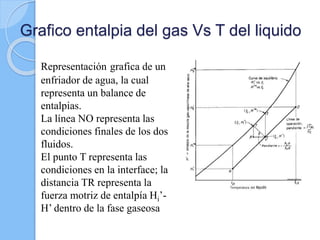
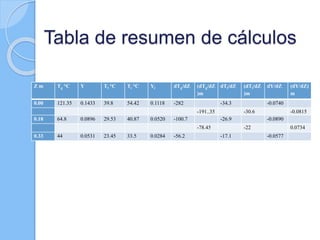
Este documento presenta información sobre humidificación y deshumidificación adiabática. Explica conceptos como coeficientes de transferencia de masa, número de unidades de transferencia, altura de unidades de transferencia y ecuaciones para calcular las condiciones de entrada y salida en una torre. También incluye un ejemplo de cálculo para determinar las condiciones de una mezcla de aire y vapor de agua al pasar por una torre de deshumidificación.

1. UNIVERSIDAD NACIONAL
AUTÓNOMA DE MÉXICO
FACULTAD DE ESTUDIOS SUPERIORES CUAUTITLÁN
TRANSFERENCIA DE MASA Y APLICACIONES DE BALANCE
PROYECTO “ HUMIDIFICACIÓN ADIABÁTICA”
Álvarez Sánchez Alicia
Melo Cruz Johanny
Herrera Silva Dina Yocelin
Rojas Santos Luz Mahelet
González Vázquez Diana Alejandra

2. INTRODUCCIÓN
 En el presente trabajo se presentara las
investigaciones bibliográficas realizadas para
conocer el tema de humidificación
adiabático, así como se presentar un
problema que ejemplificara el uso de las
ecuaciones para la terminación de las
condiciones de entrada y salida del aire y
agua de una torre, así como su altura
empacada.

3. OBJETIVOS
 Definir y determinar los coeficientes de transferencia de masa
individuales y globales kg, kl y K respectivamente.
 Definir y determinar el número de unidades de transferencia de masa de los
gases individuales y globales NTG y NTOG respectivamente.
 Definir y determinar la altura de las unidades de transferencia de masa de
los gases individuales y globales HTG y HTOG respectivamente.
 Definir las operaciones unitarias de humidificación adiabática y
deshumidificación adiabática.
 Determinar las dimensiones y condiciones de entrada y salida en una torre
rellena para la deshumidificación del aire, desarrollando un problema.

4. Humidificación adiabática de una
masa gaseosa en contacto con un
líquido.

5. DEFINICIÓN
 En la humidificación adiabática se presenta un
aumento de la humedad y la humedad relativa, a
la vez que disminuye la temperatura sin que
exista aportación de energía. El proceso es el
mismo que el que se presenta en la saturación
adiabática, sin que tenga que alcanzarse
necesariamente dicha saturación.

6. Operaciones adiabáticas
Este tipo de operación generalmente se llevan a
cabo en algún tipo de torre empacada, con un flujo
contracorriente gas- liquido, para ellos primero se
hacen las relaciones generales y posteriormente
operaciones especificas.

7.  En el proceso se verifican tres etapas:
 Precalefacción. Se calienta el aire fuera del contacto del agua
(tramo AC) hasta la temperatura tc que tiene una temperatura
bulbo húmedo.
 Humidificación adiabática. Se introduce al aire caliente en el
humidificador adiabático, en donde se satura en contacto con
agua que se encuentra a una temperatura igual a la de saturación
del aire. (Tramo CD).
 Calefacción Final. (tramo DB) El aire sale del humidificador
con la humedad deseada (la de B) y se calienta fuera del contacto
con agua hasta Tº final TB.

8.  La relación entre la temperatura del aire y su
humedad a lo largo del humidificador
adiabático está dada por la ecuación:
 Dónde: Y= humedad; YS= humedad de
saturación a la temperatura de saturación
adiabática; CH= calor especifico húmedo; λS=
calor latente de vaporización a la temperatura
de saturación adiabática; temperatura y TS=
temperatura de saturación adiabática.

9.  Para un humidificador adiabático las
diferencias de Temperaturas del liquido es:
dTl= 0 se tiene el balance de energía como:
−𝑑𝑇𝐺
𝑑𝑌
=
𝜆
𝐶 𝐻
 El balance de materia establecido para un
elemento diferencial de altura dZ queda:
𝐺𝑙2 − 𝐺𝑙1 = 𝐺′ 𝑔 𝑌2 − 𝑌1
 Debido a que Tl = Ti = Tas la velocidad de
transferencia de calor entre la corriente del
líquido y la interface queda indeterminada.
𝐶𝑙 𝐺𝑙 𝑑𝑇𝑙 = ℎ𝑙 𝑎𝑑𝑍 𝑇𝑙 − 𝑇𝑖

10.  La velocidad de transferencia de calor entre la corriente de aire y
la interface entre el aire y el agua da:
ln
𝑇𝑔1 − 𝑇𝑠𝑎
𝑇𝑔2 − 𝑇𝑠𝑎
=
ℎ 𝑔 𝑎 𝑍2 − 𝑍1
𝐺′ 𝑔 𝑚𝑒𝑑
 La velocidad de transferencia de masa entre la corriente de aire y
la interface se expresa:
ln
𝑌𝑠𝑎 − 𝑌1
𝑌𝑎𝑠 − 𝑌2
=
𝑘 𝑌 𝑎𝑀 𝑉 𝑍2 − 𝑍1
𝐺′ 𝑔
 Dónde:
 Gl= velocidad másica del agua [Kg/hm2];
 G´g= velocidad másica del aire seco [Kg/hm2];
 kY= coeficiente de transferencia de masa [moles Kg/hm2)(kg H2O
por Kg de aire seco];
 hg= coeficiente de transferencia de materia [moles Kg/h m2 atm];
 MV= peso molecular del vapor y
 Z= altura, distancia vertical sobre plano de referencia

11. Relaciones en la humidificación
adiabática
Diagrama indicativo de las
condiciones reinantes en la
humidificación adiabática.
La temperatura del agua en el
interior del humidificador es
constante y se presenta un
circuito cerrado.

12. Representa una sección de la torre de altura diferencial dz,
muestra al liquido y al gas que fluyen de un lado a otro, separador por
una interface gas-liquido
Y muestran que son diferenciales los cambios de temperatura y
humedad
Sección
interfacial

13. Enfriamiento de agua con aire

14. El agua, entibiada por el paso a través de
intercambiadores de calor, condensadores y
similares, se enfría por contacto con el aire
atmosférico para ser utilizada nuevamente.
El calor latente del agua es tan grande que
una cantidad pequeña de evaporación
produce grandes efectos de enfriamiento.

15. Grafico entalpia del gas Vs T del liquido
Representación grafica de un
enfriador de agua, la cual
representa un balance de
entalpias.
La línea NO representa las
condiciones finales de los dos
fluidos.
El punto T representa las
condiciones en la interface; la
distancia TR representa la
fuerza motriz de entalpía Hi’-
H’ dentro de la fase gaseosa

16. Unidades de transferencia de
masa.
 El numero de unidades de transferencia de
entalpia del gas NTG, es una medida de la
dificultad de la transferencia de entalpia en el
proceso.
 La altura de las unidades de transferencia de
entalpia HTG es una relación que se utiliza como
una medida del comportamiento del empaque.
𝐻 𝑇𝐺 =
𝐺′ 𝑠
𝑘 𝑌 𝑎

17.  También puede utilizarse una fuerza motriz
global que represente la diferencia en
entalpía para las fases totales, pero
expresada en función H, como la distancia
vertical SU. Esto requiere de su coeficiente
global correspondiente y lleva a números y
alturas globales de las unidades de
transferencia:

18. La diferencia entre la temperatura del líquido saliente y la
temperatura de bulbo húmedo del aire entrante, TLI-TWI llamada
la “aproximación mediante la temperatura de bulbo húmedo”,
es una medida de la fuerza motriz disponible para la difusión en
la parte terminal inferior del equipo.
La “compensación” de agua fresca en los sistemas de
recirculación de agua debe agregarse para reemplazar el agua
perdida por arrastre (“arrastre por la corriente” o “viento”), por
evaporación y “eliminación”.
El uso de los coeficientes globales de transferencia de masa no
distingue entre el enfriamiento por convección y por
evaporación del líquido, y no permite el cálculo de la humedad
o temperatura de bulbo seco del aire saliente.

19. DESHUMIDIFICACIÓN
ADIABÁTICA
La deshumidificación es el proceso de retirar el vapor
de agua contenida en el aire, llamada también humedad.
Existen diferentes procesos para remover la humedad
del aire, estos son: por enfriamiento, por el incremento
de la presión total y al poner en contacto un desecante
con el aire. En esta operación el vapor de agua se
transfiere del estado gaseoso al estado líquido.

20. Relaciones en un deshumidificador
 Se presenta la
disminución de la
temperatura y de la
humedad del aire debido
a el contacto con agua
fría, esto se debe a que en
el deshumidificador el
agua toma del aire calor
sensible y calor latente.
 En el diagrama se
muestran las relaciones
generales.

21. Cálculos deshumidificador
 Para calcular la altura de un deshumidificador, cuyo
trabajo consiste en cambiar la humedad del aire, a la
temperatura de Tg1, desde Y1 a Y2, con Gl2 de agua a
la temperatura de Tl2, el calculo puede efectuarse del
siguiente modo:
 La velocidad másica del liquido que abandona el
aparato se calcula mediante un balance de materia:
𝐺𝑙2 − 𝐺𝑙1 = 𝐺′ 𝑔 𝑌2 − 𝑌1
 Se realiza un balance de energía para determinar la
relación entre las temperaturas de salida Tl1 y Tg2.
𝐺𝑙 𝐶𝑙 𝑑𝑇𝑙 = 𝐺′ 𝑔 𝐶 𝐻 𝑑𝑇𝑔 + 𝐺𝑔 𝜆𝑑𝑌

22.  Se calculas las condiciones en la interface, Ti y Yi:
 Se obtiene un segundo punto sobre la curva que
representa la humedad Y en función de la
temperatura del gas Tg, tomando en las siguientes
expresiones los valores medios correspondientes a
pequeño intervalos.
𝑑𝑇𝑔
𝑑𝑍
=
ℎ 𝑔 𝑎 𝑇𝑔 − 𝑇𝑖
𝐺′
𝑔 𝐶 𝐻
𝑑𝑇𝑙
𝑑𝑍
=
ℎ𝑙 𝑎 𝑇𝑙 − 𝑇𝑖
𝐺𝑙 𝐶𝑙
𝑑𝑌
𝑑𝑍
=
𝑘 𝑌 𝑀 𝑉 𝑎 𝑌𝑖 − 𝑌
𝐺′ 𝑔
ℎ𝑙 𝑎 𝑇𝑖 − 𝑇𝑙 = ℎ 𝑔 𝑎 𝑇𝑔 − 𝑇𝑖 + 𝑘 𝑌 𝑎𝑀 𝑉 𝜆 𝑌 − 𝑌𝑖

23.  En Z0+ΔZ los valores de Yi y Ti se calculan
por la ecuación:
ℎ𝑙 𝑎 𝑇𝑖 − 𝑇𝑙 = ℎ 𝑔 𝑎 𝑇𝑔 − 𝑇𝑖 + 𝑘 𝑌 𝑎𝑀 𝑉 𝜆 𝑌 − 𝑌𝑖
 Este método se repite con incrementos
sucesivos hasta que la humedad del aire Y1
sea igual a la especificada, y si la
temperatura estimada para el aire entrante
Tg1 coincide a su vez con la verdadera, es
que la temperatura supuesta al principio
para el aire saliente Tg2, era correcta. Si no
es así hay que repetir todo el calculo.

24. NTG y HTG
 Para la determinación de NTG y HTG es este
proceso, la entalpía del gas es en realidad
función únicamente de su temperatura de
saturación adiabática, y permanece constante
durante toda la operación. La entalpía del
líquido a temperatura constante también es
constante.
 Por lo que se utiliza la transferencia de masa
como base de diseño y se tiene que Yas es
constante, se tiene

25. Puesto que la humedad en el equilibrio adiabático con el líquido es YA, la
eficiencia de Murphree de la etapa para la fase gaseosa es:
Si se utiliza la transferencia de calor como base para el diseño:
En donde hGa es el coeficiente volumétrico de transferencia de calor de la
transferencia de calor sensible entre el cuerpo del gas y la superficie del líquido.

26. Métodos generales
 Estos métodos se ocupan cuando no son
apropiadas las aproximaciones o cuando
en número de Lewis (LE) es diferente a 1.
 El número de Lewis se obtiene mediante
la división de números adimensionales:
𝐿𝐸 =
𝑁ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑆𝑐ℎ𝑚𝑖𝑑𝑡𝑙
𝑁ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑃𝑟𝑎𝑛𝑑𝑡𝑙

27.  Se debe de igual el lado derecho de las
ecuaciones 7.39 y 7.41 obteniéndose de esta
manera la igualdad entre Temperaturas:
Para el gradiente de Humedad:
La ecuación 7.64 se ocupara para aproximaciones bajas de vapor.

28.  Gradiente de Temperatura:
 Aquí puede utilizarse en vez de
utilizar siempre y cuando se ocupe en
velocidades bajas de transferencia.

29.  Para ocupar (superficie interfacial
específica para la transferencia de calor) y
(superficie interfacial específica para la
transferencia de masa) por separado se debe
de conocer ambos valores de lo contrario se
debe suponer que

30.  Si durante el cálculo es mayor, a
una cierta Temperatura de gas, entonces se
tiene una mayor concentración de vapor a
saturación correspondiente, se formara una
niebla en la fase gaseosa, en cuyo caso todo el
análisis se vuelve nulo y debe de escogerse
nuevas condiciones en los puntos finales de la
torre.

31. Ejemplo problema
 Una mezcla de aire y de vapor de agua a 120 °C, que contiene
0.1433 Kg de vapor de H2O por kg de aire seco, se ha de
deshumidificar en una torre rellena, por contacto con agua y en
contracorriente. La torre contiene anillos raschig de 25 mm (=1
in) y trabaja a la presión atmosférica. La temperatura del agua
que penetra a la torre es de 25 °C, el aire que abandona la torre
contendrá 0.0550 kg de agua por Kg de aire seco. La velocidad
másica del agua en la parte alta de la torre será 9760 Kg/h m2, y
la de la mezcla aire-vapor de agua en el fondo de la torre 2440
Kg/h m2, para estos caudales se estima que los valores medios
de los coeficientes de transferencia calórica son:
 hga= 4650 Kcal/h m3 °C
 hla= 42000 Kcal/h m3 °C
 Determínese la temperatura del
aire que abandona la torre y
la altura necesaria de relleno.

32. SOLUCIÓN:
 La velocidad másica del aire seco es:
𝐺′
𝑔 =
𝐺 𝑔1
1 + 𝑌1
=
2440
1.1433
= 2130 𝐾𝑔 𝑎𝑖𝑟𝑒 𝑠𝑒𝑐𝑜 ℎ 𝑚2
 La velocidad másica del liquido que abandona la torre se calcula
con un balance global de materia.
𝐺𝑙2 − 𝐺𝑙1 = 𝐺′ 𝑔 𝑌2 − 𝑌1
𝐺𝑙1 = 2130 0.1433 − 0.0550 + 9760 = 9950 𝐾𝑔 𝑎𝑖𝑟𝑒 𝑠𝑒𝑐𝑜 ℎ 𝑚2
 El calor especifico húmedo para las mezclas aire-vapor es:
 En el fondo CH1=0.304; en la cúspide CH2=0.265; promedio
CH=0.285
λ0= 595 Kcal/kg (a 0 °C)

33.  Los balances energéticos globales utilizando los estados de referencia del agua liquida a 0 °C y del aire a 0
°C dan:
𝐺′
𝑔 𝐶 𝐻1 𝑇𝑔1 + 𝜆0 𝑌1 + 𝐺𝑙2 𝐶𝑙 𝑇𝑙2 = 𝐺′
𝑔 𝐶 𝐻2 𝑇𝑔2 + 𝜆0 𝑌2 + 𝐺𝑙1 𝐶𝑙 𝑇𝑙1
2130 0.304 120 + 595 0.1433 + 9760 1 25 = 2130 0.265 𝑇𝑔2 + 595 0.0550 + 9950 1 𝑇𝑙1
 Por lo tanto:
𝑇𝑙1 = 42.3 + 0.0567𝑇𝑔2
 Se desarrolla un primer ensayo a una temperatura supuesta para el gas de salida, Tg2 de 45 °C; entonces
Tl1= 40 °C.
 Para el sistema agua-aire, el valor numérico del calor húmedo vale:
𝐶 𝐻 =
ℎ 𝑔
𝑘 𝑌 𝑀 𝑉
 Sustituyendo esta ecuación en:
ℎ𝑙 𝑎 𝑇𝑖 − 𝑇𝑙 = ℎ 𝑔 𝑎 𝑇𝑔 − 𝑇𝑖 + 𝑘 𝑌 𝑎𝑀 𝑉 𝜆 𝑌 − 𝑌𝑖
 Se obtiene:
42000 𝑇𝑖 − 𝑇𝑙 = 4650 𝑇𝑔 − 𝑇𝑖 +
4650
𝐶 𝐻
𝑌 − 𝑌𝑖 595
 Utilizando el valor medio de CH esta ecuación se reduce a:
10.30𝑇𝑖 + 2090𝑌𝑖 = 9.03𝑇𝑙 + 𝑇𝑔 + 209
 Para las condiciones del fondo de la torre, utilizando la curva de saturación, se obtiene: Ti= 55 °C y Yi=
0.114

34. Representación en la carta
psicrométrica del proceso

35.  Con estos valores se obtiene:
𝑑𝑇𝑔
𝑑𝑍
= −
4650 𝑇𝑔−𝑇 𝑖
2130 0.285
= −7.66 𝑇𝑔 − 𝑇𝑖 =
− 498 𝑒𝑛 𝑒𝑙 𝑓𝑜𝑛𝑑𝑜 𝑑𝑒 𝑙𝑎 𝑡𝑜𝑟𝑟𝑒
𝑑𝑇 𝑙
𝑑𝑍
=
42000 𝑇 𝑙−𝑇 𝑖
9930 1
= −4.23 𝑇𝑖 − 𝑇𝑙 =
− 63.45 𝑒𝑛 𝑒𝑙 𝑓𝑜𝑛𝑑𝑜 𝑑𝑒 𝑙𝑎 𝑡𝑜𝑟𝑟𝑒
𝑑𝑌
𝑑𝑍
=
4650 𝑌 𝑖−𝑌
0.285 2130
= −7.66 𝑌 − 𝑌𝑖 = −0.224 𝑒𝑛 𝑒𝑙 𝑓𝑜𝑛𝑑𝑜 𝑑𝑒 𝑙𝑎 𝑡𝑜𝑟𝑟𝑒
 Se proponen pequeños incrementos en la altura de la torre para obtener
los valores medios de las derivadas utilizadas. La humedad deseada
(H=0.0550) se alcanza cuando la temperatura de salida Tg2 es 45.46 °C
valor muy próximo al supuesto de 45 °C.
 La altura de la zona rellena de la columna estará comprendida entre
30.5 cm y 33.5 cm.

36. Tabla de resumen de cálculos
Z m Tg °C Y Tl °C Ti °C Yi dTg/dZ (dTg/dZ
)m
dTl/dZ (dTl/dZ
)m
dY/dZ (dY/dZ)
m
0.00 121.35 0.1433 39.8 54.42 0.1118 -282 -34.3 -0.0740
-191..35 -30.6 -0.0815
0.18 64.8 0.0896 29.53 40.87 0.0520 -100.7 -26.9 -0.0890
-78.45 -22 0.0734
0.33 44 0.0531 23.45 33.5 0.0284 -56.2 -17.1 -0.0577

37. BIBLIOGRAFÍA
 TREYBAL, Robert E.; “OPERACIONES
DE TRANSFERENCIA DE MASA”; 2a
edición; Mc GRAW-HILL; buenos aires
argentina; PP 845.
 http://www.ucm.es
 BROWN, George Granger; “Operaciones
Básicas de Ingeniería Química”; Editorial
Marlín, S.A.; España; 1965; PP 629.