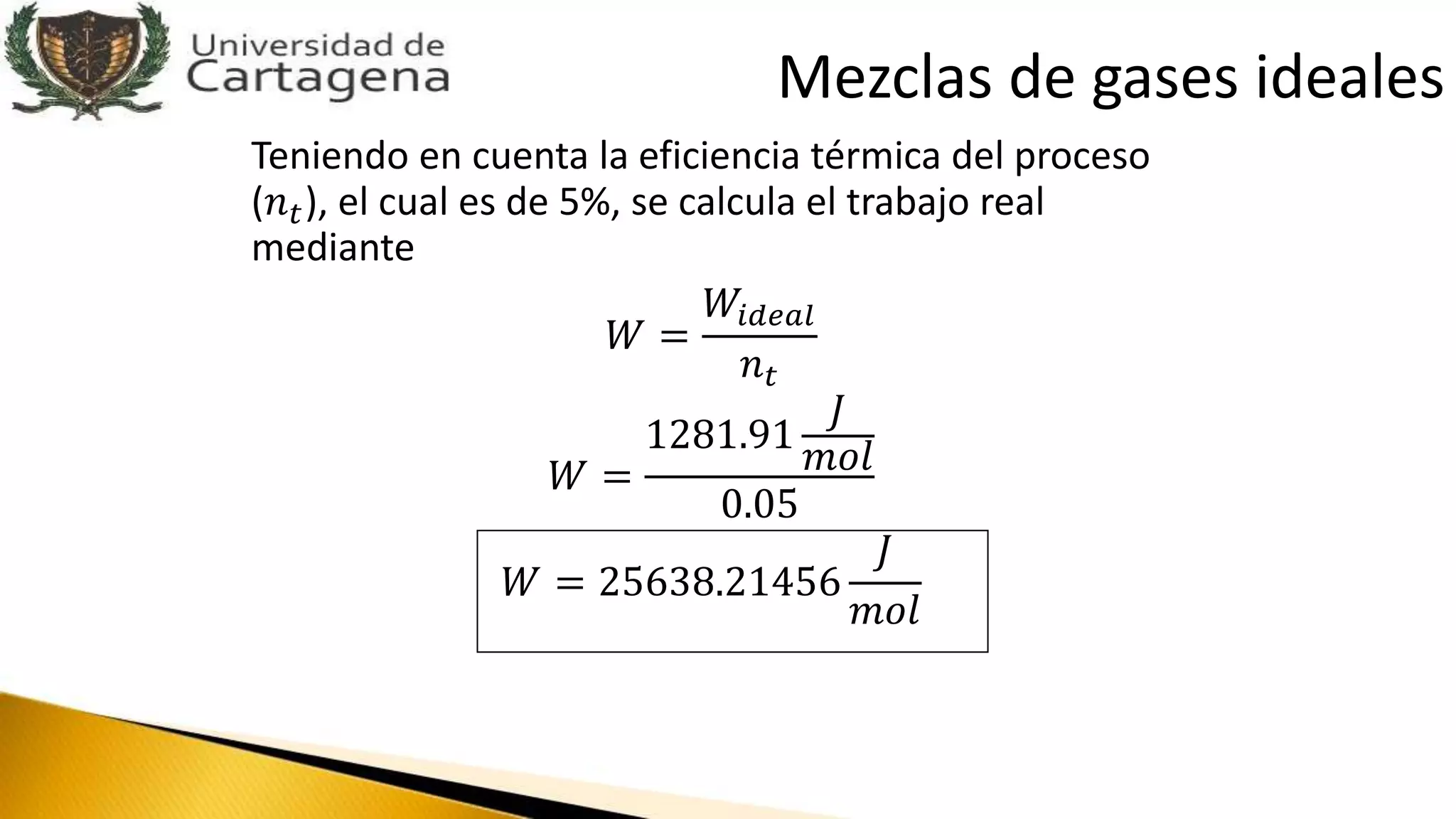
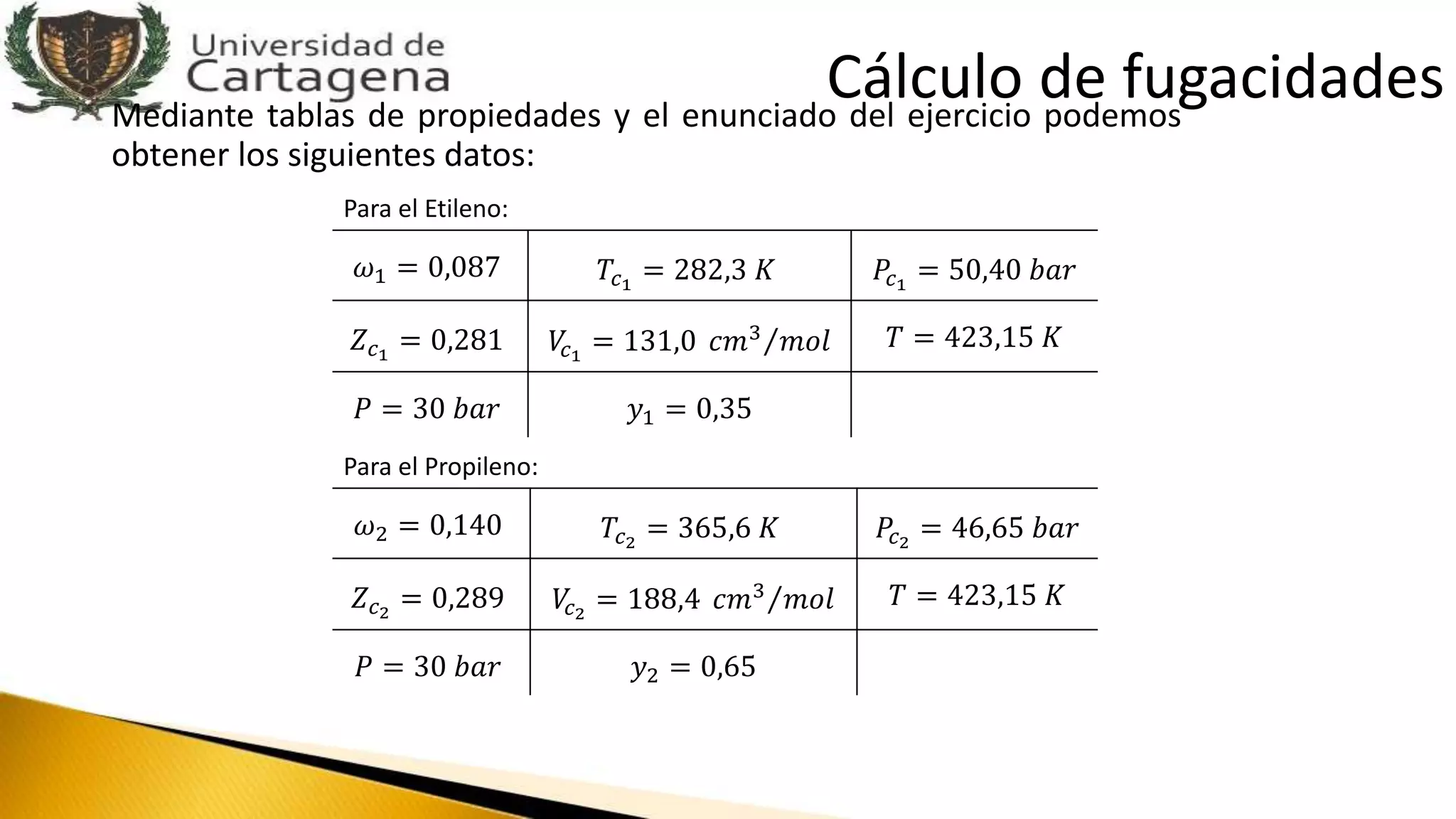
Este documento presenta varios ejercicios resueltos relacionados con propiedades molares parciales de mezclas binarias y ternarias. En el primer ejercicio, se encuentran las expresiones de los volúmenes molares parciales de los componentes de una mezcla binaria en términos de la densidad molar empírica de la mezcla. En otro ejercicio, se demuestra que una propiedad específica parcial se obtiene dividiendo la propiedad molar parcial entre la masa molar. Finalmente, se calcul

1. 4. Solved problems in Thermodynamics
of solutions (in Spanish)
Angel Darío González-Delgado
Ing. Quim. Ph. D.
Universidad de Cartagena
2016

2. Si la densidad molar de una mezcla binaria está dada por la expresión
empírica :
𝜌 = 𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2
Encuentre las expresiones correspondientes para los volúmenes parciales
molares de los componentes de la mezcla. La solución de este ejercicio es
una contribución de María del Pilar Ortiz Rincón Código: 0231320049
𝜌 = 𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2
Entonces tenemos que el volumen es igual a 𝑣 =
1
𝜌
Reemplazando valores:
𝑣 =
1
𝜌
=
1
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2
Propiedades molares parciales

3. Por medio de propiedades molares parciales de cada uno de los componentes de la mezcla,
en este caso el primer componente, tenemos que:
𝛻1 =
1
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2 − 1 − 𝑥1 +
𝑎1 + 2𝑎2 𝑥1
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2 2
Operando algebraicamente:
𝛻1 =
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥2 − 𝑎1 − 2𝑎2 𝑥1 + 𝑎1 𝑥1 + 2𝑎2 𝑥1
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2 2
Obteniendo anteriormente el volumen parcial para el primer componente, ahora
procedemos a calcular el volumen del componente numero dos:
𝛻2 =
1
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2 + 𝑥1 +
𝑎1 + 2𝑎2 𝑥1
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2 2
Propiedades molares parciales

4. Nuevamente se opera algebraicamente:
𝛻2 =
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2
+ 𝑎1 𝑥1 + 2𝑎2 𝑥1
2
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2
Sumando los términos semejantes, tenemos:
𝛻2 =
𝑎0 + 2𝑎1 𝑥1 + 3𝑎2 𝑥1
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2
Por ultimo, queda demostrado que la densidad de una mezcla binaria
es igual a:
𝑉 = 𝑥1 𝛻1 + 𝑥2 𝛻2 =
1
𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥1
2
Propiedades molares parciales

5. Demuestre que una propiedad específica parcial de una
especie en solución se obtiene por división de la propiedad
molar parcial entre la masa molar (peso molecular) de la
especie.
La solución de este ejercicio es una contribución de
David López Barbosa, Cod. 0231310026
Propiedades molares parciales

6. Se define una propiedad específica de la materia
como una magnitud intensiva obtenida como
cociente de dos magnitudes extensivas, o
equivalentemente una cantidad extensiva por
unidad de masa o volumen.
Si llamamos M a una propiedad molar cualquiera, m
la masa molar (peso molecular) de la especie, n el
número de moles de la especie, y X la propiedad
molar específica de esta especie, aplicando la
definición anterior obtenemos:
𝑛𝑋𝑖 =
𝑛𝑀𝑖
𝑚
Propiedades molares parciales

7. Debido a que una propiedad molar es intensiva, se multiplica por el numero de moles para
convertirla en extensiva, es decir que dependa de la cantidad de materia, y así poder aplicar la
definición de propiedad específica.
Si aplicamos la relación de sumabilidad:
𝑖
𝑛𝑖 𝑋𝑖 =
𝑖 𝑛𝑖 𝑀𝑖
𝑚
Donde 𝑛𝑖 son los moles de la especie pura, 𝑋𝑖 es la propiedad molar parcial específica y 𝑀𝑖 es la
propiedad molar parcial de la especie. Operando obtenemos:
𝑛𝑖 𝑋𝑖 =
𝑛𝑖 𝑀𝑖
𝑚
→ 𝑿𝒊 =
𝑴𝒊
𝒎
Esta expresión indica que una especie en solución es igual al cociente de la propiedad molar parcial
entre la masa molar (peso molecular) de la especie.
Propiedades molares parciales

8. Para una solución ternaria a T y P constantes, la dependencia de
la propiedad molar M en función de la composición está dada
por:
En donde M1, M2 y M3 son los valores de M para las especies 1,
2 y 3 puras, y C es un parámetro independiente de la
composición.
Determine una expresión para M, aplicando la ecuación:
Propiedades molares parciales

9. La solución de este ejercicio es una contribución de Angelith Marcela Bonfante
Pérez Cod. 0231220041
Para la aplicación de la ecuación todas las fracciones molares deben ser eliminados
de la ecuación dada por la relación xi= ni/n :
𝑛𝑀 = 𝑛1𝑀1 + 𝑛2𝑀2 + 𝑛3𝑀3 +
𝑛1𝑛2𝑛3
𝑛2
C
Para 𝑀1,
𝜕(𝑛𝑀)
𝜕𝑛1 𝑇,𝑃,𝑛2,𝑛3
= 𝑀1 +n2n3C
1
𝑛2 −
2𝑛1
𝑛3
𝜕𝑛
𝜕𝑛1 𝑇,𝑃,𝑛2,𝑛3
Porque n= n1+n2+n3 ,
𝜕𝑛
𝜕𝑛1 𝑇,𝑃,𝑛2,𝑛3
=1
Propiedades molares parciales

10. De donde :
𝑀1= M1 +
𝑛2𝑛3
𝑛2 1 − 2
𝑛1
𝑛
𝐶 y 𝑀1= M1+ 𝑥2 𝑥3 1 − 2𝑥1 𝐶
𝑀2= M2+ 𝑥1 𝑥3 1 − 2𝑥2 𝐶 𝑀3= M3+ 𝑥1 𝑥2 1 − 2𝑥3 𝐶
Se puede demostrar que la aplicación de la ecuación regenera la ecuación original
para M . Los valores de dilución infinita vienen dados por:
𝑀𝑖
∞
= Mi + 𝑥𝑗 𝑥 𝑘 𝐶 (j,k≠i)
Aquí 𝑥𝑗 y 𝑥 𝑘son fracciones de moles.
Propiedades molares parciales

11. La entalpía de un sistema líquido binario de las especies 1 y 2 a T y P
fijas está representada por la ecuación:
𝐻 = 400𝑥1 + 600𝑥2 + 𝑥1 𝑥2 40𝑥1 + 20𝑥2
a) Aplique la siguiente ecuación:
𝑀𝑖 ≡
𝜕 𝑛𝑀
𝜕𝑛𝑖 𝑃,𝑇,𝑛 𝑗
A la ecuación 𝐻 = −600 − 180𝑥1 − 20𝑥1
3, para demostrar que:
𝐻1 = 420 − 60𝑥1
2 + 40𝑥1
3
Y 𝐻2 = 600 + 40𝑥1
3
Propiedades molares parciales

12. b) Demuestre que las ecuaciones de 𝐻1 y𝐻2, cuando se
combinan, regeneran a la ecuación:
𝐻 = −600 − 180𝑥1 − 20𝑥1
3
c) Demuestre que las ecuaciones de𝐻1 y𝐻2 satisfacen la
ecuación de Gibbs/Duhem.
La solución de este ejercicio es una contribución de María
José De Pombo Angulo, Cod. 0231320014
Propiedades molares parciales

13. a) La entalpia para un sistema liquido binario a T y P fijas,
dada por la ecuación:
𝐻 = 400𝑥1 + 600𝑥2 + 𝑥1 𝑥2 40𝑥1 + 20𝑥2
Para ello, se deja la ecuación en términos de una de las
fracciones, siendo mayor el numero de 𝑥1, se deja la ecuación
en términos de esta, mediante la relación: En una mezcla
binaria,
𝑥1 + 𝑥2 = 1
Por lo que 𝑥2 = 1 − 𝑥1
Propiedades molares parciales

14. 𝐻 = 400𝑥1 + 600(1 − 𝑥1) + 𝑥1(1 − 𝑥1) 40𝑥1 + 20(1 − 𝑥1)
𝐻 = 400𝑥1 + 600 −600𝑥1 +40𝑥1
2
+ 20𝑥1 − 20𝑥1
2
− 40𝑥1
3
− 20𝑥1
2
+ 20𝑥1
3
𝐻 = −20𝑥1
3
− 180𝑥1
3
+ 600
Una vez teniendo la entalpia en términos de un fracción, se deriva con respecto a
esta:
𝑑𝐻
𝑑𝑥1
= −60𝑥1
2 − 180
Para calcular la entalpia molar parcial con respecto al primer componente, se utiliza
la ecuación:
𝐻1 = 𝐻 + 𝑥2
𝑑𝐻
𝑥1
Propiedades molares parciales

15. 𝐻1 = (−20𝑥1
3
− 180𝑥1
3
+ 600) + (1 − 𝑥1)(−60𝑥1
2
− 180)
Resolviendo, quedaría:
𝐻1 = 40𝑥1
3
− 60𝑥1
3
+ 420
De la misma forma, se utiliza siguiente la ecuación para hallar la
entalpia molar parcial del compuesto 2:
𝐻2 = 𝐻 + 𝑥1
𝑑𝐻
𝑥1
𝐻2 = −20𝑥1
3
− 180𝑥1
3 + 600 + 𝑥1 −60𝑥1
2 − 180
𝐻2 = 40𝑥1
3
+ 600
Propiedades molares parciales

16. b) Para comprobar que al combinarse las propiedades
molares parciales dan como resultado la propiedad total,
se aplica la relación de sumabilidad:
𝐻 = 𝑥𝑖 𝐻𝑖 = 𝑥1 𝐻1 + 𝑥2 𝐻2
𝐻 = 𝑥1 40𝑥1
3
− 60𝑥1
3 + 420 + 1 − 𝑥1 40𝑥1
3
+ 600
𝐻 = −20𝑥1
3
− 180𝑥1 + 600
Propiedades molares parciales

17. c) Para comprobar que al combinarse las propiedades molares parciales
cumplen con la ecuación de Gibbs/Duhem, se define primero la
ecuación:
𝑥1
𝑑𝐻1
𝑑𝑥1
+ 𝑥2
𝑑𝐻2
𝑑𝑥1
= 0
𝑑𝐻1
𝑑𝑥1
=
𝑑 40𝑥1
3
− 60𝑥1
3
+ 420
𝑑𝑥1
= 120𝑥1
2
− 120𝑥1
𝑑𝐻2
𝑑𝑥1
=
𝑑 40𝑥1
3
+ 600
𝑑𝑥1
= 120𝑥1
2
Propiedades molares parciales

18. 𝑥1 120𝑥1
2
− 120𝑥1 + 𝑥2 120𝑥1
2
= 0
120𝑥1
3
− 120𝑥1
2
+ (1 − 𝑥1) 120𝑥1
2
= 0
120𝑥1
3
− 120𝑥1
2
+ 120𝑥1
2
− 120𝑥1
3
= 0
0 = 0
Cumpliéndose así la ecuación de Gibbs/Duhem para las
propiedades molares parciales.
Propiedades molares parciales

19. Mezclas de gases ideales
• Una corriente de nitrógeno que fluye a la velocidad de 2 kg/s y otra corriente de
hidrógeno que fluye a la velocidad de 0.5 kg/s se mezclan adiabáticamente en un
proceso de flujo uniforme. Si se considera que los gases son ideales, cuál es la
velocidad de aumento de la entropía como resultado del proceso?
• La solución de este ejercicio es una contribución de Gilver José Caraballo Becerra,
Cod: 0231320002

20. • Una corriente de nitrógeno que fluye a la velocidad de 2 kg/s y otra corriente de
hidrógeno que fluye a la velocidad de 0.5 kg/s se mezclan adiabáticamente en un
proceso de flujo uniforme. Si se considera que los gases son ideales, cuál es la
velocidad de aumento de la entropía como resultado del proceso?
• La ecuación para la variación de la entropía de una mezcla de gases ideales es la
siguiente:
• ∆𝑆 𝑔𝑖= −𝑛𝑅 𝑦𝑖 𝑙𝑛𝑦𝑖 𝐼
• Tenemos dos flujos másicos:
• 𝑚 𝑁2 = 2 𝑘𝑔/𝑠 𝑚 𝐻2 = 0,5 𝑘𝑔/𝑠
Mezclas de gases ideales

21. Procedemos a hallar las moles de cada especie
𝑛 𝑁2 =
𝑚𝑖
𝑀 𝑁2
=
2000 𝑔
28 𝑔/𝑚𝑜𝑙
= 71, 42
𝑔
𝑚𝑜𝑙
𝑁2
𝑛 𝐻2 =
𝑚𝑖
𝑀 𝐻2
=
500 𝑔
2 𝑔/𝑚𝑜𝑙
= 250
𝑔
𝑚𝑜𝑙
𝐻2
Las moles totales serán por tanto
𝑛 𝑇 = 𝑛 𝑁2 + 𝑛 𝐻2
𝑛 𝑇 = 71,42 𝑚𝑜𝑙 + 250 𝑚𝑜𝑙 = 321, 42 𝑚𝑜𝑙
Mezclas de gases ideales

22. Las fracciones molares de cada especie serán
𝑦 𝑁2 =
𝑛𝑖
𝑛 𝑇
=
71,42 𝑚𝑜𝑙
321,42 𝑚𝑜𝑙
= 0,23
𝑦 𝐻2 =
𝑛𝑖
𝑛 𝑇
=
250 𝑚𝑜𝑙
321,42 𝑚𝑜𝑙
= 0,77
Mezclas de gases ideales

23. Considerando como base de tiempo segundos, la ecuación (I) quedaría de esta
forma:
∆𝑆 𝑔𝑖= −𝑛𝑅 𝑦𝑖 𝑙𝑛𝑦𝑖
∆𝑆 𝑔𝑖= − 321,42 𝑚𝑜𝑙 ∗ 8,314
𝐽
𝑚𝑜𝑙 ∗ 𝑘
∗ 0,23 ∗ ln 0,23 + 0,77 ∗ ln 0,77
Por lo tanto la velocidad de aumento de la entropía es
∆𝑆 𝑔𝑖= 1441, 1
𝐽
𝐾
Mezclas de gases ideales

24. ¿Cuál es el trabajo que se requiere para separación de aire (21% mol de oxígeno y
79% mol de nitrógeno) a 25ºC y 1 bar, en un proceso de flujo uniforme en
corrientes de producto de oxígeno y nitrógeno puros, también a 25ºC y 1 bar, si la
eficiencia termodinámica del proceso es 5 por ciento y si la temperatura de los
alrededores es de 300 K?
La solución de este ejercicio es una contribución de María José De Pombo Angulo,
Cod. 0231320014
Mezclas de gases ideales

25. Solución:
Consideraciones:
• Base calculo de 1 mol.
• Eficiencia térmica: 5%= 0.05
• Temperatura de los alrededores (𝑇𝜎)= 300K
• Se asume una mezcla de gases ideales, por lo que ∆𝐻 = 0
Mezclas de gases ideales

26. Se calculan las fracciones molares:
𝑥 𝑂2
= 0.21
𝑥 𝑁2
= 0.79
Se parte de la definición de entropía para una mezcla
de gases ideales (el cambio de signo es porque la
mezcla se esta separando):
∆𝑆 = 𝑅 𝑦𝑖 𝑙𝑛𝑦𝑖
∆𝑆 = 𝑅 𝑦1 𝑙𝑛𝑦1 + 𝑦2 𝑙𝑛𝑦2
∆𝑆 = 8.314
𝐽
𝑚𝑜𝑙 ∙ 𝐾
0.21ln(0.21) + 0.79𝑙𝑛0.79
Mezclas de gases ideales

27. ∆𝑆 = −4.273
𝐽
𝑚𝑜𝑙 ∙ 𝐾
Partiendo de la definición para el trabajo ideal, se
tiene que
𝑊𝑖𝑑𝑒𝑎𝑙 = ∆𝐻 − 𝑇∆𝑆
Siendo ∆𝐻 = 0, quedaría
𝑊𝑖𝑑𝑒𝑎𝑙 = −𝑇𝜎∆𝑆 = − −4.273
𝐽
𝑚𝑜𝑙 ∙ 𝐾
300𝐾
Por lo que el trabajo ideal seria 1281.91
𝐽
𝑚𝑜𝑙
Mezclas de gases ideales

28. Teniendo en cuenta la eficiencia térmica del proceso
(𝑛 𝑡), el cual es de 5%, se calcula el trabajo real
mediante
𝑊 =
𝑊𝑖𝑑𝑒𝑎𝑙
𝑛 𝑡
𝑊 =
1281.91
𝐽
𝑚𝑜𝑙
0.05
𝑊 = 25638.21456
𝐽
𝑚𝑜𝑙
Mezclas de gases ideales

29. Un recipiente, dividido en dos partes mediante una separación,
contiene 4 moles de nitrógeno a 75°C y 30 bar de un lado y 2.5
moles de argón a 130°C y 20 bar en el otro. Si se elimina la
separación y los gases se mezclan adiabática y completamente, cuál
es el cambio en la entropía? Considere al nitrógeno un gas ideal con
CV = (5/2)R y al argón un gas ideal con CV = (3/2)R.
La solución de este ejercicio es una contribución de Angelith
Marcela Bonfante Pérez Cod. 0231220041
Mezclas de gases ideales

30. Primero determinamos los volúmenes de cada gas:
𝑉𝑖,𝐴𝑟 =
𝑛 𝐴𝑟 𝑅𝑇 𝑖,𝐴𝑟
𝑝 𝑖,𝐴𝑟
=
2,5𝑚𝑜𝑙(0,08205746 𝐿 𝑎𝑡𝑚
𝑚𝑜𝑙 𝐾)(348,15𝐾)
29,60𝑎𝑡𝑚
= 2,41L
𝑉𝑖,𝑁 =
𝑛 𝑁 𝑅𝑇 𝑖,𝑁
𝑁
=
4𝑚𝑜𝑙(0,08205746 𝐿 𝑎𝑡𝑚
𝑚𝑜𝑙 𝐾)(403,15𝐾)
19,60𝑎𝑡𝑚
= 6,75L
Luego, para calcular el estado final de equilibrio y el cambio total de entropía,
supondremos que transcurre el proceso en dos etapas, una primera etapa
isocora y después una segunda etapa isoterma.
Primera etapa: Es isocora, por tanto hay un intercambio de energía interna entre
los dos medios que nos lleva a deducir la temperatura final de equilibrio.
Mezclas de gases ideales

31. ∆𝑈 𝑁2
= −∆𝑈𝐴𝑟
𝐶𝑣 𝑁2
∗ ∆𝑇𝑖,𝑁2
= −𝐶𝑣 𝐴𝑟 ∗ ∆𝑇𝑖,𝐴𝑟
5/2𝑅𝑛 𝑁2
∗ 𝑇𝑓 − 𝑇𝑖.𝑁2
= − 3
2 𝑅𝑛 𝐴𝑟 ∗ 𝑇𝑓 − 𝑇𝑖.𝐴𝑟
𝑇𝑓 = 348,25
Sabiendo que R= 0,08205746 𝐿 𝑎𝑡𝑚
𝑚𝑜𝑙 𝐾
𝐶𝑣 𝑁2
= 5/2R
𝐶𝑣 𝐴𝑟=-3/2R
Mezclas de gases ideales

32. Dado que no hay trabajo intercambiado en esta etapa entre los gases, la
energía interna se intercambia en forma de calor y por tanto el cambio de
entropía de cada gas es:
∆𝑆1,𝑁2
=
𝑖
𝑓
𝛿𝑄
𝑇
=
𝑖
𝑓
𝑑𝑈
𝑇
= 𝐶𝑣 𝑁2
𝑇𝑖
𝑇𝑓
𝑑𝑇
𝑇
= 572𝑅 ∗ 𝑛 𝑁2
𝑙𝑛
𝑇𝑓
𝑇𝑖
=
5,4630𝐽
𝐾
∆𝑆1,𝐴𝑟 =
𝑖
𝑓
𝛿𝑄
𝑇
=
𝑖
𝑓
𝑑𝑈
𝑇
=
𝐶𝑣 𝐴𝑟 𝑇𝑖
𝑇𝑓 𝑑𝑇
𝑇
3
2𝑅
∗ 𝑛 𝐴𝑟 𝑙𝑛
𝑇𝑓
𝑇𝑖
= −4,56
𝐽
𝐾
∆𝑆1 = 0,8989
𝐽
𝐾
Mezclas de gases ideales

33. Luego en la segunda etapa es isoterma, un gas se expansiona contra el otro, pero
sin cambiar la energía interna de ambos gases ya que es constante la
temperatura. La expansión se detiene cuando se equilibran las presiones, la
presión final de cada gas es:
𝑝 𝑓 =
𝑛𝑡𝑜𝑡𝑎𝑙 ∗ 𝑅𝑇𝑓
𝑉𝑡𝑜𝑡𝑎𝑙
= 20,2781 𝑎𝑡𝑚
Los volúmenes de cada uno de los gases en el equilibrio es:
𝑣 =
𝑛 𝑛2 ∗ 𝑅𝑇𝑓
𝑝 𝑓
= 5,637L
𝑣 =
𝑛 𝐴𝑟 ∗ 𝑅𝑇𝑓
𝑝 𝑓
= 3,523L
Mezclas de gases ideales

34. Dado que los gases se expanden en un proceso isotermo (sin cambio de energía
interna) entonces por el primer principio:
Q = W
Por tanto el cambio de entropía de cada gas es:
∆𝑆2,𝑁2
= 𝑖
𝑓 𝛿𝑄
𝑇
= 𝑖
𝑓 𝑑𝑤
𝑇
= 𝑉𝑖
𝑉𝑓 𝑝𝑑𝑉
𝑇
= 𝑛𝑅 𝑉𝑖
𝑉𝑓 𝑑𝑉
𝑉
= 𝑛 𝑁2
𝑅𝑙𝑛
𝑉𝑓
𝑉𝑖
=-5,992 J/K
∆𝑆2,𝐴𝑟 = 𝑖
𝑓 𝛿𝑄
𝑇
= 𝑖
𝑓 𝑑𝑤
𝑇
= 𝑉𝑖
𝑉𝑓 𝑝𝑑𝑉
𝑇
= 𝑛𝑅 𝑉𝑖
𝑉𝑓 𝑑𝑉
𝑉
= 𝑛 𝐴𝑟 𝑅𝑙𝑛
𝑉𝑓
𝑉𝑖
=7,891 J/K
∆𝑆2 = 1,899 J/K
Tras estas etapas, ya tenemos conocidas las presiones y temperaturas finales de
los gases y la entropía total de este apartado es la suma de las entropías de las
dos etapas:
∆𝑆 𝑎 = ∆𝑆1 + ∆𝑆2 = 2,798 J/K
Mezclas de gases ideales

35. Dado que la entropía es función de estado, la entropía de realizar las
etapas del apartado anterior más la entropía de mezcla de gases con
idéntica presión y temperatura es por tanto la entropía total que nos
piden calcular en este apartado. La presión y la temperatura es la misma
que la que calculamos en el apartado anterior. Luego
∆𝑆 𝑏 = ∆𝑆 𝑎 + ∆𝑆 𝑀
Siendo ∆𝑆 𝑀 la entropía de mezcla, que para nuestros dos gases es:
∆𝑆 𝑀 = −ntotal ∗ R 𝑥 𝑂2 𝑙𝑛𝑥 𝑂2 + 𝑥 𝐴𝑟 ln𝑥 𝐴𝑟
𝑥 𝑂2 y 𝑥 𝐴𝑟 son las fracciones molares , y sus valores son:
𝑥 𝑂2 =
𝑛 𝑜2
𝑛 𝑜2 + 𝑛 𝐴𝑟
= 0,615
Mezclas de gases ideales

36. 𝑥 𝐴𝑟 =
𝑛 𝐴𝑟
𝑛 𝑜2 + 𝑛 𝐴𝑟
= 0,385
Por lo tanto:
∆𝑆 𝑀 = −ntotal ∗ R 𝑥 𝑂2 𝑙𝑛𝑥 𝑂2 + 𝑥 𝐴𝑟 ln𝑥 𝐴𝑟 = 36,0161 J/K
La entropía total del proceso en este apartado es por tanto:
∆𝐒 𝐛 = ∆𝐒 𝐚 + ∆𝐒 𝐌 = 38,8141 J/K
Mezclas de gases ideales

37. • La energía de Gibbs en exceso de una mezcla liquida binaria a T y P fijas
esta dada por:
•
𝐺 𝐸
𝑅𝑇
= 𝑥1 𝑥2(−2,6𝑥1 − 1,8𝑥2)
• a) Encuentre expresiones para 𝑙𝑛𝑦1 y 𝑙𝑛𝑦2
• b) Demuestre que cuando las expresiones del inciso anterior se combinan,
la ecuación dada para 𝐺 𝐸
/𝑅𝑇 se recupera.
• c) Demuestre que estas expresiones satisfacen la ecuaciones de Gibbs/
Duhem
• La solución de este ejercicio es una contribución de Gilver José Caraballo
Becerra, Cod: 0231320002
Propiedades en exceso

38. • a)
𝐺 𝐸
𝑅𝑇
= 𝑥1 𝑥2(−2,6𝑥1 − 1,8𝑥2)
• El siguiente desarrollo justifica que 𝑙𝑛 𝑦𝑖 es una propiedad parcial con
respecto a 𝐺 𝐸
𝑅𝑇
• Sabemos que 𝑥1 + 𝑥2 = 1  𝑥2 = 1 − 𝑥1 reemplazamos 𝑥2 en la ecuación
•
𝐺 𝐸
𝑅𝑇
= 𝑥1(1 − 𝑥1)(−2,6𝑥1 − 1,8(1 − 𝑥1)) resolviendo las operaciones entre
paréntesis
•
𝐺 𝐸
𝑅𝑇
= 0,8𝑥3 + 𝑥1
2
− 1,8𝑥1
•
Propiedades en exceso

39. • ¿Por qué hacemos esto?
• Para cumplir con la ecuación de una propiedad molar parcial
• 𝑀1 = 𝑀 + (1 − 𝑥1)
𝑑𝑀
𝑑𝑥1
• Donde
𝑑𝑀
𝑑𝑥1
equivale a
𝑑𝐺 𝐸
𝑅𝑇
𝑑𝑥1
esto es igual a
•
𝑑𝑀
𝑑𝑥1
= 2,4𝑥1
2
+ 2𝑥1 − 1,8
Propiedades en exceso

40. • La ecuación para la propiedad molar parcial será:
• 𝑀1 = 𝑥1
2
− 1,8𝑥1 + 0,8𝑥1
3
+ (1 − 𝑥1)(2𝑥1 − 1,8 + 2,4𝑥1
2
)
• Resolviendo la ecuación
• 𝑀1 = −1,6𝑥1
3
+ 1,4 𝑥1
2
+ 2𝑥1 − 1,8
• Esta propiedad molar parcial equivale a 𝑙𝑛𝑦1
• Para hallar 𝑙𝑛𝑦2 usamos la ecuación
• 𝑀2 = 𝑀 − 𝑥1
𝑑𝑀
𝑑𝑥1
• Reemplazando los valores tenemos
• 𝑀2 = −1,8𝑥1 + 𝑥1
2
+ 0,8𝑥1
3
− 𝑥1 2𝑥1 + 2,4𝑥1
2
− 1,8
Propiedades en exceso

41. • Resolviendo todas las operaciones 𝑀2 = −𝑥1
2
− 1,6𝑥1
3
• Como en el caso anterior, esta ecuación es equivalente a 𝑙𝑛𝑦2
• b) Demuestre que cuando las expresiones del inciso anterior se
combinan, la ecuación dada para 𝐺 𝐸
𝑅𝑇se recupera.
• Este inciso expresa lo siguiente
• 𝑀 = 𝑥𝑖 𝑀𝑖
• La ecuación quedaría de la siguiente forma
• 𝑀 = 𝑥1 2𝑥1 + 1,4𝑥1
2
− 1,6𝑥1
3
− 1,8 + (1 − 𝑥1)(−𝑥1
2
− 1,6𝑥1
3
)
Propiedades en exceso

42. • Resolviendo las operaciones entre paréntesis
• 𝑀 = 0,8𝑥3 + 𝑥1
2
− 1,8𝑥1
• Esta ecuación es equivalente a
•
𝐺 𝐸
𝑅𝑇
= 0,8𝑥3 + 𝑥1
2
− 1,8𝑥1
Propiedades en exceso

43. • c) Demuestre que estas expresiones satisfacen la ecuación de Gibbs/Duhem
• La ecuación de Gibbs/Duhem postula que
• 𝑥𝑖 𝑑 𝑀𝑖 = 0
• Resolviendo
• Escriba aquí la ecuación.
• 𝑀1 = −1,6𝑥1
3
+ 1,4 𝑥1
2
+ 2𝑥1 − 1,8
• 𝑑𝑀1 = 2 + 2,8𝑥1 − 4,8𝑥1
2
• 𝑀2 = −𝑥1
2
− 1,6𝑥1
3
• 𝑑𝑀2 = −2𝑥1 − 4,8𝑥1
2
Propiedades en exceso

44. • Por lo tanto
• 𝑥1 2 + 2,8𝑥1 − 4,8𝑥1
2
+ 1 − 𝑥1 −2𝑥1 − 4,8𝑥1
2
= 0
• Resolviendo
• 2𝑥1 + 2,8𝑥1
2
− 4,8𝑥1
3
− 2𝑥1 − 4,8𝑥1
2
+ 2𝑥1
2
+ 4,8𝑥1
3
= 0
• Si nos damos cuenta toda la expresión se hace cero, demostrando
que si se cumple la ecuación de Gibbs/Duhem.
Propiedades en exceso

45. Para 𝑆𝑂2 a 600 k y 300 bar, determine una buena
estimación de la fugacidad y de
𝐺 𝑅
𝑅𝑇
, La solución de este
ejercicio es una contribución de Luis Rios Yepez, Cod.
0231320007
Debido al hecho que φ se puede dar en términos de Z, al
introducirse la correlación de pitzer y operando llegamos a la eq
(11.67)
φ = φ0
φ1 𝜔
Nos remitimos a la tabla B.1 para calcular las propiedades
reducidas del gas.
Pc=78,84 bar Tc=430,8 k ω=0,245
Propiedades residuales

46. Calculamos Pr y Tr
𝑃𝑟 =
𝑃
𝑃𝑐
→ 𝑃𝑟 =
300 𝑏𝑎𝑟
78,84 𝑏𝑎𝑟
→ 𝑃𝑟 = 3,805
𝑇𝑟 =
𝑇
𝑇𝑐
→ 𝑇𝑟 =
600 𝐾
430 𝑘
→ 𝑇𝑟 = 1,393
En la tabla E.15 se muestra la dependencia de estas
correlaciones con los valores antes calculados. Para las
condiciones obtenidas tenemos que:
φ0
= 0,6724
φ1
= 1,3543
Propiedades residuales

47. Reemplazando en la eq 11.67 tenemos:
φ = 0,6724 ∗ 1,3543 0,245
φ=0,7238
por definición se tiene :
𝐺 𝑅
𝑅𝑇
= ln φ
Reemplazando
𝐺 𝑅
𝑅𝑇
= ln 0,7238 →
𝑮 𝑹
𝑹𝑻
= −𝟎, 𝟑𝟐𝟑
Para la fugacidad
𝑓 = φ∗P → 𝑓 = 0,7238 ∗ 300 𝑏𝑎𝑟 → 𝒇 = 𝟐𝟏𝟕, 𝟏𝟒𝒃𝒂𝒓
Propiedades residuales

48. Se han reportado las expresiones siguientes para los coeficientes de
actividad de las especies 1 y 2 en una mezcla liquida binaria a T y P
dadas:
ln 𝛾1 = 𝑥2
2
(0,273 + 0,096𝑥1)
ln 𝛾2 = 𝑥1
2(0,273 − 0,096𝑥2)
a) Determine la expresión implicada para
𝐺 𝐸
𝑅𝑇
b) Genere expresiones para ln 𝛾1 y ln 𝛾2 a partir del resultado de A
c) Compare los resultados de B con las expresiones reportadas para
ln 𝛾1 y ln 𝛾2 Explique cualquier discrepancia. Es posible que sean
correctas las expresiones reportadas?
La solución de este ejercicio es una contribución de Luis Rios Yepez, Cod.
0231320007
Propiedades residuales

49. Por definición tenemos que :
𝐺 𝐸
𝑅𝑇
= 𝑥𝑖 𝛾𝑖
Aplicando y simplificando tenemos:
𝐺 𝐸
𝑅𝑇
= 𝑥1 𝑥2
2 0,273 + 0,096𝑥1 + 𝑥2 𝑥1
2 0,273 − 0,096𝑥2
𝑮 𝑬
𝑹𝑻
= 𝟎, 𝟐𝟕𝟑𝒙 𝟏 𝒙 𝟐
𝟐
+ 𝒙 𝟐 𝒙 𝟏
Propiedades residuales

50. Para una mezcla binaria de componentes tenemos lo siguiente
ln 𝛾1 =
𝐺 𝐸
𝑅𝑇
+ 𝑥2
𝑑
𝐺 𝐸
𝑅𝑇
𝑑𝑥1
ln 𝛾2 =
𝐺 𝐸
𝑅𝑇
− 𝑥1
𝑑
𝐺 𝐸
𝑅𝑇
𝑑𝑥1
Reemplazando 𝑥2 = 1 − 𝑥1 y resolviendo llegamos a las
siguientes expresiones
ln 𝛾1 = 0,273𝑥1 − 0,273𝑥1
2 + 1 − 𝑥1 (0,273 − 0,546𝑥1)

51. 𝐥𝐧 𝜸 𝟏 = 𝟎, 𝟐𝟕𝟑 − 𝟎, 𝟓𝟒𝟔𝒙 𝟏 + 𝟎, 𝟐𝟕𝟑𝒙 𝟏
𝟐
Para ln 𝛾2
ln 𝛾2 = 0,273𝑥1 − 0,273𝑥1
2 − 𝑥1(0,273 − 0,546𝑥1)
𝐥𝐧 𝜸 𝟐 = 𝟎, 𝟐𝟕𝟑𝒙 𝟏
𝟐
Aplicando la ecuación de gibss-duhem al cuarteto de expresiones
se observa que las dadas en el enunciado no satisfacen la
condición 𝑥𝑖 d ln 𝛾𝑖 = 0 por lo que se llega a la conclusión de
que los cambios en ln 𝛾𝑖 no suceden en una fase homogénea.
Propiedades residuales

52. Gibbs-duhem para los ln 𝛾𝑖 hallados
1 − 𝑥1 0,273𝑥1
2
+ 𝑥1 0,273 − 0,546𝑥1 + 0,273𝑥1
2
= 0
0 = 0
Gibbs-duhem para los ln 𝛾𝑖 dados
𝑥1 0,288𝑥1
2 + 0,162𝑥1 − 0,45
+ 1 − 𝑥1 0,288𝑥1
2 + 0,354𝑥1 = 0
0 ≠ 0,45𝑥1
2
− 0,804𝑥1 + 0,354
Los datos ingresados en la ultima ecuación corresponden a los
ln 𝛾𝑖 dados en el enunciado y simplificados para 𝑥2 = 1 − 𝑥1
Propiedades residuales

53. Las formas similares de las definiciones de 𝑀E y 𝑀R sugieren que las propiedades en
exceso y las propiedades residuales deben estar relacionadas en una forma sencilla
Demuestre que:
𝑀 𝐸
= 𝑀 𝑅
−
𝑖
𝑥𝑖 𝑀𝑖
𝑅
La solución de este ejercicio es una contribución de María del Pilar Ortiz Rincón Código:
0231320049
Partimos de estas dos ecuaciones
𝑀 𝐸 = 𝑀 − 𝑀 𝑖𝑑 y 𝑀 𝑅= 𝑀 − 𝑀 𝑖𝑔
Ahora procedemos a restar las dos ecuaciones
𝑀 𝐸−𝑀 𝑅 = 𝑀 − 𝑀 𝑖𝑑 − 𝑀 + 𝑀 𝑖𝑔
Propiedades residuales

54. Partimos de una propiedad termodinámica extensiva para calcular 𝑀 𝑖𝑑y 𝑀 𝑖𝑔 en
este caso H lo cambio por M
𝑀 𝑖𝑑
= 𝑖 𝑥𝑖 − 𝑅 𝑖 𝑥𝑖 𝑙𝑛𝑥𝑖 y 𝑀 𝑖𝑔
= 𝑖 𝑦𝑖 − 𝑅 𝑖 𝑀𝑖
𝑖𝑔
− 𝑅 𝑖 𝑦𝑖 𝑙𝑛𝑦𝑖
𝑀 𝐸 − 𝑀 𝑅 =
𝑖
𝑥𝑖 𝑀𝑖 − 𝑅
𝑖
𝑥𝑖 𝑙𝑛𝑥𝑖 −
𝑖
𝑥𝑖 𝑀𝑖
𝑖𝑔
+ 𝑅
𝑖
𝑦𝑖 𝑙𝑛𝑦𝑖
Procedemos a simplificar términos semejantes:
𝑀 𝑖𝑑 − 𝑀 𝑖𝑔 =
𝑖
𝑥𝑖 𝑀𝑖 −
𝑖
𝑀𝑖
𝑖𝑔
=
𝑖
𝑥𝑖 𝑀𝑖
𝑅
Propiedades residuales

55. Organizando:
𝑀 𝐸 − 𝑀 𝑅 =
𝑖
𝑥𝑖 𝑀𝑖
𝑅
𝑀 𝐸 = 𝑀 𝑅
𝑖
𝑥𝑖 𝑀𝑖
𝑅
Propiedades residuales

56. Aplique esto para la energía de Gibbs, y
demuestre que el resultado lleva a:
𝛾𝑖 =
ˆ 𝑖
𝑖
Partimos de la siguiente ecuación
𝐺 𝐸 = 𝐺𝑖
𝑅
− 𝐺𝑖
𝑅
𝐺𝑖
𝑅
= 𝐺𝑖 − 𝐺𝑖
𝑖𝑔
= 𝑅𝑇𝑙𝑛
𝑓𝑖
𝑦𝑖 𝑃
Propiedades residuales

57. Donde
𝑓 𝑖
𝑦 𝑖 𝑃
= Φ
𝐺𝑖
𝑅
= 𝐺𝑖 − 𝐺𝑖
𝑖𝑔
= 𝑅𝑇𝑙𝑛
𝑓 𝑖
𝑝
donde
𝑓 𝑖
𝑝
= Φ
Ahora procedemos a introducir las dos últimas ecuaciones en la inicial y
remplazamos el valor de Φ
𝐺 𝐸 = 𝑅𝑇𝑙𝑛 Φ − 𝑅𝑇𝑙𝑛Φ =
Φ
Φ
𝐺 𝐸
𝑅𝑇
= 𝑙𝑛Φ =
Φ
Φ
Propiedades residuales

58. Por definición
𝐺 𝐸
𝑅𝑇
= 𝑙𝑛𝜑
Igualamos
𝐺 𝐸
𝑅𝑇
y simplificamos logaritmos, obteniendo
𝜑 =
Φ
Φ
Propiedades residuales

59. Estime la fugacidad del isobutileno como un gas: a
280°C y 20 bar. Y a 280°C y 100 bar
La solución de este ejercicio es una contribución de
María José De Pombo Angulo, Cod. 0231320014
Cálculo de fugacidades

60. Solución:
Propiedades criticas del Isobutileno:
𝑇𝑐 = 418.09 𝐾
𝑃𝑐 = 40.1 𝑏𝑎𝑟
𝑤 = 0.194
Cálculo de fugacidades

61. a) Isobutileno a 280°C y 20 bar
𝑇 = 280°𝐶 = 553.15𝐾
𝑃 = 20 𝑏𝑎𝑟 = 2000𝐾𝑃𝑎
Se calculan las propiedades relativas mediante las
ecuaciones:
𝑇𝑟 =
𝑇
𝑇𝑐
= 1.32
𝑃𝑟 =
𝑃
𝑃𝑐
= 0.49
Cálculo de fugacidades

62. Utilizando una correlación generalizada para calcular
el coeficiente de fugacidad a partir de los
coeficientes viriales:
𝜙 = 𝑒𝑥𝑝
𝑃𝑟
𝑇𝑟
𝐵0 + 𝑤𝐵1
Usando las siguiente ecuaciones para hallar los
coeficientes viriales:
𝐵0 = 0.083 −
0.422
𝑇𝑟
1.6 = 0.083 −
0.422
1.321.6
= −0.18
𝐵1
= 0.139 −
0.172
𝑇𝑟
4.2 = 0.139 −
0.172
1.324.2
= 0.085
Cálculo de fugacidades

63. Reemplazando valores, se obtiene el coeficiente de
fugacidad para el isobutileno a 280°C y 20 bar:
𝜙 = 𝑒𝑥𝑝
0.49
1.32
−0.18 + (0.194)(0.085 )
𝜙 = 0.9411
Al tener el coeficiente de fugacidad, se puede hallar la
fugacidad mediante la ecuación:
𝜙 =
𝑓𝑖
𝑃
= 0.9411
𝑓𝑖 = 𝜙𝑃 = 0.9411 20𝑏𝑎𝑟 = 18.822𝑏𝑎𝑟
O 𝑓𝑖 = 𝜙𝑃 = 0.9411 2000𝐾𝑃𝑎 =
1882.216904𝐾𝑃𝑎
Cálculo de fugacidades

64. b) Isobutileno a 280°C y 100 bar
𝑇 = 280°𝐶 = 553.15𝐾
𝑃 = 100 𝑏𝑎𝑟 = 10000𝐾𝑃𝑎
Se calculan las propiedades relativas mediante las
ecuaciones:
𝑇𝑟 =
𝑇
𝑇𝑐
= 1.32
𝑃𝑟 =
𝑃
𝑃𝑐
= 2.49
Cálculo de fugacidades

65. Repitiendo los pasos anteriores:
𝜙 = 𝑒𝑥𝑝
𝑃𝑟
𝑇𝑟
𝐵0
+ 𝑤𝐵1
Usando las siguiente ecuaciones para hallar los
coeficientes viriales:
𝐵0 = −0.18
𝐵1
= 0.085
Cálculo de fugacidades

66. Reemplazando valores, se obtiene el coeficiente de
fugacidad para el isobutileno a 280°C y 100 bar:
𝜙 = 𝑒𝑥𝑝
2.49
1.32
−0.18 + (0.194)(0.085 )
𝜙 = 0.7346
𝑓𝑖 = 𝜙𝑃 = 0.7346 100𝑏𝑎𝑟 = 73.456𝑏𝑎𝑟
O 𝑓𝑖 = 𝜙𝑃 = 0.7346 10000𝐾𝑃𝑎 =
7345.925𝐾𝑃𝑎
Cálculo de fugacidades

67. 12. Estime la fugacidad del 1-buteno líquido a 120°C y 34
bar. A 120°C la presión de vapor del 1-buteno es 25.83 bar.
La solución de este ejercicio es una contribución de David
López Barbosa, Cod. 0231310026
Mediante tablas de propiedades y el enunciado del
ejercicio podemos obtener los siguientes datos para el 1-
buteno: 𝜔 = 0,191 𝑇c = 420,0 𝐾 𝑃c = 40,43 𝑏𝑎𝑟
𝑍c = 0,277 𝑉c = 239,3 𝑐𝑚3 𝑚𝑜𝑙 𝑇 = 393,15 𝐾
𝑃 = 34 𝑏𝑎𝑟 𝑃 𝑠𝑎𝑡 = 25,83 𝑏𝑎𝑟
Cálculo de fugacidades

68. Calculamos las propiedades reducidas:
𝑇𝑟 =
𝑇
𝑇𝑐
=
393,15 𝐾
420 𝐾
= 0,9361
𝑃 𝑠𝑎𝑡
𝑟 =
𝑃 𝑠𝑎𝑡
𝑃𝑐
=
25,83 𝑏𝑎𝑟
40,43 𝑏𝑎𝑟
= 0,3689
Calculamos el coeficiente de fugacidad utilizando la ecuación (11.68) del libro de
Smith, Van Ness:
ϕ = 𝑒𝑥𝑝
𝑃𝑟
𝑇𝑟
𝐵0
+ 𝜔𝐵1
Utilizando las correlaciones de Pitzer para el segundo coeficiente virial obtenemos:
𝐵0 = 0,083 −
0,422
𝑇𝑟
1,6 = 0,083 −
0,422
0,9361 1,6 = −0,3860
Cálculo de fugacidades

69. 𝐵1
= 0,139 −
0,172
𝑇𝑟
4,2 = 0,139 −
0,172
0,9361 4,2 = −0,0879
Reemplazando estos valores en la ecuación (11.68) para el coeficiente de
fugacidad obtenemos:
ϕ = 𝑒𝑥𝑝
0,3689
0,9361
−0,3860 + 0,191 −0,0879 ; ϕ = 0,8532
Este coeficiente de fugacidad equivale a ϕ 𝑠𝑎𝑡 debido a que se calculó
usando 𝑃 𝑠𝑎𝑡.
Para calcular la fugacidad utilizamos la ecuación (11.44) del libro de Smith,
Van Ness:
𝑓 = ϕ 𝑠𝑎𝑡 𝑃 𝑠𝑎𝑡 𝑒𝑥𝑝
𝑉 𝑠𝑎𝑡
(𝑃 − 𝑃 𝑠𝑎𝑡
)
𝑅𝑇
Cálculo de fugacidades

70. Para calcular 𝑉 𝑠𝑎𝑡
utilizamos la ecuación de Rackett:
𝑉 𝑠𝑎𝑡 = 𝑉𝑐 𝑍 𝑐
1−𝑇𝑟
2
7
Reemplazando valores obtenemos:
𝑉 𝑠𝑎𝑡 = 239,3 𝑐𝑚3 𝑚𝑜𝑙 0,277 1−0,9361
2
7
= 163,5199 𝑐𝑚3 𝑚𝑜𝑙
Reemplazando estos valores en la ecuación (11.44) para la fugacidad obtenemos:
𝑓 = 0,8532 25,83 𝑏𝑎𝑟 𝑒𝑥𝑝
163,5199 𝑐𝑚3 𝑚𝑜𝑙 (34 𝑏𝑎𝑟 − 25,83 𝑏𝑎𝑟)
83,1447 𝑐𝑚3 𝑏𝑎𝑟
𝑚𝑜𝑙 𝐾
393,15 𝐾
Obtenemos que la fugacidad para el 1-buteno a 120°C y 34 bar es 𝒇 = 𝟐𝟐, 𝟗𝟓𝟕𝟓 𝒃𝒂𝒓
Cálculo de fugacidades

71. 21. Para el sistema etileno(1)/propileno(2) como un gas,
estime 𝑓1, 𝑓2 𝑦 𝜙1, 𝜙2 a T=150°C, P=30 bar, y y1=0.35:
a) Por medio de la aplicación de las siguientes
ecuaciones:
ln 𝜙1 =
𝑃
𝑅𝑇
𝐵11 + 𝑦2
2 𝛿12
ln 𝜙2 =
𝑃
𝑅𝑇
𝐵22 + 𝑦1
2 𝛿12
b) Suponiendo que es una solución ideal.
La solución de este ejercicio es una contribución de David
López Barbosa, Cod. 0231310026
Cálculo de fugacidades

72. Mediante tablas de propiedades y el enunciado del ejercicio podemos
obtener los siguientes datos:
Para el Etileno:
𝜔1 = 0,087 𝑇𝑐1
= 282,3 𝐾 𝑃𝑐1
= 50,40 𝑏𝑎𝑟
𝑍 𝑐1
= 0,281 𝑉𝑐1
= 131,0 𝑐𝑚3 𝑚𝑜𝑙 𝑇 = 423,15 𝐾
𝑃 = 30 𝑏𝑎𝑟 𝑦1 = 0,35
Para el Propileno:
𝜔2 = 0,140 𝑇𝑐2
= 365,6 𝐾 𝑃𝑐2
= 46,65 𝑏𝑎𝑟
𝑍 𝑐2
= 0,289 𝑉𝑐2
= 188,4 𝑐𝑚3 𝑚𝑜𝑙 𝑇 = 423,15 𝐾
𝑃 = 30 𝑏𝑎𝑟 𝑦2 = 0,65
Cálculo de fugacidades

73. a) Podemos calcular las propiedades de la mezcla utilizando las reglas de
combinación de Prausnitz, ecuaciones (11.70-74) del libro de Smith, Van
Ness:
Si reemplazamos valores en estas ecuaciones obtenemos los siguientes
valores:
𝜔𝑖𝑗 =
𝜔𝑖 + 𝜔𝑗
2 𝑇𝑐 𝑖𝑗
= 𝑇𝑐 𝑖
𝑇𝑐 𝑗
1
2
𝑃𝑐𝑖𝑗
=
𝑍 𝑐𝑖𝑗
𝑅𝑇𝑐 𝑖𝑗
𝑉𝑐 𝑖𝑗
𝑍 𝑐𝑖𝑗
=
𝑍 𝑐𝑖
+ 𝑍 𝑐 𝑗
2
𝑉𝑐 𝑖𝑗
=
𝑉
1
3 𝑐 𝑖
+ 𝑉
1
3 𝑐 𝑗
2
3
𝑖𝑗 𝜔𝑖𝑗 𝑇𝑐 𝑖𝑗
/𝐾 𝑍 𝑐𝑖𝑗
𝑉𝑐 𝑖𝑗
/ 𝑐𝑚3 𝑚𝑜𝑙 𝑃𝑐 𝑖𝑗
/𝑏𝑎𝑟
11 0,087 282,3 0,281 131,0 50,347
22 0,140 365,6 0,289 188,4 46,629
12 0,114 321,3 0,285 158,0 48,189
Cálculo de fugacidades

74. Para calcular los coeficientes cruzados 𝐵𝑖𝑗 utilizamos la ecuación (11.69)
del libro de Smith, Van Ness:
𝐵𝑖𝑗 =
𝑅𝑇𝑐 𝑖𝑗
𝑃𝑐 𝑖𝑗
𝐵0 + 𝜔𝑖𝑗 𝐵1
Para calcular los componentes 𝐵0 y 𝐵1 necesitamos de las siguientes
ecuaciones:
Si reemplazamos valores en estas ecuaciones obtenemos los siguientes
valores:
𝑖𝑗 𝑇𝑟 𝑖𝑗 𝐵0 𝐵1 𝐵𝑖𝑗 / 𝑐𝑚3
𝑚𝑜𝑙
11 1,499 -0,138 0,108 -59,955
22 1,157 -0,251 0,046 -159,429
12 1,317 -0,189 0,085 -99,403
𝐵0 = 0,083 −
0,422
𝑇𝑟 𝑖𝑗
1,6 𝐵1 = 0,139 −
0,172
𝑇𝑟 𝑖𝑗
4,2 𝑇𝑟 𝑖𝑗
=
𝑇
𝑇𝑐 𝑖𝑗
Cálculo de fugacidades

75. Calculando 𝛿12 de acuerdo a su definición, tenemos:
𝛿12 = 2𝐵12 − 𝐵11 − 𝐵22 = 2 −99,403 + 59,955 + 159,429
= 20,578
Por lo tanto, calculando ϕ1 y ϕ2 con las ecuaciones que nos da el
enunciado del ejercicio, obtenemos:
ln 𝜙1 =
30
83,1447 423,15
−59,955 + 0,65 2
(20,578) = −0,044
ln 𝜙2 =
30
83,1447 423,15
−159,429 + 0,35 2
(20,578)
= −0,134
De donde, 𝝓 𝟏 = 𝟎, 𝟗𝟓𝟕 y 𝝓 𝟐 = 𝟎, 𝟖𝟕𝟓.
Para calcular la fugacidad utilizamos la expresión 𝑓𝑖 = ϕ𝑖 𝑦𝑖 𝑃. De aquí
obtenemos que 𝒇 𝟏 = 𝟏𝟎, 𝟐𝟑𝟕 𝒃𝒂𝒓 y 𝒇 𝟐 = 𝟏𝟕, 𝟎𝟔𝟐 𝒃𝒂𝒓.
Cálculo de fugacidades

76. b) En una solución ideal, el coeficiente de fugacidad de la especie 𝑖 es igual al
coeficiente de fugacidad de la especie pura en el mismo estado físico que la
solución y a las mismas 𝑇 y 𝑃. Por lo tanto podemos utilizar las ecuaciones
(11.68) y (11.52), respectivamente, del libro de Smith, Van Ness:
ϕ𝑖
𝑠𝑖
= ϕ𝑖 = 𝑒𝑥𝑝
𝑃𝑟
𝑇𝑟
𝐵0 + 𝜔𝐵1
𝑓𝑖
𝑠𝑖
= ϕ𝑖
𝑠𝑖
𝑦𝑖 𝑃
Calculamos los siguiente valores de 𝑃𝑟 , 𝑇𝑟 , 𝐵0 y 𝐵1 para el sistema
etileno(1)/propileno(2):
𝑖 𝑃𝑟 𝑇𝑟 𝐵0 𝐵1
1 0,595 1,499 -0,138 0,108
2 0,643 1,157 -0,251 0,046
Cálculo de fugacidades

77. Reemplazando los valores de la tabla en las ecuaciones
(11.68) y (11.52) obtenemos
ϕ1
𝑠𝑖
= 𝑒𝑥𝑝
0,595
1,499
−0,138 + 0,087 0,108 ; 𝝓 𝟏
𝒔𝒊
= 𝟎, 𝟗𝟓𝟎
ϕ2
𝑠𝑖
= 𝑒𝑥𝑝
0,643
1,157
−0,251 + 0,140 0,046 ; 𝝓 𝟐
𝒔𝒊
= 𝟎, 𝟖𝟕𝟑
𝑓1
𝑠𝑖
= 0,950 0,35 30 𝑏𝑎𝑟 ; 𝒇 𝟏
𝒔𝒊
= 𝟗, 𝟗𝟕𝟓 𝒃𝒂𝒓
𝑓2
𝑠𝑖
= 0,873 0,65 30 𝑏𝑎𝑟 ; 𝒇 𝟐
𝒔𝒊
= 𝟏𝟕, 𝟎𝟐𝟑 𝒃𝒂𝒓
Cálculo de fugacidades

78. A partir de los datos en las tablas de vapor, determine una buena
estimación de
𝑓
𝑓 𝑠𝑎𝑡 para agua liquida a 150 °C y 150 bar, donde 𝑓 𝑠𝑎𝑡es la
fugacidad del liquido saturado a 150°C. La solución de este ejercicio es una
contribución de Luis Rios Yepez, Cod. 0231320007
Para la fugacidad de sustancias puras nos remitimos a una forma especifica de la
diferencia de 𝐺𝑖 − 𝐺𝑖
𝑠𝑎𝑡
ln
𝑓
𝑓 𝑠𝑎𝑡
=
1
𝑅𝑇 𝑝 𝑠𝑎𝑡
𝑝
𝑉𝑖
𝑙
𝑑𝑝
Donde 𝑉𝑖
𝑙
representa el volumen molar de la sustancia a la 𝑝 𝑠𝑎𝑡
Cálculo de fugacidades

79. Para hallar 𝑝 𝑠𝑎𝑡
utilizaremos la ecuacion de antoine, para ello
nos remitimos a la tabla B.2 y leemos los coeficientes A, B y C
para el agua
A=16,3872 ; B=3885,7 ; C=230,170
Introduciendo y resolviendo para 𝑝 𝑠𝑎𝑡 llegamos a:
ln 𝑃 𝑠𝑎𝑡 = 𝐴 −
𝐵
𝑇 + 𝐶
→ ln 𝑃 𝑠𝑎𝑡 = 16,3872 −
3885,7
150 + 230,17
ln 𝑝 𝑠𝑎𝑡 = 6,166 → 𝑝 𝑠𝑎𝑡 = 476,395 𝑘𝑃𝑎
Cálculo de fugacidades

80. Por medio de tablas de vapor hallamos V para T y 𝑝 𝑠𝑎𝑡
V=0,001086 𝑚3
𝑘𝑔
Tenemos que 𝑉𝑖
𝑙
= 𝑉 ∗ 𝑃𝑚 donde Pm esta definido como el
peso molecular de la sustancia
𝑉𝑖
𝑙
= 0,001086 ∗ 18 → 𝑉𝑖
𝑙
= 0,0195 𝑚3
𝑘𝑚𝑜𝑙
El volumen molar resulta ser una función débil de la presión por
debajo de Pc, por lo tanto en la función integrada de ln
𝑓
𝑓 𝑠𝑎𝑡 se
toma como constante sin el riesgo de generar un error
apreciable.
Cálculo de fugacidades

81. Resolviendo tenemos
ln
𝑓
𝑓 𝑠𝑎𝑡
=
0,195(150 ∗ 100 − 476,394)
8,314 ∗ 423,15
ln
𝑓
𝑓 𝑠𝑎𝑡
= 0,0805
𝒇
𝒇 𝒔𝒂𝒕
= 𝟏, 𝟎𝟖𝟒
Cálculo de fugacidades

82. Estime la fugacidad del ciclopentano a 1100c y 275 𝑏𝑎𝑟. A 1100c, la presión de
vapor del ciclopentano es 5,267 𝑏𝑎𝑟.
La solución de este ejercicio es una contribución de Arturo Ángel Castro Castro
cod: 0231320035
Cálculo de fugacidades

83. Nos están pidiendo la fugacidad en un liquido puro, en este caso el ciclopentano,
para hallarla se tiene la formula para la fugacidad de un liquido puro que es la
siguiente: 𝑓𝑖 = Փ𝑖 𝑃𝑖
𝑠𝑎𝑡
𝐸𝑋𝑃
𝑉 𝑖 (𝑃−𝑃𝑠𝑎𝑡)
𝑅𝑇
En la cual conocemos varios valores por las tablas de vapor o por el enunciado del
ejercicio, pero nos damos cuenta que dentro de esa formula nos hace falta
obtener dos datos que no están en las tablas que son: Փ𝑖 y 𝑉𝑖 así que se debe
buscar la manera de obtenerlos.
Cálculo de fugacidades

84. A continuación se plantean las formulas para hallar los datos antes mencionados
esto que estas formulas ya se dedujeron y están en términos que se conocen,
entonces para hallar:
•Փ𝑖 = Փ0 ∗ (Փ1) 𝜔 y para 𝑉𝑖 =
𝑅𝑇
𝑃
ya teniendo estas formulas pasamos a
obtener los datos que faltan para hallar la fugacidad entonces de las ecuaciones
anteriores al revisar en la tabla obtenemos: Փ0 = 0,9354 y Փ1 = 0,9550 a
demás 𝜔 = 0,196 .
Ahora bien Փ𝑖 = (0,9354)(0,9550)0,196
= 0,9
Cálculo de fugacidades

85. Ahora pasamos a hallar 𝑉𝑖
𝑉𝑖 =
𝑅𝑇
𝑃
donde 𝑅 = 83,14
𝑐𝑚3 𝑏𝑎𝑟
𝑚𝑜𝑙 𝐾
, 𝑇 = 383,15 𝐾, 𝑃 = 275 𝑏𝑎𝑟,
Asi pues 𝑉𝑖 =
(84,14
𝑐𝑚3 𝑏𝑎𝑟
𝑚𝑜𝑙 𝐾
)(383,16 𝐾)
275 𝑏𝑎𝑟
= 115,837
𝑐𝑚3
𝑚𝑜𝑙
y asi obtenemos nuestro ultimo dato
correspondiente para la formula de fugacidad.
Entonces para encontrar la fugacidad tenemos:
𝑉𝑖 = 115,837
𝑐𝑚3
𝑚𝑜𝑙
, Փ𝑖 = 0,9, 𝑃𝑖
𝑠𝑎𝑡
= 5,267 𝑏𝑎𝑟, 𝑃 = 275 𝑏𝑎𝑟, 𝑅 = 83,14
𝑐𝑚3 𝑏𝑎𝑟
𝑚𝑜𝑙 𝐾
y 𝑇 =
383,15 𝐾
Cálculo de fugacidades

86. Ahora:
𝑓𝑖 = Փ𝑖 𝑃𝑖
𝑠𝑎𝑡
𝐸𝑋𝑃
𝑉 𝑖 (𝑃−𝑃𝑠𝑎𝑡)
𝑅𝑇
𝑓𝑖 = 0,9 5,267 𝐸𝑋𝑃
115,837
𝑐𝑚3
𝑚𝑜𝑙
(275 𝑏𝑎𝑟−5,267 𝑏𝑎𝑟)
83,14
𝑐𝑚3 𝑏𝑎𝑟
𝑚𝑜𝑙 𝐾
(383,15 𝐾)
=12,641 𝑏𝑎𝑟
Cálculo de fugacidades

87. Para el sistema Metano (1), Etano (2), Propano (3), como un gas, estime
𝒇 𝟏, 𝒇 𝟐 , 𝒇 𝟑 y ∅ 𝟏, ∅ 𝟐, ∅ 𝟑 a t = 100°C, P = 35 bar, 𝒚 𝟏 = 𝟎. 𝟐𝟏; 𝒚 𝟐 = 𝟎. 𝟒𝟑
La solución de este ejercicio es una contribución de Arturo Ángel Castro Castro
cod: 0231320035
Cálculo de fugacidades

88. a) Aplicando
ln ∅ 𝑘 =
𝑃
𝑅𝑇
𝐵 𝑘𝑘 +
1
2
𝑖 𝑗
𝑦𝑖 𝑦𝑗 2𝛿𝑖𝑘 − 𝛿𝑖𝑗
Para desarrollar la anterior ecuación debemos hallar 𝜔, 𝑇𝑐, 𝑇𝑟, 𝑃𝑐, 𝑃𝑟, 𝑉𝑐, 𝑍 𝑐
Para cada componente y para cada par de componentes, primero por
medio de la Tabla B.1 del Smith Van Ness obtenemos
𝜔1 = 0.012; 𝜔2 = 0.1; 𝜔3 = 0.152
𝑇𝑐1 = 190.6 𝐾; 𝑇𝑐2 = 305.3 𝐾; 𝑇𝑐3 = 369.8 𝐾
𝑇𝑟1 = 1.96; 𝑇𝑟2 = 1.22; 𝑇𝑟3 = 1.01
𝑃𝑐1 = 45.99 𝑏𝑎𝑟; 𝑃𝑐2 = 48.72 𝑏𝑎𝑟; 𝑃𝑐3 = 42.48 𝑏𝑎𝑟
𝑃𝑟1 = 0.76; 𝑃𝑟2 = 0.72; 𝑃𝑟3 = 0.82
𝑉𝑐1 = 98.6
𝑐𝑚3
𝑚𝑜𝑙
; 𝑉𝑐2 = 145.5
𝑐𝑚3
𝑚𝑜𝑙
; 𝑉𝑐3 = 200
𝑐𝑚3
𝑚𝑜𝑙
𝑍 𝑐1 = 0.286; 𝑍 𝑐2 = 0.279; 𝑍 𝑐3 = 0.276
Cálculo de fugacidades

89. Ahora para las parejas de componentes por medio de las formulas.
𝜔𝑖𝑗 =
𝜔 𝑖+𝜔 𝑗
2
; 𝑇𝑐𝑖𝑗 = 𝑇𝑐𝑖 ∗ 𝑇𝑐𝑗 ; 𝑍 𝑐𝑖𝑗=
𝑍 𝑖+𝑍 𝑗
2
; 𝑉𝑐𝑖𝑗 =
𝑉 𝑐𝑖
1
3+ 𝑉 𝑐𝑗
1
3
2
; 𝑃𝑐𝑖𝑗 =
𝑍 𝑐𝑖𝑗∗𝑅∗𝑇 𝑐𝑖𝑗
𝑉 𝑐𝑖𝑗
; 𝑇𝑟𝑖𝑗 =
𝑇
𝑇 𝑐𝑖𝑗
Para
𝜔𝑖𝑗 =
𝜔𝑖 + 𝜔𝑗
2
𝜔12 = 0.06; 𝜔13 = 0.08 ; 𝜔23 = 0.13
𝑇𝑐𝑖𝑗 = 𝑇𝑐𝑖 ∗ 𝑇𝑐𝑗
Cálculo de fugacidades

90. Ahora para las parejas de componentes por medio de las formulas
𝑍 𝑐𝑖𝑗=
𝑍𝑖 + 𝑍𝑗
2
𝑍 𝑐12 = 0.28; 𝑍 𝑐13 = 0.28; 𝑍 𝑐23 = 0.28
𝑉𝑐𝑖𝑗 =
𝑉𝑐𝑖
1
3 + 𝑉𝑐𝑗
1
3
2
Cálculo de fugacidades

91. 𝑉𝑐12 = 120.53
𝑐𝑚3
𝑚𝑜𝑙
; 𝑉𝑐13 = 143.38
𝑐𝑚3
𝑚𝑜𝑙
; 𝑉𝑐23 = 171.31
𝑐𝑚3
𝑚𝑜𝑙
𝑃𝑐𝑖𝑗 =
𝑍 𝑐𝑖𝑗∗ 𝑅 ∗ 𝑇𝑐𝑖𝑗
𝑉𝑐𝑖𝑗
𝑃𝑐12 = 46.59 𝑏𝑎𝑟; 𝑃𝑐13 = 43.1 𝑏𝑎𝑟; 𝑃𝑐23 = 45.66 𝑏𝑎𝑟
𝑇𝑟𝑖𝑗 =
𝑇
𝑇𝑐𝑖𝑗
𝑇𝑟12 = 1.55; 𝑇𝑟13 = 1.41; 𝑇𝑟23 = 1.11
De las ecuaciones
𝐵𝑖𝑗
0
= (𝐵0
)𝑇𝑟𝑖𝑗 ; 𝐵𝑖𝑗
1
= (𝐵1
)𝑇𝑟𝑖𝑗;
𝐵𝑖𝑗 =
𝑅∗𝑇 𝑐𝑖𝑗
𝑃 𝑐𝑖𝑗
∗ 𝐵𝑖𝑗
0
+ 𝜔𝑖𝑗 ∗ 𝐵𝑖𝑗
1
Obtenemos los valores de los coeficientes viriales y por ultimo hallamos los valores del
a siguiente ecuación para resolver el primer punto
Cálculo de fugacidades

92. 𝛿𝑖𝑗 = 2𝐵𝑖𝑗 − 𝐵𝑖𝑖 − 𝐵𝑗𝑗
𝛿12 = 30.44
𝑐𝑚3
𝑚𝑜𝑙
𝛿13 = 107.81
𝑐𝑚3
𝑚𝑜𝑙
𝛿23 = 23.48
𝑐𝑚3
𝑚𝑜𝑙
Ahora teniendo todos los valores de la ecuación del punto “a” procedemos a reemplazar y
hallar el coeficiente de fugacidad
∅ 𝑘 = 𝑒𝑥𝑝
𝑃
𝑅𝑇
𝐵 𝑘𝑘 +
1
2
𝑖 𝑗
𝑦𝑖 𝑦𝑗 2𝛿𝑖𝑘 − 𝛿𝑖𝑗
∅1 = 1.019; ∅2 = 0.881; ∅3 = 0.775
Para hallar la fugacidad de cada componente tenemos la ecuación
𝑓𝑘 = ∅ 𝑘 𝑦 𝑘 𝑃
𝑓1 = 7.49 𝑏𝑎𝑟; 𝑓2 = 13.25 𝑏𝑎𝑟; 𝑓3 = 9.76 𝑏𝑎𝑟
Cálculo de fugacidades

93. b) Para una solución ideal ∅𝑖𝑑 = ∅ de las especies puras
𝑃𝑟𝑘 =
𝑃
𝑃𝑐𝑘
Hallando
∅𝑖𝑑𝑘 = 𝑒𝑥𝑝
𝑃𝑟𝑘
𝑇𝑘,𝑘
𝐵 𝑘,𝑘
0
+ 𝜔 𝑘,𝑘 ∗ 𝐵 𝑘,𝑘
1
∅𝑖𝑑1 = 0.977; ∅𝑖𝑑2 = 0.88; ∅𝑖𝑑3 = 0.759
Para la fugacidad 𝑓𝑖𝑑𝑘 = ∅ 𝑘𝑖𝑑 𝑦 𝑘 𝑃
𝑓𝑖𝑑1 = 7.182 𝑏𝑎𝑟; 𝑓𝑖𝑑2 = 13.251; 𝑓𝑖𝑑3 = 9.569 𝑏𝑎𝑟
Cálculo de fugacidades

94. Estime la fugacidad del a) n-pentano b) isobutileno c) 1-buteno líquido
a la temperatura de su punto de ebullición normal y 200 bar.
La solución de este ejercicio es una contribución de Angelith Marcela
Bonfante Pérez Cod. 0231220041
Cálculo de fugacidades

95. a) n-pentano
Tc= 469,7 K Pc= 33,7 bar Zc= 0,270 Vc= 313,0
𝑐𝑚3
𝑚𝑜𝑙
𝜔 = 0,252 Tn= 309,2 K P = 200 bar Psat= 1,01325 bar
Tr =
𝑇𝑛
𝑇𝑐
Pr=
𝑃𝑠𝑎𝑡
𝑃𝑐
Entonces: Tr= 0,6583 Pr= 0,0301
𝑉𝑖 = 𝑉𝑐 ∗ 𝑍𝑐(1−𝑇𝑟)2/7
𝑉𝑖 = 119,4388
𝑓𝑖 = ∅𝑖 𝑠𝑎𝑡 𝑃𝑖 𝑠𝑎𝑡 exp
𝑉𝑖(𝑃 − 𝑃𝑖 𝑠𝑎𝑡)
𝑅𝑇
∅𝑖 𝑠𝑎𝑡 𝑃𝑖 𝑠𝑎𝑡 = 0,9572
Reemplazando en la ecuación tenemos:
𝒇𝒊 = 𝟐, 𝟒𝟒𝟓 𝒃𝒂𝒓
Cálculo de fugacidades

96. b) Isobutileno
Tc= 417,9 K Pc= 40,0 bar Zc= 0,275 Vc= 238,9
𝑐𝑚3
𝑚𝑜𝑙
𝜔 = 0,194 Tn= 266,3 K P = 300 bar Psat= 1,01325 bar
Tr =
𝑇𝑛
𝑇𝑐
Pr=
𝑃𝑠𝑎𝑡
𝑃𝑐
Entonces: Tr= 0,6372 Pr= 0,0253
𝑉𝑖 = 𝑉𝑐 ∗ 𝑍𝑐(1−𝑇𝑟)2/7
𝑉𝑖 = 90,8987
𝑓𝑖 = ∅𝑖 𝑠𝑎𝑡 𝑃𝑖 𝑠𝑎𝑡 exp
𝑉𝑖(𝑃 − 𝑃𝑖 𝑠𝑎𝑡)
𝑅𝑇
∅𝑖 𝑠𝑎𝑡 𝑃𝑖 𝑠𝑎𝑡 = 0,9618
Reemplazando en la ecuación tenemos:
𝒇𝒊 = 𝟑, 𝟑𝟐𝟔 𝒃𝒂𝒓
Cálculo de fugacidades

97. c) 1-butano
Tc= 420 K Pc= 40,43 bar Zc= 0,277 Vc= 239,3
𝑐𝑚3
𝑚𝑜𝑙
𝜔 = 0,191 Tn= 266,9 K P = 150 bar Psat= 1,01325 bar
Tr =
𝑇𝑛
𝑇𝑐
Pr=
𝑃𝑠𝑎𝑡
𝑃𝑐
Entonces: Tr= 0,6355 Pr= 0,0251
𝑉𝑖 = 𝑉𝑐 ∗ 𝑍𝑐(1−𝑇𝑟)2/7
𝑉𝑖 = 91,4286
𝑓𝑖 = ∅𝑖 𝑠𝑎𝑡
𝑃𝑖 𝑠𝑎𝑡
exp
𝑉𝑖(𝑃 − 𝑃𝑖 𝑠𝑎𝑡)
𝑅𝑇
∅𝑖 𝑠𝑎𝑡
𝑃𝑖 𝑠𝑎𝑡
= 0,9620
Reemplazando en la ecuación tenemos:
𝒇𝒊 = 𝟐, 𝟒𝟒𝟓 𝒃𝒂𝒓
Cálculo de fugacidades

98. El vapor de agua a 1000 (psi) y 800 (°F) experimenta un cambio isotérmico de estado
hasta una presión de 50 (psi). Determine la relación de la fugacidad entre el estado
final y el estado inicial.
La solución de este ejercicio es una contribución de María del Pilar Ortiz Rincón
Código: 0231320049
El sistema es isotérmico, es decir, que la temperatura es constante; el estado inicial
presenta una presión de 1000 psi y una temperatura de 800°F y el estado final tiene
una presión de 50 psi y 800°F.
A 1000 psi y 800°F por medio de las tablas de vapor tenemos:
𝐻1 = 3230,72
𝐾𝐽
𝐾𝑔
y 𝑆1 = 6,5008
𝐾𝐽
𝐾𝑔
Cálculo de fugacidades

99. A 50 psi y 800°F
𝐻2 = 3330,52
𝐾𝐽
𝐾𝑔
y 𝑆2 = 8,0510
𝐾𝐽
𝐾𝑔
𝑅 = 8,314
𝐽
𝐾𝑚𝑜𝑙
Cálculo de fugacidades

100. Con la siguiente ecuación tomada del libro Van Ness lograremos dar solución a
este problema:
𝑙𝑛
𝑓𝑖
𝑓𝑖
=
1
𝑅𝑇
𝐻2 − 𝐻1
𝑇
− 𝑆2 − 𝑆1
Nota: como es vapor de agua y necesitamos que la ecuación quede expresada en
unidades molares multiplicamos por la masa molar del agua.
Ahora procedemos a reemplazar valores conocidos en la ecuación anterior:
𝑙𝑛
𝑓𝑖
𝑓𝑖
=
18,015
𝑔
𝑚𝑜𝑙
8,314
𝐽
𝑚𝑜𝑙
3330,52
𝐾𝐽
𝐾𝑔 − 3230,72
𝐾𝐽
𝐾𝑔
699.7 𝐾
− 8,0510 − 6,5608
𝐾𝐽
𝐾𝑔𝐾
Cálculo de fugacidades

101. Nos quedaría que:
ln
𝑓𝑖
𝑓𝑖
= −2,9199
Despejando el logaritmo natural tendríamos que:
𝑓𝑖
𝑓𝑖
= 𝑒−2,9199
= 0,05393
La relación de la fugacidad entre un estado inicial y final
quedaría igual a 0,05393
Cálculo de fugacidades