El documento presenta 5 ejercicios de balances de materia y energía con reacciones químicas. El primer ejercicio involucra reacciones en un reactor continuo y calcula la composición molar de los productos y la selectividad. El segundo ejercicio analiza la combustión del etano con aire en exceso y calcula la composición molar de los gases de combustión. Los siguientes ejercicios presentan problemas adicionales de balances con reacciones químicas.








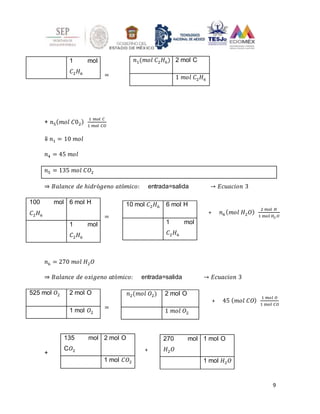


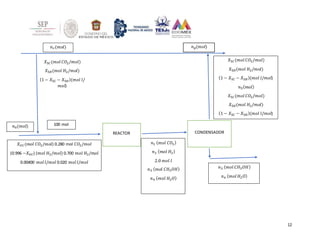







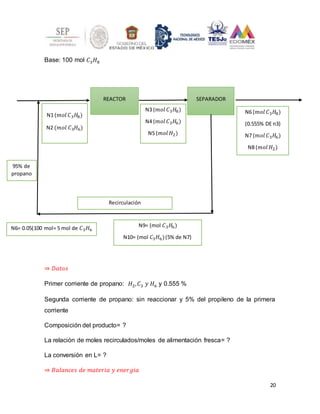
 + [𝑛7 (𝑚𝑜𝑙 𝐶3𝐻6)](3 𝑚𝑜𝑙
𝑐
𝑚𝑜𝑙
𝐶3𝐻6
N6= 5 mol → n7= 95 mol 𝐶3𝐻6
Balance general de H:
(100)(8) = 𝑛6 (8)+ 𝑛7 (6)+ 𝑛8(2) → 𝑛8 = 95 𝑚𝑜𝑙 𝐻2 → 𝐸𝑐𝑢𝑎𝑐𝑖ó𝑛 2
El producto contiene = 5 𝑚𝑜𝑙 𝐶3𝐻8 → 2.6 𝑚𝑜𝑙% 𝐶3𝐻8
95 𝑚𝑜𝑙 𝐶3𝐻6 → 48.7 𝑚𝑜𝑙% 𝐶3𝐻6
95 𝑚𝑜𝑙 𝐻2 → 48.7 𝑚𝑜𝑙 𝐻2
Relaciones dadas entre las variables del separador: → 𝐸𝑐𝑢𝑎𝑐𝑖ó𝑛 3
𝑛6 = 0.00555 𝑛3 → 𝑛3 = 900 𝑚𝑜𝑙 𝐶3𝐻8
𝑛10 = 0.00555 𝑛7 → 𝑛10 = 4.75 𝑚𝑜𝑙 𝐶3𝐻6
Balance del propano en torno a la unidad de separación: → 𝐸𝑐𝑢𝑎𝑐𝑖ó𝑛 4](https://image.slidesharecdn.com/segundadebalance-220327162721/85/segunda-de-balance-docx-21-320.jpg)

