Este documento describe el proceso de calibración utilizado para determinar parámetros en un modelo de equilibrio general computable. La calibración es un método determinista para estimar valores de parámetros cuando la estimación econométrica no es factible debido a limitaciones de datos. El documento explica cómo se calibran parámetros clave como las elasticidades de sustitución en funciones de producción utilizando información de una matriz de contabilidad social. Se proporciona un ejemplo numérico utilizando datos de Bogotá, Colombia.

1. Calibración
Juan Carlos SEGURA-ORTIZ M.Sc.
Universidad de La Salle / Escuela Colombiana de Ingeniería
Bogotá, D.C., 2004

2. Determinación de Parámetros: La Calibración
La calibración constituye una aproximación determinista de la estimación de los valores de
los parámetros en un CGE.
La estimación econométrica de un CGE es usualmente implausible por dos razones
principales:
a. En los modelos aplicados aparece tal cantidad de parámetros que su estimación
simultánea haciendo uso de series de tiempo es, al menos por el momento, implausible
debido a que se requerirían grandes cantidades de datos y resolver grandes problemas de
identificación.
b. La información de benchmark (SAM / MIP) tiene por unidades valores; su
descomposición en observaciones separadas para precios y cantidades no garantiza la
obtención de secuencias con unidades consistentes a través del tiempo, como se exige en
series de tiempo.
Para resolver estos problemas se procede de dos maneras (Keyzer & Ginsburgh, 1997):
1. Utilizando estimaciones econométricas por componentes, tomando algunos parámetros de
la literatura (pero no incorporan todas las restricciones contenidas en el modelo completo);
2. Definiendo los parámetros restantes a través de métodos de calibración (benchmarking
methods)

3. Con Keyzer y Ginsburgh [1997], el procedimiento de la calibración puede entenderse
como la selección de valores numéricos para los parámetros de las funciones de
demanda del consumidor xi(p, hi), así como para las funciones de producción yj(p) o
los requerimientos directos unitarios A(p).
En términos de las variables de la Matriz de Contabilidad Social xi*, hi*, yj*, p*, la
calibración consiste en resolver el siguiente sistema de ecuaciones:
( )
xil p* , hi* ; β, γ = xil
*
∀i ,l
[A] y ( p ; β, γ ) = y
jl
* *
jl ∀j ,l
A ( p ; β, γ ) = A
lh
* *
lh ∀l , h
β y γ son vectores de parámetros, y A* es la matriz de insumo-producto.

4. Con frecuencia algúnos parámetros clave como las elasticidades de sustitución o las
tasas de retorno a escala, ― γ ―, se toman prestados de investigaciones y trabajos
econométricos (i.e., estimados en sistemas parciales). En contraste, los parámetros en
el vector β harán las veces de incógnitas en el sistema [A].
El supuesto clave es que existe un equilibrio de alguna clase en la economía
observada de manera que la primera tarea en el ciclo de modelaje no es hallar el
equilibrio sino utilizar el equilibrio observado para determinar parámetros
consistentes con esa observación (Shoven & Whalley, 1992).
Puesto que los datos de benchmark vienen en valores (p*q), es preciso escoger
unidades particulares para poder separar precios de cantidades. Una convención muy
popular, originalmente adoptada por A. Harberger (1959, 1962) consiste en escoger
unidades para bienes y factores tales que, en el equilibrio base, tengan un precio igual
a uno (1).
Una prominente característica de la calibración es que no hay pruebas de hipótesis
para verificar si la especificación del modelo es adecuada, justamente por el carácter
determinístico del procedimiento. (Crítica Econométrica)

5. Con la convención de Harberger, en modelos aplicados, las unidades físicas de los
factores son aquellas cantidades que reportan una unidad monetaria de retorno ($1) en
el equilibrio.
Las unidades para las mercancías se derivan, de manera similar, como aquellas
cantidades que se venden por $1, netas de impuestos y subsidios, en el equilibrio.
El supuesto de que en el equilibrio el producto marginal factorial es igual en todos los
usos posibles, permite que los pagos a los factores por industria puedan ser utilizados
como observaciones de las cantidades físicas de los inputs primarios.
Con datos SAM / MIP sobre usos de factores por industria y los supuestos previos, es
posible entonces calcular parámetros para las funciones de producción del modelo.

6. Ejemplo: Calibrando una Función de Producción CES en dos factores
Una función de producción de Elasticidad de Sustitución Constante puede ser escrita
de la siguiente forma:
(
Q = A αK + (1 − α )L
µ
)
µ 1/ µ
[E1.1.]
El producto marginal del capital está dado por:
PmgK = αA(α + ((1 − α )(L / K )µ ))
(1−µ ) / µ
Note además que, dado que de [E1.1.]
(Q / A)µ = αK µ + (1 − α )Lµ [E1.2.]
Se sigue que
PmgK = αAµQ1−µ K µ −1 [E1.3.]

7. Y por simetría, PmgL = (1 − α )AµQ1−µ Lµ −1 [E1.4.]
µ −1
De manera que PmgK α K
TMSTK ,L = =   [E1.5.]
PmgL 1 − α  L 
Las demandas por K,L, se derivan de la siguiente forma: Recuerde que el problema
de minimización del costo unitario es:
min C = k ⋅ Pk + l ⋅ Pl (
s.a. A αK + (1 − α )L
µ
)
µ 1/ µ
=1
Las CPO resultantes son, justamente:
µ −1
PmgK α K PK
=   = [E1.6.]
PmgL 1 − α  L  PL
(
A αK + (1 − α )L
µ
)
µ 1/ µ
=1 [E1.7.]

8. De la CPO [E1.6.], se tiene:
µ / (µ −1)
  1 − α µ / (µ −1)  P  
kµ =    K
P 

 ⋅lµ
 α   L  
 
Reemplazando en [E1.7.] y reordenando, se tiene, finalmente:
µ / (µ −1) µ / (µ −1)
1− α   PK 
α  
P 
 ⋅ l µ + (1 − α ) ⋅ l µ = A−µ [E1.8.]
 α   L 
Expresión que expresa en forma unívoca l y de la cual puede determinarse la demanda
de éste factor de producción, por unidad de producto.

9. En efecto,
(1 − α ) 1 / (1−µ ) 1 / ( µ−1 )
PL
l=
( )
[E1.9.]
A α1 / (1−µ ) PK / (µ −1) + (1 − α ) µ / (µ −1) 1 / µ
µ 1 / (1−µ )
P
L
y de manera similar
1 / ( µ−1 )
1 / (1−µ )
α PK
k=
( )
[E1.10.]
A α1 / (1−µ ) PK / (µ −1) + (1 − α ) µ / (µ −1) 1 / µ
µ 1 / (1− µ )
P
L
Siendo k, l requerimientos unitarios de factores.

10. Premisas para la calibración CES
La calibración de esta forma es de fácil implementación, a partir de la
base de datos del Benchmark. De la SAM (MIP) se obtienen valores para
los factores (k, l) y, en el caso de un modelo con impuestos, las tasas
implícitas de impuestos del benchmark asociadas a cada factor, se
calculan de los pagos efectivos en la submatriz impuestos.
Puesto que, por la convención de Harberger, PK = PL = 1, se dispone de
los precios (netos de impuestos) de equilibrio para los factores, en el año
base.

11. Considere dos posibles isocuantas en una formulación CES:
• En el punto A las dos isocuantas
presentan la misma pendiente (igual
K
a la relación de los precios de los
σ2 σ1 factores) en una relación que resulta
consistente con los precios de los
factores.
• Esto crea un problema de
calibración porque la función tiene
A tres (3) parámetros mientras que de
la SAM se tienen solo dos piezas de
información: las isocuantas pasan a
través de un punto específico con
pendiente específica y un nivel de
producción dados los inputs
L registrados. La respuesta estándar
consiste en tomar prestada la
elasticidad de sustitución, σ.

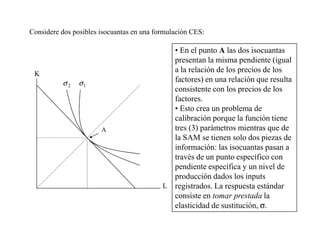
12. Tomando el valor de la elasticidad de sustitución de la literatura, aprovechando la
definición funcional de las demandas por factores [E1.9] y [E1.10.], y teniendo en
cuenta que el parámetro µ se relaciona con σ mediante la expresión:
σ=1/(1−µ)
tendremos:
l ⋅ PL =
(1 − α )σ PL− σ ⋅ PL =
(1 − α )σ PL−σ
A(α PK ) A(α PK )
σ 1 / (1− σ ) (σ −1) / σ σ 1 / (1− σ ) (σ −1) / σ
σ 1 / (1− σ )
+ (1 − α ) PL σ 1 / (1− σ )
+ (1 − α ) PL
α σ PK− σ α σ PK− σ
k ⋅ PK = ⋅ PK =
(
Aα P σ 1 / (1− σ )
K + (1 − α ) P
σ
L )
1 / (1− σ ) (σ −1) / σ
(
Aα P σ 1 / (1− σ )
K + (1 − α ) P
σ
L )
1 / (1− σ ) (σ −1) / σ

13. De manera que, si definimos,
k ⋅ PK α σ PK−σ
1
ωKL = =
l ⋅ PL (1 − α )σ PL −σ
1
Asumiendo la Convención de Harberger ( PK = PL = 1), se puede despejar α, sin
complicación:
α=
(ωKL )1 / σ
ˆ
1 + (ωKL )
1/ σ
El valor de A se deriva de las condiciones de beneficio cero que se suponen en un
modelo competitivo. Note que el costo de producir una unidad es:
C = k PK + l PL [E1.10.]
Reemplazando las demandas k, l tendremos:

14. (µ −1)
A
(
C = α1 / (1−µ ) PK / (µ −1) + (1 − α )
1 µ 1 / (1−µ ) µ / (µ −1)
PL ) µ [E1.11.]
Por lo tanto, haciendo uso del valor calibrado de α
( )
1
C = α + (1 − α )
1 σ σ
ˆ ˆ 1− σ =1
A
Resolviendo para A
( )
1
A = α + (1 − α )
σ σ 1− σ
ˆ ˆ ˆ

15. Ejemplo Numérico: SAM Bogotá (1994)
S MBogotá, 1994
A
C ponentes del V A
om alor gregado
Calibración de una F ión C Sen K L
unc E ,
AGROMIN SERVPUB BSCONSM BSKPTAL CONSTRC COMERCE SSPRIVS SSGOVRN
Remuneración a Asalariados FCTRAS 39.050 106.888 1,160.437 106.413 442.495 1,253.970 2,059.981 2,059.685
Excedente de Explotación FCTEBE 88.296 395.727 4,192.298 268.895 1,562.070 1,735.721 2,472.692 956.799
Consumo de Capital Fijo FCTCCF 1.020 27.341 87.077 9.263 67.509 64.549 180.885 24.135
Impuestos FCTTAX 3.079 -7.641 163.158 12.284 77.173 86.236 332.149 69.731
Calculado K 89.316 423.068 4,279.375 278.158 1,629.579 1,800.270 2,653.577 980.934
Calculado L 39.050 106.888 1,160.437 106.413 442.495 1,253.970 2,059.981 2,059.685
Calculado VA 128.366 529.956 5,439.812 384.571 2,072.074 3,054.240 4,713.558 3,040.619
Calculado k 0.696 0.798 0.787 0.723 0.786 0.589 0.563 0.323
Calculado l 0.304 0.202 0.213 0.277 0.214 0.411 0.437 0.677
Calculado w 2.287 3.958 3.688 2.614 3.683 1.436 1.288 0.476
Prestado σ 1.880 1.966 2.781 10.980 4.390 5.830 2.364 5.607
Calibrado µ 0.468 0.491 0.640 0.909 0.772 0.828 0.577 0.822
Calibrado δ 0.608 0.668 0.615 0.522 0.574 0.516 0.527 0.467
Calibrado A 1.915 1.800 1.866 1.980 1.913 1.994 1.993 1.976
Verificación VA^ 128.366 529.956 5,439.812 384.571 2,072.074 3,054.240 4,713.558 3,040.619
Cálculos: J
-segura@uniandes.edu.co

16. Lo mismo, con GAMS:
PARAMETER
k0(j) Capital - Agrega CCF & EBE
l0(j) Empleo -
va(j) Valor Agregado en L K en Benchmark
psi(j) Ratio k l unitario
mu(j) Exponente en CES
delta(j) Parámetro de Distribución en CES
A(j) Parámetro de Escala en CES
va_hat(j) Chequeo de la Calibración ;
k0(j) = F("FCTEBE",J) + F("FCTCCF",J) ;
l0(J) = F("FCTRAS",J) ;
va(j) = K0(j) + L0(j) ;
psi(j) = (k0(j)/va(j))/(l0(j)/va(j)) ;
mu(j) = -((1-esub(j))/esub(j)) ;
delta(j) = psi(j)**(1/esub(j)) / (1 + psi(j)**(1/esub(j))) ;
A(j) = (delta(j)**esub(j) + (1-delta(j))**esub(j))**(1/(1-esub(j))) ;
va_hat(j) = A(j)*(delta(j)*k0(j)**(mu(j)) + (1-delta(j))*l0(j)**(mu(j)))**(1/mu(j)) ;

17. ---- 166 PARAMETER report1 Datos y Resultado Calibración VA (CES)
sigma psi mu delta A VA VAhat
AGROMIN 1.8801 2.2872 0.4681 0.6083 1.9153 128.3660 128.3660
SERVPUB 1.9660 3.9580 0.4914 0.6681 1.7995 529.9561 529.9561
BSCONSM 2.7814 3.6877 0.6405 0.6152 1.8661 5439.8122 5439.8122
BSKPTAL 10.9797 2.6139 0.9089 0.5219 1.9799 384.5716 384.5716
CONSTRC 4.3897 3.6827 0.7722 0.5737 1.9130 2072.0742 2072.0742
COMERCE 5.8296 1.4357 0.8285 0.5155 1.9944 3054.2403 3054.2403
SSPRIVS 2.3636 1.2882 0.5769 0.5268 1.9933 4713.5576 4713.5576
SSGOVRN 5.6074 0.4763 0.8217 0.4670 1.9763 3040.6185 3040.6185

18. Ejemplo: Calibrando una Función de Utilidad CES en dos mercancías
Una función de utilidad CES para dos bienes se expresa:
(
u = αX 1(σ −1) / σ + (1 − α )X 2σ −1)/ σ
( )σ (σ
/ −1)
α ∈ [0,1] [E2.1.]
Los símbolos tienen el significado usual. El problema de la maximización de la utilidad:
max (
u = αX 1σ −1)/ σ + (1 − α )X 2σ −1)/ σ
( ( )
σ / (σ −1)
s.a. P X 1 + P2 X 2 ≤ M
1
Da las demandas ordinarias (i.e. de Marshall) por X1, X2:
M 
 α σ P11−σ 

X1 = [E2.2.]
P1  α σ P1−σ + (1 − α )σ P1−σ 
 1 2 
X2 =
M 
 (1 − α )σ P21−σ 
 [E2.3.]
P2  α σ P1−σ + (1 − α )σ P1−σ 
 1 2 

19. Participaciones presupuestales en CES
La participación de X1 en el presupuesto es:
X 1P  α σ P11−σ 
1
=  σ 1−σ  [E2.4.]
M α P
 1 + (1 − α )σ P2 −σ
1 

En tanto que la participación de X2 es:
X 2 P2  (1 − α )σ P21−σ
=  σ 1−σ

 [E2.5.]
M α P
 1 + (1 − α )σ P2 −σ
1 

A efectos de calibración, resulta útil la relación:
σ σ −1
P1 X 1 α σ P1σ −1  α  P 
= =   1
  [E2.6.]
P2 X 2 (1 − α ) P2
σ σ −1
 1 − α   P2 

20. Por su parte, la elasticidad-precio propio de la demanda por X1, está dada por:
∂X 1 ∂P  α σ P σ −1 + σ (1 − α )σ P2σ −1 
ξ= 1
= − σ 1 σ −1  [E2.7.]
X1 P 1
 α P
 1 + (1 − α ) P2
σ σ −1 

Note que este resultado sugiere que es posible obtener una estimación de la elasticidad
de sustitución, σ, a partir de alguna estimación de la elasticidad precio de la demanda,
si bien se trata de una función obviamente no lineal.

21. Al utilizar la convención de Harberger, la calibración del parámetro de distribución, -α-,
se logra a partir del mismo procedimiento utilizado en la CES de producción; en el caso
de la utilidad, no hay un parámetro de escala.
No obstante, como anotan Shoven y Whalley [1992], la convención de Harberger debe
ser utilizada con cautela cuando se observan distorsiones sobre los precios: impuestos,
tasas, multas. En estos casos, los precios iniciales son mayores que 1. En estos casos,
σ σ −1 σ
 α   P1 + τ X 1
σ σ −1 
PX α P1  α  σ −1
ω= 1 1 = =    =  θ
P2 X 2 (1 − α )σ P2σ −1  1 − α   P2 + τ X 2


  1−α 
De forma que el parámetro a calibrar es:
ω 1/ σ
α = 1/ σ
ˆ [E2.8.]
ω + θ (σ −1)/ σ