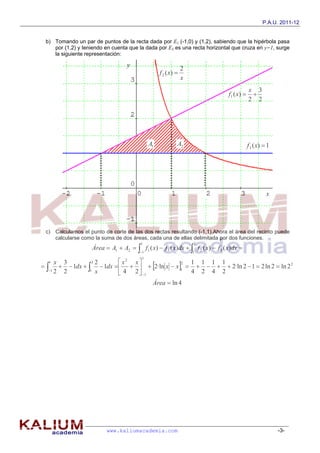
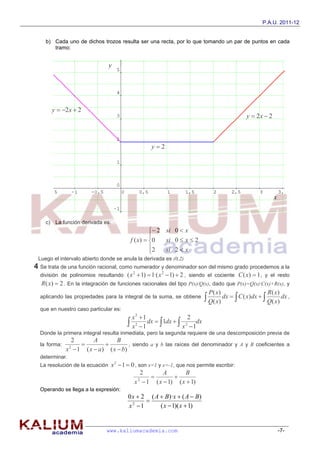
Este documento presenta la resolución de cuatro problemas de matemáticas. En el primer problema, se analiza la compatibilidad de un sistema de ecuaciones en función de un parámetro. En el segundo, se calculan dos vectores ortogonales dados. El tercer problema determina el mínimo de una función de dos variables. El cuarto encuentra los puntos de intersección de tres funciones y calcula el área de una región delimitada por ellas.

1. P.A.U. 2011-2012
MATEMÁTICAS II
Opciión A
Opc ón A
1 Para la discusión del sistema empleamos el teorema de Rouché-Fröbenius: sean las matrices de
coeficientes (A) y ampliada con los términos independientes (A*) asociadas al sistema de ecuaciones:
 1 1 2  1 1 2 a
   
A  1 1  a A*    1 1  a 1
 1 a 1 a  1 a 1  a  1
   
Procedemos al cálculo de los respectivos rangos en función del parámetro a, así igualando a cero del
determinante de A:
1 1 2
, A  1 1  a  a2  a  2  0; a1  1 ; a 2  2
1 a 1 a
Teniendo en cuenta que el rango (rg) de una matriz es el orden del mayor menor no nulo que puede
extraerse de ella, éste no puede superar el mínimo entre el número de filas y de columnas de la matriz
(3 en ambos) y que el rango de la matriz ampliada es mayor o igual al de la matriz de coeficientes por
contenerla, podemos extraer una primera conclusión:
 Si a  1 y a  2 , entonces rg(A)=rg(A*)=nº de incógnitas y el sistema es compatible determinado.
Cuando a=-1, las matrices quedan de la siguiente forma:
 1 1 2  1  1 2  1
   
A  1 1 1 A*    1 1 1 1
 1 1 0  1  1 0  1
   
1 2
Así el menor de orden 2 (extraido de A)  1  2  3 , revela que el rango de ésta es 2 y
1 1
como se observa, en la matriz ampliada la cuarta columna es proporcional a la primera y a la segunda,
por lo que no podrá extraerse ningún menor de orden tres no nulo, de lo que se concluye que:
 Si a  1 , entonces rg(A)=rg(A*)=2<nº de incógnitas y el sistema es compatible indeterminado.
Cuando a=2, las matrices son:
 1 1 2  1 1 2 2
   
A  1 1  2 A*    1 1  2 1
 1 2 3  1 2 3  1
   
1 1
Así el menor de orden 2 (extraido de A)  2  1  3 , revela que el rango de ésta es 2, y al
1 2
aplicar las transformaciones de Gauss sobre A*:
 1 1 2 2  1 1 2 2  1 1 2 2
     
A*    1 1  2 1 f 2  f1  0 0 0 3  0 3 1  3  se observa que su
 1 2 3  1 f 3  f 1  0 3 1  3 f 3  f 2  0 0 0 3
     
rango es 3, luego:
www.kaliumacademia.com -1-

2. MATEMÁTICAS II
 Si a  2 , entonces rg(A)=2≠rg(A*)=3 y el sistema es incompatible.
 
2 Del producto vectorial de dos vectores u y v , se extrae un vector
 
w1
ortogonal a ambos ( w ), por lo que bastaría con hacer dicha operación y
a continuación encontrar los vectores proporcionales a él con el módulo 
deseado, sin más que multiplicar sus coordenadas por el cociente de v
  
u
éste y del propio módulo. El problema tiene dos soluciones ( w1 y w2 )
 
que son los dos vectores de módulo 2 ortogonales a u y v y cuyos 
sentidos son opuestos entre si: w2
Realizamos el producto vectorial y determinamos su módulo:
  
i j k
     
w  u  v  1  1  1  i  k  1,0,1 ; w  12  0 2  11  2
1 2 1
Luego los vectores buscados se calculan:
 2   2 2    
wi   ·u  v    2
·u  v    2·u  v 
2 2
 
De esta forma obtenemos: w1  ( 2 ,0, 2 ) y w2  (  2 ,0, 2 ) .
3
a) El mínimo de una función puede calcularse aprovechando que la pendiente de la recta tangente
en él es nula (recta horizontal) y como el valor de ésta viene dado por el de la función derivada,
basta con encontrar los puntos que anulan a la primera derivada. El problema es que partimos de
una función de dos variables:
f ( x, y )  x  y
Pero como deben pertenecer a la parábola debe cumplirse que y  x , que al sustituir en la función
2
queda: f ( x)  x  x , cuya derivada es f ( x )  1  2 x . Igualando a cero resulta:
2
1  2 x  0 ; x   1 , de donde se concluye que en x=-1/2 existe un extremo que además se
2
comprueba que es un mínimo por ser la segunda derivada positiva ( f ( 1 / 2)  2 ). El valor de y se
obtiene sustituyendo el de x en la ecuación de la parábola: y  ( 1 / 2)  1 / 4 , luego el punto buscado
2
es:
 1 1
( x, y )    , 
 2 4
b) Al tratrarse de una función continua (como todas las polinómicas) y ser estrictamente decreciente
en el intervalo ( ,1 / 2) (la derivada es negativa para todo valor de x<-1/2) y estrictamente
creciente en el intervalo ( 1 / 2, ) (la derivada es positiva para todo valor de x>-1/2), la función
no alcanza ningún otro extremo y por tanto este mínimo es absoluto.
4
a) El cálculo de los puntos de corte de funciones pasa por resolver el sistema de ecuaciones que
forman, así:
 E1 : 2 y  x  3
  despejando x en E1: x  2 y  3 , y sustituyendo en E2: ( 2 y  3)·y  2 ;
 E 2 : x·y  2
2 y 2  3 y  2  0 , cuya soluciones son y=2 e y=-1/2, pero como sólo nos interesa el semiplano
derecho (x>0), resulta, que el punto buscado es ( x, y )  (1,2)
E3 : y  1
  , sustituyendo el resultado de E3 en E2, resulta x=2, luego el segundo punto es
 E 2 : x·y  2
( x, y )  (2,1)
www.kaliumacademia.com -2-

3. P.A.U. 2011-12
b) Tomando un par de puntos de la recta dada por E1 (-1,0) y (1,2), sabiendo que la hipérbola pasa
por (1,2) y teniendo en cuenta que la dada por E3 es una recta horizontal que cruza en y=1, surge
la siguiente representación:
y
2
f 2 ( x) 
x
x 3
f 1 ( x)  
2 2
A1 A2 f 3 ( x)  1
x
c) Calculamos el punto de corte de las dos rectas resultando (-1,1).Ahora el área del recinto puede
calcularse como la suma de dos áreas, cada una de ellas delimitada por dos funciones.
1 2
Área  A1  A2   f1 ( x)  f 3 ( x)dx   f 2 ( x)  f 3 ( x)dx 
1 1
1
 x2 x
  1dx    1dx      2·ln x  x 1      2·ln 2  1  2 ln 2  ln 2 2
1 x 3 2 2 1 1 1 1

2
1 2 2 1 x
 4 2  1 4 2 4 2
Área  ln 4
www.kaliumacademia.com -3-

5. P.A.U. 2011-2012
MATEMÁTICAS II
Opciión B
Opc ón B
1 Encontramos la matriz A realizando las operaciones indicadas:
 1 0 1  1 0 1 1 0 0  2 0 2  2 0 0
        
A  B  2·C  B·B  2·C   0  1 0 · 0  1 0   2· 1 1  1   0 1 0    2
2
2  2
 1 0 1  1 0 1
  
 0  1 1  2 0 2   0  2
     2

 0 0 2
 
A    2 1 2
 2 2 0
 
1
Para el cálculo de la matriz inversa utilizamos el resultado teórico A
1
  Adj ( A) t , así el
A
determinante de A:
0 0 2
 2 1
A   2  1 2  2·(1)13  4
2 2
2 2 0
Los adjuntos de cada elemento son:
1 2 2 2  2 1
adj11  (1)11  4 adj12  (1)1 2 4 adj13  (1)13  2
2 0 2 0 2 2
0 2 0 2 0 0
adj 21  (1) 21 4 adj 22  (1) 2 2  4 adj 23  (1) 23 0
2 0 2 0 2 2
0 2 0 2 0 0
adj31  (1) 31 2 adj32  (1) 3 2  4 adj33  (1) 3 3 0
1 2 2 2  2 1
t
 4 4  2
1 1  
Así: A  · 4  4 0  , cuyo resultado es:
4
 2 4 0
 1  1  1/ 2
 
A 1    1 1 1
1 / 2 0 0
 
www.kaliumacademia.com -5-

6. MATEMÁTICAS II
2 Para calcular la distancia del punto P a la recta r vamos a encontrar la proyección ortogonal de P sobre r
(P´), de manera que la distancia d P ,r  d P , P  PP  , para
ello:
Encontramos el plano   Ax  By  Cz  D  0 ,
perpendicular a r que pase por P, luego su vector normal

r
P
debe coincidir con el vector director de r

N  ( A, B, C )  (v1 , v 2 , v3 ) , a su vez compuesto por los
denominadores de la ecuación continua de r. Para encontrar
dicha ecuación asignamos x   en las ecuaciones d P, r
implícitas y surge:
x y 1 z

1

0

1
P
Luego nuestro plano adquiere la forma   x  z  D  0 ,
imponiendo que P verifique dicha ecuación: 3  2  D  0 ;
D=-1, con lo que el plano buscado es   x  z  1  0 .
El punto P´ es la intersección de r y de π, por lo que resolvemos el sistema de ecuaciones formado por
las respectivas ecuaciones aplicando la regla de Cramer:
1 1 1 1 1 1 1 1 1
0 0 1 1 0 1 1 0 0
x  y  z  1
 1 0 1 1 1 1 1 11 0 1
 xz 0 x  ; y  1 ; z  
 1 1 1 2 1 1 1 1 1 1 2
 x  z 1
1 0 1 1 0 1 1 0 1
1 0 1 1 0 1 1 0 1
1 1  5 5
Así el vector PP    ,1,   3,1,2    ,0, 
2 2  2 2
2 2
 5  5
Con lo que PP       0     , es decir:
2
 2  2
5 2
d P ,r 
2
3
a) Para expresar la f(x) como una función definida a trozos basta con conocer que un valor absoluto
no es más que su argumento cuado este es positivo y éste cambiado de signo cuando es
negativo por lo que resolviendo las correspondientes inecuaciones:
x0 x0

x20 x2
Resulta obvio que podemos definir la función en tres intervalos:
 x  ( x  2) si 0  x  2 x  2 si 0  x
 
f ( x)   x  ( x  2) si 0  x  2  f ( x )  2 si 0  x  2
 x  ( x  2) si 2  x 2 x  2 si 2  x
 
www.kaliumacademia.com -6-

7. P.A.U. 2011-12
b) Cada uno de dichos trozos resulta ser una recta, por lo que tomando un par de puntos en cada
tramo:
y
y  2 x  2
y  2x  2
y2
x
c) La función derivada es:
 2 si 0  x

f ( x)  0 si 0  x  2
2 si 2  x

Luego el intervalo abierto donde se anula la derivada es (0,2)
4 Se trata de una función racional, como numerador y denominador son del mismo grado procedemos a la
división de polinomios resultando ( x 2  1)  1·( x 2  1)  2 , siendo el cociente C ( x)  1 , y el resto
R ( x)  2 . En la integración de funciones racionales del tipo P(x)/Q(x), dado que P(x)=Q(x)·C(x)+R(x), y
P( x) R( x)
aplicando las propiedades para la integral de la suma, se obtiene  dx   C ( x)dx   dx ,
Q( x) Q( x)
que en nuestro caso particular es:
x2 1 2
 x 2  1 dx   1dx   x 2  1dx
Donde la primera integral resulta inmediata, pero la segunda requiere de una descomposición previa de
2 A B
la forma:   , siendo a y b las raíces del denominador y A y B coeficientes a
x  1 ( x  a ) ( x  b)
2
determinar.
La resolución de la ecuación x 2  1  0 , son x=1 y x=-1, que nos permite escribir:
2 A B
 
x  1 ( x  1) ( x  1)
2
Operando se llega a la expresión:
0 x  2 ( A  B)·x  ( A  B)

x2 1 ( x  1)( x  1)
www.kaliumacademia.com -7-

8. MATEMÁTICAS II
Eliminado los denominadores e igualando los coeficientes de los polinomios en los numeradores resulta
el sistema de ecuaciones:
A  B  0

A  B  2
Cuyas soluciones son A=1 y B=-1, con lo que nuestra integral queda:
x2 1 1 1 1 1
 x 2  1 dx   1dx   x  1  x  1dx   1dx   x  1 dx   x  1 dx
Resolviendo cada una de ellas resulta:
x2 1
 x 2  1 dx  x  ln x  1  ln x  1  C
Y simplificando:
x2 1 x 1
 x 2  1 dx  x  ln x  1  C
www.kaliumacademia.com -8-