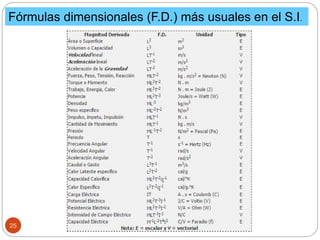
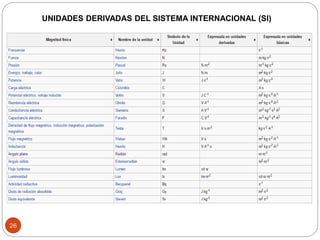
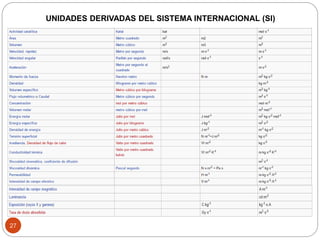
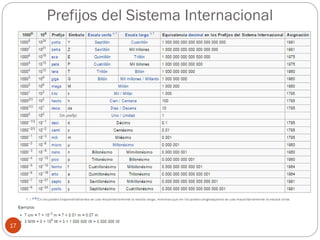
El documento presenta una introducción a la física impartida por el profesor Billy Solis. Explica brevemente qué es la física y sus objetivos, como observar el mundo a través del método científico y formular predicciones. Luego, introduce el análisis dimensional como el estudio de las relaciones entre magnitudes derivadas y fundamentales, sirviendo para comprobar fórmulas y deducir nuevas a partir de datos experimentales. Finalmente, presenta algunas magnitudes fundamentales y derivadas comúnmente usadas, así como ejemplos de aplicación del aná

1. FÍSICA
1
1°-2°-3° SECUNDARIA
Prof. Billy Solis

2. Antes de …
2
 Celulares apagados
 Lugar libre de distracciones.
 Lapiz, lapicero y papel.
 Preguntas al final
 Si no preguntan, preguntaré.
 Dudas adicionales, apoyo y consultas:
987832405

3. 3

4. ¿Qué es?
4
 Estudio del mundo y del universo.
 Aventura humana.
 Observar al mundo (método científico).
 Formular predicciones.
 Física clásica.
 Física moderna

5. Para que sirve?
5

6. Para qué sirve?
6

7. 7
Y como antes de correr uno debe de gatear,
caerse, caminar, caerse y correr… para seguir
cayéndose

8. ANALISIS DIMENSIONAL
8

9. Qué es?
Estudio de la relación entre las
magnitudes derivadas y las
fundamentales.
9

10. Expresar las relaciones entre las magnitudes
derivadas en términos de las fundamentales.
Sirven para comprobar la veracidad o falsedad
de las fórmulas físicas, haciendo uso del
principio de homogeneidad dimensional.
Sirven para deducir nuevas fórmulas a partir
de datos experimentales. (Fórmulas
Empíricas).
Objetivos del análisis dimensional
10

11. Medir = comparar
Unidad de medida = patrón de comparación
Magnitudes y unidades
11

12. CLASIFICACIÓN DE LAS
MAGNITUDES
POR SU
ORIGEN
POR SU
NATURALEZA
M. FUNDAMENTALES
M. DERIVADAS
M. ESCALARES
M. VECTORIALES
12

13. Magnitudes Fundamentales
13

14. donde a, b, c, d, e, f, g, se conocen como dimensiones
Ejemplo: área, Volumen, velocidad, aceleración, fuerza,
trabajo, energía, calor, etc.
Magnitudes derivadas
14

15. Magnitudes escalares
Valor
Unidad de medida
Ejemplo: área, volumen, longitud, tiempo,
trabajo, energía, calor, etc.
15

16. Magnitudes vectoriales
Valor numérico
Unidad de medidad
Dirección
Sentido
Ejemplo: Velocidad, aceleración, fuerza,
gravedad, etc.
16

17. Prefijos del Sistema Internacional
17

18. Ecuaciones dimensionales
Magnitudes derivadas = f (fundamentales)
Álgebra elemental (menos suma y resta)
18

19. Notación
A: magnitud "A"
[A]: ecuación dimensional de "A".
“Los corchetes se usan para
indicar dimensiones”
19

20. Propiedades de las
ecuaciones dimensionales
Cada término de una ecuación dimensional, serán iguales
dimensionalmente.
1. Principio de Homogeneidad Dimensional o Principio
de Fourier (P.H.).
20

21. Ejemplo:
En la siguiente ecuación: , luego de aplicar el principio de
homogeneidad dimensional nos debe quedar de la siguiente forma:
21

22. 2. Términos Adimensionales
Números
Ángulos
Logaritmos
Constantes numéricas
Funciones trigonométricas…
…valen 1
22

23. 3. No se cumplen la suma y la resta algebraica.
EJEMPLOS:
23

24. 4. Todas las ecuaciones dimensionales
deben expresarse como productos y nunca
dejarse como cocientes
EJEMPLOS:
El término:
Deberá expresarse como:
24

25. Fórmulas dimensionales (F.D.) más usuales en el S.I.
25

26. 26
UNIDADES DERIVADAS DEL SISTEMA INTERNACIONAL (SI)

27. 27
UNIDADES DERIVADAS DEL SISTEMA INTERNACIONAL (SI)

28. Obtención de Magnitudes
físicas dimensionales
28

29. 29
a) Ecuación dimensional para el Área:
b) Ecuación dimensional para el Volumen:
c) Ecuación dimensional para la velocidad:

30. 30
d) Ecuación dimensional para la aceleración:
e) Ecuación dimensional para la fuerza:
f) Ecuación dimensional para el trabajo:
   
 
2
2




 LT
T
L
T
T
L
t
v
a

31. 31
Ejemplo:
Sabemos que las dimensiones para la fuerza
son: M, L y T-2 lo cual indica que para M
utilizaremos el kilogramo (kg), para L el metro (m)
y para T el segundo si el sistema es el SI.

32. 32
a) Ecuación adimensional para la densidad
relativa:
Obtención de Magnitudes
físicas Adimensionales

33. 33
Problema:
Demostrar que la fórmula
es dimensionalmente válida

34. 34
Solución
Sustituyendo las magnitudes físicas por sus
dimensiones tenemos que:
Dimensionalmente la fórmula es correcta, ya que se
cumplen los principios:
L
L
T
T
L
T
T
L
L 


 2
2