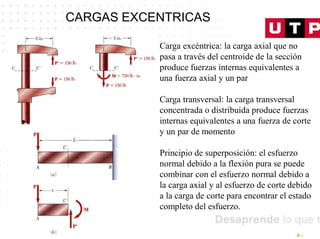
Este documento trata sobre la flexión de elementos estructurales. Explica conceptos como flexión pura, deformaciones debido a la flexión, tensiones causadas por la flexión y casos de carga axial excéntrica. También incluye ejemplos numéricos que ilustran cómo calcular tensiones máximas, la ubicación del eje neutro y cargas críticas para elementos sometidos a flexión.

1. FLEXIÓN-2
SESION
Dr. Ing. Jony Lazo Ramos

2. CONTENIDO
 Flexión pura
 Otros tipos de carga
 Elemento simétrico en flexión pura
 Deformaciones de flexión
 Deformaciones en una sección transversal
 Tensión debido a la flexión
 Ejemplos
 Caso general de carga axial excéntrica
 Ejemplos

3. Flexión pura
4 - 3
Una viga es un elemento que se somete a cargas transversales al eje
longitudinal. Si aplicamos la carga F en el plano de simetría y
perpendicular al eje x entonces se produce la flexión pura
- La viga tiene un plano de simetría
axial, que consideramos que es el
plano xy

4. 4 - 4
El par M consta de dos cargas
iguales y opuestas. M y M´ que
actúan en el mismo plano
longitudinal.
Se observa que si se efectúa un corte a través
del elemento AB en algún punto arbitrario C,
las condiciones de equilibrio de la porción AC
del elemento requieren que las fuerzas
internas en la sección sean equivalentes al par
M

5. Deformación de un elemento simétrico en
flexión pura
4 - 5
Viga con un plano de simetría en flexión pura:
 El elemento permanece simétrico, se dobla
uniformemente para formar un arco circular
 La sección transversal pasa por el centro del
arco y permanece plano
 La longitud de la parte superior disminuye
y la longitud de la parte inferior aumenta y
existe una superficie neutral que es paralela
a las superficies superior e inferior y en el
cual la longitud no cambia
 Las tensiones y las deformaciones son
negativas (de compresión) por encima del
plano neutral y positivas (tensión de
tracción) por debajo

6. Deformación debido a la flexión
4 - 6
La deformación unitaria longitudinal normal x varía linealmente con la
distancia y desde la superficie neutral.

7. • Para un material en el rango elástico,
• Formula para el momento de flexión,
4 - 7
• Para el máximo momento de flexión,
La razón I/c depende sólo de la geometría de la
sección transversal. Esta relación se denomina
módulo elástico de la sección y se representa
por S.

8. Entonces la deformación debida al momento flector M se
cuantificara por la curvatura de la superficie neutral

9. La expansión por encima de la
superficie neutra y la contracción por
debajo causan una curvatura en el
plano,
Deformación en la sección transversal
Aunque los planos de sección transversal
permanecen planos cuando se someten a
momentos de flexión, las deformaciones
en el plano son distintas de cero

10. CARGAS EXCENTRICAS
4 -
Carga excéntrica: la carga axial que no
pasa a través del centroide de la sección
produce fuerzas internas equivalentes a
una fuerza axial y un par
Carga transversal: la carga transversal
concentrada o distribuida produce fuerzas
internas equivalentes a una fuerza de corte
y un par de momento
Principio de superposición: el esfuerzo
normal debido a la flexión pura se puede
combinar con el esfuerzo normal debido a
la carga axial y al esfuerzo de corte debido
a la carga de corte para encontrar el estado
completo del esfuerzo.

11. Carga axial excéntrica en un plano de simetría
A I
x  x centrica  x flexion
 P  M y
Carga excéntrica
F  P M Pd
4 - 11
Las fuerzas internas que actúan en una sección
transversal dada pueden representarse por la fuerza
F aplicada en el centroide C de la sección y a un par
M que actúa en el plano de simetría del elemento
Las condiciones de
equilibrio del cuerpo
libre AC requieren que
la fuerza F sea igual y
opuesta a P’ y que el
momento del par M sea
igual y opuesto al
momento de P’ con
respecto a C.
La distribución de esfuerzos debida a la carga excéntrica original puede obtenerse superponiendo la
distribución uniforme del esfuerzo correspondiente a las cargas céntricas P y P’ y la distribución lineal
correspondiente a los pares flectores M y M’

12. Ejemplo
4 - 12
• Superponga la tensión uniforme debido
a la carga céntrica y la tensión lineal
debido al momento flector.
• Evalúe las tensiones máximas de
tracción y compresión en los bordes
interno y externo, respectivamente, de
la distribución de tensiones
superpuestas.
• Encuentre el eje neutral determinando
la ubicación donde el esfuerzo normal
es cero.
Se obtiene un eslabón de cadena abierto de acero con bajo contenido de carbono en la
forma que se muestra. Para una carga de 160 lb, determine (a) tensiones máximas de
tracción y compresión, (b) distancia entre el centroide de la sección y el eje neutro
SOLUCIÓN:
Encuentre la fuerza céntral y el momento
flector

14. Carga céntrica y
momento flector
P  160lb
M  Pd  160lb0.6in
104lbin
4 - 14

15. t  0 m
 8158475
c  0 m
 8158475
 t  9290psi
 c  7660psi
• Ubicación del eje neutral
815psi
4 - 15
105lbin
3.068103in4
A M
 P I  
y0
0  P  M y0
A I
y0  0.0240in
Máximas tensiones de tracción y
compresión.

16. Ejemplo
• Evaluar las cargas críticas para los esfuerzos de
tensión y compresión permitidos.
• La carga máxima permitida es la menor de las dos
cargas críticas.
Datos iniciales,
A  3103m2
Y  0.038m
I  868109 m4
4 - 16
Los mayores esfuerzos permitidos para el gancho de hierro fundido son 30
MPa en tensión y 120 MPa en compresión. Determine la máxima fuerza P que
se puede aplicar al gancho.
SOLUCIÓN:
Determine una carga céntrica equivalente y un
momento flector.
Superponga el esfuerzo debido a la carga céntrica y
al esfuerzo debido a la flexión.

17. • Evaluar cargas críticas para tensiones admisibles.
P  79.6kN
P  76.9kN
 A  377 P  30MPa
 B  1559 P  120MPa
P  77.0 kN
• Determinamos cargas centradas y de flexión equivalentes
d  0.038 0.010  0.028m
P centric load
M  Pd  0.028 P  bendingmoment
4 - 17
• Superponiendo tensiones debido a cargas céntricas y de
flexión
La máxima carga permitida