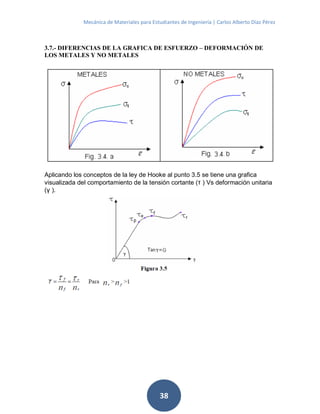
Este documento resume los conceptos básicos de la mecánica de materiales para estudiantes de ingeniería. Está dividido en 8 capítulos que cubren temas como carga axial, tracción y compresión, propiedades mecánicas de materiales, ensayos de materiales, torsión, flexión y vigas. El primer capítulo introduce los conceptos de tensión, tracción, compresión y diagrama de esfuerzo-deformación. También describe los procedimientos de ensayos de tracción y compresión para materiales dúctiles y frá











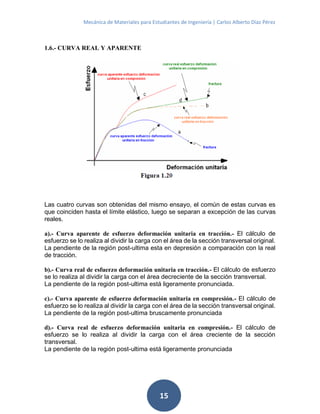






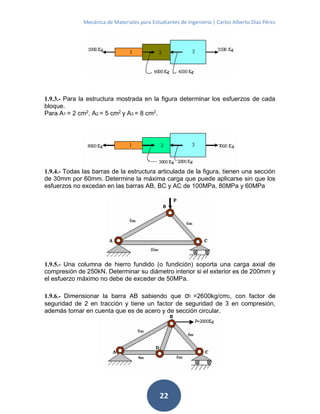
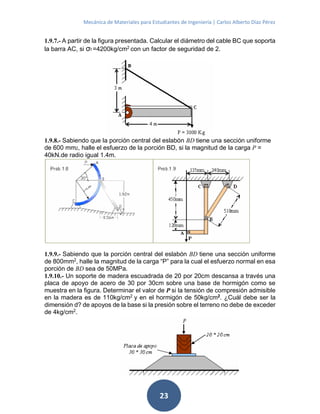






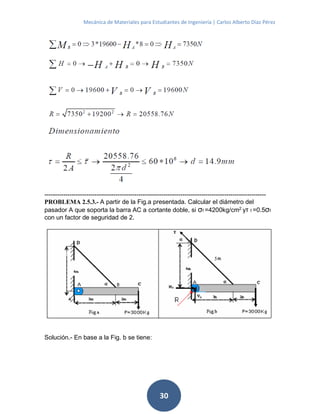
















































![Mecánica de Materiales para Estudiantes de Ingeniería | Carlos Alberto Díaz Pérez
92
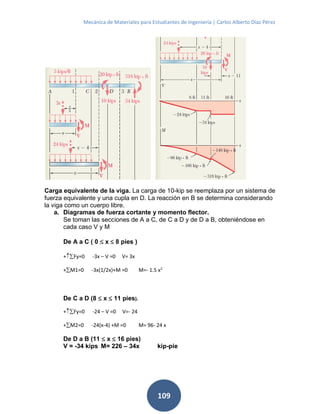
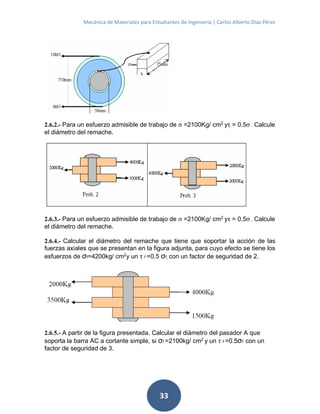
4.9 PROBLEMAS PROPUESTOS
4.9.1. Hallar el diámetro de una pieza cilíndrica de Acero con un largo de 100 cm
para que pueda soportar un momento de 1000 Kg cm. Tomar Sy´= 960 Kg/cm2
, y
fs = 2.
Hallar además la deformación.
4.9.2. Un tambor de una máquina de elevación tiene un diámetro de 30 cm y se
encuentra montado sobre un eje con un diámetro de 3 cm con Sy`= 900 Kg/cm2
.
Se pide hallar el peso máximo que puede levantar.
4.9.3. Un eje gira a 120 rpm y esta acoplado a un motor de 9 Hp por medio de una
transmisión. Si el material tiene una fluencia de S`y = 900 Kg/cm2
. Para fs = 2 se
pide calcular el diámetro del eje.
4.9.4. Hallar el ángulo de torsión del extremo libre respecto al extremo fijo del
sistema de la figura. El material es acero y las dimensiones están en cm.
]
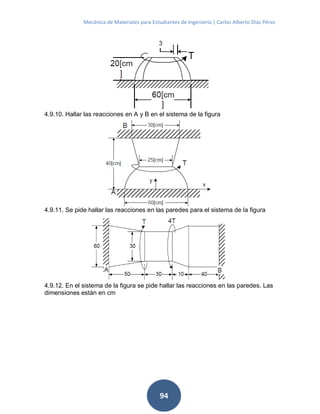
4.9.5. La pieza de la figura tiene forma cónica truncada. Se pide hallar la
deformada total y el esfuerzo máximo](https://image.slidesharecdn.com/mecanicadematerialesunprg-200802141545/85/Mecanica-de-materiales-unprg-93-320.jpg)