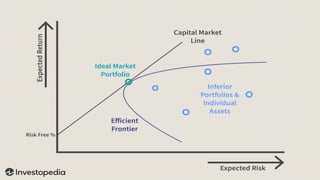
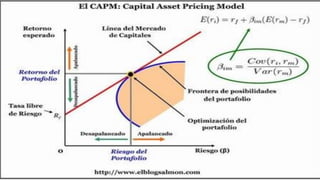
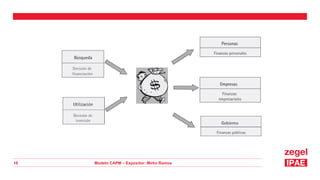
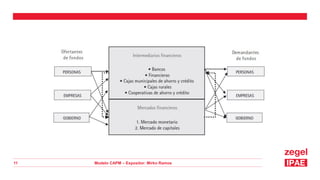
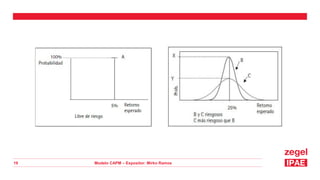
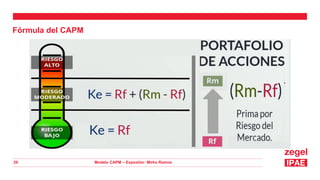
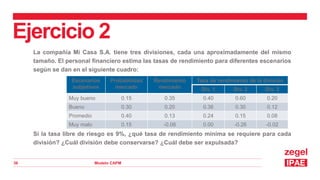
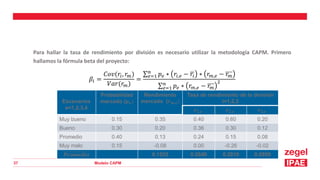
Este documento presenta una introducción al Modelo CAPM (Capital Asset Pricing Model). Explica los supuestos del modelo y define su fórmula central, la cual relaciona el rendimiento esperado de un activo con el riesgo libre, el rendimiento del mercado y el riesgo sistemático del activo medido por su beta. Luego presenta ejemplos numéricos para calcular las tasas de rendimiento esperadas usando el modelo CAPM. Finalmente, muestra cómo aplicar el modelo para tomar decisiones de inversión evaluando diferentes divisiones de una empresa.

1. 25/05/2023 1

2. Finanzas II
CAPM
Administración de Empresas

3. Modelo CAPM – Expositor: Mirko Ramos
3
Indicador de logro
Identifica los distintos riesgos asociados a un proyecto y cómo
afectan a los costos de capital.

4. Colocar aquí la imagen a tamaño completo.

5. Colocar aquí la imagen a tamaño completo.

6. Colocar aquí la imagen a tamaño completo.

7. NINGUNO ES DIGNO

8. 8 Modelo CAPM – Expositor: Mirko Ramos
• Introducción
• Definición del modelo CAPM
• Ejemplos
• Actividad en clase
• Actividad virtual
Contenido temático

9. Modelo CAPM – Expositor: Mirko Ramos
9
INTRODUCCION

10. Modelo CAPM – Expositor: Mirko Ramos
10

11. Modelo CAPM – Expositor: Mirko Ramos
11

12. Modelo CAPM – Expositor: Mirko Ramos
12
Paratomardecisiones… Quéeslomásimportante?

13. Modelo CAPM – Expositor: Mirko Ramos
13
DESTINO: CUZCO
DESTINO: ANGUIA (*)
 1,310 KM
 32 HORAS
SENTADO
 SE DETIENE
EN CADA
PUEBLO
DATO ADICIONAL: EN ANGUIA VIVE TU MAMÁ Y ESTÁ MUY GRAVE
(*) INEI 2018, UNO DE LOS TRES DISTRITOS MAS POBRES DEL PERU

14. Modelo CAPM – Expositor: Mirko Ramos
14
Paratomardecisiones… Quéeslomásimportante?
Dependerá de a dónde queremos ir
Por lo tanto, lo más importante para tomar decisiones son los
OBJETIVOS que uno tenga. Y si hablamos de las decisiones que
toman las empresas, lo más importante son los OBJETIVOS de la
empresa.

15. Modelo CAPM – Expositor: Mirko Ramos
15
La rentabilidad para los accionistas
debe ser el único objetivo?

16. Modelo CAPM
16
¿Qué pasaría si las condiciones económicas bajo las cuales una inversión
es declarada rentable, cambian drásticamente con el tiempo?
¡La rentabilidad pronosticada también variará!

17. Modelo CAPM
17
Por ello ahora consideraremos la selección de un proyecto no sólo
sobre la base del criterio del VAN o la TIR, sino tomando en cuenta
un elemento nuevo asociado al proyecto: el riesgo.

18. Modelo CAPM – Expositor: Mirko Ramos
18
PELIGRO OPORTUNIDAD
RIESGO

19. Modelo CAPM – Expositor: Mirko Ramos
19

20. Modelo CAPM
20
• Para calcular el rendimiento de un proyecto de inversión
SIN CONSIDERAR EL RIESGO, utilizábamos una tasa de
descuento(%) a la que no se consideraba el factor riesgo.
• Ahora, para un proyecto de inversión CONSIDERANDO EL
RIESGO, utilizaremos una tasa de descuento(%) a la que
se le incorporará el factor riesgo.
Entonces….

21. 21
Construcción
Modelo CAPM

22. Modelo CAPM – Expositor: Mirko Ramos
22
CAPM - SUPUESTOS
 Los inversionistas son “tomadores de préstamos” en el sentido de que todos ellos son pequeños y
sus transacciones individuales no afectarán el precio del mercado. (en Economía esto equivale a
un escenario de “competencia perfecta”)
 Se considera un solo periodo de tenencia, lo cual proporciona al modelo una visión de corto plazo
 Las posibilidades de inversión se limitan a los activos financieros transados públicamente
 Es posible prestar y pedir prestado a la tasa libre de riesgo
 Ausencia de impuestos y costos de transacción
 Todos los inversionistas son racionales optimizadores de la relación media-varianza. Es decir, todos
utilizan el modelo de selección de portafolios de Markowitz
 Existen expectativas homogéneas. Es decir, todos los inversionistas comparten la información y la
analizan de la misma manera.

23. Modelo CAPM – Expositor: Mirko Ramos
23
CAPM

24. Modelo CAPM – Expositor: Mirko Ramos
24
CAPM

25. Modelo CAPM – Expositor: Mirko Ramos
25
Fórmula del CAPM
Ke =

26. Modelo CAPM – Expositor: Mirko Ramos
26
Fórmula del CAPM

27. Modelo CAPM – Expositor: Mirko Ramos
27
Fórmula del CAPM

28. Modelo CAPM – Expositor: Mirko Ramos
28
Tasa libre de riesgo

29. Modelo CAPM – Expositor: Mirko Ramos
29
Rendimiento del mercado

30. Modelo CAPM – Expositor: Mirko Ramos
30
Prima por riesgo del mercado

31. Modelo CAPM – Expositor: Mirko Ramos
31
Beta apalancada (Beta)

32. Modelo CAPM
32
Cálculo del CAPM

33. Modelo CAPM
33
Beta apalancada

34. Modelo CAPM
34
El capital social de Aardvark Enterprises tiene una beta de 1.5 y el de Zebra
Enterprises tiene una beta de 0.7. La tasa sin riesgo es del 7% y la diferencia entre la
rentabilidad esperada del mercado y la tasa sin riesgo es del 8.5%. ¿Cuáles son las
rentabilidades esperadas de cada uno de los dos títulos? ¿Cuál es la rentabilidad
esperada de la cartera?
Ejercicio 1

35. Modelo CAPM
35
Solución:
Rentabilidad esperada de Aardvark:
19.75% = 7% + 1.5 x 8.5%
Rentabilidad esperada de Zebra:
12.95% = 7% + 0.7 x 8.5%
Rentabilidad esperada de la cartera (se asume inversión equitativa en dos
títulos): 16.35% = 0.5 x 19.75% + 0.5 x 12.95%

36. Modelo CAPM
36
Ejercicio 2
La compañía Mi Casa S.A. tiene tres divisiones, cada una aproximadamente del mismo
tamaño. El personal financiero estima las tasas de rendimiento para diferentes escenarios
según se dan en el siguiente cuadro:
Si la tasa libre de riesgo es 9%, ¿qué tasa de rendimiento mínima se requiere para cada
división? ¿Cuál división debe conservarse? ¿Cuál debe ser expulsada?
Escenarios
subjetivos
Probabilidad
mercado
Rendimiento
mercado
Tasa de rendimiento de la división
Div. 1 Div. 2 Div. 3
Muy bueno 0.15 0.35 0.40 0.60 0.20
Bueno 0.30 0.20 0.36 0.30 0.12
Promedio 0.40 0.13 0.24 0.15 0.08
Muy malo 0.15 -0.08 0.00 -0.26 -0.02

37. Modelo CAPM
37
Para hallar la tasa de rendimiento por división es necesario utilizar la metodología CAPM. Primero
hallamos la fórmula beta del proyecto:
𝛽𝑖 =
𝐶𝑜𝑣(𝑟𝑖, 𝑟𝑚)
𝑉𝑎𝑟(𝑟𝑚)
=
σ𝑒=1
𝑛
𝑝𝑒 ∗ 𝑟𝑖,𝑒 − ഥ
𝑟𝑖 ∗ 𝑟𝑚,𝑒 − 𝑟𝑚
σ𝑒=1
𝑛
𝑝𝑒 ∗ 𝑟𝑚,𝑒 − 𝑟𝑚
2
Escenarios
e=1,2,3,4
Probabilidad
mercado (𝒑𝒆)
Rendimiento
mercado (𝒓𝒎,𝒆)
Tasa de rendimiento de la división
i=1,2,3
𝒓𝟏,𝒆 𝒓𝟐,𝒆 𝒓𝟑,𝒆
Muy bueno 0.15 0.35 0.40 0.60 0.20
Bueno 0.30 0.20 0.36 0.30 0.12
Promedio 0.40 0.13 0.24 0.15 0.08
Muy malo 0.15 -0.08 0.00 -0.26 -0.02
𝑷𝒓𝒐𝒎𝒆𝒅𝒊𝒐 0.1525 0.2640 0.2010 0.0950

38. Modelo CAPM
38
• 𝛽𝑖 =
𝐶𝑜𝑣(𝑟𝑖,𝑟𝑚)
𝑉𝑎𝑟(𝑟𝑚)
=
σ𝑒=1
𝑛 𝑝𝑒∗ 𝑟𝑖,𝑒− ഥ
𝑟𝑖 ∗ 𝑟𝑚,𝑒−𝑟𝑚
σ𝑒=1
𝑛 𝑝𝑒∗ 𝑟𝑚,𝑒−𝑟𝑚
2
• Se calcula cada uno de los componentes de la fórmula beta.
• Empezamos con el denominador (la varianza):
Escenarios
e=1,2,3,4
𝒑𝒆 𝑽𝒆=(𝒓𝒎,𝒆−𝒓𝒎) 𝟐
e=1,2,3,4
Muy bueno 0.15 0.0390
Bueno 0.30 0.0023
Promedio 0.40 0.0005
Muy malo 0.15 0.0541
෍
𝒆=𝟏
𝟒
𝒑𝒆 ∗ 𝑽𝒆 0.014839 = 1.4839%

39. Modelo CAPM
39
• 𝛽𝑖 =
𝐶𝑜𝑣(𝑟𝑖,𝑟𝑚)
𝑉𝑎𝑟(𝑟𝑚)
=
σ𝑒=1
𝑛 𝑝𝑒∗ 𝑟𝑖,𝑒− ഥ
𝑟𝑖 ∗ 𝑟𝑚,𝑒−𝑟𝑚
σ𝑒=1
𝑛 𝑝𝑒∗ 𝑟𝑚,𝑒−𝑟𝑚
2
• Seguimos con el cálculo del numerador de beta:
Escenarios
e=1,2,3,4
𝒑𝒆
𝑾𝟏,𝒆= 𝒓𝟏,𝒆 − 𝒓𝟏 ∗ 𝒓𝒎,𝒆 − 𝒓𝒎
e=1,2,3,4
𝑾𝟐,𝒆= 𝒓𝟐,𝒆 − 𝒓𝟐 ∗ 𝒓𝒎,𝒆 − 𝒓𝒎
e=1,2,3,4
𝑾𝟑,𝒆= 𝒓𝟑,𝒆 − 𝒓𝟑 ∗ 𝒓𝒎,𝒆 − 𝒓𝒎
e=1,2,3,4
Muy bueno 0.15 0.0269 0.0788 0.0207
Bueno 0.30 0.0046 0.0047 0.0012
Promedio 0.40 0.0005 0.0011 0.0003
Muy malo 0.15 0.0614 0.1072 0.0267
෍
𝒆=𝟏
𝟒
𝒑𝒆 ∗ 𝑾𝒋,𝒆
0.014820 = 1.4820% 0.0298 = 2.98% 0.0076 = 0.76%

40. Modelo CAPM
40
Para tomar la decisión de cuál división debe conservarse, se compara el rendimiento mínimo que debe
ser exigido por los accionistas (según el modelo CAPM) con el rendimiento esperado (promedio).
Según el cuadro, las divisiones 2 y 3 deben ser eliminadas, porque su rendimiento promedio es más bajo
que el rendimiento exigido por el modelo CAPM. Sólo se conservaría la división 1 porque es el único que
cumple con el rendimiento exigido.
Rendimiento exigido Rendimiento promedio
División 1 15.24% 26.40%
División 2 21.54% 20.10%
División 3 12.21% 9.50%

41. Modelo CAPM – Expositor: Mirko
Ramos
41