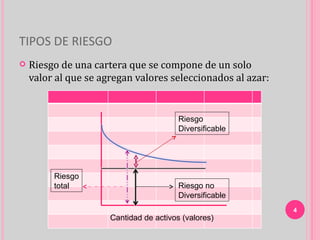
El documento presenta el Modelo de Valoración de Activos de Capital (CAPM) para determinar el rendimiento requerido de un activo. El CAPM relaciona el riesgo no diversificable de un activo con su rendimiento esperado. El riesgo se mide a través del coeficiente Beta, el cual indica la volatilidad de un activo en comparación con el mercado. El CAPM establece que el rendimiento esperado de un activo es igual a la tasa libre de riesgo más el coeficiente Beta multiplicado por la prima de riesgo del mercado.

1. MODELO DE VALUACIÓN DE ACTIVOS
DE CAPITAL.
1

2. CAPITAL ASSET PRICING MODEL (CAPM)
 Incertidumbre:
 Posibilidad
de obtener un
rendimiento menor o mayor al
rendimiento presupuestado.
 Pretendemos mayor rentabilidad a
mayor riesgo.
2

3. TIPOS DE RIESGO
 Riesgototal = Riesgo diversificable +
Riesgo no diversificable
 Riesgo diversificable: Acontecimiento
específico de la empresa (nuevos
productos de la competencia, capacidad
gerencial, etc.).
 Riesgo no diversificable: Factores de
mercado que afectan a todas la
empresas (guerras, inflación, etc.) 3

4. TIPOS DE RIESGO
 Riesgo de una cartera que se compone de un solo
valor al que se agregan valores seleccionados al azar:
Riesgo
Diversificable
Riesgo
total Riesgo no
Diversificable
4
Cantidad de activos (valores)

5. CAPITAL ASSET PRICING MODEL
CAPM
 El modelo CAPM es utilizado para determinar
teóricamente el retorno requerido sobre un activo.
 El modelo relaciona el riesgo no diversificable y el
rendimiento de todos los activos.
The CAPM is a model for pricing and individual security
or a portfolio:
rA = rf + β ( rm - rf )
5

6. CAPITAL ASSET PRICING MODEL
CAPM
 El modelo se soporta en la idea que la compensación
que buscan los inversores debe tener en cuenta:
 El valor del dinero en el tiempo.
 El riesgo que asumen.
rf = time value of the money
Risk = β A ( rm - rf )
Market premium = ( rm - rf )
6

7. CAPITAL ASSET PRICING MODEL
BETA
 El coeficiente Beta es una medida relativa del riesgo
no diversificable.
 Es una medida de la volatilidad de una acción o de un
portafolio en comparación con el mercado en su
totalidad.
 Beta es un coeficiente que expresa la comparación
entre el retorno de un activo y el retorno del mercado
durante un período de tiempo.
 Beta ajusta la prima por riesgo de mercado (rm – rf ).
7

8. CAPITAL ASSET PRICING MODEL
BETA
Los rendimientos históricos o futuros (pronosticados) de un
activo se usan pra calcular el coeficiente Beta.
30
25
Rendimiento
del activo 20 Pendiente 1,30
15
10
5
1
Pendiente 0,80
-20 -15 -10 -5 0 5 10 15 20 25 30
Rendimiento de mercado
5
10
15 8
20
25

9. CAPITAL ASSET PRICING MODEL
BETA
 La pendiente de cada línea es la Beta.
 La Beta de la línea azul es 0,80.
 La Beta de la línea naranja es 1,30:
 Esta Beta indica que la línea naranja es más sensible a los
cambios de mercado.
 La incertidumbre es mayor.
 Es más volatil.
 El inversionista requiere mayor rendimiento.
9

10. CAPITAL ASSET PRICING MODEL
BETA
 La Beta del mercado es igual a uno.
 Las Betas pueden ser positivas o
negativas.
 La norma es que sean positivas.
 La mayoría de los coeficientes Beta está
entre 0,5 y 2,0.
10

11. CAPITAL ASSET PRICING MODEL
BETA
 Si Beta es 0,5 se espera que el
rendimiento de la acción cambie 0,5%
por cada cambio de 1% del mercado.
 Si una empresa tiene una Beta de 2, se
espera que el rendimiento cambie el 2%
por cada cambio del 1% del
rendimiento del mercado en su
conjunto.
 Para llegar al rendimiento total debe
11
sumarse la rentabilidad libre de riesgo.

12. CAPITAL ASSET PRICING MODEL
LIMITACIONES
 El
CAPM sostiene que el rendimiento de
una acción se relaciona positivamente
con su rendimiento.
 Un estudio determinó para el período
1963 – 1990 que no había relación entre
la beta y el rendimiento de las acciones
(Fama y French). 12

13. CAPITAL ASSET PRICING MODEL
LIMITACIONES
 Poco después otro estudio determinó
que se cumplía la relación positiva entre
beta y rendimiento, según el período
considerado (Chan y Lakonishok).
 En los peores meses se determinó que
las acciones con altas betas tuvieron un
desempeño peor que las otras.
 En los buenos tiempos las acciones con
betas altas tuvieron mejor desempeño 13
que las acciones con betas bajas.

14. CAPITAL ASSET PRICING MODEL
LA ECUACIÓN
rA = r f + β (r m - r f )
 r A : Rentabilidad del Activo.
 r f : Rentabilidad libre de riesgo.
 r m : Rentabilidad del mercado.
 β : Coeficiente de riesgo no diversificable.
 En el paréntisis se mide la tasa de riesgo del mercado.
 r f : Por lo general se toma una letra del Tesoro de los
EE.UU. (T-bill) a tres meses, de reciente emisión.
 Se pueden usar datos históricos de 30 años para
determinar la tasa de mercado, en función de los 14
escenarios que se consideren.

15. CAPITAL ASSET PRICING MODEL
EJERCITACIÓN
 Está en consideración un proyecto con una β de 1,50.
 rf es del 7% y rm del 10%. Se espera que el
rendimiento anual sea del 11%:
l Si rm se incrementara 10%, ¿cuál sería el rendimiento
requerido del proyecto? ¿Qué pasaría si rm se redujera
un 10%?
u Utilice CAPM para encontrar el rendimiento requerido
de esta inversión?
n En base a los cálculos de b), ¿recomendaría esta
inversión? ¿Por qué?
q Si rm pasa a ser 9%, ¿Qué impacto tendría este cambio 15
en sus respuestas de b) y c).

16. CAPITAL ASSET PRICING MODEL
EJERCITACIÓN
I Cuando rm se incrementa 10%, se espera que el
rendimiento requerido se incremente 15% (1,5 x
10%). Cuando el rm se reduce 10% se espera que el
rendimiento requerido disminuya
15% [1,50 x (-10%)].
% rA = rf + [β (rm – rf)] = 7% + [1,5 x (10% - 7%)] =
11,5%
El proyecto se debe rechazar porque su rendimiento
esperado es menor que el requerido.
r rA = 7% + [1,5 x (9% - 7%)] = 10%. El proyecto es
aceptable porque el rendimiento requerido del 10% 16
ha bajado, debido a que los inversionistas se han
vuelto menos adversos al riesgo.

17. RETORNOS COMPARACIÓN
1926/1997
Categorías Promedio Risk Std.
anual premiun Deviation %
% %
Commom stocks 13,00 9,20 20,30
Small stocks 17,70 13,90 33,90
Long–term corp. bonds 6,10 2,30 8,70
Long–term gov. bonds 5,60 1,80 9,20
US T–bills 4,40 0,60 3,20
17
Inflation 3,80 4,50