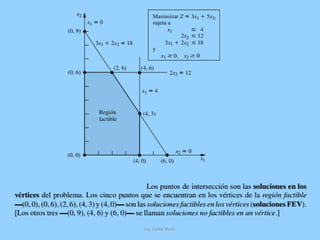
Este documento presenta una introducción al método simplex para resolver problemas de programación lineal. Explica conceptos clave como forma estándar, soluciones factibles y básicas, y cómo transformar un problema a forma estándar usando variables de holgura. También resume los objetivos y competencias de aprendizaje relacionados con el uso del método simplex para optimizar funciones lineales sujetas a restricciones.