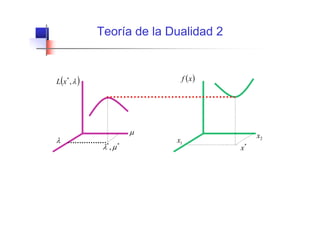
Este documento describe los problemas de programación lineal (PL), donde la función objetivo y restricciones son lineales. Explica que un problema de PL puede representarse en forma matricial minimizando o maximizando la función objetivo sujeta a restricciones lineales. También presenta ejemplos para ilustrar cómo formular problemas de la vida real como problemas de PL.