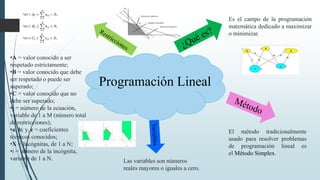
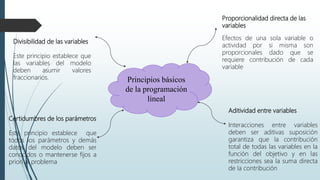
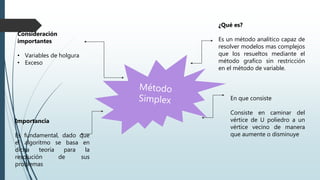
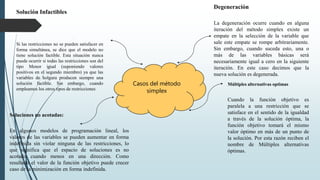
La programación lineal es un método matemático para maximizar o minimizar una función objetivo sujeto a restricciones lineales. El método tradicional para resolver problemas de programación lineal es el método simplex. Este documento describe los principios básicos, métodos y casos especiales de la programación lineal.

1. Republica bolivariana de Venezuela
Ministerio del poder popular para la educación
I.U.P” Santiago Mariño Extensión Maracay
Maracay, Estado Aragua.
Programación Lineal
Alumno:
Kenner Ortiz
C.I: 26.4791.844
Sección: SAIA

2. Programación Lineal
Es el campo de la programación
matemática dedicado a maximizar
o minimizar.
El método tradicionalmente
usado para resolver problemas
de programación lineal es
el Método Simplex.
Las variables son números
reales mayores o iguales a cero.
•A = valor conocido a ser
respetado estrictamente;
•B = valor conocido que debe
ser respetado o puede ser
superado;
•C = valor conocido que no
debe ser superado;
•j = número de la ecuación,
variable de 1 a M (número total
de restricciones);
•a; b; y, c = coeficientes
técnicos conocidos;
•X = Incógnitas, de 1 a N;
•i = número de la incógnita,
variable de 1 a N.

3. Historia de la
programación
lineal
Problema
El problema de la resolución de
un sistema lineal de
inecuaciones se remonta, al
menos, a Joseph Fourier,
después de quien nace el
método de eliminación de
Fourier-Motzkin. La
programación lineal se plantea
como un modelo matemático
desarrollado durante la Segunda
Guerra Mundial para planificar
los gastos y los retornos, a fin
de reducir los costos al ejército
y aumentar las pérdidas del
enemigo. Se mantuvo en
secreto hasta 1947. En la
posguerra, muchas industrias lo
usaron en su planificación
diaria.
Acontecimientos
• 1826 Joseph Fourier anticipa la
programación lineal. Carl
Friedrich Gauss
resuelve ecuaciones lineales por
eliminación "gaussiana".
• 1902 Gyula Farkas concibe un
método para resolver sistemas
de inecuaciones.
• 1947 George Dantzig publica
el algoritmo simplex y John von
Neumann desarrolló la teoría de
la dualidad.Se sabe que Leonid
Kantoróvich también formuló la
teoría en forma independiente.
• 1984 Narendra Karmarkar introduce
el método del punto interior para
resolver problemas de programación
lineal.

4. Principios básicos
de la programación
lineal
Proporcionalidad directa de las
variables
Efectos de una sola variable o
actividad por si misma son
proporcionales dado que se
requiere contribución de cada
variable
Aditividad entre variables
Interacciones entre variables
deben ser aditivas suposición
garantiza que la contribución
total de todas las variables en la
función del objetivo y en las
restricciones sea la suma directa
de la contribución
Divisibilidad de las variables
Este principio establece que
las variables del modelo
deben asumir valores
fraccionarios.
Certidumbres de los parámetros
Este principio establece que
todos los parámetros y demás
datos del modelo deben ser
conocidos o mantenerse fijos a
priori al problema

5. ¿Qué es?
Es un método analítico capaz de
resolver modelos mas complejos
que los resueltos mediante el
método grafico sin restricción
en el método de variable.
En que consiste
Consiste en caminar del
vértice de U poliedro a un
vértice vecino de manera
que aumente o disminuye
Importancia
Es fundamental, dado que
el algoritmo se basa en
dicha teoría para la
resolución de sus
problemas
Consideración
importantes
• Variables de holgura
• Exceso

6. Casos del método
simplex
Degeneración
La degeneración ocurre cuando en alguna
iteración del método simplex existe un
empate en la selección de la variable que
sale este empate se rompe arbitrariamente.
Sin embargo, cuando suceda esto, una o
más de las variables básicas será
necesariamente igual a cero en la siguiente
iteración. En este caso decimos que la
nueva solución es degenerada.
Múltiples alternativas optimas
Cuando la función objetivo es
paralela a una restricción que se
satisface en el sentido de la igualdad
a través de la solución óptima, la
función objetivo tomará el mismo
valor óptimo en más de un punto de
la solución. Por esta razón reciben el
nombre de Múltiples alternativas
óptimas.
Soluciones no acotadas:
En algunos modelos de programación lineal, los
valores de las variables se pueden aumentar en forma
indefinida sin violar ninguna de las restricciones, lo
que significa que el espacio de soluciones es no
acotado cuando menos en una dirección. Como
resultado el valor de la función objetivo puede crecer
caso de la minimización en forma indefinida.
Solución Infactibles
Si las restricciones no se pueden satisfacer en
forma simultánea, se dice que el modelo no
tiene solución factible. Esta situación nunca
puede ocurrir si todas las restricciones son del
tipo Menor igual (suponiendo valores
positivos en el segundo miembro) ya que las
variables de holgura producen siempre una
solución factible. Sin embargo, cuando
empleamos los otros tipos de restricciones

7. Método Gráfico
¿Qué es?
El método gráfico es un procedimiento de
solución de problemas de programación
lineal, muy limitado en cuanto al número
de variables pero muy rico en materia de
interpretación de resultados e incluso
análisis de sensibilidad.
Pasos básicos:
Determinación del espacio de las
soluciones factibles
Determinación de la solución óptima de
entre todos los puntos en el espacio de
solución factible:
Dibujar una recta con valor función
objetivo constante (contorno)
Mover dicha recta de forma paralela en la
dirección en la que se optimiza la función
objetivo
El espacio de las soluciones
factibles es un conjunto
convexo.
Si un problema de PL tiene solución
óptima, ésta es un punto extremo o
esquina del espacio de las soluciones
factibles.

8. Propiedades intrínsecas
en la linealidad
Proporcionalidad
La contribución de cada
variable de decisión en la
función objetivo y en las
restricciones es
directamente proporcional
al valor de la variable
Aditividad
La contribución total de
todas las variables en la
función objetivo y en las
restricciones es la suma de
la contribución individual de
cada variable.

9. Análisis de
sensibilidad
Si la base actual permanece
óptima después de cambiar el
coeficiente de una variable no
básica en la función objetivo,
los valores de las variables de
decisión y el valor objetivo
óptimo no cambian.
Si cambia el coeficiente de
una variable básica, los
valores de las variables de
decisión pueden
permanecer constantes,
pero el valor objetivo
óptimo puede cambiar
Si cambia el lado derecho
de una restricción los
valores de las variables de
decisión y de la función
objetivo pueden cambiar

10. Forma estándar
Variable de holgura
En las restricciones (≤) el lado
derecho representa el límite
sobre la disponibilidad de un
recurso y el lado izquierdo el
uso de ese recurso limitado.
Una holgura representa la
cantidad del recurso que no se
utiliza.
Variable de superávit
Las restricciones (≥) determinan
requerimientos mínimos de
especificaciones. Un superávit
representa el exceso del lado izquierdo
sobre el requerimiento mínimo.
Variable no restringida
El método del símplex exige
trabajar con variables no
negativas. Las variables no
restringidas pueden expresarse
como la diferencia de dos
variables no negativas.
Conversión a forma estándar
Conversión de desigualdades a igualdades
(≤): se introduce una variable de holgura
Ej: x1+x2 ≤ 3 Ù x1+x2+s1=3, s1≥0
(≥): se introduce una variable de superávit
Ej: x1+3x2 ≥7 Ù x1+3x2 – s2=7, s2≥0
Conversión de una variable no restringida a
variables no negativas:
x= x+ - x- , x+, x- ≥ 0

11. Bibliografía
• https://es.wikipedia.org/wiki/Programaci%C3%B3n_lineal
• https://saia.psm.edu.ve/pluginfile.php?file=%2F1356881%2Fmod_resource%2Fcontent%2F2%2FModelos-
PL%20%20Pricipios%20Basicos%20PL.pdf
• https://es.wikipedia.org/wiki/Programaci%C3%B3n_lineal#:~:text=La%20programaci%C3%B3n%20lineal%2
0se%20plantea,mantuvo%20en%20secreto%20hasta%201947.
• https://www.exapuni.com/carreras/apunte/Universidad%20de%20Buenos%20Aires/Ingenier%C3%ADa%20I
ndustrial/Investigaci%C3%B3n%20Operativa/Casos%20especiales%20SIMPLEX/128/0
• https://saia.psm.edu.ve/pluginfile.php?file=%2F1356883%2Fmod_resource%2Fcontent%2F1%2FMetodo%2
0Simplex.pdf
• https://saia.psm.edu.ve/pluginfile.php?file=%2F1356883%2Fmod_resource%2Fcontent%2F1%2FMetodo%2
0Simplex.pdf