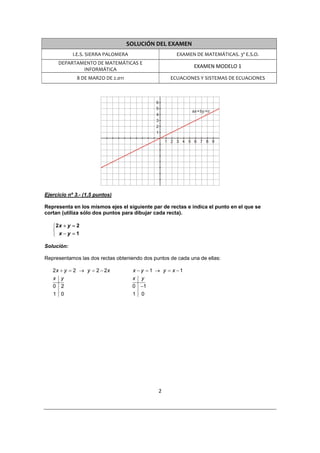
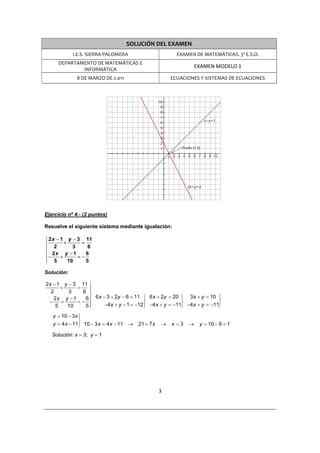
Este documento contiene la solución de un examen de matemáticas de 3er año de educación secundaria. El examen incluye 6 ejercicios sobre ecuaciones y sistemas de ecuaciones. Cada ejercicio está resuelto de manera detallada. El primer ejercicio involucra resolver dos ecuaciones. El segundo pide obtener tres puntos de una recta dada. El tercero representa dos rectas en un mismo plano y encuentra su punto de intersección.

1. SOLUCIÓN DEL EXAMEN
I.E.S. SIERRA PALOMERA EXAMEN DE MATEMÁTICAS. 3º E.S.O.
DEPARTAMENTO DE MATEMÁTICAS E
EXAMEN MODELO 1
INFORMÁTICA
8 DE MARZO DE 2.011 ECUACIONES Y SISTEMAS DE ECUACIONES
Ejercicio nº 1.-
Resuelve las siguientes ecuaciones:
2 ( x + 5 ) 3 2 x 3 ( x + 1)
a) − = − (1,5 puntos)
5 2 5 10
b) 3x2 + 3x − 6 = 0 (0,5 puntos)
Solución:
2 ( x + 5) 3 2 x 3 ( x + 1)
a) =− −
5 2 5 10
2 x + 10 3 2 x 3 x + 3
− = −
5 2 5 10
4 x + 20 15 4 x 3 x + 3
− = −
10 10 10 10
4x + 20 − 15 = 4x − 3x − 3
4x − 4x + 3x = −3 − 20 + 15
3x = −8
8
x=−
3
b ) 3x2 + 3x − 6 = 0 → x2 + x − 2 = 0
x =1
−1 ± 1 + 8 − 1 ± 9 − 1 ± 3
x= = =
2 2 2
x = −2
Ejercicio nº 2.- (1 punto)
A la vista de la siguiente gráfica, obtén tres puntos de la recta ax + by = c.
Solución:
Por ejemplo: (0, 0); (2, 1); (4, 2).
1

2. SOLUCIÓN DEL EXAMEN
I.E.S. SIERRA PALOMERA EXAMEN DE MATEMÁTICAS. 3º E.S.O.
DEPARTAMENTO DE MATEMÁTICAS E
EXAMEN MODELO 1
INFORMÁTICA
8 DE MARZO DE 2.011 ECUACIONES Y SISTEMAS DE ECUACIONES
Ejercicio nº 3.- (1,5 puntos)
Representa en los mismos ejes el siguiente par de rectas e indica el punto en el que se
cortan (utiliza sólo dos puntos para dibujar cada recta).
⎧2 x + y = 2
⎨
⎩ x−y =1
Solución:
Representamos las dos rectas obteniendo dos puntos de cada una de ellas:
2x + y = 2 → y = 2 − 2x x − y = 1 → y = x −1
x y x y
0 2 0 −1
1 0 1 0
2

3. SOLUCIÓN DEL EXAMEN
I.E.S. SIERRA PALOMERA EXAMEN DE MATEMÁTICAS. 3º E.S.O.
DEPARTAMENTO DE MATEMÁTICAS E
EXAMEN MODELO 1
INFORMÁTICA
8 DE MARZO DE 2.011 ECUACIONES Y SISTEMAS DE ECUACIONES
Ejercicio nº 4.- (2 puntos)
Resuelve el siguiente sistema mediante igualación:
⎧ 2 x − 1 y − 3 11
⎪ 2 + 3 = 6
⎪
⎨
⎪− 2 x + y − 1 = − 6
⎪ 5
⎩ 10 5
Solución:
2 x − 1 y − 3 11 ⎫
+ =
2 3 6 ⎪⎪
⎬
2x y − 1 6 ⎪ 6 x − 3 + 2y − 6 = 11 ⎫ 6 x + 2y = 20 ⎫ 3 x + y = 10 ⎫
− + =− ⎬ ⎬ ⎬
5 10 5⎪⎭ −4 x + y − 1 = −12⎭ −4 x + y = −11⎭ −4 x + y = −11⎭
y = 10 − 3 x ⎫
⎬
y = 4 x − 11⎭ 10 − 3 x = 4 x − 11 → 21 = 7 x → x=3 → y = 10 − 9 = 1
Solución: x = 3; y = 1
3

4. SOLUCIÓN DEL EXAMEN
I.E.S. SIERRA PALOMERA EXAMEN DE MATEMÁTICAS. 3º E.S.O.
DEPARTAMENTO DE MATEMÁTICAS E
EXAMEN MODELO 1
INFORMÁTICA
8 DE MARZO DE 2.011 ECUACIONES Y SISTEMAS DE ECUACIONES
Ejercicio nº 5.- (1,5 puntos)
Halla dos números sabiendo que el primero es 12 unidades mayor que el segundo; pero
que, si restáramos 3 unidades a cada uno de ellos, el primero sería el doble del segundo.
Solución:
⎧ x = y + 12
⎨
⎩x − 3 = 2 ⋅ ( y − 3)
y + 12 − 3 = 2 y − 6
15 = y
x = y + 12 = 15 + 12 = 27
Ejercicio nº 6.- (2 puntos)
Un granjero cuenta con un determinado número de jaulas para sus conejos. Si introduce 6
conejos en cada jaula quedan 4 plazas libres en una jaula. Si introduce 5 conejos en cada
jaula quedan 2 conejos libres. ¿Cuántos conejos y jaulas hay?
Solución:
Número de jaulas = x
Número de conejos = y
⎧6 x − 4 = y
⎨
⎩5x + 2 = y
6 x − 4 = 5x + 2
x=6
y = 6 x − 4 = 36 − 4 = 32
4