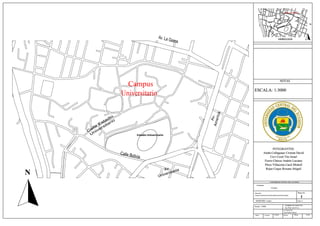
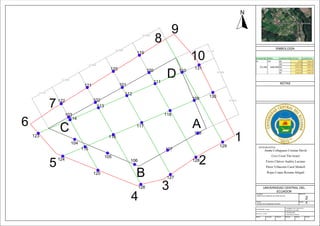
Este documento presenta el informe de una práctica de levantamiento topográfico realizada con un teodolito electrónico. El objetivo general fue obtener una representación gráfica de un terreno mediante la medición de su poligonal principal, puntos de lindero y perfiles transversales. El procedimiento incluyó la medición de ángulos horizontales, verticales y distancias inclinadas, y la elaboración de un plano del terreno en AutoCAD con sus curvas de nivel.