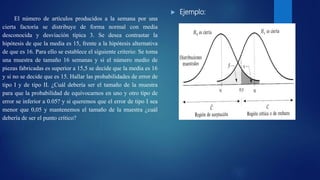
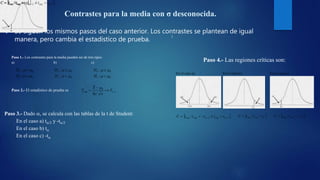
Este documento describe los pasos para realizar un contraste de hipótesis estadístico. Explica que primero se debe determinar la hipótesis nula y alternativa, elegir un nivel de significación, seleccionar un estadístico de prueba y determinar la región crítica. Luego se toma una muestra, se calcula el estadístico y se decide si se acepta o rechaza la hipótesis nula basado en si el valor calculado cae dentro o fuera de la región crítica. También discute los erro

1. DA19-EB-7-DOMINIO DEL
CONOCIMIENTO MATEMATICO EN EL
SUBNIVEL DE BASICA MEDIA III
PARALELO 03

2. "CONTRASTES DE HIPÓTESIS"
 La Inferencia Estadística consta de dos partes: Estimación y Contrastes de
Hipótesis. La primera se ha estudiado en la unidad anterior y estaba
destinada a tratar de determinar el valor de un parámetro poblacional, a
partir de lo observado en la muestra. La técnica de Contraste de Hipótesis
es preciso para establecer procedimientos para aceptar o rechazar
hipótesis estadísticas emitidas acerca de un parámetro, u otra
característica de la población.
 La única forma de saber con certeza absoluta que una hipótesis
estadística es verdadera, es examinar toda la población. Pero esto, en la
mayoría de los casos resulta, imposible (por falta de medios económicos,
imposibilidades técnicas, etc.). Por lo tanto, la decisión debe adoptarse a
partir de los resultados de una muestra de la población (supuesta
representativa), que nos inducirá a tomar la decisión sobre la verdad o
falsedad de la hipótesis. Pero es difícil ésta decisión, porque aunque
sepamos exactamente el valor del parámetro de la población, en las
muestras es muy difícil que se verifique ese valor exacto, por lo que
debemos decidir unos límites de valores del parámetro en la muestra, que
nos puedan llevar a la decisión de aceptar el valor del parámetro
poblacional.

3. Pasos en un contraste de hipótesis
 Veamos ahora los pasos que son convenientes seguir para
realizar el contraste de hipótesis:
 1º Determinar, claramente, la hipótesis nula Ho y la hipótesis
alternativa Ha.
 2º Elegir el nivel de significación.
 3º Seleccionar un estadístico cuya distribución muestral sea
conocida en el caso de que la hipótesis nula sea cierta.
 4º Determinar la región crítica.
 5º Calcular el valor del estadístico de contraste para la
muestra elegida.
 6º Sacar las conclusiones estadísticas del contraste (aceptar o
rechazar Ho).
 7º Sacar las conclusiones no estadísticas (biológicas, médicas,
económicas, etc.) a que nos llevan los resultados estadísticos.

4. PRUEBAS BILATERALES Y PRUEBAS
 Un contraste bilateral adopta en general la forma:
 H0: θ = θ0 contra H1: θ ≠ θ0
 En determinadas ocasiones el experimentador prefiere plantear directamente un
contraste de la forma:
 H0: θ = θ0 contra H1: θ > θ0
 Conocido como contraste unilateral derecho. Obviamente, otra posibilidad es el
unilateral izquierdo:
 H0: θ = θ0 contra H1: θ < θ0
 En estos tres casos, el contraste de hipótesis es simple contra compuesta.
 En la mayoría de situaciones aplicadas, se desean realmente resolver contrastes
unilaterales que comportan hipótesis compuestas. El unilateral derecho es entonces:
 H0: θ ≤ θ0 contra H1: θ > θ0
 y el izquierdo es:H0: θ ≥ θ0 contra H1: θ < θ0

5. CONTRASTES UNILATERALES Y BILATERALES
 El contraste bilateral sitúa la región de rechazo en los dos extremos (colas) de la distribución
muestral. En cambio, el contraste unilateral sitúa la región de rechazo en uno de los dos
extremos (colas) de la distribución muestral. El contraste bilateral (o de dos colas) se utiliza
cuando la Hipótesis Alternativa asigna al parámetro cualquier valor diferente al establecido en
la Hipótesis Nula.
 Ejemplo de contraste bilateral:
La Hipótesis Alternativa establece que, caso de rechazar la
Hipótesis Nula, decidimos que la proporción de la población
a que pertenece la muestra no es 0.5
 Ejemplo de contraste unilateral
 La Hipótesis Alternativa establece que, caso de rechazar la Hipótesis Nula,
decidimos que la proporción de la población a que pertenece la muestra es inferior
a 0.5

6.  Expresión general de un contraste de hipótesis.
 Un contraste de hipótesis se plantea de la siguiente forma
 Que nos indica que provisionalmente admitimos que  pertenece a 0. Si después del estudio resulta
que no es cierto, se acepta la hipótesis alternativa.
 Formas básicas de un contraste paramétrico.
 Las formas de un contraste de hipótesis depende de las especificaciones apropiadas, pero se pueden
resumir en cuatro formas básicas.
 Hipótesis simple frente a alternativa simple.
 Hipótesis simple frente a alternativa bilateral
 Contrastes unilaterales.
 Contraste bilateral.
011
00
:
:




H
H
21
10
:
:




H
H
01
00
:
:




H
H
01
00
01
00
:
:
:
:








H
H
ó
H
H
211
210
:
:




óH
H

7. Región crítica y región de aceptación.
Ante un contraste de hipótesis hay que tomar una de las dos decisiones:
Se acepta la hipótesis alternativa y se rechaza la hipótesis nula.
Se acepta la hipótesis nula y se rechaza la alternativa
Para decidir qué decisión tomar, se toma una muestra aleatoria simple y se elige un determinado estimador
puntual
 Se denomina región crítica a la constituida por el conjunto de muestras para las que se rechaza la hipótesis nula
 Se denomina región de aceptación la constituida por el conjunto de muestras para las que se acepta la hipótesis
nula.
 Se denominan valores críticos de la muestra aquellos que separan la región crítica de la región de aceptación.

θˆ (X1, X2, …,Xn)
 021 /,...,,( HrechazasexxxC n
 021 /,...,,( HaceptasexxxC n

8.  Cuando estamos ante un contraste bilateral (hipótesis alternativa bilateral) la región crítica también es
bilateral y existen dos valores críticos.
Cuando el contraste es unilateral, la región crítica también lo es y únicamente existe un valor crítico.
 Una vez determinada la región crítica se elige una M.A.S. Si esa muestra pertenece a la región crítica,
rechazamos H0 y aceptamos H1; si la muestra está en la región de aceptación, se acepta H0 y se rechaza H1.
01
00
:
:




H
H
01
00
:
:




H
H

9.  Error de tipo I y error de tipo II.
 En un contraste de hipótesis, igual que en cualquier problema de
decisión, hay varias alternativas y, por tanto, existe la posibilidad
de equivocarse. Las posibles alternativas y estados se resumen en
el siguiente cuadro.
 Error de tipo I es el cometido al rechazar H0 cuando es cierta.
 Error de tipo II es el cometido al aceptar H0 cuando es falsa.
Estados de la naturaleza
Decisión H0 verdadera H0 falsa
Aceptar H0 No hay error
Nivel de confianza
)
Error de tipo II

Rechazar H0 Error de tipo I

No hay error
Potencia (1-)

10.  Riesgo de error de tipo I para un parámetro ()
 Es la probabilidad de cometer un error de tipo I, es decir:
 Habrá tantos errores de tipo I como valores posibles de 0. Se denomina talla del error de
tipo I, o tamaño del error de tipo I, a la mayor de estas probabilidades, que se designa por ,
también denominado nivel de significación del contraste, o tamaño de la región crítica.














0
21
0
0 ),...,,(Re
)(
 CXXX
P
ciertaesH
Hchazar
P n

11.  Ejemplo:
El número de artículos producidos a la semana por una
cierta factorìa se distribuye de forma normal con media
desconocida y desviación típica 3. Se desea contrastar la
hipótesis de que la media es 15, frente a la hipótesis alternativa
de que es 16. Para ello se establece el siguiente criterio: Se toma
una muestra de tamaño 16 semanas y si el número medio de
piezas fabricadas es superior a 15,5 se decide que la media es 16
y si no se decide que es 15. Hallar las probabilidades de error de
tipo I y de tipo II. ¿Cuál debería ser el tamaño de la muestra
para que la probabilidad de equivocarnos en uno y otro tipo de
error se inferior a 0.05? y si queremos que el error de tipo I sea
menor que 0,05 y mantenemos el tamaño de la muestra ¿cuál
debería de ser el punto crítico?

12.  Solución:
 Como  y  son iguales, lo calculamos únicamente para .
luego n tiene que ser mayor o igual a 98.
Análogamente:
 con lo que, despejando, el valor de x0 ha de ser 16,23.




























16
3
155,15
16
3
15
15
5,15Re
0
0
X
PXP
ciertaesH
Hchazar
P
 = P(Z > 0,66) = 0,2546



























16
3
165,15
16
3
16
16
5,15
0
0
X
PXP
falsaesH
HAceptar
P
 = P(Z < -0,66) = 0,2546
05,0
3
155,15
3
15
15
5,15 





















nn
X
PXP
 645,1
3
155,15



n
05,0
16
3
15
16
3
15
15
00 






















xX
P
xX
P

 645,1
16
3
150



x

13. Fases a realizar en un contraste de hipótesis.
 Paso 1.- Planteamiento de las hipótesis nula y alternativa en términos estadísticos.(Recordar que por
motivos de cohesión teórica, el signo igual ha de estar siempre en la hipótesis nula).
 Paso 2.- Determinar un estadístico de prueba apropiado que se utilizará para aceptar o rechazar
la hipótesis nula, ha de cumplir:
 a) Su función de probabilidad ha de ser conocida cuando H0 se supone cierta.
 b) Debe de contener el parámetro que se quiere contrastar.
 c) Los restantes términos que intervienen han de ser conocidos o se pueden estimar a partir de la
muestra.
 Paso 3.- Fijar el nivel de significación .

 Paso 4.- Determinar la región crítica del estadístico de prueba.

 Paso 5.- Seleccionar aleatoriamente la muestra y calcular el valor del estadístico de prueba o
experimental.

 Paso 6.- Decidir e interpretar si el valor del estadístico experimentado está o no en la región crítica y
rechazar o aceptar la hipótesis nula.
)ˆ(h

14. Contrastes para la media con σ desconocida.
 Se siguen los mismos pasos del caso anterior. Los contrastes se plantean de igual
manera, pero cambia el estadístico de prueba.
01
00
:
:




H
H
01
00
:
:




H
H
01
00
:
:




H
H
Paso 1.- Los contrastes para la media pueden ser de tres tipos:
a) b) c)
)
Paso 2.- El estadístico de prueba es 1
0
exp 

 nT
nSc
X
T 

Paso 3.- Dado , se calcula con las tablas de la t de Student:
En el caso a) t/2 y -t/2
En el caso b) t
En el caso c) -t
Paso 4.- Las regiones críticas son:
En el caso a) En el caso b) En el caso c)
 2/exp2/expexp /  ttótttC   tttC  expexp /  tttC  expexp /
 2/exp2/expexp /  ttótttC  tttC  expexp / tttC  expexp / 2/exp2/expexp /  ttótttC  tttC  expexp / tttC  expexp /

15.  CONCLUSIONES
 Se rechaza la hipótesis nula (Ho), se acepta la hipótesis alterna
(H1) a un nivel de significancia de α = 0.05. La prueba resultó
ser significativa.
 La evidencia estadística no permite aceptar la aceptar la hipótesis
nula.
 Las pruebas de hipótesis y al proceso de simular, y entendiendo
este ejercicio como una actividad de investigación inicial,
además de haber sido la manera como se fundamentaron desde
un punto de vista es entonces posible concluir que la revisión y
estudio de dicha documentación constituyó un elemento esencial
del trabajo desarrollado, en tanto que permitió una mirada
sensata a los conocimientos previos sobre las pruebas de
hipótesis y una exploración rigurosa de referentes teóricos
nuevos que dieron una perspectiva mucho más amplia sobre las
temáticas estudiadas.