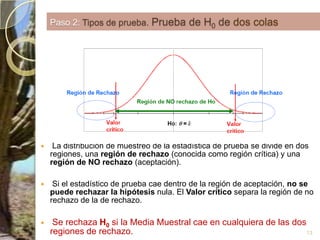
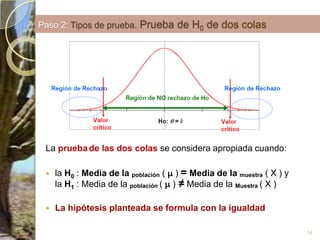
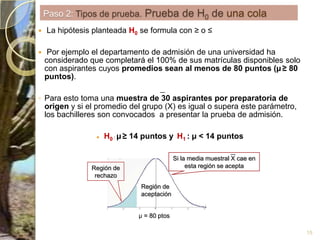
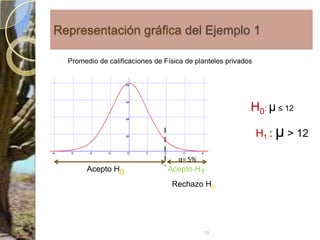
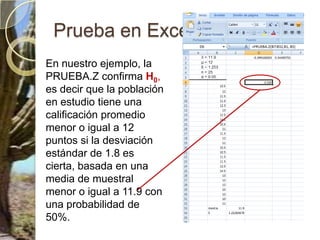
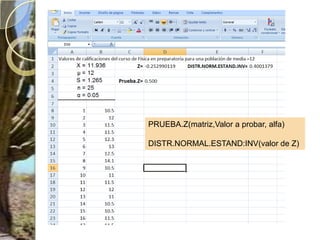
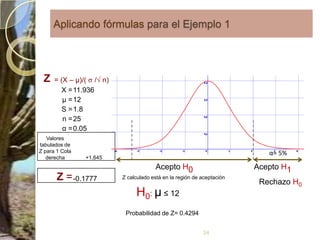
Este documento presenta los conceptos clave de las pruebas de hipótesis estadísticas, incluyendo (1) la definición de hipótesis nula e hipótesis alternativa, (2) la selección del nivel de significación, y (3) los cinco pasos del procedimiento de prueba de hipótesis - identificar la distribución muestral asociada, formular la regla de decisión, y tomar una decisión final de aceptar o rechazar la hipótesis nula. También proporciona un ejemplo numérico

1. Bondad de Ajuste y Concepto de prueba de HipótesisEstadística CIMACODr. Carlos Cáceres Martínez, presentación preparada a partir del trabajo de la Ing. María Isabel Bautista y otros mas

2. Introducción a la Inferencia Estadística2Hipótesis EstadísticaProcedimiento para probar una Hipótesis para una Muestra (uso de “Z”).Hipótesis nula (H0) e Hipótesis alternativa (H1)Nivel de significaciónTipos de pruebaDistribución muestral asociadaLa regla de decisión

3. Hipótesis EstadísticaLa Hipótesis es la aseveración que se hace sobre una población 3Será cierto o no una suposición que se ha hecho sobre un parámetro que caracteriza a una población

4. Hipótesis EstadísticaEn el análisis estadístico se hace una aseveración, se plantea una hipótesis, después se hacen las pruebas para verificar la aseveración o para determinar que no es verdadera.4

5. Hipótesis EstadísticaLa Hipótesis es la aseveración que se hace sobre una población En el análisis estadístico se hace una aseveración, se plantea una hipótesis, después se hacen las pruebas para verificar la aseveración o para determinar que no es verdadera.La prueba de hipótesis es un procedimiento basado en la evidencia muestraly la teoría de probabilidad que se emplea para determinar si la hipótesis es una afirmación razonable 5

6. Hipótesis EstadísticaUsualmente se desea probar una suposición que se ha hecho sobre un parámetro que caracteriza a una población en particular, tal como la media poblacional.6

7. Procedimiento para probar una HipótesisLa prueba de una hipótesis se realiza mediante un procedimiento sistemático de cinco pasos. Al llegar al 5º paso se puede o no rechazar la hipótesis. Esta prueba aporta una clase de prueba más allá de una duda razonable. El propósito de la prueba de hipótesis es el de hacer un juicio con respecto a la diferencia entre estadístico de muestra y un valor planteado del parámetro.7Aceptar o Rechazar

8. Procedimiento para probar una Hipótesis8La prueba de una hipótesis se realiza mediante un procedimiento sistemático de cinco pasos. Al llegar al 5º paso se puede o no rechazar la hipótesis. Esta prueba aporta una clase de prueba más allá de una duda razonable. La prueba de una hipótesis se realiza mediante un procedimiento sistemático de cinco pasos. Al llegar al 5º paso se puede o no rechazar la hipótesis. Esta prueba aporta una clase de prueba más allá de una duda razonable. Analizaremos cada paso en detalle

9. Paso 1: Definir Hipótesis nula (H0) e Hipótesis alternativa (H1)Consiste en establecer el valor supuesto del parámetro en consideración antes de empezar el muestreo. Ese valor supuesto que se desea probar se le denomina Hipótesis Nula (H0)La hipótesis nula es una afirmación que no se rechaza a menos que los datos muestrales proporcionen evidencia convincente de que es falsa. El planteamiento de la hipótesis nula siempre contiene un signo de igualdad con respecto al valor especificado del parámetro. La hipótesis alternativa (H1) se refiere a cualquier hipótesis que difiera de H0. Es una afirmación que se acepta si los datos muestrales proporcionan evidencia suficiente de que la hipótesis nula es falsa. El planteamiento de la hipótesis alternativa nunca contiene un signo de igualdad con respecto al valor especificado del parámetro9

10. Ejemplo:El jefe de la zona escolar desea probar que el promedio de calificaciones del curso de Física de secundaria (media: µ) de planteles privados es igual a 12 H0 : µ = 12Si H0 no es cierta se presentan las siguientes 3 alternativas:H1 : µ≠ 12 la media de calificaciones es diferente de 12 puntosH1:µ > 12 la media de calificaciones es mayor a 12 puntosH1: µ < 12 la media de calificaciones es menor a 12 puntos

11. 11Paso 2: Seleccionar el nivel de significaciónSe refiere a la probabilidad αde rechazar H0cuando en realidad es verdadera, cometiendo así un ERROR tipo I.O por el contrario la probabilidad βde aceptar H0 cuando en realidad es falsa, cometiendo así un ERROR tipo IIAunque no existe una regla general para seleccionar los valores de α,suele utilizarseα=0,05 (5%) y α= 0,01 (1%)y debe especificarse antes de realizar la prueba.Si por ejemplo se elige un α= 5% al diseñar una prueba entonces podemos esperar que en 5 ocasiones de cada 100 se rechazará la H0 cuando debería ser aceptada (porque por azar la muestra cae en la región de rechazo), o sea que tenemos una probabilidad = 0.95 (95%) de que no rechazaremos la H0 siendo cierta.

12. Ejemplo:Si la muestra de 25 colegios la media de las calificaciones supera los 12 puntos. Se rechaza H0. Se comete error tipo Isi la media de la población es igual a 12 puntos. Si la muestra de 25 colegios la media de las calificaciones es igual a 12 puntos. Se acepta H0. Se comete error tipo IIsi la media de la población supera los 12 puntos.

13. Md. población = Md. muestra13Paso 2: Tipos de prueba. Prueba de H0 de dos colas La distribución de muestreo de la estadística de prueba se divide en dos regiones, una región de rechazo (conocida como región crítica) y una región de NO rechazo (aceptación). Si el estadístico de prueba cae dentro de la región de aceptación, no se puede rechazar la hipótesis nula. El Valor crítico separa la región de no rechazo de la de rechazo.Se rechaza H0 si la Media Muestral cae en cualquiera de las dos regiones de rechazo.

14. Md. población = Md. muestra14Paso 2: Tipos de prueba. Prueba de H0 de dos colasLa pruebade las dos colas se considera apropiada cuando:la H0 : Media de lapoblación (μ) =Media de lamuestra ( X ) yla H1 : Media de la población (μ)≠Media de la Muestra ( X ) La hipótesis planteada se formula con la igualdad

15. 15Si la media muestral X cae en esta región se acepta Región de rechazoRegión de aceptaciónµ = 80 ptosPaso 2: Tipos de prueba. Prueba de H0 de una cola La hipótesis planteada H0 se formula con ≥ o ≤ Por ejemplo el departamento de admisión de una universidad ha considerado que completará el 100% de sus matrículas disponibles solo con aspirantes cuyos promedios sean al menos de 80 puntos (µ≥ 80 puntos). Para esto toma una muestra de 30 aspirantes por preparatoria de origen y si el promedio del grupo (X) es igual o supera este parámetro, los bachilleres son convocados a presentar la prueba de admisión.H0 : µ≥ 14 puntos y H1: µ < 14 puntos16Paso 3: Identificar la Distribución Muestralasociada Se refiere al valor determinado a partir de la información muestral que se utiliza para aceptar o rechazar la hipótesis nula H0Existen muchos estadísticos de prueba, en nuestro caso utilizaremos los estadísticos Z para distribución normal de la población y t “t de student” para la muestra. La elección de uno de estos depende del tamaño de la muestras, si las muestras son grandes (mayor a 30 observaciones) el estadístico recomendado es el de la Distribución Normal Estándar (z) , o en caso de muestras pequeñas utilizar el estadístico t .En las pruebas de hipótesis para la media de la población (μ), cuando se conoce la desviación estándar (σ) poblacional, o cuando el valor de la muestra es grande (30 o más), el valor estadístico de prueba es z y se determina a partir de:

16. Caso ejemplo 1Promedio de calificaciones del curso de Física de de planteles privados. Se conoceμ y σPaso 1Paso 2Nivel de significación α = 0,05 (5%), que es la probabilidad de cometer error tipo I, es decir rechazar H0 cuando esta es verdadera. Nivel de confianza 95%Paso 3El estadístico apropiado es Z ya que se dijo que la distribución es normal. Para hacer el cálculo se utiliza Excel, función “PRUEBA.Z”17Paso 3: Identificar la Distribución Muestralasociada

17. Representación gráfica del Ejemplo 1 18Promedio de calificaciones de Física de planteles privadosH0: µ≤ 12H1 : µ > 12α= 5%Acepto H0Acepto H1Rechazo H0

18. 19Paso 4: Formular la regla de decisiónSe establece las condiciones específicas en la que se rechaza la hipótesis nula H0y las condiciones en que no se rechaza la hipótesis nula. La región de rechazo define la ubicación de todos los valores que son tan grandes o tan pequeños, que la probabilidad de que se presenten bajo la suposición de que la hipótesis nula es verdadera, es muy remota

19. Prueba en ExcelEn nuestro ejemplo, la PRUEBA.Z confirma H0, es decir que la población en estudio tiene una calificación promedio menor o igual a 12 puntos si la desviación estándar de 1.8 es cierta, basada en una media de muestral menor o igual a 11.9 con una probabilidad de 50%.

20. DISTR.NORM.ESTAND.INVCaso ejemplo 1 Regresamos a el calculo con otra herramientaPromedio de calificaciones de física de 9º de planteles privados. Se conoceμyσPaso 1Paso 2Nivel de significación α = 0,05 (5%), que es la probabilidad de cometer error tipo I, es decir rechazar H0cuando esta es verdaderaPaso 3El estadístico apropiado es Zya que se dijo que la distribución es normal. Para hacer el cálculo se utiliza Excel, función “PRUEBA.Z” Utiliza DISTR.NORM.ESTAND.INVPaso 4Si Z es ≥ 95% ( 1- α) se acepta que el promedio de notas de los planteles privados de la zona escolar no están alcanzando los objetivos de aprendizaje de Física

21. PRUEBA.Z(matriz,Valor a probar, alfa)DISTR.NORMAL.ESTAND:INV(valor de Z)

22. 23Paso 5: Tomar una decisiónEn este último paso de la prueba de hipótesis, se calcula el estadístico de prueba, se compara con el valor crítico y se toma la decisión de rechazar o no la hipótesis nula. Tenga presente que en una prueba de hipótesis solo se puede tomar una de dos decisiones: aceptar o rechazar la hipótesis nula.

23. Aplicando fórmulas para el Ejemplo 1 24α= 5%Acepto H0Acepto H1Z calculado está en la región de aceptaciónRechazo H0H0:µ≤ 12Probabilidad de Z= 0.4294

24. Lista de ReferenciasMendenhall, Willian. (1978), Estadística para Administradores y Economía. Universidad Nacional Autónoma de México. Grupo Editorial Iberoamérica. México.Navarro, A. (2000), Estadística Aplicada al área económica y empresarial. Ediciones de la Universidad Ezequiel Zamora. Colección Docencia Universitaria. Barinas, Venezuela Tarjeta de referencia rápida: Funciones estadísticas de Excelhttp://support.microsoft.com/kb/828296/es25