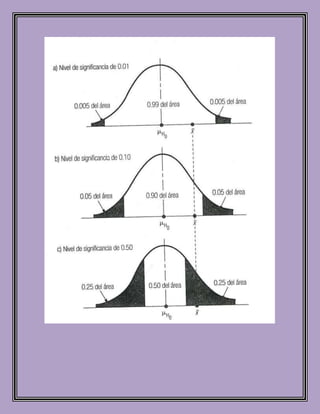
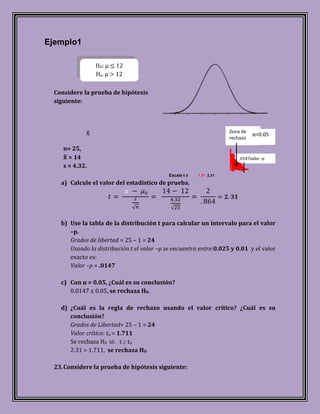
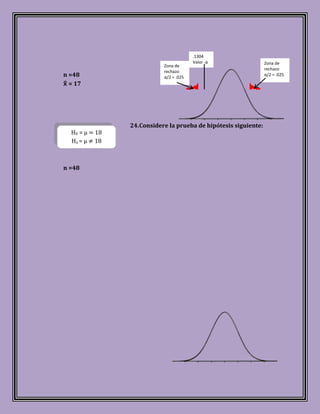
Este documento describe las pruebas de hipótesis, un procedimiento estadístico para decidir cuál de dos hipótesis complementarias sobre un parámetro de población es más probable basado en una muestra. Se definen las hipótesis nula e hipótesis alternativa, y se explican conceptos como los niveles de significancia, los tipos de errores, y cómo usar estadísticos de prueba y valores críticos para decidir si rechazar o no la hipótesis nula. El documento también proporciona ejemplos numéric

1. 17/4/2012
PRUEBAS DE
HIPÓTESIS
| Rosa Helida Yaneth Meza Reyes

2. PRUEBAS DE HIPÓTESIS
Es un procedimiento estadístico que comienza con una suposiciónque se hace con respecto
a un parámetro de población, luego se recolectan datos demuestra, se producen estadísticas
de muestra y se usa esta información para decidir quétan probable es que sean correctas
nuestras suposiciones acerca del parámetro depoblación en estudio.
Ejemplos de hipótesis pueden ser: Se desea
a) Probar si las ventas diaria de un abasto son 1 Mio de bolívares o no
b) Probar si la proporción de individuos que compran algún artículo en una tienda es
o no mayor del 0.3.
Objetivo de la prueba de hipótesis
Decidir, basado en una muestra de una población, cuál de dos hipótesis complementarias
es cierta. Las dos hipótesis complementarias se denominan hipótesis nula e hipótesis
alternativa.
Conceptos Básicos
Hipótesis Nula (H0)
Representa la hipótesis que mantendremos cierta a no ser que los datos indiquen su
Falsedad. Esta hipótesis nunca se considera aceptada, en realidad lo que se quiere decir es
que no hay suficiente evidencia estadística para rechazarla por lo que aceptar H 0 no
garantiza que H0 sea cierta.
Hipótesis Alternativa (H1)
Hipótesis que se acepta cuando los datos no respaldan la hipótesis nula.
Tipos de pruebas
a) Pruebas de hipótesis de 2 extremos o bilaterales. Estas pruebas son del tipo:
Ho: 0 11H :
b) Pruebas de hipótesis de un extremo o unilateral.
b.1) Ho: 0 11H :
b.2) Ho: 0 11H :

3. Metodología:
La lógica de una prueba de hipótesis es similar a la de un juicio penal, donde debe decidirse
si el acusado es inocente o culpable y el juicio consiste en aportar evidencia para rechazar
la hipótesis de inocencia más allá de cualquier duda razonable. Por su parte una prueba de
hipótesis analiza si los datos observados permitan rechazar la hipótesis nula, comprobando
si éstos tienen una probabilidad de aparecer lo suficientementepequeña cuando es cierta la
hipótesis nula.
Las etapas de una prueba de hipótesis son:
a) Definir la hipótesis nula a contrastar.
b) Definir una medida de discrepancia entre los datos muéstrales y la hipótesis Ho.
Supongamos que el parámetro de interés es la media de una población y que a partir de
una muestra hemos obtenido su estimador x , entonces debemos medir de
alguna manera la discrepancia entre ambos, que denotaremos como d( , x) .
c) Decidir qué discrepancia consideramos inadmisibles con Ho, es decir, a partir de
que valor de d, la discrepancia es muy grande como para atribuirse al azar y
considerar que Ho pueda ser cierta. Para ello debemos entonces:
Tomar la muestra
Calcular el estimador del parámetro, en nuestro ejemplo x
Calcular la medida de discrepancia d.
Tomar la decisión: Si d es “pequeña”, aceptar Ho, si es lo
“suficientemente “grande, rechazarla y aceptar H1.
Es por ello que necesitamos establecer una Regla de Decisión mediante la cual sea
Especificado:
a) La medida de discrepancia.
b) Un criterio que nos permita juzgar qué discrepancia son “ demasiado grandes”
a) Medidas de discrepancias:
Es natural considerar medidas de discrepancias del tipo:, de las que será posible conocer su
distribución de probabilidad..
Si las hipótesis son bilaterales el signo de la desviación entre ˆ
0 _no es importante, sin embargo cuando la hipótesis es unilateral el signo de la
discrepancia sí lo es.
b) Calculo de un valor mínimo c d para la discrepancia para la aceptación de Ho.
Para ello definamos:

4. Nivel de Significancia.
Para realizar una prueba de hipótesis dividiremos el rango de discrepancias que puede
observarse cuando Ho es cierta en dos regiones: una región de aceptación de Ho y otra de
rechazo.
Se consideran discrepancias “ demasiado grandes” , las que tienen una probabilidad
pequeña de ocurrir si Ho es cierta. A este valor lo llamamos nivel de significación:
generalmente tomamos valores de 0.1,0.05,0.01 o 0,005.
El nivel de significación puede interpretarse también como la probabilidad que
estamos dispuestos a asumir de rechazar Ho cuando esta es cierta.
Cabe destacar que mientras más alto sea el nivel de significancia que se utiliza para
probar una hipótesis, mayor será la probabilidad de rechazar una hipótesis nula cuando
escierta.
En la siguiente figura se muestran tres niveles de significancia distintos:

6. Región de Rechazo:
Una vez fijado , la región de rechazo se determina a partir de la distribución de
probabilidad de d( , x) cuando Ho es cierta. Como esta distribución es conocida
elegiremosc d de manera que discrepancias mayores de c d tengan probabilidad de ocurrir
menor de ,si Ho es cierta.
La región de rechazo será c d dy la de no rechazo será por consiguiente: c d d
Tipos de errores
Cuando se decide sobre el rechazo de una hipótesis se pueden cometer dos
Error tipo l se presenta si la hipótesis nula Ho es rechazada cuando es verdadera y debía ser
aceptada. La probabilidad de cometer un error tipo I se denomina con la letra alfa α
Un error tipo II, se denota con la letra griega β se presenta si la hipótesis nula es aceptada cuando de
hecho es falsa y debía ser rechazada.
Existe un equilibrio entre los dos tipos de errores, la probabilidad de cometer un tipo de
error puede reducirse sólo si deseamos incrementar la probabilidad de cometer el otro.
Tipos de pruebas
a) Pruebas de hipótesis de 2 extremos o bilaterales.
Es una prueba en la que H0 se rechaza si el valor de la muestra es significativamente mayor
o menor que el valor hipotetizado del parámetro de población. Esta prueba involucra dos
regiones de rechazo
b) Pruebas de hipótesis de 1 extremo o unilaterales Es una prueba en la que sólo hay una
región de rechazo, es decir, sólo nos interesa si el valor observado se desvía del valor
hipotetizado en una dirección. Pueden ser:
b.1) Prueba de extremo inferior
Es una prueba en la que si hay un valor de muestra que se encuentra Significativamente por
debajo del valor de la población hipotetizado, nos llevará a Rechazar la hipótesis nula.
Gráficamente:
b.2) Prueba de extremo superior
Es una prueba en la que si hay un valor de muestra que se encuentra significativamente por
encima del valor de la población hipotetizado, nos llevará a rechazar la hipótesis nula.
Gráficamente:

7. Ejemplo1
H 0: µ 12
Ha: µ 12
Considere la prueba de hipótesis
siguiente:
 Zona de
α=0.05
rechazo
n= 25,
 = 14 .0147valor -p
s = 4.32.
Escala t 0 1.71 2.31
a) Calcule el valor del estadístico de prueba.
b) Use la tabla de la distribución t para calcular un intervalo para el valor
–p.
Grados de libertad = 25 – 1 = 24
Usando la distribución t el valor –p se encuentra entre:0.025 y 0.01 y el valor
exacto es:
Valor –p = .0147
c) Con α = 0.05, ¿Cuál es su conclusión?
0.0147 ≤ 0.05, se rechaza H0.
d) ¿Cuál es la regla de rechazo usando el valor crítico? ¿Cuál es su
conclusión?
Grados de Libertad= 25 – 1 = 24
Valor crítico: tα = 1.711
Se rechaza H0 si: t tα
2.31 > 1.711, se rechaza H0.
23. Considere la prueba de hipótesis siguiente:

8. .1304
Valor -p Zona de
Zona de
rechazo
rechazo
n =48 α/2 = .025
α/2 = .025
 = 17
24. Considere la prueba de hipótesis siguiente:
H0 = µ 18
Ha = µ 18
n =48

9. Ejemplo 2
Determine si la región de rechazo es de la cola derecha, de la cola
izquierda o de dos colas.
a. H0 : = 15, H1 : 15, =.05
b. H0 : p  0.7, H1 : p > 0.7, =.02
Solución: La forma de la región de rechazo está determinada por
la hipótesis alterna.
a. H1 : 15 significa que la región está en ambas colas.
.05/2 .05/2
b. H1 : p > 7 significa que la región está en la cola
derecha.
.02

10. Ejemplo 3: En el Ejemplo 1a, presumamos que la región de
rechazo es parte de la curva normal estándar. Complete el dibujo de
la región crítica para los valores siguientes:
a.  .05
=
Solución:
a. Del ejemplo 1(a), tenemos:
De la tabla de la
.05/2=0.025 .05/2=0.025
distribución normal, la
-1.96 1.96 P(Z z) =.025
corresponde a un valor
Z= -1.96. Por simetría la
P(Z>z)=.025 corresponde
a Z= 1.96.

11. Ejemplo 4: En el ejemplo 1a, presumamos que la región de rechazo
es parte de la curva t. Complete el dibujo de la región de rechazo
para:
a.  = .05 y  = 14
Solución:
a. Del ejemplo 1(a),  = .05, y = 14, tenemos:
.05/2=0.025 .05/2=0.025
De la tabla de la
distribución t, la
-2.086 2.086
P(T t) =.025
corresponde a un valor t=
-2.086. Por simetría la
P(T>t)=.025 corresponde
a t= 2.086.

12. Ejemplo 5:
Establezca las hipótesis nula y alterna.
a. Las millas por galón (mpg) promedio de un nuevo
modelo de automóvil es 32.
b. Más del 65% de los empleados de un colegio aportan
a Fondos Unidos.
c. En promedio, los empleados de cierta compañía
viven a no más de 15 millas de la misma.
d. Al menos un 60% de la población adulta de una
comunidad votará en las próximas elecciones
Presidenciales.
e. El peso promedio de un pollo para asar es de al
menos cuatro libras.
Solución:
a. H0 : = 32 b. H0 : p .65 c. H0 : 15
H1 : 32 H1 : p < .65 H1 : > 15
d. H0 : p .6 e. H0 : 4
H1 : p < .6 H1 : < 4

13. Ejemplo 6
De una población se toma una muestra de 40 observaciones. La
media muestral es de 102 y la desviación estándar 5. De otra
población se toma una muestra de 50 observaciones. La media
muestral es ahora 99 y la desviación estándar es 6. Realice la
siguiente prueba de hipótesis usando como nivel de significancia 0,04.
Ho: u1 =
u2
Ho:
u1 ≠ u2
a) Es esta una prueba de una o de dos colas?
Esta es una prueba de hipótesis de dos colas
b) Establezca la regla de decisión
Si Z > que le valor crítico, se rechaza la hipótesis nula y se acepta la
hipótesis alternativa
c) Calcule el valor del estadístico de prueba
Si Z > que el valor crítico, se rechaza la hipótesis nula y se
acepta H1

14. d) Cuál es su decisión respecto a la hipótesis nula?
Como su valor calculado Z (2,59) > 2,05; se rechaza la hipótesis
nula y se acepta la hipótesis alternativa
Si Z tabulada es 0,5 - 0,02 = 0,48 este valor en la tabla es 2,05
e) Cuál es el valor p?
Z = 2,59 Area 0,4952
0,5 - 0,4952 = 0,0048 * 2 = 0,0096

15. Ejemplo 7
Un artículo reciente, publicado en el diario USA today, indica que solo
a uno de cada tres egresados de una universidad les espera un puesto
de trabajo. En una investigación a 200 egresados recientes de su
universidad, se encontró que 80 tenían un puesto de trabajo. Puede
concluirse en el nivel de significancia 0,02, que en su universidad la
proporción de estudiantes que tienen trabajo es mayor?

16. Ejemplo 8
Para H1:  > valor aceptado, la región de rechazo está dada por:
(Cola derecha, z ó t)
Para H1 :  < valor aceptado, la región de rechazo está
dada por:
(Cola izquierda, z ó t)
Para H1 :   valor aceptado, la región de rechazo es
de dos colas y está dada por:
/2 /2 (2-colas, z ó t)