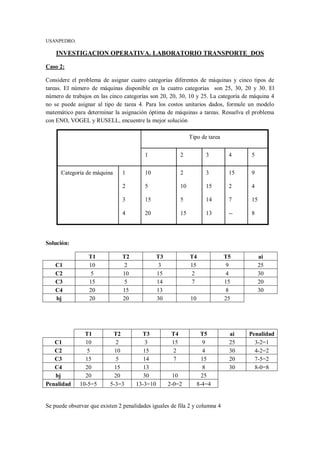
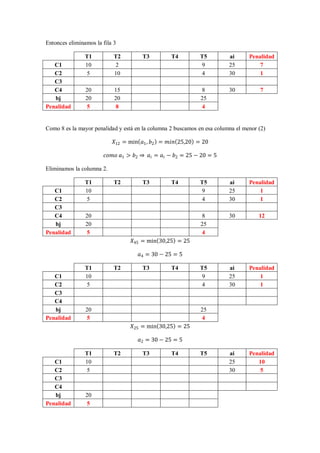
El resumen es el siguiente: 1) Se debe asignar cuatro categorías de máquinas con capacidades de 25, 30, 20 y 30 a cinco tipos de tareas con demandas de 20, 20, 30, 10 y 25. 2) Se formula un modelo matemático para determinar la asignación óptima que minimice las penalidades. 3) Usando el método de mínimas penalidades se resuelve el problema asignando máquinas a tareas de forma óptima con un costo total de 690.

1. USANPEDRO.
INVESTIGACION OPERATIVA. LABORATORIO TRANSPORTE_DOS
Caso 2:
Considere el problema de asignar cuatro categorías diferentes de máquinas y cinco tipos de
tareas. El número de máquinas disponible en la cuatro categorías son 25, 30, 20 y 30. El
número de trabajos en las cinco categorías son 20, 20, 30, 10 y 25. La categoría de máquina 4
no se puede asignar al tipo de tarea 4. Para los costos unitarios dados, formule un modelo
matemático para determinar la asignación óptima de máquinas a tareas. Resuelva el problema
con ENO, VOGEL y RUSELL, encuentre la mejor solución
Tipo de tarea
1 2 3 4 5
Categoría de máquina 1 10 2 3 15 9
2 5 10 15 2 4
3 15 5 14 7 15
4 20 15 13 -- 8
Solución:
T1 T2 T3 T4 T5 ai
C1 10 2 3 15 9 25
C2 5 10 15 2 4 30
C3 15 5 14 7 15 20
C4 20 15 13 8 30
bj 20 20 30 10 25
T1 T2 T3 T4 T5 ai Penalidad
C1 10 2 3 15 9 25 3-2=1
C2 5 10 15 2 4 30 4-2=2
C3 15 5 14 7 15 20 7-5=2
C4 20 15 13 8 30 8-0=8
bj 20 20 30 10 25
Penalidad 10-5=5 5-3=3 13-3=10 2-0=2 8-4=4
Se puede observar que existen 2 penalidades iguales de fila 2 y columna 4

2. 24 = min a2 , b4 = min 30,10 = 10
2 > 4 : ℎ = −
2 = 2 − 4 = 30 − 10 = 20 4
T1 T2 T3 T4 T5 ai Penalidad
C1 10 2 3 9 25 1
10
C2 5 10 15 4 30 2
C3 15 5 14 15 20 9
C4 20 15 13 8 30 5
bj 20 20 30 25
Penalidad 5 3 10 4
Como 10 es la mayor penalidad y está en la columna 3 buscamos en esa columna el menor (3),
luego se introduce en la base
13 = min 1 , 3 = 25,10 = 10
1 > 3 = −
1 = 1 − 3 = 25 − 10 = 15
Entonces eliminamos la columna 3
T1 T2 T3 T4 T5 ai Penalidad
C1 10 2 9 25 7
C2 5 10 4 30 1
C3 15 5 15 20 10
C4 20 15 8 30 7
bj 20 20 25
Penalidad 5 3 4
Como 10 es la mayor penalidad y está en la fila 3 buscamos en esa fila el menor (5); luego se
introduce en la base.
32 = min 3 , 2 = 20,20 = 20
3 > 2 = −
3 = 3 − 2 = 20 − 20 = 0

3. Entonces eliminamos la fila 3
T1 T2 T3 T4 T5 ai Penalidad
C1 10 2 9 25 7
C2 5 10 4 30 1
C3
C4 20 15 8 30 7
bj 20 20 25
Penalidad 5 8 4
Como 8 es la mayor penalidad y está en la columna 2 buscamos en esa columna el menor (2)
12 = min 1 , 2 = 25,20 = 20
1 > 2 = − 2 = 25 − 20 = 5
Eliminamos la columna 2.
T1 T2 T3 T4 T5 ai Penalidad
C1 10 9 25 1
C2 5 4 30 1
C3
C4 20 8 30 12
bj 20 25
Penalidad 5 4
45 = min 30,25 = 25
4 = 30 − 25 = 5
T1 T2 T3 T4 T5 ai Penalidad
C1 10 9 25 1
C2 5 4 30 1
C3
C4
bj 20 25
Penalidad 5 4
25 = min 30,25 = 25
2 = 30 − 25 = 5
T1 T2 T3 T4 T5 ai Penalidad
C1 10 25 10
C2 5 30 5
C3
C4
bj 20
Penalidad 5

4. 11 = min 25,20 = 20
1 = 25 − 20 = 5
T1 T2 T3 T4 T5 ai Penalidad
C1
C2 5 30 5
C3
C4
bj 20
Penalidad 5
21 = min 30,20 = 20
2 = 30 − 20 = 10
La solución queda como sigue:
T1 T2 T3 T4 T5 ai
C1 10 2 3 15 9 25
20 20 10
C2 5 10 15 2 4 30
10 25
C3 15 5 14 7 15 20
20
C4 20 15 13 8 30
25
bj 20 20 30 10 25
La asignación óptima de máquinas y tareas es:
= 10 20 + 2 20 + 3 10 + 2 10 + 4 25 + 5 20 + 8 25
= 690

5. Caso 1:
Tres ciudades se abastecen de electricidad de tres centrales eléctricas con capacidades de 25, 40
y 30 megawatts (MW). Las demandas máximas en las tres ciudades se estiman en 30, 35 y 25
MW. El precio por MW en las tres ciudades se muestra en la tabla.
Durante el mes de agosto hay un aumento del 20% en la demanda de cada ciudad. Que se puede
satisfacer comprando electricidad a otra red, a una tasa elevada de US$ 1000 por MW. Sin
embargo, la red no está conectada con la ciudad 3. La empresa eléctrica desea determinar el plan
más económico para distribuir y comprar la energía adicional.
Ciudad
1 2 3
Planta 1 $ 600 $ 700 $ 400
2 $ 320 $ 300 $ 350
3 $ 500 $ 480 $ 450