Descargar para leer sin conexión
Subido porJacinto González Pachón
Tema4b ud2
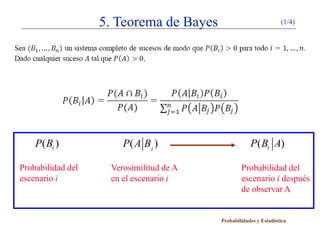
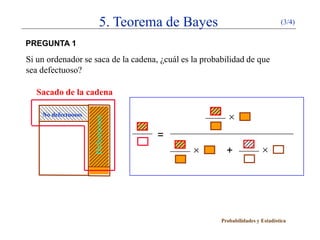
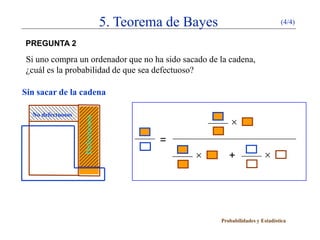
El documento presenta un esquema inicial sobre conceptos básicos de probabilidad como la probabilidad condicionada, el teorema de la probabilidad compuesta, la independencia de sucesos y el teorema de la probabilidad total. Luego, explica el teorema de Bayes a través de un ejemplo sobre la detección de defectos en ordenadores y dos preguntas relacionadas con la probabilidad de que un ordenador sea defectuoso en diferentes escenarios.
Tema4b ud2
- 1. Esquema inicial 1. Introduccióna la probabilidad condicionada 2. Teorema de la probabilidad compuesta o producto 3. Independencia de sucesos 4. Teorema de la Probabilidad Total 5. Teorema de Bayes Probabilidades y Estadística
- 2. 4. Teorema dela probabilidad total (1/2) k k = f• j ∑ fij = = 1= 1 i i ∑ f ji × fi• Estadística Descriptiva Probabilidades y Estadística
- 3. 4. Teorema dela probabilidad total (2/2) EJEMPLO Dos cajas contienen chips grandes y chips pequeños. La primera contiene 60 grandes y 40 pequeños. Mientras que la segunda contiene 20 grandes y 10 pequeños. Se selecciona una caja al azar y se extrae un chips, ¿cuál es la proba- bilidad de que sea un chip grande? Probabilidades y Estadística
- 4. Esquema inicial 1. Introduccióna la probabilidad condicionada 2. Teorema de la probabilidad compuesta o producto 3. Independencia de sucesos 4. Teorema de la Probabilidad Total 5. Teorema de Bayes Probabilidades y Estadística
- 5. 5. Teorema deBayes (1/4) P( Bi ) P( A Bi ) P( Bi A) Probabilidad del Verosimilitud de A Probabilidad del escenario i en el escenario i escenario i después de observar A Probabilidades y Estadística
- 6. 5. Teorema deBayes (2/4) EJEMPLO Supóngase que el 30% de los ordenadores fabricados por una planta son defectuosos. Si un ordenador es defectuoso, la probabilidad de que un controlador lo detecte y lo saque de la cadena de producción es 0.9. Si no es defectuoso, la probabilidad de que lo saque es 0.2. ESCENARIO Sacado de la cadena Defectuosos Sacado de la cadena No Defectuosos Probabilidades y Estadística
- 7. 5. Teorema deBayes (3/4) PREGUNTA 1 Si un ordenador se saca de la cadena, ¿cuál es la probabilidad de que sea defectuoso? Sacado de la cadena No defectuosos × Defectuosos = × + × Probabilidades y Estadística
- 8. 5. Teorema deBayes (4/4) PREGUNTA 2 Si uno compra un ordenador que no ha sido sacado de la cadena, ¿cuál es la probabilidad de que sea defectuoso? Sin sacar de la cadena No defectuosos × Defectuosos = × + × Probabilidades y Estadística