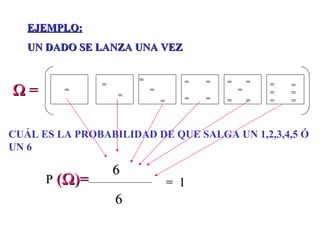
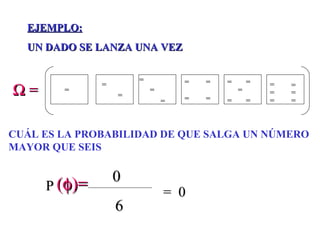
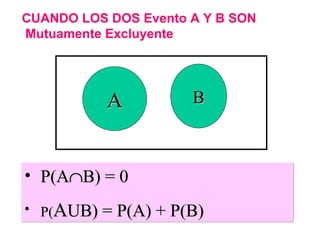
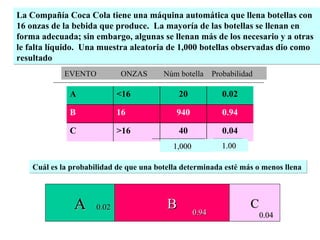
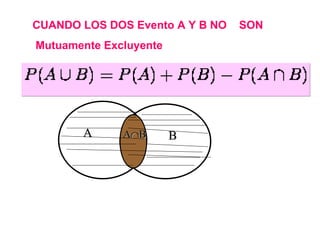
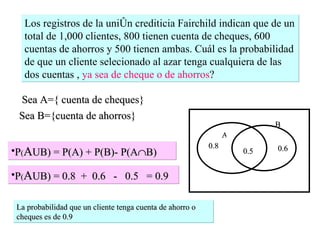
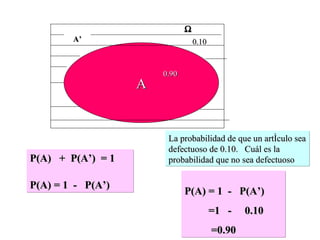
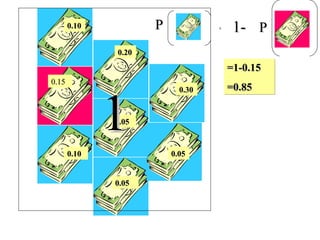
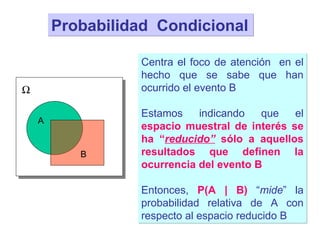
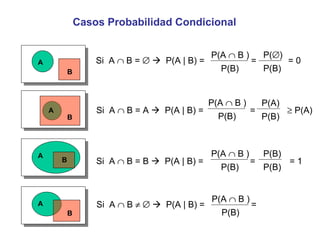
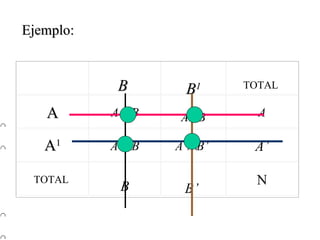
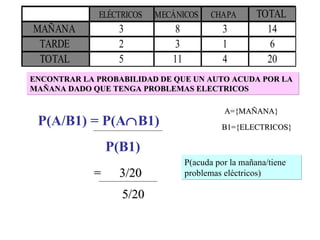
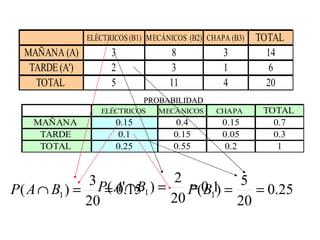
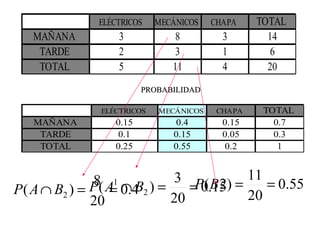
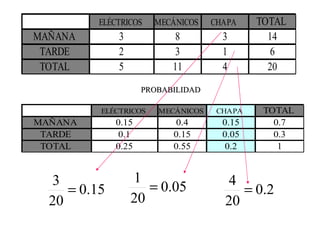
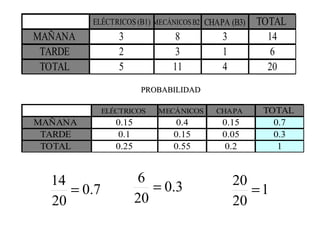
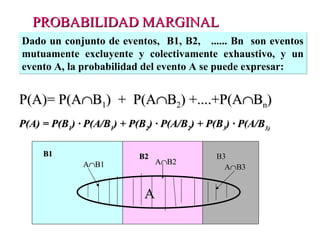
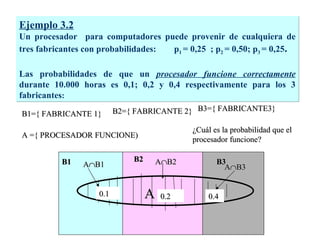
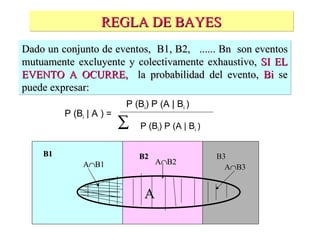
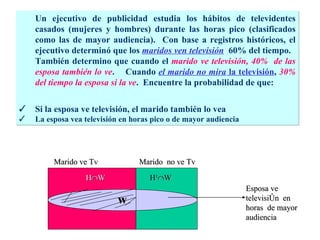
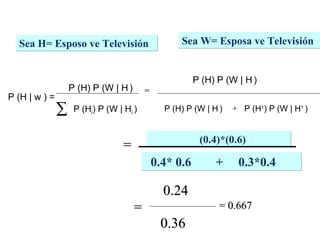
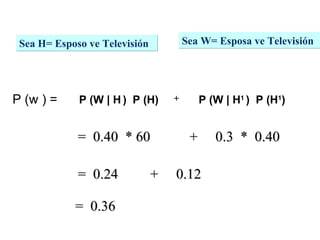
El documento define la probabilidad como una medida numérica asociada a eventos en un experimento aleatorio, que cumple ciertas propiedades. Presenta ejemplos de cálculo de probabilidades para lanzar un dado y analiza conceptos como eventos mutuamente excluyentes, eventos independientes y probabilidad condicional.

1. Probabilidad Definición: Dado un experimento E y el espacio de muestreo  respectivo, a cada evento A le asociamos un número real P ( A ), el cual es la probabilidad de A y satisface las siguientes propiedades: P (  )=1

2.  = EJEMPLO: UN DADO SE LANZA UNA VEZ CUÁL ES LA PROBABILIDAD DE QUE SALGA UN 1,2,3,4,5 Ó UN 6 (  )= P 6 6 = 1                     

3.  = EJEMPLO: UN DADO SE LANZA UNA VEZ CUÁL ES LA PROBABILIDAD DE QUE SALGA UN NÚMERO MAYOR QUE SEIS (  )= P 0 6 = 0                     

4. A B CUANDO LOS DOS Evento A Y B SON Mutuamente Excluyente P(A  B) = 0 P( A UB) = P(A) + P(B)

5. Si A 1 , A 2 , ... , A k , son mutuamente excluyentes dos a dos, entonces: P( A 1 UA 2 U... UA k ) = P( A 1 ) + P( A 2 ) + ... + P( A k )

6. La Compañía Coca Cola tiene una máquina automática que llena botellas con 16 onzas de la bebida que produce. La mayoría de las botellas se llenan en forma adecuada; sin embargo, algunas se llenan más de los necesario y a otras le falta líquido. Una muestra aleatoria de 1,000 botellas observadas dio como resultado EVENTO ONZAS Núm botella Probabilidad 1,000 1.00 Cuál es la probabilidad de que una botella determinada esté más o menos llena A B C 0.02 0.94 0.04 0.04 40 >16 C 0.94 940 16 B 0.02 20 <16 A

7. P ( A UC) = P(A) + P(C)- P(A  C) P ( A UC) = 0.02 + 0.04 - 0 = 0.06 La probabilidad de que una botella determinada esté más o menos llena es de 0.06.

8. CUANDO LOS DOS Evento A Y B NO SON Mutuamente Excluyente A B A  B

9. Los registros de la unión crediticia Fairchild indican que de un total de 1,000 clientes, 800 tienen cuenta de cheques, 600 cuentas de ahorros y 500 tienen ambas. Cuál es la probabilidad de que un cliente selecionado al azar tenga cualquiera de las dos cuentas , ya sea de cheque o de ahorros ? Sea A={ cuenta de cheques} Sea B={cuenta de ahorros} P ( A UB) = P(A) + P(B)- P(A  B) P ( A UB) = 0.8 + 0.6 - 0.5 = 0.9 0.5 0.8 0.6 A B La probabilidad que un cliente tenga cuenta de ahorro o cheques es de 0.9

10. A A’  P(A) + P(A’) = 1 P(A) = 1 - P(A’) La probabilidad de que un artículo sea defectuoso de 0.10. Cuál es la probabilidad que no sea defectuoso P(A) = 1 - P(A’) =1 - 0.10 =0.90 0.90 0.10

11. 0.10 0.20 0.30 0.05 0.05 0.10 0.05 0.15 = 1- =1-0.15 =0.85 1 P P

12. Probabilidad Condicional A  Centra el foco de atención en el hecho que se sabe que han ocurrido el evento B Estamos indicando que el espacio muestral de interés se ha “ reducido” sólo a aquellos resultados que definen la ocurrencia del evento B Entonces, P(A | B) “ mide ” la probabilidad relativa de A con respecto al espacio reducido B B

13. Probabilidad Condicional Sean A, B dos sucesos tal que P(B) > 0. La probabilidad de A condicionada a la ocurrencia de B, denotada como P(A/B) : P(A/B) = P(A  B) P(B) Propiedades: 1. P(A/B)  0 2. P(  /B) = 1 3. P(  A i /B) =  P(A i /B) con A i  A j =  ,  i, j : i  j

14. Casos Probabilidad Condicional A B Si A  B = A  P(A | B) = =  P(A) P(A  B ) P(B) P(A) P(B) A B Si A  B = B  P(A | B) = = = 1 P(A  B ) P(B) P(B) P(B) A B Si A  B =   P(A | B) = = = 0 P(A  B ) P(B) P(  ) P(B) A B Si A  B    P(A | B) = = P(A  B ) P(B)

15. Eventos independientes Dos eventos, A y B , son independientes si la ocurrencia de uno no tiene que ver con la ocurrencia de otro. A es independiente de B si y sólo si: Esto implica que: Independientes es diferente a mutuamente exclusivos La probabilidad de B dado que A ha ocurrido La probabilidad de A dado que B ha ocurrido

16. Una compañía está considerado introducir dos nuevos productos en un mercado local. El gerente cree que la posibilidad de éxito es de alrededor del 50% para el primero y de 75% para el segundo ¿Cuál es la probabilidad de que ambos productos tengan éxito. Ambas probabilidades son subjetivas porque estan basada en la opinión del gerente (experto). P(A  B) = P(A) x P(B) =0.5 x 0.75 =0.375 A B U

17. Eventos dependientes Dos eventos, A y B , son dependientes si la ocurrencia de uno AFECTA la ocurrencia de otro P(A  B) = P(A) P(A/B)

18. SUCESOS DEPENDIENTES EL SUCESO “PERSONA QUE FUMA ” CAMBIA LA PROBABILIDAD DE TENER “ CANCER DE PULMÓN” YA QUE SE HA ESTABLECIDO UNA RELACIÓN MÉDICA ENTRE ESTOS DOS SUCESOS

19. Los datos históricos muestran que el 10% de las lavadoras de una lavandería automática necesitan motor nuevo durante los primeros dos años de operación. De aquellas que necesitan motores nuevos , el 25% también necesita una correa de transmisión nueva durante el mismo periodo. ¿Cúal es la probabilidad de que una lavadora necesite tanto un nuevo motor como una correa de transmisión nueva durante los primeros dos años?

20. Probabilidad dependiente 100% lavadoras Evento A = { necesite motor nuevo} B = { necesite correa de trasmisión} Cuál es la probabilidad que una lavadora necesite un motor nuevo y correa de transmisión? P(A  B) = P(A) P(A/B) =0.10 x 0.25 =0.025 Se sabe que el 10% de las lavadoras necesita de un motor nuevo después de 2 años de operación Se ha encontrado que el 25% de las lavadoras que necesitan motor nuevo también necesitan de una correa nueva Por lo tanto el 90% no requieren de motor nuevo durante los dos años de operación

21. TABLA 2 X 2

22. Ejemplo: B B 1 TOTAL A A  B A  B A A 1 A’  B A’  B’ A’ TOTAL B B’ N

23. Ejemplo: B B 1 TOTAL A P( A  B ) P(A  B 1 ) P( A ) A 1 P( A’  B) P(A’  B’) P( A’ ) TOTAL P( B ) P(B’) 1

24. RAZONES POR LA QUE INGRESAN LOS AUTOMOVILES A UN TALLER SEGÚN HORARIO B1= {ELECTRICOS} B2={MECANICOS} B3={CHAPA} EVENTOS A={MAÑANA} A’={TARDE}

26. ENCONTRAR LA PROBABILIDAD DE QUE UN AUTO ACUDA POR LA MAÑANA DADO QUE TENGA PROBLEMAS ELECTRICOS P(A/B1) = P(A  B1) P(B1) A={MAÑANA} B1={ELECTRICOS} P(acuda por la mañana/tiene problemas eléctricos) = 3/20 5/20

27. PROBABILIDAD

28. PROBABILIDAD

29. PROBABILIDAD

30. PROBABILIDAD

31. PROBABILIDAD MARGINAL P(A)= P(A  B 1 ) + P(A  B 2 ) +....+P(A  B n ) Dado un conjunto de eventos, B1, B2, ...... Bn son eventos mutuamente excluyente y colectivamente exhaustivo, y un evento A, la probabilidad del evento A se puede expresar: B1 B2 B3 A  B1 A  B2 A  B3 A P(A) = P(B 1 ) · P(A/B 1 ) + P(B 2 ) · P(A/B 2 ) + P(B 3 ) · P(A/B 3)

32. Ejemplo 3.2 Un procesador para computadores puede provenir de cualquiera de tres fabricantes con probabilidades: p 1 = 0,25 ; p 2 = 0,50; p 3 = 0,25 . Las probabilidades de que un procesador funcione correctamente durante 10.000 horas es 0,1; 0,2 y 0,4 respectivamente para los 3 fabricantes : B1={ FABRICANTE 1} B3={ FABRICANTE3} B2={ FABRICANTE 2} A ={ PROCESADOR FUNCIONE) B1 B2 B3 A  B1 A  B2 A  B3 A 0.1 0.2 0.4 ¿Cuál es la probabilidad que el procesador funcione?

33. Solución = 0,25 *0.1+ 0,5*0.2 + 0,25*0,4 = 0,225. P(A)= P(A  B 1 ) + P(A  B 2 ) +P(A  B 3 ) P(A) = P(B 1 ) · P(A/B 1 ) + P(B 2 ) · P(A/B 2 ) + P(B 3 ) · P(A/B 3)

34. REGLA DE BAYES Dado un conjunto de eventos, B1, B2, ...... Bn son eventos mutuamente excluyente y colectivamente exhaustivo, SI EL EVENTO A OCURRE, la probabilidad del evento, Bi se puede expresar: B1 B2 B3 A  B1 A  B2 A  B3 A  P (B i | A ) = P (B i ) P ( A | B i ) P (B i ) P ( A | B i )

35. Un ejecutivo de publicidad estudia los hábitos de televidentes casados (mujeres y hombres) durante las horas pico (clasificados como las de mayor audiencia). Con base a registros históricos, el ejecutivo determinó que los maridos ven televisión 60% del tiempo. También determino que cuando el marido ve televisión, 40% de las esposa también lo ve . Cuando el marido no mira la televisión , 30% del tiempo la esposa si la ve . Encuentre la probabilidad de que: Si la esposa ve televisión, el marido también lo vea La esposa vea televisión en horas pico o de mayor audiencia

36. Un ejecutivo de publicidad estudia los hábitos de televidentes casados (mujeres y hombres) durante las horas pico (clasificados como las de mayor audiencia). Con base a registros históricos, el ejecutivo determinó que los maridos ven televisión 60% del tiempo. También determino que cuando el marido ve televisión, 40% de las esposa también lo ve . Cuando el marido no mira la televisión , 30% del tiempo la esposa si la ve . Encuentre la probabilidad de que: Si la esposa ve televisión, el marido también lo vea La esposa vea televisión en horas pico o de mayor audiencia Marido ve Tv Marido no ve Tv Esposa ve televisión en horas de mayor audiencia H  W w H 1  W

37. Sea H= Esposo ve Televisión 0.4* 0.6 + 0.3*0.4 (0.4)*(0.6) 0.24 0.36 = 0.667  P ( H | w ) = P ( H ) P ( W | H ) P ( H i ) P ( W | H i ) = = = P ( H ) P ( W | H ) P ( H 1 ) P ( W | H 1 ) Sea W= Esposa ve Televisión P ( H ) P ( W | H ) +

38. Sea H= Esposo ve Televisión Sea W= Esposa ve Televisión P (w ) = P ( W | H ) P ( H ) P ( W | H 1 ) P ( H 1 ) + = 0.40 * 60 + 0.3 * 0.40 = 0.24 + 0.12 = 0.36