Más contenido relacionado
Similar a Tema5_euclideo.pdf
Similar a Tema5_euclideo.pdf (20)
Último
Último (20)
Tema5_euclideo.pdf
- 1. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal Tema 5: Espacio Euclídeo Matemáticas I IITV Tema 5: Espacio Euclídeo
- 2. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal Contenidos 1 Concepto de producto escalar y espacio euclídeo 2 Módulo de un vector, ángulo, distancia y ortogonalidad 3 Proceso de ortonormalización de Gramm-Schmidt 4 Variedad lineal ortogonal Tema 5: Espacio Euclídeo
- 3. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal Producto escalar En Rn, un producto escalar es una aplicacion < ·, · >: Rn × Rn −→ R que verica: 1 x + y, z = x, z + y, z , ∀x, y, z ∈ Rn 2 λx, y = λ x, y , x, λy = λ x, y , ∀x, y ∈ Rn, ∀λ ∈ R 3 x, x ≥ 0, x, x = 0 ⇐⇒ x = 0; ∀x ∈ Rn 4 x, y = y, x , ∀x, y ∈ Rn Espacio euclídeo Un espacio euclídeo es un espacio vectorial dotado de un producto escalar: (V, ·, · ) Tema 5: Espacio Euclídeo
- 4. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal Nota Usaremos el producto escalar usual que viene dado por x1 · · xn , y1 · · yn = x1y1 + . . . + xnyn Ejemplo Sean en R4 los vectores x = 1 2 −1 3 , y = −1 1 2 0 x, y = 1 2 −1 3 , −1 1 2 0 = −1 + 2 − 2 + 0 = −1 Tema 5: Espacio Euclídeo
- 5. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal Módulo o norma Se dene la norma o módulo de un vector x ∈ Rn como ||x|| = √ x, x Propiedades 1 ||x|| ≥ 0, ∀x ∈ Rn 2 ||x|| = 0 ⇐⇒ x = 0 3 ||λx|| = |λ|||x|| 4 ||x + y|| ≤ ||x|| + ||y|| 5 | x, y | ≤ ||x|| ||y|| Expresión trigonométrica de producto escalar Se verica que x, y = ||x|| ||y||cos( z}|{ x, y ) Tema 5: Espacio Euclídeo
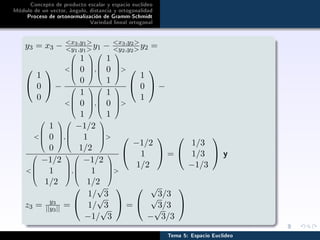
- 6. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal Ángulo Se dene el ángulo que forman dos vectores x, y ∈ Rn como el único α ∈ [0, π] tal que cos(α) = x,y ||x|| ||y|| Perpendicularidad Dos vectores, x, y ∈ Rn son perpendiculares u ortogonales (x ⊥ y) si x, y = 0. Un vector se dice normalizado o untario si ||x|| = 1. Nota Si x 6= 0, entonces y = x ||x|| es unitario. Tema 5: Espacio Euclídeo
- 7. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal base ortogonal y ortonormal Una base B = {u1, . . . , un} es ortogonal si ui, uj = 0, ∀1 ≤ i j ≤ n. La base B es ortonormal si además se verica ||uk|| = 1, ∀1 ≤ k ≤ n. Proceso de ortonormalización de Gram-Schmidt Dada una base B = {x1, . . . , xn}, construímos una base ortogonal B0 = {y1, . . . , yn} y otra ortonormal B00 = {z1, . . . , zn} Tema 5: Espacio Euclídeo
- 8. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal Proceso de ortonormalización de Gram-Schmidt y1 = x1, z1 = y1 ||y1|| y2 = x2 + λy1, y2, y1 = 0, x2 + λy1, y1 = x2, y1 +λ y1, y1 = 0, λ = −x2,y1 y1,y1 . Así, y2 = x2 − x2,y1 y1,y1 y1, z2 = y2 ||y2|| y3 = x3 + λy1 + µy2, como y3, y1 = x3 + λy1 + µy2, y1 = 0, deducimos que λ = −x3,y1 y1,y1 . Además, como y3, y2 = x3 + λy1 + µy2, y2 = 0, obtenemos que µ = −x3,y2 y2,y2 . Así que y3 = x3 − x3,y1 y1,y1 y1 − x3,y2 y2,y2 y2, z3 = y3 ||y3|| . Tema 5: Espacio Euclídeo
- 9. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal Ejemplo Ortonormalizar la base B = { 1 0 1 , 0 1 1 , 1 0 0 } Sea y1 = x1 = 1 0 1 , z1 = y1 ||y1|| = 1 √ 2 0 1 √ 2 . Ahora y2 = x2 − x2,y1 y1,y1 y1 = 0 1 1 − 0 1 1 , 1 0 1 2 1 0 1 = −1/2 1 1/2 y z2 = y2 ||y2|| = − √ 6 6 √ 6 3 √ 6 6 Tema 5: Espacio Euclídeo
- 10. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal y3 = x3 − x3,y1 y1,y1 y1 − x3,y2 y2,y2 y2 = 1 0 0 − 1 0 0 , 1 0 1 1 0 1 , 1 0 1 1 0 1 − 1 0 0 , −1/2 1 1/2 −1/2 1 1/2 , −1/2 1 1/2 −1/2 1 1/2 = 1/3 1/3 −1/3 y z3 = y3 ||y3|| = 1/ √ 3 1/ √ 3 −1/ √ 3 = √ 3/3 √ 3/3 − √ 3/3 Tema 5: Espacio Euclídeo
- 11. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal Variedad lineal ortogonal Dada una variedad lineal, L ∈ Rn, la variedad lineal ortogonal a L es L⊥ = {y ∈ Rn | x, y = 0, ∀x ∈ L} Nota 1 Las variedades ortogonales son variedades complementarias. 2 Si {a1, a2, . . . , an} es base de L, entonces todo vector x ∈ L⊥ verica x, ai = 0, ∀1 ≤ i ≤ n. De hecho las ecuaciones implícitas de L⊥ son x, a1 = 0 x, a2 = 0 . . . x, an = 0 Tema 5: Espacio Euclídeo
- 12. Concepto de producto escalar y espacio euclídeo Módulo de un vector, ángulo, distancia y ortogonalidad Proceso de ortonormalización de Gramm-Schmidt Variedad lineal ortogonal Ejemplo Calcular la variedad lineal ortogonal a L cuya base es BL = { 1 1 1 , 1 1 0 }. 0 = x y z , 1 1 1 = x + y + z 0 = x y z , 1 1 0 = x + y Por tanto unas ecuaciones implícitas de L⊥ son x + y + z = 0 x + y = 0 Tema 5: Espacio Euclídeo