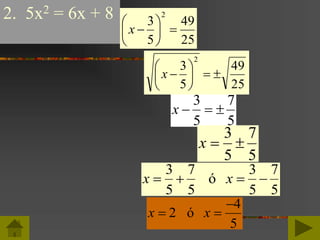
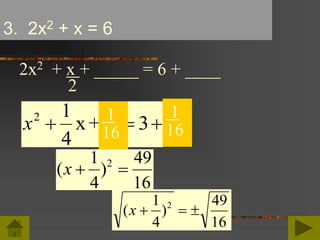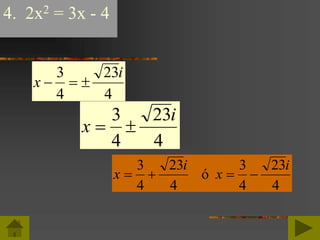Este documento trata sobre las funciones cuadráticas. Primero, describe las propiedades de las funciones cuadráticas, incluidas sus formas estándar y de vértice. Luego, explica cómo encontrar las soluciones o ceros de una función cuadrática mediante métodos como la factorización, la raíz cuadrada y completando al cuadrado. Finalmente, presenta la fórmula cuadrática y cómo usarla para hallar las soluciones.

1. Funciones
Cuadráticas

2. Índice
 Propiedades de las funciones cuadráticas
 Solución de una función cuadrática
 Formas para hallar una solución

3. Propiedades de una ecuación
cuadrática
 Forma estándar cuadrática:
ax2 + bx + c = 0 ; a ≠ 0
donde x es una variable y a , b y c son
constantes.

4. Propiedades de una ecuación
cuadrática
 Forma Vértice:
y = a(x – h)2 + k
Vértice es el punto más bajo o más alto de la parábola.
El vértice siempre es: (h, k)

5. Solución de una ecuación
cuadrática
 La solución de una ecuación cuadrática es
lo mismo que hallar los ceros de la
ecuación cuadrática.
 Los ceros de una ecuación cuadrática son
los puntos donde la parábola intercepta el
eje de x.

6. Formas de hallar la solución de
una función cuadrática
Factorización
Raíz cuadrada
Completando al cuadrado
Fórmula Cuadrática

7. Hallando la solución por
factorización

8. Ejemplo 1
Halla la solución mediante factorización:
x2 – 8x + 7 = 0
Observemos si hay factores comunes.
La otra forma de factorizar un trinomio es por tanteo :
( ___ ____ ) ( _____ _____)
Observemos si es cuadrado perfecto.
x x
Factores de x2
Factores de 7 que sumado o restado de a -8
-7 -1

9. Por lo tanto
x2 – 8x + 7 = 0
(x-7) (x-1) = 0
(x-7) = 0 ó (x-1) = 0 Propiedad del producto
de cero
x = 7 ó x = 1
Esto implica que los ceros de esa
parábola son (7,0) y (1,0)

10. Ejemplo 2
Halla la solución mediante factorización:
6x2 – 19x – 7 = 0
( ) ( ) = 02x 3x-7 + 1
Verifica que el término del
medio sea -19x
2x
-21x(2x – 7) = 0 ó (3x + 1) = 0
x = 7/2
ó x = -1/3
Los cero son (3 ½, 0) y (-1/3, 0 )

11. Ejemplo 3
Halla la solución mediante factorización:
x2 - 6x + 5 = 0
( ) ( ) = 0x x- 5 - 1
(x – 5) = 0 ( x – 1 )= 0
x = 5 ó x = 1
Los puntos son (5,0) y ( 1 ,0)

12. Ejemplo 4
Halla la solución mediante factorización:
2x2 = 3x
2x2 - 3x = 0 Igualamos a cero
Hay un factor común por lo tanto la factorización sérá:
x ( 2x – 3) = 0
x = 0 ó x = 3/2
Los interceptos son: (0,0) y (3/2,0)

13. Hallando la solución por
raíz cuadrada

14. Solución por raíz cuadrada:
2
3
x
2
2

Ejemplo 1: 2x2 – 3 = 0
2x2 = 3Despejemos por la variable
x2 = 3/2
2
6

Los interceptos son: ( , 0) y ( , 0)2
6
2
6


15. Solución por raíz cuadrada:
9x
Ejemplo 2 3x2 + 27 = 0
3x2 = -27
x2 = -27/3
x2 = -9
ix 3
Los interceptos son: (3i, 0) y (-3i, 0)

16. Solución por raíz cuadrada:
4
5
)
2
1( x
2
5
)
2
1( x
2
5
2
1
x
Ejemplo 3 (x + ½ )2 = 5/4
Primero elimina el exponente 2
Ahora elimino el 1/2
Los interceptos son:
)
2
5-1-
(y)0,
2
51
(


17. Importante:
Para resolver por raíz cuadrada la
ecuación debe tener dos términos.

18. Ejercicios:
Hoja fotocopiada p. 3

19. Hallando la solución
completando al cuadrado

20. Repasemos
Multiplica mentalmente:
1. (x+3)2
2. (x-4)2
3. (2x-7)2
4. (3x+2)2

21. Solución
Multiplica mentalmente:
1. (x+3)2
2. (x-4)2
3. (2x-7)2
4. (3x+2)2
x2 + 6x + 9
x2 – 8x + 16
4x2 – 28x + 49
9x2 + 12x + 4

22. Generalización:
El resultado de la multiplicación mentalmente del
cuadrado de un binomio :
1. Siempre será un trinomio
2. El primer y tercer término es el cuadrado
del primer y segundo término del binomio.
3. El segundo término es el doble del producto
del primer y segundo término del binomio.

23. Factoriza cada trinomio si es posible
1. x2 – 12x + 36
2. m2 + 10m + 25
3. 4t2 – 20t + 25
4. h2 – 7h + 49
5. y2 + 14y + 14
6. 9 – 6t – t2

24. Solución
1. (x – 6)2
2. (m + 5)2
3. (2t – 5)2
4. No
factorizable
5. No factorizable
6. No factorizable

25. ¿Cómo saber si un trinomio es cuadrado
perfecto?
1. El primer y tercer término son
cuadrados perfectos y positivos.
2. El segundo término es el doble del
producto de un factor de primer y tercer
termino del trinomio.

26. ¿Cómo completar al cuadrado un
trinomio?
Para completar el cuadrado de
un trinomio, se debe obtener el
tercer término.

27. ¿Cómo completar al cuadrado un
trinomio?
El tercer término se obtiene
dividiendo el segundo término por 2 y
cuadralo.

28. Generalización:
22
2
22













b
x
b
bxx

29. Ejercicios:
Completa al cuadrado.
1.x2 + 2x + _____
2.x2 –12x + _____
3.x2 + 3x + _____
1
36
9
4

30. Ejemplos:
Resuelve cada ecuación cuadrática,
completando al cuadrado.
1.x2 - 8x = -36
x2 - 8x + ____= -36
-8
2
( )2 = 16
16 +16

31. Ejemplos:
Resuelve cada ecuación cuadrática,
completando al cuadrado.
x2 - 8x + 16 = -20
(x – 4)2 = -20
x   4 20
x i  4 2 5 x i 4 2 5

32. 1. Escribe la ecuación en la
forma x2 + bx + ___ = c
Pasos para resolver una ecuación
cuadrática, completando al cuadrado.

33. Pasos para resolver una ecuación
cuadrática, completando al cuadrado.
2. Busca el tercer término y
suma éste al termino c.

34. Pasos para resolver una ecuación
cuadrática, completando al cuadrado.
Obten la raíz cuadrada del
binomio y del término c.

35. Pasos para resolver una ecuación
cuadrática, completando al cuadrado.
4. Despeja para x.

36. 2. 5x2 = 6x + 8
5x2 - 3x +____= 8 + ___
( )2 ( ) 2
1( )
5
x2 – 3x + ____ = 8
5 5
3
5
=
3
5
9
25 
9
25
25
9
25
40
5
3
2






x

37. 2. 5x2 = 6x + 8
25
49
5
3
2






x
x   
3
5
7
5
25
49
5
3
2






x
x  
3
5
7
5
x x   
3
5
7
5
3
5
7
5
ó
x x 

2
4
5
ó

38. 3. 2x2 + x = 6
2x2 + x + _____ = 6 + ____
2
x2 1
4
3  x+
(x  
1
4
49
16
)2
(x   
1
4
49
16
)2
1
16
1
16

39. 3. 2x2 + x = 6
(x   
1
4
7
4
)
x   
1
4
7
4
x    
1
4
7
4
7
4
ó x = -
1
4
x  
3
2
ó x = -2

40. 4. 2x2 = 3x - 4
2x2 –3x + ____= -4 + _____
2
1( )
2
x2 – 3x + ____= -2 + ____
4
9
16
( )x  
3
4
23
16
2
9
16

41. 4. 2x2 = 3x - 4
x
i
  
3
4
23
4
x
i
 
3
4
23
4
x
i
x
i
   
3
4
23
4
3
4
23
4
ó

42. Intenta
Halla el conjunto de solución completando
al cuadrado:
1. x2 + 6x – 2 = 0
2. 2x2 –4x + 3 = 0
3. x2 + 8x = 3

43. Ejercicios de Práctica
Hoja fotocopiada p.4 A, B y C
Advanced Algebra p. 237
(1-6) (9-20)

44. Hallando la solución
fórmula cuadrática

45. ¿Sabes el objetivo de usar la
fórmula cuadrática?

46. Esta se deriva de la ecuación
ax2 + bx + c = 0

47. Y ¿Cómo se usa?
Ejemplo 1:
Halla los valores de la variable en la
ecuación 2x2 + 6x + 1 = 0
a = 2 ; b = 6 ; c = 1
Al sustituir en la fórmula
cuadrática obtendremos:

48. Y ¿Cómo se usa?
Ejemplo 1:
x
b b ac
a

  2
4
2 )2(2
)1)(2(466 2


4
8366 

x 
 6 28
4 4
726 
 4
72
4
6



2
7
2
3



x 
 3 7
2

49. Ejemplo 1:
Halla los valores de la variable en la
ecuación 2x2 = -6x - 7
a = 2 ; b = 6 c = 7
x
b b ac
a

  2
4
2
2x2 + 6x + 7 = 0

50. Ejemplo 1:
Halla los valores de la variable en la
ecuación 2x2 = -6x - 7
x 
  6 6 4 2 7
2 2
2
( ) ( )( )
( ) 4
56366 

4
206 

x
i

 6 2 5
4 4
52
4
6 i



2
5
2
3 i



2
53
ó
2
53 i
x
i
x





51. El discriminante

52. El discriminante nos puede indicar si
la solución de una función
cuadrática es una o dos reales; o
complejas.

53. El discriminante nos puede indicar si
la solución de una función
cuadrática es una o dos reales; o
complejas.

54. Discriminante
Y....
El discriminante es la parte
de la ecuación cuadrática
b2- 4ac

55. Discriminante
Y....
Si b2 – 4ac es:
> 0 tiene dos interceptos en x
= 0 tiene un intercepto en x
< 0 no tiene intercepto en x

56. En otras palabras:
Si el discriminante es:
> 0 Tendrá dos soluciones reales
< 0 Tendrá soluciones complejas o no
reales
= 0 Tendrá solo una solución real

57. Ejemplo 1:
Halla el discriminante para determinar si la
solución es real o compleja.
1.x2+ 5x – 14 = 0
2.3x2 –7x + 5 = 0
3.x2 – 2x +1 = 0

58. Solución:
1. 81 Implica que tiene dos soluciones
reales
2. -11
Implica que tiene dos soluciones
complejas
3. 0
Implica que tiene una solución
real

59. Ejemplo 2:
Halla los valores de la variable en la
ecuación x2 - x - 1 = 0 , utilizando la
fórmula cuadrática.
a = 1 ; b = -1 c = -1

60. Solución:
Halla los valores de la variable en la
ecuación x2 - x - 1 = 0
a = 1 ; b = -1 c = -1
x
b b ac
a

  2
4
2
)1(2
)1)(1(4)1(1 2

x 
 1 1 4
2 2
51


61. ¿Cómo se halla los interceptos en
una función cuadrática?
Si le das valor de cero a la y podrás
encontrar los valores de x y éstos
serán los interceptos de la función
cuadrática.

62. Ejemplo 3:
Indica cuántos interceptos en x tiene las
siguientes funciones cuadráticas.
1.x2+ 5x – 14 = 0
2.3x2 –7x + 5 = 0
3.x2 – 2x +1 = 0

63. Solución:
1. 81 Implica que tiene dos soluciones
reales
2. -11
Implica que tiene dos soluciones
complejas
3. 0
Implica que tiene una solución
real

64. Intercepto en y:
Si y = 2x2 – 3x + 5 ¿Cuál
será el intercepto en y?

65. Intercepto en y:
Si le damos valor de x = 0 ...
O sea y = 5

66. Intercepto en y:
Obtendremos que y = 2(0)2 –3(0) + 5

67. Intercepto en y:
O sea y = 5

68. Intercepto en y:
El intercepto en y será (0,5).

69. Ejemplos:
Halla los interceptos de x de las siguientes
funciones cuadráticas.
1.y = x2+ 5x – 14
2.y = 3x2 –7x + 5
3.y = x2 – 2x +1

70. Solución:
1. Los puntos son: (-7,0) y (2,0)
2. No tiene interceptos
3. El punto es (1,0)

71. Ahora podrás hacer la
gráfica de una función
cuadrática con:

72. Con los puntos reflejos

73. El vértice y
su eje de simetria

74. Con los interceptos ( si lo tiene)

75. Recuerda que...

76. Para obtener los valores de x hay
varias formas:

77. Factorización

78. Raíz Cuadrada

79. Completando al cuadrado

80. Fórmula cuadrática

81. Ejercicios:
Libro Guía...