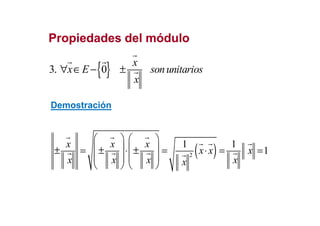
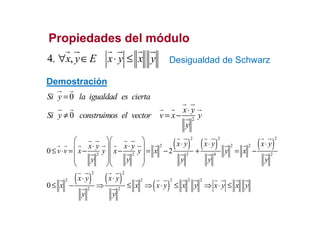
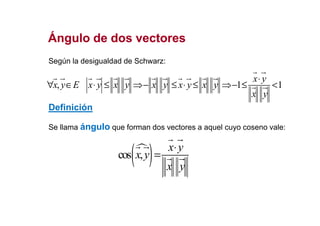
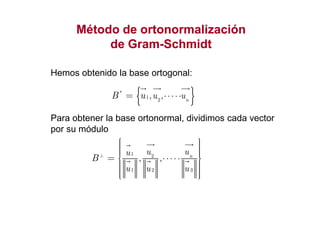
Este documento describe los conceptos fundamentales de los espacios vectoriales euclídeos, incluyendo el producto escalar, módulo de un vector, propiedades del módulo, ángulo entre vectores, ortogonalidad, subespacios ortogonales y bases ortonormales. También presenta el método de Gram-Schmidt para obtener una base ortonormal a partir de una base cualquiera.

1. ESPACIOSESPACIOS VECTORIALESVECTORIALES
EUCLÍDEOSEUCLÍDEOSEUCLÍDEOSEUCLÍDEOS
Sección Departamental de Matemáticas. Algeciras.

2. Producto escalarProducto escalar
Sea E un espacio vectorial.
Un producto escalar es una aplicación de
que a cada par de vectores le asocia un número real
que representamos por y que cumple las siguientes
propiedades:
( ),x y
x y⋅
E E en× ℝ
propiedades:
{ }
( ) ( ) ( )
1. 0 0
2. ,
3. , , ,
x E x x
x y E x y y x
x y z E x y z x z y zλ α λ α λ α
∀ ∈ − ⋅ >
∀ ∈ ⋅ = ⋅
∀ ∈ ∀ ∈ + ⋅ = ⋅ + ⋅ℝ
Un espacio vectorial euclídeo es un espacio vectorial en el
que hay definido un producto escalar.

3. Módulo de un vectorMódulo de un vector
= + ⋅
Se define el módulo o longitud de un vector de un
espacio vectorial euclídeo y se denota por a:
x
x
x x x= + ⋅
Si se dice que el vector es unitario.1x =

4. 1. 0 0x x= ⇔ =
Propiedades del móduloPropiedades del módulo
Demostración
0 0 0 0x x x x x x= ⇒+ ⋅ = ⇒ ⋅ = ⇒ =
0 0 0x x x x= ⇒ ⋅ = ⇒ =
2. y x E x xλ λ λ∀ ∈ ∀ ∈ =ℝ
Demostración
( ) ( ) ( )2
x x x x x x x xλ λ λ λ λ λ= ⋅ = ⋅ = ⋅ =

5. { }3. 0
x
x E sonunitarios
x
∀ ∈ − ±
Propiedades del móduloPropiedades del módulo
Demostración
( )2
1 1
1
x x x
x x x
x x x xx
   
   ± = ± ⋅ ± = ⋅ = =
   
   

6. 4. ,x y E x y x y∀ ∈ ⋅ ≤
Propiedades del móduloPropiedades del módulo
Demostración
0Si y la igualdad es cierta=
Desigualdad de Schwarz
0
x y
Si y construimos el vector v x y
⋅
≠ = − 2
0
x y
Si y construimos el vector v x y
y
⋅
≠ = −
( ) ( ) ( )
2 2 2
2 2 2
2 2 2 4 2
0 2
x y x y x yx y x y
v v x y x y x y x
y y y y y
   ⋅ ⋅ ⋅⋅ ⋅  ≤ ⋅ = − − = − + = −
    
  
( ) ( )
( )
2 2
22 2 2 2
2 2
0
x y x y
x x x y x y x y x y
y y
⋅ ⋅
≤ − ⇒ ≤ ⇒ ⋅ ≤ ⇒ ⋅ ≤

7. 5. ,x y E x y x y∀ ∈ + ≤ +
Propiedades del móduloPropiedades del módulo
Desigualdad Triangular
( )( ) ( ) ( )
22 2 2 2 2
2 2x y x y x y x x y y x x y y x y+ = + + = + ⋅ + ≤ + + = +
Demostración
De donde
( )( ) ( ) ( )2 2x y x y x y x x y y x x y y x y+ = + + = + ⋅ + ≤ + + = +
( )
22
x y x y x y x y+ ≤ + ⇒ + ≤ +

8. 6. ,x y E x y x y∀ ∈ − ≥ −
Propiedades del móduloPropiedades del módulo
Demostración
x x y y x y y x y x y
y x y x y x x y x y x x y x y x y
 = + − ≤ − + ⇒ − ≤ −

= + − ≤ − + ⇒ − ≤ − = − ⇒ − − ≤ −
Luego
x y x y x y x y x y− − ≤ − ≤ − ⇒ − ≤ −

9. , 1 1
x y
x y E x y x y x y x y x y
x y
⋅
∀ ∈ ⋅ ≤ ⇒− ≤ ⋅ ≤ ⇒− ≤ <
Ángulo de dos vectoresÁngulo de dos vectores
Definición
Según la desigualdad de Schwarz:
( )cos ,
x y
x y
x y
⋅
=
Se llama ángulo que forman dos vectores a aquel cuyo coseno vale:

10. OrtogonalidadOrtogonalidad
Definición
Sea V un espacio vectorial euclídeo
Se dice que dos vectores son ortogonales si,x y V∈
0x y x y⊥ ⇔ ⋅ =
Se dice que dos vectores son ortogonales si
su producto escalar es nulo.
,x y V∈

11. 1. 0 0x V x∀ ∈ ⋅ =
Propiedades de la ortogonalidadPropiedades de la ortogonalidad
Demostración
{ } 22. , 0 ,Si x y V y x y x y π∈ − ⊥ ⇒ =
Demostración
En efecto, si
( ) ( ) 2
0
cos , cos , 0 ,x y x y x y
x y
π= ⇒ = ⇒ =
0x y x y⊥ ⇒ ⋅ =
Luego:

12. Propiedades de la ortogonalidadPropiedades de la ortogonalidad
Demostración
0x y x y⊥ ⇒ ⋅ =
2 2 2
3. ,x y V son x y x y x y∈ ⊥ ⇔ + = +
De igual forma:
2 2 2 2 2 2
2Como x y x x y y x y x y+ = + ⋅ + ⇒ + = +
2 2 2
2 0 0Si x y x y x y x y x y+ = + ⇒ ⋅ = ⇒ ⋅ = ⇒ ⊥

13. SubespaciosSubespacios ortogonalesortogonales
Sea V un espacio vectorial euclídeo. Sea S un
subespacio vectorial de V
x V∈
Definición
0y S x y∀ ∈ ⋅ =
x S⊥Lo representamos por:
Se dice que un vector es ortogonal a S
si:
x V∈

14. SubespaciosSubespacios ortogonalesortogonales
se verifica que 0x S y y L x y∀ ∈ ∀ ∈ ⋅ =
Dos subespacios S y L de V , son ortogonales si:
Definición
se verifica que 0x S y y L x y∀ ∈ ∀ ∈ ⋅ =
S L⊥Lo representamos por:

15. SubespaciosSubespacios ortogonalesortogonales
Dos subespacios S y L de V , son ortogonales si y
solo sí los vectores de una base de S son ortogonales
a los de una base de L
Proposición 1
Demostración
Si se verifica que 0S L x S y y L x y⊥ ⇒ ∀ ∈ ∀ ∈ ⋅ =
Demostración
Sea una base de S y
una base de L
{ }1
2
, ,S n
u uB u ⋅⋅⋅⋅⋅=
{ }1
2
, ,L n
v vB v ⋅⋅⋅⋅⋅=
Luego 0 ,i j
u v i j⋅ = ∀
. .c n
⇒
ya que ,i j
u S y v L i j∈ ∈ ∀

16. SubespaciosSubespacios ortogonalesortogonales
Si
. .c s
⇐
1
n
i i
i
x S x x u
=
∈ ⇒ = ∑
Si
1
n
j j
j
y L y y v
=
∈ ⇒ = ∑
( )1 1 1 1
Luego 0
n n n n
i i j j i j i j
i j i j
x y x u y v x y u v
= = = =
⋅ = ⋅ = ⋅ =∑ ∑ ∑∑
Ya que 0 ,i j
u v i j⋅ = ∀ por tanto S L⊥

17. Base ortogonalBase ortogonal
Definición
Sea una base de un espacio
vectorial euclídeo V
{ }1
2
, , n
u uB u ⋅⋅⋅⋅⋅=
Se dice que B es una base ortogonal si sus vectores
0i j
u u i j⋅ = ∀ ≠
Se dice que B es una base ortogonal si sus vectores
son ortogonales dos a dos:

18. Base ortonormalBase ortonormal
Definición
Sea una base de un espacio
vectorial euclídeo V
{ }1
2
, , n
u uB u ⋅⋅⋅⋅⋅=
Se dice que B es una base ortonormal si sus vectores
0
1
i j
i
u u i j
u i
 ⋅ = ∀ ≠
 = ∀
Se dice que B es una base ortonormal si sus vectores
son ortogonales dos a dos y unitarios:

19. Teorema
Si es un conjunto finito de vectores
ortogonales dos a dos, no nulos de V, entonces es libre.
{ }1
2
, , n
u uH u ⋅⋅⋅⋅⋅=
( )
n n n
Demostración
( )1 1 1
0 0 0
n n n
i i j i i i j i
i i i
Sea u u u u uλ λ λ
= = =
= ⇒ ⋅ = ⇒ ⋅ = ⇒∑ ∑ ∑
( )
2
0 0 0j j j j j j ju u ya que u u uλ λ⋅ = ⇒ = ⋅ = ≠
y se verifica j∀

20. Producto escalar y módulo de un vectorProducto escalar y módulo de un vector
referido a una base ortonormalreferido a una base ortonormal
Sea una base ortonormal de V{ }1
2
, , n
u uB u ⋅⋅⋅⋅⋅=
1
n
i i
i
x V x x u
=
∈ ⇒ = ∑
1
n
j j
j
y V y y u
=
∈ ⇒ = ∑
( )1 1 1 1 1 1
Luego
n n n n n n
i i j j i j i j i j
i j i j i j
x y x u y u x y u u x y
= = = = = =
⋅ = ⋅ = ⋅ =∑ ∑ ∑∑ ∑∑
1i=
1 1 2 2
matricialmente
t
n n
x y x y x y x y x y⋅ = = + +⋅⋅⋅⋅⋅+
2 2 2 2
1 2 3
Y n
x x x x x x x=+ ⋅ =+ + + +⋅⋅⋅⋅+

21. Método de ortonormalizaciónMétodo de ortonormalización
de Gramde Gram--SchmidtSchmidt
Método para obtener una base ortonormal de V a partir
de una base cualquiera { }1
2
, , n
e eB e ⋅⋅⋅⋅⋅=
Primero obtenemos una base ortogonal { }*
1, ,u uB u ⋅⋅⋅⋅⋅=Primero obtenemos una base ortogonal { }1
2
, , n
u uB u ⋅⋅⋅⋅⋅=
1 1
2 2 1 1
3 3 1 1 2 2
1
1 1 2 2 1
n
n n n
u e
u e u
u e u u
u e u u u
α
λ λ
β β β −
−
 = = + = + +
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ = + + + ⋅ ⋅ ⋅ ⋅ +

22. Método de ortonormalizaciónMétodo de ortonormalización
de Gramde Gram--SchmidtSchmidt
Y hallamos los escalares haciendo 0i j
u u i j⋅ = ∀ ≠
Por tanto:
( ) 1 2
1 2 1 1 1 2 1 1 1 11 2
0 0
u e
u e u u e u uu u α α α
⋅
= ⇒ ⋅ + = ⋅ + ⋅ = ⇒ = −⋅ ( )1 2 1 1 1 2 1 1 1 1
1 1
1 2
u u
u u α α α
⋅
⋅
1 3
3 1 1 1 1
1 1
1 1 3 2 1 2
0 0
u e
u u
u u
u u e u uu β ββ ⇒
⋅
⋅ = ⇒ + ⋅ = = −
⋅
⋅ + ⋅
2 3
3 1 2 1 2
2 2
2 2 3 2 2 2
0 0
u e
u u
u u
u u e u uu β ββ ⇒
⋅
⋅ = ⇒ + ⋅ = = −
⋅
⋅ + ⋅

23. Método de ortonormalizaciónMétodo de ortonormalización
de Gramde Gram--SchmidtSchmidt
Siguiendo este proceso obtendríamos:
1 2
1
1 1
2 2
u e
u
u u
u e
⋅
= −
⋅
1 1
u e=
u e u e⋅ ⋅1 3 2 3
1 2
1 1 2 2
3 3
u e u e
u u
u u u u
u e
⋅ ⋅
= − −
⋅ ⋅
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
1 2 1
1 2 1
1 1 2 2 1 1
n n n n
n
n n
n n
u e u e u e
u u u
u u u u u u
u e −
−
− −
⋅ ⋅ ⋅
= − −
⋅ ⋅ ⋅
⋅⋅⋅⋅⋅⋅−

24. Método de ortonormalizaciónMétodo de ortonormalización
de Gramde Gram--SchmidtSchmidt
Hemos obtenido la base ortogonal:
{ }*
1
2
, , n
u uB u ⋅⋅⋅⋅⋅=
Para obtener la base ortonormal, dividimos cada vectorPara obtener la base ortonormal, dividimos cada vector
por su módulo
1 2
1 2 3
, , n
u uu
u u u
B⊥
     ⋅⋅⋅⋅⋅ 
     
=

25. Suplemento ortogonalSuplemento ortogonal
Sea V un espacio vectorial euclídeo. Sea L un
subespacio vectorial de V.
{ }
Definimos el conjunto:
L x V⊥
= ∈{ }0x u u L⋅ = ∀ ∈
Veamos que dicho conjunto es un subespacio
vectorial de V , denominado suplemento ortogonal
de L.

26. Suplemento ortogonalSuplemento ortogonal
Proposión 1Proposión 1
1. , veamos quex y L x y L⊥ ⊥
∈ + ∈
Demostración
es un subespacio vectorialL⊥
1. , veamos quex y L x y L⊥ ⊥
∈ + ∈
( ) 0 0 0x y u x u y u u L x y L⊥
+ ⋅ = ⋅ + ⋅ = + = ∀ ∈ ⇒ + ∈
2. veamos quex L x Lλ λ⊥ ⊥
∈ ∈ ∈ℝ
( ) ( ) 0 0x u x u u L x Lλ λ λ λ ⊥
⋅ = ⋅ = ∀ ∈ ⇒ ∈

27. Suplemento ortogonalSuplemento ortogonal
Proposión 2Proposión 2
{ }0L L⊥
∩ =
0 0
x L x V
Si x L L x x x
x L
⊥
⊥
 ∈ ⇒ ∈
∈ ∩ ⇒ ⇒ ⋅ = ⇒ =
∈
Demostración

28. Suplemento ortogonalSuplemento ortogonal
Proposión 3Proposión 3
Por cumplir estas tres proposiciones es suplemento
L L V⊥
+ =
L⊥
Por cumplir estas tres proposiciones es suplemento
ortogonal de
Este suplemento de es único.
L
L
L

29. Proyección ortogonalProyección ortogonal
Por ser y subespacios suplementarios de VL⊥
L
,x V se tiene x u v con u L v L⊥
∀ ∈ = + ∈ ∈
u L se llama proyección ortogonal de x a lo largo de L∈
v L se llama proyección ortogonal de x a lo largo de L⊥
∈

30. Proyección de un vector sobre otroProyección de un vector sobre otro
El vector proyección de un vector
sobre un vector es:
u V∈ y V∈
x V∈
x y
u x
x x
⋅
=
⋅
Sea L x y V y x v con v Lλ ⊥
=< > ∈ ⇒ = + ∈
x x⋅
Demostración
( )0 0Si v L v x v x y x xλ⊥
∈ ⇒ ⊥ ⇒ ⋅ = ⇒ − ⋅ = ⇒
0
y x x y
y x x x u x
x x x x
λ λ
⋅ ⋅
⋅ − ⋅ = ⇒ = ⇒ =
⋅ ⋅