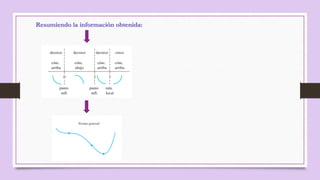
La función f(x)=x^3/5 es cóncava hacia arriba en los intervalos (-∞,0) y (2,∞), y es cóncava hacia abajo en el intervalo (0,2). La función es decreciente en los intervalos (-∞,0) y (0,3), y es creciente en el intervalo (3,∞). Los puntos críticos son x=0 y x=3, donde x=3 es un punto de mínimo local. Los puntos de inflexión son x=0 y x=2.

1. Concavidad de una
función.

2. La función 𝑓 𝑥 =
𝑥3
5
es una función creciente es su dominio, pero con un
comportamiento distinto conforme 𝑥 crece, en los intervalos −∞, 0 𝑦 0, ∞ .
Las pendientes de las rectas tangentes a la gráfica de la
función en el intervalo −∞, 0 disminuyen quedando la
gráfica de 𝑓 por debajo de todas estas rectas. Mientras
que las pendientes de las rectas tangentes a la gráfica de
𝑓 en el intervalo 0, ∞ aumentan quedando la gráfica de
𝑓 por arriba de todas estas rectas.

3. Definición: La gráfica de una función diferenciable 𝑓 es:
• Cóncava hacia arriba en un intervalo abierto I si 𝒇′ es creciente en I con lo
cual la gráfica de 𝑓 se encuentra arriba de todas sus rectas tangentes en el
intervalo I
• Cóncava hacia abajo en un intervalo abierto I si 𝒇′ es decreciente en I con
lo cual la gráfica de 𝑓 se encuentra debajo de todas sus rectas tangentes en el
intervalo I

6. Observación:
El punto de una curva 𝑦 = 𝑓(𝑥) donde 𝑓 es continua allí y 𝑓′′ es positiva de un lado y
negativa del otro es un punto de inflexión. En tal punto 𝒇′′ es cero o no está definida.

7. Prueba de la derivada segunda para extremos locales
Si 𝑓′′ es continua en un intervalo abierto que contiene a 𝑐
1. Si 𝑓′
𝑐 = 0 𝑦 𝑓′′
𝑐 < 0 entonces 𝑓 tiene un máximo local en 𝑐.
2. Si 𝑓′
𝑐 = 0 𝑦 𝑓′′
𝑐 > 0 entonces 𝑓 tiene un mínimo local en 𝑐.
3. Si 𝑓′
𝑐 = 0 𝑦 𝑓′′
𝑐 = 0 el criterio no es concluyente, 𝑓 puede tener en 𝑐 un máximo local
o un mínimo local o nada.

8. Prueba de la derivada segunda para extremos locales
Si 𝑓′′ es continua en un intervalo abierto que contiene a 𝑐
1. Si 𝑓′
𝑐 = 0 𝑦 𝑓′′
𝑐 < 0 entonces 𝑓 tiene un máximo local en 𝑐.
2. Si 𝑓′
𝑐 = 0 𝑦 𝑓′′
𝑐 > 0 entonces 𝑓 tiene un mínimo local en 𝑐.
3. Si 𝑓′
𝑐 = 0 𝑦 𝑓′′
𝑐 = 0 el criterio no es concluyente, 𝑓 puede tener en 𝑐 un máximo local
o un mínimo local o nada.

9. Juntas, 𝑓′ y 𝑓′′, nos indican la forma de la gráfica de una función, esto es, dónde se localizan los
números críticos y lo que sucede en un número crítico, dónde es creciente la función, dónde es
decreciente y cómo abre la curva de acuerdo con su concavidad.
Ejercicio: Dada la función 𝑓 𝑥 = 𝑥4
− 4𝑥3
− 10
1) Determinar los intervalos en los que 𝑓 es creciente y los intervalos donde 𝑓 es decreciente.
2) Determinar dónde la gráfica de 𝑓 es cóncava hacia arriba y dónde es cóncava hacia abajo.
3) Identificar algunos puntos específicos, tales como los puntos máximos y mínimos locales, los
puntos de inflexión.
4) Realizar un bosquejo general de la gráfica de 𝑓.

10. 𝒇 𝒙 = 𝒙𝟒
− 𝟒𝒙𝟑
− 𝟏𝟎
1) El dominio de 𝑓 es ℝ.
𝑓′
𝑥 = 4𝑥3
− 12𝑥2
, su dominio es ℝ. Así que los números críticos de 𝑓 se alcanzan sólo en los
ceros de 𝑓′
.
𝑓′
𝑥 = 4𝑥3
− 12𝑥2
= 4𝑥2
𝑥 − 3 , 𝑓′
es cero en 𝑥 = 0 y 𝑥 = 3
Intervalos Signo 𝒙𝟐 Signo (𝑥 − 𝟑) Signo 𝑓’ Comportamiento de 𝑓
(−∞, 0) + − − 𝑓 decrece en (−∞, 0)
(0,3) + − − 𝑓 decrece en (0,3)
(3, ∞) + + + 𝑓 crece en (3, ∞)
Por medio del criterio de la primera derivada para extremos locales y la tabla anterior, vemos que
no hay extremo local en 𝑥 = 0 y hay un mínimo local en 𝑥 = 3.

11. 𝒇 𝒙 = 𝒙𝟒
− 𝟒𝒙𝟑
− 𝟏𝟎
2) 𝑓′′
𝑥 = 12𝑥2
− 24𝑥, su dominio es ℝ.
𝑓′′
𝑥 = 12𝑥2
− 24𝑥 = 12𝑥 𝑥 − 2 , 𝑓′′
es cero en 𝑥 = 0 y en 𝑥 = 2
Intervalos Signo 𝒙 Signo (𝑥 − 𝟐) Signo 𝑓’’ Comportamiento de 𝑓
(−∞, 0) − − + 𝑓cóncava hacia arriba en
(−∞, 0)
(0,2) + − − 𝑓cóncava hacia abajo en
(0,2)
(2, ∞) + + + 𝑓cóncava hacia arriba en
(2, ∞)
Por medio de la información del cuadro la gráfica de 𝑓 tiene en 𝑃(0, 𝑓(0)) y en 𝑄(2, 𝑓(2)) puntos
de inflexión.

12. Resumiendo la información obtenida:

13. Resumiendo la información obtenida:

14. Resumiendo la información obtenida: