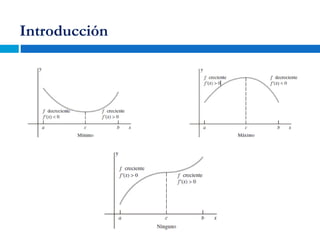
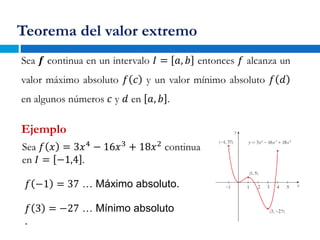
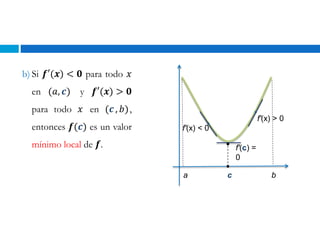
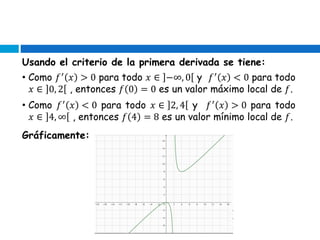
Este documento presenta los conceptos fundamentales de la derivada, incluyendo cómo determinar puntos críticos, intervalos de crecimiento y decrecimiento, y extremos locales de una función. Explica cómo usar la derivada, el teorema de monotonía y el criterio de la primera derivada para analizar funciones. El documento proporciona ejemplos detallados para ilustrar cada concepto.

1. APPLICATIONS OF THE
DERIVATIVE
Mg. Billy Toribio Aranda
Facultad de Ingeniería
MATEMÁTICA II

2. • Determinar los puntos críticos de una función usando la
derivada, mostrando orden y claridad en el manejo de la
información.
• Determinar los intervalos de crecimiento y decrecimiento de
una función usando el teorema de monotonía, mostrando
una actitud responsable y participativa.
• Identificar los extremos locales de una función haciendo uso
del criterio de la primera derivada, mostrando una actitud
analítica y responsable de la información.
En esta sesión de clase aprenderás:

3. Contenidos
 Introducción.
 Teorema del valor extremo.
 Definición de punto critico.
 Teorema de monotonía.
 Criterio de la primera derivada.

4. Introducción

5. Teorema del valor extremo
Sea 𝒇 continua en un intervalo 𝐼 = 𝑎, 𝑏 entonces 𝑓 alcanza un
valor máximo absoluto 𝑓 𝑐 y un valor mínimo absoluto 𝑓 𝑑
en algunos números 𝑐 y 𝑑 en 𝑎, 𝑏 .
Ejemplo
Sea 𝑓 𝑥 = 3𝑥4
− 16𝑥3
+ 18𝑥2
continua
en 𝐼 = −1,4 .
𝑓 −1 = 37 … Máximo absoluto.
𝑓 3 = −27 … Mínimo absoluto
.

6. Definición de punto crítico
Un punto crítico de una función 𝑓 es algún
numero 𝑐 en el dominio de 𝑓 en el cual
𝑓′ 𝑐 = 0 0 𝑓′ 𝑐 no existe.

7. Determine los puntos críticos de las siguientes
funciones
𝑎) 𝑓 𝑥 = 𝑥3
− 3𝑥2
− 9𝑥 + 2
Solución
Derivando la función 𝑓, se tiene:
𝑓′
𝑥 = 3𝑥2
− 6𝑥 − 9
Ahora igualamos la 𝑓′
𝑥 a cero, tenemos:
𝑓′
𝑥 = 0
3𝑥2
− 6𝑥 − 9 = 0 𝐷𝑖𝑣𝑖𝑑𝑖𝑒𝑛𝑑𝑜 𝑝𝑜𝑟 3
𝑥2
− 2𝑥 − 3 = 0
𝐹𝑎𝑐𝑡𝑜𝑟𝑖𝑧𝑎𝑛𝑑𝑜
𝑥 − 3 𝑥 + 1 = 0
Por tanto los puntos críticos de la función son:
𝑥 = 3 ∨ 𝑥 = −1

8. b) 𝑓 𝑥 =
𝑥2
𝑥−2
Derivando la función 𝑓, se tiene:
𝑓′
𝑥 =
𝑥2 ′
𝑥 − 2 − 𝑥2
𝑥 − 2 ′
𝑥 − 2 2
Solución
𝑓′
𝑥 =
2𝑥 𝑥 − 2 − 𝑥2
𝑥 − 2 2
𝑓′
𝑥 =
2𝑥2
− 4𝑥 − 𝑥2
𝑥 − 2 2
𝑓′
𝑥 =
𝑥2
− 4𝑥
𝑥 − 2 2

9. Ahora igualamos la 𝑓′
𝑥 a cero, tenemos:
𝑓′
𝑥 = 0
𝑥2
− 4𝑥
𝑥 − 2 2
= 0
𝐹𝑎𝑐𝑡𝑜𝑟𝑖𝑧𝑎𝑛𝑑𝑜
𝑥 𝑥 − 4
𝑥 − 2 2
= 0
𝑥 𝑥 − 4 = 0
Por tanto los puntos críticos de la función son:
𝑥 = 0 ∨ 𝑥 = 4

10. Ojo
Si 𝑥 = 2, y evaluando la derivada 𝑓′
𝑥 en este punto, se tiene:
𝑓′
2 =
22
− 4 2
2 − 2 2
𝑓′
2 =
−4
0
De esta ultima expresión se deduce que la 𝑓′
2 no existe, lo
cual satisface una parte de la definición de punto critico,
ademas 𝑥 = 2 ∉ 𝐷𝑜𝑚 𝑓 .
Por tanto 𝑥 = 2 no es punto critico de la función.

11. Ejercicios (Homework)
Determine los puntos críticos en cada una de las funciones.
a) 𝑓 𝑥 = 𝑥4
− 2𝑥2
b) 𝑓 𝑥 =
𝑥
𝑥+3
c) 𝑓 𝑥 = 2𝑥3
− 3𝑥2
− 12𝑥 + 15

12. Teorema de monotonía
Sea 𝒇 continua en un intervalo 𝐼 = 𝑎, 𝑏 y derivable en el
intervalo abierto 𝑎, 𝑏 .
1) Si 𝑓′
𝑥 > 0 ∀ 𝑥 ∈ 𝑎, 𝑏 , entonces 𝑓 es creciente en 𝐼.
2) Si 𝑓′
𝑥 < 0 ∀ 𝑥 ∈ 𝑎, 𝑏 , entonces 𝑓 es decreciente en 𝐼.
Geométricamente, se tiene:

13. Sea 𝒇 continua en un intervalo abierto (𝒂 , 𝒃) que contiene un
punto crítico 𝒄. Entonces:
1) Si 𝒇′(𝒙) > 𝟎 para todo 𝑥
en (𝑎, 𝒄) y 𝒇′(𝒙) < 𝟎 para
todo 𝑥 en (𝒄, 𝑏), entonces
𝒇(𝒄) es un valor máximo
local de 𝒇.
f'(c) = 0
a c b
Criterio de la primera derivada

14. b) Si 𝒇′(𝒙) < 𝟎 para todo 𝑥
en (𝑎, 𝒄) y 𝒇′(𝒙) > 𝟎
para todo 𝑥 en (𝒄, 𝑏),
entonces 𝒇(𝒄) es un valor
mínimo local de 𝒇. f'(c) =
0
f'(x) > 0
f'(x) < 0
a c b

15. 1) 𝑓 𝑥 = 𝑥3
− 3𝑥2
Determine los intervalos de crecimiento y los
extremos relativos de las siguientes funciones.
Solución
Derivando la función 𝑓, se tiene:
𝑓′
𝑥 = 3𝑥2
− 6𝑥
𝑓′
𝑥 = 3𝑥 𝑥 − 2
Igualando la 𝑓′
𝑥 a cero:
𝑓′
𝑥 = 0
3𝑥 𝑥 − 2 = 0
Los puntos críticos de 𝑓 son:
𝑥 = 0 ∨ 𝑥 = 2

16. Ubicamos estos puntos críticos en la recta:
0 2
𝑓′ 𝑓′ 𝑓′
∙ ∙
Analizamos la derivada en cada uno de estos intervalos:
• Si 𝑥 = −1, y como 𝑓′
−1 > 0, entonces 𝑓 es creciente en
el intervalo 𝐼 = −∞, 0 .
• Si 𝑥 = 1, y como 𝑓′
1 < 0, entonces 𝑓 es decreciente en
el intervalo 𝐼 = 0, 2 .
• Si 𝑥 = 3, y como 𝑓′
3 > 0, entonces 𝑓 es creciente en el
intervalo 𝐼 = 2, ∞ .

17. Usando el criterio de la primera derivada se tiene:
• Como 𝑓′
𝑥 > 0 para todo 𝑥 ∈ −∞, 0 y 𝑓′
𝑥 < 0 para todo
𝑥 ∈ 0, 2 , entonces 𝑓 0 = 0 es un valor máximo local de 𝑓.
• Como 𝑓′
𝑥 < 0 para todo 𝑥 ∈ 0, 2 y 𝑓′
𝑥 > 0 para todo
𝑥 ∈ 2, ∞ , entonces 𝑓 2 = −4 es un valor mínimo local de
𝑓.
Gráficamente:

18. 2) 𝑓 𝑥 = 𝑥3
−
3
2
𝑥2
Solución
Derivando la función 𝑓, se tiene:
𝑓′
𝑥 = 3𝑥2
− 3𝑥
𝑓′
𝑥 = 3𝑥 𝑥 − 1
Igualando la 𝑓′
𝑥 a cero:
𝑓′
𝑥 = 0
3𝑥 𝑥 − 1 = 0
Los puntos críticos de 𝑓 son:
𝑥 = 0 ∨ 𝑥 = 1

19. Ubicamos estos puntos críticos en la recta:
𝑓′ 𝑓′ 𝑓′
∙ ∙
0 1
Analizamos la derivada en cada uno de estos intervalos:
• Si 𝑥 = −1, y como 𝑓′
−1 > 0, entonces 𝑓 es creciente en
el intervalo 𝐼 = −∞, 0 .
• Si 𝑥 =
1
2
, y como 𝑓′ 1
2
< 0, entonces 𝑓 es decreciente en
el intervalo 𝐼 = 0, 1 .
• Si 𝑥 = 2, y como 𝑓′
2 > 0, entonces 𝑓 es creciente en el
intervalo 𝐼 = 1, ∞ .

20. Usando el criterio de la primera derivada se tiene:
• Como 𝑓′
𝑥 > 0 para todo 𝑥 ∈ −∞, 0 y 𝑓′
𝑥 < 0 para todo
𝑥 ∈ 0, 1 , entonces 𝑓 0 = 0 es un valor máximo local de 𝑓.
• Como 𝑓′
𝑥 < 0 para todo 𝑥 ∈ 0, 1 y 𝑓′
𝑥 > 0 para todo
𝑥 ∈ 1, ∞ , entonces 𝑓 1 = −
1
2
es un valor mínimo local de
𝑓.
Gráficamente:

21. 3) 𝑓 𝑥 =
𝑥2
𝑥 − 2
Solución
Derivando la función 𝑓, se tiene:
𝑓′
𝑥 =
2𝑥 𝑥 − 2 − 𝑥2
𝑥 − 2 2
𝑓′
𝑥 =
2𝑥 𝑥 − 2 − 𝑥2
𝑥 − 2 2
𝑓′
𝑥 =
𝑥2
− 4𝑥
𝑥 − 2 2
𝑓′
𝑥 =
𝑥 𝑥 − 4
𝑥 − 2 2

22. Igualando la 𝑓′
𝑥 a cero:
𝑓′
𝑥 = 0
𝑥 𝑥 − 4
𝑥 − 2 2
= 0
Los puntos críticos de 𝑓 son:
𝑥 = 0 ∨ 𝑥 = 4

23. Si 𝑥 = 2, y evaluando la derivada 𝑓′
𝑥 en este punto, se tiene:
𝑓′
2 =
2 2 − 4
2 − 2 2
𝑓′
2 =
−4
0
De esta ultima expresión se deduce que la 𝑓′
2 no existe, lo
cual satisface una parte de la definición de punto critico,
ademas 𝑥 = 2 ∉ 𝐷𝑜𝑚 𝑓 .
Por tanto 𝑥 = 2 no es punto critico de la función.
Ojo

24. Ubicamos estos puntos críticos en la recta y el punto 𝑥 = 2.
𝑓′ 𝑓′ 𝑓′
0 4
2
𝑓′
Analizamos la derivada en cada uno de estos intervalos:
• Si 𝑥 = −1, y como 𝑓′
−1 > 0, entonces 𝑓 es creciente en
el intervalo 𝐼 = −∞, 0 .
• Si 𝑥 = 1, y como 𝑓′
1 < 0, entonces 𝑓 es decreciente en el
intervalo 𝐼 = 0, 2 .
• Si 𝑥 = 3, y como 𝑓′
3 < 0, entonces 𝑓 es decreciente en el
intervalo 𝐼 = 2, 4 .
• Si 𝑥 = 5, y como 𝑓′
5 > 0, entonces 𝑓 es creciente en el
intervalo 𝐼 = 4, ∞ .
∙ ∙
°

25. Usando el criterio de la primera derivada se tiene:
• Como 𝑓′
𝑥 > 0 para todo 𝑥 ∈ −∞, 0 y 𝑓′
𝑥 < 0 para todo
𝑥 ∈ 0, 2 , entonces 𝑓 0 = 0 es un valor máximo local de 𝑓.
• Como 𝑓′
𝑥 < 0 para todo 𝑥 ∈ 2, 4 y 𝑓′
𝑥 > 0 para todo
𝑥 ∈ 4, ∞ , entonces 𝑓 4 = 8 es un valor mínimo local de 𝑓.
Gráficamente:

26. Ejercicios (Homework)
Determine los intervalos de crecimiento y los
extremos relativos de las siguientes funciones.
a) 𝑓 𝑥 = 2𝑥3
− 3𝑥2
− 36𝑥 + 7
b) 𝑓 𝑥 =
𝑥4+1
𝑥2
c) 𝑓 𝑥 = 𝑥 +
4
𝑥

27. ¡Ojo! Recuerda que
debes resolver los
ejercicios de la hoja de
trabajo de la semana 3;
esto te ayudará a
enriquecer los temas
vistos en clase.