El documento explica conceptos clave sobre funciones crecientes, decrecientes, derivadas, valores críticos, máximos y mínimos de funciones. Incluye ejemplos y ejercicios resueltos sobre cómo determinar los intervalos donde una función es creciente o decreciente, y los valores máximos y mínimos, usando la derivada primera y segunda. También cubre puntos de inflexión y concavidad.

2. FUNCIONES CRECIENTES Y DECRECIENTES
Y SU RELACIÓN CON LA DERIVADA
Sea f una función continua con ecuación y = f(x), definida en un
intervalo [a, b]. La siguiente es la representación gráfica de f en
el intervalo [a, b].

3. FUNCIONES CRECIENTES Y DECRECIENTES
Y SU RELACIÓN CON LA DERIVADA
En la representación
gráfica anterior puede
observarse la función f
es:
1. Creciente en los intervalos ]a, x3[ , ]x5, x6[
2. Decreciente en los intervalos ]x3, x5[ , ]x6, b[

4. FUNCIONES CRECIENTES Y DECRECIENTES
Y SU RELACIÓN CON LA DERIVADA
También se tiene que
cuando la pendiente de
la recta tangente es
positiva, la función f
crece; y cuando la
pendiente de la recta
tangente es negativa, la
función decrece.
Note además que en los puntos (x3, f(x3)) , (x5, f (x5)) y
(x6, f (x6)) la recta tangente es horizontal, por lo que su
pendiente es cero, es decir, la primera derivada de la
función se anula en cada uno de esos puntos.

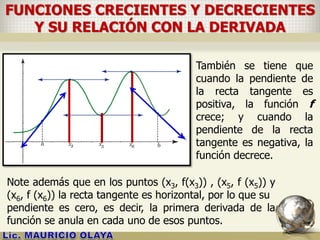
5. FUNCIONES CRECIENTES Y DECRECIENTES
Y SU RELACIÓN CON LA DERIVADA
Sea f una función continua en un intervalo cerrado [a,
b] y derivable en el intervalo abierto ]a, b[.
1. Si f’ (x) > 0 para toda x en ]a, b[, entonces la
función f es creciente en [a, b].
2. Si f’ (x) < 0 para toda x en ]a, b[, entonces la
función f es decreciente en [a, b].

6. FUNCIONES CRECIENTES Y DECRECIENTES
Y SU RELACIÓN CON LA DERIVADA
EJERCICIO
1. Determinemos los intervalos en que crece o decrece
la función con ecuación 𝒇 𝒙 =
𝟏
𝟐
𝒙 𝟐
− 𝟒𝒙 + 𝟏

7. FUNCIONES CRECIENTES Y DECRECIENTES
Y SU RELACIÓN CON LA DERIVADA
EJERCICIO
2. Determinemos los intervalos en que crece o decrece
la función con ecuación 𝒇 𝒙 = 𝒙 𝟐
+
𝟏
𝒙 𝟐 con 𝒙 ≠ 𝟎.

8. VALOR MÁXIMO Y VALOR MÍNIMO DE UNA
FUNCIÓN REAL
Si 𝒇 es una función dada, entonces 𝒇(𝒄) es un valor máximo
relativo de 𝒇, si existe un intervalo abierto 𝒂, 𝒃 tal que 𝒂 <
𝒄 < 𝒃 y 𝒇(𝒄) ≥ 𝒇(𝒙) para 𝒙 ∈ 𝒂, 𝒃 , siendo 𝒙 un valor del
dominio de la función.
Si 𝒇(𝒄) ≥ 𝒇(𝒙) para toda 𝒙 en el dominio de 𝒇, entonces 𝒇(𝒄) es
el valor máximo de 𝒇 o máximo absoluto.

9. VALOR MÁXIMO Y VALOR MÍNIMO DE UNA
FUNCIÓN REAL
Si 𝒇 es una función dada, entonces 𝒇(𝒄) es un valor mínimo
relativo de 𝒇, si existe un intervalo abierto 𝒂, 𝒃 tal que 𝒂 <
𝒄 < 𝒃 y 𝒇(𝒄) ≤ 𝒇(𝒙) para 𝒙 ∈ 𝒂, 𝒃 , siendo 𝒙 un valor del
dominio de la función.
Si 𝒇(𝒄) ≤ 𝒇(𝒙) para toda 𝒙 en el dominio de 𝒇, entonces 𝒇(𝒄) es
el valor mínimo de 𝒇 o mínimo absoluto.

10. VALOR MÁXIMO Y VALOR MÍNIMO DE UNA
FUNCIÓN REAL
Considere una función 𝒇 definida en un intervalo 𝒄, 𝒅 , cuya
representación gráfica es la siguiente:
Note que 𝒇(𝒙 𝟏) , es un
máximo relativo y 𝒇(𝒙 𝟑)
es el máximo valor que
toma la función en el
intervalo en que está
definida. Similarmente,
𝒇(𝒙 𝟒) es un valor mínimo
relativo y 𝒇(𝒙 𝟐) es el
mínimo absoluto de la
función en 𝒄, 𝒅 .

11. VALOR MÁXIMO Y VALOR MÍNIMO DE UNA
FUNCIÓN REAL
Sea 𝒄 un punto interior del dominio de una función 𝒇. Si 𝒇(𝒄)
es un valor máximo relativo de 𝒇 y si existe 𝒇′(𝒄) entonces
𝒇′ 𝒄 = 𝟎.
Sea 𝒄 un punto interior del dominio de una función 𝒇. Si 𝒇(𝒄)
es un valor mínimo relativo de 𝒇 y si 𝒇′(𝒄) existe, entonces
𝒇′ 𝒄 = 𝟎.
Observación: El recíproco de los teoremas anteriores
no es cierto. Es decir, el hecho de que 𝒇′ 𝒄 = 𝟎, no
implica que en 𝒙 = 𝒄 exista un máximo o un mínimo.

12. VALORES CRÍTICOS DE UNA
FUNCIÓN REAL
Sea 𝒇 una función. Recibe el nombre de valores críticos del
dominio de 𝒇, aquellos en los que 𝒇′(𝒙) es igual a cero o en los
que 𝒇′(𝒙) no existe.

13. VALORES CRÍTICOS DE UNA
FUNCIÓN REAL
EJERCICIO
Determinemos los puntos críticos de las funciones con
ecuaciones:
1. 𝒇 𝒙 = 𝟐𝒙 𝟐 − 𝒙 𝟒, 𝒙 ∈ ℝ
2. 𝑓 𝑥 = 𝑥 −
1
𝑥
, 𝑥 > 0

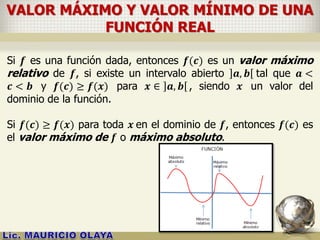
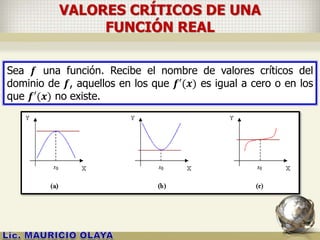
14. CRÍTERIOS DE LA PRIMERA DERIVADA
Sea 𝒇 una función continua en un intervalo cerrado 𝒂, 𝒃 , que
es derivable en todo punto del intervalo abierto ]𝒂, 𝒃[. Sea 𝒄 en
]a, b[ tal que 𝒇′ 𝒄 = 𝟎 o 𝒇′(𝒄) no existe.
a) Si 𝒇′(𝒙) es positiva para
todo 𝒙 < 𝒄 , y negativa para
todo 𝒙 > 𝒄, entonces 𝒇(𝒄) es
un valor máximo relativo de
𝒇(𝒙).

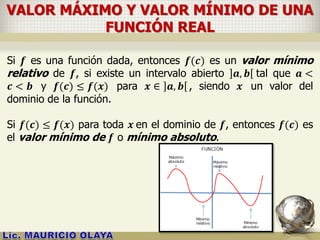
15. CRÍTERIOS DE LA PRIMERA DERIVADA
Sea 𝒇 una función continua en un intervalo cerrado 𝒂, 𝒃 , que
es derivable en todo punto del intervalo abierto ]𝒂, 𝒃[. Sea 𝒄 en
]a, b[ tal que 𝒇′
𝒄 = 𝟎 o 𝒇′(𝒄) no existe.
b) Si 𝒇′(𝒙) es negativa para
toda 𝒙 < 𝒄, y positiva para
toda 𝒙 > 𝒄, entonces 𝒇(𝒄) es
un mínimo relativo de 𝒇(𝒙).

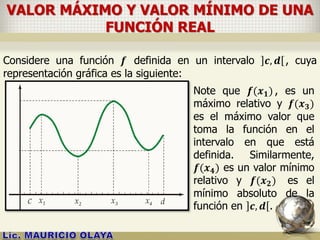
16. CRÍTERIOS DE LA PRIMERA DERIVADA
Sea 𝒇 una función continua en un intervalo cerrado 𝒂, 𝒃 , que
es derivable en todo punto del intervalo abierto ]𝒂, 𝒃[. Sea 𝒄 en
]a, b[ tal que 𝒇′
𝒄 = 𝟎 o 𝒇′(𝒄) no existe.
c) Si 𝒇′(𝒙) es positiva para
todo 𝒙 < 𝒄 y también lo es
para todo 𝒙 > 𝒄; o si 𝒇′(𝒙) es
negativa para todo 𝒙 < 𝒄 y a
su vez para todo 𝒙 > 𝒄 ,
entonces 𝒇(𝒄) no es un valor
máximo relativo ni un valor
mínimo relativo de 𝒇(𝒙).

17. CRÍTERIOS DE LA PRIMERA DERIVADA
En los siguientes ejercicios determinar los valores extremos de la
función cuya ecuación se da. Para ello, se calcula la primera
derivada de la función, luego se determinan los valores críticos,
a continuación se hallan los intervalos donde la función crece o
decrece y por último se realiza una bosquejo de la gráfica.
1. 𝒇 𝒙 = 𝟒𝒙 −
𝟏
𝟑
𝒙 𝟑
2. 𝒇 𝒙 = 𝟑𝒙 𝟒 − 𝟒𝒙 𝟑
3. 𝒇 𝒙 = 𝒙 𝟑 −
𝟑
𝟐
𝒙 𝟐
4. 𝒇 𝒙 = 𝒙 𝟐 +
𝟏
𝒙 𝟐

18. CÓNCAVIDAD HACIA ARRIBA Y
CÓNCAVIDAD HACIA ABAJO
Sea 𝒇 derivable en un intervalo abierto 𝒂, 𝒃 . La gráfica de 𝒇 es
cóncava hacia arriba sobre 𝒂, 𝒃 si 𝒇 ′(𝒙) es creciente en el
intervalo y cóncava hacia abajo en 𝒂, 𝒃 si 𝒇 ′(𝒙) es
decreciente en el intervalo.

19. CÓNCAVIDAD HACIA ARRIBA Y
CÓNCAVIDAD HACIA ABAJO
Si 𝒇 es una función tal que 𝒇′′(𝒙) > 𝟎 cuando 𝒙 ∈ 𝒂, 𝒃 ,
entonces la gráfica de 𝒇 es cóncava hacia arriba sobre 𝒂, 𝒃 .
Si 𝒇 es una función tal que 𝒇′′(𝒙) < 𝟎 cuando 𝒙 ∈ 𝒂, 𝒃 ,
entonces la gráfica de 𝒇 es cóncava hacia abajo sobre 𝒂, 𝒃 .

20. PUNTOS DE INFLEXIÓN
Se dice que (𝒙 𝟎, 𝒇(𝒙 𝟎)) es un punto de inflexión de la gráfica de
una función 𝒇, si existe un intervalo 𝒂, 𝒃 tal que 𝒙 𝟎 ∈ 𝒂, 𝒃 , y
la gráfica de 𝒇 es cóncava hacia arriba sobre 𝒂, 𝒙 𝟎 , y cóncava
hacia abajo sobre 𝒙 𝟎, 𝒃 , o viceversa.
Si (𝒙 𝟎, 𝒇(𝒙 𝟎)) es un punto de inflexión de la gráfica de 𝒇 y si
𝒇′′(𝒙 𝟎) existe, entonces 𝒇′′ 𝒙 𝟎 = 𝟎.

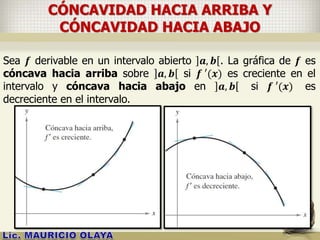
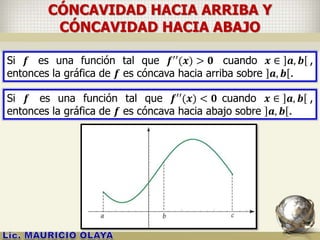
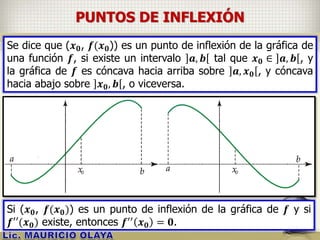
21. PUNTOS DE INFLEXIÓN
Si:
i. 𝒇 es una función continua sobre un intervalo 𝑰,
ii. 𝒙 𝟎 es un punto interior de I tal que 𝒇′′
𝒙 𝟎 = 𝟎, ó 𝒇′′
𝒙 𝟎 existe, y
iii. Si existe un intervalo ]𝒂, 𝒃[ con 𝒙 𝟎 ∈]𝒂, 𝒃[, (]𝒂, 𝒃[ ∈ 𝑰) tal que:
 𝒇′′
𝒙 𝟎 > 𝟎 cuando 𝒙 ∈ 𝒂, 𝒙 𝟎 y 𝒇′′
𝒙 𝟎 < 𝟎 cuando 𝒙 ∈ 𝒙 𝟎, 𝒃 ,
entonces (𝒙 𝟎, 𝒇(𝒙 𝟎)) es un punto de inflexión de la gráfica de 𝒇.
 𝒇′′
𝒙 𝟎 < 𝟎 cuando 𝒙 ∈ 𝒂, 𝒙 𝟎 y 𝒇′′
𝒙 𝟎 > 𝟎 cuando 𝒙 ∈ 𝒙 𝟎, 𝒃 ,
entonces (𝒙 𝟎, 𝒇(𝒙 𝟎)) es un punto de inflexión de la gráfica de 𝒇.
 𝒇′′ 𝒙 𝟎 > 𝟎 cuando 𝒙 ∈ 𝒂, 𝒙 𝟎 y 𝒇′′ 𝒙 𝟎 > 𝟎 cuando 𝒙 ∈ 𝒙 𝟎, 𝒃 , o
bien, 𝒇′′ 𝒙 𝟎 < 𝟎 cuando 𝒙 ∈ 𝒂, 𝒙 𝟎 y 𝒇′′ 𝒙 𝟎 < 𝟎 cuando 𝒙 ∈ 𝒙 𝟎, 𝒃
entonces (𝒙 𝟎, 𝒇(𝒙 𝟎)) no es un punto de inflexión de la gráfica de 𝒇.

22. CRITERIOS DE LA SEGUNDA DERIVADA
Analizar la función 𝒇 𝒙 =
𝒙 𝟒
𝟏𝟐
+
𝒙 𝟑
𝟔
− 𝒙 𝟐
+ 𝟏

23. CRITERIOS DE LA SEGUNDA DERIVADA
Analizar la función 𝒇 𝒙 =
𝒙 𝟐+𝟏
𝒙 𝟐−𝟒

24. BIBLIOGRAFÍA
 Cálculo diferencial e integral, con aplicaciones.. Elsie
Hernández S, primera edición, Revista digital Matemática-
Educación e Internet.
 Cálculo 1 de una variable, novena edición, Ron Larson,
Bruce H. Edwards, Ed. Mc Graw Hill