Este documento presenta los conceptos fundamentales del cálculo diferencial como el teorema de Rolle, funciones crecientes y decrecientes, valores críticos, extremos relativos, concavidad y puntos de inflexión. Además, incluye criterios de evaluación y ejemplos resueltos para aplicar estos conceptos en el análisis y trazado de gráficas de funciones.

1. CALCULO I (MAT-101)
Docente: Ing. Isaac Checa
A.

2. Teorema de Rolle
Teorema del Valor Medio
Funciones Crecientes y Decrecientes
Valor Crítico
Extremos Relativos,
Criterio de la Primera Derivada
Criterio de la segunda derivada,
Concavidad
Puntos de Inflexión
Problemas Resueltos
Práctica Nº 4 (Primera Parte)
Volver a la página principal

3. COMPETENCIAS ESPECÍFICAS
• Establece, a partir de los diferentes teoremas, los
valores máximos y mínimos, los intervalos de
crecimiento y decrecimiento, las concavidades y los
posibles puntos de inflexión de una función para
aplicarlos en el trazado de su gráfica.
• Analiza el comportamiento de las funciones por medio
del cálculo diferencial y calcula sus extremos relativos
los que tienen aplicación en problemas reales.
• Desarrolla habilidades para interpretar el
comportamiento de funciones de acuerdo a su análisis
por medio de las derivadas.

4. CRITERIOS DE EVALUACIÓN
• Calcula la derivada de una función real sobre la base de la
definición
• Calcula las derivadas aplicando las distintas reglas de
derivación
• Interpreta funciones crecientes y decrecientes
• Interpreta y grafica una función real aplicando derivadas
• Calcula la derivada de una función de dos variables sobre la
base de la definición
• Aplica el concepto de derivada y sus diferentes teoremas para
resolver problemas de máximos y mínimos.
• Utiliza la regla de L` Hôpital para calcular límites con
indeterminaciones específicas

5. Sea f una función continua en el intervalo [a,b] y
derivable en el intervalo abierto (a,b) tal que
f(a)=f(b). Entonces existe al menos un punto c
(a,b) tal que f’(c)=0
f ’(c)=0
f(a)=f(b)
a c b
Volver a índice aplicaciones de la derivada, gráficos

6. Sea una función continua en el intervalo cerrado
[a,b], derivable en el intervalo abierto (a,b).
Entonces existe un punto c (a,b) tal que:
f(b)
f ‘(c) f (b) f (a)
f ' (c )
b a
ß
ß
f(a)
a c b
Volver a índice aplicaciones de la derivada, gráficos

7. Una función es creciente en un intervalo dado si
para dos números cualesquiera x1 y x2 se tiene
que x1 < x2 f(x1) < f(x2)
y es decreciente si
x1 < x2 f(x1) > f(x2)
constante
f ‘(x)<0
f ‘(x)>0
a b c d

8. Si f ’(x)>0 f(x) es creciente en (a,b)
Si f ’(x)<0 f(x) es decreciente en (c,d)
Si f ’(x)=0 f(x) es constante (b,c)
Valor crítico de una función es todo
punto c de la misma para el cual f ’(c)=0
o bien f ’(c) no existe
Volver a índice aplicaciones de la derivada, gráficos

9. Un máximo relativo de una función es todo punto
c, f(c) de (a,b), para el cual se cumple que f(x)
f(c) para todo x de (a,b).
Un mínimo relativo de una función es todo punto
c, f(c) de (a,b), para el cual se cumple que f(x)
f(c) para todo x de (a,b).
Una función tiene un Máx.r.
mínimo o un máximo
relativo en un punto
c cuando c es un
Mínimo r.
valor crítico de f.

10. Signo de GRÁFICO Signo de c, f(c)
f ‘ en f ‘ en (c,b)
(a,c) a c b
MÁXIMO
+ -

11. Signo de GRÁFICO Signo de c, f(c)
f ‘ en f ‘ en (c,b)
(a,c) a c b
MÁXIMO
+ -
MÍNIMO
- +

12. Signo de GRÁFICO Signo de c, f(c)
f ‘ en f ‘ en (c,b)
(a,c) a c b
MÁXIMO
+ -
MÍNIMO
- +
NINGUNO
+ +

13. Signo de GRÁFICO Signo de c, f(c)
f ‘ en f ‘ en (c,b)
(a,c) a c b
MÁXIMO
+ -
MÍNIMO
- +
NINGUNO
+ +
NINGUNO
- -

14. Ejemplo. Hallar máximos, mínimos y graficar la
siguiente función
f(x) = x2 + 3x – 4 f ’(x) = 2x + 3 = 0
Valor Crítico x = -3/2
f ’(-2) = 2(-2) + 3 < 0 (-) f ’(0) = 2(0) + 3 > 0 (+)
El signo de la derivada antes y después del valor
crítico varía de (-) a (+) por tanto la función tiene
un mínimo en x = -3/2
f(-3/2) = (-3/2)2 + 3 (-3/2) – 4
= 9/4 – 9/2 – 4 ; X Y
y = -25/4
0 -4
1 0
-4 0
Volver a índice aplicaciones de la derivada, gráficos

15. y y
Cóncava
Cóncava hacia arriba
hacia abajo
x x
y’ y’
f ”(c)<0 f ”(c)>0
x x
a c b a c b

16. Sea f una función cuya segunda derivada existe
en el intervalo (a,b). Entonces:
Si f ’’(x)>0 para todo x en (a,b), la gráfica de f
es cóncava hacia arriba en (a,b).
Si f ’’(x)<0 para todo x en (a,b), la gráfica de f
es cóncava hacia abajo en (a,b).
Si además la función contiene un punto c tal que
f’(c)=0, entonces:
Si f ’’(c)>0, f(c) es un mínimo relativo.
Si f ’’(c)<0, f(c) es un máximo relativo.
Volver a índice aplicaciones de la derivada, gráficos

17. Si la gráfica de una función continua posee una
tangente en un punto en el que su concavidad
cambia de hacia arriba a hacia abajo, o viceversa,
este punto se denomina punto de inflexión.
Si (c,f(c)) es un punto de inflexión, entonces o
bien f’’(c)=0 o f’’(c) no existe.

18. y
Cóncava Cóncava
hacia arriba hacia arriba
Cóncava
hacia abajo
Cóncava Cóncava
Cóncava
hacia arriba hacia abajo
hacia abajo
x
Volver a índice aplicaciones de la derivada, gráficos

19. Ejemplo. Determinar máximos y mínimos relativos,
puntos de inflexión y grafique
f(x) = 2x3 + 3x2 – 12x
Solución
f ’(x) = 6x2 + 6x –12 = 0
x2 + x –2 = (x-1) (x+2) = 0
x=1 ; x=-2 Valores críticos
f ’’(x) = 12x + 6
f’’(1)>0 , la función tiene un mínimo en x = 1 ; y =-7
f’’(-2)<0, la función tiene un máximo en x=-2 ; y =20
Haciendo f’’(x) = 0 se tiene
12 x + 6 = 0 ; x = -1/2 por tanto,
el punto x = -1/2 ; y = 6,5 es un punto de inflexión.

20. (-2,20)
f(x) = 2x3 + 3x2 – 12x
(-1/2, 6,5)
(1,-7)

21. Hallar máximos mínimos puntos de inflexión y
graficar… 4
2 1 x 1
y x 2
y
x x2
3 2
y ' 2x 2x 2x 3
0
x
2 x4 2 0 x 4
1 1
y " 2 6x 4
f "(1) 0 f "( 1) 0
Existen dos mínimos en: x=1 y=2 ; x=-1 y=2
La función es simétrica al eje y
Tiene una asíntota vertical en x=0

22. 2 1
y x 2
x

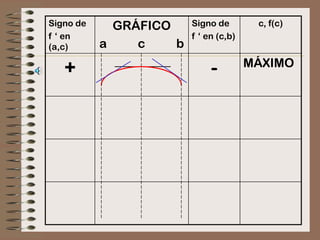
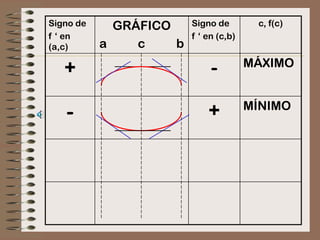
23. Hallar los extremos relativos y graficar...
f(x) = 2xe-x + 4 en [-1,1]
Resp. Máx (1, (2/e) + 4). Mínimo (-1, -2e+4)
f ‘(x) = 2e-x – 2xe-x = 2e-x(1 – x) = 0
valor crítico: x = 1
f’’(x) = - 2e-x - 2e-x + 2xe-x = 2e-x ( x – 2 )
f’’(1) = 2e-1(-1) = -2e-1
como es menor a cero la función tiene un
máximo en
x=1 , y=4,73

24. Máximo (1, (2/e) + 4)=(1, 4.73)
Para el valor x=-1
f(-1) = -2e+4 que
constituye un mínimo
en el intervalo de
análisis de [-1,1]
Mínimo (-1, -2e+4)

25. Graficar
x 2 x 2
f ( x)
x2 4x 3 ( x 1)( x 3)
x=1 ; x=3 asíntotas verticales
(1)( x 2
4 x 3) ( x 2)(2 x 4)
f '( x) 2 2
( x 4 x 3)
x2 4 x 3 2 x2 4 x 4 x 8 x2 4x 5
2 2 2 2
( x 4 x 3) ( x 4 x 3)
x2 4 x 5
2 2
0 No existen valores criticos
( x 4 x 3)

26. x 2
lim 2 0 y 0 Asíntota horizontal
x x 4x 3
(2 x 4)( x 2 4 x 3) ( x 2 4 x 5)(2 x 4)
f "( x)
(x 2 - 4·x + 3)4
2(x-2)( x 2 4 x 7)
0
(x 2 - 4·x + 3)3
Por tanto x=2 ; y=0 es el punto de inflexión

27. x y
4 2/3
2,5 -2/3
2 0
0 -2/3
Volver a índice aplicaciones de la derivada, gráficos

28. Determinar los extremos relativos, puntos de inflexión y
graficar.
1.- f(x) = x3 – 6x2 + 15
Resp. Max.Rel. (0, 15); Min.Rel.(4, -17)
2.- f(x) = x1/3 + 1 Resp. No tiene extremos.
3.- f(x) = (x2 – 2x + 1) / (x + 1)
Resp.(-3, -8) Máximo Relativo (1, 0) Mínimo Relativo
4.- Hallar a, b ,c y d tales que la función f(x)=ax3 + bx2 +
cx +d tenga un mínimo relativo en (0,0) y un máximo
relativo en (2,2).
Resp. a = -1/2 ; b =3/2 ; c = d = 0.
5.- f(x) = 2x3 – 3x2 – 12x + 8
6.- f(x) = x2 / (x2 + 1)

29. 7.- f(x) = x / (x2 - 4) Resp. (0, 0) Punto de Inflexión
8.- Un fabricante ha calculado que el costo total
c de la explotación de una cierta instalación esta
dado por c = 0,5x2 + 15x + 5000, donde x es el
número de unidades producidas. ¿A qué nivel de
producción será mínimo el costo medio por
unidad? (El costo medio por unidad viene dado
por c/x)
Resp. x = 387,3
En los ejercicios 9 al 14 determine los extremos
absolutos de la función en el intervalo indicado.
9.- f(x) = x2 (x2 – 2) + 1 en [-3, 0]
Resp. Max. (-3, 64) Min. (-1, 0)

30. 10.- f(x) = x / (x2 + 2x +2) en [-3, 0]
Resp. Máximo (0, 0). Mínimo (-√2, -(√2+1)/2
11.- f(x) = 2ln (1 + x2) + 2 en [0, 2]
12.- f(x) = arctag (1 + x2 ) en [-1, 1]
13.- f(x) = -ln (1 + x2 ) en [-2, 2]
14.- f(x) = x4 – 32x + 4 [0,2]
FIN de Aplicaciones de la derivada, gráficas
Volver a la página principal
Volver a índice aplicaciones de la derivada, gráficos