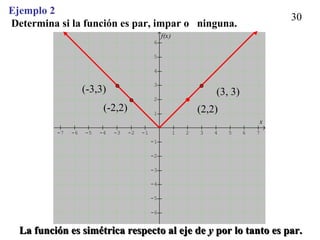
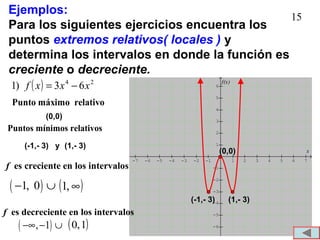
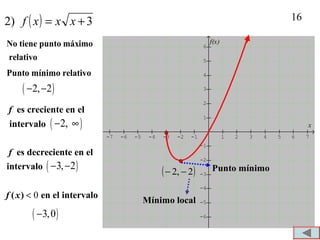
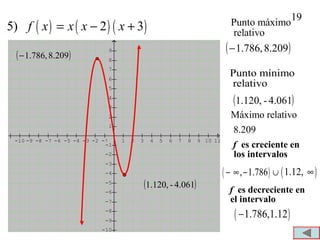
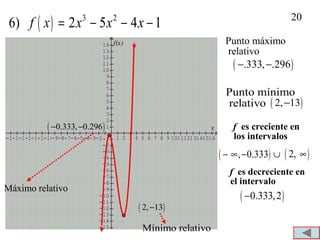
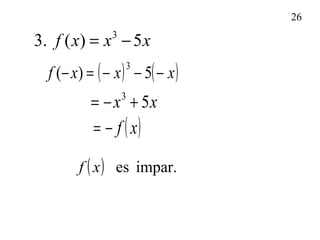1. El documento presenta definiciones y ejemplos relacionados con funciones crecientes, decrecientes y constantes, extremos locales, e identificar funciones pares e impares. 2. Se definen funciones crecientes, decrecientes y constantes usando gráficas e intervalos. También se explican extremos locales y cómo identificarlos. 3. Se proveen ejemplos para practicar la identificación de intervalos donde funciones son crecientes, decrecientes o constantes, así como la detección de extremos locales.

1. 1
Funciones Crecientes, Decrecientes y Constantes
Extremos Locales
Funciones Pares e Impares

2. 2
Objetivos:Objetivos:
1.1. Determinar los intervalos en donde laDeterminar los intervalos en donde la
gráfica de una función es creciente,gráfica de una función es creciente,
decreciente o constante.decreciente o constante.
2.2. Definir y hallar extremos locales en laDefinir y hallar extremos locales en la
gráfica de una función.gráfica de una función.
3.3. Determinar los intervalos en donde laDeterminar los intervalos en donde la
función es positiva o es negativa.función es positiva o es negativa.
5. Determinar si una función es par,impar o5. Determinar si una función es par,impar o
ninguna.ninguna.
6.6. Determinar la simetría de una función
usando la gráfica.

3. 3
Definiciones:Definiciones:
Una funciónUna función ff eses crecientecreciente en un intervalo abiertoen un intervalo abierto II sisi
siempre quesiempre que tenemos quetenemos que
para cualquier escogido depara cualquier escogido de xx11 yy xx22 enen I.I.
1 2x x<1 2( ) ( )f x f x<
Aclaración:Aclaración: Si nos movemos a la derecha sobreSi nos movemos a la derecha sobre
el eje deel eje de xx la gráfica de la función va subiendo.la gráfica de la función va subiendo.
Página Inicial

4. 4
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
1x
( )1xf
2x
( )2xf
21 xx <
( ) ( )21 xfxf <
Ilustración de una función creciente

5. 5
DefiniciónDefinición
Una funciónUna función ff eses decrecientedecreciente en un intervalo abiertoen un intervalo abierto I,I,
si para cualquier escogido desi para cualquier escogido de xx11 yy xx22 enen II, con, con xx11 << xx22,,
tenemos quetenemos que
ff((xx11) >) > ff((xx22).).
Aclaración:Aclaración: Si nos movemos a la derecha sobre el eje deSi nos movemos a la derecha sobre el eje de
x la gráfica de la función va bajando.x la gráfica de la función va bajando.

6. 6
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
1x
( )1xf
2x
( )2xf
21 xx <
( ) ( )1 2f x f x>
Ilustración de una función decreciente

7. 8
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
1x 2x
21 xx <
( ) ( )21 xfxf =
Ilustración de una función constante

8. 9
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
Ejemplos:
Use las gráficas para encontrar los intervalosUse las gráficas para encontrar los intervalos
en donde la función esen donde la función es crecientecreciente,, decrecientedecreciente
oo constanteconstante..
[ )1,∞
Creciente en:
( )∞∞− ,
( ) .0≥xfDetermina los intervalos en dondeetermina los intervalos en donde
( ) 0f x en≥

9. 10
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
(-6, -3)
(-4, 4)
(-1, 1)
(6, -3)(2, -3)
Creciente
Decreciente
Constante en
( )2,6
( )-4,2
( )-6,-4

10. 11
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
( )3,3−
( )2, 5− ( )0,5
( )2,1 ( )4, 1
Creciente en:
( )5, 2− − ∪ ( )4, ∞
Decreciente en:
Constante en:
( )2,0− ∪ ( )2,4
( )0,2
( )5,0−
( ) .0≥xfDetermina los intervalos en dondeetermina los intervalos en donde [ )5,− ∞

11. 12
Una función f tiene un máximo local (relativo) en
x = c si existe un intervalo abierto I que contiene a c
tal que, para todo x en I, f(x) < f(c).
Llamamos a f (c) el máximo local (relativo) de f en c.
Definiciones:Definiciones:
Una función f tiene un mínimo local (relativo) en
x = c si existe un intervalo abierto I que contiene a c
tal que f (x) > f (c) para todo x en I.
Llamamos a f (c) el mínimo local (relativo) de f en c.
Página Inicial

12. 13
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
f(x)
x
Ejemplo:Ejemplo:
Encuentra el máximo y/o mínimo local de la función.Encuentra el máximo y/o mínimo local de la función.
( )3, 2− −
Decreciente en:
( ), 3−∞ −
Creciente en:
( )3,− ∞
Punto mínimo
f no tiene punto
máximo local
Punto mínimo
( )3, 2− −
es el mínimo
local
2−

13. 14
Ejemplos:
Para los siguientes ejercicios encuentra los
puntos extremos relativos( locales ) y
determina los intervalos en donde la función es
creciente o decreciente.
( ) 24
63)1 xxxf −=
( ) 3)2 += xxxf
( ) 2
3) 3 4 2f x x x= − −
( ) 3
4) 3f x x x= −
( ) ( ) ( )5) 2 3f x x x x= − +
( ) 3 2
6) 2 5 4 1f x x x x= − − −
( ) 2
7) 4f x x x= −
Solución
Solución
Solución
Solución
Solución
Solución
Solución

14. 15
Ejemplos:
Para los siguientes ejercicios encuentra los
puntos extremos relativos( locales ) y
determina los intervalos en donde la función es
creciente o decreciente.
( ) 24
63)1 xxxf −=
Punto máximo relativo
es creciente en los intervalosf
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
f(x)
x(0,0)
(1,- 3)(-1,- 3)
Puntos mínimos relativos
Punto máximo relativo
(0,0)
(-1,- 3) y (1,- 3)
es decreciente en los intervalosf
( ), 1−∞ − ∪ ( )1,0
( )1, 0− ∪ ( )∞,1

15. 16
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
f(x)
x
( ) 3)2 += xxxf
( )2,2 −− Punto mínimo
es creciente en el
intervalo
f
Punto mínimo relativo
No tiene punto máximo
relativo
es decreciente en el
intervalo
f
( )3, 2− −
( )2,− ∞
0<( ) en el intervalof x
( )3,0−
( )2, 2− −
Mínimo local

16. 17
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
f(x)
x
( ) 2
3) 3 4 2f x x x= − −
2 10
,
3 3
 
− ÷
 
2 4
3( ) 2
3
y x x= − −
24 4 4
3 3 2
9 3 9
y x x
   
+ = − + − ÷  ÷
   
2
10 2
3
3 3
y x
 
+ = − ÷
 
2
1 10 2
3 3 3
y x
   
+ = − ÷  ÷
   
24 4 4
2 3
3 3 9
y x x
 
+ + = − + ÷
 
Punto mínimo
es creciente en los intervalosf
es decreciente en los intervalosf
2
,
3
 
−∞ ÷
 
2
,
3
 
∞ ÷
 
Mínimo local

17. 18
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
f(x)
x
( ) 3
4) 3f x x x= −
( )2,1−
( )2-,1
Máximo relativo
Mínimo relativo
( ) ( ), 3 0, 3−∞ ∪
3
0 3x x= −
( )2
0 3x x= −
2
0 ; 3 0x x= − =
0 ; 3x x= = ±
( ) 0.f x <
Determina losetermina los
intervalos enintervalos en
dondedonde

18. 19
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 11
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
( ) ( ) ( )5) 2 3f x x x x= − +
( )8.209,786.1−
( )4.061-,120.1
Punto máximo
relativo
Punto mínimo
relativo
Máximo relativo
8.209
( )8.209,786.1−
( )4.061-,120.1
es creciente en
los intervalos
f
es decreciente en
el intervalo
f
( )1.786,1.12−
( )1.12, ∞( ), 1.786− ∞ − ∪

19. 20
-16-15-14-13-12-11-10-9-8-7-6-5-4-3-2-1 1 2 3 4 5 6 7 8 9 10111213141516
-15
-14
-13
-12
-11
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14 f(x)
x
Máximo relativo
( ) 3 2
6) 2 5 4 1f x x x x= − − −
( )0.333, 0.296− −
( )2, 13−
Mínimo relativo
Punto máximo
relativo
Punto mínimo
relativo
( ).333, .296− −
( )2, 13−
es creciente en
los intervalos
f
es decreciente en
el intervalo
f
( )0.333,2−
( )2, ∞( ), 0.333− ∞ − ∪

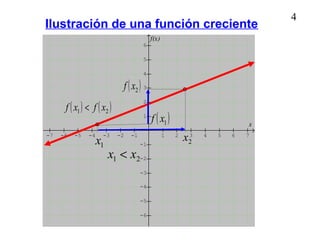
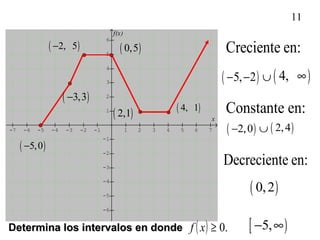
20. 21
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
f(x)
x
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
( ) 2
7) 4f x x x= −
( )2, 4−
Punto mínimo relativo
( )0,0 ( )0,4
Interceptos en x
( ] [ ), 0 4,−∞ ∞U
( )4 0x x − =
0; 4 0x x= − =
( )
2
(2) 2 4(2)
4
f = −
= −
( ) .0≥xf
Determina losetermina los
intervalos enintervalos en
dondedonde

21. 22
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
DefiniciónDefinición
Una funciónUna función f,f, eses parpar si para cada númerosi para cada número xx en elen el
dominio dedominio de ff el númeroel número -x-x también está en el dominio,también está en el dominio,
y se cumple quey se cumple que ( ) ( )f x f x− =
( ))(, xfx
xx−
( )f x( )f x−( ), ( )x f x− −
Página Inicial

22. 23
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
Definición
Una función f es impar si para cada número x en el
dominio de f , el número -x también está en el dominio
de f y se cumple que )()( xfxf −=−
( ))(, xfx
x
x−
( )f x
( )f x−
( ), ( )x f x− −

23. 24
2
1. ( ) 3 4f x x= +
( )
2
( ) 3 4f x x− = − +
43 2
+= x
( )xf=
( ) par.esxf
Ejemplos:
Determina si la función es par, impar o ninguna.

24. 25
2
2. ( ) 5 1f x x x= − +
( ) ( ) 15)(
2
+−−−=− xxxf
152
++= xx
( )xf≠
( ) no es par, ni es impar.f x

25. 26
3
3. ( ) 5f x x x= −
( ) ( )xxxf −−−=− 5)(
3
xx 53
+−=
( )xf−=
( ) impar.esxf

26. 27
2
4. ( ) 3 4 2f x x x= − −
=− )( xf ( ) ( ) 243
2
−−−− xx
243 2
−+= xx
( ) impar.esnopar;esnoxf

27. 28
Teorema:Teorema:
Una función esUna función es parpar si y solo si su gráfica essi y solo si su gráfica es
simétricasimétrica con respecto alcon respecto al eje de yeje de y..
Una función esUna función es imparimpar si y solo si su gráfica essi y solo si su gráfica es
simétricasimétrica concon respecto al origen.respecto al origen.

28. 29Ejemplo 1
Determina si las función es par, impar o ninguna.
La función es simétrica respecto al eje deLa función es simétrica respecto al eje de yy por lo tanto es par.por lo tanto es par.
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)

29. 30
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
(3, 3)(-3,3)
(-2,2) (2,2)
La función es simétrica respecto al eje deLa función es simétrica respecto al eje de yy por lo tanto es par.por lo tanto es par.
Ejemplo 2
Determina si la función es par, impar o ninguna.

30. 31
La función es simétrica respecto al origen por lo tanto es impar.La función es simétrica respecto al origen por lo tanto es impar.
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
Ejemplo 3
Determina si la función es par, impar o ninguna.

31. 32
La función no tiene simetría , por lo tanto no es par ni impar.La función no tiene simetría , por lo tanto no es par ni impar.
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
f(x)
Ejemplo 4
Determina si la función es par, impar o ninguna.