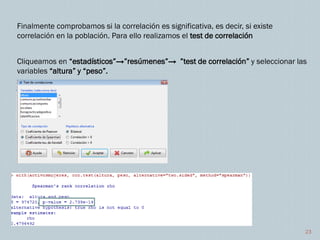
Este documento describe un análisis de correlación entre las variables de altura y peso en un conjunto de datos de salud, filtrando primero por sexo. Para los varones, se encontró una correlación positiva baja pero significativa entre altura y peso. Para las mujeres, hubo una correlación positiva moderada y significativa. En ambos casos, las variables no siguieron una distribución normal, por lo que se usó la prueba de correlación de Spearman en lugar de Pearson.

1. TEST DE CORRELACIÓN
Lucia Zabala Sánchez-Noriega Subgrupo 9. Grupo 2
1

2. Para comenzar, en R Commander, cargar el conjunto de datos activosdesalud.
EJERCICIO: Determina si existe relación y como de fuerte es entre las variables
altura y peso, filtrando el conjunto de datos por sexo
2

3. En primer lugar, filtraremos la variable sexo para varones. Para ello
cliqueamos en “Datos”→“Conjunto de datos activos” → “Filtrar el
conjunto de datos activos”.
Una vez filtrada, comprobaremos si las
variables altura y peso siguen una
distribución normal. Seguiremos los
siguientes pasos:
1. Histograma
2. Grafico QQ
3. Realizar el test de normalidad
3
Conjunto de datos filtrando la
variable sexo para varones :
sexo==“Varon”

4. VARIABLE PESO EN VARONES
HISTOGRAMA GRÁFICA QQ
Cliquear en “ Graficas”, “Histograma” y
seleccionar la variable “peso”
Cliquear en “Gráficas”, “grafica de comparación
de cuartiles” y seleccionar variable “peso”
4

5. Realizamos el test de normalidad de Kolmogorov-Smirnov puesto que el tamaño
maestral es superior a 50 (n =51).
Para ello cliqueamos en “estadísticos”→“resúmenes”→“test de normalidad”
5

6. 6
Observando el histograma parece que la variable peso no sigue una distribución
normal, pero no puede asegurarse.
Observando la grafica QQ encontramos algunos valores que se salen de la línea,
pero no podemos decidir si sigue o no una distribución normal.
Finalmente, al realizar el test de normalidad de Kolmogorov-Slimrov comprobamos
que la variable peso sigue una distribución normal; pues el p valor = 0,05356 > α
(0,05) luego se acepta la Hipótesis nula (H0).
Luego concluimos que, la variable “peso “sigue una distribución normal.
 H0 : las medias muestrales se distribuyen normalmente
 H1: las medias muestrales NO se distribuyen normalmente
NOTA

7. VARIABLE ALTURA EN VARONES
HISTOGRAMA GRÁFICA QQ
7

8. 8
Observando el histograma, podemos deducir que la variable altura no sigue
una distribución normal aunque no podemos confirmarlo aún.
Según la gráfica QQ , parece que la variable altura sigue una distribución
normal a pesar de que algunos datos estén más dispersos.
Para comprobar si sigue o no distribución normal realizaremos finalmente el
test de normalidad para la variable “altura”

9. 9
Realizamos el test de normalidad de Kolmogorov-Slimrov para comprar si la
variable altura sigue o no una distribución normal.
Para ello cliqueamos en “estadísticos”→ “resúmenes”→“test de normalidad”
y seleccionamos la variable altura.
El resultado del test de normalidad es p-valor =0,0267 ; luego el p-valor
es < α (0,05) por lo que se rechaza la Hipótesis nula (H0) y se acepta la
alterna (H1). Concluimos que la variable “altura” no se distribuye
normalmente.
 H0 : las medias muestrales se distribuyen normalmente
 H1: las medias muestrales NO se distribuyen normalmente
NOTA

10. 10
Puesto que una de las variables (“altura”) no se distribuye normalmente, no
podemos realizar el test de correlación de Pearson ya que no se cumple una de
las condiciones.
Luego, realizaremos el test de correlación de Rho de Spearman
En primer lugar, realizaremos una aproximación visual del grado de correlación a
través de la nube de puntos o grafico de dispersión.
En R Commander cliqueamos en “Gráficas” → “Diagrama de dispersión” y
seleccionar “Línea de mínimos cuadrados”
Observando la nube de
puntos, a simple vista
podemos ver que hay
correlación lineal
directa. Confirmaremos
la correlación con el test
de Rho de Spearman
En el eje X variable independiente

11. 11
Seguidamente, calculamos la matriz de correlación para valorar la fuerza de
correlación entre las variables “peso” y “altura”
El coeficiente Rho de Spearman es 0,3593082 por lo que ambas variables se
correlacionan de forma lineal o directa, siendo el grado de correlación bajo.

12. 12
Cliqueamos en “estadísticos”→”resúmenes”→ ”test de correlación”
Finalmente comprobamos si la correlación es significativa, es decir, si existe
correlación en la población. Para ello realizamos el test de correlación

13. 13
El resultado del p-valor es < α ( 0,009612 < 0,05), por lo que se rechaza la
hipótesis nula H0 y se acepta la hipótesis alterna. Luego, en la población existe
correlación entre las variables “peso” y “altura” en varones.
 H0:ρ = 0 (El coeficiente de correlación obtenido procede de una población
cuya correlación es cero: no hay correlación entre variables)
 H1: ρ ≠ 0 (El coeficiente de correlación obtenido procede de una población
cuyo coeficiente de correlación es distinto de cero: hay correlación entre
variables

14. 14
Volvemos a filtrar la base de datos “activossalud”, esta vez quedándonos
solo con las mujeres de la variable “sexo”. Para ello realizamos la misma
operación que en el caso anterior: Datos”→“Conjunto de datos activos” →
“Filtrar el conjunto de datos activos”.
Filtrar la variable
sexo para mujeres :
sexo==“Mujer”
Una vez filtrada, comprobaremos si las variables altura y peso siguen una distribución
normal. Seguiremos los siguientes pasos:
1. Histograma
2. Grafico QQ
3. Realizar el test de normalidad

15. VARIABLE PESO EN MUJERES
HISTOGRAMA GRÁFICO QQ
15

16. 16
Realizamos el test de normalidad de Kolmogorov-Smirnov puesto que el tamaño
maestral es superior a 50 (n =240).
Seguimos el mismo procedimiento que en el caso anterior, cliqueando en
“estadísticos”→“resúmenes”→“test de normalidad” y seleccionando variable
“peso”

17. 17
Observando el histograma podemos pensar que la variable “peso” no sigue una
distribución normal, pero no es seguro.
Según la grafica QQ, parece que sigue una distribución normal.
Finalmente, realizando el test de normalidad de Kolmogorov-Slimrov comprobamos
que la variable “peso” no sigue una distribución normal, pues el p-valor es < α
(0,0003874< 0,05) y por tanto se rechaza la hipótesis nula H0.
Luego, concluimos que la variable “peso” no sigue una distribución normal.
 H0 : las medias muestrales se distribuyen normalmente
 H1: las medias muestrales NO se distribuyen normalmente
NOTA

18. VARIABLE ALTURA EN MUJERES
HISTOGRAMA GRAFICO QQ
18
Cliquear en “ Graficas”, “Histograma” y
seleccionar la variable “peso”
Cliquear en “Gráficas”, “grafica de comparación
de cuartiles” y seleccionar variable “peso”

19. 19
Realizamos el test de normalidad de Kolmogorov-Smirnov puesto que el tamaño
maestral es superior a 50 (n =240), cliqueando en
“estadísticos”→“resúmenes”→“test de normalidad” y seleccionando variable
“altura”

20. 20
Observando el histograma, la variable “altura” parece que sigue una distribución
normal.
Según la gráfica QQ, también parece que sigue una distribución normal, pero
tendremos que comprobar con el test de normalidad.
Finalmente, realizamos el test de normalidad de Kolmogorov-Slimrov para comprobar
si la variable “altura” sigue o no una distribución normal. El p-valor es <α (0,001657 <
0,05), luego se rechaza la hipótesis nula H0 y se acepta la alterna H1
Luego, concluimos que la variable “altura” no se distribuye normalmente.
 H0 : las medias muestrales se distribuyen normalmente
 H1: las medias muestrales NO se distribuyen normalmente
NOTA

21. 21
Puesto que ninguna de las dos variables “peso” y “altura” se distribuye
normalmente, no podemos realizar el test de correlación de Pearson ya que no se
cumple una de las condiciones.
Realizaremos el test de correlación de Rho de Spearman
En primer lugar, al igual que en el caso anterior, realizaremos una aproximación
visual del grado de correlación a través de la nube de puntos o grafico de
dispersión.
En R Commander cliqueamos en “Gráficas” → “Diagrama de dispersión” y
seleccionar “Línea de mínimos cuadrados”
Observando la nube de
puntos, deducimos que
hay correlación lineal
directa entre las dos
variables, pero lo
confirmaremos a
continuación.

22. 22
Seguidamente, calculamos la matriz de correlación para valorar la fuerza de
correlación entre las variables “peso” y “altura”.
Seguimos el mismo procedimiento que en el caso de los varones. Cliquear en
“estadísticos” →“resúmenes” →“matriz de correlación” y seleccionar
variables “peso” y “altura” .
Marcar coeficiente de Spearman.
El coeficiente Rho de Spearman es 0,4796 por lo que ambas variables se
correlacionan de forma lineal o directa, siendo el grado de correlación moderado.

23. 23
Finalmente comprobamos si la correlación es significativa, es decir, si existe
correlación en la población. Para ello realizamos el test de correlación
Cliqueamos en “estadísticos”→”resúmenes”→ ”test de correlación” y seleccionar las
variables “altura” y “peso”.

24. 24
El resultado del p-valor es < α (2,7392e -14 < 0,05), por lo que se rechaza la
hipótesis nula H0 y se acepta la hipótesis alterna H1.
Luego, en la población existe correlación entre las variables “peso” y “altura” en
mujeres.
 H0:ρ = 0 (El coeficiente de correlación obtenido procede de una población
cuya correlación es cero: no hay correlación entre variables)
 H1: ρ ≠ 0 (El coeficiente de correlación obtenido procede de una población
cuyo coeficiente de correlación es distinto de cero: hay correlación entre
variables
CONTRASTE DE HIPÓTESIS

25. 25
FIN