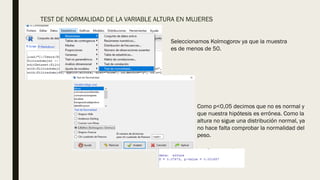
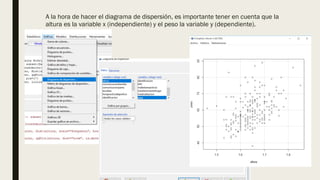
Este documento describe un análisis de correlación entre el peso y la altura de hombres y mujeres utilizando datos de salud. Se filtran los datos por sexo y se realizan pruebas de normalidad, diagramas de dispersión, matrices de correlación y pruebas de correlación de Spearman. Los resultados muestran una correlación positiva débil entre el peso y la altura tanto en mujeres como en hombres.

1. TAREA 8
CORRELACIÓN DE VARIABLES

2. En esta ocasión vamos a realizar la
correlación entre las variables peso y
altura, diferenciando por sexos. Para ello,
utilizaremos el programa R y el conjunto de
datos activossalud, al igual que en las
tareas anteriores.

3. En primer lugar, vamos a filtrar el conjunto de datos para poder observar la correlación
de las variables peso y altura solo en las mujeres.
Para ello, tras cargar el conjunto de datos, realizamos la siguiente ruta:
Conjunto de datos activo → Filtrar el conjunto de datos → variable: sexo → expresión
de selección: sexo==“Mujer”→ nombre del nuevo conjunto de datos: filtradomujer.

4. Comprobamos la eficacia de nuestra operación seleccionando la opción “Visualizar
datos”.
Como vemos, hemos filtrado correctamente los resultados.

5. Tras esto, comprobaremos si las variables siguen una distribución normal. Para ello,
realizaremos en primer lugar un histograma, en segundo lugar un gráfico de comparación
de cuantiles y, por último, un test de normalidad tanto de la altura como del peso
HISTOGRAMA DE LA
VARIABLE ALTURA
GRÁFICO DE COMPARACIÓN DE
CUANTILES DE LA VARIABLE ALTURA

6. TEST DE NORMALIDAD DE LA VARIABLE ALTURA EN MUJERES
Seleccionamos Kolmogorov ya que la muestra
es de menos de 50.
Como p<0,05 decimos que no es normal y
que nuestra hipótesis es errónea. Como la
altura no sigue una distribución normal, ya
no hace falta comprobar la normalidad del
peso.

7. A continuación realizaremos un análisis de correlación para conocer la relación de las
variables en cuestión. Para ello, primero haremos un diagrama de dispersión, una
matriz de correlaciones y un test de correlación.

8. A la hora de hacer el diagrama de dispersión, es importante tener en cuenta que la
altura es la variable x (independiente) y el peso la variable y (dependiente).

9. A continuación, comprobamos los resultados de la gráfica realizando una matriz de
correlación. Como estamos utilizando 2 variables que no presentan normalidad,
utilizaremos Spearman:

10. Por último, hacemos el test de correlación, a fin de sacar conclusiones.

11. Como vemos, hay una correlación positiva débil (puesto que es menor que 0,5 y por
tanto se aproxima al 0).
Además, el valor de p es inferior a 0,05, por lo que aceptamos la hipótesis alternativa,
es decir, que la altura sí influye en el peso.
Con esto, habríamos terminado la primera parte de la tarea.

12. Ahora pasaremos a realizar la correlación de la altura y el peso en los hombres. Para
ello, tendremos que cargar de nuevo el conjunto de datos y repetir el proceso de
filtrado, en este caso en varones.
Cargamos los datos y volvemos a tener 291 filas y 40 columnas.

13. Realizamos el filtrado.

14. Repetimos el proceso realizado previamente en las mujeres para calcular si las
variables siguen una distribución normal o no, estudiando el histograma, la gráfica de
comparación de cuantiles y el test de normalidad (se podría realizar solamente este
último).
HISTOGRAMA
COMPARACIÓN DE CUANTILES
TEST DE NORMALIDAD

15. El resultado del test de normalidad ha sido un valor de p menos a 0,05, por lo que las
variables no siguen una distribución normal. Debido a esto último, podemos
permitirnos no realizar el mismo proceso en la variable peso.
A continuación vamos a realizar un análisis de correlación. Para ello, haremos un
diagrama de dispersión, una matriz de correlaciones y por último un test de correlación.
Al igual que el caso anterior, debido a la distribución no normal de la variables,
utilizaremos Spearman.

16. DIAGRAMA DE DISPERSIÓN MATRIZ DE CORRELACIONES
TEST DE CORRELACIONES
Según el rho, vuelve a haber una correlación positiva débil.
Por otro lado, el valor de p es inferior a 0,05, por lo que rechazamos
la hipótesis nula y aceptamos la alternativa (la altura influye en el
peso.

17. FIN
¡GRACIAS POR SU ATENCIÓN!