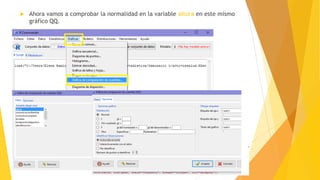
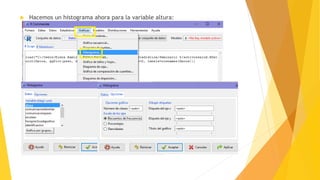
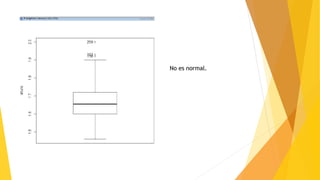
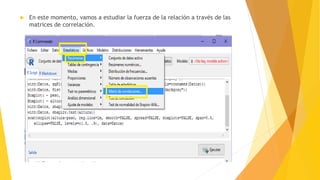
Este documento describe los pasos para analizar la relación entre las variables altura y peso. Inicialmente, se comprueba la normalidad de ambas variables a través de gráficos QQ, histogramas y diagrama de cajas, así como la prueba de Shapiro-Wilk, determinando que no siguen una distribución normal. Luego, el gráfico de dispersión muestra una relación positiva entre las variables. Finalmente, el coeficiente de correlación de Spearman de 0.6224 indica una relación fuerte entre la altura y el peso.

1. Seminario VIII: Análisis bivariado
con variables cuantitativas.
ELENA RAMÍREZ CALERO.

2. Normalidad y linealidad. Diagrama de
dispersión. Coeficientes de correlación de
Pearson y Rho de Spearman
EJERCICIO:
Determina que si existe
relación y como de fuerte es
entre las variables altura y
peso.

3. Instrucciones.
 Realizar un gráfico de dispersión para ver la
linealidad. Ver el grafico. Si tenemos claro que es
lineal (línea) usamos Pearson, si no usamos las dos
(Pearson y Spearman). Si tenemos muy claro que no
es lineal usamos la curva de Spearman directamente.
 Comprobar también la normalidad de las dos variables
por método gráfico box-plot (diagrama de cajas,
histogramas), y grafico q-q. También usaremos
Shapiro-Will.
 Contraste de hipótesis.

4.  Para realizar la asociación entre las variables altura y peso, lo primero es
comprobar la normalidad, para ello realizamos la comprobación con
diferentes pruebas en cada una de las variables, la primera será la variable
peso en una gráfica QQ.

5. Este sería el gráfico
resultante del proceso.
Como podemos observar,
esta variable no sigue una
distribución normal, ya que,
aunque hay algunos puntos
que están en el lugar de la
línea roja (que se
corresponde de la
normalidad), la gran mayoría
de los puntos se sale de ella.

6.  Ahora vamos a comprobar la normalidad en la variable altura en este mismo
gráfico QQ.

7. Vemos el resultado del
procedimiento. En este
caso comprobamos que
tampoco es normal ya
que al igual que ocurría
anteriormente, aunque
algunos puntos se
ajustan a la
normalidad, la mayoría
de ellos están fuera por
lo que la distribución no
puede considerarse
normal.

8.  A continuación, vamos a comprobar la normalidad con el histograma.

9. El histograma
resultante corrobora
la información antes
obtenida, la
distribución no es
normal si no que
está sesgada hacia
un lado.

10.  Hacemos un histograma ahora para la variable altura:

11. Tampoco en este
caso se ve
normalidad, no se
ajusta mucho el
histograma de
nuestra distribución
con la campana de
Gauss.

12.  Cómo último método gráfico para comprobar la normalidad, utilizamos el
diagrama de cajas o gráfico box plot.

13. Sigue sin haber
normalidad en la
variable peso.

14. Hacemos
lo mismo
con la
variable
altura.

15. No es normal.

16. Test de Shapiro- Wilk.
 La última prueba para asegurarnos de la normalidad es el test de Shapiro Wilk
en ambas variables.

17. Peso.
Altura.
Ho: hay normalidad. P>0,05
H1: no hay normalidad. P<0,05
Las dos distribuciones tienen una p valor menor que 0,05
por lo que rechazamos Ho y decimos que ninguna sigue la
normalidad.

18. Regresión y correlación.
Al haber comprobado que las
variables no son normales,
pasamos a comprobar la relación
entre las variables (regresión) y la
fortaleza de esta posible relación
(correlación).

19. Regresión.
 Para ver la regresión realizamos un diagrama de dispersión:

20. Viendo el resultado
obtenido podemos ver
que existe relación
entre ambas
variables. Esto se
puede ver al
comprobar que la
recta tiene pendiente
y que, por lo general,
a mayor altura hay
mayor peso.

21.  En este momento, vamos a estudiar la fuerza de la relación a través de las
matrices de correlación.

22. En este paso
seleccionamos las dos
variables pulsando la
tecla “control”. A
continuación
seleccionamos el
coeficiente de Spearman
ya que hemos
comprobado que las
distribuciones no son
normales y tampoco
tiene linealidad.

23. La relación entre las dos variables es
de 0,6224, por lo que la relación es
buena y más bien fuerte, ya que el
coeficiente de correlación va de 0 a 1.

24.  Podemos asegurarnos calculando la correlación de la siguiente forma.
Seleccionamos las
variables, el
coeficiente de
Spearman, la
hipótesis
alternativa
bilateral y le
damos a aceptar.

25. Comprobamos que sale el
mismo resultado. Podemos
rechazar nuestra Ho antes
citada ya que la p valor es
menor a 0,05
Concluimos
que existe
una gran
relación
entre las
variables
altura y
peso.