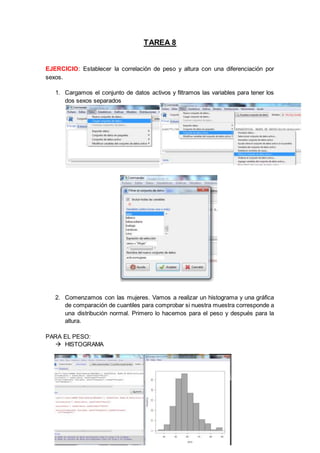
Este documento describe los pasos para establecer la correlación entre el peso y la altura de mujeres y hombres. Se realizan histogramas, gráficas de cuantiles y pruebas de normalidad para determinar si el peso y la altura siguen distribuciones normales. Luego, se crean diagramas de dispersión, matrices de correlación y pruebas de correlación usando el coeficiente de Spearman para analizar la correlación entre el peso y la altura dentro de cada sexo.

1. TAREA 8
EJERCICIO: Establecer la correlación de peso y altura con una diferenciación por
sexos.
1. Cargamos el conjunto de datos activos y filtramos las variables para tener los
dos sexos separados
2. Comenzamos con las mujeres. Vamos a realizar un histograma y una gráfica
de comparación de cuantiles para comprobar si nuestra muestra corresponde a
una distribución normal. Primero lo hacemos para el peso y después para la
altura.
PARA EL PESO:
 HISTOGRAMA

2.  GRÁFICA DE COMPARACIÓN DE CUANTILES
 TEST DE NORMALIDAD PARA EL PESO EN MUJERES.
Usamos Kolmogorov porque se trata
de una muestra grande (n>50)
Como p<0.05 podemos afirmar que la
variable “peso” no sigue una
distribución normal.

3. Vamos a hacer lo mismo con la altura:
 HISTOGRAMA.
 GRÁFICA DE COMPARACIÓN DE CUANTILES
 TEST DE NORMALIDAD PARA LA ALTURA
Como p es menor a 0,05
podemos afirmar que la
variable altura no
corresponde a una
distribución normal.

4. 3. A continuación vamos a realizar un diagrama de dispersión, matriz de
correlación y test de correlación para las dos variables (altura y peso). Para el
test y la matriz de correlación vamos a utilizar el coeficiente de Spearman.
 DIAGRAMA DE DISPERSIÓN
 MATRIZ DE CORRELACIÓN

5.  TEST DE CORRELACIÓN
4. Vamos a hacer lo mismo con los hombres.
PESO: HISTOGRAMA, GRÁFICA DE COMPARACIÓN DE CUANTILES Y TEST DE
NORMALIDAD.

6. La variable “peso” en el hombre si
corresponde a una distribución normal
porque p>0.05

7. ALTURA: HISTOGRAMA, GRÁFICA DE COMPARACIÓN DE CUANTILES Y TEST
DE NORMALIDAD.
Como p<0,05 podemos decir
que la variable “altura” no
corresponde a una distribución
normal en el hombre.

8. 5. Vamos a realizar ahora el diagrama de dispersión, la matriz de correlación y el
test de correlación. Como solo una de las variables corresponde con una
distribución normal, vamos a emplear el Coeficiente de Spearman
 DIAGRAMA DE DISPERSIÓN
 MATRIZ DE CORRELACIÓN Y TEST DE CORRELACIÓN