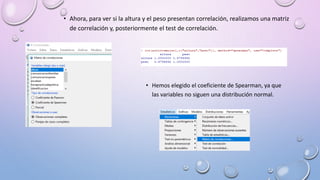
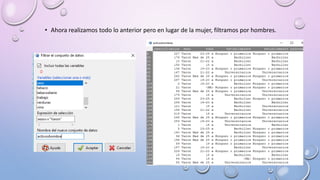
El documento describe un análisis estadístico que establece la correlación entre el peso y la altura diferenciado por sexo. Se realizan pruebas de normalidad, diagramas de dispersión, matrices de correlación y pruebas de correlación de Spearman para determinar si existe una relación entre el peso y la altura en mujeres y hombres. Los resultados muestran que existe una correlación significativa entre el peso y la altura tanto en mujeres como en hombres.

1. TAREA 9
ESTADÍSTICA Y TICS
ROCÍO DEL PILAR SUTIL ARENAS SUBGRUPO 5

2. EJERCICIO
• Tenemos que establecer la correlación entre las variables peso y altura, diferenciado por sexos.
• Estudiamos la relación que tiene el peso y la altura en los hombres, y posteriormente en las
mujeres.

3. • Para hacer la correlación entre peso
y altura, debemos de filtrar el
conjunto de datos a solo mujeres.

4. • Ahora debemos ver si las variables “altura” y “peso” siguen
una distribución normal o no.
• Primero realizaremos el histograma y la gráfica QQ para la
altura.

5. • Para saber si la variable altura sigue una distribución normal,
debemos de hacer el test de normalidad para la “altura”.
• Utilizamos el test de normalidad “Kolmogorov – Smirnov”
debido a que el tamaño de la muestra es mayor de 50.
• Una vez realizamos el test, vemos que el valor de “p”
es menor de 0,05. Por lo tanto, podemos decir que la
altura no presenta una distribución normal.

6. Ahora realizamos lo mismo con el peso.
Realizamos las gráficas, que parecen indicarnos que el
peso no se distribuye normalmente. Para asegurarnos
realizamos el test de normalidad.
Una vez realizado el test vemos que el valor de “p” es
muy inferior a 0,05. por lo tanto, podemos decir que el
peso no sigue una distribución normal.

7. • Después de haber realizado lo anterior, ahora sí vamos a ver si existe relación entre la altura y el
peso en la mujer. Para ello realizamos un diagrama de dispersión.

8. • Ahora, para ver si la altura y el peso presentan correlación, realizamos una matriz
de correlación y, posteriormente el test de correlación.
• Hemos elegido el coeficiente de Spearman, ya que
las variables no siguen una distribución normal.

9. • Ahora realizamos el test de correlación.
• Observamos el valor de “p” y vemos que es muy inferior a
0,05. por lo tanto, rechazamos la hipótesis nula y decimos
que la altura y el peso están relacionados en la mujer.

10. • Ahora realizamos todo lo anterior pero en lugar de la mujer, filtramos por hombres.

11. • Vemos si la altura presenta una distribución normal en el hombre.
• Vemos que “p” es menor que
0,05 y que la altura no sigue
una distribución normal.

12. • Vemos si el peso presenta una distribución normal en el hombre.
• Vemos que “p” es mayor que
0,05 y que la altura sigue una
distribución normal.

13. • Diagrama de dispersión, matriz de correlación y test de correlación entre altura y
peso.
• Como el valor de “p” es
menor que 0,05, podemos
decir que si hay correlación
entre la atura y el peso en el
hombre. Por lo tanto,
rechazamos la hipótesis nula.