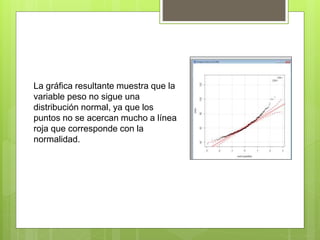
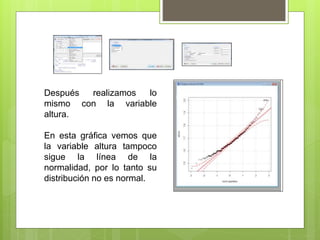
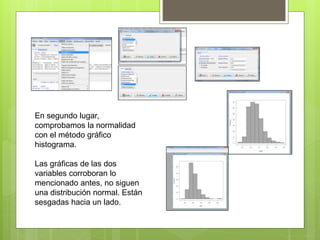
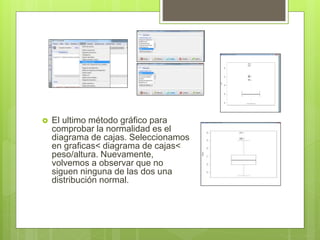
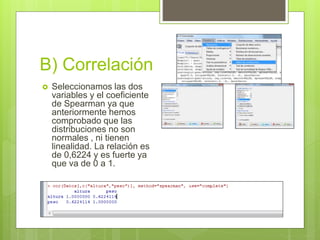
Este documento describe un ejercicio para determinar la relación entre las variables altura y peso mediante diferentes métodos. Se comprueba la normalidad de ambas variables con gráficos de QQ, histograma y cajas, así como con la prueba de Shapiro-Wilk, encontrando que no siguen una distribución normal. Se realiza una regresión mostrando una relación positiva entre altura y peso, y una correlación de Spearman de 0.6224 indicando una fuerte asociación entre las variables.

1. SEMINARIO
VIII
Pilar Gordillo González

2. EJERCICIO
 Determina si existe relación y cómo de fuerte
es entre las variables altura y peso.
 Para realizar la asociación entre las variables
altura y peso, comprobamos la normalidad de
cada una de las variables con métodos
gráficos (QQ, Histograma y diagrama de
cajas) y Shapiro Wilk.

3.  Empezamos con la variable peso y la gráfica
QQ. Seleccionando en Gráficas< Graficas de
comparación de cuartiles< aceptar

4. La gráfica resultante muestra que la
variable peso no sigue una
distribución normal, ya que los
puntos no se acercan mucho a línea
roja que corresponde con la
normalidad.

5. Después realizamos lo
mismo con la variable
altura.
En esta gráfica vemos que
la variable altura tampoco
sigue la línea de la
normalidad, por lo tanto su
distribución no es normal.

6. En segundo lugar,
comprobamos la normalidad
con el método gráfico
histograma.
Las gráficas de las dos
variables corroboran lo
mencionado antes, no siguen
una distribución normal. Están
sesgadas hacia un lado.

7.  El ultimo método gráfico para
comprobar la normalidad es el
diagrama de cajas. Seleccionamos
en graficas< diagrama de cajas<
peso/altura. Nuevamente,
volvemos a observar que no
siguen ninguna de las dos una
distribución normal.

8. SHAPIRO WILK
 El test se hace para ambas variables:
 Estadísticos< Resumenes< Test de
normalidad de Shapiro Wilk.

9.  Nuestras hipótesis son:
 Ho: la variable altura sigue una distribución
normal.
 H1: la variable altura no sigue una distribución
normal.
Al ser el p valor menor de 0,05, decimos que es
test es significativo, rechazando Ho y aceptando
H1, por lo tanto la variable peso no sigue una
distribución normal.

10.  Nuestras hipótesis son:
 Ho: la variable peso sigue una distribución
normal.
 H1: la variable peso no sigue una distribución
normal.
Al ser el p valor menor de 0,05, decimos que es
test es significativo, rechazando Ho y aceptando
H1, por lo tanto la variable peso no sigue una
distribución normal.

11. REGRESIÓN Y CORRELACIÓN
 Comprobamos la relación entre las variables:
regresión. Usamos un diagrama de
dispersión.
 Comprobamos la fortaleza de la relación:
correlación. Utilizamos matrices de
correlación.

12. A) Regresión
 En la gráfica se puede
observar que la recta
tienen pendiente y que
generalmente a mayor
altura mayor peso. Por lo
tanto podemos decir que
hay relación entre las
variables peso y altura.

13. B) Correlación
 Seleccionamos las dos
variables y el coeficiente
de Spearman ya que
anteriormente hemos
comprobado que las
distribuciones no son
normales , ni tienen
linealidad. La relación es
de 0,6224 y es fuerte ya
que va de 0 a 1.

14.  Para comprobar la
correlación usamos el test de
correlación: Estadísticos <
Resúmenes < Test de
correlación.
 Sale el mismo resultado,
rechazamos la Ho ya que la
p valor es menor que 0,05,
con lo que aclaramos que
hay una gran asociación
entre las variables peso y
altura.