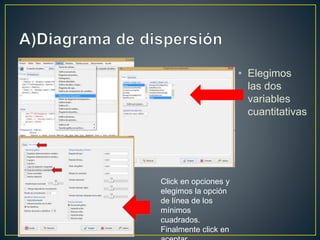
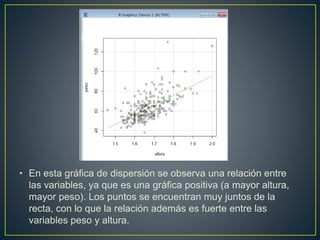
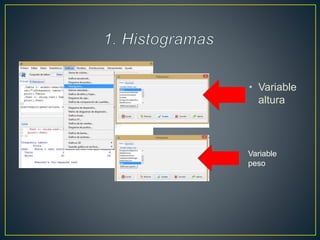
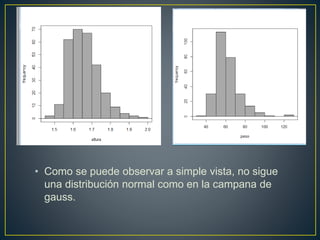
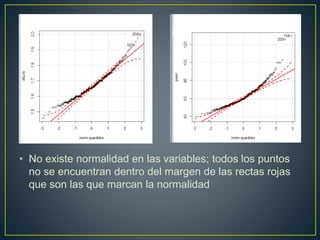
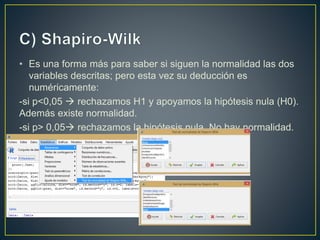
El documento analiza la relación entre el peso y la altura de individuos utilizando diferentes métodos estadísticos. No se encontró evidencia de normalidad en las variables a través de histogramas y pruebas estadísticas. El diagrama de dispersión mostró una relación positiva fuerte entre las variables. El coeficiente de correlación de Spearman fue de 0.631, indicando también una fuerte relación positiva entre el peso y la altura.

1. JESÚS SABORIDO RAMÍREZ
SUBGRUPO 14
ESTADÍSTICA Y TICS

2. • Estudiar dos variables cuantitativas (el peso y la altura) y
analizar la relación que hay entre ambas y como de
fuerte la relación en caso de que exista.
• Hay que utilizar:
 Normalidad y linealidad
 Diagrama de dispersión
 Coeficientes de correlación de Pearson y Rho
Spearman.

3. • Elegimos
las dos
variables
cuantitativas
Click en opciones y
elegimos la opción
de línea de los
mínimos
cuadrados.
Finalmente click en

4. • En esta gráfica de dispersión se observa una relación entre
las variables, ya que es una gráfica positiva (a mayor altura,
mayor peso). Los puntos se encuentran muy juntos de la
recta, con lo que la relación además es fuerte entre las
variables peso y altura.

5. • HISTOGRAMAS
• GRÁFICO DE CUARTILES

6. • Variable
altura
Variable
peso

7. • Como se puede observar a simple vista, no sigue
una distribución normal como en la campana de
gauss.

8. ALTURA
PESO

9. • No existe normalidad en las variables; todos los puntos
no se encuentran dentro del margen de las rectas rojas
que son las que marcan la normalidad

10. • Es una forma más para saber si siguen la normalidad las dos
variables descritas; pero esta vez su deducción es
numéricamente:
-si p<0,05  rechazamos H1 y apoyamos la hipótesis nula (H0).
Además existe normalidad.
-si p> 0,05 rechazamos la hipótesis nula. No hay normalidad.

11. • En ambos casos apreciamos como p-value> 0,05;
podemos concluir que no siguen una distribución normal.
ALTURA
PESO

12. • Se utiliza solo cuando las variables no siguen una
distribución normal, sirve para ver el grado de relación
que existe entre ambas (coeficiente de Spearman).
Para elegir las dos
variables hay que pulsar
en la tecla «Ctrl» y click
en las dos variables
(altura y peso). Después
click en aceptar

13. • Al comparar ambas variables vemos como tienen una
relación de 0,6311292 (siendo la correlación perfecta 1).
Por tanto, determinamos que existe una relación muy
fuerte entre ambas variables.