Texto docente 8 básico

básico
RafaelHumbertoArancibiaRojas
Edición especial para el Ministerio de Educación. Prohibida su comercialización.
Guía Didáctica del Docente
Tomo
2

Guía Didáctica del Docente - Tomo 2
Matemática 8° básico
Familias tipográficas empleadas en este libro:
Chaparral Pro, Myriad Pro
Rafael Humberto Arancibia Rojas
Profesor de Matemática y Computación
Universidad de Santiago de Chile
Magíster en educación mención gestión educacional
Universidad Metropolitana de Ciencias de la Educación
CL0000000001141 MATE_8B_GDD_Iniciales_Tomo_2_5929.indd 1 1/8/2020 12:03:11 PM

La Guía Didáctica del Docente Matemática 8° básico es una obra colectiva, creada y diseñada
por el Departamento de Investigaciones Educativas de Editorial Santillana, bajo la dirección de:
RODOLFO HIDALGO CAPRILE
SUBDIRECCIÓN EDITORIAL
Cristian Gúmera Valenzuela
COORDINACIÓN ÁREA MATEMÁTICA
Cristian Gúmera Valenzuela
EDICIÓN
Dafne Milenka Vanjorek Suljgoi
AUTORÍA
Rafael Humberto Arancibia Rojas
CORRECCIÓN DE ESTILO
Departamento de estilo Santillana
SUBDIRECCIÓN DE DISEÑO
Verónica Román Soto
DISEÑO Y DIAGRAMACIÓN
Alvaro Pérez Montenegro
FOTOGRAFÍAS
Archivo Santillana
Getty Images
Shutterstock
DOCUMENTACIÓN
Cristian Bustos Chavarría
PRODUCCIÓN
Rosana Padilla Cencever
Las lecturas que hemos seleccionado e incorporado en este texto de estudio han sido escogidas por su calidad lingüística y
didáctica. La lectura de las mismas y las actividades que se realizan facilitan el aprendizaje de los alumnos y alumnas. Agradecemos
a todos los autores por su colaboración.
Quedan rigurosamente prohibidas, sin la autorización escrita de los titulares del copyright, bajo las sanciones establecidas en
las leyes, la reproducción total o parcial de esta obra por cualquier medio o procedimiento, comprendidos la reprografía y el
tratamiento informático, y la distribución en ejemplares de ella mediante alquiler o préstamo público.
La editorial ha hecho todo lo posible por conseguir los permisos correspondientes para las obras con copyright que aparecen en
el presente texto. Cualquier error u omisión será rectificado en futuras impresiones a medida que la información esté disponible.
En este libro se usan de manera inclusiva términos como “los niños”, “los padres”, “los hijos”, “los apoderados”, “profesores” y otros que se refieren
a hombres y mujeres.
De acuerdo con la norma de la Real Academia Española, el uso del masculino se basa en su condición de término genérico, no marcado en la oposición
masculino/femenino; por ello se emplea el masculino para aludir conjuntamente a ambos sexos, con independencia del número de individuos que
formen parte del conjunto. Este uso evita, además, la saturación gráfica de otras fórmulas, que puede dificultar la comprensión de lectura y limitar
la fluidez de lo expresado.
©2019 – Santillana del Pacífico S. A. de Ediciones
Andrés Bello 2299, Piso 10, oficinas 1001 y 1002,
Providencia, Santiago, Chile.
ISBN Obra completa: 978-956-15-3506-0
ISBN Tomo 2: 978-956-15-3508-4
Inscripción Nº: 310.626
Se terminó de imprimir esta 1ª edición de 7.354 ejemplares en el mes de enero del año 2020.
Impreso en Chile por Aimpresores S.A.
www.santillana.cl
CL0000000001141 MATE_8B_GDD_Iniciales_Tomo_2_5929.indd 2 17-01-20 14:54

Presentación
E
l diseño y la construcción de la Guía Didáctica del Docente Matemática 8°
básico apunta al desarrollo de los estudiantes del nivel en la asignatura
de Matemática en función de lo establecido en las Bases Curriculares.
Para ello, se atiende de manera integrada tanto los contenidos como
las habilidades y actitudes que las herramientas curriculares declaran,
tales como números, álgebra, geometría, modelación, representación
y búsqueda de soluciones a situaciones problema.
En ese sentido, junto con exhibir un nivel acorde a la edad, con los contenidos y
requerimientos de los alumnos, la presente propuesta favorece el desarrollo de
diversas habilidades, las que dicen relación no solo con su desarrollo cognitivo y sus
correspondientes ritmos de aprendizaje, sino también con las habilidades disciplinares
que la asignatura promueve y, además, las del siglo 21, valiéndose para ello de variadas
actividades que permiten practicarlas, a lo largo del año, de manera sistemática
y progresiva.
El enfoque didáctico se plantea desde el modelo de la instrucción explícita (Archer y
Hughes, 2011). El proceso de aprendizaje es guiado y mediado por el docente, quien
expone las metas y el sentido de cada una de las tareas. En la Guía Didáctica se entregan
las herramientas para que el profesor modele las habilidades, secuenciándolas en pasos
pequeños, apoye y retroalimente la práctica, y así conduzca a los estudiantes a instancias
de práctica independiente, las que propenden al dominio de la habilidad.
Las unidades se han diseñado a partir de una meta establecida de antemano y
con criterios de evaluación definidos y públicos. Cada una se organiza a partir de
una pregunta esencial o tópico generativo (Stone, 2005) que incentiva la reflexión
de los alumnos y que busca conectarse con sus intereses, con miras a crear un
espacio significativo para construir el aprendizaje. Todas las lecturas, actividades y
procedimientos propuestos atienden a la pregunta esencial, de manera que los niños
se vean estimulados a reflexionar al respecto e inicien un trabajo a lo largo del cual
irán desarrollando sus propias respuestas. Para articular este trabajo se dan a conocer
los objetivos de cada unidad (McTighe y Wiggins, 2004), de modo que el estudiante
conozca de antemano los aprendizajes que desarrollará.
Las planificaciones, orientaciones y materiales complementarios que componen
la Guía Didáctica del Docente apuntan a apoyar la labor del profesor en cuanto a
proponer y potenciar situaciones de aprendizaje significativas y auténticas en el aula,
en consonancia con lo referido en las Bases Curriculares. “Esta propuesta tiene como
propósito formativo enriquecer la comprensión de la realidad, facilitar la selección de
estrategias para resolver problemas y contribuir al desarrollo del pensamiento crítico
y autónomo en todos los estudiantes, integrando y articulando los ejes temáticos
definidos para la asignatura” (Bases Curriculares, 2015).
Esperamos que esta Guía Didáctica permita orientar, apoyar y enriquecer
su ejercicio profesional.
III
Presentación

Índice
Organización y uso de la Guía Didáctica del Docente ..................................................VI
Planificación anual .................................................................................................................................VIII
Planificación semestral .......................................................................................................................234
Planificación de la Unidad 3 ............................................................................................................236
Presentación de la Unidad 3 ...........................................................................................................238
Orientaciones y planificaciones de clase ............................................................................... 240
(Planificaciones clases 65 a 94)
Solucionario Texto del Estudiante ..............................................................................................298
Orientaciones y solucionario Cuaderno de Actividades ............................................. 306
Actividades complementarias .......................................................................................................324
• Actividades complementarias: refuerzo – Lección 1 ..................................................... 324
• Actividades complementarias: ampliación – Lección 1 ............................................... 325
Solucionario Actividades complementarias ........................................................................ 330
Instrumentos de evaluación ...........................................................................................................334
• Instrumentos de evaluación: Evaluación diagnóstica ................................................... 334
• Instrumentos de evaluación: Evaluación de proceso – Lección 1 y 2 ................. 336
• Instrumentos de evaluación: Evaluación de proceso – Lección 3 ......................... 338
• Instrumentos de evaluación: Evaluación formativa ........................................................ 340
• Instrumentos de evaluación: Evaluación final ....................................................................341
Solucionario Instrumentos de evaluación ............................................................................ 343
IV Índice

Planificación semestral .......................................................................................................................348
Planificación de la Unidad 4 ............................................................................................................350
Presentación de la Unidad 4 ...........................................................................................................352
Orientaciones y planificaciones de clase ............................................................................... 354
(Planificaciones clases 95 a 114)
Solucionario Texto del Estudiante ..............................................................................................390
Orientaciones y solucionario Cuaderno de Actividades ............................................. 398
Actividades complementarias .......................................................................................................410
Solucionario Actividades complementarias ........................................................................ 414
Instrumentos de evaluación ...........................................................................................................416
• Instrumentos de evaluación: Evaluación diagnóstica ................................................... 416
• Instrumentos de evaluación: Evaluación formativa ........................................................ 422
• Instrumentos de evaluación: Evaluación final ....................................................................423
Solucionario Instrumentos de evaluación ............................................................................ 425
Bibliografía .................................................................................................................................................430
Sitios web ....................................................................................................................................................431
V
V
Índice

Organización y uso de la Guía Didáctica del Docente
La Guía Didáctica del Docente presenta la siguiente estructura:
Planificación anual,
planificaciones semestrales
y de unidad.
Planificaciones clase a clase, con orientaciones
y tiempos estimados para su inicio, desarrollo
y cierre, y las siguientes cápsulas:
Planificación anual
Unidad Sección / Lección
1
La era digital
¿Cómo puedes relacionar
los números con la tecnología?
Evaluación diagnóstica
Lección 1: Números enteros
Lección 2: Números racionales
Lección 3: Potencias, raíz cuadrada y porcentajes
Evaluación final
Síntesis y Repaso
2
Medioambiente
¿Cómo podemos aplicar el álgebra
en el cuidado del medioambiente?
Lección 1: Expresiones algebraicas
Lección 2: Ecuaciones e inecuaciones
Lección 3: Funciones
Evaluación final
Síntesis y Repaso
3
La geometría del arte
¿Cómo se relaciona la geometría y el arte?
Lección 1: Área y volumen de prismas y cilindros
Lección 2: Teorema de Pitágoras
Lección 3: Transformaciones isométricas
Evaluación final
Síntesis y Repaso
4
El deporte
¿Cómo se relacionan la estadística
y la probabilidad con el deporte?
Lección 1: Estadística
Lección 2: Probabilidades
Evaluación final
Síntesis y Repaso
8 Guía Didáctica del Docente • Matemática 8°B
Orientaciones y planificaciones de clase
Unidad
1
Propósito de la unidad
Profundizar en las operaciones con
números enteros y números racionales.
Además, ampliar el estudio de potencias.
Objetivos de aprendizaje
OA 1 , OA 2 , OA 3 , OA 4 y OA 5
(2 horas pedagógicas) /
págs. 8 y 9
Planificación
Clase 1
Conocimientos y experiencias previos
Para resolver las actividades propuestas es necesario que el estudiante
repase:
• adición y sustracción de números enteros
• adición y sustracción de fracciones positivas
• multiplicación y división de decimales positivos
• potencias de base 10 con exponente natural.
Orientaciones y
planificaciones de clase
Actitudes
A lo largo de esta unidad trabajarán las
siguientes actitudes:
OA A Abordar de manera flexible
y creativa la búsqueda de soluciones
a problemas de la vida diaria, de la
sociedad en general, o propios de otras
asignaturas.
OA C Demostrar interés, esfuerzo
y perseverancia y rigor frente a la
resolución de problemas y la búsqueda
de nuevas soluciones para problemas
reales.
OA D Trabajar en equipo, en forma
responsable y proactiva, ayudando a
los otros, considerando y respetando
los aportes de todos, y manifestando
disposición a entender sus argumentos
en las soluciones de los problemas.
Gestión de la clase
Inicio 15 minutos
Comente con sus estudiantes
“continuaremos profundizando en las
operaciones con números enteros y
números racionales”. Luego comparta
situaciones problemas de la vida diaria
donde es posible realizar operaciones
con estos números.
Desarrollo 60 minutos
Invite a sus estudiantes a observar las
imágenes y pregunte:
• ¿De qué forma se relacionan los números
con los aparatos tecnológicos que
utilizas?
• ¿Cómo crees tú que los conjuntos
numéricos que conoces se utilizan para
el desarrollo de nueva tecnología?
• ¿Conoces algún invento actual que su
funcionamiento depende de operaciones
numéricas?
Invite a sus estudiantes a desarrollar, de
forma individual, la evaluación diagnóstica
en sus cuadernos.
Cierre 15 minutos
Revise junto a sus estudiantes la evaluación
diagnóstica. Invítelos a reflexionar acerca
de errores y/o dificultades que tuvieron al
desarrollar esta.
Notas para el docente
Invite a sus estudiantes a reflexionar acerca del uso de redes sociales.
Luego pregunte:
• ¿Quéelementosmatemáticosreconocenenelfuncionamientoderedes
sociales como: Facebook, Instagram, Whatsapp?
• ¿Necesitamossabermatemáticaparahacerusodelatecnología?Explica
describiendo situaciones cotidianas.
• ¿Quéentiendenporprogramación?Sinoconoceneltérmino,invítelosa
investigarquéeslaprogramaciónycómoserelacionaconlamatemática
y los números.
En Chile (enero 2018) hay un total de 28115115 teléfonos móviles, más de 10 millones por sobre
la cantidad de habitantes del país. Por otra parte, un estudio muestra que los chilenos pasan 5 horas
diarias conectados al teléfono. Como si fuera poco, Chile es líder en el uso de redes sociales.
| Matemática 8ºB
8
¿Cómo puedes relacionar
los números con la tecnología?
Es imposible imaginar la tecnología sin los números, porque son
la base de todos los algoritmos que permiten hacer funcionar,
por ejemplo, las aplicaciones que usamos en nuestro telefóno móvil.
• ¿Cuáles crees que son la ventajas y desventajas del uso actual
de la tecnología?
• ¿En qué situaciones cotidianas se utilizan los números negativos?
¿Y las fracciones o porcentajes?
1. Resuelve las siguientes operaciones.
a. (–4) + (–6) – (–2) b. 3 • 1,25
2. Calcula el valor de cada potencia.
a. 105
b. 107
3. Resuelve los siguientes problemas.
a. Un submarino se encuentra inicialmente a 32 m de
profundidad y luego desciende 23 m más. ¿A qué
profundidad se halla el submarino?
b. En una encuesta quedó reflejado que el 70% de las
personas reconocía haber caminado en la calle mirando
su celular en más de una oportunidad. Si respondieron
la encuesta 1500 personas, ¿a qué cantidad corresponde
dicho porcentaje?
Lección 1
Números
enteros
Página10
Lección 2
Números
racionales
Página22
Lección 3
Potencias, raíz cuadrada
y porcentajes
Página38
La era
digital
1
Unidad
En esta unidad estudiarás los números enteros, los números
racionales, las potencias y raíces, y las variaciones porcentuales
a través de sus representaciones y del uso de las operaciones, las
que te serán útiles para la resolución de situaciones problema.
Matemática 8ºB | 9
17
16 Guía Didáctica del Docente • Unidad 1 Guía Didáctica del Docente • Matemática 8°B
Planificación Semestral
Unidad
Tiempo
estimado*
Clases
Sección /
Lección
Objetivos de aprendizaje Indicadores de evaluación
Guía Didáctica
del Docente
Actitud
Unidad
1
2 1
Inicio de
unidad
• Evaluación diagnóstica pág. 106
OA A
OA C
OA D
OA E
OA F
12 2 a 7
Lección 1
Números
enteros
OA 1 Mostrar que comprenden la multiplicación y la división de números enteros:
• Representándolos de manera concreta, pictórica y simbólica.
• Aplicando procedimientos usados en la multiplicación y la división de números naturales.
• Aplicando la regla de los signos de la operación.
• Resolviendo problemas rutinarios y no rutinarios.
• Representan la multiplicación por -1 de manera concreta.
• Desarrollan la regla de los signos en ejemplos concretos o en la recta numérica.
• Representan la multiplicación y división de números enteros positivos y negativos.
• Aplican la regla de los signos de las multiplicaciones y de las divisiones en ejercicios rutinarios.
• Resuelven problemas cotidianos que requieren la multiplicación o división de números enteros.
• Actividades de refuerzo pág. 96
• Actividades de ampliación pág. 97
18 8 a 16
Lección 2
Números
racionales
OA 2 Utilizar las operaciones de multiplicación y división con los números racionales
en el contexto de la resolución de problemas:
• Representándolos en la recta numérica.
• Involucrando diferentes conjuntos numéricos (fracciones, decimales y números enteros).
• Representan operaciones con fracciones negativas y decimales negativos en la recta numérica.
• Realizan ejercicios rutinarios que involucren las cuatro operaciones con fracciones y decimales.
• Reconocen la operación matemática adecuada en problemas sencillos para resolverlos.
• Resuelven problemas que involucren la multiplicación y la división de números racionales.
• Utilizan diferente notación simbólica para un número racional (decimal, fraccionaria, mixta).
• Evaluación de proceso lección 1 y 2
pág. 108
26 17 a 29
Lección 3
Potencias,
raíz cuadrada
y porcentajes
OA 3 Explicar la multiplicación y la división de potencias de base natural y exponente natural
hasta 3, de manera concreta, pictórica y simbólica.
OA 4 Mostrar que comprenden las raíces cuadradas de números naturales:
• Estimándolas de manera intuitiva.
• Representándolas de manera concreta, pictórica y simbólica.
• Aplicándolo a situaciones geométricas y en la vida diaria.
OA 5 Resolver problemas que involucran variaciones porcentuales en contextos diversos,
usando representaciones pictóricas y registrando el proceso de manera simbólica; por
ejemplo: el interés anual del ahorro.
• Representan potencias de base y exponente natural hasta 3.
• Representan la multiplicación, la división y la potencia de potencias de exponente natural hasta 3.
• Descubren, comunican y aplican las propiedades de la multiplicación y división de potencias.
• Ubican la posición aproximada de raíces no exactas en la recta numérica.
• Aplican la raíz cuadrada en la solución de problemas de la vida cotidiana.
• Relacionan porcentajes rebajados y aumentados con situaciones reales.
• Identifican, en expresiones de la vida diaria, los términos involucrados en el cálculo porcentual.
• Expresan porcentajes aumentados o rebajados con números decimales y viceversa.
• Determinan el porcentaje de promociones.
• Evaluación de proceso lección 3
pág 110
6 30 y 32
Fin de
unidad
OA 1, OA 2, OA 3, OA 4, OA 5
• Evaluación formativa pág. 112
• Evaluación final pág. 113
Unidad
2
2 33
Inicio de
unidad
10 2 a 6
Lección 1
Expresiones
algebraicas
OA 6 Mostrar que comprenden las operaciones de expresiones algebraicas:
• Representándolas de manera pictórica y simbólica.
• Relacionándolas con el área de cuadrados, rectángulos y volúmenes de paralelepípedos.
• Determinando formas factorizadas.
• Modelan la propiedad distributiva de la multiplicación sobre la suma.
• Transforman productos en sumas y sumas en productos, en ejercicios rutinarios.
• Elaboran expresiones algebraicas a base de composiciones de áreas y perímetros de figuras 2D.
• Desarrollan y reducen términos algebraicos que incluyen sumas y productos.
• Actividades de ampliación pág 205
16 42 a 49
Lección 2
Ecuaciones e
inecuaciones
OA 8 Modelar situaciones de la vida diaria y de otras asignaturas, usando ecuaciones lineales
de la forma: ax = b; x
a
= b, a ≠ 0 ; ax + b = c; x
a
+ b = c; ax = b + cx; a(x + b) = c; ax + b = cx + d.
OA 9 Resolver inecuaciones lineales con coeficientes racionales en el contexto de la resolución
de problemas, por medio de representaciones gráficas, simbólicas, de manera manual y/o con
software educativo.
• Representan pictóricamente ecuaciones mediante balanzas.
• Modelan situaciones que requieren de una ecuación o inecuación y resuelven problemas.
• Representan inecuaciones de manera concreta, pictórica o simbólica.
• Resuelven inecuaciones de la forma ax + b < c o ax + b > c en ejercicios rutinarios.
• Evaluación de proceso lección 1 y 2
pág. 216
24 50 a 61
Lección 3
Funciones
OA 7 Mostrar que comprenden la noción de función por medio de un cambio lineal:
Utilizando tablas; usando metáforas de máquinas; estableciendo reglas entre x e y;
representando de manera gráfica (plano cartesiano, diagramas de Venn), de manera manual
y/o con software educativo
OA 10 Mostrar que comprenden la función afín:
Generalizándola como la suma de una constante con una función lineal; trasladando
funciones lineales en el plano cartesiano; determinando el cambio constante de un intervalo
a otro, de manera gráfica y simbólica, de manera manual y/o con software educativo;
relacionándola con el interés simple; utilizándola para resolver problemas de la vida diaria.
• Descubren el concepto de función mediante la relación de proporcionalidad directa.
• Representan la noción de función de manera concreta, pictórica o simbólica.
• Elaboran las tablas y gráficos correspondientes, basados en ecuaciones de funciones lineales.
• Representan la linealidad f(kx) = kf(x) y f(x1
+ x2
) = f(x1
) + f(x2
) en tablas y gráficos.
• Identifican la pendiente del gráfico de la función f(x) = a • x con el factor a.
• Modelan situaciones de la vida cotidiana o de ciencias con funciones lineales o afines.
• Representan tablas y gráficos pertenecientes a cambios con una base fija y tasa de cambio constante.
• Elaboran, basados en los gráficos, la ecuación de la función afín f(x) = a • x + b.
• Diferencian modelos afines, lineales y de proporcionalidad inversa.
• Evaluación de proceso lección 3
pág. 218
6 62 y 64
Fin de
unidad
OA 6, OA 7, OA 8, OA 9, OA 10
Presentación de la Unidad 1
Sección/Lección
Tiempo estimado
(horas pedagógicas)
Clases OA
Texto del estudiante/
Cuaderno de actividades
Páginas del texto
del estudiante
Páginas del
cuaderno de
actividades
Páginas de la guía didáctica del docente
Planificación
de clases
Recursos
Inicio de unidad 2 1 –
• Inicio de unidad y evaluación
diagnóstica
8 y 9 – 16 y 17 • Evaluación diagnóstica pág. 106
Lección 1
Números Enteros
12 2 a 7 OA 1
• Multiplicación de números enteros
• División de números enteros
• Evaluación lección 1
10 a 21 6 a 15 18 a 29
Lección 2
Números
racionales
18 8 a 16 OA 2
• El conjunto de los números racionales
• Fracciones y números decimales
• Adición y sustracción de números
racionales
• Multiplicación y división de números
racionales
22 a 37 16 a 25 30 a 45
• Evaluación de proceso lección 1 y 2 pág. 108
Lección 3
Potencias, raíz
cuadrada y
porcentajes
26 17 a 29
OA 3
OA 4
OA 5
• Multiplicación de potencias
• División de potencias
• Raíz cuadrada
• Variaciones porcentuales
38 a 59 26 a 35 46 a 67
• Evaluación de proceso lección 3 pág. 110
Fin de unidad 6 30 y 32
OA 1
OA 2
OA 3
OA 4
OA 5
• Evaluación final
• Síntesis y repaso
60 a 63 36 y 37 68 a 71
La era digital
¿Cómo puedes relacionar los números con la tecnología?
Planificaciones
• Dificultades y errores frecuentes: se
sugieren actividades para detectar
y aclarar los posibles errores de los
estudiantes.
• Uso de recursos tecnológicos:
se proponen actividades
complementarias haciendo
uso de la tecnología.
• Solucionario: se indican las páginas
donde se pueden revisar las
soluciones de las actividades.
• Notas para el docente: orientaciones
generales enfocadas en el
tratamiento del contenido,
desarrollo de las actividades
e instancias metacognitivas.
• Desarrollo del pensamiento: se
proponen actividades y preguntas
para estimular el desarrollo del
pensamiento matemático.
• Conocimientos y experiencias
previos: se presentan los
conocimientos que el estudiante
debe recordar y preguntas orientadas
a activar las experiencias previas.
• Conexión interdisciplinaria: se
relacionan los contenidos trabajados
con otras disciplinas y ejes.
• Opciones para profundizar:
se proponen actividades de
profundización e información
complementaria.
• Ambientes de aprendizaje: se
sugieren instancias para promover
las actitudes y un ambiente
positivo en el aula.
VI Organización y uso de la Guía Didáctica del Docente

• Evaluación
diagnóstica
Nombre: Curso: Fecha:
Instrumentos de evaluación: Evaluación diagnóstica
Material
fotocopiable
Marca la opción correcta en los ítems 1 al 10.
1. ¿Cuál de las siguientes frases no se relaciona
con el número –12?
A. Variación de 12 ºC.
B. Nació en el año 12 a. C.
C. Temperatura de 12 ºC bajo cero.
D. 12 metros bajo el nivel del mar.
2. Los números que están ordenados de mayor
a menor son:
A. –69; –67; –72; –77
B. –175; –157; –152; –125
C. –304; –290; –189; –205
D. –754; –762; –775; –789
3. ¿Cuál es el resultado de (–4) – (12) + (–6) – (–2)?
A. –24
B. –20
C. –10
D. –8
4. Aristófanes, autor de comedias, nació en el año
386 a. C. ¿Cuántos años han pasado desde su
nacimiento hasta el año 2015?
A. 1628
B. 1629
C. 2400
D. 2401
5. Si se corta una cuerda de 3 m de longitud en
trozos de 1
4
m, ¿cuántos pedazos se obtienen?
A. 4
B. 7
C. 12
D. 25
6. ¿Cuál es el resultado de b
2
7 •
3
5 l :
4
35?
A.
2
3
B.
3
2
C.
6
25
D.
25
6
7. Felipe recorre en bicicleta 16,1 km en una hora.
¿Cuántos kilómetros recorrerá en 2,3 horas?
A. 14,02 km
B. 18,52 km
C. 30,70 km
D. 37,03 km
8. En un curso de 35 estudiantes, el 40 % son
mujeres. ¿Cuántos estudiantes son hombres?
A. 14
B. 17
C. 21
D. 35
9. ¿Qué alternativa corresponde al desarrollo
de 105
?
A. 10 • 5
B. 10 • 10 • 10 • 10 • 10
C. 10 + 10 + 10 + 10 + 10
D. 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5
10.La arista de un cubo mide 10 cm.
¿Cuál es el volumen del cubo?
A. 10 cm3
B. 100 cm3
C. 1000 cm3
D. 10000 cm3
Guía Didáctica del Docente • Unidad 1
106
• Evaluación
de proceso
Instrumentos de evaluación: Evaluación proceso
a. 8 • 2 + 8
b. 12 • (–5) – 4
c. (–10) • 3 + 8 • 12
d. (–5 + 16) • (40 – 8)
e. (42 – 7) • (–1 500)
f. (–58) • (–8 – 15)
g. 50 • (–50) + 50 – (–50)
h. (–88 + 8) • (–888)
i. –30 : 6 + 25
j. 80 • 2 + 90 : (–9)
k. (–64) : (–4) – 50
l. 100 • 16 : 4
m. 7 – 56 : 7 + 42
n. –550 : (–50) + 505
ñ. 25 – 1 246 : (–2)
o. 136 : (–8) • 4
2. Completa con“positivo”o“negativo”.
a. Si multiplicas tres números negativos,
el producto es .
b. Si multiplicas dos números negativos y
uno positivo, el producto es .
c. Si multiplicas cinco números negativos y
dos positivos, el producto es .
3. Completa con =, < o >.
a. (–1) • (–3) (–9) : (–3)
b. (–9) + 2 (–3) + (–7)
c. (–4) • 9 • (–1) (–2) • (–3) • 4
d. (–6) : 3 • 0 (–6) : 3
e. (–10) • (–10) (–10) • 10
f. 12 : (–3) 8 : (–2)
g. 1 –(–1)
4. Completa la tabla y luego responde.
x 2x 2x – 3
–3
1
–8
–7
a. Nicolás dice que si x es un número entero, en
la segunda columna siempre va a resultar un
número par. ¿Estás de acuerdo? ¿Por qué?
b. Andrea dice que si x es un número entero,
en la última columna siempre va a resultar un
número impar. ¿Estás de acuerdo? ¿Por qué?
5. Ubica los siguientes números en la recta numérica.
1,8 –0,25 – 3
4
0,9 1
3
–5
3
1,5
–2 –1 0 1 2
6. Resuelve y completa la siguiente tabla.
+ – 1
2
– 3
4
12
5
7
10
– 1
5
–1,2
0,5
–8,35
108 Guía Didáctica del Docente • Unidad 1
Material
fotocopiable
Lección 1 y 2
Unidad
1
Material
fotocopiable
Instrumentos de evaluación: Evaluación final
1. El producto entre –10, –2 y 5 es:
A. –100 B. –20 C. 100 D. 20
2. Las temperaturas mínima y la máxima
registradas durante un día fueron –2 °C en la
mañana y 23°C en la tarde. ¿Cuál es la variación
entre estas temperaturas?
A. Aumento de 21 °C.
B. Aumento de 25 °C.
C. Disminución de 21 °C.
D. Disminución de 25 °C.
3. Un buzo se sumergió 15 metros en 1 hora.
Si cada 15 minutos bajó la misma cantidad
de metros, ¿cuántos metros se sumergió
en 45 minutos?
A. 11,25 m
B. 7,5 m
C. 3,75 m
D. 1,5 m
4. Las temperaturas registradas durante tres días
se muestran en la siguiente tabla:
Lunes Martes Miércoles
Mínima –3 ºC –4 ºC –2 ºC
Máxima 21 ºC 18 ºC 24 ºC
¿Cuál es el promedio de las temperaturas
mínimas y de las máximas registradas durante
los tres días?
A. El promedio es –3 ºC la mínima y 21 ºC
la máxima.
B. El promedio es –3 ºC la mínima y 22 ºC
la máxima.
C. El promedio es –1 ºC la mínima y 21 ºC
la máxima.
D. El promedio es –1 ºC la mínima y 24 ºC
la máxima.
5. ¿Cuál de las siguientes alternativas representa
el valor de A en la recta numérica?
–2 A –1 0
A. –1 1
4
B. –1 1
2
C. –1 3
4
D. –2 1
4
6. ¿Cuál es el valor de 10,5 – 1
2
+ 0,2?
A. 11,2
B. 10,2
C. –10,2
D. –11,2
7. Luis tiene 154 llaveros de distintos lugares del
mundo. Si 7
11
corresponden a Sudamérica,
¿cuántos llaveros son de otros lugares?
A. 14 llaveros.
B. 22 llaveros.
C. 56 llaveros.
D. 98 llaveros.
8. ¿Cuál de las siguientes potencias es equivalente
a la expresión 4 • (28
: 4)2
?
A. 26
B. 212
C. 214
D. 222
9. Un tipo de bacteria se divide en dos cada
8 minutos. ¿Cuántas bacterias habrá a partir
de una de ellas pasados 88 minutos?
A. 28
bacterias.
B. 211
bacterias.
C. 288
bacterias.
D. 888
bacterias.
Guía Didáctica del Docente • Matemática 8° básico 113
• Evaluaciones
formativas
Instrumentos de evaluación: Evaluación formativa
Material
fotocopiable
a. 5 • 3
b. 45 : (–9)
c. (–28) : (–4)
d. (–5) • (–8)
e. (–4) • 3
f. –90 : (–10)
g. 54 : (–1)
h. (–7) • (–2)
i. (–10) • 1
j. –200 : (–40)
k. 192 : (–8)
l. (–1 240) • (–3)
a. 0,4 • 3,1
b. – 1
3
: 5
24
c. –1,2 : (–0,2) + 0,5
d. 1
8
• (–0,25)
e. 3
4
+ 5
4
– 1
4
f. 0,5 : 1
3
g. 2
5
• 1 1
10
: 1
5
h. – 5
6
+ 0,57 • 5
4
3. Marca con una el número que debe ir en
el recuadro para que se cumpla la igualdad.
a. 1
2
• = 1
–1
2
2
b. –0,3=–0,3 0,03 0,63
c. 2
5
: = 6
35
3
7
7
3
d. + 1 4
5
= 11
5
4
2
5
4. Completa la siguiente tabla.
a b a2
b2
a2
• b2
2 1
10 5
4 3
5. Calcula el resultado de cada expresión. Para
ello, utiliza las propiedades de las potencias.
a. 22
b. 52
c. 3 • 33
d. 53
• 23
e. 33
• 33
f. 73
• 7
g. 23
: 22
h. 33
: 33
i. 83
: 43
j. 1003
: 103
k. 23
: 2 • 22
l. 43
: 42
: 2
m. 32
• 42
n. (52
)3
: 52
ñ. (82
: 8) • 8
6. Calcula el valor de las siguientes raíces.
a. 1
b. 9
c. 100
d. 0
e. 25
f. 81
7. Aproxima las siguientes raíces cuadradas al
número natural más próximo. Luego, ubícalas
en la recta numérica.
a. 3
b. 14
c. 50
d. 32
e. 18
f. 20
g. 1000
h. 65
i. 89
8. Completa y calcula los valores finales.
a. Aumento del 10% sobre $300.
110% • =
b. Descuento del 3% de $2 500.
• $2500 =
9. Francisco pagó $253000 por un refrigerador.
Si estaba con un 8% de descuento, ¿cuál era
el valor del refrigerador sin el descuento?
¿Cuánto dinero se ahorró Francisco?
10.El precio de un televisor de 32 pulgadas es
de $350000. Si está en oferta con un 30% de
descuento, ¿cuánto se deberá pagar luego de
aplicado el descuento?
11.La medida de uno de los lados de un cuadrado
es 23 cm. Si esta aumenta en un 20%, ¿cuál es
el perímetro del cuadrado?
112
• Solucionarios
Unidad
1
Material
fotocopiable
Solucionario Instrumentos de evaluación
1. A
2. D
3. B
4. D
5. C
6. B
7. D
8. C
9. B
10. C
11. La temperatura es de –16 °C.
12. a. 1050 estudiantes.
b. 225 estudiantes.
c. Representan
7
10
del total.
Objetivos de aprendizaje ítems Indicadores de logro
• Representar y ordenar números enteros.
• Resolver adiciones y sustracciones entre números enteros.
• Resolver problemas utilizando números enteros.
1, 2, 3,
4 y 11
Logrado: 3 ítems correctos o más.
Por lograr: menos de 3 ítems correctos.
• Resolver multiplicaciones y divisiones de fracciones y números
decimales positivos.
• Resolver problemas que involucren la multiplicación y la división de fracciones
y de decimales positivos.
• Resolver problemas que involucren las cuatro operaciones con fracciones y
decimales.
5, 6 y 7
• Calcular porcentajes y aplicarlo en distintas situaciones. 8 y 12
Logrado: 2 ítems correctos.
• Calcular el valor de una potencia de base 10 con exponente natural.
• Resolver problemas usando potencias.
9 y 10
• Fichas de ampliación: actividades
de profundización relacionadas
con lo desarrollado en
cada lección.
Unidad
1
Material
fotocopiable
Actividades complementarias: ampliación
1. Completa la representación en la que el número escrito
en cada casilla corresponde al producto de los números
de las dos casillas inferiores.
a. Agustín utiliza su bicicleta para hacer deporte. Cada día recorre 12 km en la mañana y 5 km en la tarde.
¿Cuántos kilómetros recorre en total al cabo de 4 días?
b. Un submarino descendió hasta una profundidad de 36 m en 3 etapas. Si en cada etapa se sumergió
la misma cantidad de metros, ¿cuántos metros descendió el submarino en cada etapa?
c. Un buzo en una laguna descendió 8 m en una hora. Si cada hora bajó la misma cantidad de metros,
¿cuántos metros bajó en 4 horas?
d. Francisca tiene un saldo negativo de $12000 en su línea de crédito. Si cada día que pasa le cobran $450
de intereses por mora, ¿cuánto dinero deberá pagar en la línea de crédito al cabo de 6 días para dejar
la deuda en $0?
e. Una cámara de frío se encuentra a –18 °C. Si cada 4 minutos aumenta la misma cantidad de grados y
luego de 24 minutos alcanza una temperatura de 0 °C, ¿cuántos grados aumenta cada 8 minutos?
8
5
–400
–20000
Lección 1
• Fichas de refuerzo: actividades
para reforzar los conocimientos
y habilidades trabajados en
cada lección.
Actividades complementarias: refuerzo
Material
fotocopiable
1. Resuelve cada multiplicación.
a. 3 • 4 =
b. (–2) • 12 =
c. (–6) • 6 =
d. (–3) • 5 • (–1) =
e. (–2) • (–13) • (–8) =
f. (–7) • 9 =
g. 4 • 8 =
h. 10 • 14 =
i. (–4) • (–1) • (–1) =
j. 1 • (–11) • (–5) =
2. Resuelve cada división.
a. 36 : (–18) =
b. –10 : (–5) =
c. 23 : (–1) =
d. 104 : (–13) =
e. –42 : 14 =
f. 11 : (–11) =
g. –56 : (–7) =
h. 0 : (–9) =
i. –144 : (–12) =
j. 81 : (–3) =
3. Completa la siguiente tabla.
a b c a • b a : –b a • b • c –c : a
5 –1 200
–12 –4 –96
150 30 –1050
–126 6 378
a. Un pulpo se encuentra a 6 metros de profundidad respecto del nivel del mar. Si desciende 3 metros
cada minuto, ¿a qué profundidad estará después de 5 minutos?
b. Si las temperaturas mínimas registradas durante 5 días de una semana son:
Lunes Martes Miércoles Jueves Viernes
–3 °C 1 °C 0 °C –2 °C –1 °C
¿Cuál fue la temperatura promedio durante los 5 días?
96
Lección 1
• Solucionario
Solucionario Actividades complementarias
Refuerzo
1. a. 12
b. –24
c. –36
d. 15
e. –208
f. –63
g. 32
h. 140
i. –4
j. 605
2. a. –2
b. 2
c. –23
d. –8
e. –3
f. –1
g. 8
h. 0
i. 12
j. –27
3.
a b c a • b a : –b a • b • c –c : a
5 –1 200 –5 5 –1000 –40
–12 –4 –96 48 –48 –4608 –8
150 30 –1050 4500 5 –4725000 7
–126 6 378 –756 –21 –285768 3
4. a. Estará a 21 m de profundidad.
b. La temperatura promedio fue de –1 °C.
Ampliación
1.
–400
–20000
–5
8
50
–10 8
1
–5
2
2. a. Anda 68 km.
b. Descendió 12 m en cada etapa.
c. Bajó 32 m en 4 horas.
d. Deberá pagar $14700.
e. Aumenta 6 °C.
102 Guía Didáctica del Docente • Unidad 1
Material
fotocopiable
• Solucionario del Texto del Estudiante. • Solucionario del Cuaderno de Actividades
Actividades complementarias
Instrumentos de evaluación
Solucionario Unidad 1
Página 9
• Las ventajas es que la tecnología ayuda a la humanidad
facilitando ciertas actividades en la vida cotidiana, así como
también en el desarrollo de las áreas del conocimiento
humano. Una desventaja es que en la actualidad el ser
humano está volviéndose muy dependiente de esta, se están
generando nuevas fuentes de contaminación.
• Los negativos se pueden utilizar en temperaturas o economía,
las fracciones y porcentajes sirven para dividir cosas o para
descuentos.
Evaluación diagnostica
1. a. –8
b. 3,75
c. 100000
d. 10000000
2. a. Se encuentra a 55 m de profundidad.
b. Corresponde a 1050 personas.
Página 10
Números enteros
Lección 1
Multiplicación de números enteros
• –800
• Proporciona una referencia de la posición y alabeo del avión
respecto al horizonte.
• –700
• Significa que se está descendiendo a 500 fpm. Se representa
con –500
• –700 • 15 = –10500. El avión habrá descendido 10500 pies
• Se deben multiplicar los 220m por los 8 minutos de descenso,
lo cual representa un descenso de 1760 m, lo cual significa
que la altitud del avión a los 8 minutos es de 8040 m
• Situación 1: Un avión se encuentra descendiendo a 500 fpm y
en un instante aumenta su velocidad de descenso en 200 fpm
¿a que velocidad se encuentra descendiendo? Se encuentra
descendiendo a 700 fpm, debido a que –500 + (–200) = –700
Situación 2: Un avión desciende a 300 fpm y en un instante
duplcia su velocidad ¿A que velocidad llega? Llega a 600 fmp,
esto ya que –300 • 2 = –600.
Página 14
Actividades
1. a. 16
4 4 4 4
b. –12
–2 –2 –2 –2 –2 –2
c. –21
3 3 3
3 3 3
3
d. –32
–4
–4
–4
–4
–4
–4
–4
2. –11 < –10 < –1 < 4 < 6 < 21
c.
–9 –8 –7 –6 –5 –4
+(–3) +(–3) +(–3)
–3 –2 –1 0
b.
–16 –14 –12 –10 –8 –6
+(–1) +(–1) +(–1) +(–1) +(–1) +(–1) +(–1) +(–1)
–4 –2 0
d.
–28 –24 –20 –16 –12 –8
+(–7) +(–7) +(–7) +(–7)
–4 0
0 2 4 6 8 10
+4 +4 +4 +4 +4
12 14 16 18 20
3. a.
4. Actividad en clase
Página 15
5. a. –16
b. 150
c. –630
d. 5
e. –288
f. 4
6. Si la cantidad de números negativos es par, el resultado será
positivo, si es impar el resultado será negativo.
7. a. +
b. –
c. +
d. +
8. Al multiplicar por –1 un entero positivo, se obtiene el mismo
número, pero con signo opuesto. Lo mismo ocurre al
multiplicar por –1 un entero negativo.
9. a. Debe pagar $4980
b. El cargo se puede relacionar con –4980.
10. a. –2750
b. 447
c. –4694
d. 1420
e. 605
f. –825
11.–25 • 3 • (–8) • (–12) = –75 • 96 = –7200
72 Guía Didáctica del Docente • Solucionario Unidad 1
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
10
a
15
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
1
del
Programa
de
Estudio.
Multiplicación
de
números
enteros
1.
Representa
en
la
recta
numérica
cada
multiplicación
y
calcula
el
producto.
a.
4
•
(–4)
=
–20
–15
–10
–5
0
5
10
15
20
b.
5
•
(–3)
=
–20
–15
–10
–5
0
5
10
15
20
c.
(–2)
•
6
=
–20
–15
–10
–5
0
5
10
15
20
d.
(–8)
•
1
=
–20
–15
–10
–5
0
5
10
15
20
2.
Resuelve
las
siguientes
multiplicaciones:
a.
(–5)
•
6
=
b.
(–1)
•
(–10)
=
c.
1
•
(–1)
=
d.
(–8)
•
4
=
e.
(–3)
•
(–9)
=
f.
17
•
(–4)
=
g.
(–8)
•
8
=
h.
(–15)
•
0
=
i.
30
•
(–2)
=
3.
Respetando
la
prioridad
de
las
operaciones,
calcula
el
resultado
de
cada
expresión.
a.
5
•
(–3)
+
(–2)
•
9
=
b.
(–4)
•
(–3)
•
(–2)
•
(–3)
=
c.
(–2)
•
(–6)
+
10
•
(–3)
=
d.
(–3)
•
(5
+
4)
•
(–2)
=
Unidad
1
•
La
era
digital
Números
enteros
Lección
1
6
|
Unidad
1
6
4.
Calcula
el
número
de
salida
para
cada
número
de
entrada
ingresado.
Entrada
–5
–3
4
7
Salida
Salida
•
(–3)
•
2
•
4
•
(–1)
Entrada
Si
es
positivo
o
cero
Si
es
negativo
5.
Identifica
y
explica
el
error
cometido
en
cada
caso
y
corrígelo.
a.
(–5)
•
4
=
20
Corrección:
Error:
b.
(–3)
•
(–3)
•
3
=
9
Corrección:
Error:
c.
0
•
(–17)
=
–17
Corrección:
Error:
1
Unidad
7
7
Lección
1
•
Números
enteros
|
80
Cuaderno
de
Actividades
•
Unidad
1
–16
–15
–12
–8
–30
–32
–64
10
6
–48
–84
10
27
0
–1
–33
–18
54
72
–68
–60
5
•
(–3)
+
(–2)
•
9
(–2)
•
(–6)
+
10
•(–2)
(–4)
•
(–3)
•
(–2)
•
(–3)
(–3)
•
(5
+
4)
•
(–2)
–15
+
–
18
–33
12
+
(–30
)
–18
(–5)
•
4=
–20
(–3)
•
(–3)
•
3
=
9
•
3
=
27
0
•
(–17)
=
0
–24
•
(–3)
72
–12
•
(–2)
•
(–3)
(–3)
•
9
•
(–2)
–27
•
(–2)
54
No
se
utilizó
bien
la
regla
Solo
se
multiplicaron
Cualquier
número
multiplicado
de
los
signos.
dos
factores.
por
cero
es
cero.
Solucionarios
VII
Organización y uso de la Guía Didáctica del Docente

Unidad Sección / Lección OA Actitudes
1
La era digital
¿Cómo puedes
relacionar los
números con
la tecnología?
OA 1
OA 2
OA 3
OA 4
OA 5
OA A: Abordar de manera flexible y creativa la búsqueda
de soluciones a problemas de la vida diaria, de la
sociedad en general, o propios de otras asignaturas.
OA C: Demostrar interés, esfuerzo, perseverancia y rigor
frente a la resolución de problemas y la búsqueda de
nuevas soluciones para problemas reales.
OA D: Trabajar en equipo, en forma responsable
y proactiva, ayudando a los otros, considerando y
respetando los aportes de todos, y manifestando
Lección 2: Números racionales
Lección 3: Potencias, raíz cuadrada y porcentajes
Evaluación final
Síntesis y Repaso
2
Medioambiente
¿Cómo podemos
aplicar el álgebra
en el cuidado del
medioambiente?
OA 6
OA 7
OA 8
OA 9
OA 10
OA C: Demostrar interés, esfuerzo, perseverancia y rigor
frente a la resolución de problemas y la búsqueda de
nuevas soluciones para problemas reales.
OA E: Mostrar una actitud crítica al evaluar las
evidencias e informaciones matemáticas y valorar el
aporte de los datos cuantitativos en la comprensión de
la realidad social.
OA F: Usar de manera responsable y efectiva las
tecnologías de la comunicación en la obtención de
información, dando crédito al trabajo de otros y
respetando la propiedad y la privacidad de las personas.
Lección 1: Expresiones algebraicas
Lección 2: Ecuaciones e inecuaciones
Lección 3: Funciones
Evaluación final
Síntesis y Repaso
3
La geometría
del arte
¿Cómo se relaciona la
geometría y el arte?
OA 11
OA 12
OA 13
OA 14
OA B: Demostrarcuriosidad,interésporresolverdesafíos
matemáticos,conconfianzaenlaspropiascapacidades,
inclusocuandonoseconsigueun resultado inmediato.
OA C: Demostrarinterés,esfuerzo,perseveranciayrigor
frentea laresoluciónde problemasylabúsquedadenuevas
solucionesparaproblemas reales.
OA D: Trabajarenequipo,enformaresponsableyproactiva,
ayudandoalosotros,considerandoyrespetandolosaportes
detodos,ymanifestandodisposiciónaentendersus
argumentosen lassolucionesdelosproblemas.
Evaluación final
Síntesis y Repaso
4
El deporte
¿Cómo se relacionan
la estadística
y la probabilidad
con el deporte?
OA 15
OA 16
OA 17
OA D: Trabajar en equipo, en forma responsable
y proactiva, ayudando a los otros, considerando y
respetando los aportes de todos, y manifestando
disposición a entender sus argumentos en las soluciones
de los problemas.
OA E: Mostrar una actitud crítica al evaluar las
evidencias e informaciones matemáticas y valorar el
aporte de los datos cuantitativos en la comprensión
de la realidad social.
OA F: Usar de manera responsable y efectiva las
tecnologías de la comunicación en la obtención de
información, dando crédito al trabajo de otros y
respetando la propiedad y la privacidad de las personas.
Evaluación final
Síntesis y Repaso
VIII Planificación anual

Habilidades*
Tiempo estimado
(Horas
pedagógicas)
a. Resolver problemas utilizando estrategias tales como:
• Destacar la información dada. • Descartar información irrelevante.
• Usar un proceso de ensayo y error sistemático. • Usar problemas similares.
• Aplicar procesos reversibles.
c.
Utilizar sus propias palabras, gráficos y símbolos matemáticos para presentar sus ideas o soluciones.
h.
Usar modelos, realizando cálculos, estimaciones y simulaciones, tanto manualmente como con ayuda de
instrumentos para resolver problemas de otras asignaturas y de la vida diaria.
k.
Elegir y utilizar representaciones concretas, pictóricas y simbólicas para enunciados y situaciones en contextos
diversos (tablas, gráficos, recta numérica, entre otros).
m.
Representar y ejemplificar utilizando analogías, metáforas y situaciones familiares para resolver problemas.
64
b.
Evaluar procedimientos y comprobar resultados propios y de otros de un problema matemático.
c.
e. Explicar y fundamentar:
• Soluciones propias y los procedimientos utilizados.
•
Resultados mediante definiciones, axiomas, propiedades y teoremas.
i.
Seleccionar y ajustar modelos, para resolver problemas asociados a ecuaciones e inecuaciones de
la forma ax + b ,,= c (a,b,c ∈ N) comparando dependencias lineales.
j. Evaluar la pertinencia de modelos:
• En relación con el problema presentado.
• Considerando sus limitaciones.
l.
Relacionar y contrastar información entre distintos niveles de representación.
64
c.
e. Explicar y fundamentar:
• Soluciones propias y los procedimientos utilizados.
• Resultados mediante definiciones, axiomas, propiedades y teoremas.
f.
Fundamentar conjeturas dando ejemplos y contraejemplos.
g. Evaluar la argumentación de otros dando razones.
h.
Usar modelos, realizando cálculos, estimaciones y simulaciones, tanto manualmente como con ayuda
de instrumentos para resolver problemas de otras asignaturas y de la vida diaria.
60
c.
d.
Describir relaciones y situaciones matemáticas de manera verbal y usando símbolos.
f.
Fundamentar conjeturas dando ejemplos y contraejemplos.
h.
Usar modelos, realizando cálculos, estimaciones y simulaciones, tanto manualmente como con ayuda de
instrumentos para resolver problemas de otras asignaturas y de la vida diaria.
k.
Elegir y utilizar representaciones concretas, pictóricas y simbólicas para enunciados y situaciones en contextos
diversos (tablas, gráficos, recta numérica, entre otros).
l.
Relacionar y contrastar información entre distintos niveles de representación.
40
* Las habilidades se trabajan de forma transversal y continua, pero en cada unidad se enfatiza las presentadas.
IX
IX

Planificación semestral
Unidad
Tiempo
estimado*
Clases
Sección /
Lección
Objetivos de Aprendizaje
Actitud
Unidad
3
2 65 Inicio de unidad
OA B
OA C
OA D
14 62 a 72
Lección 1
Área y volumen
de prismas y
cilindros
OA 11 Desarrollar las fórmulas para encontrar el área de superficies y el volumen
de prismas rectos con diferentes bases y cilindros: :
• Estimando de manera intuitiva área de superficie y volumen.
• Desplegando la red de prismas rectos para encontrar la fórmula del área de
superficie
• Transfiriendo la fórmula del volumen de un cubo (base por altura) en prismas
diversos y cilindros.
• Aplicando las fórmulas a la resolución de problemas geométricos y de la vida diaria.
16 73 a 80
Lección 2
Teorema de
Pitágoras
OA 12 Explicar, de manera concreta, pictórica y simbólica, la validez del teorema de
Pitágoras y aplicar a la resolución de problemas geométricos y de la vida cotidiana,
de manera manual y/o con software educativo.
22 81 a 91
Lección 3
Transformaciones
isométricas
OA 13 Describir la posición y el movimiento (traslaciones, rotaciones y reflexiones)
de figuras 2D, de manera manual y/o con software educativo, utilizando:
• Los vectores para la traslación.
• Los ejes del plano cartesiano como ejes de reflexión.
• Los puntos del plano para las rotaciones.
OA 14 Componer rotaciones, traslaciones y reflexiones en el plano cartesiano y en
el espacio, de manera manual y/o con software educativo, y aplicar a las simetrías de
polígonos y poliedros, y a la resolución de problemas geométricos relacionados con
el arte.
6 92 a 94 Fin de unidad OA 11, OA 12, OA 13, OA 14
Unidad
4
OA D
OA E
OA F
16
96 a
103
Lección 1
Estadística
OA 15 Mostrar que comprenden las medidas de posición, percentiles y cuartiles:
• Identificando la población que está sobre o bajo el percentil.
• Representándolas con diagramas, incluyendo el diagrama de cajón, de manera
manual y/o con software educativo.
• Utilizándolas para comparar poblaciones.
OA 16 Evaluar la forma en que los datos están presentados:
• Comparando la información de los mismos datos representada en distintos tipos de
gráficos para determinar fortalezas y debilidades de cada uno.
• Justificando la elección del gráfico para una determinada situación y su
correspondiente conjunto de datos.
• Detectando manipulaciones de gráficos para representar datos.
16
104 a
111
Lección 2
Probabilidades
OA 17 Explicar el principio combinatorio multiplicativo:
• A partir de situaciones concretas.
• Representándolo con tablas y árboles regulares, de manera manual y/o con software
educativo.
• Utilizándolo para calcular la probabilidad de un evento compuesto.
6
112 a
114
Fin de unidad OA 15, OA 16, OA 17
*Horas pedagógicas
234 Planificación semestral
CL0000000001141 MATE_8B_GDD_U3_Txt_5837.indd 234 1/8/2020 12:04:53 PM

Unidad
3
Habilidades Indicadores de evaluación
Guía Didáctica
del Docente
OAH c
OAH e
OAH f
OAH g
OAH h
• Arman y despliegan cajas de forma de prismas rectos.
• Elaboran redes de prismas rectos de diferentes bases y calculan las áreas de las superficies.
• Resuelven problemas cotidianos que involucran el volumen y el área de prismas rectos.
• Confeccionan de manera concreta modelos de cilindros y los comparan con modelos o
dibujos de prismas a base de polígonos regulares.
• Transfieren la fórmula del volumen de un cubo para determinar la del volumen de un cilindro.
• Calculan el área de cilindros en ejercicios rutinarios.
• Resuelven problemas cotidianos relacionados con el área y el volumen de cilindros.
• Actividades de ampliación
pág. 325
• Descubren el teorema de Pitágoras concreta o pictóricamente.
• Dibujan triángulos rectángulos con los cuadrados respectivos encima de los catetos y
la hipotenusa, y verifican la validez del teorema de Pitágoras.
• Estiman las raíces cuadradas que resultan al aplicar el teorema de Pitágoras.
• Verifican con las medidas dadas de un triángulo si es rectángulo o no.
• Calculan el largo del lado faltante para que un triángulo sea rectángulo y lo verifican.
pág. 327
• Evaluación de proceso
Lección 1 y 2 pág. 336
• Realizan traslaciones en el plano con vectores dados.
• Determinan el vector entre la imagen y la preimagen de 2 figuras 2D.
• Reflexionan figuras 2D según los ejes dados, de manera concreta y pictórica.
• Determinan el eje de reflexión entre la imagen y la preimagen de dos figuras 2D.
• Identifican rotaciones, reflexiones y traslaciones en situaciones cotidianas.
• Realizan traslaciones, reflexiones y rotaciones y reconocen las propiedades.
• Realizan teselados con figuras 2D, según los patrones dados.
• Identifican patrones de teselados dados, descubriendo las propiedades de la congruencia.
• Reconocen transformaciones isométricas dadas en el plano.
• Realizan combinaciones de traslaciones, reflexiones y rotaciones y reconocen las propiedades.
pág. 329
Lección 3 pág 338
OAH c
OAH d
OAH f
OAH h
OAH k
OAH l
• Organizan y agrupan datos en tablas o esquemas para formar distribuciones de frecuencias.
• Calculan, describen e interpretan las medidas de posición (cuartiles y percentiles).
• Representan las medidas de posición por medio de diagramas de cajón.
• Reconocen cuándo es adecuado utilizar alguna de las medidas para analizar una muestra.
• Comparan muestras de poblaciones, utilizando algunas de las medidas de tendencia.
• Explican la elección de tipos de gráficos para representar determinada información.
pág. 411
Lección 1 pág. 418
• Simulan experimentos que involucran elecciones al azar equiprobables reiteradas
(de pocos pasos) y describen pictóricamente los resultados, vía árboles.
(de pocos pasos).
pág. 413
235
Planificación semestral 235

Planificación Unidad 3
Sección/Lección
Tiempo estimado
Clases OA
Texto del Estudiante/
Cuaderno de Actividades
diagnóstica
Lección 1
Área y volumen
de prismas y
cilindros
14 66 a 72 OA 11
• Área de prismas y cilindros
• Volumen de prismas y cilindros
• Evaluación Lección 1
Lección 2
Teorema de
Pitágoras
16 73 a 80 OA 12
• Teorema de Pitágoras
• Aplicaciones del teorema de Pitágoras
Lección 3
Transformaciones
isométricas
22 81 a 91
OA 13
OA 14
• Traslación
• Rotación
• Reflexión
• Composición de transformaciones
isométricas
• Transformaciones isométricas en el
espacio
Fin de unidad 6 92 a 94
OA 11
OA 12
OA 13
OA 14
¿Cómo se relacionan la geometría y el arte?
236 Planificación Unidad 3

Unidad
3
Páginas del Texto
del Estudiante
Páginas del
Cuaderno de
Actividades
Páginas de la Guía Didáctica del Docente
Planificación
de clases
Recursos
118 a 135 76 a 85 242 a 259
136 a 147 86 a 93 260 a 271
• Evaluación de proceso Lección 1 y 2 pág. 336
148 a 169 94 a 107 272 a 293
• Evaluación de proceso Lección 3 pág. 338
170 a 173 108 y 109 294 a 297
237
Planificación Unidad 3 237

Unidad
3
¿Cómo se relacionan la geometría y el arte?
En esta unidad los estudiantes descubren y aplican las fórmulas del área de superficies y del volumen
de prismas rectos y de cilindros. Para ello, comienzan con cuerpos conocidos, como el cubo, y trabajan
con sus redes para determinar las relaciones entre largo, ancho y alto, necesarias para desarrollar el
nuevo conocimiento.
Se trabaja el teorema de Pitágoras, que se introduce, desde lo concreto de sus aplicaciones, con dibujos
explicativos y con una demostración matemática, pero sencilla. Se resuelven problemas que involucren
dicho teorema en contextos como la geometría, la construcción y el arte.
Además, se describen movimientos como la traslación, la rotación y la reflexión. Se comienza con algunos
sencillos, para continuar con la composición de dos o más de estos movimientos; la motivación puede
provenir del arte o de la matemática. También se sugiere usar medios visuales o material concreto para
ayudar a los estudiantes a desarrollar su capacidad espacial.
238 Presentación de la Unidad 3

Unidad
3
Ruta de aprendizaje de la Unidad 3
(Preguntas específicas
relacionadas con la temática
de la unidad, las imágenes
y el texto introductorio)
Enuncia 5 ramas del arte
en las que la geometría juega
un papel fundamental
Lecciones que se articulan según los
Objetivos de Aprendizaje de la unidad.
Evaluación de la Lección 1
Evaluación final
¿Cómo se relacionan
la geometría y el arte?
•
Traslación
• Rotación
• Reflexión
•
Composición de transformaciones
isométricas
•
Transformaciones isométricas
en el espacio
Lección 1: Área y volumen de prismas y
cilindros
•
Área de prismas y cilindros
• Volumen de prismas y cilindros
• Aplicaciones del teorema de Pitágoras
La estructura de la unidad se muestra a continuación:
239

Propósito
En esta clase los estudiantes conocerán
la estrecha relación entre la geometría y
el arte.
OA 11 , OA 12 , OA 13 , OA 14
Planificación
Actitudes
A lo largo de esta unidad trabajarás las
OA B Demostrar curiosidad e interés
por resolver desafíos matemáticos, con
confianza en las propias capacidades,
incluso cuando no se consigue un
resultado inmediato.
OA C Demostrar interés,
esfuerzo, perseverancia y rigor
frente a la resolución de problemas
y la búsqueda de nuevas soluciones
para problemas reales.
los aportes de todos y manifestando
Orientaciones y
Conexión interdisciplinaria
Invite a sus estudiantes a indagar acerca de la relación entre geometría
y arte solicitando que busquen imágenes de distintas manifestaciones
artísticas en las que se aprecien figuras geométricas.
Para profundizar en este tema, dígales que lean el documento
«Los secretos geométricos en diseño y arquitectura», disponible en:
imarrero.webs.ull.es/sctm05/modulo3lp/3/calsina.pdf
págs. 116 y 117
Clase 65
La geometría
del arte
3
Unidad
¿Cómo se relaciona la geometría y el arte?
En esta unidad estudiarás el área y el volumen de prismas rectos y de
cilindros; el teorema de Pitágoras y las transformaciones isométricas
para resolver diversos problemas geométricos y de la vida cotidiana.
Matemática y Arte han estado siempre estrechamente vinculadas: el número de oro,
las simetrías, las proporciones, la geometría, son elementos presentes en el arte; no
en vano muchos grandes artistas de la historia han sido grandes matemáticos; se
han apoyado en la matemática para expresar la realidad con un lenguaje artístico.
• Enuncia 5 ramas del arte donde la geometría juega un papel fundamental.
Lección 1
Área y volumen de
prismas y cilindros
Página118
Lección 2
Teorema
de Pitágoras
Página136
Lección 3
Transformaciones
isométricas
Página148
1. Calcula:
a. Si el largo de un rectángulo mide 8 cm y el ancho 2,5 cm menos,
¿cuál es su área?
b. ¿Cuál es el perímetro (P) de una circunferencia de radio 5 cm?
Considera π ≈ 3,14.
c. ¿Cuál es el área (A) de un círculo de radio 11 cm?
2. El perímetro de un triángulo equilátero mide 18 cm
y la altura mide 5,2 cm. Calcula el área del triángulo.
3. ¿Cuántas caras tienen los siguientes cuerpos geométricos?
| Matemática 8ºB
116
CL0000000001018 MATE_8B_Texto_U3_L1_5353.indd 116 12/17/2019 9:32:13 AM CL0000000001018 MA
240 Orientaciones y planificaciones de clase • Unidad 3

Unidad
3
Inicio 15 minutos
Analice junto con sus estudiantes la
situación planteada preguntando qué
aportes creen que hace la geometría
al arte y comparta con ellos el propósito
de la unidad.
Pídales a sus estudiantes que respondan
la evaluación de diagnóstico de forma
independiente y que registren las
respuestas en sus cuadernos.
Una vez terminada la evaluación, resuelva
cada una de las actividades en la pizarra
y corrija los errores cometidos por sus
estudiantes durante el desarrollo.
Cierre 15 minutos
Reflexione junto con ellos acerca
de las dificultades que tuvieron y
los errores cometidos.
Para apoyar su labor docente le ofrecemos
las imágenes de la unidad en el link
http://www.recursostic.cl/lic19/mat8_u3.
Opciones para profundizar
La geometría es importante para el desarrollo lógico-matemático por lo
que es necesario acercarla a los estudiantes de una forma significativa
y motivadora. Carmen Leandro afirma que una manera de hacer
esto es a través de diversos recursos artísticos que permitan que la
geometría entre en la sala de clases sirviendo el arte como punto de
partida para su introducción de manera sistemática, y como base de un
trabajo continuo que permita un enriquecimiento en su formación.
Puede obtener más información y conocer algunas actividades
propuestas por la autora en el siguiente link:
https://www.um.es/documents/299436/550133/
LEANDRO+BARQUERO,+CARMEN+M.pdf
2/17/2019 9:32:13 AM
PirámidedelMuseodelLouvre.
Inaugurada el 29 de marzo del año 1989.
CL0000000001018 MATE_8B_Texto_U3_L1_5353.indd 117 12/17/2019 9:32:14 AM
241
Orientaciones y planificaciones de clase • Unidad 3

Propósito
En esta clase los estudiantes comprenderán
los procedimientos para calcular el área de
prismas y cilindros.
OA 11
(2 horas pedagógicas)
Inicio 15 minutos
Invite a sus estudiantes a analizar la
situación planteada abordando la técnica
del cubismo. Solicíteles que investiguen
y expliquen esta técnica. Puede analizar
en conjunto con ellos los cuadros cubistas
expuestos en el siguiente link:
https://www.todocuadros.cl/estilos-arte/
cubismo/
• Luego, pídales realizar la actividad
propuesta. Puede utilizar esta instancia
para motivar a los alumnos, por
ejemplo, mediante la planificación de
una exposición de las obras creadas,
que puede trabajar en conjunto con la
asignatura de artes.
Para profundizar en la corriente artística del cubismo, especialmente
en lo referente a la «cuarta dimensión», se sugiere leer el documento
disponible en:
www.usc.es/revistas/index.php/quintana/article/download/1535/3081
Planificación
Ambiente de aprendizaje
Motive a sus estudiantes a mantener
un ambiente de respeto frente a las
opiniones o respuestas de cada uno
de los estudiantes del curso.
págs. 118 a 121
Clase 66
Actitudes
OA B
• Utiliza la técnica del cubismo para deconstruir un prisma y luego crea tu propia obra de arte.
En esta lección podrás descubrir y aplicar
las fórmulas del área de superficies y del
volumen de prismas rectos y de cilindros.
Área y volumen de prismas y cilindros
Lección 1
De un cubo 3D se pueden ver a lo más 3 de sus lados. Sin
embargo, 4-dimensional se podrían ver sus 6 lados a la vez.
Lo que hicieron los cubistas fue deconstruir el cubo 3D en
sus 6 facetas. Luego pintar las facetas en un lienzo 2D. Ahora
podríamos“ver el cubo”como si fuéramos de la cuarta dimensión.
Guitarraymandolina. Juan Gris. Madrid 1919.
1
3
4
6
5
3
1
4
2
5
6
2
El cubismo es un movimiento artístico que
rompe la estructura del arte tradicional.
Surge a principios del siglo XX tras las
investigaciones llevadas a cabo por pintores
como Pablo Picasso, Georges Braque y
Juan Gris, entre otros.
118 | Unidad 3
E
T
P
¿
P
2
l
E
D
CL0000000001018 MA
242

Unidad
3
Analice los ejemplos junto con sus
estudiantes y pregúnteles:
• ¿Cómo definirían un prisma?
• ¿Cómo definirían un prisma recto?
• ¿Qué representa el área de un prisma?
Formalice la definición de poliedro, prisma
y prisma recto considerando la información
de Aprende. Recuerde a sus estudiantes
las expresiones para el cálculo de áreas de
triángulos y cuadriláteros.
Solicíteles que establezcan una expresión
general para calcular el área de un
prisma recto.
Apoye el análisis de sus estudiantes a partir de la visualización de
redes de prismas disponible de un applet de GeoGebra en:
www.geogebra.org/m/zKYBrBG6
Puede trabajar en la construcción de
un prisma triangular y un prisma
rectangular mediante las redes de los
siguientes links:
https://www.curriculumnacional.cl/614/
articles-24674_recurso_jpg.jpg
articles-24675_recurso_jpg.jpg
Pue
fun
de h
rep
med
el s
http
arti
n.
9.
2/17/2019 9:32:15 AM
Ejemplo 1
Tamara tiene una caja en la que guarda sus útiles escolares. Ella quiere forrarla con papel.
Para ello, desarma la caja, como se muestra en la siguiente imagen.
¿Cómo podría saber Tamara cuánto papel requiere para forrar la caja?
Para saber cuánto papel utilizará, Tamara desarma la caja obteniendo una red formada por
2 triángulos y tres rectángulos. Entonces, si calcula el área de cada una de estas figuras y
las suma, tendrá el área total, y podrá dar respuesta a su interrogante.
Ejemplo 2
Dibuja la red geométrica del siguiente prisma recto de base cuadrada.
1 Dibujamos la figura geométrica que corresponde a sus caras basales.
2 Del mismo modo que en , identificamos la figura geométrica que
corresponde a cada una de sus caras laterales. Luego, las dibujamos.
Las caras laterales del prisma recto
son rectángulos congruentes entre sí.
3 Por último, dibujamos la red geométrica completa con sus dos caras basales
y sus 4 caras laterales.
Distintos cuerpos geométricos se pueden construir
a partir de figuras en el plano denominadas
red geométrica o red de construcción.
• Un poliedro es un cuerpo geométrico cuyas caras son polígonos y pueden ser regulares
(cuando todas sus caras son polígonos regulares y congruentes entre sí) o no regulares.
• Un prisma es un poliedro cuyas caras laterales son paralelógramos y sus caras basales son
paralelas y corresponden a polígonos congruentes
• Un prisma recto es aquel cuyas caras laterales son rectángulos o cuadrados. La altura de un
prisma recto coincide con su arista lateral.
Aprende
3
Unidad
119
Lección 1 • Área y volumen de prismas y cilindros |
243

Desarrollo continuación
Recuerde a sus estudiantes las
características de los polígonos regulares
definiendo apotema. Determine el área
del polígono regular a partir de triángulos
isósceles con vértice en el centro y altura
igual a la apotema.
Analice el ejemplo 3 junto con sus
estudiantes y solicíteles que apliquen la
expresión algebraica determinada para el
área de un prisma recto para comprobar
el resultado.
Formalice los conceptos estudiados en
el ejemplo 3 a partir de la información
contenida en Aprende.
Promueva un ambiente positivo al
interior del aula. Para ello se sugiere:
• Fomentar el desarrollo de la
empatía entre todos los estudiantes
invitándolos, por ejemplo, a respetar
a sus compañeros y escuchar sus
opiniones con la atención que les
gustarían recibir.
• Aumentar la motivación y el interés
por el aprendizaje mediante la
aplicación de los aprendizajes en
situaciones de la vida cotidiana.
Invite a sus estudiantes a profundizar en el estudio de poliedros y
a analizar los antecedentes históricos de estos a partir de la lectura
del documento «Poliedros», disponible en:
ww.unirioja.es/cu/luhernan/Divul/Polipdf.pdf
Ejemplo 3
Calcula el área total del siguiente prisma recto de base
un hexágono regular.
1 Dibujamos la red geométrica que permite construir el prisma
de base hexagonal y la completamos con las medidas
del cuerpo geométrico.
2 Calculamos el área (A) de una de sus caras laterales y de una
de sus caras basales.
Área cara lateral.
A = (12 • 6) cm2
A = 72 cm2
6 cm
12 cm
Área cara basal
6 cm
5 cm A = 36 • 5 cm2
= 90 cm2
2
3 Calcular el área total (AT) del prisma equivale a sumar el área lateral (AL) con el área
de las caras basales (AB).
AL = (72 • 6) cm2
= 432 cm2
AB = 90 cm2
6 veces el área de una cara lateral, ya que el prisma
tiene 6 caras laterales de iguales dimensiones.
Luego, reemplazamos los valores en la fórmula,
con lo que obtenemos:
AT = AL + 2AB
AT = (432 + 2 • 90) cm2
= 612 cm2
Para calcular el área total (AT) de un prisma se suman el área lateral (AL) con el área de las caras
basales (AB).
• AL = PB • h, donde PB es el perímetro
de la base del prisma y h la altura.
• AB = área del polígono de la base
del prisma.
Apotema Base
h: altura
Base
Área total (AT) de un prisma: AT = AL + AB + AB = AL + 2 • AB
Aprende
12 cm
6 cm
5 cm
• Elárea(A)deunpolígonoregularestá
dadapor:
A= P•a
2
a
• dondePrepresentael perímetrodel
polígonoya eslamedidadelaapotema.
Lección 1
120 | Unidad 3
E
S
d
CL0000000001018 MA
244

Unidad
3
Solicite a sus estudiantes que analicen
el ejemplo 4 relacionando la base de
un polígono regular con el aumento de
sus lados. Invítelos a dibujar el cuerpo
geométrico resultante al aumentar los
lados del polígono regular de la base.
Luego, puede pedir a algún estudiante que
lea en voz alta la información contenida en
Aprende y asegúrese de la comprensión de
todos los alumnos.
Cierre 15 minutos
Solicite a sus estudiantes que establezcan
las diferencias entre poliedros y cuerpos
redondos y determinen ejemplos
de objetos de uso cotidiano en los
que se puedan visualizar. Para esto
puede plantear preguntas como: ¿qué
características tienen las caras de los
poliedros?, ¿y las de los cuerpos redondos?
El software GeoGebra permite trabajar con cuerpos geométricos en su
vista 3D apoyando el estudio de las características de estos. Por ello es
fundamental que pueda incorporar este recurso dentro del desarrollo
de la clase. Una sugerencia didáctica utilizando GeoGebra está
disponible en:
https://thales.cica.es/epsilon/sites/thales.cica.es.epsilon/files/%5Bfield_
volumen-formatted%5D/epsilon90_3.pdf
2/17/2019 9:32:15 AM
Ejemplo 4
Si se aumenta sucesivamente la cantidad de lados del polígono regular que forma la base
de un prisma recto, ¿cuál es la red geométrica del nuevo cuerpo?
1 Construimos la red geométrica del prisma y notamos que al aumentar la cantidad de lados
de la base también aumenta la cantidad de caras laterales.
O
O
a
a
h O
O
a
a
h O
O
a
a
h
2 Si se sigue con el proceso de aumentar la cantidad de lados de la base del prisma, el polígono
regular se asemeja a un círculo. Por lo tanto, la medida de su apotema a se acerca a la medida
del radio r del círculo.
3 Al asemejarse la base a un círculo, la red geométrica del cuerpo resultante será la siguiente:
Cara basal
Superficie lateral
Cara basal
O
O
r
h
r
Aquellos cuerpos geométricos que tienen al menos una superficie curva se denominan cuerpos
redondos, por ejemplo, el cilindro. Para determinar la superficie de un cilindro, calculamos el
área de cada una de las figuras que componen su red geométrica.
Aprende
3
Unidad
121
245

Propósito
En esta clase los estudiantes continuarán
con el cálculo de áreas de prismas y cilindros
aplicando diferentes procedimientos.
OA 11
Inicio 15 minutos
Recuerde a sus estudiantes los contenidos
tratados la clase anterior preguntando:
• ¿Qué es un poliedro? ¿Cuál(es) es (son)
la(s) diferencia(s) entre poliedros y
cuerpos redondos?
Analice junto con sus estudiantes el
ejemplo 5 e identifique las figuras
geométricas que componen el cilindro y
permítales que verbalicen el procedimiento
para determinar el área de este.
Formalice la expresión para calcular el
área de un cilindro recto apoyado en la
información contenida en Aprende.
Planificación
págs. 122 a 125
Clase 67
Actitudes
OA B , OA D
Para apoyar la formalización de las características del cilindro recto y
para reforzar su análisis como sólido de revolución se sugiere utilizar
un applet de GeoGebra disponible en:
www.geogebra.org/m/Bms3UV6t
Ejemplo 5
Calcula el área total del cuerpo geométrico correspondiente a la siguiente red.
1 Identificamos las figuras que forman la red geométrica.
Círculo
Rectángulo
Círculo
6 cm
O
O
1,5 cm
1,5 cm
2 Calculamos el área de la base del cuerpo geométrico considerando que el radio (r) de cada
círculo mide 1,5 cm y aproximamos π a 3,14.
AB = πr2
= 3,14 • 1,52
= 3,14 • 2,25 = 7,065 cm2
3 Para calcular el área lateral (AL ), necesitamos la medida
del largo del rectángulo, ya que el ancho mide 6 cm.
Al construir el cuerpo geométrico, notamos que el largo
del rectángulo coincide con el perímetro de la base.
Luego, el área lateral (AL ) es igual a:
AL = PB • 6 = 2πr • 6
= 2 • 3,14 • 1,5 • 6
= 56,52 cm2
Perímetro de la base
4 Luego, calculamos el área total (AT ) y obtenemos:
AT = AL + AB + AB = (56,52 + 7,065 + 7,065) cm2
= 70,65 cm2
6 cm
O
O
1,5 cm
1,5 cm
• Un cilindro recto es un cuerpo redondo o cuerpo
de rotación que se genera a partir de un rectángulo
que se hace girar considerando uno de sus lados
como eje de rotación.
h: altura del cilindro r: radio de la base L: eje de rotación
• Para calcular el área total (AT ) de un cilindro se suman
el área lateral (AL ) con el área de las caras basales (AB ).
AT = AL + AB + AB = 2πrh + πr2
+ πr2
= 2πrh + 2πr2
= 2πr(h + r)
Aprende
L
h
r
L
h
r
Área lateral
Base
• Uncilindroesrectocuandosualturah
esperpendicularalascarasbasalesen
suscentros,delocontrario,sediceque
es oblicuo.
h Cilindrorecto
h Cilindrooblicuo
Lección 1
122 | Unidad 3
1
2
3
CL0000000001018 MA
246

Unidad
3
Pida a sus estudiantes que desarrollen
las actividades individualmente y que
registren las respuestas en sus cuadernos.
Guíe a sus estudiantes para que hagan
una representación prolija de la red de
cada prisma de la actividad 1 utilizando
adecuadamente herramientas como la regla.
Permita que los alumnos expongan sus
procedimientos en la resolución de las
actividades 2 y 3. Puede estimular esto
mediante preguntas como:
• ¿Qué pasos seguiste para resolver esta
actividad?
• ¿Crees que se puede resolver mediante
otra estrategia?, ¿por qué?
• ¿Cómo puedes verificar el resultado
obtenido? Explica.
Procure que ambos estudiantes
justifiquen sus resoluciones
y afirmaciones.
Promueva la participación de
todos los estudiantes en un clima
de respeto. Para ello, se sugiere tener
los nombres de todos los alumnos en
palos de helado e ir sacando al azar
cada vez que se plantea una pregunta.
De esta forma puede asegurarse de
que todos tengan la oportunidad
de expresarse y comunicar sus
razonamientos.
Valore la diversidad de
representaciones para desarrollar
la habilidad de representar en
sus estudiantes.
Solucionario
Para revisar las soluciones de las actividades
propuestas utilice la sección Solucionario
páginas 298 a la 305.
Para la comprensión del área de cuerpos geométricos es fundamental
la comprensión del área de figuras geométricas por lo que puede
profundizar en esto mediante las actividades digitales propuestas
en el siguiente link:
https://www.curriculumnacional.cl/614/w3-article-70560.html
2/17/2019 9:32:15 AM
1. Construye la red geométrica de cada uno de los prismas.
a. c.
b. d.
2. Calcula el área basal (AB), área lateral (AL) y el área total (AT) de los siguientes
cuerpos geométricos cuya base es un polígono regular. Comprueba con una calculadora.
a = 6,9 cm
10 cm
8 cm a
b.
Considera π ≈ 3,14
7,6 cm
15 cm
d.
a = 6,8 cm
28 cm
10 cm
a
f.
Base cuadrada.
4,5 cm
3 cm
a.
Considera π ≈ 3,14
2,5 cm
8,5 cm
e.
a = 6,9 cm
c.
11 cm
8 cm
a
3. Analiza las siguientes redes y cuerpos geométricos y luego realiza lo pedido.
a. Identifica el cuerpo geométrico que se
puede construir con la siguiente red.
b. Un dado, con forma de cubo, se muestra
desde distintas vistas.
Identifica la red geométrica que permite
construir el dado.
Actividades
3
Unidad
123
247

Actitudes
Recuerde a sus estudiantes que al
enfrentarse a un desafío, aun cuando
no obtengan el resultado de manera
inmediata, deben perseverar y confiar
en sus propias capacidades.
Todos pueden aprender
A los estudiantes que presentan dificultades en la actividad 6
solicíteles que representen cada una de las caras de los cuerpos
geométricos dados y determinen su área.
Solicite a sus estudiantes que desarrollen
las actividades en parejas y registren las
resoluciones en sus cuadernos.
Luego, guíelos en el análisis de sus
procedimientos mediante preguntas como:
• ¿Qué fue lo primero que hicieron al
resolver las actividades propuestas?
• ¿Te fue útil considerar el valor de
π = 3,14?, ¿por qué?
• ¿Qué estrategias puedes usar para
comprobar tus resultados?
4. Dibuja los cilindros generados al rotar cada uno de los rectángulos en torno al eje L.
Luego, calcula su área total (AT ). Considera π ≈ 3,14.
b. L
8,5 cm
3 cm
L
4 cm
8 cm
d.
a. L
5 cm
10 cm
c. L
4 cm
7 cm
5. Resuelve los siguientes problemas. Considera π ≈ 3,14.
a. Una carpa tiene las medidas que muestra la imagen.
¿Cuánta tela se utilizó en su fabricación?
b. Un cubo de arista igual a 4 cm se puede dividir por la mitad
de dos formas, como muestra la imagen. ¿A qué cuerpo
geométrico corresponden las mitades con mayor área?
c. El diámetro de la base de un cilindro mide 7 cm y la altura,
9 cm. ¿Cuánto miden el ancho y el largo del rectángulo
que lo generó?
d. ¿Cuál es el área de un tronco de madera cilíndrico recto de
2 m de altura y diámetro basal de 46 cm?
e. ¿Cuántos centímetros cuadrados de material se utiliza, como mínimo, para construir una lata
de duraznos en conserva que tiene base circular de 5 cm de radio y una altura de 12 cm?
f. Una lata de salsa de tomates tiene 12 cm de altura y 3,5 cm de radio. ¿Cuántos metros
cuadrados de papel se necesitan para fabricar las etiquetas de 3000 latas de tomates?
g. Una moneda mide 26 mm de diámetro y 1 mm de alto. ¿Cuál es el área mínima del papel
que se utiliza para envolver 50 monedas iguales apiladas?
h. Si las medidas de un prisma de base rectangular se reducen a la mitad, ¿en cuánto
disminuye su área total?
6. Calcula el área total (AT ) de los siguientes cuerpos. Para ello, calcula el área de cada cara
y luego súmalas. Compara tus resultados con los de tus compañeros.
c.
120 cm
40 cm
180 cm
120 cm
40 cm
70 cm
a.
4 cm
1,33 cm
1,33 cm
4 cm
4 cm
b. Base cuadrada
35 cm
35 cm
20 cm
40 cm
20 cm
1,5 m
1 m
80 cm
1,2 m
Lección 1
124 | Unidad 3
•
•
7
8
9
1
CL0000000001018 MA
248

Unidad
3
la actividad 9 utilizando 2 hojas
rectangulares idénticas dispuestas
según las indicaciones dadas. Oriéntelos
a justificar sus respuestas a partir de
los cálculos correspondientes.
Una vez terminada la actividad, solicite
que algunos estudiantes presenten
sus resoluciones en la pizarra para que
en conjunto analicen las respuestas y
corrijan los errores cometidos.
Cierre 15 minutos
Para finalizar, invite a sus estudiantes
a que reflexionen acerca del trabajo
realizado a partir de las respuestas
a las preguntas planteadas.
Ampliando el conocimiento
Solicite a sus estudiantes completar el siguiente cuadro considerando
π ≈ 3,14.
r h AB
AL
AT
3,5 cm 236,76 cm2
10 cm 904,32 cm2
0,1 m 30,14 m2
10 cm 1 130,4 cm2
6,5 mm
4 mm 339,12 m2
565,2 m2
Se sugiere desarrollar esta clase como
práctica y retroalimentación utilizando
el Cuaderno de Actividades,
Planificación
Clase 68
m
a
2/17/2019 9:32:16 AM
Reflexiona y responde
• Explica cómo calcular el área de prismas y cilindros a partir de sus redes geométricas y aplicando
las fórmulas.
• ¿Cómo planificaste tu trabajo y los procedimientos que utilizaste? Comenta con tu curso.
7. Analiza la siguiente situación y luego responde.
Un juego está formado por un soporte con forma de prisma recto de base rectangular
en el que se encajan dos piezas, una con forma de cilindro y la otra con forma de prisma
de base triangular, como muestra la imagen.
20 cm
8,94 cm
8,94 cm
1,5 cm
8 cm
8 cm
1,5 cm
8 cm
10 cm
1,5 cm
a. ¿Cuál es el área total (AT ) del soporte cuando
las piezas están encajadas en él?
b. ¿Cuál es el área total (AT ) de las piezas
del juego? Considera π ≈ 3,14.
8. En las plantas para almacenar hidrocarburos (compuesto químico formado por carbono e
hidrógeno) existen grandes depósitos de forma cilíndrica.
a. ¿Cuál es el área lateral (AL) que tiene un depósito de 6 m de radio y 10 m de altura?
b. ¿De qué área se dispone para colocar letreros de advertencia en la superficie lateral
de un tanque si puede utilizarse el 12% del área lateral del cilindro?
9. Reúnete con un compañero o compañera y desarrollen
la siguiente actividad. Consigan dos hojas de papel de
forma rectangular y del mismo tamaño. Enrollen una
de ellas a lo largo, y la otra, a lo ancho, como muestra
la imagen. ¿Cuál de los dos rollos de papel tiene
mayor área lateral (AL)? Explica.
10.Josefina dice que en la siguiente red geométrica la medida
del largo del rectángulo es 24 cm. ¿Es correcto lo que afirma?
¿Por qué? Si se duplica la altura del cilindro correspondiente
a la red geométrica y se mantiene el diámetro de la base,
¿se duplica el área lateral? ¿Ocurre lo mismo si se duplica
el diámetro y se mantiene la altura? Considera π ≈ 3,14.
16 cm
r
8 cm
CuadernodeActividades
Páginas76a79.
3
Unidad
125
249

Promueva un ambiente positivo al interior del aula. Para ello
se sugiere estimular la motivación y el interés por el aprendizaje
mediante, por ejemplo, la manipulación de cubos iguales que le
permitan formar cubos más grandes y así establecer la relación
con el volumen.
Propósito
y aplicarán el cálculo del volumen de
prismas y cilindros en situaciones diversas.
OA 11
Inicio 15 minutos
Recuerde los conceptos tratados las clases
anteriores caracterizando prismas y
cilindros. Registre en la pizarra los tópicos
más relevantes a modo de resumen.
situación y solicíteles que compartan sus
respuestas a las preguntas planteadas.
Planificación
Actitudes
OA D
págs. 126 a 129
Clase 69
• ¿Qué crees fue lo que motivó a la banda
a utilizar un prisma en su disco?
• ¿Cuáles son las características de un prisma?
En marzo de 1973 fue publicado el octavo
álbum de la banda británica Pink Floyd, el cual
es reconocido no solo por su alta calidad musical,
también por tener una de las carátulas más
icónicas de la historia.
Volumen de prismas y cilindros
Su portada es la sencilla imagen de un prisma
que refracta la luz en los colores del arcoíris.
Lección 1 Área y volumen de prismas y cilindros
| Unidad 3
126
E
S
l
e
¿
E
C
CL0000000001018 MA
250

Unidad
3
Solicite a sus estudiantes que analicen
cada uno de los ejemplos planteados.
Oriéntelos para que establezcan la relación
entre la cantidad de cubos que caben
como máximo al interior de la caja y el
volumen de esta. Invítelos a verbalizar
qué entienden por volumen de un
cuerpo geométrico.
Puede complementar la información dada
en el ejemplo 2, mediante el conversor
de unidades de medida de volumen del
siguiente link.
http://www.semergencantabria.org/calc/
arcalc.htm
Desarrollo del pensamiento matemático
Invite a sus estudiantes a trabajar en la conversión entre unidades
de volumen utilizando un applet de GeoGebra disponible en:
www.geogebra.org/m/kfFHwCeQ
Luego plantee preguntas como: ¿crees que es útil el uso de la tecnología
para la conversión entre unidades de medida?, ¿por qué? ¿Qué unidad
de medida crees que es más adecuada para expresar el volumen de una
piscina? Justifica tu respuesta.
Para iniciar y motivar el trabajo con
el volumen de cuerpos geométricos,
puede proponer a los alumnos el juego
del siguiente link:
articles-26307_recurso_pdf.pdf
2/17/2019 9:32:18 AM
Ejemplo 1
Se quieren guardar de forma ordenada cubos de arista igual a 1 cm en
la caja que se muestra en la imagen, es decir, que no queden espacios
entre ellos.
¿Cuántos cubos caben como máximo en la caja?
1 Como el ancho del prisma mide 3 cm entonces se pueden poner
3 cubos de 1 cm, como de largo mide 4 cm podemos poner 4 cubos
de 1 cm.
Por lo tanto, en la base caben 12 cubos.
2 Como el prisma tiene 10 cm de altura, se pueden poner 10 bases
como las anteriores de 12 cubos.
Por lo que, en el prisma caben 120 cubos como máximo.
Ejemplo 2
Calcula el volumen del siguiente prisma recto de base rectangular.
1 El volumen del prisma se puede relacionar con la cantidad
de cubos de 1 cm de arista que se necesitan para formar
un cuerpo con sus dimensiones.
2 A partir de las medidas de la base del prisma podemos disponer
los cubos de la siguiente forma:
Para formar la base del prisma
se necesitan (8 • 4) cubos.
4 cubos
8 cubos
3 Luego, como la arista de cada cubo mide 1 cm, necesitamos
6 de los pisos construidos en el paso anterior para formar
el prisma.
Cada cubo ocupa un espacio de 1 cm3
.
4 cubos
8 cubos
6 cubos
Cada piso tiene (8 • 4) cubos, luego se requieren (6 • 8 • 4) cubos
para formar el prisma. Entonces, el volumen del prisma es:
(6 • 8 • 4) cm3
= 192 cm3
• Lasunidadesdevolumenaumentano
disminuyende1000en1000,como
se muestraenlossiguientesdiagramas.
cm3
mm3
• 1000
: 1000
dm3
cm3
• 1000
: 1000
m3
dm3
• 1000
: 1000
8 cm
6 cm
4 cm
10 cm
4 cm
3 cm
3
Unidad
127
251

Para la comprensión de los contenidos
planteadosenestaspáginasesfundamental
estimular el interés y la perseverancia de
los estudiantes para lo que se sugiere
verificar la comprensión de los alumnos
constantemente y establecer relaciones
con situaciones cotidianas con el objetivo
de otorgar sentido al aprendizaje.
Analice en conjunto con los estudiante el
ejemplo 3 y luego, formalice el concepto de
volumen de un cuerpo geométrico a partir
de la información contenida en la primera
sección Aprende.
Luego, analice el paso a paso para el
cálculo del volumen del prisma dado en
el ejemplo 4 y pida a sus estudiantes que
establezcan una estrategia para determinar
el volumen de un paralelepípedo y que lo
contrasten con la información contenida en
la segunda sección Aprende.
Dificultades y errores frecuentes
Algunos estudiantes pueden cometer errores al no considerar los cubos
que no se ven en la imagen y que forman los cuerpos geométricos del
ejemplo 3. Para ello, es importante recordar que los cuerpos geométricos
formados corresponden a prismas y, de ser posible, representarlos con
material concreto.
Ejemplo 3
Si la arista de los cubos que forman los siguientes prismas
mide 1 cm, ¿cuál de ellos tiene mayor volumen?
1 Contamos la cantidad de cubos que se requieren para formar cada prisma.
12 cubos 12 cubos
2 Cada cubo ocupa un espacio de 1 cm3
, por lo tanto calculamos el volumen de cada prisma
para luego compararlos.
12 cm3
12 cm3
3 Ambos prismas ocupan el mismo espacio, por lo tanto tienen el mismo volumen.
El volumen es la porción de espacio que ocupa un cuerpo. Un cubo de 1 cm de arista tiene un
volumen igual a 1 cm3
(un centímetro cúbico).
Aprende
Ejemplo 4
Calcula el volumen del siguiente prisma recto de base rectangular.
1 La base del prisma corresponde a un rectángulo cuyos lados
miden 5 cm y 4 cm y su altura (h) es 7 cm.
2 El área basal (Ab) del prisma corresponde a:
Ab = (5 • 4) cm2
= 20 cm2
.
3 Finalmente el volumen (V) del prisma es:
V = Ab • h = (20 • 7) cm3
= 140 cm3
.
El volumen (V) de un prisma se puede determinar calculando
el producto del área basal (AB ) por la medida de su altura (h).
V = AB • h
Aprende
h
AB
7 cm
4 cm
5 cm
Lección 1
128 | Unidad 3
E
U
q
•
•
•
E
S
t
d
e
CL0000000001018 MA
252

Unidad
3
Analice los procedimientos expuestos en
el ejemplo 5. Solicite que sus estudiantes
establezcan una estrategia que permita
determinar el volumen del cilindro
comparando el procedimiento con el
usado para un prisma recto. Para ello
puede preguntar: ¿qué características
tiene un prisma recto?, ¿y un cilindro?,
¿qué semejanzas y diferencias tienen estos
cuerpos geométricos?
Formalice el volumen del cilindro apoyado
en la información contenida en Aprende.
Cierre 15 minutos
Guíe a sus estudiantes a plantear una
expresión algebraica que permita
determinar el volumen de un
paralelepípedo y de un cilindro recto.
La longitud, el área y el volumen se aplican tanto a objetos como
a los seres vivos. Es posible analizar cómo afectan los cambios en
estas dimensiones gracias a la geometría por lo que puede invitar
a los estudiantes a analizar los casos propuestos en la lectura del
siguiente link:
https://www.curriculumnacional.cl/614/articles-26311_recurso_pdf.pdf
2/17/2019 9:32:18 AM
Ejemplo 5
Un recipiente está conformado por un prisma recto de base cuadrada
que contiene un cilindro, como se muestra en la figura.
• ¿Cuáles son las dimensiones del cilindro?
El cilindro tiene como diámetro 20 cm. Por lo tanto su radio es 10 cm.
Y la altura del cilindro es la misma que la del prisma. Es decir, 32 cm.
• ¿Cuál es el volumen del prisma?
El volumen del prisma se calcula Ab • h. Y como, el área de la base del prisma es 400 cm3
y la altura es 32 cm, el volumen es de 12800 cm3
.
• ¿La capacidad del cilindro será mayor o menor que la del prisma?
La capacidad del cilindro es menor que la del prisma, pues la medida de la base del cilindro
es menor que la del prisma.
El volumen de un cilindro se asemejará cada vez más al volumen de un prisma recto de base
un polígono regular a medida que la cantidad de lados de la base del prisma aumenta.
Aprende
Ejemplo 6
Si se llena al ras un prisma de base cuadrada con arena y se vacía
todo el contenido en un cilindro de la misma altura y cuya área
de la base es igual a la del prisma, ¿cuánta arena puede contener
el cilindro?
1 La cantidad de arena que contiene el prisma es igual
al producto entre su área basal y su altura, pues este
se encuentra completamente lleno con arena.
2 Notamos que el cilindro se llenará completamente con la arena,
ya que tiene igual área basal y altura que el prisma, por lo tanto
su volumen es igual al del prisma.
3 Calculamos el volumen (V) del cilindro utilizando la expresión
que permite determinar el volumen de un prisma.
Consideramos π ≈ 3,14.
V = AB • h = πr2
• h = 3,14 • (2,3)2
• 5 cm3
= 83,053 cm3
Altura del cilindro.
Área de la base
del cilindro.
Cantidad de arena.
• Paracalcularelvolumen (V)entre
dos cuerposgeométricossedetermina
elvolumendecadaunoyluegoseresta
el mayorconelmenorvolumen.
V1 – V2 = VF
5 cm
2,3 cm
32 cm
20 cm
20 cm
3
Unidad
129
253

Propósito
En esta clase los estudiantes calcularán
el volumen de prismas y cilindros en
situaciones diversas.
OA 11
Planificación
Inicio 15 minutos
Analice la información contenida en el
recuadro relacionándola con la expresión
algebraica determinada en la clase anterior.
Solicite a sus estudiantes que verbalicen los
procedimientos expuestos en los ejemplos.
Guíe a sus estudiantes durante el
estudio de los ejemplos aquí presentados
enfatizando en las variables que permiten
determinar el volumen de un cilindro:
área de la base (Ab
), altura del cilindro (h)
y volumen (V).
págs. 130 a 133
Clase 70
Actitudes
OA C ; OA D
Para apoyar la formalización del volumen de un cilindro y su relación
con el volumen de poliedros se recomienda utilizar un applet de
GeoGebra disponible en:
https://www.geogebra.org/m/rb4jzcam
El volumen (V) de un cilindro se asemeja al de un prisma. Para calcularlo se
determina el área de la base (AB) y se multiplica por la medida de su altura.
Es decir, el volumen (V) de un cilindro está dado por:
V = AB • h = πr2
• h
donde r es el radio de la base y h la altura del cilindro.
Aprende
h
r
Ejemplo 7
Calcula el volumen del siguiente cilindro.
1 Para calcular el volumen del cilindro podemos utilizar la siguiente
expresión: V = AB • h, donde AB es el área de la base del cilindro
y h es su altura.
2 Identificamos el radio de la base del cilindro (r) y su altura (h).
Luego, calculamos su volumen (V) considerando π ≈ 3,14.
El radio (r) de la base del cilindro mide 3 : 2 = 1,5 cm.
Diámetro de la
base del cilindro.
Altura (h) del cilindro.
8 cm
3 cm
V = AB • h = πr2
• h = 3,14 • (1,5)2
• 8 cm3
= 56,52 cm3
Ejemplo 8
Calcula el volumen del siguiente cuerpo geométrico considerando
que sus caras basales son semicírculos.
1 Notamos que el cuerpo geométrico representa la mitad de un cilindro.
2 Calculamos el volumen (V) del cilindro. Consideramos π ≈ 3,14.
V = AB • h
V = πr2
• h
V = 3,14 • (2,5)2
• 12 cm3
V = 235,5 cm3
12 cm
5 cm
Diámetro de la
base del cilindro.
Altura (h) del cilindro.
3 Calculamos la mitad del volumen obtenido.
V : 2 = (235,5 : 2) cm3
= 117,75 cm3
Volumen del cuerpo geométrico.
8 cm
3 cm
12 cm
5 cm
Lección 1
130 | Unidad 3
1
2
3
CL0000000001018 MA
254

Unidad
3
Es importante promover en todo
momento un ambiente de respeto y
compañerismo en el que todas las
opiniones y dudas sean escuchadas
y al mismo tiempo resueltas.
las actividades en sus cuadernos.
Note que en la actividad 1 se solicita
comprobar los resultados obtenidos
utilizando una calculadora. Puede
sugerir a los estudiantes crear una tabla
de dos columnas para que escriban en
una el resultado obtenido manualmente
y en la otra, el resultado obtenido usando
calculadora. Luego, pídales compararlos.
Enfatice la importancia de expresar
el volumen de cada una de las
figuras en las unidades de medida
correspondientes.
Solucionario
Puede profundizar el trabajo con el volumen de cuerpos geométricos
mediante la actividad propuesta en el siguiente link:
2/17/2019 9:32:19 AM
1. Calcula el volumen (V) de los siguientes cuerpos geométricos. Considera π ≈ 3,14 y
comprueba con tu calculadora.
a.
10 cm
4 cm
4 cm
7 cm
2 cm
c. g.
8 cm
5,2 cm
6 cm
e.
19 cm
6 cm
8 cm
d.
4 cm
2 cm
3 cm
3 cm
b.
1
4
de círculo.
Base:
8 cm
6,5 cm
12 cm
4 cm
3 cm
9 cm
9 cm
h.
f.
11 cm
6 cm
2 cm
2. Con las siguientes redes geométricas se pueden construir polígonos regulares. Calcula el área
de la base (AB ) y el volumen (V) de los respectivos polígonos, sabiendo que:
b. a = 8,7 cm, l = 10 cm y h = 15 cm.
h
a
l
a. a = 4,3 cm, l = 5 cm y h = 12 cm.
h
a
l
3. Ordena los siguientes cuerpos geométricos desde el de menor al de mayor volumen.
A
10 cm
5 cm
B
8 cm
5 cm
C
12 cm
8 cm
Actividades
3
Unidad
131
255

Para el desarrollo de las actividades
planteadas en estas páginas es
recomenadle estimular la perseverancia
de los alumnos y motivarlos a
resolver, verificar y corregir sus
resoluciones cuando sea necesario.
Además, puede permitirles trabajar
en parejas para buscar diferentes
estartegias de resolución y generar
un aprendizaje colaborativo.
Solicite a sus estudiantes que bosquejen los
cuerpos geométricos involucrados en cada
una de las actividades incorporando las
medidas indicadas.
En la actividad 6 solicite a sus estudiantes
que bosquejen los cilindros generados al
rotar el rectángulo en el eje indicado.
En el siguiente link encontrará un listado de las fórmulas para el
cálculo del área y volumen de diferentes cuerpos geométricos:
https://www.geogebra.org/m/z6Ehy4P7
Puede solicitar a los estudiantes copiarlo en una cartulina para
tenerlo en la sala de clases.
4. Los depósitos cilíndricos A y B tienen la misma altura, pero
la medida del radio de B es el doble de la del radio de A. Si
se va a llenar con agua el recipiente B utilizando el A, ¿cuántas
veces hay que vaciar el contenido de A en el de B para llenarlo?
5. Considerando π ≈ 3,14. Calcula:
a. El perímetro de la base, el área de la base y el volumen, de un cilindro de radio 5,5 cm
y altura 12 cm.
b. El radio, el perímetro de la base y el área de la base de un cilindro de altura 15 cm y
volumen 4710 cm3
.
c. El radio, el área de la base y el volumen de un cilindro que tiene un perímetro basal
de 12,56 cm y altura 11 cm.
6. Calcula el volumen (V) de los cilindros generados al rotar cada uno de los rectángulos
en torno al eje L. Considera π ≈ 3,14.
b. L
4 cm
1,5 cm
c.
L
0,5 cm
5 cm
d. L
7 cm
7 cm
a.
L
6 cm
10 cm
7. Resuelve los siguientes problemas. Considerando π ≈ 3,14.
a. Un florero con forma de prisma recto tiene una altura de 25 cm. Su base es un pentágono
regular de lado igual a 6 cm y su apotema mide 4,13 cm. ¿Cuántos centímetros cúbicos (cm3
)
de agua contiene si se llenó hasta 10 cm del borde?
b. Con 72 cubos de 1 cm3
se forma un prisma recto de caras rectangulares. Si se utilizan
4 cubos para el largo y 6 cubos para el alto, ¿cuántos se necesitan para el ancho?
c. Las dimensiones de un contenedor y de las cajas que se van a almacenar en él se
muestran en la imagen. ¿Cuántas cajas se pueden guardar en él de modo que este
quede totalmente lleno?
30 cm
60 cm
40 cm
Caja
3 m
18 m
8 m
Contenedor
d. Gloria preparó una torta cilíndrica de dos pisos de 8 cm de altura cada uno. El más grande
tiene 32 cm de diámetro y el otro, 13 cm de radio. ¿Qué volumen ocupa la torta?
e. La capacidad de una taza con forma cilíndrica es de 254,34 cm3
. Si el diámetro de la base
mide 6 cm, ¿cuál es la altura de la taza?
h B
A
Lección 1
132 | Unidad 3
8
•
•
•
CL0000000001018 MA
256

Unidad
3
Una vez que todos terminen la actividad,
revise cada uno de los ejercicios en la
pizarra, mientras los estudiantes corrigen
sus respuestas detectando errores y
definiendo dificultades encontradas.
Cierre 15 minutos
Invite a sus estudiantes a compartir
sus reflexiones acerca de las preguntas
planteadas en Reflexiona y responde.
páginas 80 a 83.
Planificación
Clase 71
Para profundizar el trabajo con el volumen de cuerpos geométricos,
proponga a los estudiantes resolver las actividades del siguiente link:
https://www.geogebra.org/m/nscyq2cu
Considere que los alumnos pueden trabajar de forma autónoma y
recibir retroalimentación del trabajo realizado.
2/17/2019 9:32:19 AM
f. En una pastelería venden mermeladas en dos envases distintos.
Uno de ellos tiene una altura de 11 cm y el diámetro de su base
mide 8 cm, y el otro mide 8 cm de alto y 11 cm de diámetro.
¿Cuál de los dos envases contiene mayor cantidad de mermelada?
g. La densidad (δ) de un material corresponde a la razón entre
su masa y su volumen. Si la densidad del bronce (δbronce)
es 8,9
g
cm3
y la densidad de la plata (δplata) es 10,46
g
cm3
,
¿cuál es la masa de los siguientes cilindros de bronce y
de plata? (Considera π ≈ 3,14).
h. ¿Es correcto afirmar que el volumen del prisma recto
de base triangular es la mitad del volumen del prisma
de base rectangular? ¿Por qué?
Comenta con tus compañeros.
8. Verifica si las siguientes afirmaciones son verdaderas o falsas. Justifica en cada caso.
a. Al duplicar la medida de la arista de un cubo, su volumen también se duplica.
b. Si se triplica la altura de un prisma de base rectangular, su volumen también se triplica.
c. Al disminuir a la mitad las medidas de un prisma de base rectangular, su volumen
disminuye a la cuarta parte.
d. Al duplicar las medidas de la base de un prisma de base rectangular y al disminuir
a la cuarta parte su altura, su volumen no varía.
e. Al duplicar la medida de la altura de un cilindro, su volumen no varía.
f. Si se triplica la medida del radio de un cilindro, su volumen también se triplica.
g. Al disminuir a la mitad las medidas de un cilindro, su volumen disminuye a la octava parte.
h. Al disminuir a la mitad la medida del radio de un cilindro y al cuadruplicar su altura,
su volumen no varía.
• ¿Qué situaciones puedes resolver mediante el cálculo de volumen de prismas y cilindros?
• ¿Cómo puedes comprobar si el volumen de prismas o cilindros es correcto?
• ¿Qué estrategias utilizaste para resolver los problemas? ¿Cuáles usaron tus compañeros?
Páginas80a83.
h
4 cm
6 cm
2 cm
10 cm
Bronce
3 cm
Plata
3 cm
4 cm
3
Unidad
133
257

Propósito
Evaluar los objetivos desarrollados en
la Lección 1.
Objetivo de la clase
Evaluar formativamente las habilidades y
conocimientos adquiridos en la Lección 1.
Planificación
Inicio 15 minutos
Recuerde los contenidos tratados en la
lección y registre en la pizarra un cuadro
sinóptico con los tópicos más relevantes
a modo de resumen.
Solicite a sus estudiantes que respondan
la evaluación individualmente y registren
sus respuestas en sus cuadernos. Enfatice
la importancia de expresar en unidades de
volumen cada una de las respuestas que
así lo ameriten.
Para complementar el estudio de área y volumen de cuerpos
geométricos se sugiere la lectura del documento «Medida de
magnitudes y su didáctica para maestros» disponible en:
www.ugr.es/~jgodino/edumat-maestros/manual/5_Medida.pdf
págs. 134 y 135
Clase 72
1. Calcula el área y el volumen de los siguientes cuerpos geométricos.
a.
2,5 cm
8,5 cm
b.
12 cm
12 cm
12 cm
c.
5 cm
2,5 cm
2 cm 1,5 cm
2. Calcula el área y el volumen de los prismas que se describen a continuación. Considera que
en cada caso se presenta la vista superior.
b. Prisma de 9 cm de altura.
10 cm
5 cm
d. Prisma de 18 cm de altura.
8 cm
8 cm
a. Prisma de 12 cm de altura.
10 cm
5 cm
c. Prisma de 1,5 m de altura.
30 cm
30 cm
30 cm
30 cm
30 cm
30 cm
25,98 cm
a
3. Miguel tiene tres cilindros de 1 m de altura. Calcula sus radios a partir de la información
de cada uno de ellos que se entrega a continuación:
a. Su volumen es 900π.
b. Su área lateral es 1600π.
c. Su área basal es 200π.
Evaluación Lección 1
| Unidad 3
134
4
5
6
7
•
•
•
CL0000000001018 MA
258

Unidad
3
Permita que sus estudiantes intercambien
sus resoluciones para que entre pares
corrijan sus actividades. Registre cada una
de las respuestas en la pizarra y resuelva las
dudas que surjan a partir de la corrección.
Cierre 15 minutos
Invite a sus estudiantes a reflexionar
acerca del trabajo de la evaluación y a
responder las preguntas planteadas.
Ínstelos a reforzar los contenidos con
menor grado de asimilación.
Al finalizar la evaluación, realice una discusión plenaria en la que
los estudiantes puedan comentar con sus compañeros las principales
dificultades que tuvieron al trabajar en esta lección.
Solucionario
2/17/2019 9:32:20 AM
4. Un diseñador realiza un bosquejo de una caja de 18 cm de altura cuya base es un triángulo
rectángulo y sus catetos miden 4 cm y 3 cm. Si no queda conforme con este bosquejo y
aumenta al doble la longitud del cateto de menor longitud, ¿cómo debe variar la altura
de la caja para conservar su capacidad?
5. Se está diseñando un recipiente para contener la leche extraída
en una lechería. Una de las opciones considera un cilindro cuya
altura mide 4 m y su radio 3 m, como se muestra en la imagen.
Otra opción considera el doble del radio del recipiente anterior.
¿De qué manera debe variar su altura para que en ambos
recipientes se pueda guardar la misma cantidad de leche?
6. Sofía quiere recubrir una superficie con el cartón de los rollos de papel higiénico que ha
juntado en su casa. Para hacerlo, primero determinó las medidas de uno de estos cilindros,
obteniendo los valores de su altura y su diámetro: 10 cm y 5 cm, respectivamente.
a. ¿Qué superficie puede recubrir con 1 rollo?
b. ¿Cuántos rollos necesita para recubrir 1 m2
? ¿Cuánto cartón sobra del último rollo ocupado?
7. María tiene dos tubos de ensayo cilíndricos rectos con las siguientes características:
a. ¿Cuánto líquido contiene el Tubo A si su nivel marca 10 cm?
b. ¿Cuánto líquido puede contener como máximo el Tubo B ?
c. ¿Cuál de los tubos puede contener más líquido?
Tubo de
ensayo A
1,6 cm
18 cm
Tubo de
ensayo B
1,6 cm
18 cm
• ¿En qué situaciones puedes aplicar lo aprendido sobre área y volumen? Ejemplifica.
• ¿Qué pasos sigues para calcular el área y el volumen de prismas y cilindros?
• ¿Cómo puedes verificar el área de prismas y cilindros?, ¿y el volumen?
Páginas84y85.
4 cm
3 cm
3
Unidad
Evaluación Lección 1 | 135
259

Propósito
el teorema de Pitágoras, el cual aplicarán
para resolver diversos problemas
geométricos.
OA 12
Planificación
Inicio 15 minutos
Para comenzar, pida a sus estudiantes que
observen la fotografía y lean la información
sobre la pirámide Kefrén.
Guíe a sus estudiantes a través del
ejemplo 1 para que puedan explicar la
validez del teorema de Pitágoras utilizando
la representación pictórica planteada.
Para activar los conocimientos previos, formule
las siguientes preguntas:
• ¿Qué es una raíz cuadrada?
• ¿Qué es una potencia?
• ¿Qué es un número cuadrado perfecto?
págs. 136 y 137
Clase 73
Actitudes
OA B
Teorema de Pitágoras
Lección 2
Ejemplo 1
Explica la validez del teorema de Pitágoras.
Según las medidas del siguiente rectángulo, verifica que
la suma de las áreas de los cuadrados pequeños es igual
al área del cuadrado de mayor tamaño.
1 Notamos que el rectángulo está formado por 4 triángulos
congruentes. Calculamos el área (A) del rectángulo:
A = (2 • 1) cm2
= 2 cm2
2 El cuadrado de mayor tamaño está formado por 4 triángulos congruentes iguales
a los que forman el rectángulo. Por lo tanto, su área es 2 cm2
.
3 Los cuadrados de menor medida están formados por dos triángulos congruentes iguales a
los que forman el rectángulo. Luego, el área de cada uno es igual a (2 : 2) cm2
, es decir, 1 cm2
.
4 Sumamos las áreas de los cuadrados de menor tamaño y
verificamos que el resultado es igual al área del cuadrado
de mayor medida.
1 cm
1 cm
1 cm
1 cm2
+ 1 cm2
= 2 cm2
Área cuadrados pequeños. Área cuadrado grande.
La pirámide de Kefrén, fue la primera gran
pirámide que se construyó basándose en
el llamado triángulo sagrado egipcio,
de proporciones 3 - 4 - 5.
• ¿Cómo crees se relacionan matemáticamente
los números del triángulo sagrado?
En esta lección aplicarás el teorema de
Pitágoras para resolver diversos problemas
geométricos y de la vida cotidiana.
136 | Unidad 3
E
¿
q
CL0000000001018 MA
260

Unidad
3
las actividades en parejas y que registren
las respuestas en sus cuadernos.
Cierre 15 minutos
Finalice la clase formalizando el teorema
de Pitágoras y sus propiedades con ayuda
de la información en Aprende.
Muestre a sus estudiantes los tríos pitagóricos principales y desafíelos
a encontrar otros amplificando los términos.
Explique que varias civilizaciones antiguas trabajaron con tríos
pitagóricos, por ejemplo: los egipcios, los chinos, etc.
e.
2/17/2019 9:40:10 AM
Ejemplo 2
¿Cuál es la distancia máxima que una persona puede nadar en una piscina de forma rectangular
que mide 24 m de largo y 10 m de ancho si solo puede hacerlo en línea recta?
1 Si solo puede nadar en línea recta, la distancia
máxima (x) corresponde a la diagonal de la
superficie de la piscina.
2 Notamos que la diagonal de la piscina determina
dos triángulos rectángulos.
3 Aplicamos el teorema de Pitágoras para calcular
la medida de la diagonal (x) de la piscina.
Catetos
Hipotenusa
24 cm
10 cm
x
• En un triángulo rectángulo, el teorema de Pitágoras establece
que la suma de los cuadrados de las medidas de los catetos es
igual al cuadrado de la medida de la hipotenusa.
En el triángulo ABC, a y b representan las medidas de los catetos
y c la medida de la hipotenusa.
Si un trío de números naturales cumple con el teorema de Pitágoras,
estos números son llamados trío pitagórico.
• El recíproco del teorema de Pitágoras establece que si se tienen
3 segmentos de medidas a, b y c que cumplen con la igualdad:
a2
+ b2
= c2
entonces el triángulo formado por estos segmentos es
un triángulo rectángulo.
Aprende
a2
+ b2
= c2
a
b
c
A
C
B
a
b
c
A
C
B
x2
= 242
+ 102
x2
= 576 + 100
x2
= 676
x = 676 m
x = 26 m
24 cm
10 cm
3
Unidad
137
Lección 2 • Teorema de Pitágoras |
261

Propósito
En esta clase los estudiantes aplicarán
el teorema de Pitágoras para resolver
problemas diversos.
OA 12
Planificación
Inicio 15 minutos
Para comenzar, recuerde a sus estudiantes
el teorema de Pitágoras y las propiedades
estudiadas en la clase anterior.
Invite a sus estudiantes a desarrollar
las actividades en pareja, a intercambiar
ideas y a crear estrategias de manera
colaborativa.
Actitudes
OA B
Solucionario
págs. 138 y 139
Clase 74
Puede proponer las actividades de los siguientes links para profundizar
el trabajo con el teorema de Pitágoras:
1. Calcula la medida del lado desconocido (x) en cada triángulo.
d.
4,8 cm
2 cm
x
b.
12 cm
5 cm
x
c.
15 cm
8 cm
x
a. 6 cm
8 cm
x
2. Calcula el perímetro (P) y el área (A) de cada triángulo.
a.
15 cm
9 cm
x
b.
26 cm
24 cm
x
c.
1,8 cm
3 cm
x
d.
2,5 cm
2 cm
x
3. Calcula las medidas que faltan en cada figura. Utiliza una calculadora si es necesario.
a.
y
12 cm
3 cm
4 cm
x
b.
y
25 cm
17 cm
x
z
8 cm
c.
y
12 cm
x
20 cm
29 cm
4. Evalúa si los siguientes tríos de números forman tríos pitagóricos. Considera a y b como
la medida de los catetos y c como la medida de la hipotenusa.
a. b. c. d.
a 9 5 15 21
b 12 2 36 28
c 15 13 39 35
Actividades
Lección 2
138 | Unidad 3
5
6
7
•
•
CL0000000001018 MA
262

Unidad
3
En la actividad 5 recuerde a sus estudiantes
que el teorema de Pitágoras se cumple solo
en triángulos rectángulos. Esto también
permite determinar cuándo un triángulo
es rectángulo.
Cierre 15 minutos
Para finalizar, pregunte a sus estudiantes
en qué situaciones de la vida cotidiana
se puede utilizar el teorema de Pitágoras.
Además, invítelos a reflexionar acerca
del trabajo realizado y a responder las
preguntas planteadas en Reflexiona
y responde.
Puede complementar el trabajo con el teorema de Pitágoras mediante
la lección propuesta en la planificación del siguiente link: https://www.
curriculumnacional.cl/614/articles-131868_recurso_4.pdf
Además, considere que en el siguiente link encontrará la guía del
estudiante correspondiente: https://www.curriculumnacional.cl/614/
articles-131868_recurso_10.pdf
páginas 86 y 87.
Planificación
Clase 75
m
2/17/2019 9:40:10 AM
5. Identifica los triángulos rectángulos y justifica tu elección.
d.
11 cm
10 cm
9 cm
b. 4,5 cm
7,5 cm
6 cm
a.
50 cm
40 cm
30 cm
c.
12 cm
14 cm
9 cm
6. Calcula el perímetro (P) y el área (A) de las siguientes figuras. Si es necesario, utiliza
una calculadora.
a.
A
D C
B
8 cm
17 cm
c.
A
C
B
24 cm 32 cm
14,4 cm
b.
A
D C
B
3 cm
4 cm
a. Reúnete con un compañero o compañera y construyan un triángulo rectángulo cuyos
lados midan 4,5 cm, 6 cm y 7,5 cm. Sobre cada uno de ellos dibujen un triángulo isósceles
con base en el lado y 3 cm de altura. ¿Es cierto que el área del triángulo construido sobre
la hipotenusa es igual a la suma de las áreas de los otros dos triángulos? ¿Por qué?
b. Diego y Francisco trotan en una cancha rectangular
como la que se muestra. Diego da 8 vueltas completas
a la cancha. Francisco trota solo por el camino marcado
con rojo y da 10 vueltas. ¿Quién recorrió una mayor
cantidad de metros?
• ¿Qué pasos sigues al aplicar el teorema de Pitágoras?
• ¿Qué es un trío pitagórico? Ejemplifica.
Páginas86y87.
50 cm
90 cm
3
Unidad
139
263

Propósito
aplicaciones del teorema de Pitágoras en
diversas situaciones contextualizadas.
OA 12
Planificación
Inicio 15 minutos
observen la imagen del puente Malleco
y lean la situación del cambio de vigas
(diagonales) que se plantea.
ejemplo 1 para que apliquen el teorema
de Pitágoras para calcular la altura de
un triángulo equilátero.
Pregunte:
• ¿Qué es la altura de un triángulo?
• ¿Qué características tiene?
Dificultades y errores frecuentes
Un error frecuente que cometen los estudiantes cuando aplican el teorema
de Pitágoras para determinar la medida desconocida de un segmento es
la de igualar siempre el cuadrado del segmento desconocido con la suma
de los cuadrados de los otros segmentos.
Para abordar este error, muestre cómo evaluar correctamente los valores
de los catetos y la hipotenusa en la expresión:
a2
+ b2
= c2
Actitudes
OA B
págs. 140 Y 141
Clase 76
Aplicaciones del teorema de Pitágoras
El viaducto del Malleco es un puente ferroviario chileno ubicado
sobre el río Malleco, en la ciudad de Collipulli, Región de La Araucanía.
Con sus 102 m de altura, es el segundo puente más alto de Chile.
En 1990 fue decretado monumento histórico.
Ejemplo 1
¿Cuál es la medida de la altura h en el triángulo?
1 En un triángulo equilátero y en un triángulo isósceles la altura (h)
correspondiente a la base divide a esta en dos segmentos de igual
medida. Por lo tanto, se cumple:
AD = DB = 2,5 cm
2 Notamos que la altura h divide al triángulo ABC en dos triángulos rectángulos congruentes.
En el triángulo rectángulo DBC, h representa uno de sus catetos, por lo tanto podemos aplicar
el teorema de Pitágoras para calcular su medida.
h2
+ 2,52
= 52
h2
+ 6,25 = 25
h2
= 25 – 6,25
h2
= 18,75
h = 18,75 cm ≈ 4,33 cm Utilizamos una calculadora
para obtener la raíz cuadrada.
5 cm
2,5 cm
C
h
B
D
5 cm 5 cm
5 cm
C
A
h
B
D
• Si un ingeniero quiere cambiar las vigas marcadas por
unas más resistentes, ¿qué largo debiesen tener?
24 m
7 m
Lección 2
140 | Unidad 3
E
E
d
¿
2
E
C
d
CL0000000001018 MA
264

Unidad
3
Guíe a sus estudiantes en el ejemplo 3,
ya que se pide calcular la diagonal de un
paralelepípedo, para lo cual es necesario
plantear el teorema de Pitágoras en dos
ocasiones: primero para calcular la diagonal
de la base, y luego para calcular la diagonal
del prisma.
Cierre 15 minutos
En una plenaria, invite a sus estudiantes
a compartir sus apreciaciones sobre
los contenidos estudiados y las
situaciones abordadas.
Comente a sus estudiantes que para saber más acerca del teorema
de Pitágoras, deben visitar el siguiente sitio web:
http://mimosa.pntic.mec.es/ clobo/geoweb/trian9.htm
2/17/2019 9:40:11 AM
Ejemplo 2
En una habitación de 2,4 m de altura se quiere ubicar un mueble
de 60 cm de profundidad. Si se debe inclinar para trasladarlo,
¿cuál es la altura máxima que puede tener para no rayar el techo?
1 En el mueble podemos formar un triángulo rectángulo
en el que h representa su altura.
h
0,6 m
2,4 m
Igualamos las unidades
de medida.
h
60 cm
2,4 m
En esta posición la diagonal
del mueble coincide con
la altura de la habitación.
2 Aplicamos el teorema de Pitágoras para calcular la medida de la altura (h).
h2
+ 0,62
= 2,42
h2
+ 0,36 = 5,76
h2
= 5,4
h = 5,4 ≈ 2,32 m
Ejemplo 3
Calcula la medida de la diagonal del siguiente prisma recto
de base rectangular.
1 Calculamos la medida de la diagonal de la base (x) aplicando
el teorema de Pitágoras.
9,6 cm
5 cm
7,2 cm
x
9,6 cm
7,2 cm
x
x2
= (7,2)2
+ (9,6)2
x2
= 51,84 + 92,16
x2
= 144
x = 144
x = 12 cm
2 Calculamos la medida de la diagonal del prisma (y).
Expresamos la medida
de la diagonal del prisma.
y2
= 52
+ 122
y2
= 25 + 144
y2
= 169
y = 169
y = 13 cm
Aplicamos el teorema
de Pitágoras.
9,6 cm
5 cm
7,2 cm
y
12 cm
12 cm
5 cm
y
Altura máxima del mueble.
9,6 cm
5 cm
7,2 cm
60 cm
2,4 m
El teorema de Pitágoras se puede aplicar para calcular las medidas en figuras o cuerpos
geométricos, y así poder determinar su área y su perímetro.
Aprende
3
Unidad
141
265

Propósito
el Teorema de Pitágoras para abordar
problemas en contextos diversos.
Objetivo de Aprendizaje
OA 12
Planificación
Inicio 15 minutos
Antes de comenzar la actividad, pida a
un estudiante que explique el teorema
de Pitágoras y que muestre un ejemplo
de aplicación basándose en lo realizado
la clase anterior.
En la actividad 4 los estudiantes deben
aplicar propiedades del plano cartesiano
para determinar la magnitud de distintos
tramos. Para ello, recuerde la notación
de puntos usando un par ordenado
de coordenadas, en el que la primera
corresponde a la posición respecto
al eje X y la segunda respecto al eje Y.
Para activar los conocimientos previos, plantee
las siguientes preguntas:
• ¿Qué indica el teorema de Pitágoras?
• ¿Qué propiedades del teorema de Pitágoras conoces?
• ¿Qué situaciones de la vida cotidiana se pueden abordar aplicando
el teorema de Pitágoras?
Actitudes
OA C ; OA D
págs. 142 y 143
Clase 77
1. Calcula el área (A) de los siguientes polígonos.
a = apotema
b.
50 cm
a
a
h = altura
a.
6 cm 6 cm
6 cm
C
A
h
B
h = altura
c.
7,5 cm 7,5 cm
3 cm
R
P
h
Q
a = apotema
d. Hexágono regular
2 cm
a
2. Determina lo solicitado en cada caso. Si es necesario, utiliza una calculadora.
a. El área de un rectángulo de largo igual a 6 cm cuya diagonal mide 6,5 cm.
b. El perímetro de un rombo cuyas diagonales miden 12 cm y 16 cm (Recuerda que
en un rombo sus diagonales se dimidian y son perpendiculares).
c. El área de un cuadrado de diagonal igual a 8 cm.
d. El perímetro de un triángulo equilátero cuya altura mide 28 cm.
e. La altura de un trapecio isósceles de bases 8 dm y 10 dm de longitud, y lados iguales a 7 dm.
3. Calcula la medida de la diagonal de los siguientes prismas.
b.
8 cm
1,2 cm
6 cm
a.
5 cm
5 cm
5 cm
c.
15 cm
20 cm
4. Analiza la información y representa las componentes perpendiculares de los siguientes
vectores y calcula su magnitud. Si es necesario, utiliza una calculadora.
Y
O X
1
2
3
–2
4
5
–1
4 5
–1 3
–2 2
1
v = (3, 4)
||v|| = 32
+ 42
= 25 = 5
Y
O X
1
2
3
–2
4
5
–1
4 5
–1 3
–2 2
1
v = (3, 4)
vy = (0, 4)
vx = (0, 3)
Al representar un vector v en el plano
cartesiano es posible representar sus
componentes (vx, vy) y calcular su
magnitud ||v|| = vx
2
+ vy
2
. Por ejemplo,
al representar las componentes del
vector v = (3, 4) y calcular su magnitud
se obtiene:
a. v = (2, –3)
b. v = (–6, –4)
c. v = (–2, 3)
d. v = (–5, 4)
e. v = (–4, 4)
f. v = (3, –4)
Actividades
Lección 2
142 | Unidad 3
•
•
•
5
6
CL0000000001018 MA
266

Unidad
3
Al abordar los problemas propuestos,
comparta las siguientes estrategias con
sus estudiantes:
• Destacar la información relevante.
• Destacar los distractores del enunciado.
• Utilizar sus propias palabras para
describir el problema.
• Evaluar diferentes procedimientos
de resolución.
• Comprobar que los resultados son
coherentes con la situación resuelta.
Cierre 15 minutos
Para finalizar, invite a sus estudiantes a
contestar las preguntas de Reflexiona y
responde, y a compartir las respuestas con
sus compañeros.
Invite a sus estudiantes a visitar el sitio:
ttps://www.geogebra.org/m/YQjYdtCc
En él aparece una animación del teorema de Pitágoras.
Pida a sus estudiantes investigar acerca de esta representación y ver
cómo se puede extender el teorema a otras figuras geométricas, más
allá de los triángulos.
páginas 88 a 91.
Planificación
Clase 78
Solucionario
.
m
2/17/2019 9:40:12 AM
• ¿En qué situaciones de la vida cotidiana puedes aplicar estos nuevos conocimientos
y habilidades?
• ¿Qué datos necesitas para aplicar el teorema de Pitágoras? Ejemplifica.
• ¿Cómo puedes demostrar tus aprendizajes sobre el teorema de Pitágoras? Explica.
a. Una escalera de 3 m está apoyada contra un árbol perpendicular al suelo. Si la distancia
de la base de la escalera al árbol es de 1 m, ¿a qué distancia del suelo se encuentra la parte
más alta de la escalera?
b. Una rampa tiene una altura de 11 m y su punto de inicio está a 60 m de distancia de la pared.
¿Cuál es la longitud de la rampa?
c. Julieta está encumbrando un volantín con un hilo de 100 m. Cuando el hilo está totalmente
tenso, la altura del volantín al nivel de su mano es de 80 m. Sin considerar la estatura de
Julieta, ¿a qué distancia se encuentra ella de este punto?
d. En el trapecio PQRV se han trazado las alturas PS y QT. Si ST mide 10 cm, TV mide 17 cm,
RV 24 cm y PV 13 cm, ¿cuál es el perímetro y cuál es el área del trapecio PQRV?
e. Se necesita pasar un espejo de forma cuadrada, cuyos lados miden 210 cm, por una puerta
que mide 84 cm de ancho y 205 cm de alto. ¿Podrá realizarse la operación?
f. En las construcciones antiguas, para marcar los ángulos rectos desarrollaron un ingenioso
método que consistía en una cuerda cerrada que tenía 12 nudos, entre los cuales existía
igual distancia. ¿Por qué es posible construir un ángulo recto con esta cuerda? Justifica.
6. Analiza las siguientes preguntas respecto del triángulo de la figura y luego responde.
a. ¿Los lados AC y BC son perpendiculares? b. ¿Cuánto mide CD?
C
A B
D
48 cm
36 cm
21,6 cm
60 cm
Páginas88a91.
3
Unidad
143
267

Propósito
En esta clase los estudiantes demostrarán,
utilizando un recurso tecnológico, que para
cualquier triángulo rectángulo se cumple
que la suma de las áreas de los cuadrados
construidos sobre sus catetos es igual al
área del cuadrado construido sobre su
hipotenusa.
OA 12
Planificación
Inicio 15 minutos
Antes de comenzar la actividad, pida a
un estudiante que explique el teorema
de Pitágoras y que muestre un ejemplo
de aplicación basándose en lo realizado
la clase anterior.
Usemos la tecnología
Pida a sus estudiantes que visiten el sitio web:
https://www.geogebra.org, en el que podrán utilizar el software GeoGebra
de forma online.
págs. 144 y 145
Clase 79
Actitudes
OA C , OA D
1 Construye un segmento.
Pincha , selecciona , luego pincha
en dos puntos del plano. Habrás creado
el segmento AB.
2 Traza una perpendicular al segmento AB.
Pincha , luego pincha sobre cualquier
punto del segmento AB, y desplaza la recta
hasta el extremo B. Habrás trazado la recta
perpendicular al segmento AB que pasa
por B.
3 Sobre la recta crea el punto C.
Pincha , selecciona“punto”y haz clic en
cualquier lugar sobre la recta. Habrás creado
el punto C sobre la recta.
4 Dibuja el segmento AC.
Selecciona , pincha , luego haz clic
sobre A y C. Habrás creado el segmento AC.
5 Construye el polígono ABC.
Selecciona , pincha sobre A, B, C, A
y habrás construido el polígono ABC.
6 Construye los cuadrados sobre cada lado
del triángulo ABC.
Selecciona , luego selecciona“ polígono
regular”. Haz clic sobre A y luego sobre C,
aparecerá un cuadro donde debes poner el
número de lados del polígono que quieres
construir, en este caso 4.
Herramientas tecnológicas
En la siguiente actividad podrás demostrar que en cualquier triángulo rectángulo se cumple que la
suma de las áreas de los cuadrados construidos sobre los catetos es igual al área del cuadrado
construido sobre la hipotenusa. Para ello, utilizaremos el programa GeoGebra.
Instrucciones
Lección 2
144 | Unidad 3
R
1
2
3
1
CL0000000001018 MA
268

Unidad
3
Guíe a sus estudiantes en la construcción
del teorema de Pitágoras en GeoGebra.
A los estudiantes que tienen mayor dominio
del software, pídales que definan polígonos de
n lados utilizando un deslizador de variable n
con valores 3, 4, 5, 6, entre otros.
Cierre 15 minutos
Finalice la clase preguntando a
sus estudiantes:
• ¿Qué fue lo más difícil de aprender
en esta lección?
• ¿Qué propiedades tiene el teorema
de Pitágoras?
A los estudiantes que tienen mayor dominio del software, pídales
que definan no solo un cuadrado, sino también polígonos de n lados
utilizando un deslizador de variable n con valores 3, 4, 5, 6, etc.
Conduzca a sus estudiantes a diseñar la generalización dinámica
del teorema de Pitágoras planteada la clase anterior en el sitio web
https://www.geogebra.org/m/YQjYdtCc
Luego reflexione sobre el trabajo realizado con preguntas como: ¿qué
pasos seguiste para definir los polígonos?, ¿podrías haberlo hecho de
otra forma?, ¿por qué?
2/17/2019 9:40:12 AM
Responde:
1. ¿Cómo se relaciona la suma de las áreas de los cuadrados construidos sobre los catetos
y el área del cuadrado construido sobre la hipotenusa?
2. ¿Crees que esta relación varía según el triángulo que se considere? ¿Por qué?
3. ¿Qué relación existe entre la fórmula a2
+ b2
= c2
y las áreas de los cuadrados?
Comenta con tu curso.
9 Suma las áreas de los cuadrados construidos sobre los catetos y compárala con el área
del cuadrado construido sobre la hipotenusa.
10 Repite el procedimiento construyendo un triángulo distinto.
7 Construye los cuadrados sobre los otros
lados del triángulo, siguiendo las mismas
indicaciones del paso pero considerando
los otros puntos.
8 Calcula el área de cada cuadrado.
Selecciona , y pincha sobre área, .
Haz clic sobre cada uno de los cuadrados
construidos y obtendrás el área de ellos.
3
Unidad
145
269

Propósito
Evaluar los objetivos desarrollados en la
Lección 2.
Inicio 15 minutos
Para comenzar la clase, pregunte a sus
estudiantes los conceptos estudiados
la clase anterior, por ejemplo:
• ¿Qué nombre reciben los lados de un
triángulo rectángulo?
• ¿Qué plantea el teorema de Pitágoras?
• ¿Qué son los tríos pitagóricos? Señalen
un ejemplo.
Solicite a sus estudiantes que respondan
las actividades de la evaluación en
sus cuadernos.
Planificación
Invite a sus estudiantes a explorar relaciones en el teorema de Pitágoras
a partir del tangrama disponible en: www.geogebra.org/m/grgaz2mN
Luego, guíe la reflexión de los estudiantes con preguntas como: ¿qué
sucede al mover un vértice azul en el triángulo?, ¿cómo puedes explicar
esto mediante el teorema de Pitágoras?
págs. 146 y 147
Clase 80
1. Calcula la medida del lado desconocido (x) en cada triángulo. Comprueba con tu
calculadora.
a.
16 cm
x
20 cm
b.
12 cm
9 cm
x
c.
4,5 cm
7,5 cm
x
d.
13 cm
12 cm
x
2. Determina si los siguientes números forman tríos pitagóricos.
a. 1, 2 y 3
b. 2, 3 y 4
c. 3, 4 y 5
d. 7, 24 y 25
e. 5, 11 y 12
f. 8, 15 y 17
3. Calcula la medida de la hipotenusa de los triángulos que hacen referencia al siguiente
triángulo, que es rectángulo en el vértice A:
21 cm
20 cm
C
A B
a. Hipotenusa del triángulo ABC.
b. Hipotenusa del triángulo cuyos catetos miden
el doble de los catetos del triángulo ABC.
c. Hipotenusa del triángulo cuyos catetos miden
la mitad de los catetos del triángulo ABC.
4. Calcula la medida de la diagonal d de los siguientes prismas rectos:
12 cm
4 cm
3 cm
d
a.
7,2 cm
5,6 cm
3,3 cm
d
b.
Balanza B
| Unidad 3
146
5
6
•
•
•
CL0000000001018 MA
270

Unidad
3
Una vez que todos los estudiantes
terminen la actividad, solicite que algunos
presenten sus resoluciones en la pizarra
para que el resto analice las respuestas
y corrija los errores.
Cierre 15 minutos
acerca del trabajo realizado y a compartir
las respuestas a las preguntas planteadas
en Reflexiona y responde.
Desarrolle la metacognición en los estudiantes y promueva la
participación de todos. Para ello, puede otorgar un tiempo para
reflexionar y discutir las siguientes preguntas:
• ¿En qué situaciones cotidianas es posible utilizar las funciones?
• ¿Qué fue lo más difícil de entender de este tema?
• ¿Cómo se relaciona lo aprendido con los contenidos anteriores?
Solucionario
2/17/2019 9:40:13 AM
5. Calcula el área total (AT) y el volumen (V) de los siguientes cuerpos geométricos.
Si es necesario, utiliza calculadora. Considera π ≈ 3,14.
c.
25 cm
18 cm
9 cm
b.
52 cm
48 cm
a.
8,5 cm
20 cm
9 cm
a. Una escalera con una extensión de 8 m se encuentra apoyada en una pared. Si el punto de
contacto con el suelo está a 2 metros de la base de dicha pared, ¿cuál es la altura alcanzada
por la escalera?
b. Un televisor es un aparato electrónico destinado a la recepción y reproducción de señales
de televisión. Gracias a los grandes avances tecnológicos, se ha hecho posible la invención
de múltiples televisores con caracteres innovadores, los cuales son cada vez más livianos y
tan delgados que pueden ser colgados en la pared como un cuadro más de la casa.
Este televisor es de 26 pulgadas,
es decir, esa es la medida de la
diagonal de su pantalla. Su alto mide
14 pulgadas y su largo, 22 pulgadas.
Este televisor es de
22 pulgadas y su largo
mide 18 pulgadas.
El alto de este televisor es
de 30 pulgadas y tiene
40 pulgadas de largo.
Este televisor es de
40 pulgadas y su alto
mide 22 pulgadas.
1
2
3
4
• Según las dimensiones del primer televisor, ¿se cumple el teorema de Pitágoras? Justifica.
• ¿Cuál es la medida del alto del televisor ?
• ¿Cuánto mide el largo del televisor ?
• ¿De cuántas pulgadas es el televisor ?
• ¿Cómo puedes superar las dificultades tuviste en el desarrollo de la lección? Explica.
• ¿Crees que respetar y considerar los aportes de tus compañeros favorece a tu aprendizaje? ¿Por qué?
• Representa algunos ejemplos de triángulos en los que puedas aplicar el teorema de Pitágoras.
Páginas92y93.
3
Unidad
271

Propósito
En esta clase estudiarán las
transformaciones isométricas a través
de traslaciones, rotaciones y reflexiones
en el plano y el espacio.
OA 13
Inicio 15 minutos
Para comenzar la clase, invite a sus
estudiantes a observar las imágenes
de frisos decorativos y pregunte:
• ¿Hay una imagen o figura que se repita?
• ¿Cómo se llama este proceso?
ejemplo 1, en el que deben trabajar
con los pares ordenados del triángulo
para trasladarlo por el plano cartesiano.
Formalice con ayuda del recuadro.
Promueva un ambiente de compañerismo y de respeto al interior del
aula con el fin de que todos los estudiantes se sientan en confianza
para compartir sus inquietudes o respuestas. Para ello, puede guiar
a los estudiantes a elaborar en conjunto las reglas para el trabajo en
clases en las que se considere, por ejemplo, levantar la mano para
hablar, evitar interrupciones y escuchar con atención.
Planificación
págs. 148 a 151
Clase 81
Actitudes
OA B , OA C
Palacio de la Alhambra. Granada, España.
Ejemplo 1
Traslada en el plano cartesiano el triángulo ABC, de vértices A(–4, –2), B(–2, –2) y C(–5, 2), con
respecto al vector v = (6, 3) y determina las coordenadas de los vértices del triángulo A'B'C'.
1 Como el vector de traslación es v = (6, 3), el triángulo ABC se traslada 6 unidades
hacia la derecha y 3 unidades hacia arriba.
7 unidades
3 unidades
Y
O X
1
2
3
–2
4
5
–1
4 5
–1 3
–2 2
–3 1
–4
–5
A'
A
C'
C
B'
B
v
2 Las coordenadas de los vértices del triángulo A´B´C´ son A'(2, 1), B'(4, 1) y C'(1, 5).
Lección 3 Transformaciones isométricas
• Isometría:esdeorigengriegoysignifica
“igualmedida”(iso=igualo mismo,
metría=medir).
En esta lección podrás realizar traslaciones,
rotaciones y reflexiones de figuras en el
plano cartesiano y en el espacio.
Traslación
Los frisos decorativos son una larga banda
pintada, esculpida o incluso caligrafiada.
• ¿Dónde has visto construcciones como la que se muestra en la imagen?
148 | Unidad 3
E
D
s
CL0000000001018 MA
272

Unidad
3
Indique a sus estudiantes que un trabajo colaborativo se realiza
cuando todos aportan al desarrollo del problema. Pídales que trabajen
colaborativamente y que cada uno sea capaz de explicar cómo
resolvieron los problemas.
ejemplo 2 para que comprendan la
traslación de una figura en el plano
cartesiano utilizando un vector.
Enfatice en los valores que pueden
tomar las variables a y b cuando
el vector traslación es (a, b).
En el siguiente link encontrará un
applet de Geogebra relacionado con
la traslación:
https://www.geogebra.org/m/E8VPVUCX
Utilice este recurso para que los
estudiantes visualicen la traslación al
manipular digitalmente el vector dado.
2/17/2019 9:30:26 AM
Ejemplo 2
Determina el vector de traslación respecto al cual se trasladó el rectángulo ABCD para obtener
su imagen A'B'C'D'.
Y
O X
1
2
–3
–4
3
–2
–1
4 5
–1 3
–2 2
–3 1
–4
–5
4
5
A'
A
D'
D
C'
C
B'
B
1 Escogemos uno de los vértices del rectángulo ABCD. En este
caso elegiremos el vértice A, y contamos las unidades que
se trasladó hasta el vértice A'.
2 Como el vértice A se trasladó 7 unidades a la izquierda y
5 unidades hacia arriba en el plano cartesiano, la primera
componente del vector buscado será –7 y la segunda, 5.
Es decir, el vector de traslación es v = (–7, 5).
3 Podemos comprobar nuestra solución restando
las coordenadas de A' con las de A.
Las coordenadas de A' son (–5, 2) y las de A son (2, –3). Luego,
realizamos la sustracción:
v = (–5, 2) – (2, –3)
= (–5 – 2, 2 – (–3))
= (–7, 5)
Lo anterior se cumple con cualquier pareja de vértices correspondientes, es decir, si
consideramos que las coordenadas de B' son (–2, 2) y las de B son (5, –3) obtenemos:
v = (–2, 2) – (5, –3)
= (–2 – 5, 2 – (–3))
= (–7, 5)
• Sienunvectorv=(a,b)aesigualacero,
lafiguranosetrasladahorizontalmente
(izquierdaoderecha).Sibesigualacero,
la figuranosetrasladaverticalmente
(arriba oabajo).
• Una traslación de una figura geométrica desplaza todos los puntos
de ella en una misma magnitud, dirección y sentido.
• Al trasladar un punto A, le corresponderá otro punto A' donde
AA' = v, que es el vector de traslación.
Aprende
Y
O X
1
2
–3
–4
–5
3
–2
–1
4 5
–1 3
–2 2
–3 1
–4
–5
A'
A
D'
D
C'
C
B'
B
4
5
7 unidades
5 unidades
v
C
C'
A
A'
B
B'
v
3
Unidad
149
Lección 3 • Transformaciones isométricas |
273

Guíe a sus estudiantes a través de las
actividades propuestas y pídales que las
desarrollen en sus cuadernos trabajando
en parejas.
Aproveche el ejemplo 3 para profundizar
en el contenido de esta lección y plantee
diferentes situaciones a sus estudiantes,
por ejemplo:
¿Con qué vector puedo trasladar el
cuadrado de tal forma que el vértice M
coincida con el punto G?, ¿cómo
lo supiste?
Cuando trasladamos el cuadrado de tal
forma que el punto L quede en el punto
(0, 2), ¿qué coordenadas tiene ahora el
vértice en K?, ¿cómo puedes verificar
tu afirmación?
Solucionario
1. Traslada cada punto según el vector dado e indica las coordenadas resultantes.
a. P(5, 3) según el vector v = (0, 3).
b. Q(–2, 6) según el vector u = (3, 0).
c. R(–3, –4) según el vector w = (–3, –4).
d. S(4, –5) según el vector z = (–2, 8).
e. T(10, 8) según el vector h = (–5, –8).
f. U(12, –10) según el vector k = (–10, 6).
2. Aplica a cada figura una traslación según el vector indicado y escribe las coordenadas
de los vértices de la figura imagen.
a. Y
O X
1
–4
2
–3
3
–2
–1
–1
–2 2
–3 1
–4
–5
–6
–7
A
B
C
D
v = (–1, –1)
b Y
O X
1
–4
2
–3
3
–2
–1
–1
–2 2
–3 1
–4
–5
–6
–7
C E
D
F
G
A
B
w = (4, 2)
3. A partir del plano cartesiano, realiza las siguientes actividades.
a. Determina las componentes del vector que traslada
el triángulo EFG al triángulo E'F'G'.
b. ¿Cuáles son las componentes del vector que traslada
el triángulo E'F'G' al triángulo EFG?
c. ¿Qué relación existe entre las componentes de los vectores
encontrados en las preguntas a. y b.?
d. Traslada el cuadrado JKLM de acuerdo con el vector z y
determina las coordenadas de los nuevos vértices.
4. Sea A(9, –12) imagen del punto B(5, –16). Con esta información, responde.
a. ¿Cuál es el vector que traslada a B en A?
b. Si A se traslada con respecto al vector de la pregunta anterior, ¿cuáles serían
las coordenadas de su imagen?
• Explica cómo trasladar figuras en el plano cartesiano respecto de un vector.
Páginas94y95.
Actividades
Y
O X
1
–4
–5
2
–3
3
4
5
–2
–1
–1 3
–2 2
–3 1
–4
–5
–6
–7
G
F
E
M
L
K
J
G'
F'
E'
z
Lección 3
150 | Unidad 3
T
U
l
CL0000000001018 MA
274

Unidad
3
Invite a sus estudiantes a trabajar
utilizando el software Geogebra.
Motívelos a crear traslaciones de figuras
más complejas y a que les planteen a sus
compañeros preguntas para que descubran
qué vector utilizaron al trasladar la
figura original.
Cierre 15 minutos
Para finalizar, desarrolle una plenaria
en la que los estudiantes puedan
intercambiar sus inquietudes y señalar
las dificultades que se les presentaron al
trabajar trasladando figuras en el plano
cartesiano usando vectores.
Permita que sus estudiantes determinen
analíticamente un punto imagen basados
en otro punto dado considerando un
vector de traslación a partir del análisis
de los resultados obtenidos al ejecutar
el siguiente applet de GeoGebra:
www.geogebra.org/m/ePuHUmeU
Luego, pídales explicar sus
procedimientos y compararlos
con sus compañeros. Finalmente,
formule las siguientes preguntas: ¿los
procedimientos empleados son iguales
que los de tus compañeros?, ¿por qué?
X
2/17/2019 9:30:26 AM
Traslación de un pentágono
Usando el programa GeoGebra, puedes construir transformaciones isométricas mediante
los siguientes pasos.
1 Utiliza una hoja nueva, presiona el botón derecho y selecciona ejes. Presiona nuevamente
el botón derecho y selecciona cuadrícula.
2 En las herramientas del software, selecciona
Polígono . Luego, en la cuadrícula dibuja
un polígono haciendo clic en distintos puntos.
Recuerda que el último clic siempre se debe
hacer sobre el primer vértice que generaste.
4 Para trasladar la figura respecto al vector,
selecciona la herramienta traslada objeto
acorde a vector . Al usar esta herramienta,
haz clic primero sobre el objeto a trasladar y
luego sobre el vector de traslación.
3 Dibuja un vector presionando la herramienta
vector entre dos puntos .
Nota:
la aplicación Geogebra, creada por Markus Hohenwarter, fue incluida
en este texto con fines de enseñanza y a título meramente ejemplar.
3
Unidad
151
275

Propósito
qué es la rotación y cómo realizarla en
el plano cartesiano.
OA 13
Inicio 15 minutos
Comience la clase pidiendo a sus
estudiantes que observen las fotografías y
pídales que digan qué ven en cada una de
ellas. ¿Qué ocurrió? ¿Qué se hizo con el
cuadro para obtener la segunda imagen?
Analice el ejemplo 1 junto con sus
estudiantes y mencione el sentido que
toma el ángulo para realizar la rotación
de la figura, el cual puede ser horario
o antihorario.
Planificación
Guíe a sus estudiantes a analizar expresiones cotidianas en las que se
utilicen conceptos matemáticos como por ejemplo «cambio radical en
180°». Invítelos a explicar estas expresiones y a interpretarlas desde
un punto de vista matemático.
Actitudes
OA B , OA C
págs. 152 y 153
Clase 82
Rotación
Al observar el siguiente cuadro desde un lado, se pueden ver manzanas, peras, uvas e higos
ubicados en un cesto.
Al darle vuelta, como si se soltara la fruta, repentinamente aparece un retrato en el que se pueden
distinguir los ojos y otros aspectos del rostro.
Ejemplo 1
Utilizando regla y compás rota el triángulo ABC, respecto al punto O, en 90°.
Para rotar un triángulo ABC con respecto a un punto O y ángulo
de rotación 90º en sentido antihorario, utilizaremos regla, compás
y transportador.
1 Dibujamos una circunferencia con centro O y radio OC y con
un transportador determinaremos un ángulo de 90º. Luego,
marcamos la imagen C' en la circunferencia, como se observa
en la figura .
2 Repetimos el mismo procedimiento para los demás vértices
y luego unimos los puntos, con lo que obtenemos la imagen
del triángulo, como se observa en la figura .
• ¿Qué movimiento se debe aplicar al cuadro para lograr visualizar el retrato? Descríbelo.
Figura 1
Figura 2
A
C
C'
B O
A
C
C'
A'
B
O
B'
Testareversibileconcestodifrutta(Cestadefrutas). Giuseppe Arcimboldo. Italia, 1590.
Si se ubica el origen de coordenadas en el punto O,
¿cuáles son las coordenadas del triángulo ABC y A'B'C'?
Lección 3
152 | Unidad 3
E
D
i
E
I
A
CL0000000001018 MA
276

Unidad
3
Guíe a sus estudiantes a través de
los ejemplos rotando las figuras
en el plano cartesiano.
Destaque qué ocurre cuando se rotan
figuras con un ángulo de 180 grados
con centro de rotación en el origen.
Cierre 15 minutos
Finalice la clase recordando a sus
estudiantes qué es una rotación, qué
representa el punto de rotación y de qué
tipo puede ser el ángulo de rotación.
Invite a sus estudiantes a conocer interesantes aplicaciones de la rotación
utilizando el software GeoGebra en:
https://www.geogebra.org/m/bTevssdC
2/17/2019 9:30:27 AM
• Para identificar el ángulo de rotación de una figura, se une uno de los
vértices de la figura original con el de la figura imagen pasando por el
centro de rotación y luego se mide el ángulo que se forma.
• Una rotación es una transformación isométrica en la cual todos los
puntossemuevenrespectodeunpuntofijollamadocentroderotación
(O) en un determinado ángulo, llamado ángulo de rotación (α).
• El ángulo de rotación puede tener sentido antihorario (positivo) o
sentido horario (negativo).
C
A
B
O
α
C' A'
B'
Aprende
Ejemplo 2
Determina el ángulo de rotación respecto del cual se rotó el cuadrilátero ABCD para obtener su
imagen A'B'C'D'. Considera que O es el centro de rotación.
1 Trazamos un segmento que pase por O y que una uno de los vértices con su imagen, en este
caso D y D'.
2 Identificamos el ángulo de rotación, que es 180º.
Y
O X
1
2
–3
–4
3
4
–2
–1
4 5
–1 3
–2 2
–3 1
–4
–5
A'
A
D'
D
C'
C
B'
B
180º
Y
O X
1
2
–3
–4
3
4
–2
–1
4 5
–1 3
–2 2
–3 1
–4
–5
A'
A
D'
D
C'
C
B'
B
Ejemplo 3
Identifica el ángulo de rotación que se le aplicó al triángulo ABC para obtener el triángulo
A'B'C' considerando que P es el centro de rotación.
1 Trazamos un segmento que una A con P y otro que una P con A'.
2 Medimos el ángulo que se forma, que en este caso es 90º.
Y
O X
1
2
–3
–4
3
4
–2
–1
4 5
–1 3
–2 2
–3 1
–4
–5
A'
A
P
C'
C
B'
B
Y
O X
1
2
–3
–4
3
4
–2
–1
4 5
–1 3
–2 2
–3 1
–4
–5
A'
A
P
C'
C
B'
B
• SiserotaunpuntoA(x,y)en180º
concentroderotaciónelorigenO
(0,0),lascoordenadasdel punto
resultanteseránA’(–x,–y).
3
Unidad
153
277

Propósito
rotaciones de figuras en el plano
cartesiano.
OA 13
Inicio 15 minutos
Para comenzar la clase, pregunte a sus
estudiantes: ¿qué características tiene una
rotación? ¿Qué se necesita para rotar una
figura en el plano cartesiano?
Invítelos a compartir las respuestas con sus
compañeros respetando las ideas de los otros.
Invite a sus estudiantes a trabajar en las
actividades de esta lección recurriendo a la
materia del cuaderno cuando sea necesario.
Planificación
Motive a sus estudiantes a trabajar las rotaciones utilizando regla y
compás. Invítelos a comprobar sus construcciones con el compás, de
tal forma que midan distancias con él sin usar la regla graduada.
Actitudes
OA B , OA D
págs. 154 y 155
Clase 83
1. Determina la imagen de los siguientes puntos al rotarlos en el ángulo dado respecto
del origen.
a. A(2, 5) en un ángulo de 90º en sentido antihorario.
b. B(–6, 7) en un ángulo de 180º en sentido horario.
c. C(2, 5) en un ángulo de 270º en sentido antihorario.
2. Determina el punto al cual se le aplicaron las rotaciones, con respecto al origen, indicadas
a continuación.
a. D'(–6, 9), su rotación fue en un ángulo de 180º en sentido antihorario.
b. E'(3, –5), su rotación fue en un ángulo de 90º en sentido antihorario.
c. F'(–1, –4), su rotación fue en un ángulo de 270º en sentido horario.
3. Rota las siguientes figuras en el ángulo indicado y con centro en A.
a. Ángulo de 90º en
sentido horario.
b. Ángulo de 90º en
sentido antihorario.
c. Ángulo de 270º en
Y
O X
A
Y
O X
A
Y
O X
A
4. Determina el ángulo respecto al cual se rotaron las siguientes figuras para obtener
sus imágenes. Considera el centro de rotación en cada caso.
a. Centro de rotación A. b. Centro de rotación O. c. Centro de rotación P.
Y
O X
P
A
D
B
C
B'
A'
C'
D'
Y
O X
A
B
C
B'
C'
Y
O X
E D
C
B
A
F
B' A'
C' F'
E'
D'
• ¿Qué pasos debes seguir para rotar figuras en el plano cartesiano? Explica con tus palabras.
• ¿Qué elementos se deben considerar al rotar figuras en el plano cartesiano?
Páginas96y97.
Actividades
Lección 3
154 | Unidad 3
R
1
R
CL0000000001018 MA
278

Unidad
3
Para esta actividad, pida a sus
estudiantes que trabajen utilizando
el software GeoGebra.
Actitudes
Cierre 15 minutos
Finalice la clase preguntando a sus
estudiantes qué fue lo más difícil al aplicar
rotaciones a figuras en el plano cartesiano.
Solucionario
Invite a sus estudiantes a analizar la rotación de otras figuras
utilizando un applet de GeoGebra disponible en:
https://www.geogebra.org/m/uzv5njww
2/17/2019 9:30:28 AM
Responde:
1. Luego de realizar los pasos anteriores, responde.
a. ¿Cuánto mide cada ángulo interior de la figura inicial
y de la imagen?, ¿cómo se relacionan?
b. Calcula el perímetro, el área y las medidas de cada lado
de ambas figuras usando las herramientas del software.
¿Qué observas? ¿Ocurrirá lo mismo en cualquier
transformación isométrica?, ¿por qué?
Rotación de un triángulo
2 En las herramientas del software, selecciona Polígono . Luego, en la cuadrícula dibuja un
triángulo haciendo tres clics en distintos puntos; el cuarto clic lo debes hacer sobre el vértice
del primer clic del triángulo.
3 Selecciona la herramienta Nuevo Punto .
Haz clic en cualquier parte de la cuadrícula
para dibujar el centro de rotación.
4 Selecciona . Haz clic sobre el triángulo y,
luego, sobre el centro de rotación. Aparecerá
una tabla en la cual debes ingresar el ángulo
de rotación, puede ser 70º (o el que tú
quieras). Una vez ingresado el ángulo de
rotación, presiona OK; aparecerá la imagen
rotada en sentido horario.
5 Selecciona la herramienta Ángulo . Haz
clic sobre cada vértice correspondiente
al ángulo interior del triángulo, en sentido
antihorario; aparecerán las medidas de
los ángulos interiores como se muestra en
la figura.
Nota:
la aplicación
Geogebra, creada por
Markus Hohenwarter, fue
incluida en este texto con fines
de enseñanza y a título
meramenteejemplar.
3
Unidad
155
279

Propósito
qué es la reflexión de figuras planas.
OA 13
Inicio 15 minutos
Invite a sus estudiantes a mirar
las imágenes y a responder las
preguntas planteadas.
Analice con sus estudiantes el ejemplo 1 y
enfatice la reflexión respecto de una recta.
Apóyese en la información del recuadro
destacando las características del punto
y su imagen.
Planificación
Invite a sus estudiantes a identificar y comprobar las características
planteadas en el recuadro en la situación del ejemplo 1.
Actitudes
OA C , OA D
págs. 156 a 159
Clase 84
• ¿En cuál de ellos consideras que hay más simetrías? ¿Por qué?
• Averigua a qué corrientes artísticas se relacionan estas pinturas.
Luego, comparte tu investigación con tu curso.
Algunos objetos o diseños deben parte de su belleza a la presencia
de simetrías. Observa las siguientes pinturas.
Reflexión
Una reflexión es una transformación isométrica en la que a cada punto de una figura se le
asocia otro punto, llamado imagen. El punto y su imagen deben estar a igual distancia de una
recta llamada eje de reflexión o de simetría y el segmento que une el punto con su imagen
debe ser perpendicular a ella.
Y
O X
Eje de reflexión
A
B
C
D
E
C'
E'
A'
B'
D'
Por ejemplo, al pentágono ABCDE se le aplicó una
reflexión con respecto al eje Y en el plano cartesiano.
Aprende
NascitadiVenere(ElnacimientodeVenus).
Sandro Botticelli. Italia, 1484.
LesDemoisellesd'Avignon(LasseñoritasdeAvignon).
Pablo Picasso. España, 1907.
Lección 3
156 | Unidad 3
E
R
1
CL0000000001018 MA
280

Unidad
3
Apoyándose en el recuadro, aclare a sus
estudiantes los dos tipos de simetrías
en el plano cartesiano: axial y central,
reconociendo en cada una de ellas las
características de la simetría.
Invite a sus estudiantes a buscar imágenes de expresiones artísticas en
las que se visualice algún tipo de simetría y a identificar el eje o centro
de simetría.
Utilice la applet de GeoGebra del link
https://www.geogebra.org/m/Tjkq9eB3
para que los estudiantes analicen una
reflexión al manipular digitalmente
el eje de simetría.
2/17/2019 9:30:29 AM
Ejemplo
Realiza una reflexión al triángulo ABC, de vértices A(2, 1), B(6, 2) y C(1, 5), con respecto al eje X.
1 Representamos el triángulo ABC en el
plano cartesiano y dibujamos los puntos
simétricos a sus vértices con respecto
al eje X.
2 Unimos los puntos y dibujamos el triángulo
A'B'C', que es la imagen del triángulo ABC.
Y
O X
1
–4
–5
2
–3
3
–2
4
5
–1
4 5 6 7
–1 3
–2 2
–3 1
–4
–5
A'
A
C'
C
B'
B
Y
O X
1
–4
–5
2
–3
3
–2
4
5
–1
4 5 6 7
–1 3
–2 2
–3 1
–4
–5
A'
A
C'
C
B'
B
• La simetría axial es una reflexión en la que
todos los puntos de la figura original y su
imagen están a igual distancia de una recta.
• La simetríacentral es una reflexión en la que
todos los puntos de la figura original y sus
respectivas imágenes están a igual distancia
de un punto, llamado punto de simetría.
B
C
D
A
A'
D'
C'
B'
O
L
B
C
A
B'
C'
A'
Aprende
Actividades
1. Una línea de simetría divide a una figura en dos partes simétricas. Encuentra la o las líneas
de simetría en las siguientes figuras.
a. b. c. d.
3
Unidad
157
281

Invite a sus estudiantes a desarrollar las
actividades en parejas y a resolver cada una
de ellas en sus respectivos cuadernos.
Actitudes
Indique a sus estudiantes que pueden imaginar un espejo sobre el eje de
simetría de las figuras originales para visualizar la imagen que se forma
con la reflexión. Luego, pregunte a sus estudiantes qué es el eje de reflexión.
Solucionario
2. Realiza las siguientes actividades.
a. Refleja el pentágono
ABCDE respecto al eje X.
b. Refleja el triángulo ABC
respecto al eje Y.
c. Refleja el triángulo ABC
respecto al eje X.
Y
O X
1
–4
–5
2
–3
3
–2
4
5
–1
4 5
–1 3
–2 2
–3 1
–4
–5
D C
B
A
E
Y
O X
1
–4
–5
2
–3
3
–2
4
5
–1
4 5
–1 3
–2 2
–3 1
–4
–5
A
C
B
Y
O X
1
–4
–5
2
–3
3
–2
4
5
–1
4 5
–1 3
–2 2
–3 1
–4
–5
C
A
B
3. Observa el siguiente plano cartesiano y realiza las actividades.
Y
O X
1
–4
–5
2
–3
3
–2
4
5
–1
4 5 6
–1 3
–2 2
–3 1
–4
–5
F
A N
H
M P
B
C
D
E
P'
a. ¿Cuáles son las coordenadas del punto que se obtuvo al aplicar una reflexión
al punto H con respecto al eje Y?
b. ¿Qué punto se obtuvo al aplicar una reflexión al punto P con respecto al eje X?
c. Al aplicar una reflexión al punto M con respecto al eje X resulta el punto M'.
¿Cuáles son sus coordenadas? Y si se aplica una reflexión con respecto al eje X
al punto M', ¿cuáles son sus coordenadas?
d. Al aplicar una reflexión al punto M con respecto al eje Y resulta el punto M''.
¿Cuáles son sus coordenadas?
e. Al aplicar una reflexión al punto N con respecto al eje X resulta el punto N'.
¿Cuáles son sus coordenadas?
• ¿Qué es una reflexión? Ejemplifica.
• ¿Qué diferencias reconoces entre una rotación y una reflexión?
Páginas98y99.
Lección 3
158 | Unidad 3
R
1
R
CL0000000001018 MA
282

Unidad
3
Pida a sus estudiantes que realicen la
reflexión de un cuadrilátero utilizando
GeoGebra según las instrucciones.
Cierre 15 minutos
En una plenaria, guíe a sus estudiantes
a analizar el trabajo desarrollado y a
reflexionar acerca de la utilización de
la reflexión en la vida cotidiana.
Explique que se trata de un trabajo colaborativo, en el que deben ser
capaces de explicar cómo desarrollaron cada actividad.
páginas 94 a 99.
Planificación
Clase 85
2/17/2019 9:30:30 AM
Responde:
1. Luego de realizar los pasos anteriores, responde.
a. ¿Cuánto mide cada lado de la figura inicial y de la imagen?, ¿cómo se relacionan?
b. Calcula el perímetro y el área de ambas figuras usando las herramientas del software
y compáralas.
c. ¿Ocurrirá lo mismo en cualquier polígono al que apliques una reflexión?, ¿cómo lo supiste?
d. En una nueva aplicación de GeoGebra, dibuja otro polígono (que no sea cuadrilátero),
realiza los mismos pasos anteriores y responde las preguntas a., b. y c..
Reflexión de un cuadrilátero
2 En las herramientas del software, selecciona
Polígono . Luego, en la cuadrícula dibuja
un triángulo haciendo tres clics en distintos
puntos; el quinto clic lo debes hacer sobre
el vértice del primer clic del cuadrilátero.
3 Selecciona la herramienta Recta que pasa
por Dos Puntos . En la cuadrícula, haz
dos clics en distintos puntos para dibujar
el eje de simetría, como se muestra en
la figura.
4 Selecciona la herramienta Refleja objeto
en recta . Haz clic sobre el cuadrilátero
y, luego, sobre la recta y aparecerá la
siguiente imagen.
5 Selecciona la herramienta Distancia o
Longitud . Haz clic sobre cada lado
de la figura inicial y, luego, sobre cada
lado de la imagen; aparecerán las medidas
de todos los lados.
3
Unidad
159
283

Propósito
la composición de transformaciones
isométricas.
OA 14
Inicio 15 minutos
Comience la clase recordando lo estudiado
las clases anteriores:
• traslación
• rotación
• reflexión
de figuras en el plano cartesiano.
Analice junto con sus estudiantes
la imagen e invítelos a responder
las preguntas planteadas.
Luego, con ayuda del recuadro,
presente el concepto de composición
de transformaciones isométricas.
Invite a sus estudiantes a trabajar en un ambiente de respeto, en el
que las opiniones e ideas de los compañeros sean valoradas.
Planificación
Actitudes
OA B , OA C
págs. 160 y 161
Clase 86
Composición de
transformaciones isométricas
La composición de transformaciones isométricas consiste en aplicar una transformación
isométrica a una figura y sobre la figura imagen aplicar otra transformación isométrica, y
así sucesivamente.
Aprende
Ejemplo 1
Traslada el triángulo ABC, de vértices A(–4, –2), B(–1, 2) y C(–3, 2), respecto del vector v = (5, 3).
Luego, refleja su figura imagen respecto del eje X.
1 Representamos el triángulo ABC en el plano cartesiano.
2 Trasladamos el triángulo ABC respecto del vector v = (5, 3).
Observa la imagen y responde.
• ¿Qué transformación isométrica es necesario aplicar a la figura para obtener la figura ?,
¿y para obtener la figura ?
1
2
3
El holandés Maurits Cornelis Escher es un
artista cuyo trabajo ha interesado a muchos
matemáticos porque utiliza patrones de
figuras que cubren una superficie plana
sin superponer las figuras ni dejar espacios
libres entre ellas.
Lección 3
160 | Unidad 3
E
U
c
CL0000000001018 MA
284

Unidad
3
Explique a sus estudiantes qué se
entiende por teselación apoyándose en la
información del recuadro y enfatice en la
característica que deben cumplir las figuras
para poder teselar un plano: la suma de los
ángulos que concurren a un vértice debe
ser 360 grados.
Cierre 15 minutos
Finalice la clase promoviendo la
metacognición de sus estudiantes a través
de las siguientes preguntas:
• ¿Qué fue lo más difícil de comprender
en esta clase?
• ¿Cómo se relaciona la composición
de transformaciones isométricas
con lo estudiado anteriormente?
Invite a sus estudiantes a desarrollar una teselación utilizando GeoGebra
y apoyados en tutoriales disponibles en internet, como por ejemplo:
www.youtube.com/watch?v=K3oRceAf2R8
www.youtube.com/watch?v=qz_xepU6_lM
www.youtube.com/watch?v=pjq1NM-w3XY
2/17/2019 9:30:31 AM
3 Finalmente, reflejamos el triángulo A'B'C' respecto al eje X. Las coordenadas del triángulo
resultante son A''(1, –1), B''(4, –5) y C''(2, –5).
Y
O X
1
–4
–5
2
–3
3
–2
4
5
–1
4 5
–1 3
–2 2
–3 1
–4
–5
B
A
C
Y
O X
1
–4
–5
2
–3
3
–2
4
5
–1
4 5
–1 3
–2 2
–3 1
–4
–5
B
A
C
A'
C' B'
Figura 1 Figura 2
Y
O X
1
–4
–5
2
–3
3
–2
4
5
–1
4 5
–1 3
–2 2
–3 1
–4
–5
B
A
C
A'
A
''
C'
C''
B'
B''
Figura 3
Una teselación es una regularidad o patrón de figuras que cubre
completamente una superficie plana y que cumple con dos
condiciones: que no queden espacios y que no se sobrepongan
las figuras.
Las teselaciones se pueden crear usando transformaciones
isométricas sobre una o varias figuras. La suma de los ángulos
de las figuras que concurren a un vértice es 360º.
120º
120º
120º
Aprende
Ejemplo 2
Una familia quiere poner baldosas con forma de hexágono regular en su patio, de manera que
cubran todo el piso. ¿Cómo se puede crear un diseño para el piso?
1 Dibujamos un hexágono inicial ABCDEF que represente una baldosa.
2 Le aplicamos reflexiones respecto de los segmentos FA, AB, BC y CD. Las reflexiones las puedes
construir con regla y compás. Obtenemos lo siguiente:
3 Luego, a esta nueva figura le aplicamos sucesivas traslaciones hacia la derecha. Puedes
trasladar cada uno de los puntos de la figura con regla y compás. Así, seguimos aplicando
transformaciones isométricas hasta cubrir el piso por completo.
D
F
C
A
B
E
Figura 1 Figura 2 Figura 3
3
Unidad
161
285

Propósito
En esta clase los estudiantes reconocerán
las transformaciones isométricas y figuras
con las que es posible teselar.
OA 14
Inicio 15 minutos
Recuerde a sus estudiantes los conceptos
asociados a función, función lineal y
función afín. Solicite a sus estudiantes
que den ejemplos en los que se aplique este
tipo de funciones en problemas de la vida
diaria.
Solicite a sus estudiantes realizar
la actividad de forma individual y
registrar sus respuestas en su cuaderno.
Planificación
Para activar conocimientos previos, recuerde a sus estudiantes las
propiedades de la traslación en el plano cartesiano, las propiedades
y características de la rotación y los tipos de reflexión. Entregue un
ejemplo de cada transformación.
Actitudes
OA B , OA C
págs. 162 y 163
Clase 87
1. ¿Qué transformaciones isométricas se le aplicaron a la figura A para obtener la figura C
pasando por B?
C
B
A
2. Escribe las transformaciones isométricas aplicadas al triángulo ABC para lograr
la siguiente teselación.
A
C
B
3. Describe mediante qué transformaciones aplicadas al triángulo ABC se puede construir
el siguiente diseño.
C
B
A
4. Identifica con cuál o cuáles de las siguientes figuras es posible teselar un plano. Luego,
construye teselaciones en tu cuaderno a partir de las figuras seleccionadas y describe
las transformaciones isométricas que aplicaste para teselar.
a. b. c. d.
Actividades
Lección 3
162 | Unidad 3
5
6
7
8
•
•
•
CL0000000001018 MA
286

Unidad
3
Guíe a sus estudiantes durante el trabajo
de las actividades. Enfatice la importancia
de la perseverancia y el orden al trabajar
con transformaciones isométricas en el
plano cartesiano.
Cierre 15 minutos
Para finalizar, invite a sus estudiantes
a reflexionar, a responder las preguntas
planteadas y a compartir las respuestas
con sus compañeros.
Como repaso, utilice un applet de GeoGebra (disponible en
www.geogebra.org/m/kCFgZXeK) que le permitirá visualizar
las transformaciones isométricas estudiadas.
Solucionario
páginas 100 a 103.
Planificación
Clase 88
2/17/2019 9:30:39 AM
5. Reúnete con un compañero o compañera y dibujen cada uno un cuadrilátero en el plano
cartesiano con los vértices que prefieran y aplíquenle una reflexión respecto al eje X. Luego,
roten la imagen con respecto al origen en 180º y finalmente apliquen una traslación respecto
del vector v = (2, –2). Comparen sus resultados.
6. Traslada el triángulo ABC respecto del vector u = (3, 0) y
luego refléjalo con respecto al eje Y. Si inviertes el orden de
las transformaciones, ¿cambian las coordenadas de los vértices
de la figura imagen? ¿Qué puedes concluir?
7. A la figura ABCDEF se le ha aplicado una rotación en 90º con
respecto al punto P. Copia en tu cuaderno la figura y construye
con regla y compás, mediante traslaciones y reflexiones, una
transformación isométrica equivalente a esa rotación.
8. El Tetris es un videojuego en el cual se deben aplicar repetidas veces transformaciones
isométricas a figuras diferentes para hacerlas encajar. Considerando la jugada que
aparece en la imagen, ¿qué transformaciones isométricas debes realizar para hacer
encajar correctamente la figura 1 en A?, ¿y para encajar la figura 2 en B?
2
1
A
B
• Explica qué es una teselación y cómo se relaciona con las transformaciones isométricas.
• ¿Qué conocimientos previos te ayudaron a comprender las teselaciones?
• ¿Cómo puedes comprobar que una teselación es correcta?
Páginas100a103.
A
D
B
F
E
C E'
D' C'
B'
A'
F'
P
Y
O X
B
C
A
3
Unidad
163
287

Propósito
En esta clase los estudiantes
comprenderán las transformaciones
isométricas en el espacio.
OA 14
Inicio 15 minutos
Invite a sus estudiantes a observar la
fotografía y a comentar la relación que
existe entre los movimientos de una
bailarina y las trasformaciones isométricas.
Guíe a sus estudiantes para que
determinen los planos de simetría
de diferentes cuerpos geométricos.
Planificación
Recuerde a sus estudiantes la reflexión estudiada en clases anteriores
y haga la relación (en la simetría axial) del eje de simetría y el plano de
simetría en el caso de los sólidos.
Actitudes
OA B , OA D
págs. 164 a 167
Clase 89
• ¿Cómo se relacionan los movimientos del cuerpo
con las transformaciones isométricas?
• Si una persona realiza un giro, ¿lo está llevando
a cabo en el plano o en el espacio?
Un cuerpo geométrico puede tener uno o varios planos de simetría,
los cuales dividen al cuerpo en dos partes iguales.
Aprende
Ejemplo 1
Dibuja el o los planos de simetría de un cubo.
1 Dibujamos un cubo para poder identificar los planos de simetría
que tiene.
2 Un cuerpo puede tener planos de simetría horizontal, vertical o
diédricos, por lo que comenzaremos analizando si el cubo tiene
planos de simetría horizontales o verticales.
en el espacio
El ser humano siempre se ha comunicado
utilizando su cuerpo. En principio, la danza
tenía un componente ritual, celebrada en
ceremonias de fecundidad, caza, guerra,
religión, entre otras.
164 | Unidad 3
E
D
a
a
E
D
a
e
p
CL0000000001018 MA
288

Unidad
3
Formalice los conceptos de cuerpo
generado por rotación y cuerpo generado
por traslación apoyándose en la
información en Aprende.
Invite a sus estudiantes a conversar sobre
sólidos conocidos en la vida cotidiana
que podrían ser generados por rotación
o traslación.
Motive a sus estudiantes a mantener un ambiente de respeto frente a
las opiniones o respuestas de cada uno de los estudiantes del curso.
2/17/2019 9:30:40 AM
3 El cubo tiene dos planos de simetría verticales y uno horizontal. Luego, identificamos los planos
de simetría diédricos.
Concluimos que el cubo tiene 6 planos
de simetría diédricos, por lo que en total
el cubo tiene 9 planos de simetría.
• Un cuerpo es generado por rotación o es un sólido de revolución si
se puede obtener mediante la rotación de una curva o de una figura
plana en torno a un eje. Se llama generatriz a la figura plana que,
por su movimiento, forma un sólido geométrico.
• Un cuerpo es generado por traslación si se puede obtener
mediante el desplazamiento de una figura plana.
Aprende
Ejemplo 2
Dibuja el cuerpo que se genera
al rotar la siguiente figura
alrededor del eje indicado.
1 Copiamos la figura usando
el eje como eje de simetría.
2 Dibujamos el cuerpo
dándole el volumen
correspondiente.
Ejemplo 3
Dibuja el cuerpo que se genera
al trasladar la siguiente figura
en dirección perpendicular al
plano que contiene esta hoja.
1 Trasladamos el hexágono
en forma perpendicular
al plano para construir
el cuerpo geométrico.
2 Finalmente, dibujamos el
cuerpo geométrico, que
en este caso es un prisma
recto de base hexagonal.
3
Unidad
165
289

Comience la actividad promoviendo la
participación de todos los estudiantes
en un clima de respeto.
Destaque la importancia de compartir las
dificultades explicando que muchas veces
el error es una muy buena oportunidad
para aprender.
Aproveche esta lección y motive a sus estudiantes a investigar más
sobre estructuras de arte antiguas que representan sólidos que pueden
ser generados por rotación o traslación.
Además, invítelos a recopilar información acerca de obras de arte que
se encuentren en nuestro país, por ejemplo: las obras del Parque de las
Esculturas en Santiago.
http://www.plataformaurbana.cl/archive/2012/04/24/
guia-urbana-de-santiago-parque-de-las-esculturas/
Solucionario
1. Determina si los siguientes son planos de simetría de los cuerpos geométricos que
se muestran a continuación.
e.
c.
a.
b. f.
d.
2. Dibuja el eje de simetría de los siguientes cuerpos generados por rotación.
a. b. c. d.
3. Dibuja un plano de simetría en los siguientes cuerpos geométricos.
a. c. d.
b.
4. Dibuja el cuerpo que se genera al rotar las siguientes figuras alrededor del eje indicado.
b. c. d.
a.
Actividades
Lección 3
166 | Unidad 3
5
6
7
8
•
•
•
CL0000000001018 MA
290

Unidad
3
Guíe a sus estudiantes para determinar
los planos de simetría de diferentes objetos
o animales.
Cierre 15 minutos
Permita que sus estudiantes comparen
entre ellos sus respuestas. Oriente a aquellos
estudiantes que presentaron dificultades
o cometieron errores durante el desarrollo
de la actividad. Invite a sus estudiantes
a compartir sus reflexiones acerca de
las preguntas de Reflexiona y responde.
Desarrolle la habilidad de resolver problemas en sus estudiantes
compartiendo con ellos las siguientes estrategias:
• Utilizar sus propias palabras para describir el problema.
• Evaluar diferentes procedimientos de resolución.
• Comprobar que los resultados son coherentes con la situación
resuelta.
páginas 104 y 105.
Planificación
Clase 90
2/17/2019 9:30:40 AM
5. Dibuja el cuerpo que se genera al trasladar las siguientes figuras en dirección perpendicular
al plano que contiene esta hoja.
b. d.
a. c.
6. Identifica el (los) plano(s) de simetría que puedes observar en las siguientes imágenes
presentes en la naturaleza.
7. Realiza en tu cuaderno la reflexión del siguiente cuerpo cuyo
centro de simetría es el punto O. Compara lo obtenido con
tus compañeros y analicen sus diferencias.
8. Verifica si son verdaderas o falsas las siguientes afirmaciones. Justifica las falsas.
a. Un prisma es un sólido de revolución.
b. La esfera es el único cuerpo que posee más de un plano de simetría.
c. Por la altura de un cono pasa un plano de simetría.
d. Un cilindro solo tiene un plano de simetría.
e. Cualquier plano paralelo a la base de un cilindro es un plano de simetría.
f. Los conos tienen infinitos planos de simetría.
O
• ¿Qué entiendes por planos de simetría de un cuerpo geométrico? Explica con tus palabras.
• ¿Qué transformaciones isométricas en el espacio necesitas ejercitar más? ¿Por qué?
• ¿Qué ejemplos de transformaciones en el espacio reconoces en la vida cotidiana?
Páginas104y105.
3
Unidad
167
291

Propósito
la Lección 3.
Inicio 15 minutos
Comience la clase recordando los conceptos
clave estudiados en esta lección:
• Transformaciones isométricas
• Traslación
• Reflexión
• Rotación
• Composición de transformaciones
isométricas
• Sólidos generados por rotación
y traslación
la evaluación de forma individual
y registren sus respuestas en sus
respectivos cuadernos. Actitudes
Recuerde a sus estudiantes que al enfrentarse a un desafío, aun
cuando no obtengan el resultado de manera inmediata, deben
perseverar y confiar en sus propias capacidades.
Planificación
págs. 168 y 169
Clase 91
1. En tu cuaderno, aplica las transformaciones isométricas pedidas en cada caso.
a. Rotación del triángulo ABC respecto del
punto O(0, 0) en 90º en sentido horario.
Y
O X
1
–4
–5
2
–3
–2
–1
4 5 6
–1 3
–2 2
1
C
B
A
c. Reflexión del pentágono FGHIJ respecto
del eje X y trasladar su imagen según
el vector v = (0, –2).
Y
O X
1
–4
–5
2
–3
–2
–1
4 5 6
–1 3
–2 2
1
H
I
J
F
G
Y
O X
1
2
3
–2
4
5
6
–1
4 5 6
–1 3
–2 2
1
P
M
N
O
b. Traslación del rectángulo MNOP con
respecto al vector v = (2, –4).
d. Reflexión del cuerpo que se representa
a continuación respecto de la recta H.
H
2. Verifica si cada afirmación es verdadera o falsa.
a. Al rotar un cuerpo, este puede cambiar de forma.
b. Al aplicar una transformación isométrica a una figura geométrica, esta puede cambiar
de forma.
c. Para aplicar una reflexión a una figura es necesario conocer el vector en que se reflejará.
d. Para aplicar una rotación a una figura se necesita conocer el centro de rotación y el ángulo
de rotación.
3. A partir de las coordenadas de los vértices de las siguientes figuras y sus respectivas
imágenes, determina el ángulo de rotación que se les aplicó. Todas las rotaciones son
con respecto al origen y en sentido antihorario.
Figura Vértices Imágenes
Triángulo A(6, 1) B(5, –1) C(8, 1) A'(–6, –1) B'(–5, 1) C'(–8, –1)
Cuadrilátero A(1, 3) B(2, 4) C(4, 4) D(3, 3) A'(3, –1) B'(4, –2) C'(4, –4) D'(3, –3)
Cuadrilátero A(–4, –2) B(–3, –1) C(–2, –3) D(–5, –4) A'(2, –4) B'(1, –3) C'(3, –2) D'(4, –5)
| Unidad 3
168
4
5
•
•
•
CL0000000001018 MA
292

Unidad
3
Aproveche la situación planteada con el
mapa mundial para profundizar en la
aplicación de transformaciones isométricas.
Plantee nuevas situaciones respecto a
los barcos e invite a sus estudiantes a
formular preguntas a sus compañeros
para que determinen qué transformación
isométrica se utilizó.
Cierre 15 minutos
Analice las respuestas obtenidas por sus
estudiantes, determine el nivel de logro e
inste a reforzar a aquellos estudiantes que
presentaron mayores dificultades en el
desarrollo de la síntesis.
Al finalizar la evaluación, realice una discusión plenaria en la que
los estudiantes puedan comentar con sus compañeros sobre las
principales dificultades que tuvieron al trabajar en esta unidad.
Solucionario
2/17/2019 9:30:41 AM
4. En el plano cartesiano realiza las siguientes actividades.
a. Aplicar una reflexión al triángulo FGH con respecto al eje X.
Determina las coordenadas de los vértices de la figura imagen.
b. Aplicar una reflexión al pentágono ABCDE con respecto
al eje Y. Determina las coordenadas de los vértices de
la figura imagen.
c. Aplicar una simetría central a cada uno de los polígonos con
respecto al origen. Determina las coordenadas de los vértices
de cada figura imagen.
5. Observa el siguiente mapa y luego responde.
Quito
Brasilia
Lesotho
Antananarivo
Cairo
Londres
Meridiano
de
Greenwich
a. En relación con los barcos negros, ¿qué transformación isométrica se aplicó para
ir de un barco a otro?
b. En relación con los barcos rojos:
• ¿Cómo se llama la transformación isométrica que permite ir de uno a otro?
• ¿En qué ángulo se realizó dicha transformación?
c. En relación con las ciudades, determina aquellas que son el reflejo de otra
con respecto a la línea del ecuador y al meridiano de Greenwich.
• ¿Qué entiendes por una transformación isométrica?
• ¿Cuál transformación isométrica crees que es más compleja de aplicar? ¿Por qué?
• ¿En qué situaciones cotidianas puedes observar transformaciones isométricas? Comparte tus
ideas con tus compañeros.
Páginas106y107.
Y
O X
1
–4
–5
2
–3
3
–2
4
5
–1
4 5
–1 3
–2 2
–3 1
–4
–5
G
H
F
A
E
D
C
B
3
Unidad
169
Evaluación Lección 3 |
293

Propósito
la Unidad 3.
conocimientos adquiridos en la Unidad 3.
Inicio 15 minutos
Comience la clase promoviendo la
participación de todos los estudiantes
en un ambiente de respeto.
Destaque la importancia de compartir
las dificultades en el aprendizaje de la
unidad explicando que muchas veces el
error es una muy buena oportunidad
para el aprendizaje.
Motive a los estudiantes a desarrollar
las actividades propuestas como
evaluación final. Guíelos a considerar
los aprendizajes en las lecciones 1 y 2,
explique las instrucciones para desarrollar
cada actividad y apóyelos en caso de ser
necesario.
Planificación
En la página web: www.bdigital.unal.edu.co/7739/1/
sergioandresmontesalarcon.2012. pdf
encontrará el trabajo de Sergio Montes, en el que se muestran distintas
actividades, las que permiten aplicar los contenidos relacionados con
transformaciones isométricas valiéndose del juego Pac-Man, lo que es
un estímulo para los estudiantes.
págs. 170 y 171
Clase 92
1. Calcula el área total (AT ) y el volumen (V) de cada cuerpo. Considera π ≈ 3,14.
3,5 m
4,5 m
6,5 m
b. e.
16 cm
36 cm
4 cm
f.
a cm
a cm
a cm
cm
50
c.
9 cm
12 cm
a.
5 cm
9 cm
1 cm
d.
15 cm
6 cm
2. Calcula el valor de x en cada caso.
c. Sea ABCD un rectángulo.
0,5 m
1,2 m
D
A
C
B
x
b. Sea MNOP un cuadrado.
P
M
O
N
x
cm
162
a.
1,6 cm
x
1,2 cm
3. Resuelve los siguientes problemas. Considera π ≈ 3,14.
a. Un tubo que transporta agua tiene un diámetro interior de 25 cm. ¿Cuánta cantidad
de agua como máximo puede contener en 120 cm de extensión?
b. Se quiere cubrir con papel una caja con forma de prisma que mide 35 cm de largo, 18 cm
de ancho y 16 cm de alto. ¿Cuántos centímetros cuadrados de papel se necesitan como
mínimo si se cubren todas las caras de la caja?
c. La diagonal de la base rectangular de un prisma mide 25 cm y uno de sus lados mide 24 cm.
Si la altura del prisma es de 8 m, ¿cuál es su área? ¿Cuál es su volumen?
Evaluación final
| Unidad 3
170
4
5
6
•
•
CL0000000001018 MA
294

Unidad
3
Analice junto con sus estudiantes los
aprendizajes de la Lección 3 e invítelos a
realizar las actividades y a registrar sus
respuestas en sus cuadernos.
Cierre 15 minutos
Analice las respuestas obtenidas por sus
estudiantes, determine el nivel de logro
e inste a reforzar a aquellos estudiantes
que presentaron mayores dificultades
en el desarrollo de la síntesis.
Desarrolle la habilidad de resolver problemas en sus estudiantes
compartiendo con ellos las siguientes estrategias:
• Utilizar sus propias palabras para describir el problema.
• Evaluar diferentes procedimientos de resolución.
• Comprobar que los resultados sean coherentes con la situación
resuelta.
Solucionario
páginas 108 y 109.
Planificación
Clase 93
.
m
.
2/17/2019 9:30:42 AM
d. En un envase cilíndrico alcanzan 75π m3
de agua. Si el perímetro de su base es de 10π m,
¿cuál es su altura?
e. Se aplica una rotación en torno al origen en 270º en sentido antihorario sobre el punto
S(–5, 5), y sobre su imagen se aplica una reflexión respecto del eje Y. ¿Cuáles son las
coordenadas del punto resultante?
4. Al cuadrilátero ABCD aplícale una rotación en 270º en sentido antihorario con respecto
al origen; a su imagen, aplícale una reflexión con respecto al eje X, y al resultado de esta
reflexión aplícale una traslación con respecto al vector v = (1, –2).
Y
O X
1
2
3
–2
4
5
–1
4 5
–1 3
–2 2
–3 1
–4
–5
D
A
B
C
5. Observa la siguiente teselación y responde las preguntas.
a. ¿Qué figuras geométricas componen la teselación?
b. ¿Por qué es posible realizar la teselación con esas figuras?
c. Construye con regla y compás esta teselación en tu cuaderno.
• ¿Qué contenido necesitas ejercitar más? ¿Por qué?
• ¿Cómo solucionaste las dificultades que tuviste en el desarrollo de la unidad?
Páginas108y109.
3
Unidad
Evaluación final | 171
295

Propósito
En esta clase se realizará una síntesis con
los conocimientos más importantes de las
lecciones de la Unidad 3.
Sintetizar y repasar los conocimientos
adquiridos en la Unidad 3.
Inicio 15 minutos
Para comenzar, explique a sus estudiantes
que se realizará una síntesis de los
contenidos estudiados en esta unidad,
considerando los conceptos de:
• Área y volumen de prismas y cilindros
• Transformaciones isométricas
la información contenida en los
recuadros y motívelos a explicar cada
una de las propiedades utilizando sus
propias palabras.
Invite a sus estudiantes a compartir con sus compañeros sus
aprensiones y dificultades respecto de los contenidos de geometría
estudiados en esta unidad.
Planificación
págs. 172 y 173
Clase 94
Lección 1
Lección 2
1. Calcula el área basal (AB ), área lateral (AL )
y el área total (AT ) de los siguientes
prismas rectos en los cuales su base
es un polígono regular.
a = 6,2 cm
8 cm
3 cm a
b.
4,5 cm
3 cm
a.
Base cuadrada.
2. Calcula el área basal (AB ), área lateral (AL )
y el área total (AT ) de los siguientes cilindros.
b.
4 cm
10 cm
a.
19 cm
12 cm
3. Calcula el volumen (V) de los siguientes
cuerpos geométricos. Considera π ≈ 3,14.
b.
10 cm
3 cm
a.
5 cm
2 cm 1,5 cm
• Si la medida de tres segmentos cumple la relación del teorema de Pitágoras,
entonces estos tres segmentos forman un triángulo rectángulo.
• Área total (AT ) de un prisma: se
suman el área lateral (AL ) con el área
de las caras basales (AB ).
AT = AL + 2AB
• Área total (AT ) de un cilindro: se
suman el área lateral (AL ) con el área
de las caras basales (AB ).
AT = AL + 2AB
= 2πrh + 2πr2
= 2πr(h + r)
• Volumen (V) de un prisma: se calcula
el producto del área basal (AB ) por
la medida de su altura (h).
V = AB • h
• Volumen (V) de un cilindro: se calcula
el producto del área basal (AB ) por
la medida de su altura (h).
V = AB • h = πr2
• h
h: altura del cilindro r: radio de la base
• En un triángulo rectángulo, el teorema de Pitágoras
establece que la suma de los cuadrados de los
catetos es igual al cuadrado de la medida de
hipotenusa.
Es decir: a2
+ b2
= c2
c
b
a
hipotenusa
cateto
cateto
Síntesisy Repaso
| Unidad 3
172
1
1
2
CL0000000001018 MA
296

Unidad
3
Guíe a sus estudiantes en el trabajo con
transformaciones isométricas en el plano
cartesiano, cuidando la notación de los
puntos de cada figura, respetando el
orden del par ordenado.
Invítelos a generalizar en la notación de
los puntos cuando se aplica una traslación,
una rotación o una reflexión.
Cierre 15 minutos
Desarrolle la metacognición en sus
estudiantes. Para ello, pregúnteles:
• ¿Qué fue lo más difícil de aprender
en esta unidad?
• ¿Cómo puedo relacionar estos
conocimientos con las unidades
anteriores?
Invite a sus estudiantes a visitar los recursos que ofrece la página web
del software GeoGebra https://www.geogebra.org/t/transformations en el
que podrán ver de forma dinámica la aplicación de las transformaciones
isométricas.
Solucionario
.
m
2/17/2019 9:30:43 AM
Lección 3
1. Calcula la medida que falta en cada
triangulo rectángulo.
a.
a
15 m
8 m
b.
20 dm
a
24 dm
2. Determina cuáles de las siguientes
medidas corresponden a las de un
triángulo rectángulo.
a. 12 cm, 16 cm y 20 cm
b. 13 m, 12 m y 10 m
3. La cara frontal de una carpa es un
triángulo isósceles cuya base mide
1,6 metros y cada uno de los lados
iguales mide 170 centímetros. Calcula
la altura en centímetros de esa carpa.
1. Dado un triángulo de vértices A = (–5, –3);
B = (2, –1) y C = (1, 4). ¿Cuáles son las
coordenadas del vértice si el triángulo
ABC se traslada 2 unidades a la derecha
y 3 unidades hacia arriba?
2. Dibuja en un plano cartesiano el triángulo
de vértices A(1, 1), B(3, 1) y C(1, 4) y
aplícale sucesivamente las siguientes
transformaciones:
• Una reflexión respecto del eje X.
• Una rotación en 90° en sentido horario
respecto del origen.
• Una traslación de acuerdo con el vector
de traslación v = (–2, 3).
3. Si al punto (–6, –1) se le aplica una traslación
T(4, 3) y luego una rotación en 180° con
respecto al origen, entonces, ¿cuáles son
las coordenadas del nuevo punto?
4. De las siguientes figuras geométricas,
¿cuál(es) de ellas puede(n) teselar
(embaldosar) una superficie plana?
Justifica tu respuesta.
• Hexágono regular
• Pentágono Regular
• Triángulo equilátero
Una transformación isométrica es un cambio en la posición de una figura en el plano
o en el espacio, sin variar su forma ni su tamaño.
• Traslación: todos los
puntos de una figura
se desplazan en una
misma magnitud,
dirección y sentido.
Se puede representar
por un vector.
• Rotación: todos los
puntos de una figura
se mueven respecto de
un punto fijo o centro
en un cierto ángulo
de rotación.
• Reflexión: a cada
punto se le asocia un
punto que está a la
misma distancia de
una recta llamada eje
de reflexión.
3
Unidad
173
Síntesis y Repaso |
297

1. a. Su área mide 44 cm2
b. El perímetro es 31,4 cm
c. Su área mide 379,94 cm2
2. 15,6 cm2
3. Prisma de base triangular: 5 caras
Prisma de base pentagonal: 7 caras
Página 118
Lección 1
• Actividad a cargo del estudiante.
Página 123
Actividades
c.
1. a.
b. d.
2. a. Ab = 9 cm2
; AL = 54 cm2
; AT = 72 cm2
b. Ab = 165,6 cm2
; AL = 480 cm2
; AT = 811,2 cm2
c. Ab = 55,2 cm2
; AL = 264 cm2
; AT = 319,2 cm2
d. Ab = 706,5 cm2
; AL = 715,92 cm2
; AT = 2128,92 cm2
e. Ab = 19,625 cm2
; AL = 133,45 cm2
; AT = 172,7 cm2
f. Ab = 170 cm2
; AL = 1.400 cm2
; AT = 1740 cm2
3. a. b.
Página 124
Actividades
4. a. AT = 942 cm2 c. AT = 615,44 cm2
b. AT = 165,792 cm2 d. AT = 301,44 cm2
5. a. Se usaron 5,76 m2
de tela.
b. Dividir la figura en dos paralelepípedos genera una
mayor área, ya que se originan más caras de dimensiones
comparables a las de la primera división.
c. 9 cm de lato y 3,5 cm de ancho.
d. Su área es de 3,221012 m2
.
e. Se necesitan 533,8 cm2
de material.
f. Se necesitan 79,128 m2
de papel.
g. Se necesitan 4 082 mm2
de papel.
h. Su área total disminuye a un cuarto de la original.
6. a. 101 307 cm2
b. 13 000 cm2
c. 76 000 cm2
Página 125
7. a. El área total del soporte con las piezas es de 490 cm2
.
b. El área total de las piezas es de 240,98 cm2
.
8. a. El área lateral es de: 376,8 m2
.
b. Se dispone de 45,216 m2
.
9. Ambos rollos tienen igual área lateral, ya que se usa la misma
cantidad de material.
10. No es correcto lo que afirma Josefina, ya que el perímetro
del circulo es de 25,12, luego, el largo del rectángulo tiene la
misma medida.
Al duplicar la altura y mantener el diámetro, se duplica el área
lateral. Lo mismo ocurre al duplicar el diámetro y mantener
la altura.
Página 126
Volumen de prismas y cilindros
• Respuesta a cargo del estudiante.
• Un prisma es un poliedro cuyas caras laterales son
paralelogramos y sus caras basales son paralelas y
corresponden a polígonos congruentes.
Página 131
Actividades
1. a. 502,4 cm3
b. 265,33 cm3
c. 56 cm3
d. 127,16 cm3
e. 456 cm3
298 Solucionario Texto del Estudiante • Unidad 3
Solucionario Texto del Estudiante
CL0000000001141 MATE_8B_GDD_U3_MF_5834.indd 298 1/8/2020 12:10:32 PM

Unidad
3
f. 1 208,9 cm3
g. 748,8 cm3
h. 828 cm3
2. a. AB = 10,75 cm2
V = 129 cm3
b. AB = 261cm2
V = 3 915 cm3
3. B, C y A
Página 132
4. Se debe vaciar 4 veces el contenido de A para llenar B.
5. a. Perímetro base: 34,54 cm
Ab = 94,985 cm2
V = 1.139,82 cm3
b. Perímetro base: 62,8 cm
Radio: 10 cm
Ab = 314 cm2
c. Radio: 2 cm
Ab = 12,56 cm2
V = 138,16 cm3
6. a. 1 130,4 cm3
b. 28,26 cm3
c. 3,925 cm3
d. 1 077,02 cm3
7. a. Contiene 929,25 cm3
.
b. Se necesitan 3 cubos para el ancho.
c. Se pueden guardar 6 000 cajas.
d. La tora tiene un volumen de 10 676 cm3
.
e. La altura de la taza es de 9 cm.
Página 133
f. El envase de mayor diámetro contiene más mermelada.
Su capacidad es de 759,88 cm3
, mientras que la del otro
envase es de 552,64 cm3
.
g. Masa del cilindro de cobre: 2 515,14 g
Masa del cilindro de plata: 1 576,53 g
h. La afirmación es correcta, ya que tienen la misma
profundidad, y el área del triángulo en la base es la mitad
del área del rectángulo en la base. Sus volúmenes son 48
cm3
y 24 cm2
, respectivamente.
8. a. F. Su volumen aumenta 6 veces.
b. V. Ya que la fórmula es V = Ah, con lo que A(3h) = 3V
c. F. Su volumen disminuye 6 veces.
d. F. Su volumen aumenta 6 veces.
e. F. Su volumen aumenta al doble.
f. F. Su volumen aumenta 9 veces.
g. F. Disminuye a una sexta parte.
h. F. Su volumen aumenta 6 veces.
Página 134
1. a. AT = 172,7 cm2
; V = 166,813 cm3
b. AT = 864 cm2
; V = 1.728 cm3
c. AT = 33 cm2
; V = 7,5 cm3
2. a. 300 cm3
b. 450 cm3
c. 350.730 cm3
d. 1 152 cm3
3. a. Radio es de 30 m
b. Radio es de 800 m
c. Radio es de 10 2 m
Página 135
4. La altura debe disminuir a la mitad para conservar
la capacidad siendo esta de 9 cm.
5. La altura debe disminuir a un cuarto de la original para
conservar la capacidad, siendo esta de 1 m.
6. a. Cubre una superficie de 196,25 cm2
.
b. Para cubrir 1 m2
necesita 51 rollos, sobrándole 8,75 cm2
.
7. a. El tubo A contiene 20,096 cm3
.
b. El tubo B puede contener, como máximo, 36,1728 cm3
.
c. Ambos tubos pueden contener la misma cantidad de
líquido, ya que poseen el mismo volumen.
Página 136
Lección 2
• Se relacionan mediante 32
+ 42
= 52
.
Página 138
Actividades
1. a. x = 10 cm
b. x = 13 cm
c. x = 17 cm
d. x = 5,2 cm
2. a. P = 36 cm; A = 54 cm2
b. P = 60 cm; A = 120 cm2
c. P = 7,2 cm; A = 2,16 cm2
d. P = 6 cm; A = 1,5 cm2
3. a. x = 5 cm; y = 13 cm
b. x = 15 cm; y = 10 cm; z = 2 41
c. x = 4 34 cm; y = 21 cm
4. a. Es trío pitagórico.
b. No es trío pitagórico.
c. Es trío pitagórico.
d. Es trío pitagórico.
299
Solucionario Texto del Estudiante • Unidad 3

5. a. Triángulo rectángulo, ya que sus lados siguen el teorema
de Pitágoras.
b. Triángulo rectángulo, ya que sus lados siguen el teorema
de Pitágoras.
c. No es triángulo rectángulo, ya que sus lados no siguen el
teorema de Pitágoras.
d. No es triángulo rectángulo, ya que sus lados no siguen el
teorema de Pitágoras.
6. a. P = 31 cm; A = 120 cm2
b. P = 18 cm; A = 15 cm2
c. P = 96 cm; A = 384 cm2
7. a. La relación anterior no se cumple, ya que el área del
triángulo sobre la hipotenusa es 11,25 cm2
, mientras que la
suma de los otros dos es 15,75 cm.
b. Francisco recorrió más camino que Diego. Este recorre
solamente 1 120 m, mientras que Francisco recorre
100 106 + 1 400 m.
Página 140
Aplicaciones del teorema de Pitágoras
• 25 m
Página 142
Actividades
1. a. 9 3 cm2
b. 5 000 cm2
c. 9 6
2
cm2
d. 6 3 cm2
2. a. 15 cm2
b. 40 cm
c. 32 cm2
d. 168 3 cm
e. 4 3 dm
3. a. 5 3 cm
b. 2 634
5
cm
c. 25 cm
4. a. 13
b. 2 13
c. 13
d. 41
e. 4 2
f. 5
Página 143
Actividades
5. a. La parte más alta de la escalera se encuentra
a 2 2 m del suelo.
b. La longitud de la rampa es de 61 m.
c. Julieta se encuentra a 60 m del punto.
d. El perímetro es de 60 cm, mientras que su área es
de 240 30 cm2
.
e. Sí, debido a que la diagonal de la puerta es de,
aproximadamente, 221,54 cm. Mayor al lado de 210 del
cuadrado.
f. Es posible, ya que se forma el trío pitagórico
con 3 + 4 + 5 = 12.
6. a. Sí, ya que siguen el teorema de Pitágoras.
b. Mide 28,8 cm.
Página 145
1. La suma de las áreas de los cuadrados sobre los catetos es
igual al área del cuadrado construido sobre la hipotenusa.
2. Se cumple solamente para triángulos rectángulos, ya que se
deriva del teorema de Pitágoras.
3. Sean a y b las medidas de los catetos y c la medida
de la hipotenusa, se tiene que la relación de las áreas es
a2
+ b2
= c2
, lo que es justamente el teorema de Pitágoras,
razón por la que se cumple la relación anterior.
Página 146
1. a. 12 cm
b. 15 cm
c. 6 cm
2. a.
b.
c.
d.
e.
f.
3. a. 29 cm
b. 58 cm
c. 14,5 cm
4. a. 13 cm
b. 9,7 cm
Página 147
5. a. AT = 1 539 cm2
; V = 4 590 cm3
b. AT = 8 540,8 cm2
; V = 60 288 cm3
c. AT = 306 3 + 675 cm2
; V = 2 025 3
2
cm3

Unidad
3
6. a. La altura que alcanza la escalera es de 2 15 m
b. •
Al parecer no se cumple con Pitágoras, pero se llega a un
valor muy cercano (diagonal de 26,07 pulgadas). Esto se
debe a que se aproximan los resultados.
• Su alto mide aproximadamente 12,65 pulgadas.
• Su largo mide aproximadamente 33,4 pulgadas.
• El televisor 4 es de 50 pulgadas.
Página 148
Lección 3
Traslación
• Se aplican sucesivas traslaciones.
Página 150
Actividades
1. a. (5, 6)
b. (1, 6)
c. (–6, –8)
d. (2, 3)
e. (5, 0)
f. (2, –4)
2. a. b.
3. a. v = (1, 1)
b. w = (–1, –1)
c. Sus respectivas coordenadas son inversos aditivos.
d. M' (3, –2); J' (2, –3); K' (3, –4); L' (4, –3)
4. a. v = (4, 4)
b. A'' (13, –8)
Página 152
Rotación
• Se debe aplicar una rotación. Se rotó en 180° en torno a un
punto central entre los cuadros.
Página 154
Actividades
1. a. A' (–5, 2)
b. B' (6, –7)
c. C' (5, –2)
2. a. D(6, –9) b. E(–5, –3) c. F(–4, 1)
3. a.
b.
c.
4. a. 90° Sentido horario
b. 180°
c. 90° Sentido antihorario
Página 155
1. a. La medida de los ángulos se mantiene en la figura inicial y
en la imagen al rotar.
b. La medida de los lados se mantiene en la figura inicial
y en la imagen al rotar. Esto es común con todas las
transformaciones isométricas.
Página 156
Reflexión
• En la primera figura hay más simetrías.
Página 158
Actividades
1. Una línea de simetría divide a una figura en dos partes simétricas. Encuentra la o las líneas
2. Realiza las siguientes actividades.
a. Refleja el pentágono
ABCDE respecto al
eje X.
b. Refleja el triángulo ABC
respecto al eje Y.
c. Determina el eje de
reflexión respecto
al cual se reflejó
el triángulo ABC
para obtener su
imagen A'B'C'.
Y
2
3
4
5
Y
2
3
4
5
C
B
Y
2
3
4
5
A'
B'
Actividades
Lección 3
b. c. d.
1. a.
301

2. a.
b.
c.
3. a. (4, 1)
b. (–2, 2)
c. M' (–4, 2); M (–4, –2)
d. M'' (4, –2)
e. N' (6, –5)
Página 159
1. a. Los lados de la figura original, como de su imagen, tienen
la misma medida.
b. Ejemplo 1: Perímetro: 16 cm; Área: 16 cm2
para ambas
figuras.
Ejemplo 2: Perímetro: 24 cm; Área: 36 cm2
para ambas
figuras.
c. Ocurre lo mismo. Se conservan las medidas, ya que se
trata de una transformación isométrica.
d. Actividad a cargo del estudiante.
Página 160
Composición de transformaciones isométricas
• Se aplica una rotación a la figura 1 para obtener la figura 2. Se
aplica una traslación a la figura 1 para obtener la figura 3.
Página 162
Actividades
1. Se realizó una rotación en 180° para llegar a B, luego, se
realizó una reflexión para llegar a C.
2. Se puede realizar mediante una serie de reflexiones. Primero
una en torno a su lado AC. Luego, a esta imagen generada
se le realiza otra reflexión en torno a su lado B'C'. Se repite
el proceso hasta completar la figura (Nota: también se
puede generar mediante rotaciones con sus respectivas
traslaciones).
3. Se puede formar la figura mediante una serie de reflexiones
del triángulo ABC en torno a la recta dibujada. También se
puede lograr lo mismo mediante rotaciones en torno a un
punto central de la recta.
4. a. Sí se puede teselar un plano con la figura.
b. Sí se puede teselar un plano con la figura.
c. No es posible teselar un plano con la figura.
d. Sí se puede teselar un plano con la figura.
Página 163
5. Respuesta variada; a continuación, dos ejemplos.
6.
Si se invierte el orden de las transformaciones, no se obtiene
la figura en la misma posición, luego, no son operaciones
conmutativas.

Unidad
3
7. Se puede llegar al mismo resultado mediante una reflexión
por una recta diagonal qur forme un ángulo de 45° con el
eje X, seguida de una reflexión en torno a su lado B'C', y
finalmente una traslación para acomodar la figura generada
en la posición en que se pide.
8. Hay más respuestas posibles, pero la más simple es:
Para encajar 1 en A se puede realizar una rotación en 90°
sentido antihorario, seguido de una traslación.
Para encajar 2 en B se puede realizar una rotación en 90°
sentido horario, seguida de una traslación.
Página 164
Transformaciones isométricas en el espacio
• Se relacionan en que partes de él se mueven, o rotan, sin
cambiar sus dimensiones.
• Si una persona realiza un giro, este sucede fuera del plano, en
el espacio.
Página 166
Actividades
1. a. No es plano de simetría.
b. Es plano de simetría.
c. Es plano de simetría.
d. Es plano de simetría.
e. Es plano de simetría.
f. No es plano de simetría.
e.
c.
a.
b. f.
d.
Actividades
Lección 3
166 | Unidad 3
b. c. d.
2. a.
Nota: la esfera tiene infinitos ejes de rotación, se marcaron 2.
e.
c.
a.
b. f.
d.
Actividades
Lección 3
166 | Unidad 3
b. c. d.
3. a.
e.
c.
a.
b. f.
d.
Actividades
Lección 3
166 | Unidad 3
b. c. d.
4. a.
Página 167
5. a.
c.
b.
d.
5. Dibuja el cuerpo que se genera al trasladar las siguientes figuras en dirección perpendicular
al plano que contiene esta hoja.
b. d.
a. c.
6. Dibuja el (los) plano(s) de simetría que puedes observar en las siguientes imágenes
presentes en la naturaleza.
7. Realiza la reflexión del siguiente cuerpo cuyo centro de simetría
es el punto O. Compara lo obtenido con tus compañeros
y analicen sus diferencias.
8. Determina si son verdaderas (V) o falsas (F) las siguientes afirmaciones. Justifica las falsas.
a. Un prisma es un sólido de revolución.
b. La esfera es el único cuerpo que posee más de un plano de simetría.
c. Por la altura de un cono pasa un plano de simetría.
d. Un cilindro solo tiene un plano de simetría.
e. Cualquier plano paralelo a la base de un cilindro es plano de simetría.
f. Los conos tienen infinitos planos de simetría.
O
• ¿Qué entiendes por planos de simetría de un cuerpo geométrico?
• ¿En qué te gustaría profundizar en tus conocimientos?
Cuadernodeactividades
Páginas28y29.
3
Unidad
167
6.
7.
O
8. a. F. Es un sólido de traslación.
b. F. Hay otros cuerpos con más planos de simetría, por
ejemplo, el cubo tiene 9.
c. V.
d. F. Tiene infinitos planos de simetría.
e. F. El único plano de simetría de un cilindro paralelo a la
base es el que pasa por la mitad de su altura.
f. V.
303

1. a.
b.
c.
d.
2. a. F.
b. F.
c. F.
d. V.
3. • 180°
• 270
• 90°
Página 169
4. a. F' (–3,–3); H' (–5, –2); G' (–4,–4)
b. A' (–3,3); B (0,1); C (–2,1); D (–3,–1); E (–4,1)
c. A' (–3,–3); B' (0,–1); C' (–2,–1); D' (–3,1); E' (–4,–1); F' (3,–3);
G' (4,–4); H' (5,–2)
5. a. Se aplicó una traslación.
b. • Se aplicó una rotación.
• En 90°.
c. El Cairo es reflejo de Lesotho respecto a la línea del
ecuador, y Brasilia es reflejo de Antananarivo respecto al
meridiano de Greenwich.
Página 170
Evaluación final
1. a. AT = 118 cm2
; V = 45 cm3
b. AT = 135,5 cm2
; V = 102,375 cm3
c. AT = 1 582,56 cm2
; V = 4 069,44 cm3
d. AT = 791,28 cm2
; V = 1 695,6 cm3
e. AT = 1 569 cm2
; V = 2 304 cm3
f. AT = 5 000 cm2
; V = 125 000 3
9
cm3
2. a. 2 cm
b. 9 cm
c. 0,65 cm

Unidad
3
3. a. La cantidad máxima que puede contener es de 58.875
cm3
.
b. Se necesitan 2 956 cm2
de papel.
c. Su área total es de 832 cm2
, y su volumen es de 1 344 cm3
.
Página 171
d. La altura del cilindro es de 3 m.
e. Las coordenadas del punto resultante son: A'' (–5, 5).
4.
5. a. La teselación está compuesta por cuadrados, triángulos
equiláteros y hexágonos regulares.
b. Es posible realizar la teselación, ya que se tiene que la
suma de los ángulos internos de todas las figuras que
comparten un vértice suman 360°.
c. Pregunta variada. A continuación, se muestran 2 ejemplos:
6. Nota: Hay más planos de simetría posibles.
d. En un envase cilíndrico alcanzan 75π m3
de agua. Si el perímetro de su base es de 10π m,
¿cuál es su altura?
e. Se aplica una rotación en 270º en sentido antihorario sobre el punto S(–5, 5), y sobre
su imagen se aplica una reflexión respecto del eje Y. ¿Cuáles son las coordenadas del
punto resultante?
4. Al cuadrilátero ABCD aplícale una rotación en 270º en sentido antihorario con respecto
al origen; a su imagen, aplícale una reflexión con respecto al eje X, y al resultado de esta
reflexión aplícale una traslación con respecto al vector v = (1, –2).
Y
O X
1
2
3
–2
4
5
–1
4 5
–1 3
–2 2
–3 1
–4
–5
D
A
B
C
5. Observa la siguiente teselación y responde las preguntas.
a. ¿Qué figuras geométricas componen la teselación?
b. ¿Por qué es posible realizar la teselación con esas figuras?
c. Construye con regla y compás esta teselación en tu cuaderno.
• ¿Crees que debes repasar algún contenido?, ¿por qué?
• ¿Pudiste solucionar las dificultades que hayas tenido en el desarrollo de la unidad?
3
Unidad
Evaluación Final | 171
Página 172
Síntesis y Repaso
Lección 1
1. a. AB = 9 cm2
; AL = 54 cm2
; AT = 72 cm2
b. AB = 55,8 cm2
; AL = 144 cm2
; AT = 255,6 cm2
2. a. AB = 113,04 cm2
; AL = 339,12 cm2
; AT = 565,2 cm2
b. AB = 50,24 cm2
; AL = 252,2 cm2
; AT = 351,68 cm2
3. a. 7,5 cm3
b. 282,6 cm3
Página 173
Lección 2 Teorema de Pitágoras
1. a. a = 17 cm
b. a = 4 61 dm
2. a. Corresponde a triángulo rectángulo.
b. No corresponde a triángulo rectángulo.
3. La altura de la capa es de 150 cm.
1. A' (–3, 0), B' (4, 2), C' (3, 7)
2.
3. A'' (2, –2)
4. a. Sí se puede teselar, ya que sus ángulos internos son de
120°, con lo que se puede dividir el ángulo de 360° sin
dejar espacios.
b. No se puede teselar, ya que sus ángulos internos son de
108°, con lo que no se puede dividir el ángulo de 360° sin
dejar espacios.
c. Sí se puede teselar, ya que sus ángulos internos son de
60°, con lo que se puede dividir el ángulo de 360° sin dejar
espacios.
305

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
118
a
125
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
11
de
las
Bases
Curriculares.
Área
de
prismas
y
cilindros
1.
Calcula
el
área
total
(A
T
)
de
los
siguientes
prismas
rectos
cuya
base
es
un
polígono
regular.
a.
A
T
=
7
cm
13
cm
A
T
=
e.
6
cm
8
cm
5
cm
c.
A
T
=
6
cm
10
cm
5
cm
d.
A
T
=
4
cm
4
cm
10
cm
b.
A
T
=
5
cm
8
cm
4,3
cm
f.
A
T
=
9
cm
4
cm
4
cm
3,5
cm
4
cm
2.
Se
quiere
cubrir
con
cerámicas
rectangulares
de
100
cm
2
de
superficie
toda
el
área
lateral
de
un
pedestal.
El
pedestal,
de
forma
de
prisma
pentagonal
regular,
tiene
15
dm
de
altura
y
en
la
base
8
dm
de
lado.
¿Cuántas
cerámicas
se
necesitarán
para
cubrir
el
área
lateral
del pedestal?
Unidad
3
•
La
geometría
del
arte
Área
y
volumen
de
prismas
y
cilindros
Lección
1
76
|
Unidad
3
76
CL0000000001052
MATE_8B_CUAD_U3_5668.indd
76
12/17/2019
9:48:09
AM
3.
Resuelve
los
siguientes
problemas.
Comprueba
tus
resultados
con
una
calculadora.
a.
Florencia
va
a
pintar
varios
cubos
de
6
cm
de
arista
para
formar
una
torre.
Si
el
rendimiento
de
una
lata
de
pintura
es
de
2 m
2
,
¿cuántos
cubos
alcanza
a
pintar
con
una
sola
lata
de
pintura?
b.
Con
el
mínimo
de
papel
que
se
necesita
para
envolver
una
caja
de
10
cm
por
8
cm
por
4 cm,
¿se
puede
envolver
un
cubo
de
arista
9 cm?
Calcula
cuánto
falta
o
cuánto
sobra.
c.
Las
dimensiones
de
un
pliego
de
papel
son
1
m
y
60
cm.
Si
los
pliegos
se
venden
completos
y
cada
uno
cuesta
$600,
¿cuánto
se
gasta
en
envolver
12
cubos
de
20
cm
de
arista?
d.
Valentina
quiere
construir
con
alambres
un
prisma
de
base
cuadrada
y
luego
forrarlo
con
tela.
Si
la
base
tiene
120
cm
de
lado
y
la
altura
es
de
80
cm,
¿cuánto
alambre
necesita?,
¿y cuánta
tela?
e.
¿Qué
cantidad
de
madera
aglomerada
se
utilizará
para
hacer
una
bodega
con
forma
de
paralelepípedo
recto
de
dimensiones
1,4
m
de
largo,
1,2
m
de
ancho
y
2
m
de
alto?
3
Unidad
77
Lección
1
•
Área
y
volumen
de
prismas
y
cilindros
|
CL0000000001052
77
12/17/2019
9:48:09
AM
Área
y
volumen
de
prismas
y
cilindros
Lección
1
3
Unidad
306
Cuaderno
de
Actividades
•
Unidad
3
462
cm
2
141,5
cm
2
540
cm
2
192
cm
2
468
cm
2
122
cm
2
92
cubos.
No
se
puede,
faltan
182
cm
2
.
13,76
m
2
1 280
cm
de
alambre,
67 200
cm
2
de
tela.
600
cerámicas
$3
000
Orientaciones y solucionario Cuaderno de Actividades

Unidad
3
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
118
a
125
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
11
de
las
Bases
Curriculares.
4.
Calcula
el
área
pedida
en
cada
caso.
Área
basal:
Área
lateral:
Área
total:
a.
11
cm
4
cm
Área
basal:
Área
lateral:
Área
total:
c.
5
cm
30
mm
Área
basal:
Área
lateral:
Área
total:
b.
34
cm
26
mm
5.
Resuelve
los
siguientes
problemas.
Considera
π
≈
3,14.
a.
Se
necesita
poner
etiquetas
en
la
cara
curva
de
tarros
de
conserva
de
8
cm
de
diámetro
y
15
cm
de
altura.
Si
se
debe
disponer
de
2
cm
de
largo
extra
para
poder
pegar
cada
etiqueta,
¿cuántos
cm
2
de
papel
se
necesitan
para
cada
etiqueta?
b.
¿Cuántos
litros
de
pintura
se
necesitan
para
pintar
por
fuera
la
cara
curva
de
un
estanque
cilíndrico
de
10
m
de
diámetro
y
15
m
de
altura
si
cada
litro
de
pintura
cubre
4,5
m
2
?
c.
Se
construirá
un
tanque
de
combustible
de
360
m
3
de
volumen.
Puede
construirse
en forma de
prisma
de
base
cuadrada
si
mide
36
m
2
de
base
y
altura
10
m,
o
en
forma
cilíndrica
de
3,3 m
de
radio
y
10 m
de
altura.
Si
el
costo
de
la
construcción
depende
del área total
del
tanque,
¿cuál
de
las
dos
formas
del
tanque
es
la
más
conveniente?
Área
y
volumen
de
prismas
y
cilindros
Lección
1
78
|
Unidad
3
CL0000000001052
78
12/17/2019
9:48:09
AM
d.
Con
una
hoja
de
papel
de
21
cm
de
ancho
y
27
cm
de
largo
se
pueden
construir
dos cilindros
distintos,
uniendo
sus
lados
opuestos.
¿Cuáles
son
sus
radios?
6.
Si
las
figuras
representan
las
bases
y
el
manto
de
un
cilindro,
¿cuánto
mide
el
largo
del rectángulo?
8
cm
8
cm
20
cm
Marca
la
opción
correcta.
Justifica
en
cada
caso.
7.
¿Cuál
es
el
área
lateral
de
un
cilindro
recto
cuya
base
tiene
3,5
m
de
radio
y
su
altura
mide 12 m?
A.
340,69
m
2
B.
76,93
m
2
C.
461,58
m
2
D.
263,76
m
2
8.
¿Cuál
es
el
área
total
de
este
cilindro?
Considera
π
≈
3,14.
A.
4
710
cm
2
B.
6
660
cm
2
C.
13
140
cm
2
D.
52
020
cm
2
9.
¿Cuánto
mide
la
altura
de
un
cilindro
si
su
área
total
es
90π
cm
2
y
su
radio
basal
es
5
cm?
A.
3
cm
B.
4
cm
C.
9
cm
D.
12
cm
10.
¿Cuál
es
el
área
total
de
un
cilindro
recto
de
altura
10 cm
y
radio
7
cm?
Considera
π
≈
3,14.
A.
439,6
cm
2
B.
307,72
cm
2
C.
747,32
cm
2
D.
1
067,6
cm
2
11.
Un
maestro
pinta
la
superficie
lateral
de
un
estanque
cilíndrico
de
20
m
de
diámetro
y
15
m
de
altura,
y
cobra
$750
el
metro
cuadrado.
¿Cuánto
se
le
debe
cancelar
por
el
trabajo
hecho?
Considera
π
≈
3,14.
A.
$706
500
B.
$1
125
000
C.
$
1
350
000
D.
$
3
375
000
12
cm
119
cm
3
Unidad
79
Lección
1
•
Área
y
volumen
de
prismas
y
cilindros
|
CL0000000001052
79
12/17/2019
9:48:09
AM
Cuaderno
de
Actividades
•
Unidad
3
307
6
406,2
cm
2
3,5
cm
y
9
cm,
aproximadamente.
104,7L
aproximadamente.
El
con
forma
de
prisma.
16
π
169
π
225
π
88
π
884
π
150
π
120
π
1222
π
600
π
16π
cm.

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
126
a
133
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
11
de
las
Bases
Curriculares.
Volumen
de
prismas
y
cilindros
1.
Calcula
el
volumen
(V
)
de
los
siguientes
prismas.
80
cm
30
cm
35
cm
a.
V
=
7
cm
25
cm
2
b.
V
=
2.
Resuelve
los
siguientes
problemas.
Comprueba
tus
resultados
con
una
calculadora.
a.
El
volumen
de
un
prisma
de
base
rectangular
es
24
m
3
.
Si
el
largo
de
la
base
es
4
m
y
su ancho
es
3
m,
¿cuál
es
la
altura
del
prisma?
b.
¿Cuántos
cubitos
de
2,5
cm
de
arista
caben
en
un
prisma
de
base
cuadrada
si
la
arista
de
la base
mide
5 cm
y
la
altura
mide
10
cm?
c.
La
altura
de
un
prisma
mide
10
cm
y
su
base
es
un
triángulo
rectángulo
cuyos
catetos
miden
5
cm
y
8
cm.
¿Cuál
es
su
volumen?
d.
Si
el
prisma
de
base
triangular
A
tiene
la
misma
base
que
el
prisma
B,
pero
tiene
el
triple
de
su
altura,
¿qué
puedes
decir
del
volumen
del
prisma
A
respecto
del
volumen
del
prisma
B?
Área
y
volumen
de
prismas
y
cilindros
Lección
1
80
|
Unidad
3
CL0000000001052
80
12/17/2019
9:48:09
AM
3.
Una
empresa
que
vende
jugo
de
fruta
en
envases
con
forma
de
paralelepípedo
recto,
de
medidas
11
cm,
6
cm
y
15
cm,
decide
cambiar
dichos
envases
por
otros
en
los
que
disminuye
un
10%
el
área
de
la
base
y
aumenta
un
10%
la
altura.
a.
El
volumen
del
nuevo
envase,
¿es
mayor
o
menor
que
el
del
antiguo?
b.
Si
mantienen
el
mismo
precio,
¿es
positivo
para
los
consumidores?
4.
Una
tina
con
forma
de
prisma
tiene
150
cm
de
largo,
60
cm
de
ancho
y
50
cm
de
alto.
a.
¿Cuántos
litros
de
agua
caben
en
la
tina?
b.
Si
se
vierte
agua
hasta
cierto
nivel
de
una
tina
y
luego,
cuando
se
sumerge
completamente
un
niño,
aumenta
el
nivel
en
5
cm.
¿Cuál
es
el
volumen
del
niño?
5.
La
directora
de
una
escuela
decidió
que
se
construya
un
cajón
de
arena
para
que
jueguen
los
niños
de
kínder.
Luego
consiguió
que
una
empresa
le
donara
1,5
m
3
de
arena.
La
parvularia
le
indicó
que
el
cajón
debía
contener
arena
al
menos
hasta
30
cm
de
su
altura.
a.
Si
ocupa
un
antiguo
cajón
de
3
m
de
largo
y
2
m
de
ancho
y
vierte
en
él
la
arena
recibida,
¿alcanzará
para
cubrir
la
altura
sugerida
por
la
educadora?
b.
¿Cuál
debe
ser
la
superficie
del
cajón
para
que
la
arena
quede
a
buena
altura?
6.
Uno
de
los
primeros
computadores
electrónicos
medía
15
m
de
largo,
4
m
de
ancho
y
3 m
de
alto.
Actualmente,
un
notebook
puede
medir
30
cm
de
largo,
20
cm
de
ancho
y
2
cm
de
alto.
¿Cuántas
veces
mayor
es
el
volumen
del
antiguo
computador
respecto
del
notebook
actual?
3
Unidad
81
Lección
1
•
Área
y
volumen
de
prismas
y
cilindros
|
CL0000000001052
81
12/17/2019
9:48:10
AM
Área
y
volumen
de
prismas
y
cilindros
Lección
1
3
Unidad
308
Cuaderno
de
Actividades
•
Unidad
3
84 000
cm
3
175
cm
3
2
m
16
cubitos
200
m
3
Es
el
triple
también.
150 000
veces.
Menor
No,
ya
que
es
menor
cantidad
de
jugo.
450L
4 500
cm
3
No.
5
m
2

Unidad
3
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
126
a
133
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
11
de
las
Bases
Curriculares.
7.
Calcula
el
volumen
(V
)
de
cada
cilindro.
Considera
π
≈
3,14.
c.
20
cm
12
cm
V
=
b.
34
cm
26
cm
V
=
a.
5
cm
3
cm
V
=
8.
Resuelve
los
siguientes
problemas.
Considera
π
≈
3,14
y
comprueba
con
una
calculadora.
a.
En
una
lata
cilíndrica
de
jugo
natural
se
indica
que
el
contenido
es
de
300
cm³.
Si
el
diámetro
de
la
lata
es
de
5
cm,
¿cuál
será,
aproximadamente,
la
altura
del
envase?
b.
Un
fabricante
de
conservas
necesita
decidir
qué
envase
cilíndrico
es
mejor
para
su
producto.
Si
un
cilindro
es
el
doble
de
ancho
que
el
otro,
pero
la
mitad
del
alto,
¿cuál
de
los
dos
envases
tiene
mayor
capacidad?
Explica.
c.
El
cilindro
fonográfico
fue
el
primer
método
utilizado
para
grabar
y
reproducir
sonidos.
Hacia
1890,
algunas
empresas
decidieron
estandarizar
sus
medidas;
fue
así
como
se
produjeron
cilindros
fonográficos
de
10
cm
de
altura
y
5,7
cm
de
diámetro.
¿Cuál
era
el volumen
de
un cilindro
fonográfico?
d.
Una
torta
de
novios
tiene
tres
pisos,
cada
uno
en
forma
de
cilindro.
El
primer
piso
tiene
40 cm
de
diámetro,
el
segundo,
30
cm
y
el
tercero,
20
cm.
Cada
uno
tiene
una
altura
de
12 cm.
Calcula
el
volumen
total
de
la
torta.
Área
y
volumen
de
prismas
y
cilindros
Lección
1
82
|
Unidad
3
CL0000000001052
82
12/17/2019
9:48:10
AM
e.
El
radio
del
cilindro
A
tiene
el
doble
de
la
medida
del
radio
del
cilindro
B.
Si
son
de
igual
altura,
¿en
qué
razón
están
sus
volúmenes?
9.
Don
Javier
es
un
artesano
y
elabora
vasos
de
greda
con
forma
de
cilindro
cuyas
dimensiones
se
muestran
en
la
figura.
h
1
=
20
cm
r
1
=
9
cm
h
2
=
19
cm
r
2
=
7
cm
a.
Si
están
diseñados
para
que
el
vaso
pequeño
se
guarde
dentro
del grande,
¿cuál
es
la capacidad
del
vaso
grande?
b.
¿Cuánta
greda
se
ha
ocupado
para
fabricar
el
vaso
grande?
c.
Si
el
vaso
pequeño
se
fabrica
con
similar
grosor
de
las
paredes
y de
la
base,
¿cuál
es
su capacidad?
10.
En
una
industria
de
enlatados
se
utilizan
recipientes
con
forma
cilíndrica
para
contener
alimentos
como
se
muestra
en
la
imagen.
4
cm
12
cm
8
cm
6
cm
a.
¿Cuál
de
los
dos
recipientes
tiene
mayor
capacidad?
b.
¿En
cuál
de
los
recipientes
se
usa
mayor
cantidad
de
aluminio
para su
elaboración?
c.
Si
en
cada
recipiente
la
etiqueta
cubre
toda
la
superficie
lateral,
¿en
cuál
de
las
dos
etiquetas
se
emplea
mayor
cantidad
de
papel?
3
Unidad
83
Lección
1
•
Área
y
volumen
de
prismas
y
cilindros
|
CL0000000001052
83
12/17/2019
9:48:10
AM
Cuaderno
de
Actividades
•
Unidad
3
309
8
35,325
cm
3
18 042,44
cm
3
2 260
cm
3
15,3
cm
El
de
radio
doble
de
base.
255,0456
cm
3
.
27 318
cm
3
4
es
a
1.
2 769,48
cm
3
El
de
altura
4
cm.
2 317,32
cm
3
En
el
de
altura
4
cm.
1 664,2
cm
3
En
el
de
altura
4
cm.

Orientaciones
de
uso
•
Estas
páginas
comprenden
una
evaluación
formativa
de
la
Lección
1
Área
de
prismas
y
cilindros.
Aborda
el
Objetivo
de
Aprendizaje
11
de
las
Bases
Curriculares.
A
partir
de
la
siguiente
información,
responde
de
la
pregunta
1
a
la
6.
Se
quieren
construir
dos
tipos
de
cajas
con
tapa
y
con
forma
de
prisma.
La
caja
1,
de
100
cm
de
altura
y
de
base
rectangular
de
30
cm
por
40
cm.
Y
la
caja
2,
de
80 cm
de
altura
y
con
base
cuadrada
de
lado
50
cm.
¿Qué
tipo
de
caja
resulta
más
conveniente
para
ahorrar
material?
1.
¿Cuáles
son
los
datos
suficientes
para
resolver
el
problema?
A.
Las
dimensiones
de
la
caja
1.
B.
Las
dimensiones
de
la
caja
2.
C.
El
volumen
de
las
cajas
1
y
2.
D.
Las
dimensiones
de
las
cajas
1
y
2.
2.
¿Qué
es
lo
que
se
pregunta?
A.
El
área
de
las
cajas.
B.
La
caja
con
menor
volumen.
C.
La
caja
en
la
que
se
ahorra
más
material.
D.
La
caja
que
tiene
una
menor
altura.
3.
¿Cuál
es
el
área
de
la
caja
1?
A.
8
200
cm
2
B.
10
500
cm
2
C.
16
400
cm
2
D.
21
000
cm
2
4.
¿Cuál
es
el
área
de
la
caja
2?
A.
9
250
cm
2
B.
10
500
cm
2
C.
18
500
cm
2
D.
21
000
cm
2
5.
¿Cuál
es
el
volumen
de
la
caja
1?
A.
12
000
cm
3
B.
120
000
cm
3
C.
164
000
cm
3
D.
720
000
cm
3
6.
¿Cuál
es
la
respuesta
al
problema?
A.
La
caja
1.
B.
La
caja
2.
C.
Ambas
cajas.
D.
Ninguna
de
las
cajas.
Evaluación
Lección
1
|
Unidad
3
84
CL0000000001052
84
12/17/2019
9:48:10
AM
•
¿Cómo
calculas
el
área
de
prismas
y
cilindros?
Explica
paso
a
paso.
•
¿Qué
datos
son
necesarios
cuando
calculas
el
volumen
de
prismas
y
cilindros?
Ejemplifica.
Reflexiona
y
responde
Reflexiona
y
responde
A
partir
de
la
siguiente
información,
marca
la
respuesta
correcta
en
las
preguntas
7
a
la
12.
En
una
florería
se
utilizan
baldes
cilíndricos
para
mantener
las
flores
en
agua.
Si
tienen
15 baldes
de
40
cm
de
diámetro
y
40
cm
de
alto,
¿cuántos
cm
3
de
agua
se
utilizan
a
diario si
se
llenan
completamente?
Considera
π
≈
3,14.
7.
¿Cuáles
son
los
datos
suficientes
para
resolver
el
problema?
A.
La
cantidad
de
baldes.
B.
La
cantidad
y
forma
de
los
baldes.
C.
La
forma
y
dimensiones
de
los
baldes.
D.
La
cantidad,
forma
y
dimensiones
de
los
baldes.
8.
¿Qué
es
lo
que
se
pregunta?
A.
La
capacidad
de
un
balde.
B.
Los
cm
3
de
agua
que
se
utilizan diariamente.
C.
Los
cm
3
de
agua
que
se
utilizan
para llenar
un
balde.
D.
La
cantidad
de
agua
necesaria
para
ocupar
la
mitad
de
los
baldes.
9.
¿Cuál
es
el
volumen
de
1
balde?
A.
8
240
cm
3
B.
16
000
cm
3
C.
50
240
cm
3
D.
200
960
cm
3
10.
¿Cuál
es
la
respuesta
al
problema?
A.
50
240
cm
3
de
agua.
B.
200
960
cm
3
de
agua.
C.
753
600
cm
3
de
agua.
D.
3
014
400
cm
3
de
agua.
11.
¿Cuál
es
el
área
lateral
de
1
balde?
A.
10
048
cm
2
B.
5
024
cm
2
C.
1
600
cm
2
D.
331,2
cm
2
12.
¿Cuánta
agua
se
utilizaría
si
los
baldes
se
ocuparan
solo
hasta
la
mitad
de
su capacidad?
A.
376
800
cm
3
B.
753
600
cm
3
C.
1
130
400
cm
3
D.
1
507
200
cm
3
3
Unidad
85
Evaluación
Lección
1
|
CL0000000001052
85
12/17/2019
9:48:10
AM
3
Unidad
310
Cuaderno
de
Actividades
•
Unidad
3

Unidad
3
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
136
a
139
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
12
de
las
Bases
Curriculares.
Teorema
de
Pitágoras
1.
Calcula
la
medida
pedida
en
cada
caso.
a.
x
=
15
cm
9
cm
x
C
A
B
b.
x
=
x
13
cm
9
cm
A
C
B
c.
x
=
x
B
C
A
7
cm
4
cm
2.
Calcula
la
medida
faltante,
dados
los
catetos
(c)
o
la
hipotenusa
(h)
en
los
siguientes
triángulos
rectángulos.
a.
c
1
=
7
cm;
c
2
=
12
cm
b.
c
1
=
5
cm;
c
2
=
12
cm
c.
c
1
=
3
cm;
c
2
=
5
cm
d.
h
=
10
cm;
c
2
=
8
cm
e.
h
=
5
cm;
c
2
=
2
cm
f.
h
=
8
cm;
c
2
=
4
cm
3.
Comprueba
si
los
siguientes
números
forman
un
trío
pitagórico.
a.
7,
24
y
25.
b.
9,
15
y
20.
c.
17,
19
y
26.
d.
10,
24
y
36.
e.
4,5;
6
y
7,5.
f.
1,8;
2,4
y
3.
4.
Observa
las
figuras
y
resuelve.
a.
Calcula
el
perímetro
(P
)
del siguiente triángulo.
b.
¿Cuál
es
el
perímetro
(P
)
del siguiente rectángulo?
1
7
c
m
8
cm
26
cm
7
cm
24
cm
P
=
P
=
Teorema
de
Pitágoras
Lección
2
86
|
Unidad
3
CL0000000001052
86
12/17/2019
9:48:10
AM
5.
Responde
las
siguientes
preguntas.
Justifica
tu
respuesta.
a.
Los
lados
de
un
rectángulo
son
12
cm
y
15 cm.
¿Cuánto
mide
la
diagonal?
b.
¿Cuál
es
la
altura
de
un
trapecio
isósceles
de
bases
8
dm
y
10
dm
de
longitud,
y
lados
iguales de
7
dm?
c.
Las
diagonales
de
un
rombo
miden
12
cm
y
16
cm.
¿Cuál
es
la
medida
de
cada
uno
de
sus lados?
d.
¿Cuál
es
la
medida
de
la
altura
de
un
triángulo
equilátero
de
lado
6
cm?
e.
El
perímetro
de
un
cuadrado
mide
20
cm.
¿Cuánto
mide
su
diagonal?
Marca
la
opción
correcta
del
ítem
6
y
del
7.
Justifica
en
cada
caso.
6.
Marca
la
opción
que
muestra
la
medida,
en
centímetros,
de
los
lados
de
un triángulo rectángulo.
A.
1,
2
y
3.
B.
9,
16
y
25.
C.
2,
4
y
16.
D.
9,
12
y
15.
7.
¿Cuál
de
las
siguientes
alternativas
representa
un
triángulo
rectángulo?
8
mm
10
mm
6
mm
b.
d.
13
mm
12
mm
3
mm
a.
5
mm
3
mm
7
mm
c.
5
mm
9
mm
13
mm
3
Unidad
87
Lección
2
•
Teorema
de
Pitágoras
|
CL0000000001052
87
12/17/2019
9:48:10
AM
Cuaderno
de
Actividades
•
Unidad
3
311
0
4
cm
≈
13,89
cm
Sí
6
cm
No
13
cm
No
≈
4,58
cm
Sí
≈
5,83
cm
No
≈
6,93
cm
Sí
≈
15,81
cm
≈
15,81
cm
68
cm
46
cm
Mide
aproximadamente
19,21
cm.
La
altura
es,
aproximadamente,
6,93
dm.
Los
lados
miden
10
cm.
La
altura
mide,
aproximadamente,
5,2
cm.
La
diagonal
mide,
aproximadamente,
7,07
cm.

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
140
a
145
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
12
de
las
Bases
Curriculares.
Aplicaciones
del
teorema
de
Pitágoras
1.
La
figura
representa
un
poste
(CD)
sujeto
por
dos
cables,
AD
y
DB.
8,49
m
6
m
8
m
D
C
A
B
a.
Aproximadamente,
¿a
qué
distancia
se
encuentran
los
extremos
inferiores
de
los
cables?
b.
¿Cuánto
cable
se
utilizó
para
sujetar
el
poste?
2.
Resuelve
los
siguientes
problemas.
Puedes
utilizar
una
calculadora
para
realizar
los
cálculos.
a.
Un
terreno
mide
100
m
de
largo
por
50
m
de
ancho.
Pedro
recorre
el
ancho
y
el
largo
y
Juan
cruza
por
la
diagonal.
Aproximadamente,
¿cuántos
metros
de
caminata
se
ahorra
Juan?
b.
Un
poste
de
10
m
de
altura
se
afirmará
mediante
cables
desde
la
parte
más
alta
hasta
dos puntos
ubicados
en
el
suelo,
a
3
m
y
4
m
del
poste.
Aproximadamente,
¿cuánto
cable
se necesita?
c.
Para
tejer
chales
a
telar,
Patricia
quiere
construir
un
bastidor
de
madera
en
forma
de
triángulo
isósceles.
Si
la
base
debe
medir
120 cm
y
la
altura
80
cm,
¿cuánta
madera
necesita para
hacer
el
bastidor?
Teorema
de
Pitágoras
Lección
2
88
|
Unidad
3
CL0000000001052
88
12/17/2019
9:48:10
AM
d.
Una
escalera
se
ha
apoyado
a
3
m
de
la
base
de
una
pared,
de
tal
forma
que
la
altura
que
alcanza
es
de
2
m.
¿Cuál
es
la
longitud
de
la
escalera?
e.
Una
rampa
tiene
una
altura
de
11
m
y
su
punto
de
inicio
se
encuentra
a
60
m
de
distancia
de
una
pared.
¿Cuál
es
la
longitud
de
la
rampa?
f.
Desde
el
balcón
de
un
edificio
se
ve
una
plaza
a
85
m,
pero
desde
la
base
del
edificio
está
a 84 m.
¿A
qué
altura
se
encuentra
ese
balcón?
g.
Julieta
está
encumbrando
un
volantín
con
un
hilo
de
100
m.
Cuando
el
hilo
está
totalmente
tenso,
la
altura
del
volantín
al
suelo
es
de
80
m.
Sin
considerar
la
altura
de
Julieta,
¿a
qué
distancia
se
encuentra
ella
de
este
punto?
Marca
la
opción
correcta.
Justifica
en
cada
caso.
3.
Una
escalera
de
6
m
de
largo
se
apoya
en
una
muralla
a
una
altura
de
5
m
desde
el
suelo.
¿A qué
distancia
desde
la
base
de
la
muralla
se
encuentra
el
pie
de
la
escalera?
A.
1
m
B.
3
m
C.
3,3
m
D.
6,4
m
4.
La
plaza
central
de
una
villa
está
representada
en
la
figura.
Al
salir
a
trotar
alrededor
de
la plaza
y
dar
10
vueltas,
¿cuántos
metros
se
recorren?
A.
420
m
B.
500
m
C.
650
m
D.
720
m
24
m
18
m
3
Unidad
89
Lección
2
•
Teorema
de
Pitágoras
|
CL0000000001052
89
12/17/2019
9:48:11
AM
Teorema
de
Pitágoras
Lección
2
3
Unidad
312
Cuaderno
de
Actividades
•
Unidad
3
Se
encuentran
a
14
m,
aproximadamente.
Se
utilizaron
18,49
m.
Se
ahorra
38
m,
aproximadamente.
Pedro:
150
m
Juan:
112
m
La
escalera
mide
3,6
m,
aproximadamente.
La
rampa
mide
61
m.
Se
encuentra
a
13
m.
Se
encuentra
a
60
m.
Se
necesitan
21,21
m
de
cable,
aproximadamente.
Necesita
320
m
de
madera.
116
109
+
≈
21,21
60
2
+
80
2
=
x
2
100
=
x
2
2
+
3
2
=
x
2
3,6
≈
x
11
2
+
60
2
=
x
2
x
2
+
84
2
=
85
2
80
2
+
x
2
=
100
2
61
=
x
x
=
13
x
=
60

Unidad
3
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
140
a
145
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
12
de
las
Bases
Curriculares.
Herramientas
tecnológicas
1
Construir
un
segmento.
Presiona
y
luego
;
así
al
seleccionar
dos
puntos
del
plano
cartesiano
habrás
dibujado
el
segmento
AB.
2
Ahora
para
trazar
un
segmento
perpendicular
al
segmento
AB.
Pincha
,
luego
al
presionar
sobre
cualquier
punto
del
segmento
AB
y
desplazar
la
recta
hasta
el
extremo
B.
Se
dibujará
la
recta
perpendicular
al
segmento
AB
que
pasa
por B.
3
Dibujar
un
punto
C
sobre
la
recta.
Presiona
y
selecciona
“
punto”,
luego
clic
en
cualquier
lugar
sobre
la
recta.
De
esta
manera
habrás
dibujado
el
punto
C
sobre
la
recta.
4
Crear
el
segmento
AC.
Selecciona
,
pincha
,
luego
haz
clic
sobre
A
y
C.
Habrás
creado
el
segmento
AC.
5
Construir
un
triángulo
ABC.
Selecciona
y
presiona
sobre
los
puntos
A,
B,
C.
Luego
habrás
construido
el
triángulo
ABC.
6
Dibujar
cuadrados
sobre
cada
lado
del
triángulo
ABC.
Presiona
y
luego
selecciona
“polígono
regular”.
Haz
clic
sobre
A
y
luego
sobre
C,
aparecerá
un
cuadro
donde
debes
poner
la
cantidad
de
lados
del
polígono
que
en
este
caso
son
4.
Debes seguir
esta
misma
secuencia
para
dibujar
los
demás
cuadrados.
En
esta
sección,
podrás
demostrar
que
en
cualquier
triángulo
rectángulo
se
cumple
que:
“La
suma
de
las
áreas
de
los
cuadrados
construidos
sobre
los
catetos
es
igual
al
área
del
cuadrado
construido
sobre
la
hipotenusa”.
Para
demostrar
esta
formación,
utilizaremos
el
software
Geogebra.
Instrucciones
No
ta
:
la
apl
icac
ión
Geo
geb
ra,
cre
ada
por
Ma
rku
s
Hoh
enw
arte
r,
fue
inc
luid
a
en
est
e
tex
to
con
fine
s
de
ens
eña
nza
y
a
títu
lo
me
ram
ent
e
eje
mp
lar.
Teorema
de
Pitágoras
Lección
2
90
|
Unidad
3
CL0000000001052
90
12/17/2019
9:48:11
AM
Analiza
1.
¿Cómo
son
las
áreas
de
los
cuadrados
dibujados
sobre
los
lados
del
triángulo
ABC?
2.
¿Qué
relación
existe
entre
la
fórmula:
a
2
+
b
2
=
c
2
y
la
comparación
que
se
hizo
con
las áreas correspondientes?
8
Para
comprobar
el
teorema
de
Pitágoras,
puedes
sumar
las
áreas
de
los
cuadrados
construidos
sobre
los
catetos
y
comparas
el
resultado
obtenido
con
el
área
del
cuadrado
construido
sobre
la hipotenusa.
7
Calcular
el
área
de
cada
cuadrado
construido
sobre
los
lados
del
triángulo
ABC.
Selecciona
,
y
presiona
sobre
área,
.
Haz
clic
sobre
cada
uno
de
los
cuadrados
construidos
y
obtendrás
el
área
correspondiente.
3
Unidad
91
Lección
2
•
Teorema
de
Pitágoras
|
CL0000000001052
91
12/17/2019
9:48:11
AM
Cuaderno
de
Actividades
•
Unidad
3
313
2
El
área
del
poligono
2,
más
el
área
del
poligono
3,
es
igual
al
área
del
polígono
1.
Las
comparaciones
hechas
comprueban
que
la
fórmula
se
cumple.

Orientaciones
de
uso
•
Estas
páginas
comprenden
una
evaluación
formativa
de
la
Lección
2
Teorema
de
Pitágoras.
Aborda
el
Objetivo
de
Aprendizaje
12
de
las
Bases
Curriculares.
A
partir
de
la
siguiente
información,
responde
de
la
pregunta
1
a
la
4.
1.
¿Cuáles
son
los
datos
suficientes
para
resolver
el
problema?
A.
Medida
de
la
escalera.
B.
Distancia
desde
el
suelo
hasta
donde
está
apoyada
la
escalera
en
la
pared.
C.
Distancia
desde
el
suelo
hasta
donde
está
apoyada
la
escalera
en
la
pared
y
la
medida
de
la
escalera.
D.
Distancia
desde
el
suelo
hasta
donde
está
apoyada
la
escalera
en
la
pared
y
la
medida
de
la
pared.
2.
¿Qué
es
lo
que
se
pregunta?
A.
La
medida
de
la
pared.
B.
La
medida
de
la
escalera.
C.
La
distancia
desde
el
suelo
hasta
donde
está
apoyada
la
escalera.
D.
La
distancia
entre
el
pie
de
la
escalera
y
la
pared.
3.
¿Qué
estrategia
se
utilizó
para
resolver
el
problema?
A.
Ensayo
y
error.
B.
Plantear
una
ecuación.
C.
Plantear
una
inecuación.
D.
Usar
una
representación
gráfica.
4.
¿Cuál
es
la
respuesta
al
problema?
A.
Se
encuentra
a
8
m.
B.
Se
encuentra
a
64
m.
C.
Se
encuentra
a
225
m.
D.
Se
encuentra
a
289
m.
Una
escalera
está
apoyada
en
una
pared
vertical
a
15
m
del
suelo.
Si
la
escalera
mide
17
m,
¿a
qué
distancia
de
la
pared
se
encuentra
el
pie
de
la
escalera?
Luego
de
elegir
la
estrategia,
el
problema
se
resuelve
de
la siguiente
manera:
x
2
+
15
2
=
17
2
x
2
+
225
=
289
x
2
=
64
x
=
8
x:
distancia
entre
la
pared
y
la
escalera.
Evaluación
Lección
2
|
Unidad
3
92
CL0000000001052
92
12/17/2019
9:48:11
AM
•
¿Qué
fue
lo
que
te
produjo
mayor
dificultad
en
el
desarrollo
de
la
lección?
Justifica
tu
respuesta.
•
¿Qué
características
debe
tener
un
triángulo
para
aplicar
el
teorema
de
Pitágoras?
Ejemplifica.
Reflexiona
y
responde
Reflexiona
y
responde
A
partir
de
la
siguiente
información,
marca
la
respuesta
correcta
en
las
preguntas
5
a
la
10.
Un
cable
que
está
totalmente
tenso
va
desde
la
cima
de
una
torre
hasta
el
suelo
y
mide
50
m.
Si
la
distancia
en
el
suelo
entre
el
cable
y
la
base
de
la
torre
es
de
30
m,
¿cuál
es
la
altura
de
la
torre?
5.
¿Cuáles
son
los
datos
suficientes
para
resolver
el
problema?
A.
Medida
del
cable.
B.
Distancia
en
el
suelo
entre
el
cable
y
la base
de
la
torre.
C.
Distancia
en
el
suelo
entre
el
cable
y
la
base
de
la
torre
y
la
medida
del
cable.
D.
Distancia
en
el
suelo
entre
el
cable
y
la base
de
la
torre
y
el
tipo
de
torre.
6.
¿Qué
es
lo
que
se
pregunta?
A.
La
medida
del
cable.
B.
La
altura
de
la
torre.
C.
Distancia
entre
el
cable
y
la
torre.
D.
Distancia
entre
el
cable
y
el
suelo.
7.
¿Cuál
es
la
respuesta
al
problema?
A.
20
m
B.
40
m
C.
80
m
D.
120
m
8.
¿Cuál
es
la
suma
entre
la
medida
del
cable
y
de
la
torre?
A.
70
m
B.
80
m
C.
90
m
D.
100
m
9.
Si
otro
cable
mide
13
m
y
está
afirmado
en la
torre
a
12
m
desde
el
suelo,
¿cuál
es la
distancia
en
el
suelo
entre
el
cable
y la
torre?
A.
5
m
B.
12
m
C.
13
m
D.
30
m
10.
¿A
qué
distancia
se
encuentran
los dos cables
en
el
suelo?
A.
5
m
B.
25
m
C.
30
m
D.
35
m
3
Unidad
93
Evaluación
Lección
2
|
CL0000000001052
93
12/17/2019
9:48:11
AM
3
Unidad
314
Cuaderno
de
Actividades
•
Unidad
3

Unidad
3
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
148
a
151
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
13
y
14
de
las
Bases
Curriculares.
Traslación
1.
Verifica
si
las
siguientes
expresiones
son
verdaderas
(V)
o
falsas
(F).
Justifica
en
cada
caso.
a.
Al
aplicar
una
traslación,
todos
los
puntos
de
la
figura
se
mueven
en
una
misma
magnitud
y
dirección.
Justificación:
b.
Al
aplicar
una
transformación
isométrica
a
una
figura,
puede
cambiar
el
tamaño
de la figura,
pero
no
su
forma.
Justificación:
c.
Para
trasladar
una
figura,
es
necesario
conocer
el
vector
de
traslación.
Justificación:
d.
El
vector
de
traslación
es
siempre
paralelo
a
los
trazos
que
unen
cada
par
de
puntos correspondientes.
Justificación:
2.
Marca
el
vector
de
traslación,
partiendo
desde
A
en
cada
caso.
a.
A
b.
A
3.
Ubica
los
siguientes
vectores
en
el
plano
cartesiano.
A(6,
1)
B(5,
–1)
C(–2,
–3)
D(–5,
–4)
E(3,
–1)
F(4,
–2)
Y
O
X
1
–4
–5
2
–3
3
–2
4
5
–1
4
5
6
7
–1
3
–2
2
–3
1
–4
–5
–6
–7
Transformaciones
isométricas
Lección
3
94
|
Unidad
3
CL0000000001052
94
12/17/2019
9:48:11
AM
4.
Completa
la
tabla
con
el
punto,
el
vector
o
la
imagen
del
punto
después
de
una
traslación
según
corresponda.
P(x,
y)
P(1,
3)
P(–2,
–4)
P(1,
5)
P(0,
3)
v
v
=
(1,
–2)
v
=
(–3,
–5)
v
=
(3,
–2)
P'(x,
y)
P'(0,
3)
P'(7,
2)
P'(5,
1)
5.
Dibuja
la
imagen
del
pentágono
de
la
figura
al
aplicarle
una
traslación
de
vector
v(3,
3).
¿Cuáles
son
sus
coordenadas?
Y
O
X
1
2
3
4
5
6
7
4
5
6
7
8
9
10
11
12
13
14
3
2
1
D
C
B
A
E
6.
Usando
regla
y
compás,
traslada
cada
figura
según
el
vector
dado
para
cada
una.
a.
b.
7.
Un
cuadrado
tiene
como
vértices
los
puntos
A(–1,
1),
B(1,
1),
C(1,
–1)
y
D(–1,
–1).
Determina su
imagen
trasladada
por
el
vector
v(4,
2).
8.
Se
ha
trasladado
el
triángulo
de
vértices
A(1,
3),
B(3,
4)
y
C(2,
2)
y
la
imagen
del
vértice
C
es el
punto
C'(1,
–1).
a.
¿Cuáles
son
las
coordenadas
del
vector
que
define
la
traslación?
b.
Determina
las
coordenadas
de
los
vértices
A'
y
B'.
3
Unidad
95
Lección
3
•
Transformaciones
isométricas
|
CL0000000001052
95
12/17/2019
9:48:11
AM
Cuaderno
de
Actividades
•
Unidad
3
315
4
A'
(3,
3),
B'
(5,
3),
C'
(5,
1),
D'
(3,
1)
v
(–1,
–3)
No
cambia
ni
tamaño,
ni
forma.
A'
(0,
0);
B'
(2,
1)
V
F
V
V
v
(2,
7)
v
(4,
–4)
P
(11,
7)
P'
(2,
1)
P'
(3,
1)
D
C
F
E
D
A
B'
A'
E'
D'
C'

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
152
a
155
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
13
y
14
de
las
Bases
Curriculares.
Rotación
1.
Verifica
si
las
siguientes
expresiones
son
verdaderas
(V)
o
falsas
(F).
Justifica
las
falsas.
a.
Para
rotar
un
triángulo,
solo
es
necesario
conocer
el
ángulo
de
rotación.
Justificación:
b.
Cuando
tienen
el
mismo
centro
de
rotación,
dos
rotaciones
siempre
mueven
los puntos
de
la
figura
igual.
Justificación:
c.
Rotar
una
figura
en
180º
en
sentido
antihorario
es
equivalente
a
rotar
la
misma
figura
en
180º
en
sentido
horario.
Justificación:
2.
Un
pentágono
tiene
como
vértices
los
puntos
A(3,
0),
B(2,
5),
C(–3,
2),
D(–1,
–4)
y
E(2,
–3).
Encuentra
las
coordenadas
de
los
vértices
de
su
imagen
si
lo
rotamos
con
centro
en
el
origen
y
ángulo
de
90º.
3.
Una
figura
tiene
simetría
rotacional
si
se
puede
hacer
que
coincida
exactamente
sobre
el original
cuando
se
rota
alrededor
de
un
punto
fijo
con
un
ángulo
menor
que
360º.
a.
Determina
cuál
o
cuáles
de
ellas
tienen
simetría
rotacional.
I.
II.
III.
b.
Para
las
figuras
que
tengan
simetría
rotacional,
ubica
el
centro
de
rotación
y
el
menor
ángulo
de
rotación
con
el
que
la
imagen
coincide
con
la
figura
original.
Transformaciones
isométricas
Lección
3
96
|
Unidad
3
CL0000000001052
96
12/17/2019
9:48:12
AM
Marca
la
opción
correcta.
Justifica
en
cada
caso.
4.
¿Cuál
de
estas
figuras
no
tiene
simetría?
A.
Un
triángulo
escaleno.
B.
Un
eneágono
regular.
C.
Un
trapecio
isósceles.
D.
Un
pentágono.
5.
En
la
imagen,
se
aplicó
una
rotación
con
centro
en
O
y
ángulo
de
rotación
de:
A.
60º
B.
360º
C.
90º
D.
180º
6.
La
imagen
de
una
figura
coincide
exactamente
con
la
figura
original,
si
se
rotó
en:
A.
90º
en
sentido
horario.
B.
180º
en
sentido
antihorario.
C.
360º
en
sentido
horario.
D.
540º
en
sentido
antihorario.
7.
Al
aplicar
una
rotación,
con
el
centro
en
un
punto
de
la
figura,
siempre
se
cumple
que:
A.
una
recta
de
la
figura
queda
fija.
B.
un
punto
de
la
figura
queda
fijo.
C.
todos
los
puntos
de
la
figura
cambian
de
posición.
D.
todos
los
puntos
de
la
figura
quedan
igual.
8.
Si
el
centro
de
rotación
coincide
con
uno
de
los
vértices
de
una
figura,
¿qué
ocurre
al aplicar una
rotación
en
180º?
A.
Ningún
punto
de
la
figura
queda
fijo.
B.
Un
punto
de
la
figura
queda
fijo.
C.
Los
vértices
de
la
figura
cambian
de
posición.
D.
Todos
los
puntos
de
la
figura
cambian
de
posición.
O
3
Unidad
97
Lección
3
•
Transformaciones
isométricas
|
CL0000000001052
97
12/17/2019
9:48:12
AM
Transformaciones
isométricas
Lección
3
3
Unidad
316
Cuaderno
de
Actividades
•
Unidad
3
A'
(0,
3),
B'
(–5,
2),
C'
(–2,
–3),
D'
(4,
1),
E'
(3,
2)
También
se
necesita
el
centro
de
rotación.
Ya
que
para
quede
igual
debe
tener
el
mismo
ángulo
de
rotación.
F
F
V
I.
Centro
de
la
figura,
120º.
II.
Centro
de
la
figura,
180º.
III.
Centro
de
la
figura,
90º.

Unidad
3
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
156
a
159
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
13
y
14
de
las
Bases
Curriculares.
Reflexión
1.
Verifica
si
las
siguientes
expresiones
son
verdaderas
(V)
o
falsas
(F).
Justifica
en
cada
caso.
a.
Para
reflejar
una
figura,
es
necesario
conocer
el
vector
que
determina
la
reflexión.
Justificación:
b.
Un
dibujo
se
dice
simétrico
si
algún
eje
de
simetría
pasa
por
él.
Justificación:
c.
Al
aplicar
una
reflexión,
todos
los
puntos
de
la
figura
se
mueven
en
una
misma
dirección
y
sentido.
Justificación:
d.
La
estrella
de
la
bandera
nacional
tiene
3
ejes
de
simetría.
Justificación:
2.
Encuentra
todas
las
líneas
de
simetría
de
las
siguientes
figuras.
a.
c.
b.
d.
3.
Encierra
las
letras
y
los
números
donde
se
puedan
trazar
líneas
de
simetría.
Transformaciones
isométricas
Lección
3
98
|
Unidad
3
CL0000000001052
98
12/17/2019
9:48:12
AM
4.
Usando
regla
y
compás,
aplica
la
reflexión
según
el
eje
de
reflexión
dado.
a.
b.
5.
Un
triángulo
tiene
por
vértices
los
puntos
A(–2,
4),
B(1,
5)
y
C(–1,
5).
a.
¿Cuáles
son
las
coordenadas
del
ΔA'B'C'
si
corresponde
a
una
simetría
central
cuyo
centro es
el
origen?
b.
¿Cuáles
son
las
coordenadas
del
ΔA'B'C'
si
corresponde
a
una
simetría
axial
con
eje
en el eje X?
Marca
la
opción
correcta.
6.
¿En
cuál
de
los
siguientes
casos
se
representa
mejor
una
reflexión
según
la
recta
dada?
A.
B.
D.
C.
7.
¿En
qué
figura
no
se
ha
trazado
una
línea
de
simetría?
A.
C.
B.
D.
3
Unidad
99
Lección
3
•
Transformaciones
isométricas
|
CL0000000001052
99
12/17/2019
9:48:12
AM
Cuaderno
de
Actividades
•
Unidad
3
317
6
A'
(2,
–4),
B'
(–1,
–5),
C'
(1,
–5)
A'
(2,
4),
B'
(–1,
5),
C'
(1,
5)
Es
necesario
conocer
el
eje
de
simetría.
Todos
los
puntos
se
posicionan
a
la
misma
distancia,
en
perpendicular,
Tiene
5
ejes.
del eje
de
simetría.
F
V
F
F

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
160
a
163
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
13
y
14
de
las
Bases
Curriculares.
Composición
de
transformaciones
isométricas
1.
Usando
regla
y
compás,
traslada
el
ΔABC
según
el
vector
DT
y,
luego,
traslada
la
imagen
obtenida
según
el
vector
FK.
C
B
T
F
K
A
D
¿Podrías
trasladar
el
ΔABC
original,
según
un
solo
vector,
y
obtener
la
segunda
imagen?
2.
Si
A'B'C'D'
es
imagen
de
ABCD
y
ABCD
es
imagen
de
A'B'C'D',
entonces:
Y
O
X
1
–4
–5
–6
2
–3
3
–2
4
5
6
–1
4
5
6
7
8
–1
3
–2
2
–3
1
–4
–5
–6
–7
–8
C'
C
C
B'
B
B
D'
D
D
A'
A
A
a.
¿Cuáles
son
los
vectores
asociados
a
cada
traslación?
b.
¿Cuál
es
el
vector
que
lleva
directamente
el
cuadrado
ABCD
al
ABCD?
Transformaciones
isométricas
Lección
3
100
|
Unidad
3
CL0000000001052
100
12/17/2019
9:48:12
AM
3.
Si
se
traslada
el
punto
P(0,
5)
aplicando
el
vector
v
=
(3,
4)
y
a
continuación
el
vector
w
=
(2,
1):
a.
¿Cuál
es
el
punto
imagen
P'?
b.
Si
después
de
realizar
ambas
traslaciones
se
obtiene
el
punto
Q'(2,
–2),
¿cuál
es
el
punto
original?
4.
Se
ha
trasladado
el
punto
A(–3,
5)
aplicando
los
vectores:
v
=
(2,
5),
u
=
(–1,
–2)
y
w
=
(6,
–5)
consecutivamente.
a.
¿Cuáles
son
las
coordenadas
del
punto
de
llegada
A'?
b.
Dado
el
punto
P(3,
–5)
y
utilizando
los
mismos
vectores
de
traslación,
¿cuál
es
el
punto
P'?
5.
Un
punto
A
se
traslada
según
el
vector
v
=
(3,
4)
y,
a
continuación,
se
aplica
otra
traslación
según
el
vector
w
=
(–2,
–1).
Si
después
de
realizar
estas
traslaciones
se
obtiene
como
imagen
el
punto
A'(2,
–2),
¿cuáles
son
las
coordenadas
del
punto
A?
6.
Dibuja
el
ΔA'B'C'
aplicando
una
rotación
de
centro
O
y
ángulo
de
90º
al
ΔABC.
Luego
aplica
una
rotación
de
centro
O
y
ángulo
de
90º
para
dibujar
el
ΔABC.
Por
último,
toma
el
ΔABC
y
rótalo,
con
centro
en
O
y
ángulo
de
180º.
¿Qué
ocurre?
Justifica
tu
respuesta.
B
A
C
O
3
Unidad
101
Lección
3
•
Transformaciones
isométricas
|
CL0000000001052
101
12/17/2019
9:48:12
AM
Transformaciones
isométricas
Lección
3
3
Unidad
318
Cuaderno
de
Actividades
•
Unidad
3
Sí,
con
el
v
(6,
2)
El
primero
es
(8,
0)
y
el
segundo
es
(–8,
–4).
(0,
–4)
(5,
10)
(–3,
–7)
(4,
)
(10,
–7)
(1,
–5)
Vuelve
a
la
posición
inicial.
C''
B''
C'
A'
A''
B''
C''
B'
A''
C'
A'
B'

Unidad
3
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
160
a
163
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
13
y
14
de
las
Bases
Curriculares.
7.
Determina
F',
la
figura
imagen
de
F
respecto
de
la
reflexión
por
el
eje
E,
y
luego
ubica
F'',
la imagen
de
F'
respecto
de
la
reflexión
por
el
eje
E'.
¿Con
qué
transformación
podrías
pasar de
F
a
F''
directamente?
8.
Identifica
los
movimientos
que
permiten
pasar
de
la
figura
A
a
la
figura
A
pasando
por
A'
e indica
sus
componentes.
b.
A
A'
A
a.
A
A
A'
c.
Según
las
figuras
anteriores,
¿se
puede
pasar
de
A
hasta
A’’
directamente?
Indica
en
cada
caso
la
transformación
necesaria.
9.
Un
punto
A
se
rota
en
90°
en
torno
al
origen,
y
luego
se
aplica
otra
rotación
en
–90°
en
torno
al
origen.
Si
después
de
realizar
estas
rotaciones
se
obtiene
como
imagen
el
punto
A(15, –11),
¿cuáles
son
las
coordenadas
del
punto
A?
Justifica.
E'
E
F
Transformaciones
isométricas
Lección
3
102
|
Unidad
3
CL0000000001052
102
12/17/2019
9:48:13
AM
10.
Se
refleja
el
cuadrilátero
de
vértices
A(–4,
1),
B(–2,
4),
C(–4,
7)
y
D(–6,
4)
primero
en
torno
al
eje
Y
y
luego
en
torno
al
eje
X.
¿Qué
transformación
isométrica
puede
reemplazar
a
esta composición?
11.
Analiza
si
los
siguientes
diseños
pueden
generar
una
teselación.
Justifica
tu
respuesta.
a.
c.
b.
d.
Marca
la
opción
correcta.
Justifica
en
cada
caso.
12.
Una
traslación
con
vector
(4,
2)
seguida
de
otra
traslación
con
vector
(–2,
4)
corresponde
a:
A.
una
reflexión.
B.
una
traslación
de
vector
(–8,
8).
C.
una
traslación
de
vector
(0,
8).
D.
una
traslación
de
vector
(2,
6).
13.
Al
mover
el
triángulo
A
mediante
reflexión
sobre
el
eje
Y,
y
luego
el
A'
mediante
reflexión
sobre
el
eje X,
la
única
transformación
que
permite
pasar
desde
A
a
A
corresponde
a:
A.
Reflexión.
B.
Traslación.
C.
Simetría.
D.
Rotación
en
180º.
A
A'
A
3
Unidad
103
Lección
3
•
Transformaciones
isométricas
|
CL0000000001052
103
12/17/2019
9:48:13
AM
Cuaderno
de
Actividades
•
Unidad
3
319
8
Traslación.
No,
ya
que
no
se
puede
Sí,
ya
que
se
puede
No,
ya
que
no
se
puede
Sí,
ya
que
se
puede
El
punto
A
es
(15,
–11),
ya
que
al
rotar
en
90º
y
recubrir
una
superficie
recubrir
una
superficie
recubrir
una
superficie
recubrir
una
superficie
luego
en
–90º
se
anulan.
sin
dejar
espacios.
sin
dejar
espacios.
sin
dejar
espacios.
sin
dejar
espacios.
Sí,
en
a.
con
el
v
(–5,
–1);
en
b.
con
una
rotación
de
180º
con
centro
en
el
origen.
Composición
de
traslaciones.
Composición
de
reflexiones.
En
torno
al
eje
Y:
A'
(–4,
–1),
B'
(–2,
–4),
C'
(–4,
–7)
y
D'
(–6,
–4)
En
torno
al
eje
X:
A''
(4,
–1),
B''
(2,
–4),
C''
(4,
–7)
y
D''
(6,
–4)
A'
A''

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
164
a
167
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
13
y
14
de
las
Bases
Curriculares.
Transformaciones
isométricas
en
el
espacio
1.
Aplica
el
concepto
de
simetría.
Luego,
dibuja
el
eje
o
punto
y
completa
con
el
tipo
de
simetría.
Simetría:
a.
Simetría:
b.
2.
Realiza
la
simetría
y
completa
con
el
tipo
en
cada
caso.
Simetría:
b.
E
D
A
B
C
L
Simetría:
a.
P
F
E
B
A
D
C
Marca
la
opción
correcta.
3.
¿Qué
tipo
de
simetría
se
le
aplicó
al
cuerpo
geométrico
de
la
figura?
A.
Simetría
espacial
respecto
a
un
eje.
B.
Simetría
espacial
respecto
a
un
punto.
C.
Simetría
espacial
respecto
a
un
plano.
D.
Simetría
espacial
respecto
a
una
recta.
Transformaciones
isométricas
Lección
3
104
|
Unidad
3
CL0000000001052
104
12/17/2019
9:48:13
AM
4.
¿Cuál
es
el
cuerpo
generado
por
la
rotación
de
la
siguiente
figura?
A.
B.
C.
D.
5.
¿Qué
tipo
de
simetría
se
le
aplicó
al
cuerpo
geométrico
de
la
figura?
A.
Simetría
espacial
respecto
a
un
eje.
B.
Simetría
espacial
respecto
a
un
punto.
C.
Simetría
espacial
respecto
a
un
plano.
D.
Simetría
espacial
respecto
a
una
recta.
6.
¿Con
cuál
de
los
siguientes
cuerpos
geométricos
no
es
posible
rellenar
completamente
el espacio?
A.
Cubo.
B.
Prisma
de
base
hexagonal.
C.
Cilindro.
D.
Prisma
de
base
triangular.
7.
¿Cuál
es
la
generatriz
del
siguiente
cuerpo
generado
por
rotación?
A.
B.
C.
D.
3
Unidad
105
Lección
3
•
Transformaciones
isométricas
|
CL0000000001052
105
12/17/2019
9:48:13
AM
Evaluación
Lección
3
3
Unidad
320
Cuaderno
de
Actividades
•
Unidad
3
Espacial
con
respecto
a
un
punto.
Espacial
con
respecto
a
un
plano.
Espacial
con
respecto
a
un
eje.
Espacial
con
respecto
a
un
eje.
F'
D'
A'
B'
C'
E'
E'
C'
A'
B'
D'

Unidad
3
Orientaciones
de
uso
•
Estas
páginas
comprenden
una
evaluación
formativa
de
la
Lección
3
Transformaciones
isométricas.
Aborda
los
Objetivos
de
Aprendizaje
13
y
14
de
las
Bases
Curriculares.
A
partir
de
la
siguiente
información,
responde
de
la
pregunta
1
a
la
4.
1.
¿Cuáles
son
los
datos
suficientes
para
resolver
el
problema?
A.
Los
extremos
de
una
diagonal
del
rectángulo.
B.
El
eje
respecto
al
que
es
reflejado
el
rectángulo.
C.
Las
coordenadas
de
los
vértices
A,
B
y
C.
D.
Las
coordenadas
de
la
diagonal
y
el
eje
respecto
al
que
es
reflejado
el
rectángulo.
2.
¿Qué
es
lo
que
se
pregunta?
A.
Las
coordenadas
de
los
vértices
B
y
D,
luego
de
aplicar
la
reflexión.
B.
Las
coordenadas
de
los
vértices
B
y
D,
antes
de
aplicar
la
reflexión.
C.
Las
coordenadas
de
los
vértices
A
y
C,
luego
de
aplicar
la
reflexión.
D.
Las
coordenadas
de
los
vértices
A
y
C,
antes
de
aplicar
la
reflexión.
3.
¿Qué
estrategia
se
utilizó
para
resolver
el
problema?
A.
Ensayo
y
error.
B.
Plantear
una
ecuación.
C.
Usar
propiedades
numéricas.
D.
Construir
un
plano
cartesiano.
4.
¿Cuál
es
la
respuesta
al
problema?
A.
B’(4,
–2)
y
D(2,
4)
B.
B’(4,
2)
y
D(–2,
–4)
C.
B’(4,
–2)
y
D(–2,
–4)
D.
B’(–4,
–2)
y
D(–2,
–4)
Los
puntos
extremos
de
una
de
las
diagonales
de
un
rectángulo
ABCD
son
A(–2,
2)
y
C(4,
4).
Si
el
rectángulo
ABCD
es
reflejado
respecto
al
eje
X,
¿cuáles
son
las
coordenadas
de
los
vértices
B
y
D,
luego
de
aplicar
la
reflexión?
Luego
de
elegir
la
estrategia,
el
problema
se
resuelve
de
la siguiente
manera:
Y
O
X
1
–4
–5
2
–3
3
–2
4
5
–1
4
5
6
–1
3
–2
2
–3
1
–4
–5
–6
C'
B
B'
C
D'
A
A'
D
Evaluación
Lección
3
|
Unidad
3
106
CL0000000001052
106
12/17/2019
9:48:13
AM
•
¿En
qué
situaciones
puedes
observar
transformaciones
isométricas?
•
¿Qué
pasos
sigues
para
aplicar
las
distintas
transformaciones
isométricas?
Explica
cada
caso.
Reflexiona
y
responde
Reflexiona
y
responde
A
partir
de
la
siguiente
información,
marca
la
respuesta
correcta
en
las
preguntas
5
a
la
10.
Los
vértices
de
un
triángulo
ABC
son
A(1,
1),
B(4,
1)
y
C(4,
3).
Si
al
triángulo
se
le
aplica
una rotación
de
180°
en
torno
al
origen
y
luego
una
traslación
según
el
vector
v
=
(2,
0),
¿cuáles
son
las
coordenadas
de
A
luego
de
aplicadas
las
transformaciones
isométricas?
5.
¿Cuáles
son
los
datos
suficientes
para
resolver
el
problema?
A.
Los
vértices
del
triángulo.
B.
El
ángulo
y
centro
de
rotación.
C.
Los
vértices
del
triángulo
y
el
ángulo
y
centro
de
rotación.
D.
Los
vértices
del
triángulo,
el
ángulo
y
centro
de
rotación
y
el
vector
de
traslación.
6.
¿Qué
es
lo
que
se
pregunta?
A.
Las
coordenadas
de
A
luego
de
aplicar
la
rotación.
B.
Las
coordenadas
de
A
luego
de
aplicadas
las
transformaciones
isométricas.
C.
Las
coordenadas
de
B
y
C
luego
de
aplicadas
las
transformaciones
isométricas.
D.
La
figura
resultante
luego
de
aplicada
la
rotación.
7.
¿Qué
tipo
de
triángulo
es
ABC?
A.
Equilátero.
B.
Isósceles.
C.
Rectángulo.
D.
Obtusángulo.
8.
¿Cuál
es
la
respuesta
al
problema?
A.
A’’(1,
–1)
B.
A’’(–1,
–1)
C.
A’’(–1,
3)
D.
A’’(1,
–3)
9.
¿Cuáles
son
las
coordenadas
de
B
luego
de
aplicadas
las
transformaciones
isométricas?
A.
B’’(2,
–1)
B.
B’’(–2,
–1)
C.
B’’(–4,
–1)
D.
B’’(–4,
–3)
10.
¿Cuáles
son
las
coordenadas
de
C
luego
de
aplicadas
las
transformaciones
isométricas?
A.
C’’(–4,
–5)
B.
C’’(–4,
–3)
C.
C’’(–2,
–3)
D.
C’’(2,
–5)
3
Unidad
107
Evaluación
Lección
3
|
CL0000000001052
107
12/17/2019
9:48:13
AM
Cuaderno
de
Actividades
•
Unidad
3
321
0

Orientaciones
de
uso
•
Estas
páginas
comprenden
una
evaluación
formativa
de
la
Unidad
3
La
geometría
del
arte.
Aborda
los
Objetivos
de
Aprendizaje
11,
12,
13
y
14
de
las
Bases
Curriculares.
Marca
la
alternativa
correcta.
Justifica
en
cada
caso.
1.
¿Cuál
es
el
volumen
de
un
prisma
cuya
área
basal
es
25
cm
2
y
su
altura
mide
7
cm?
A.
175
cm
3
B.
32
cm
3
C.
18
cm
3
D.
3,5
cm
3
2.
¿Cuál
es
el
volumen
del
siguiente
prisma
de
base
cuadrada?
4
cm
8
cm
A.
16
cm
3
B.
32
cm
3
C.
36
cm
3
D.
128
cm
3
3.
Un
vaso
de
forma
cilíndrica
se
pinta
por
su
parte
exterior,
por
lo
que
se
cubre
una
superficie
de
56
π
cm
2
.
Si
el
radio
del
fondo
del
vaso
mide
4
cm,
¿cuál
es
su
altura?
A.
5
cm
B.
6
cm
C.
6,5
cm
D.
14
cm
4.
¿Cuál
es
el
área
del
triángulo
ABC?
C
B
A
25
cm
7
cm
A.
18
cm
2
B.
32
cm
2
C.
84
cm
2
D.
87,5
cm
2
Evaluación
final
|
Unidad
3
108
CL0000000001052
108
12/17/2019
9:48:13
AM
5.
¿Cuál
de
las
siguientes
alternativas
corresponde
a
las
medidas
de
los
lados
de
un triángulo rectángulo?
A.
12
cm,
35
cm,
37
cm
B.
13
cm,
36
cm,
37
cm
C.
33
cm,
56
cm,
64
cm
D.
36
cm,
77
cm,
83
cm
6.
¿Cuál
de
las
siguientes
transformaciones
se
aplicó
al
triángulo
ABC?
B
C
A
C'
A'
A.
Traslación.
B.
Rotación.
C.
Reflexión.
D.
Homotecia.
7.
Un
segmento
AB
se
traslada
según
el
vector
u,
y
luego
su
imagen
es
trasladada
según
el vector v.
¿Qué
vector
traslada
al
segmento
AB
desde
su
posición
inicial
hasta
su
posición final?
B
v
u
A
C.
D.
A.
B.
•
¿Qué
contenidos
crees
que
debes
repasar?
¿Por
qué?
•
¿Cuáles
crees
que
son
los
conceptos
clave
de
la
unidad?
Justifica
con
tres
argumentos.
Reflexiona
y
responde
3
Unidad
Evaluación
final
|
109
CL0000000001052
109
12/17/2019
9:48:13
AM
322
Cuaderno
de
Actividades
•
Unidad
3

Unidad
3
Cuaderno
de
Actividades
•
Unidad
3
323
2

Material
fotocopiable
1. Construye la red geométrica de los siguientes cuerpos.
a.
b.
c.
d.
2. Calcula el área total (AT) y el volumen (V) de los siguientes cuerpos. Considera π ≈ 3,14.
3 cm
3 cm
10 cm
AT =
V =
a.
3 cm
4 cm
12 cm
5 cm
AT =
V =
b.
13 cm
6 cm
AT =
V =
c.
324 Actividades complementarias • Unidad 3
Lección 1

Unidad
3
Material
fotocopiable
a. Dado un prisma cuya base cuadrada tiene un perímetro de 16 cm. Si la medida de su altura es el triple de
la medida de una de las aristas de su base, ¿cuál es el área total (AT) del prisma?
b. El volumen de un prisma, cuya base es un triángulo de altura 8 cm, tiene un volumen de 96 cm2
.
Si la altura del prisma mide 4 cm, ¿cuánto mide la base del triángulo?
c. El área de la cara lateral de un cilindro es 251,2 cm2
. Si la altura de este cuerpo mide 5 cm, ¿cuál es su
volumen? Considera π ≈ 3,14.
d. La medida del lado de un cuadrado, que es base de un prisma de altura 8 cm, se duplica. ¿En cuánto
aumenta su volumen?
e. El siguiente cuerpo está formado por dos cilindros. ¿Cuál es su área? ¿Cuál es su volumen?
9 cm
7 cm
7 cm
2 cm
325
Actividades complementarias • Unidad 3
Lección 1

Material
fotocopiable
1. Calcula el valor de x en cada caso.
x =
a.
8 cm
x
10 cm
x =
c.
26 cm
x
10 cm
x =
e.
15 cm
x
12 cm
x =
b.
24 m
x
7 m
x =
d. 21 dm
x
29 dm
x =
f.
1,3 m
x
0,5 m
2. Sean p q r las medidas de los lados de un triángulo. ¿Cuál es la condición que se debe cumplir para
que el triángulo sea rectángulo?
3. La diagonal de un rectángulo mide 2,9 cm. Si el ancho mide 0,9 cm menos que la diagonal,
¿cuánto mide su largo?
Lección 2

Unidad
3
Material
fotocopiable
a. Un terreno rectangular se dividirá por su diagonal instalando una cerca compuesta por tres alambres
de púas. Si el largo del terreno mide 150 m y su ancho 80 m, ¿cuántos metros de alambre de púas se
deberán utilizar?
b. ¿Cuál es el área total del prisma?
c. En la imagen se muestra el dibujo de un estanque con forma cilíndrica. Si su radio mide 12 m y
el segmento AB mide 26 m, ¿cuál es su capacidad? Considera π ≈ 3,14.
d. Una escalera cuya extensión máxima es de 25 m se apoya en el suelo a 7 m de la base de un edificio.
¿Cuál es la distancia desde el suelo al punto donde se apoya la escalera en el edificio?
e. El triángulo ABC es isósceles y AC = BC. ¿Cuál es el valor de x?
f. La siguiente figura representa una caja con forma de cubo. ¿Cuál es la distancia entre los vértices A y B?
A
B
8 cm
x
17 cm
A
C
B
A
B
10 cm
x
12 cm
15 cm
25 cm
327
Lección 2

Material
fotocopiable
1. Marca con una la transformación isométrica
aplicada en cada caso.
–1 1 2 3 4 5
–2
–3
–4
–5
–1
1
2
3
4
5
Y
X
O
B'
C'
A'
A B
C
a.
Reflexión respecto al eje X.
Traslación según el vector v = (3, –1).

Rotación en 180º y centro de rotación
en el origen.
–1 1 2 3 4 5
–2
–3
–4
–5
–1
1
2
3
4
5
Y
X
O
C'
D'
A'
B'
C
D
B
A
b.
Reflexión respecto al eje Y.
Traslación según el vector v = (8, 0).

Rotación en 90° en sentido horario y
centro de rotación en el origen.
–1 1 2 3 4 5
–2
–3
–4
–5
–1
1
2
3
4
5
Y
X
O
A'
A
B'
B C'
C
c.
Traslación según el vector u = (2, 0).

Rotación en 180° y centro de rotación
en el origen.
2. Responde.
a. Si al triángulo ABC, con vértices A(1, 4),
B(3, 5) y C(4, 3), se le aplica una rotación
de 180° con centro en el origen, ¿cuáles
serán las coordenadas de los vértices de
la figura imagen?
b. Al trasladar un cuadrado de vértices E(–20, 14),
F(–16, 14), G(–16, 18), H(–20, 18), se obtiene la
figura imagen cuyos vértices son E'(–4, 8),
F(0, 8), G(0, 12), H(–4, 12). ¿Cuál es el vector de
traslación?
c. ¿Qué cuerpo geométrico se forma al girar el
siguiente triángulo en torno al eje indicado?
.
3. Analiza si las siguientes afirmaciones son
verdaderas (V) o falsas (F).
a.
En las composiciones de transformaciones
isométricas no importa el orden en que
se aplique cada transformación.
b.
Hay tres tipos de reflexiones en el plano
cartesiano.
c.
En el espacio se puede hacer una reflexión
respecto a un punto.
d.
Todos los cuerpos geométricos son
generados por revolución de una
figura geométrica.
Lección 3

Unidad
3
Material
fotocopiable
1. Aplica las siguientes transformaciones isométricas y luego completa las coordenadas de los vértices
de cada figura.
–2 2 4 6 8 12
10 14 16 18 20 22 24 26 28
–4
–6
–8
–12–10
–14
–16
–18
–20
–22
X
–2
–6
2
4
6
8
10
12
14
16
18
–4
Y
O
C
D
B
A
a. Rota el cuadrilátero ABCD en 180° respecto del punto P(–4, 9), luego refleja la imagen A'B'C'D' respecto
al eje X y finalmente traslada A''B''C''D'' según el vector v = (–8, 10).
b. Completa.
• Las coordenadas de ABCD son A( , ), B( , ), C( , ) y D( , ).
• Las coordenadas de A'B'C'D' son A'( , ), B'( , ), C'( , ) y D'( , ).
• Las coordenadas de A''B''C''D'' son A''( , ), B''( , ), C''( , ) y D''( , ).
• Las coordenadas de A'''B'''C'''D''' son A'''( , ), B'''( , ), C'''( , ) y D'''( , ).
2. Dibuja la figura que al rotar alrededor del eje genera los siguientes cuerpos.
a. b.
329
Lección 3

Refuerzo
1. a. c.
d.
b.
2. a. AT = 138 cm2
; V = 90 cm3
b. AT = 156 cm2
; V = 72 cm3
c. AT = 715,92 cm2
; V = 1 469,52 cm3
Ampliación
1. a. El área total del prisma es 224 cm2
.
b. La base del triángulo que es la cara basal del prisma mide 6 cm.
c. El volumen del cilindro es de 1 004,8 cm3
.
d. El volumen del prisma se cuadruplica.
e. El área del cuerpo es 923,16 cm2
. Su volumen 1 934,24 cm3
.
330
Material
fotocopiable
Solucionario Actividades complementarias • Unidad 3

Unidad
3
Material
fotocopiable
Refuerzo
1. a. x = 6 cm
b. x = 25 m
c. x = 24 cm
d. x = 20 dm
e. x = 9 cm
f. x = 1,2 m
2. p2
+ q2
= r2
3. El largo del rectángulo mide 2,1 cm.
Ampliación
1. a. Se deberán utilizar 510 m de alambre de púas.
b. El área total del prisma de base triangular es 1 020 cm2
.
c. La capacidad del estanque es 4 521,6 m3
.
d. La escalera se apoya en el edificio a 24 m desde el suelo.
e. x = 30 cm
f. La distancia entre los vértices A y B es aproximadamente 17 cm.
331

Refuerzo
1. a.
Traslación según el vector v = (3, –1).
b.
Rotación en 90º y centro de rotación en el origen
y sentido horario.
c.
2. a. A(–1, –4), B(–3, –5), C(–4, –2)
b. v = (16, –6)
c. Un cono.
3. a. F
b. F
c. V
d. F
Ampliación
1. a.
–2 2 4 6 8 12
10 14 16 18 20 22 24 26 28
–4
–6
–8
–12–10
–14
–16
–18
–20
–22
X
–2
–6
–8
–10
2
4
6
8
10
12
14
16
18
–4
Y
O
C
D
D'
A'
B'
C'
D'''
B'''
A'''
B
A
A''
C'' B''
D''
C'''
b. • Las coordenadas de ABCD son A(–14, 12), B(–18, 8), C(–14, 8) y D(–8, 10).
• Las coordenadas de A'B'C'D' son A'(6, 6), B'(10, 10), C'(6, 10) y D'(0, 8).
• Las coordenadas de A''B''C''D'' son A''(6, –6), B''(10, –10), C''(6, –10) y D''(0, –8).
• Las coordenadas de A'''B'''C'''D''' son A'''(–2, 4), B'''(2, 0), C'''(–2, 0) y D'''(–8, 2).
2. a.
b.
332
Material
fotocopiable

Unidad
3
333

Material
fotocopiable
1. Si el largo de un rectángulo mide 8 cm y
el ancho 2,5 cm menos, ¿cuál es su área?
A. 20 cm2
B. 27 cm2
C. 44 cm2
D. 84 cm2
2. Si b es la medida de la base de un triángulo y h
la medida de su altura, ¿qué expresión permite
calcular su área (A)?
A. A = b + h
B. A = b • h
C. A =
b + h
2
D. A =
b • h
2
3. ¿Cuál es el perímetro (P) de una circunferencia
de radio 5 cm? Considera π ≈ 3,14.
A. P = 6,28 cm
B. P = 15,7 cm
C. P = 31,4 cm
D. P = 78,5 cm
4. ¿Cuál es el área (A) de una circunferencia
de radio 11 cm? Considera π = 3,14.
A. 379,94 cm2
B. 759,88 cm2
C. 75 988 cm2
D. 151 976 cm2
5. En el triángulo ABC, ¿cuál es la medida
del BACB?
A. 42º
B. 83º
C. 97º
D. 125º
6. Si el triángulo DEF es rectángulo, ¿cuál es la
medida que corresponde a la hipotenusa?
A. 5 cm
B. 12 cm
C. 13 cm
F
E
D
13 cm
12 cm
5 cm
D. 7 cm
7. ¿Cuál de las siguientes opciones representa una
traslación del rectángulo ABCD?
A
A'
B'
D'
C'
D
B
C
A.
A A'
B'
D'
C'
D
B
C
C.
A
A' B'
D' C'
D
B
C
B.
A
A'
B'
D'
C'
D
B
C
D.
8. ¿Cuáles son las coordenadas de los vértices
del triángulo GHI representado en el
plano cartesiano?
–1 1 2 3 4 5
–2
–3
–4
–5
X
–1
–3
1
2
3
4
–2
–4
Y
H
G I
O
A. G(–4, 2), H(–4, –4), I(4, 2)
B. G(–2, 4), H(–4, –4), I(2, 4)
C. G(4, –2), H(4, –4), I(2, 4)
D. G(4, 2), H(4, 4), I(4, 2)
C
A
B
55º
42º
334 Instrumentos de evaluación • Unidad 3

Unidad
3
Material
fotocopiable
Resuelve los siguientes problemas.
9. Si el triángulo ABC es rectángulo en B, determina las medidas de los ángulos x, y y z.
C
A
z
B
142º
y
x
10. Traslada el cuadrilátero DEFG 5 unidades a la derecha y 3 unidades hacia abajo y luego refléjalo con
respecto a la recta L.
F
D
E
G L
335
Instrumentos de evaluación • Unidad 3

Instrumentos de evaluación: Evaluación de proceso
1. Escribe el nombre del cuerpo geométrico que
se puede armar con cada una de las siguientes
redes geométricas.
b.
a. c.
2. Resuelve los problemas en tu cuaderno.
a. El área total de un cubo es 150 m2
. ¿Cuál es
la medida de su arista?
b. La arista de un cubo mide 22
5
m. ¿Cuál es
su área?
c. Vicente debe pintar por fuera una caja con
forma de cubo cuya arista mide 12 m. Si un
tarro de pintura le alcanza para cubrir 20 m2
,
¿cuántos de ellos utilizará si debe aplicar
dos manos?
d. La distancia mínima entre dos vértices en un
cubo es 6,3 cm. ¿Cuál es su área?
e. Para una maqueta Francisca necesita cubrir,
con un papel especial, una caja con forma de
prisma de base rectangular cuyas medidas son
12 cm, 25 cm y 17 cm. Si el papel vale $120
el centímetro cuadrado, ¿cuánto gastará?
f. Camilo pintará una estructura formada por
dos cubos, en la que la arista de uno de ellos
mide el doble de la del otro. Si una de las
caras del menor se dispone sobre una de las
del mayor como se muestra en la figura, ¿cuál
es la medida de la superficie visible?
18 cm
g. El área total de un cilindro es 251,2 m2
. Si el área
de su base mide 12 m2
, ¿cuál es su área lateral?
h. El radio de un cilindro es de 1
2
cm y su altura
mide el triple de ese radio. ¿Cuál es su área total?
3. Calcula el volumen (V) de los siguientes
cuerpos geométricos.
2 cm 3 cm
3 cm
a.
1
1
2
cm
1
1
2
cm
11
2
cm
b.
9 cm
15 cm
c.
336
Material
fotocopiable
Lección 1 y 2

Unidad
3
Material
fotocopiable
a. La base de un prisma es un triángulo
rectángulo cuyos catetos miden 12 cm y 9 cm.
Si su altura mide 8 cm, ¿cuál es su volumen?
b. Una piscina tiene forma de prisma de base
rectangular. Si su largo es de 15 m, su ancho
de 4 m y su profundidad de 2 m, ¿con cuántos
litros de agua se llena?
c. ¿Cuál es el volumen de un cilindro en el cual
el radio de su base es 5 cm y la medida de su
altura es el doble de la medida de su diámetro?
5 cm
d. Un cilindro tiene 5 m de altura y el área de su
base es de 254,34 m2
. ¿Cuál es su volumen?
e. En un prisma que tiene como base un
pentágono regular, su apotema mide 2,75 cm
y su altura 4,5 cm. Si la arista basal mide 4 cm,
¿cuál es su volumen?
5. Determina cuál(es) de los siguientes tríos de
longitudes permite(n) formar un triángulo
rectángulo.
a. 10 cm, 8 cm y 6 cm.
b. 5 cm, 12 cm y 13 cm.
c. 6 cm, 12 cm y 15 cm.
d. 0,3 m, 0,4 m y 0,5 m.
6. Dos cables de igual longitud sostienen una
antena a una altura de 8 m. Si las distancias de
los puntos de fijación de los cables al suelo es
de 12 m, ¿cuántos metros de cable se utilizaron
para sostener la antena?
Marca la opción correcta del ítem 7 al 12.
7. ¿Cuál es el área total del cuerpo que se
representa a continuación?
A. 42 cm2
B. 62,5 cm2
C. 73 cm2
D. 36,5 cm2
8. ¿Cuál es el área del cuerpo que se muestra
a continuación?
A. 72π cm2
B. 84π cm2
C. 180π cm2
D. 252π cm2
9. El área de la cara de un cubo es 9 m2
. ¿Cuál es
su volumen?
A. 27 m3
B. 54 m3
C. 81 m3
D. 729 m3
10. Un edificio está formado por dos prismas de
base rectangular, como se muestra en la figura.
¿Cuál es la superficie que queda a la intemperie?
A. 626 m2
B. 706 m2
C. 857 m2
D. 1 396 m2
11. ¿Cuál es el volumen del cuerpo que se muestra
a continuación?
A. 37,1 cm3
B. 98 cm3
C. 259,7 cm3
D. 519,4 cm3
12. El área de la base de un cilindro es 25π cm2
. Si su
volumen es 200π cm3
, ¿cuál es su altura?
A. 8 cm
B. 8π cm
C. 225 cm
D. 225π cm
3 cm
3,5 cm
4 cm
6 cm
15 cm
3 m
15 m
10 m
8 m
7 m 4 m
7 cm
14 cm
5,3 cm
337

1. Dibuja en tu cuaderno y aplica la transformación
isométrica pedida.
a. Traslación respecto del vector v = (4, –1).
Y
X
O
A
B
C
D
b. Simetría respecto del eje Y.
Y
X
O
A B
E
C
D
c. Rotación respecto del punto A y en 90º en
Y
X
O
A
B
E
C
D
d. Simetría respecto del punto P.
Y
X
O
A
B
P
C
2. Dibuja los elementos pedidos en cada caso.
a. El eje de simetría entre la figura original y
su figura imagen.
A
A'
D'
C'
B'
B C
D
b. El centro de rotación aplicado al triángulo ABC.
Y
X
O
A
A'
C'
B'
B
C
3. Aplica la o las transformaciones solicitadas
en cada caso en tu cuaderno y escribe las
coordenadas de la imagen resultante.
a. Sobre el punto M(2, –3) se aplica una traslación
con respecto al vector v = (2, 5) y luego una
reflexión respecto del eje X.
b. Sobre el punto P(3, –4) se aplica una reflexión
respecto del punto A(4, 7).
c. Se aplica una reflexión respecto del eje X sobre
el punto F(–5, –7).
d. Sobre el punto P(–5, 8) se aplica una reflexión
respecto del eje Y, luego una reflexión
respecto del eje X.
e. Sobre el triángulo ABC con A(3, 4), B(–3, 1) y
C(1, –5), se aplica una rotación respecto del
punto O(0, 0) en 90º en sentido horario y
luego una reflexión respecto del eje Y.
338
Material
fotocopiable
Lección 3

Unidad
3
Material
fotocopiable
4. Determina la transformación isométrica
realizada en cada caso.
v
a.
H
b.
L
c.
5. Determina los planos de simetría del siguiente
cuerpo geométrico.
6. Aplica una reflexión respecto del plano sobre
el cuerpo que se representa a continuación.
Marca la opción correcta del ítem 7 al 11.
Puedes hacer los cálculos en tu cuaderno.
7. Al aplicar una traslación al punto A(–7, –1)
resulta la imagen A'(8, –5). ¿Cuál fue el vector
de traslación aplicado?
A. v = (15, 4)
B. v = (–15, 4)
C. v = (15, –4)
D. v = (–15, –4)
8. Si se aplica una rotación respecto del origen
sobre el punto M(8, –5) en un ángulo de 270º
en sentido antihorario, ¿cuál es el punto que
se obtiene como imagen?
A. M'(5, 8)
B. M'(–8, 5)
C. M'(5, –8)
D. M'(–5, –8)
9. Se aplica sobre el punto H(3, –5) una reflexión
respecto del eje X. ¿Cuál es su imagen?
A. H'(3, 5)
B. H'(–5, 3)
C. H'(–3, 5)
D. H'(–3, –5)
10. ¿Con cuál de estos polígonos es posible
construir una teselación en el plano?
A. Eneágono regular.
B. Pentágono regular.
C. Hexágono regular.
D. Heptágono regular.
11. Respecto de las transformaciones isométricas
aplicadas en el espacio, ¿cuál de las siguientes
afirmaciones es falsa?
A. Su área mantiene su valor.
B. Su posición es la que varía.
C. El volumen del cuerpo varía.
D. Las aristas no se modifican en su longitud.
339

Material
fotocopiable
1. Calcula el área total (AT) y el volumen (V) de
cada cuerpo.
3,7 cm
6 cm
1,1 cm
a.
6 cm
2 cm
b.
2. Calcula el valor de x en cada caso
4,4 cm
x
3,3 cm
a.
13 m
x
12 m
b.
3. Determina las coordenadas de la imagen
resultante en cada caso.
a. Se aplica una traslación sobre el punto H(4, –2)
con respecto al vector v = (4, –2).
b. Se aplica una reflexión respecto del eje X sobre
el punto L(7, 3).
c. Se aplica una rotación respecto del punto
O(0, 0) sobre el punto J(3, 5) en 90º en
sentido horario.
4. Reconoce las transformaciones isométricas
aplicadas.
Y
X
O
D
D'
A
A'
B
B'
C
C'
a.
Y
X
O
F
A
E
E'
D
D'
C
B
A'
F'
C'
b.
a. La arista de un cubo mide 5 cm. ¿Cuál es
su área?
b. El radio de un cilindro mide 4,5 cm y su altura
es de 4 cm. ¿Cuál es su área?
c. La base de un prisma tiene un área de 45 cm2
.
Si su altura es de 6 cm, ¿cuál es su volumen?
d. ¿Cuál es el área de un triángulo rectángulo
cuya hipotenusa mide 10 cm y uno de los
catetos mide 6 cm?
e. El volumen de un cilindro es de 48π m3
. Si su
altura es de 3 m, ¿cuánto suman las áreas de
sus caras basales?
f. En el cuerpo que se representa a continuación,
la diagonal de la base mide 3 cm. ¿Cuál es
su volumen?
2,4 cm
5 cm
g. En la figura se muestra un triángulo rectángulo
en C. ¿Cuál es el área del cuadrado que
se observa?
18 cm
24 cm
B
A
C
h. Se aplica una traslación del punto A(2, 7) y se
obtiene el punto A'(–5, 8). ¿Cuál es el vector
de traslación?
i. Se aplica una rotación con centro en O(0, 0)
en un ángulo de 180º en sentido antihorario
sobre el punto E(2, –6). ¿Cuál es la imagen
que se obtiene?

Unidad
3
Material
fotocopiable
1. ¿Cuál es el área total del prisma que se construye
con la siguiente red geométrica? Considera que
la base del prisma es un triángulo equilátero de
altura h ≈ 5,2 cm.
17 cm
6 cm
A. 102 cm2
B. 306 cm2
C. 337,2 cm2
D. No se puede
determinar.
2. ¿Cuál es el área basal de la siguiente pirámide de
base cuadrada?
h
3 cm
A. 5 cm2
B. 9 cm2
C. 1 215 cm2
D. 2 025 cm2
3. ¿Cuál de los siguientes paralelepípedos no tiene
un volumen igual a 216 cm3
?
3 cm
9 cm
8 cm
A.
6 cm
6 cm
6 cm
B.
2 cm
9 cm
27 cm
C.
2 cm
18 cm
6 cm
D.
4. ¿Cuánto mide la altura (h) del siguiente
triángulo equilátero?
18 cm
h
A. 3 cm
B. 243 cm
C. 315 cm
D. 1 458 cm
5. ¿Cuánto mide el largo de un rectángulo si
su ancho mide 9 cm y su diagonal 15 cm?
A. 6 cm
B. 12 cm
C. 14 cm
D. 144 cm
6. ¿Cuánto miden las diagonales del siguiente rombo?
A
B
C
D
E
5 cm
A. 3 y 4 cm
B. 5 y 6 cm
C. 6 y 8 cm
D. 8 y 9 cm
341

Material
fotocopiable
7. A un triángulo ABC con vértices en A(2, 3),
B(5, 6) y C(8, 5) se le aplica una rotación de
90° en sentido horario y centro de rotación
en el origen. ¿Cuáles son las coordenadas
de la figura imagen?
A. A'(3, –2), B'(6, –5) y C'(5, –8)
B. A'(3, 2), B'(6, 5) y C'(5, 8)
C. A'(–3, –2), B'(–6, 5) y C'(5, –8)
D. A'(–3, 2), B'(6, –5) y C'(5, –8)
8. ¿Qué transformación se aplicó en EFGHI para
obtener la imagen E'F'G'H'I'?
L
E F
G
G'
F' E'
I'
H'
H
I
P
A. Reflexión respecto a L.
B. Rotación en 180° con centro en P.
C. Traslación según el vector (4, 0).
D. Rotación en 90° con centro en P y
sentido horario.
9. Respecto a las transformaciones isométricas,
¿cuál de las siguientes afirmaciones
es verdadera?
A. La simetría axial es una reflexión en la que se
utiliza el punto de simetría.
B. En una traslación todos los puntos se mueven
respecto de un punto fijo.
C. En una rotación se desplazan los puntos
de una figura en igual magnitud, dirección
y sentido.
D. La simetría central es un tipo de reflexión.
10. ¿Cuál es una condición que debe cumplir
siempre una teselación?
A. Las figuras pueden sobreponerse.
B. Las figuras deben ser congruentes.
C. Las figuras deben ser polígonos regulares.
D. No deben quedar espacios entre las figuras.
11. ¿Qué transformaciones se aplican a ABCDE
para obtener el siguiente diseño?
E A
D
B
C
A. Rotación.
B. Traslación.
C. Reflexión – simetría central.
D. Reflexión – simetría axial.
12. ¿Qué composiciones de transformaciones
isométricas se aplicaron a la figura A?
A
A'
A'''
A''
A. Traslación – reflexión – traslación – reflexión.
B. Reflexión – traslación – reflexión – traslación.
C. Reflexión – rotación – reflexión – rotación.
D. Rotación – reflexión – rotación – reflexión.

Unidad
3
Material
fotocopiable
1. C
2. D
3. C
4. A
5. B
6. C
7. B
8. A
9. x = 38º; y = 52º; z = 128º.
10.
F
D
E
G
F'
D'
E'
G' F''
D''
E''
G''
Objetivos de Aprendizaje ítems Indicadores de logro
• Calcular el área de un triángulo y de un paralelógramo.
• Calcular el perímetro y el área de un círculo.
1, 2, 3 y 4
• Determinar la medida de ángulos en el triángulo e identificar catetos e
hipotenusa en triángulos rectángulos.
5, 6 y 9
• Realizar transformaciones isométricas de figuras geométricas.
• Identificar puntos en el plano cartesiano.
7, 8 y 10
343
Solucionario Instrumentos de evaluación • Unidad 3

Material
fotocopiable
Evaluación de proceso Lección 1 y 2.
• Calcular el área de prismas y cilindros.
• Resolver problemas que involucran el cálculo del área de prismas y cilindros.
1, 2, 7, 8, 9
y 10
• Calcular el volumen de prismas y cilindros.
• Resolver problemas que involucran el cálculo del volumen de prismas y
cilindros.
3, 4, 11 y 12
• Verificar con las medidas dadas de un triángulo si es rectángulo o no.
• Resolver problemas de la vida diaria para calcular la medida de lados
desconocidos y no accesibles.
5 y 6
1. a. Prisma de base triangular.
b. Prisma de base hexagonal.
c. Prisma de base pentagonal.
2. a. La arista mide 5 cm.
b. El área del cubo es 34,56 m2
.
c. Vicente debe utilizar 87 tarros de pintura.
d. El área del cubo es 79,38 cm2
.
e. Francisca gastará $ 222 960.
f. La medida de la superficie visible es 2 268 cm2
.
g. El área lateral del cilindro es 257 cm2
.
h. El área total del cilindro mide 6,28 cm2
.
3. a. V = 18 cm3
b. V = 3,375 cm3
c. V = 607,5 cm3
4. a. El volumen del prisma es 432 cm3
.
b. La piscina se llena con 120 000 L de agua.
c. El volumen del cilindro es 1 570 cm3
.
d. El volumen del cilindro es 1 271,7 m3
.
e. El volumen del prisma es 123,75 cm3
.
5. a. Sí
b. Sí
c. No
d. Sí
6. Para sostener la antena se utilizaron 28,84 m de cable.
7. C
8. D
9. A
10. B
11. C
12. A
344 Solucionario Instrumentos de evaluación • Unidad 3

Unidad
3
Material
fotocopiable
1. a.
Y
X
O
A
A'
B
B'
C
C'
D
D'
b.
Y
X
O
A
A' B
B'
E
E'
C
C' D
D'
c.
Y
X
O
A
B
E
C
D
D'
E'
C'
B'
d.
Y
X
O
A
A'
C'
B'
B
P
C
2. a.
A
A'
D'
C'
B'
B C
D
b.
Y
X
O
A
A'
C'
B'
B
C
3. a. (4, –2)
b. (5, 18)
c. (–5, 7)
d. (5, –8)
e. A'(–4, –3); B'(–1, 3); C'(5, –1)
4. a. Traslación respecto a v.
b. Reflexión respecto a H.
c. Rotación respecto a L.
5. 6.
7. C
8. D
9. A
10. C
11. C
Evaluación de proceso Lección 3.
• Realizar traslaciones en el plano cartesiano con vectores dados.
• Determinar el vector de traslación entre la imagen y la preimagen de 2 figuras.
• Reflexionar figuras según los ejes dados.
• Determinar el eje de reflexión entre la imagen y la preimagen de dos figuras.
• Realizar rotaciones de figuras dados el centro y ángulo de rotación.
• Determinar el centro y ángulo de rotación entre la imagen y la preimagen de dos figuras.
1, 2, 7, 8 y 9
Logrado:3ítemscorrectosomás.
Por lograr: menos de 3 ítems
correctos.
• Realizar composiciones de traslaciones, reflexiones y rotaciones.
• Identificar polígonos con los cuales es posible construir una teselación en el plano.
• Reconocer transformaciones isométricas dadas en el plano y en el espacio, identificando
puntos importantes, como vector de traslación, centro de rotación, ángulo de rotación,
eje o punto de reflexión.
• Determinar los planos de simetría de cuerpos geométricos.
3, 4, 5, 6, 10
y 11
Logrado:4ítemscorrectosomás.
Por lograr: menos de 4 ítems
correctos.
345

Material
fotocopiable
Evaluación formativa
1. a. A = 65,74 cm2
; V = 24,42 cm3
b. A = 354,02 cm2
; V = 280 cm3
2. a. 5,5 cm
b. 5 m
3. a. H'(8, –4)
b. L'(7, –3)
c. J'(5, –3)
4. a. Traslación.
b. Reflexión.
5. a. 150 cm2
b. 76,5π cm2
c. 270 cm3
d. 24 cm2
e. 32π cm2
f. 21,6 cm3
g. 900 cm2
h. (–7, 1)
i. (–2, 6)

Unidad
3
Material
fotocopiable
Evaluación final
1. C
2. B
3. C
4. B
5. B
6. C
7. A
8. B
9. D
10. D
11. B
12. B
• Desarrollar las fórmulas para encontrar el área de superficies y el volumen de
prismas rectos con diferentes bases y cilindros:
-
- estimando de manera intuitiva área de superficie y volumen
-
- desplegando la red de prismas rectos para encontrar la fórmula del área de
superficie
-
- transfiriendo la fórmula del volumen de un cubo (base por altura) en prismas
diversos y cilindros
-
- aplicando las fórmulas a la resolución de problemas geométricos y de la
vida diaria.
1, 2, 3, 4, 5,
6 y 7
• Explicar, de manera concreta, pictórica y simbólica, la validez del teorema de
Pitágoras y aplicarlo a la resolución de problemas geométricos y de la vida
cotidiana, de manera manual y/o con software educativo.
4, 5 y 6
• Describir la posición y el movimiento (traslaciones, rotaciones y reflexiones)
-
- los vectores para la traslación
-
- los ejes del plano cartesiano como ejes de reflexión
-
- los puntos del plano para las rotaciones.
7, 8 y 9
• Componer rotaciones, traslaciones y reflexiones en el plano cartesiano y en
el espacio, de manera manual y/o con software educativo, y aplicarlas a las
simetrías de polígonos y poliedros, y a la resolución de problemas geométricos
relacionados con el arte.
10, 11 y 12
347

*Horas pedagógicas
Unidad
Tiempo
estimado*
Clases
Sección /
Lección
Actitud
Unidad
3
OA B
OA C
OA D
14 62 a 72
Lección 1
Área y volumen
de prismas y
cilindros
OA 11 Desarrollar las fórmulas para encontrar el área de superficies y el volumen
de prismas rectos con diferentes bases y cilindros: :
• Estimando de manera intuitiva área de superficie y volumen.
• Desplegando la red de prismas rectos para encontrar la fórmula del área de
superficie
• Transfiriendo la fórmula del volumen de un cubo (base por altura) en prismas
diversos y cilindros.
• Aplicando las fórmulas a la resolución de problemas geométricos y de la vida diaria.
16 73 a 80
Lección 2
Teorema de
Pitágoras
OA 12 Explicar, de manera concreta, pictórica y simbólica, la validez del teorema de
Pitágoras y aplicar a la resolución de problemas geométricos y de la vida cotidiana,
22 81 a 91
Lección 3
Transformaciones
isométricas
OA 13 Describir la posición y el movimiento (traslaciones, rotaciones y reflexiones)
• Los vectores para la traslación.
• Los ejes del plano cartesiano como ejes de reflexión.
• Los puntos del plano para las rotaciones.
OA 14 Componer rotaciones, traslaciones y reflexiones en el plano cartesiano y en
el espacio, de manera manual y/o con software educativo, y aplicar a las simetrías de
polígonos y poliedros, y a la resolución de problemas geométricos relacionados con
el arte.
6 92 a 94 Fin de unidad OA 11, OA 12, OA 13, OA 14
Unidad
4
OA D
OA E
OA F
16
96 a
103
Lección 1
Estadística
OA 15 Mostrar que comprenden las medidas de posición, percentiles y cuartiles:
• Identificando la población que está sobre o bajo el percentil.
• Representándolas con diagramas, incluyendo el diagrama de cajón, de manera
manual y/o con software educativo.
• Utilizándolas para comparar poblaciones.
OA 16 Evaluar la forma en que los datos están presentados:
• Comparando la información de los mismos datos representada en distintos tipos de
gráficos para determinar fortalezas y debilidades de cada uno.
• Justificando la elección del gráfico para una determinada situación y su
• Detectando manipulaciones de gráficos para representar datos.
16
104 a
111
Lección 2
Probabilidades
OA 17 Explicar el principio combinatorio multiplicativo:
• A partir de situaciones concretas.
• Representándolo con tablas y árboles regulares, de manera manual y/o con software
educativo.
• Utilizándolo para calcular la probabilidad de un evento compuesto.
6
112 a
114
Fin de unidad OA 15, OA 16, OA 17
348 Planificación semestral

Unidad
4
Habilidades Indicadores de evaluación
Guía Didáctica
del Docente
OAH c
OAH e
OAH f
OAH g
OAH h
• Arman y despliegan cajas de forma de prismas rectos.
• Elaboran redes de prismas rectos de diferentes bases y calculan las áreas de las superficies.
• Resuelven problemas cotidianos que involucran el volumen y el área de prismas rectos.
• Confeccionan de manera concreta modelos de cilindros y los comparan con modelos o
dibujos de prismas a base de polígonos regulares.
• Transfieren la fórmula del volumen de un cubo para determinar la del volumen de un cilindro.
• Calculan el área de cilindros en ejercicios rutinarios.
• Resuelven problemas cotidianos relacionados con el área y el volumen de cilindros.
pág. 325
• Descubren el teorema de Pitágoras concreta o pictóricamente.
• Dibujan triángulos rectángulos con los cuadrados respectivos encima de los catetos y
la hipotenusa, y verifican la validez del teorema de Pitágoras.
• Estiman las raíces cuadradas que resultan al aplicar el teorema de Pitágoras.
• Verifican con las medidas dadas de un triángulo si es rectángulo o no.
• Calculan el largo del lado faltante para que un triángulo sea rectángulo y lo verifican.
pág. 327
Lección 1 y 2 pág. 336
• Realizan traslaciones en el plano con vectores dados.
• Determinan el vector entre la imagen y la preimagen de 2 figuras 2D.
• Reflexionan figuras 2D según los ejes dados, de manera concreta y pictórica.
• Determinan el eje de reflexión entre la imagen y la preimagen de dos figuras 2D.
• Identifican rotaciones, reflexiones y traslaciones en situaciones cotidianas.
• Realizan traslaciones, reflexiones y rotaciones y reconocen las propiedades.
• Realizan teselados con figuras 2D, según los patrones dados.
• Identifican patrones de teselados dados, descubriendo las propiedades de la congruencia.
• Reconocen transformaciones isométricas dadas en el plano.
• Realizan combinaciones de traslaciones, reflexiones y rotaciones y reconocen las propiedades.
pág. 329
Lección 3 pág 338
OAH c
OAH d
OAH f
OAH h
OAH k
OAH l
• Organizan y agrupan datos en tablas o esquemas para formar distribuciones de frecuencias.
• Calculan, describen e interpretan las medidas de posición (cuartiles y percentiles).
• Representan las medidas de posición por medio de diagramas de cajón.
• Reconocen cuándo es adecuado utilizar alguna de las medidas para analizar una muestra.
• Comparan muestras de poblaciones, utilizando algunas de las medidas de tendencia.
• Explican la elección de tipos de gráficos para representar determinada información.
pág. 411
(de pocos pasos) y describen pictóricamente los resultados, vía árboles.
(de pocos pasos).
pág. 413
349
Planificación semestral 349

Sección/Lección
Tiempo estimado
Clases OA
Texto del Estudiante/
Cuaderno de Actividades
diagnóstica
Lección 1
Estadística
16 96 a 103
OA 15
OA 16
• Representaciones gráficas
• Medidas de posición
Lección 2
Probabilidades
16 104 a 111 OA 17
• Principio multiplicativo
• Cálculo de probabilidades
Fin de unidad 6 112 a 114
OA 15
OA 16
OA 17
El deporte
¿Cómo se relacionan la estadística y la probabilidad con el deporte?
350 Planificación Unidad 4

Unidad
4
Páginas del Texto
del Estudiante
Páginas del
Cuaderno de
Actividades
Páginas de la Guía Didáctica del Docente
Planificación
de clases
Recursos
176 a 191 110 a 121 356 a 371
192 a 205 122 a 131 372 a 385
206 a 209 132 y 133 386 a 389
351
Planificación Unidad 4 351

Unidad
4
¿Cómo se relacionan la estadística y la probabilidad con el deporte?
El deporte
En esta unidad los estudiantes trabajan en la comprensión de elementos de un estudio estadístico.
La unidad se inicia con la interpretación y construcción de diferentes tipos de gráficos, como el gráfico
de línea, el gráfico de barra, el gráfico circular y el histograma, con el propósito de que el estudiante
decida la pertinencia de cada uno de estos según una situación dada.
Luego, se trabajan las medidas de posición introduciendo los conceptos de cuartiles y percentiles para
situaciones en las que existe una distribución de datos. Estos conocimientos se aplican en la interpretación
y construcción de diagramas de cajón.
En la última lección se abordan técnicas de conteo con las cuales los estudiantes pueden determinar el
número de combinaciones posibles en situaciones dadas y así aplicarlo al cálculo de elementos de un
espacio muestral de un experimento dado. Para ello, los estudiantes aplican el principio multiplicativo
en diferentes situaciones y lo representan utilizando diagramas de árbol.
Finalmente, calculan la probabilidad de un suceso considerando la regla de Laplace.
352 Presentación de la Unidad 4

Unidad
4
Ruta de aprendizaje de la Unidad 4
(Preguntas específicas relacionadas
con la temática de la unidad, las
imágenes y el texto introductorio)
• ¿Cómo puedes decidir cuándo un
deportista es mejor que otro?
• ¿Cómo se puede utilizar la
estadística en el ámbito del
deporte? Da algunos ejemplos.
• ¿Cuál crees que es la probabilidad
de marcar un gol el último minuto
en un partido de fútbol? Explica.
El deporte
Lecciones que se articulan según los
Objetivos de Aprendizaje de la unidad.
Evaluación final
• Representaciones gráficas
• Medidas de posición
• Principio multiplicativo
• Cálculo de probabilidades
La estructura de la unidad se muestra a continuación:
353

Propósito
En esta unidad los estudiantes
comprenderán conceptos clave de
estadística y el uso de representaciones
gráficas para presentar grandes cantidades
de información.
OA 15 , OA 16 , OA 17
Planificación
Orientaciones y
Para el desarrollo de la unidad, los estudiantes deberán repasar:
• Muestreo
• Tablas de frecuencias absolutas y relativas
• Medidas de tendencia central y rango
• Probabilidades de eventos
Actitudes
A lo largo de esta unidad trabajarás las
los aportes de todos, y manifestando
OA E Mostrar una actitud crítica al
evaluar las evidencias e informaciones
matemáticas y valorar el aporte de los
datos cuantitativos en la comprensión
de la realidad social.
OA F Usar de manera responsable
y efectiva las tecnologías de la
comunicación en la obtención de
información, dando crédito al trabajo
de otros y respetando la propiedad y la
privacidad de las personas.
págs. 174 y 175
Clase 95
El deporte
4
Unidad
| Matemática 8ºB
174
L
E
e
•
•
•
CL0000000001018 MA

Unidad
4
Inicio 15 minutos
Comparta con sus estudiantes el propósito
de la unidad. Analice junto con ellos la
fotografía e invítelos a compartir sus
respuestas acerca de las preguntas planteadas.
Invite a sus estudiantes a realizar
la evaluación diagnóstica de forma
individual, registrando las respuestas en
su cuaderno. Una vez finalizada, revise
cada uno de los ejercicios en la pizarra,
corrigiendo posibles errores cometidos.
Cierre 15 minutos
Permita que sus estudiantes comenten
las dificultades que presentaron en
esta actividad con el fin de reforzar
los contenidos involucrados.
El azar es inherente a nuestra vida cotidiana y podemos establecer
distintas aplicaciones para el cálculo de probabilidades. En ocasiones
nuestra percepción y/o intuición pueden afectar negativamente este
cálculo de probabilidades, por lo que es necesario reforzar estos
conceptos para el análisis de acciones frente a la incertidumbre:
El documento “Razonamiento probabilístico en la vida cotidiana:
un desafío educativo” (disponible en: https://www.ugr.es/~batanero/
pages/ARTICULOS/ConferenciaThales2006.pdf) permite abordar esta
problemática desde una mirada didáctica.
Para apoyar su labor docente le ofrecemos
las imágenes de la unidad en el link
http://www.recursostic.cl/lic19/mat8_u4.
2/17/2019 9:31:19 AM
1. Escribe el espacio muestral del experimento
aleatorio de “lanzar dos monedas”.
2. En una caja hay fichas numeradas del
1 al 8 y se extrae una al lanzar. ¿Cuál es
la probabilidad de obtener el número 5?
3. ¿Cuál es la probabilidad de obtener menos
de 4 puntos al lanzar un dado?
4. Los siguientes datos corresponden a la
cantidad de veces que un grupo de niños
y de niñas juega fútbol a la semana.
1 – 4 – 3 – 1 – 4 – 1 – 2 – 7 – 5 – 1 – 3 – 1
0 – 3 – 2 – 1 – 4 – 3 – 5 – 2 – 3 – 4 – 6 – 4 – 5
a. Representa los datos en una tabla.
b. ¿Cuál es el promedio? ¿cómo interpretas
este valor?
Lección 1
Estadística
Página176
Lección 2
Probabilidad
Página192
En esta unidad estudiarás las medidas de posición
y utilizarás diversos gráficos para representar los
datos. Además, aplicarás el principio multiplicativo
para calcular la probabilidad de un evento.
Los números juegan un papel cada vez más importante en el deporte.
En las competencias la relación con las Matemáticas es palpable, por
ejemplo, en las etapas de clasificaciones.
• ¿Cómo puedes decidir cuándo un deportista es mejor que otro?
• ¿Cómo se puede utilizar la estadística en el ámbito del deporte?
Da algunos ejemplos.
• ¿Cuál crees que es la probabilidad de marcar un gol el último minuto
en un partido de fútbol? Explica.
355

Propósito
algunas de las representaciones gráficas
más importantes en estadística para
presentar información.
OA 16
Inicio 15 minutos
la situación propuesta, invitándolos
a compartir las respuestas de las
preguntas planteadas.
Reflexione junto con ellos acerca
de las ventajas y/o desventajas de
representar una serie de datos a
partir de gráficos estadísticos.
Planificación
Para profundizar en las dificultades que presentan algunos gráficos
estadísticos para los estudiantes se sugiere la lectura del documento
“Construcción y razonamiento de gráficos estadísticos en la
formación de profesores” disponible en: funes.uniandes.edu.co/1277/1/
Espinel2008Construccion_SEIEM_99.pdf
págs. 176 a 179
Clase 96
Actitudes
OA D , OA F
Representaciones gráficas
Analiza la información y responde.
• ¿A qué atribuyes el sedentarismo de los chilenos?
• ¿Cuántas horas dedicas semanalmente a realizar
actividad física?
• ¿Reconoces la importancia de practicar actividad física?
Estadística
Lección 1
En esta lección trabajarás con las
medidas de posición y representarás
los datos utilizando diagramas
y gráficos.
El gráfico muestra uno de los resultados de la“encuesta nacional de hábitos de actividad física y
deporte”encabezada por el Ministerio del Deporte y ejecutada por la Universidad de Concepción.
La encuesta fue aplicada a 6025 personas de 18 años y más, entre los meses de octubre y
noviembre del año 2018.
2006 2012
2009 2015 2018
Años
20
40
60
100
80
Activos + Medianamente practicantes
0
26,4% 29,3% 29,4% 31,8% 33,8%
20
40
60
100
80
Inactivos
0
73,6% 70,7% 70,6% 68,1% 66,2%
176 | Unidad 4
E
P
f
•
E
L
e
CL0000000001018 MA

Unidad
4
Analice junto con sus estudiantes los
ejemplos propuestos, invitándolos a
extraer conclusiones de los datos a
partir de la representación.
Estudie la utilidad de cada uno de los
gráficos apoyado de la información
contenida en Aprende. Permita que sus
estudiantes determinen ejemplos de
variables que puedan ser representadas
con estos gráficos.
Es importante promover en todo
momento un ambiente de respeto y
compañerismo, en el que todas las
opiniones y dudas sean escuchadas
y, al mismo tiempo, resueltas. Para
ello puede, por ejemplo, motivar
a los estudiantes a escribir una
pregunta relacionada con el contenido
trabajado en esta lección en un papel
e intercambiarla con un compañero
o una compañera quien deberá
responderla para lo que puede contar
con el apoyo y guía del profesor.
Invite a sus estudiantes agruparse con 2 o 3 compañeros y visitar
la página del Instituto Nacional de Estadísticas (INE):
wwww.ine.cl
Pídales buscar estadísticas de algún tema de su interés, analizar la
forma en que se organiza y presenta esta información (gráficos, tablas
u otros), y presentar sus conclusiones a sus compañeros.
2/17/2019 9:31:21 AM
Ejemplo 1
Para la creación de los talleres del colegio se les preguntó a los estudiantes cuál es su deporte
favorito. Los datos se representaron en los siguientes gráficos.
¿Cuál es tu deporte favorito?
f
2
4
6
12
10
8
Fútbol Básquetbol Tenis Atletismo
0
¿Cuál es tu deporte favorito?
f
2
4
6
12
10
8
Fútbol Básquetbol Tenis Atletismo
0
• ¿Cuál de los gráficos crees que es más adecuado para representar la información anterior?
El gráfico de barras es el más adecuado para representar la información por que permite
comparar las frecuencias de las distintas variables.
• El gráfico de barras se utiliza para comparar las frecuencias de variables cualitativas o
cuantitativas. Pueden ser de barras simples o múltiples.
• Los gráficos de líneas son representaciones útiles para comunicar información referida
a valores numéricos que varían en el tiempo.
Aprende
Ejemplo 2
Los números de calzado de los estudiantes de un 8° básico se encuentran representados
en el siguiente gráfico de barras. Escribe tres conclusiones a partir de él.
Número de calzado de los estudiantes de 8º básico
Nº de calzado
Frecuencia
(
f
)
1
2
3
6
5
4
36 37 38 39 40 41 42
0
1 Al observar el gráfico, podemos notar que la barra de mayor altura corresponde al número 40.
Esto quiere decir que el número de calzado que presenta mayor frecuencia es 40.
2 Del mismo modo, los números de calzado que presentan menor frecuencia son 38 y 42.
3 Hay 30 estudiantes en el 8° básico. Esto se obtiene al sumar la frecuencia de cada número
de calzado.
4
Unidad
177
Lección 1 • Estadística |
357

Solicite a sus estudiantes que reproduzcan el gráfico circular utilizando
GeoGebra y basándose en el siguiente tutorial: http://ggbkursus.dk/
geogebra/3-kan-det-meste/lav-cirkeldiagram-geogebra/?lang=es
ejemplo 3 y solicíteles que expliquen
el procedimiento para el cálculo
de porcentajes.
Guíe a sus estudiantes a extraer la
información del gráfico circular y a
organizarla en una tabla de distribución
de frecuencias.
Oriente a sus estudiantes a representar las
características de estas gráficas apoyado de
la información contenida en Aprende.
Considere las siguientes applet
de GeoGebra para profundizar lo
trabajado con relación a gráficos
circulares e histogramas:
https://www.geogebra.org/m/fhqgmthj
https://www.geogebra.org/m/dPZQcwAQ
Los recursos dados se pueden
manipular digitalmente para analizar
los efectos de los cambios en los datos.
Ejemplo 3
Se realizó una encuesta a 300 estudiantes de un colegio sobre los dispositivos de
almacenamiento de música que más utilizan. La información obtenida se representó
en el siguiente gráfico.
Dispositivos de almacenamiento
de música
Ipod
MP3
Teléfono móvil
Otros
Tipos de almacenamiento
32%
48%
9%
11%
¿Cuántos estudiantes prefieren almacenar su música en un Ipod o en un MP3?
1 Calculamos los porcentajes.
Ipod
32% de 300 = 0,32 • 300 = 96 estudiantes.
MP3
9% de 300 = 0,09 • 300 = 27 estudiantes.
2 Sumamos las cantidades obtenidas.
Cantidad de estudiantes que guardan
su música en un Ipod o en un MP3.
96 + 27 = 123 estudiantes.
• En un gráfico circular, cada sector representa un valor de la variable expresado como un
porcentaje. En general, este tipo de gráficos se utilizan para saber cómo se comporta una
variable respecto de un todo.
• El histograma es un gráfico formado por barras contiguas, donde cada una representa un
intervalo de valores. Sirve para expresar información sobre datos que están agrupados. El
polígono de frecuencias se obtiene uniendo los puntos correspondientes a la marca de clase
de cada intervalo (punto medio del intervalo).
Aprende
Estadística
Lección 1
178 | Unidad 4
E
E
p
CL0000000001018 MA

Unidad
4
Invite a sus estudiantes a analizar el
ejemplo 4, en el que se representan datos
utilizando un histograma.
Formalice lo trabajado mediante la
información de Aprende. Luego, solicite
a sus estudiantes que reproduzcan los
gráficos presentados considerando las
sugerencias dadas.
Cierre 15 minutos
En una plenaria, analicen qué tipos de
variables se pueden representar con cada
uno de los gráficos estadísticos estudiados,
destacando ventajas o desventajas de estos.
Invite a sus estudiantes a analizar por qué el ángulo de cada sector
circular se determina utilizando esa expresión. Oriente el análisis a
partir de ejemplos con datos simulados.
2/17/2019 9:31:22 AM
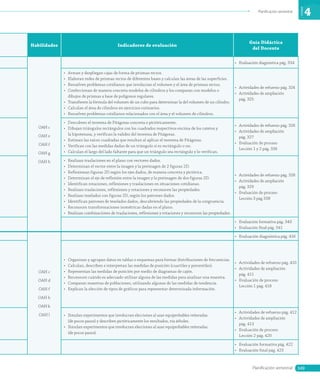
Ejemplo 4
En la siguiente tabla se muestran los puntos obtenidos por un grupo de estudiantes en una
prueba. Construye el histograma y el polígono de frecuencias correspondiente a los datos.
Puntos obtenidos en una prueba
Puntos f
[10, 20[ 5
[20, 30[ 6
[30, 40[ 4
[40, 50] 2
1 En los ejes coordenados marcamos las frecuencias en el eje vertical, y los intervalos
en el horizontal.
2 Sobre cada intervalo dibujamos barras cuya altura corresponde a la frecuencia.
3 Para realizar el polígono de frecuencias unimos con una línea poligonal las marcas
de clase de cada intervalo.
Puntos obtenidos en una prueba
f
1
2
3
6
5
4
10 20 30 40
0
Puntos
Para construir un gráfico circular debes trazar una circunferencia y marcar con un punto su centro.
Luego dibujas su radio y a partir de él trazas los ángulos adyacentes, que corresponden a cada
uno de los porcentajes encontrados. Cada ángulo a lo puedes calcular mediante la expresión:
α = f • 360º
n
donde n es el total de datos y f la frecuencia absoluta de cada dato.
Aprende
• Elintervalo[30,40[correspondeatodos
los númerosmayoresoigualesa30y
menoresque40,es decir,seincluye
el30,peronoel40.
• Elintervalo[40,50]correspondeatodos
los númerosmayoresoigualesa40
ymenoresoigualesque50,esdecir,
se incluyen40y50.
4
Unidad
179
359

Propósito
En esta clase los estudiantes resolverán
problemas presentando e interpretando
información a través de gráficos circulares,
de barra e histogramas.
OA 16
Inicio 15 minutos
Recuerde a sus estudiantes los conceptos
estudiados la clase anterior e invítelos a
plantear ejemplos en los que se podrían
utilizar cada uno de los gráficos vistos.
Solicite a sus estudiantes que realicen
las actividades en parejas, registrando
las resoluciones en sus cuadernos.
Planificación
Actitudes
Enfatice la responsabilidad y actitud crítica en sus estudiantes al
momento de resolver las actividades de manera grupal. Para ello.
guíelos a reflexionar sobre esto con preguntas como: ¿desarrollamos
completamente la actividad? ¿Qué estrategias utilizamos para verificar
los resultados obtenidos? ¿Cuál fue mi aporte en el trabajo realizado?,
¿y el de mis compañeros?
Actitudes
OA D , OA F
págs. 180 y 181
Clase 97
Solucionario
1. Lee las siguientes situaciones y determina qué tipo de gráfico realizarías para representarlas
y explica en cada caso tu elección.
a. El porcentaje de computadores vendidos durante los últimos 5 años.
b. Las comidas preferidas por un grupo de personas.
c. La cantidad de aviones que despegan de un aeropuerto entre las 7:00 y las 21:00 horas.
d. La cantidad de asistentes a las películas que están en cartelera.
e. El porcentaje de nacimientos en un hospital entre enero y julio.
f. El porcentaje de refrigeradores vendidos durante los últimos 6 meses.
2. Observa las siguientes representaciones gráficas y luego responde.
a. El gráfico representa las respuestas de
un grupo de estudiantes a la siguiente
pregunta: ¿Qué mascota tienes?
¿Cuántos estudiantes tienen como
mascota un gato o un roedor?
b. El gráfico representa los deportes favoritos
de un grupo de jóvenes.
• Si 165 jóvenes prefieren el fútbol,
¿cuántos prefieren el vóleibol?
• ¿Cuántos jóvenes prefieren el atletismo
o el tenis?
• ¿Cuántos jóvenes fueron encuestados?
c. Durante una obra de teatro se registra
la edad de los asistentes y se representa
en el siguiente histograma.
• ¿Qué intervalo de edad presenta
mayor frecuencia?
• ¿Qué intervalo de edad presenta
menor frecuencia?
• La entrada de los menores de edad tiene
un precio de $5 000, los adultos menores
de 70 años pagan $10 000 y a partir de
los 70 años cancelan $7 500. ¿Cuánto
dinero se recaudó por entradas?
• ¿Cuántas personas de menos de 44 años
asistieron a la obra de teatro?
Actividades
¿Qué mascota tienes?
Mascota
Frecuencia
(
f
)
1
2
3
6
7
8
5
4
Perro Gato Ave Pez Roedor Reptil Otro
0
Edad de los asistentes al teatro
Edad
(años)
Frecuencia
(
f
)
5
15
20
23
25
13
10
5 18 31 44 57 70 83
0
Deportes favoritos
Fútbol
Atletismo
Tenis
Vóleibol
Básquetbol
Deportes
30%
5% 10%
25%
20%
Estadística
Lección 1
180 | Unidad 4
3
4
5
•
•
•
CL0000000001018 MA

Unidad
4
a algunas parejas que expongan sus
resoluciones, mientras el resto de sus
compañeros las analizan y apoyan la
corrección de estas.
Cierre 15 minutos
Para finalizar, invite a sus estudiantes a
compartir sus reflexiones acerca de las
preguntas planteadas en Reflexiona y
responde.
La lectura e interpretación de gráficos son destrezas que deben modelarse.
Generalmente, los estudiantes no tienen dificultades con identificar
información literal en diferentes gráficos, pero sí las presentan en la
interpretación de los datos en gráficos que incluyen habilidades como
comparar cantidades, relacionar la información con el contexto dado, entre
otras, lo que puede llevarlos a cometer errores. Además, se pueden presentar
errores relacionados con la comprensión de los diferentes tipos de gráficos
y su utilidad que conduzcan a los estudiantes a una elección incorrecta
del tipo de gráfico según el contexto, por lo que se sugiere el trabajo con
situaciones contextualizadas y en las que existan espacios de reflexión
para que los estudiantes puedan considerar las ventajas y desventajas del
uso de diferentes representaciones gráficas.
páginas 110 a 113.
Planificación
Clase 98
l
2/17/2019 9:31:22 AM
1
Unidad
3. Analiza las siguientes preguntas y luego responde. Compara tus respuestas con las
de tus compañeros.
a. ¿Qué semejanzas hay entre un gráfico de barras y un histograma?, ¿y en qué se diferencian?
b. ¿Qué diferencias hay entre un gráfico de barras y un gráfico de líneas?, ¿y en qué se asemejan?
c. ¿Cuándo es útil representar la información en un gráfico circular?
4. En un colegio se hizo una encuesta a un grupo de estudiantes acerca de qué actividad
prefieren realizar en su tiempo libre.
a. Copia la tabla y el gráfico en tu cuaderno considerando los datos faltantes en cada caso.
Salir con amigos
Practicar un deporte
Ver películas
Usar el computador
Actividad
Actividad preferida
Actividad f
Salir con amigos ?
Practicar un deporte ?
Ver películas ?
Usar el computador ?
Total 150
Actividad preferida
30%
10%
20%
%
?
b. Construye un gráfico de barras con la información.
c. ¿Cuántos de los encuestados prefieren salir con amigos o practicar un deporte?
¿Es cierto que no alcanzan a ser un tercio del total de encuestados? Justifica.
d. ¿Es verdad que más de la mitad de la cantidad de encuestados prefieren usar
el computador o ver películas?
5. Construye un gráfico de líneas y un gráfico de barras que represente la siguiente situación
y luego responde.
En la tabla se muestra la cantidad de juguetes vendidos durante 5 meses en una tienda.
Juguetes vendidos en una tienda
Mes Enero Febrero Marzo Abril Mayo
Cantidad de juguetes 80 65 50 60 75
¿Qué gráfico consideras que es el adecuado para representar la situación? Justifica.
Páginas110a113.
• ¿Qué aprendiste? ¿Cómo lo aprendiste?
• ¿En qué situaciones puedes aplicar estos conocimientos?
• ¿Cuáles son las principales diferencias y semejanzas entre las representaciones gráficas trabajadas?
4
Unidad
181
361

Propósito
las principales medidas de posición, como
los cuartiles y percentiles.
OA 15
Inicio 15 minutos
situación presentada en el texto del
estudiante. Para motivarlos en el
aprendizaje del contenido matemático,
pídales investigar sobre las especialidades
del ciclismo que se muestran, sus
principales exponentes, los lugares en que
se practica, las competencias que existen,
entre otras.
Luego, invítelos a responder las preguntas
planteadas.
Planificación
Es importante promover en todo momento un ambiente de respeto y
compañerismo, en el que todos se sientan en confianza para compartir
sus ideas u opiniones. Para esto es importante enfatizar a diario en el
respeto de los turnos de habla.
Actitudes
OA D , OA F
págs. 182 a 185
Clase 99
• ¿Qué sabes del ciclismo? ¿Qué te parece este tipo de deporte?
• Lee la siguiente información y luego responde.
– La estatura, en centímetros, de los seleccionados de un grupo
de ciclistas son:
160, 168, 164, 170, 162, 166, 172, 164,
168, 164, 162, 160, 168, 170, 160, 162
– ¿Cuál es el dato mayor y cuál el dato menor?
– Ordena los datos de menor a mayor y encierra los valores que
dividen al conjunto de datos en 4 grupos con igual cantidad
de elementos.
Medidas de posición
Es una especialidad del ciclismo, en
que el deportista junto con su máquina
recorre distancias urbanas y rurales
en forma individual y grupal.
Es una especialidad del ciclismo, que
se practica en una pista o velódromo
que puede tener distintas medidas,
500, 333, 250 o 200 metros.
Especialidad del ciclismo que tiene
lugar en terrenos montañosos o en
aquellos que presentan una orografía
similar, con pendientes y rutas sinuosas.
El BMX se originó a comienzos
de los años 1970 en California.
Cuando los jóvenes intentaban
imitar a los campeones de
motocross con sus bicicletas.
Ruta
Pista
BMT
BMX
Estadística
Lección 1
182 | Unidad 4
E
L
a
S
l
CL0000000001018 MA

Unidad
4
el ejemplo 1 e invítelos a verbalizar
el procedimiento propuesto.
Defina cuartiles apoyado por la
información contenida en Aprende y
solicite a sus estudiantes que determinen
los cuartiles faltantes en el ejemplo 1.
Destaque que en el caso de que se obtenga
un decimal en la fórmula para encontrar la
ubicación del cuartil, se debe determinar
el sucesor de la parte entera de la
cantidad obtenida.
Se sugiere la lectura del documento “Identificación y análisis de
los errores cometidos por los alumnos en Estadística Descriptiva”,
disponible en https://rieoei.org/historico/expe/1729Puerto.pdf, con el
fin de tener las herramientas didácticas que permitan orientar a sus
estudiantes que presenten dificultades en el área.
2/17/2019 9:31:23 AM
Ejemplo 1
Los siguientes datos son los puntajes obtenidos en relación con una prueba de admisión
a una empresa.
100 - 121 - 134 - 123 - 142 - 118 - 123 - 142 - 126 - 127 - 131 - 98 - 116
Si para postular a la empresa se debe estar sobre el 50% de los mejores puntajes de todos
los que rindieron la prueba, ¿cuál es el puntaje de corte?
1 Debemos calcular Q2, por lo que ordenamos los datos de forma creciente.
98 - 100 - 116 - 118 - 121 - 123 - 123 - 126 - 127 - 131 - 134 - 142 – 142
2 Identificamos el puntaje que divide a los datos en dos partes iguales.
98 - 100 - 116 - 118 - 121 - 123 - 123 - 126 - 127 - 131 - 134 - 142 – 142
3 El dato encerrado es el valor de Q2, el cual separa el 50 % de los datos de la distribución,
por lo tanto para postular a la empresa se debe obtener un puntaje superior a 123.
Una de las medidas de posición son los cuartiles (Qk , con k = 1, 2, 3), que corresponden
a tres valores que dividen una distribución de datos en cuatro partes iguales.
25% 25% 25% 25%
Q1 Q2 Q3
Para calcular el cuartil Qk se deben ordenar los n datos en forma creciente y calcular n • k
4
.
• Si resulta un número entero, Qk es igual al promedio entre el dato que se ubica en esa posición
y el dato siguiente.
• Si resulta un número decimal, Qk es igual al dato que ocupa la posición ; n • k
E+ 1
4
.
Aprende
4
Unidad
183
363

ejemplo 3 y compare el procedimiento
propuesto con el del ejemplo anterior.
Defina percentiles apoyado en la
información contenida en Aprende.
Señale que los percentiles 25, 50 y
75 equivalen a los cuartiles 1, 2 y 3,
respectivamente.
la tabla de transformaciones de
puntajes de la Prueba de Selección
Universitaria, destacando cómo se
utilizan percentiles y determinando
la interpretación de estos.
Para profundizar en la comprensión de percentiles y cuartiles puede
invitar a los estudiantes a explorar la applet del siguiente link:
https://www.geogebra.org/m/ZYWRJSSJ
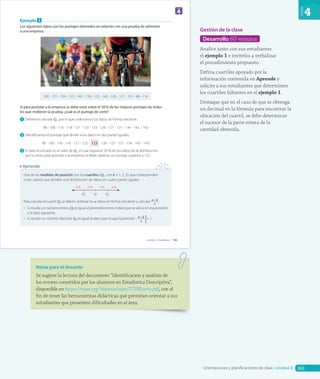
Ejemplo 3
Se quiere seleccionar a un grupo de estudiantes para competir en las olimpiadas de atletismo.
Las marcas (en metros) obtenidas por los estudiantes en una prueba son las siguientes:
52,4 - 56,3 - 57,5 - 65,3 - 65,3 - 66,5 - 66,8 - 67,9 - 68,7
69,3 - 70,2 - 71,4 - 72,4 - 74,7 - 74,9 - 75,5 - 75,6
Si se selecciona el 90% de las mejores marcas, ¿cuántos estudiantes no fueron seleccionados?
1 Debemos calcular P10, ya que los estudiantes no seleccionados equivalen al 10%.
P10
= 17 • 10 = 170 = 1,7
100 100
Como 1,7 es un número decimal, calculamos [1,7] + 1 = 1 + 1 = 2.
2 Como los datos ya están ordenados de forma creciente, identificamos aquel dato que ocupa
la posición 2.
Posición 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Dato 52,4 56,3 57,5 65,3 65,3 66,5 66,8 67,9 68,7 69,3 70,2 71,4 72,4 74,7 74,9 75,5 75,6
3 Luego, el valor de P10 corresponde a 56,3, por lo tanto 2 estudiantes no fueron seleccionados.
Los percentiles (Pk, con k = 1, 2, 3,…, 99 ) corresponden a los 99 valores de una distribución
que la dividen en 100 partes iguales. La diferencia entre dos percentiles consecutivos
corresponde al 1% de la distribución.
Para calcular el percentil Pk se deben ordenar los n datos en forma creciente y calcular n • k
100
.
• Si resulta un número entero, Pk es igual al promedio entre el dato que se ubica en esa posición
y el dato siguiente.
• Si resulta un número decimal, Pk es igual al dato que ocupa la posición ;
n • k
E+ 1
100
.
Aprende
Estadística
Lección 1
184 | Unidad 4
E
L
e
¿
¿
CL0000000001018 MA

Unidad
4
ejemplo 4 y caracterice cada uno de los
elementos que componen el diagrama
de cajón.
Establezca el método para la construcción
de las bandas del diagrama.
En una plenaria, analice junto con sus
estudiantes qué información de la muestra
se puede extraer de este tipo de gráficos.
Cierre 15 minutos
Invite a sus estudiantes a destacar los
tópicos más importantes estudiados
en la clase, incentivando que planteen
ejemplos en los que sea posible aplicar
estos contenidos.
Promueva un ambiente adecuado de aprendizaje en el que todos los
estudiantes sientan la confianza de exponer sus ideas y plantear sus
dudas. Para incentivar la participación puede motivar a los estudiantes
a plantear, al menos, una pregunta antes de finalizar la clase.
/17/2019 9:31:24 AM
Ejemplo 4
Los minutos que tardaron los estudiantes en responder un examen están representados
en el siguiente diagrama.
Datomayor
Datomenor Q3
Me
Q1
32
30 34 36 38 40 42 44 46 48 50 52 54 60
56 62
58 64 66
Minutos
¿Al cabo de cuántos minutos el 50% de los estudiantes terminó de contestar el examen?
¿Cuántos minutos tardaron en contestar el examen todos los estudiantes?
1 La mediana separa el 50% de los datos, por lo tanto a los
52 minutos la mitad de los estudiantes termina el examen.
2 Para determinar el tiempo que tardaron en responder
el examen todos los estudiantes basta que observemos
el dato mayor de la distribución de datos. Es decir, tardaron
66 minutos en responder el examen.
Para construir un diagrama de cajón se traza una recta graduada a partir de los datos y
se construye un rectángulo (cajón) cuyos extremos deben estar ubicados sobre Q1 y Q3.
Así, la medida del largo de la caja es Q3 – Q1 = Ric, donde Ric corresponde al recorrido
intercuartil o rango intercuartil, es decir, a la variabilidad de los datos con respecto a
la mediana (Me).
Dentro del cajón se traza una línea vertical en el lugar de la mediana (Me); de esta manera,
se divide el conjunto de datos en dos partes porcentualmente iguales. Luego, se trazan
dos líneas, a ambos lados del cajón, desde sus extremos hasta los valores del dato menor
y del mayor de la distribución.
Dato mayor
Dato menor Q3
Me
Q1
Al observar un diagrama de cajón es posible obtener conclusiones respecto de la distribución
de la variable en estudio. Si uno de los cajones tiene mayor área, quiere decir que los datos
que se ubican entre determinados cuartiles están más dispersos.
Aprende
• Undiagramadecajónesuna
representaciónquepermitevisualizar
algunascaracterísticasdelapoblacióna
partirdelasmedidasdetendenciacentral
ydeposición.
4
Unidad
185
365

Propósito
En esta clase los estudiantes construirán
diagramas de cajón para presentar
información y determinarán la posición
de datos según cuartiles y percentiles.
OA 15
Inicio 15 minutos
ejemplo 3 e invítelos a reproducir estas
construcciones en sus cuadernos y a extraer
conclusiones de las muestras a partir de
la gráfica.
Para la resolución de las actividades
propuestas en estas páginas, solicite a sus
estudiantes trabajar en parejas, registrando
las respuestas en sus respectivos
cuadernos. De esta forma se puede generar
un aprendizaje colaborativo en el que los
alumnos consideren diferentes estrategias
de resolución.
Planificación
Habilidades del siglo XXI
Una de las habilidades del siglo XXI es el pensamiento crítico, el
cual nos permite razonar, tomar decisiones y resolver problemas.
Para profundizar en este tema se sugiere visitar el sitio web:
www.educarchile.cl/ech/pro/app/detalle?ID=219623es=219836
Actitudes
OA D , OA E , OA F
págs. 186 a 189
Clase 100
1. Calcula las medidas de posición pedidas para cada distribución de datos.
a. 2 - 3 - 5 - 6 - 7 - 9 - 10 - 11 - 13
Calcula Q1, Q2, y Q3 .
d. 1,2 - 3,4 - 5,6 - 7,9 - 10,2 - 7,8
Calcula P10, Q3, y P75 .
b. 4 - 6 - 8 - 17 - 23 - 43 - 53 - 56
Calcula Q1, Q2, y P50 .
e. 16 - 15 - 28 - 20 - 17 - 9 - 11 - 24
Calcula P10, Q3, y P35 .
c. 50 - 52 - 53 - 55 - 56 - 58 - 61 - 62 - 64
Calcula P20, P50 y P80 .
f. 100 - 102 - 103 - 100 - 106 - 110 - 100
Calcula Q1, P12 y P92 .
Ejemplo 3
Las notas obtenidas por los estudiantes de dos 8° básicos en una evaluación son las siguientes:
Notas 8° A
6,5 - 5,2 - 7,0 - 4,8 - 3,5 - 5,8 - 6,6 - 3,7 - 4,5 - 5,2 - 6,3 - 7,0 - 5,5 - 6,5
4,9 6,8 - 5,6 - 5,5 - 5,8 - 6,0 - 5,5 - 4,8 - 4,2 - 5,9 - 7,0 - 6,4 - 4,0 - 4,0
Notas 8° B
5,4 - 5,4 - 7,0 - 6,8 - 3,4 - 4,8 - 6,2 - 3,8 - 5,5 - 6,2 - 6,6 - 6,0 - 5,0 - 6,4
3,8 - 3,8 - 6,6 - 5,7 - 5,5 - 7,0 - 6,5 - 5,8 - 3,2 - 5,5 - 6,6 - 6,8 - 7,0 - 3,2
Construye un diagrama de cajón para cada distribución de datos.
1 Determinamos los valores necesarios para construir el diagrama de cajón correspondiente
a cada curso.
8° A
Dato menor 3,5
Dato mayor 7,0
Primer cuartil 4,8
Mediana 5,55
Tercer cuartil 6,45
Recorrido intercuartil 1,65
8° B
Dato menor 3,2
Dato mayor 7,0
Primer cuartil 4,9
Mediana 5,75
Tercer cuartil 6,6
Recorrido intercuartil 1,7
2 Construimos los diagramas de cajón.
4,0
3,5 4,5 5,0 5,5 6,0 6,5 7,0
Notas
Notas 8° A
4,0
3,5 4,5 5,0 5,5 6,0 6,5 7,0
Notas
Notas 8° B
Actividades
Estadística
Lección 1
186 | Unidad 4
2
3
4
5
CL0000000001018 MA

Unidad
4
Note que en la resolución de las actividades
propuestas es necesario que los estudiantes
sean meticulosos en el manejo de
la información, lo que les permitirá
evitar errores. Por lo tanto, destaque
la importancia de ordenar los datos no
tabulados para determinar la medida de
posición pedida.
Para el desarrollo de la actividad es
fundamental que los estudiantes
demuestren interés y perseverancia en
la resolución de problemas, junto con
respetar las opiniones de sus pares.
Solucionario
propuestas u tilice la sección Solucionario
Puede profundizar el trabajo relacionado con medidas de posición
considerando el material del siguiente link:
Aquí encontrará orientaciones para el trabajo con sus estudiantes.
Además, en el siguiente link se presenta el material de trabajo para
los alumnos:
https://www.curriculumnacional.cl/614/articles-91390_recurso_2.pdf
2/17/2019 9:31:24 AM
2. Analiza cada situación y luego calcula las medidas de posición solicitadas.
a. Una empresa realizó una encuesta a
80 personas para conocer la cantidad
de horas diarias que ven televisión.
Los resultados fueron los siguientes.
b. Se aplicó una prueba a un grupo
de estudiantes de octavo básico.
Los resultados fueron los siguientes.
Puntos 75 88 90 95 100 105 110
f 6 6 9 18 10 11 15
Calcula Q1, Q2, Q3, P10, P60 y P90 .
Cantidad de horas 1 2 3 4
f 4 15 16 45
Calcula Q1, Q2, P50, Q3, P75, P80 y P99 .
3. Analiza cada situación y luego responde.
a. Los datos corresponden a la cantidad de automóviles que transitan por un peaje, ubicado
en las afueras de la ciudad, durante las últimas dos semanas.
192 - 168 - 206 - 232 - 230 - 243 - 145 - 194 - 227 - 173 - 183 - 158 - 154 - 176 - 181
¿Cuál es el valor del primer cuartil de los datos?, ¿y del tercer cuartil?
b. A un grupo de estudiantes se les preguntó acerca de la cantidad de hermanos que tiene
cada uno. Las respuestas fueron las siguientes:
2 - 3 - 1 - 4 - 5 - 2 - 1 - 2 - 3 - 2 - 1 - 4 - 5 - 2 - 1 - 3 - 2 - 1 - 2 - 3 - 2 - 3 - 4
¿Cuántos estudiantes se ubican bajo el segundo cuartil? ¿Cuántos hermanos tienen?
c. El equipo de gimnasia artística de un colegio elaboró una encuesta acerca de la estatura
(en metros) de sus integrantes. Los resultados fueron los siguientes. ¿Cuántos estudiantes
se ubican sobre el percentil 80? ¿Cuál es su estatura?
1,57 - 1,55 - 1,67 - 1,72 - 1,71 - 1,67 - 1,60 - 1,63 - 1,51 - 1,55
1,60 - 1,62 - 1,69 - 1,49 - 1,63 - 1,50 - 1,70 - 1,47 - 1,56 - 1,61
4. Lancen 24 veces un dado y anoten los resultados obtenidos. Luego, respondan
las siguientes preguntas.
a. ¿Qué puntaje se obtiene en el 25% o menos de los lanzamientos?
b. ¿Qué puntaje se obtiene en el 75% o más de los lanzamientos?
5. Los datos corresponden a la cantidad de mascotas que tienen los 25 estudiantes de un curso.
Cantidad de mascotas 1 2 3 4 5 6
f 2 7 10 3 2 1
¿Es posible afirmar que el 50% de los estudiantes del curso tiene 2 mascotas o menos? Justifica.
4
Unidad
187
367

que algunas parejas expongan sus
resoluciones en la pizarra. Invite al resto
de los estudiantes a analizar las
resoluciones propuestas, corrigiendo
posibles errores cometidos.
acerca del trabajo realizado y solicíteles que
compartan sus respuestas a las preguntas
planteadas en el recuadro.
Se sugiere la applet del siguiente link para profundizar la comprensión
respecto de los diagramas de cajón:
ttps://www.geogebra.org/m/PdyFSKKv
6. Reúnete con un compañero o compañera y resuelvan el siguiente problema.
En una empresa de mensajería se asigna un presupuesto diario para la gasolina que gastan en
sus motos los 10 mensajeros que trabajan allí. El gerente de operaciones le plantea al tesorero
que el dinero presupuestado no alcanza, pues el 85% de los mensajeros gastaron más de
lo asignado. El gasto en combustible de la semana anterior se registra a continuación.
Mensajero 1 2 3 4 5 6 7 8 9 10
Gasto ($) 24000 23000 21000 28000 26000 24500 21800 27000 23400 22300
a. ¿Cuál fue el presupuesto asignado por mensajero?
b. ¿Qué medida de posición usarías para calcular este valor?
c. ¿Qué significado tiene el valor del percentil 15 en este caso?
7. En un laboratorio se está experimentando con una bacteria benigna que se pretende usar en la
elaboración de un nuevo medicamento. A continuación se muestran los tiempos, en minutos,
de reproducción de 25 cultivos de esta bacteria. Calcula el percentil 80 e interpreta este valor.
60 - 47 - 82 - 95 - 88 - 77 - 39 - 90 - 63 - 68 - 64 - 58
94 - 55 - 89 - 72 - 50 - 92 - 90 - 77 - 86 - 58 - 78 - 86 - 44
8. Identifica en cada diagrama de cajón los valores de Q1, Q3, Me, Ric, el dato menor y el dato
mayor de la distribución de datos.
33
23 43 53 63 73
a.
33
23 43 53 63 73
b.
33
23 43 53 63 73
c.
9. Los siguientes datos corresponden a las masas corporales, en kilogramos, de los integrantes
de un equipo de fútbol.
70 - 75 - 80 - 75 - 70 - 78 - 78 - 70 - 80 - 75 - 78 - 80
75 - 74 - 70 - 74 - 75 - 75 - 74 - 75 - 75 - 71 - 70 - 78
Construye un diagrama de cajón para la distribución de datos.
• Al calcular medidas de posición, ¿cuál crees que es el error más frecuente de cometer?, ¿qué
puedes hacer para no cometerlo?
• ¿Piensas que intercambiar opiniones con tus compañeros aporta a tu aprendizaje?, ¿por qué?
Páginas114a119.
Estadística
Lección 1
188 | Unidad 4
E
S
CL0000000001018 MA

Unidad
4
Solicite a sus estudiantes que trabajen
en la actividad con herramientas
tecnológicas en parejas, utilizando
una planilla de cálculo. Guíe a sus
estudiantes, a determinar las medidas
de posición solicitadas, destacando a
aquellos que ayuden en la construcción
del diagrama de cajón.
Cierre 15 minutos
Para el cierre de la clase, invite a sus
estudiantes a reflexionar acerca del uso
de medidas de posición y a destacar las
ventajas y/o desventajas de representar un
conjunto de datos utilizando un diagrama
de cajón.
Actitudes
Enfatice la responsabilidad y actitud crítica en sus estudiantes
al momento de resolver las actividades en parejas.
páginas 114 a 119.
Planificación
Clase 101
2/17/2019 9:31:24 AM
En esta actividad usarás una planilla de cálculo para simular el lanzamiento de un dado.
Sigue las instrucciones.
1 En una hoja de cálculo escribe en la celda A2“Edades”, luego en la misma columna A escribe
las edades de 13 de tus compañeros y compañeras.
2 En la celda C3 escribe moda, en la celda C4 escribe media, y en la celda C5 escribe mediana.
3 En la celda F3 escribe q1, en la celda F4 escribe q2, y en la celda f5 escribe q3.
4 En la celda I3 escribe p1, en la celda I4 escribe p10, en la celda I5 escribe p25, en la celda I6
escribe p50, en la celda I7 escribe p75 y en la celda I8 escribe p90.
5 Luego, en tu cuaderno construye el diagrama de cajón que representa la situación.
Celda Fórmula ¿Qué hace?
D3 =MODA(A3:A15) Calcula la moda
D4 =PROMEDIO(A3:A15) Calcula le media
D5 =MEDIANA(A3:A15) Calcula la mediana
G3 =CUARTIL(A3:A15;1) Calcula el cuartil 1
G4 =CUARTIL(A3:A15;2) Calcul el cuartil 2
G5 =CUARTIL(A3:A15;3) Calcula el cuartil 3
J3 =PERCENTIL(A3:A15;0,01) Calcula el percentil 1
4
Unidad
189
369

Propósito
la Lección 1.
Objetivos de la clase
Inicio 15 minutos
Recuerde lo estudiado en las clases
anteriores, registrando en la pizarra
los tópicos claves a modo de resumen.
Solicite a sus estudiantes que realicen
las actividades en parejas, registrando
Planificación
págs. 190 y 191
Clase 102
Solucionario
propuestas, utilice la sección Solucionario
Para complementar y profundizar el trabajo de la lección, puede
utilizar las sugerencias de actividades del siguiente link:
Considere que el material correspondiente para los estudiantes está
disponible en: https://www.curriculumnacional.cl/614/articles-91392_
recurso2_pdf.pdf
1. Un grupo de pasajeros espera en el aeropuerto la salida de su avión. Este hará varias escalas
antes de llegar a París (Francia): San Pablo (Brasil), Madrid (España) y Barcelona (España).
Los destinos de los pasajeros se muestran en la siguiente tabla:
Ciudad San Pablo Madrid Barcelona París
Cantidad de pasajeros 18 6 15 9
Tabla 1 Destinos del grupo de pasajeros
a. Construye una tabla que contenga con los porcentajes de pasajeros que se dirigen a cada
uno de los lugares señalados.
b. ¿Cuál de los gráficos circulares representa correctamente los datos de la ?
Gráfico 1
Destinos del grupo
de pasajeros
Gráfico 2
Destinos del grupo
de pasajeros
c. ¿Es correcto afirmar que más de la mitad de los pasajeros va a España? ¿Por qué?
d. Construye un gráfico de barras con la información de la .
2. Una empresa de informática otorgará becas de estudio a los interesados en profundizar
sus conocimientos en programación. Para seleccionar a los beneficiados, aplicó un test de
conocimientos y habilidades en el tema. Los puntajes de los postulantes se representan
en el gráfico de barras que está a continuación:
Puntaje en el test de los postulantes a la beca
Puntaje obtenido
Cantidad
de
postulantes
1
2
3
4
5
6
7
1 2 3 4 5 6 7 8 9 10
0
| Unidad 4
190
3
4
•
•
CL0000000001018 MA

Unidad
4
Una vez que todos los estudiantes
terminen la actividad, solicite que
algunas parejas presenten sus resultados
mientras el resto de sus compañeros los
analizan, corrigiendo errores cometidos.
Cierre 15 minutos
Finalice la clase invitando a sus
estudiantes a responder las preguntas
para la reflexión en sus cuadernos y
a compartirlas con sus compañeros
de curso.
Actitudes
perseverar y confiar en sus propias capacidades. Para ello, motívelos
a probar con diferentes estrategias de resolución en las actividades
de modo de que puedan experimentar y analizar la efectividad de
cada una.
páginas 120 y 121.
Planificación
Clase 103
2/17/2019 9:31:25 AM
1
Unidad
a. Calcula los cuartiles Q1, Q2 y Q3 de los puntajes del test.
b. Construye un diagrama de cajón para la distribución de los puntajes del test.
c. Si la empresa pide como requisito para dar la beca que el postulante se encuentre sobre
el percentil 70 de los puntajes del test, ¿cuántos de ellos obtendrán la beca?
d. A los postulantes que no accedieron a la beca, pero que obtuvieron un puntaje igual
o superior al segundo cuartil, la empresa les dará la oportunidad de repetir el test.
¿Cuántos de los que rindieron el test cumplen con este requisito y podrán repetir
la prueba?
3. Construye un diagrama de cajón con cada grupo de datos y plantea conclusiones.
Datos correspondientes a la cantidad de animales que tiene un grupo de campesinos
en cada uno de sus predios.
24 - 28 - 40 - 30 - 20 - 65 - 30 - 20
40 - 15 - 23 - 18 -16 - 20 - 30 - 40
20 - 30 - 18 - 20
4. Analiza la información entregada en el siguiente gráfico, construye el diagrama de cajón
respectivo y establece conclusiones.
Cantidad de días a la semana que un
grupo de personas realiza actividad física.
Cantidad de días
Cantidad
de
personas
2
4
6
8
10
12
14
16
1 2 3 4 5 6 7
0
• Lo que has aprendido sobre estadística, ¿con qué conocimientos previos lo puedes relacionar?
• ¿Qué dificultades tuviste en el desarrollo de la lección? ¿Cómo las pudiste superar?
Páginas120y121.
4
Unidad
371

Propósito
En esta clase los estudiantes aprenderán a
calcular la cantidad total de combinaciones
posibles utilizando el principio
multiplicativo.
OA 17
Planificación
Inicio 15 minutos
Invite a sus estudiantes a leer la información
de la fotografía y a analizar los datos del
torneo interescolar por parejas.
Pregunte a sus estudiantes sobre el valor
de la probabilidad que tiene cada equipo
de ganar el campeonato.
Para esta unidad los estudiantes deben recordar:
• ¿Qué es un experimento?
• ¿Qué es un suceso?
• ¿Qué es la probabilidad y cómo se calcula?
• ¿Para qué sirve la regla de Laplace?
Actitudes
OA D
págs. 192 y 193
Clase 104
Lección 2 Probabilidades
En esta lección podrás aplicar el principio
multiplicativo para calcular la probabilidad
de un evento compuesto y representar los
resultados usando diagramas o tablas.
Torneo interescolar
Principio multiplicativo
Organiza un campeonato de básquetbol con 8 equipos, en donde ocurra una eliminación doble.
De acuerdo a esto responde:
• ¿Cuántos partidos debe jugar un equipo para coronarse campeón?
• ¿Qué probabilidad tiene cada equipo de ganar el campeonato?
Para poder participar en un torneo de tenis,
la pareja de dobles debe sortear las siguientes
rondas para llegar a la final del campeonato:
1.ª ronda, cuartos de final, semifinal y final.
Pareja 2
Pareja 8
Pareja 9
Pareja 15
Pareja 2
Pareja 4
Pareja 6
Pareja 8
Pareja 9
Pareja 11
Pareja 13
Pareja 15
Pareja 1
Pareja 2
Pareja 3
Pareja 4
Pareja 9
Pareja 10
Pareja 11
Pareja 12
Pareja 5
Pareja 6
Pareja 7
Pareja 8
Pareja 13
Pareja 14
Pareja 15
Pareja 16
192 | Unidad 4
E
M
d
CL0000000001018 MA

Unidad
4
el ejemplo 1 y guíelos a través de
los pasos para calcular la cantidad
posible de combinaciones diseñando
un diagrama de árbol y aplicando el
principio multiplicativo.
Cierre 15 minutos
Finalice la clase formalizando los
conceptos de principio multiplicativo
y diagrama de árbol apoyándose en la
información de Aprende.
Para apoyar la formalización respecto a la definición de diagrama de
árbol dada en Aprende, puede analizar con sus estudiantes el ejemplo
dado en un applet de GeoGebra disponible en:
https://www.geogebra.org/m/hRJ7KNzr
2/17/2019 9:39:15 AM
Ejemplo 1
Marcelo tiene 3 camisetas (roja, verde y azul) y 2 pantalones (negro, café). ¿De cuántas formas
distintas puede escoger Marcelo una chaqueta con un pantalón?
1 Determinamos los siguientes conjuntos:
A: Los tipos de camiseta.
B: Los tipos de pantalón.
2 Calculamos la cardinalidad de cada conjunto.
#A = 3 #B = 2
3 Hay 6 maneras de combinar los elementos de los conjuntos, ya que por el principio multiplicativo
podemos calcular el producto entre la cantidad de elementos de cada conjunto, es decir,
3 • 2 = 6. Lo anterior lo podemos visualizar en un diagrama de árbol.
Camisetas
Pantalones
Roja
Negro Negro
Negro
Café Café
Café
Verde Azul
• El principio multiplicativo es una técnica de conteo en la que si un conjunto está compuesto
por n1 elementos, otro conjunto por n2 elementos, y así sucesivamente con k conjuntos
diferentes, entonces la cantidad de maneras de combinar los elementos de los conjuntos es:
n1 • n2 • … • nk
• El diagrama de árbol es una representación gráfica que permite mostrar los resultados
posibles al aplicar el principio multiplicativo.
Aprende
• LacardinalidaddeunconjuntoA(#A)
correspondealacantidaddeelementos
contenidosenél.
4
Unidad
193
Lección 2 • Probabilidades |
373

Propósito
el principio multiplicativo para
calcular las combinaciones posibles
en situaciones diversas.
OA 17
Planificación
Inicio 15 minutos
Comience la clase recordando a los
estudiantes los conceptos estudiados la
clase anterior: principio multiplicativo
y diagrama de árbol.
Pida a sus estudiantes que analicen
el ejemplo 2 identificando los pasos
para calcular el espacio muestral del
experimento de lanzar dos dados
de 6 caras.
Motive a sus estudiantes a mantener un ambiente de respeto frente a
las opiniones y/o respuestas de cada uno de los estudiantes del curso.
Actitudes
OA D , OA F
págs. 194 a 197
Clase 105
Ejemplo 2
Al lanzar un dado de seis caras dos veces, ¿cuál es la cantidad de resultados posibles?
1 Para determinar la cantidad de resultados posibles, utilizaremos un diagrama de árbol, en el cual
se escriben de forma ramificada los elementos de cada lanzamiento.
Primer lanzamiento
Segundo lanzamiento
1
1 2 3 4 5 6
2
1 2 3 4 5 6
3
1 2 3 4 5 6
Primer lanzamiento
Segundo lanzamiento
4
1 2 3 4 5 6
5
1 2 3 4 5 6
6
1 2 3 4 5 6
2 Podemos observar que cada camino corresponde a una combinación posible, por ejemplo,
(1, 1) o (2, 3). Todas las combinaciones posibles también se pueden representar en una tabla.
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
3 Por lo tanto, la cantidad de combinaciones son 36, ya que en cada lanzamiento hay 6 posibles
resultados (1, 2, 3, 4, 5 y 6) y son 2 lanzamientos, es decir, 6 • 6 = 36.
Ejemplo 3
En un festival se otorgan premios a los tres primeros lugares.
Quedaron seleccionadas 5 personas: Claudia, Nicolás, Hernán,
Viviana y Daniela. Si los jueces otorgaron el primer lugar a
Daniela, ¿de cuántas formas se podrían entregar los premios?
1 Determinamos la cantidad de elementos de
cada conjunto.
A: Primer lugar #A = 1
B: Segundo lugar #B = 4
C: Tercer lugar #C = 3
2 La cantidad de formas que se pueden entregar los premios
está dado por: 1 • 4 • 3 = 12.
3 Las combinaciones las podemos ver en un diagrama de árbol.
Daniela
1º lugar
2º lugar
3º lugar
Claudia
Hernán
Nicolás
Viviana
Nicolás
Claudia
Claudia
Claudia
Hernán
Nicolás
Hernán
Nicolás
Viviana
Viviana
Viviana
Hernán
Probabilidades
Lección 2
194 | Unidad 4
1
2
3
CL0000000001018 MA

Unidad
4
Guíe a sus estudiantes en el desarrollo de
estas actividades e invítelos a trabajar de
manera ordenada, con perseverancia al
enfrentar desafíos matemáticos.
Puede apoyar el desarrollo de estrategias
metacognitivas con preguntas como:
• ¿Cómo puedes determinar si en una
situación se puede aplicar el principio
multiplicativo? Explica.
• ¿Qué pasos seguiste para resolver
esta actividad?, ¿por qué hiciste esto
primero?
• ¿Qué consideras importante al construir
un diagrama de árbol?, ¿por qué?
Promueva un ambiente positivo al interior del aula enfatizando en el
desarrollo de la empatía, la motivación y el interés por el aprendizaje.
Para motivar a los estudiantes en el contenido abordado en estas
páginas puede establecer relaciones con casos cotidianos en los que los
alumnos puedan apreciar la utilidad de los aprendizajes.
Solucionario
l
2/17/2019 9:39:15 AM
1. Determina si en las siguientes situaciones se puede utilizar el principio multiplicativo.
a. Luis quiere viajar a una ciudad pasando por cinco lugares. Puede llegar a cada uno en bus,
tren o avión. ¿De cuántas formas puede llegar Luis a la ciudad?
b. Tomar una ficha de una urna donde se encuentran tres fichas de diferente color.
c. Lanzar un dado cuatro veces consecutivas y observar el resultado de cada lanzamiento.
d. En la final de fútbol del campeonato de un colegio hay cuatro equipos que se disputan
el primer y segundo lugar (campeón y subcampeón). ¿De cuántas maneras diferentes los
equipos pueden ubicarse en dichos lugares?
e. Lanzar una moneda cinco veces y observar los resultados.
f. Sacar tres bolitas, en forma consecutiva, de una bolsa en la que hay 3 bolitas azules,
2 verdes, 4 rojas y una blanca.
2. En un restaurante se pueden armar distintos menús formados por un sándwich,
un condimento y un acompañamiento.
a. Completa en tu cuaderno el diagrama de árbol con todos los menús posibles.
Hamburguesa
Lomo
Pollo
Mayonesa
Salsa
puré
puré
ensalada
ensalada
Sándwich Condimento Acompañamiento
?
?
?
?
b. ¿Cuántos menús de los que escribiste tendrán puré como acompañamiento?
c. ¿Cuántos menús tendrán mayonesa y puré?
3. Calcula la cantidad de combinaciones posibles en cada una de las siguientes situaciones
y represéntalas mediante un diagrama de árbol.
a. Un médico general clasifica a sus pacientes de acuerdo con su sexo (masculino o femenino)
y por su tipo de sangre (A, B, AB, O).
b. Patricia y sus amigas fueron a comprar jugos. Al pedirlos les dieron las siguientes posibilidades:
tamaño del vaso: grande y pequeño, sabores del jugo: naranja, mango y manzana, además,
colores del vaso: rojo, amarillo o verde.
c. Claudia tiene 2 blusas, una azul y otra verde. Además, tiene 3 faldas: una roja, una negra
y otra violeta.
Actividades
4
Unidad
195
375

Acompañe a sus estudiantes en el
desarrollo de las actividades 5, 6 y 7, ya
que requieren de la organización de gran
cantidad de información. En estos casos,
proponga diferentes formas de representar
y distribuir la información, conservando
un orden determinado que evita errores
en el conteo.
Luego, represente y calcule las
combinaciones posibles en cada situación
utilizando el principio multiplicativo.
Puede profundizar en la actividad 6, proponiendo a sus estudiantes más
dígitos para formular la clave, como por ejemplo: 0, 1, 2, 3, 4 y 5. Incluso
aumentar los dígitos cada vez para conjeturar una generalización del
número de combinaciones posibles.
En este tipo de actividades lo relevante del trabajo es organizar la
información, evitando errores en el conteo de las combinaciones posibles.
4. ¿Cuántas posibilidades distintas hay de ubicar los sobres uno en cada buzón?
Dibuja un diagrama de árbol que represente la situación.
5. Observa el siguiente diagrama de árbol.
Rojo
Azul Verde Blanco
Blanco
Azul Rojo Blanco
Azul
Rojo Verde Blanco
Blanco
Rojo Verde Azul
a. Realiza un listado con los posibles resultados representados en el diagrama de árbol.
b. Escribe una situación que pueda modelarse con la información.
6. Por seguridad, Andrés cambia mensualmente la clave de su cuenta de ahorros. Para esto,
utiliza todas las combinaciones de cuatro números que puede realizar con los dígitos
del 0 al 3, de modo que en cada clave no se repite ninguno. En estas condiciones,
¿cuántos meses pasa Andrés sin repetir ninguna clave?
7. Dos amigas se mandan mensajes secretos usando estos símbolos:
a. ¿Cuántos mensajes se pueden formar que tengan 7 símbolos, todos distintos?
b. De todos los mensajes que calculaste, ¿cuántos empiezan con y terminan con ?
c. ¿Cuántos mensajes se pueden armar que tengan 4 símbolos, todos diferentes?
d. ¿Cuántos mensajes se pueden armar que tengan 3 símbolos si estos se pueden repetir?
Probabilidades
Lección 2
196 | Unidad 4
•
•
•
8
9
CL0000000001018 MA

Unidad
4
Otorgue un tiempo antes de finalizar la
clase para realizar una discusión plenaria
sobre el trabajo realizado.
Invite a participar a todos sus estudiantes
y a que compartan sus apreciaciones
guiándose por las preguntas para la
reflexión:
• ¿Cómo representamos situaciones con
el diagrama de árbol? ¿Crees que es útil
esta representación?
• ¿En qué ámbitos de la vida cotidiana
se podría utilizar?
Cierre 15 minutos
Finalice la clase recordando la definición
de principio multiplicativo y cuándo es
posible utilizarlo.
En la actividad 9, para determinar la cantidad posible de movimientos
se puede ajustar el problema para plantearlo sobre un tablero de ajedrez.
Luego, se puede extender este problema utilizando un caballo para llegar
a una torre en una esquina del tablero.
El problema original, todavía sin resolver, se llama El problema del
caballo. https://www.abc.es/ciencia/abci-problema-caballo-pasa-todas-casillas-
sin-repetir-ninguna-201801080953_noticia.html
páginas 122 a 125.
Planificación
Clase 106
2/17/2019 9:39:15 AM
• Explica en qué consiste el principio multiplicativo.
• ¿Crees que es útil representar datos en un diagrama de árbol?, ¿por qué?
• ¿Cómo aporta a tu aprendizaje respetar las opiniones de tus compañeros y compañeras?
8. Para un campeonato de ciclismo se necesita determinar el orden en que irán los deportistas
en la fila. Los seleccionados son Mauricio, Boris, Diego y Fabián.
a. Construye un diagrama de árbol que represente la situación.
b. ¿De cuántas maneras diferentes se puede ubicar a los deportistas?
c. Si Boris siempre debe ir en el primer lugar, ¿de cuántas formas se pueden ordenar?
d. El entrenador dice que al ubicar a Boris y a Mauricio siempre en los dos primeros
puestos genera la misma cantidad de formaciones que si los ubica siempre en
los últimos dos puestos. ¿Está en lo correcto el entrenador? Compara tu respuesta
con la de tus compañeros.
9. Lee la información y luego responde. Guíate por el ejemplo.
En el siguiente diagrama, para ir de la posición inicial ( ) a la posición final ( ) hay que hacer
un recorrido moviéndose a la derecha (D) o hacia arriba (A) sucesivamente.
Ejemplo: un recorrido posible es AADDD:
a. ¿Cuántos recorridos distintos se pueden realizar? Represéntalos usando un diagrama.
b. ¿Cuántos de los recorridos comienzan con el movimiento hacia la derecha?
c. ¿En cuántos de los recorridos el último movimiento es hacia arriba?
Páginas122a125.
4
Unidad
197
377

Propósito
En esta clase los estudiantes aprenderán
a calcular la probabilidad de un evento
compuesto determinando el espacio
muestral a través de diagramas y
el principio multiplicativo.
OA 17
Planificación
Inicio 15 minutos
observen la fotografía y comenten sus
experiencias con este deporte. Pregúnteles:
¿por qué consideran importante practicar
algún deporte?
Pida a sus estudiantes que lean la
información sobre el lanzamiento de una
moneda para determinar quién inicia
el juego y que comenten en qué otros
deportes se utiliza una técnica similar.
Generalmente, los estudiantes preguntan qué sucedería si la moneda
cae de canto, o bien, por qué no se considera esa posibilidad dentro
del espacio muestral.
Puede compartir con sus estudiantes una noticia anecdótica
al respecto, en la que en un partido de fútbol la moneda
que lanzó el árbitro cayó de canto. En el siguiente sitio se
encuentra el video: https://www.quo.es/ser-humano/a62280/
que-probabilidad-hay-de-que-una-moneda-caiga-de-canto/
Desde el punto de vista matemático, en situaciones normales el valor
de la probabilidad de que la moneda caiga de canto es despreciable, y
por ello no se considera.
Actitudes
OA D , OA E , OA F
págs. 198 y 199
Clase 107
Cálculo de probabilidades
Antes de iniciar un partido de vóleibol el primer árbitro realiza
un sorteo en presencia de los capitanes de ambos equipos.
Para el sorteo se utiliza una moneda que es lanzada al aire.
Quien eligió la cara de la moneda que aparece hacia arriba es
el ganador del sorteo y es él quien decide el derecho a sacar
o recibir el saque o el lado del campo.
• En un partido de vóleibol, ¿cuál es la probabilidad que tiene un equipo de hacer
el saque inicial del juego?
• ¿Qué otro deporte utiliza una moneda para determinar quién inicia el juego?
Averigua y luego comenta con tu curso.
Lección 2 Probabilidades
198 | Unidad 4
E
E
s
CL0000000001018 MA

Unidad
4
ejemplo 1, utilizando un diagrama de
árbol para determinar el espacio muestral
al lanzar 4 monedas.
Para realizar el cálculo, recuerde la regla
de Laplace.
Cierre 15 minutos
Finalice la clase pidiendo a sus
estudiantes que compartan con sus
compañeros sus apreciaciones sobre el
uso de diagramas de árbol para poder
calcular probabilidades compuestas.
Para calcular la probabilidad del evento, recuerde la regla de Laplace
a sus estudiantes, indicando que, en el valor de la probabilidad de
un evento es igual al cociente entre el número de casos favorables
al evento y el número total de casos (o cantidad de elementos del
espacio muestral).
2/17/2019 9:39:16 AM
Ejemplo 1
En el experimento aleatorio de lanzar cuatro monedas, ¿cuál es la probabilidad de obtener
solo dos caras?
1 Determinamos el espacio muestral del experimento. Para eso, podemos construir un diagrama
de árbol donde la cantidad de elementos es igual a 16.
C
C S C S C S C S
C S C S
C S
S
C S C S C S C S
C S C S
C S
2 Si el suceso A consiste en que en solo dos de las monedas se obtenga cara, entonces la cantidad
de elementos de A es 6. En el diagrama lo podemos ver de la siguiente manera:
C
C S C S C S C S
C S C S
C S
S
C S C S C S C S
C S C S
C S
3 Finalmente, calculamos la probabilidad usando la regla de Laplace.
P(A) = 6 = 3 = 0,375
16 8
4 La probabilidad de obtener solo dos caras al lanzar 4 monedas es de 3
8
, de 0,375 o de un 37,5 %.
Si en un experimento aleatorio todos los resultados posibles son equiprobables y el espacio
muestral es finito, entonces se puede calcular la probabilidad de ocurrencia mediante la regla
de Laplace.
La regla de Laplace establece que la probabilidad de ocurrencia de un suceso A es el cociente
entre la cantidad de casos favorables y la cantidad de casos posibles.
P(A) = Cantidad de casos favorables = #A
Cantidad de casos posibles #Ω
Aprende
4
Unidad
199
379

Propósito
En esta clase los estudiantes calcularán
la probabilidad de un evento compuesto
determinando su espacio muestral a través
de diagramas de árbol.
OA 17
Planificación
Inicio 15 minutos
Comience la clase recordando a sus
estudiantes los conceptos estudiados
la clase anterior.
Con apoyo del recuadro Aprende, detalle
a los estudiantes el término de sucesos
equiprobables entregando ejemplos
suficientes. Plantee además situaciones
de sucesos no equiprobables, como
dados cargados, para que identifiquen
las diferencias.
Actitudes
perseverar y confiar en sus propias capacidades.
págs. 200 a 203
Clase 108
Actitudes
OA D , OA E , OA F
Ejemplo 2
¿Cuál es la probabilidad de obtener un múltiplo de 3 al lanzar un dado de seis caras?
1 Determinamos el espacio muestral (Ω) y el suceso de obtener un múltiplo de 3.
Ω = {1, 2, 3, 4, 5, 6} #Ω = 6
A = {3, 6} #A = 2
2 Calculamos la probabilidad de obtener un múltiplo de 3.
P(A) = 2 = 1
6 3
• Se dice que dos sucesos son equiprobables si tienen la misma probabilidad de ocurrencia.
• La probabilidad de un suceso se puede expresar como una fracción, como un número decimal
o como un porcentaje. Por ejemplo, la probabilidad de obtener una cara al lanzar una moneda
es de 0,5 o de
1
2
o de un 50 %.
Aprende
Ejemplo 3
Un experimento aleatorio consiste en extraer al azar una bolita de una caja, luego lanzar
una moneda y finalmente girar una ruleta.
¿Cuál es la probabilidad de obtener una bolita roja, un sello en la moneda y obtener el color
verde o azul en la ruleta?
1 Representamos la situación con un diagrama de árbol.
Ro Az Ve Am Ro Az Ve Am
C S
C S
C S
Podemos observar que la cantidad de combinaciones posibles es igual a 24.
2 Sea A: obtener una bolita roja, un sello en la moneda y obtener el color verde o azul en la ruleta.
C S
C S
C S
3 Finalmente, calculamos la probabilidad: P(A) = 2 = 1
24 12
.
Probabilidades
Lección 2
200 | Unidad 4
1
2
3
4
5
6
CL0000000001018 MA

Unidad
4
Pida a sus estudiantes que trabajen
las actividades en parejas, respetando
las opiniones de los otros compañeros
y generando un trabajo de forma
colaborativa, lo cual significa construir
juntos una solución.
Indique que cada integrante del grupo
debe ser capaz de explicar cómo
resolvieron cada actividad.
Promueva la participación de todos los estudiantes en un clima
de respeto.
Valore la diversidad de ideas y representaciones para desarrollar la
habilidad de representar en sus estudiantes.
Solucionario
2/17/2019 9:39:17 AM
1. Identifica los casos favorables para cada suceso.
a. Obtener un número primo al extraer una bolita de las 30 numeradas del 1 al 30 de
una tómbola.
b. Obtener una vocal al extraer una tarjeta de una caja con las letras de la palabra destino.
c. Obtener un múltiplo de 4 al sumar los puntajes de las caras superiores al lanzar dos dados.
2. Calcula la probabilidad de cada suceso teniendo en cuenta el experimento aleatorio
de lanzar dos monedas.
a. En las dos monedas se obtiene cara.
b. En la segunda moneda se obtiene sello.
c. En la primera moneda se obtiene cara y en la segunda sello.
3. Una baraja de naipe inglés tiene 52 cartas en total, separadas en cuatro pintas:
diamante, corazón, trébol y pica. Si se escoge una carta al azar, calcula la probabilidad
de los siguientes sucesos.
a. A: obtener un diamante.
b. B: obtener un número 3.
c. C: no obtener un número 10.
d. D: obtener una carta de pinta roja.
4. Escribe el espacio muestral del experimento «suma de puntos al lanzar dos dados».
Y luego, responde las preguntas.
a. ¿De cuántas maneras distintas se puede obtener una suma igual a 2?
b. ¿Cuál es la probabilidad de que la suma de los puntos sea 12?
5. En una caja hay 15 bolitas iguales numeradas del 1 al 15 y se extrae una al azar.
Ordena los sucesos del menos probable al más probable.
a. A: obtener un número primo.
b. B: obtener un número impar.
c. C: obtener un múltiplo de 7.
d. D: obtener un número menor que 15.
6. Se lanzan dos dados de 8 caras. Calcula las siguientes probabilidades.
a. Obtener números iguales en ambos dados.
b. Obtener un punto en cada dado.
c. Obtener un número par de puntos en un dado y
un número primo en el otro.
Actividades
4
Unidad
201
381

Para la actividad 7.c., recuerde a sus
estudiantes que los números primos son
aquellos cuyo divisor es 1 y ellos mismos,
por ejemplo: el 2, el 3, el 5, el 7, etc.
Puede extender el problema 7.c.
utilizando un dado de 20 caras o bien,
dos dados de 12, pidiendo calcular
la probabilidad de que la suma de los
números obtenidos sea un número primo.
Desarrolle la habilidad de argumentar y comunicar, pidiendo
a los estudiantes que utilicen su conocimiento matemático para
tomar decisiones a partir de la información dada en cada una de las
actividades y que luego argumenten sus decisiones.
a. ¿Cuál es la probabilidad de que al hacer girar cada una de las ruletas se obtenga el color verde?
2 3
1
b. Una secretaria tiene que guardar tres cartas en sus sobres. Si guarda al azar una carta en
cada uno de los sobres, ¿cuál es la probabilidad de que, al menos, una de las cartas vaya
en el sobre que le corresponde?
c. Eduardo tiene un dado con doce caras numeradas del 1 al 12, como el de
la imagen. Juega con Mario así: si al arrojarlo se obtiene un número primo
en la cara superior, gana Eduardo, y si sale un múltiplo de 4, gana Mario.
¿Los dos tienen las mismas posibilidades de ganar? Anota con qué números
gana cada uno de ellos.
d. ¿En qué situación la probabilidad de un suceso es 1?, ¿y cuándo la probabilidad de un
suceso es 0? Es posible que un suceso tenga probabilidad 1,5?, ¿por qué? Comenta tus
respuestas con tus compañeros.
e. Andrés y Juan son hermanos y quieren decidir a dónde irán de vacaciones. Para ello,
Juan propone lanzar dos monedas. Si se obtiene una cara y un sello Andrés escogerá
el lugar. Si se obtienen dos caras o dos sellos, Juan elegirá. Andrés dice quen esto
es injusto porque Juan tiene más posibilidades de ganar. Juan le dice que ambos
tienennla misma posibilidad de ganar o perder. ¿Cuál de los hermanos crees que
está en lo correcto? Justifica tu respuesta.
8. Analiza la siguiente información y luego responde.
En un juego caen al azar tres series de fichas cuadradas: una verde, una amarilla y otra roja. Para
ganar, deben alinearse tres fichas del mismo color de forma horizontal o en diagonal. En cada
situación, ¿qué probabilidad hay de ganar cuando caiga la tercera serie de fichas?
a. b. c. d.
• ¿Qué conocías acerca del cálculo de probabilidades?, ¿qué sabes ahora?
• ¿En qué situaciones cotidianas puedes usar estos contenidos?
Páginas126a129.
Probabilidades
Lección 2
202 | Unidad 4
R
1
E
S
CL0000000001018 MA

Unidad
4
Acompañe a sus estudiantes en el
trabajo con la herramienta tecnológica,
enfatizando el cuidado con la notación de
las fórmulas.
Invite a sus estudiantes a responder en
su cuaderno las preguntas planteadas.
Cierre 15 minutos
Finalice la clase pidiendo a sus estudiantes
que compartan con sus compañeros sus
apreciaciones sobre el uso de diagramas
de árbol para calcular probabilidades.
Proponga a sus estudiantes utilizar la hoja de cálculo que ofrece el
software GeoGebra.
Invítelos a ver la aplicación disponible en https://www.geogebra.org/m/
y99VEspS
En ella se puede ver una planilla como la que realizaron, con un dado
que muestra la cara con el número que resulta del lanzamiento.
páginas 126 a 129.
Planificación
Clase 109
?
2/17/2019 9:39:18 AM
Responde
1. Luego de realizar los pasos anteriores, construye en tu cuaderno una tabla de frecuencias
para esta situación y responde:
a. ¿Cuál es la frecuencia relativa cuando el número del dado es 3?, ¿cuál es la probabilidad
de que salga 3?, ¿se relacionan ambos valores?
b. ¿Cuál es el espacio muestral del experimento?, ¿los resultados son equiprobables?, ¿por qué?
c. En una nueva planilla repite el mismo procedimiento hasta las celdas B50 y C100. ¿Qué
sucede con la frecuencia relativa y la probabilidad en cada caso?, ¿qué puedes concluir?
En esta actividad deberás usar una planilla de cálculo para simular el lanzamiento de un dado.
Sigue las instrucciones que se presentan a continuación.
1 En una hoja de cálculo escribe en la celda A1 la
función =ALEATORIO(). Esta función creará un
número decimal aleatorio entre 0 y 1. Cada vez que
hagas un cambio en la hoja de cálculo, generará
un nuevo número.
2 Queremos obtener un número entre 1 y 6, que son
las posibilidades de un dado. Escribe en la celda A2 la
función =ALEATORIO()*5. Al escribir esta función, el
número que se cree estará multiplicado por 5, por lo
que el número generado es un decimal entre 0 y 5.
3 Para quitar la parte decimal, escribe en otra celda la
función: =REDONDEAR(ALEATORIO() *5; 0). El primer
argumento de la función es el número que queremos
redondear (el número generado aleatoriamente) y el
segundo argumento, el número de decimales al que
queremos que se redondee ese número (0 decimales).
Se obtendrán números enteros desde el 0 al 5.
4 Para que los posibles números vayan desde el 1
al 6, basta escribir en la celda A4 la función
=REDONDEAR(ALEATORIO()*5; 0) + 1. Esta función
le suma 1 a cada número generado aleatoriamente.
5 Copia esta función desde la celda B1 hasta la celda B20.
4
Unidad
203
383

Para el desarrollo de la evaluación es fundamental que los estudiantes
demuestren interés y perseverancia en la resolución de problemas. Para
esto es importante otorgar el tiempo que requiera cada alumno para
el desarrollo completo de las actividades propuestas, considerando
la verificación de las resoluciones y motivarlos constantemente en
su aprendizaje.
Propósito
la Lección 2.
conocimientos adquiridos en la Lección 2
Inicio 15 minutos
Repase los contenidos tratados en la lección
preguntando:
• ¿Qué es la probabilidad de un evento?
• ¿Qué es el espacio muestral?
• ¿Qué es el principio multiplicativo?
• ¿Para qué sirve un diagrama de árbol?
Solicite a sus estudiantes que realicen la
evaluación de manera independiente y que
registren las respuestas en sus cuadernos.
Planificación
págs. 204 y 205
Clase 110
Solucionario
1. Representa los siguientes experimentos aleatorios utilizando diagramas de árbol.
a. El lanzamiento de tres monedas.
b. El lanzamiento de dos dados de seis caras.
c. El lanzamiento de una moneda y un dado de seis caras.
d. El género de las siguientes 4 personas que entrarán en una tienda de música.
e. La elección de un libro de ciencias y uno humanista de entre 5 de ciencias y 3 humanistas.
f. La elección de un menú entre 3 entradas y 6 platos de fondo.
2. Para cada representación de experimentos aleatorios plantea un problema a resolver.
c.
Falda
Pantalón
Blusa
Polera
Zapatillas
Sandalias
Zapatillas
Sandalias
Zapatillas
Sandalias
Blusa
Polera
Zapatillas
Sandalias
b.
Francisco
Vicente
Trinidad
Trinidad
Alondra
Alondra
Isidora
Isidora
a.
Azul
Amarillo
Amarillo
Rojo
Café
Café
3. Analiza la siguiente situación y luego responde.
Se lanzarán dos dados al aire y se sumarán los puntos que se obtengan en sus caras superiores.
a. ¿Cuál es la probabilidad de obtener como suma 8 puntos?
b. ¿Cuál es la probabilidad de obtener menos de 5 puntos como suma?
c. ¿Cuál es la probabilidad de obtener como suma más de 9 puntos?
d. ¿Cuál es la probabilidad de obtener números iguales en ambos dados?
e. ¿Cuál es la probabilidad de no obtener como suma un número mayor que 10?
f. ¿Cuál es la probabilidad de que la suma sea menor que 2?
| Unidad 4
204
4
5
6
7
•
•
CL0000000001018 MA

Unidad
4
Pida a sus estudiantes que respondan las
preguntas planteadas en sus cuadernos
teniendo en consideración los contenidos
que han aprendido hasta ahora.
Cierre 15 minutos
Permita que sus estudiantes comparen
entre ellos sus respuestas y oriente a
aquellos estudiantes que presentaron
dificultades en el desarrollo de
la evaluación.
Actitudes
Recuerde a sus estudiantes que al enfrentarse a un desafío, aun cuando
no obtengan el resultado de manera inmediata, deben perseverar y
confiar en sus propias capacidades.
páginas 130 y 131.
Planificación
Clase 111
2/17/2019 9:39:18 AM
4. Analiza la siguiente situación, represéntala y luego responde.
Se lanzarán cinco monedas al aire y se observará el resultado obtenido.
a. ¿Cuál es la probabilidad de obtener 5 caras?
b. ¿Cuál es la probabilidad de obtener 3 sellos?
c. ¿Cuál es la probabilidad de obtener al menos un sello?
d. ¿Cuál es la probabilidad de obtener como máximo 3 caras?
e. ¿Cuál es la probabilidad de obtener dos sellos exactamente?
f. ¿Cuál es la probabilidad de obtener una cara y 4 sellos?
5. Con los dígitos 3, 6, 7, 8 y 9 se formarán números de tres cifras distintas.
a. ¿Cuántos números diferentes se pueden formar?
b. ¿Cuál es la probabilidad de que el número formado sea par?
6. ¿Qué recipiente conviene elegir al extraer al azar una llave y que esta abra el candado?
Hay 12 llaves y
solo una lo abre.
Recipiente A
Hay 25 llaves y
lo pueden abrir 5.
Recipiente B
Hay 42 llaves y
lo pueden abrir 7.
Recipiente C
7. En un restaurante, el menú incluye 4 tipos de entrada, 3 posibilidades de platos de fondo
y 2 postres diferentes.
a. ¿Cómo armarías tu menú?
b. ¿De cuántas maneras distintas
crees que se puede elegir
el menú?
Entradas
• Sopa de verduras
• Sopa de pollo
• Ensalada surtida
• Palta reina
Plato de fondo
• Arroz con carne
• Fetuchini
• Pastel de verduras
Postres
• Ensalada de frutas
• Flan
Menú
• ¿Qué entiendes por probabilidad? Explica.
• ¿Cómo compartiste tus ideas y puntos de vista con tus compañeras y compañeros?
Páginas130y131.
4
Unidad
385

Propósito
la Lección 4.
conocimientos adquiridos en la Unidad 4.
Inicio 15 minutos
Comience la clase recordando los conceptos
clave estudiados en esta unidad:
Tablas de frecuencias, histogramas,
probabilidades, espacio muestral y
diagramas de árbol.
Pida a sus estudiantes que aborden la
evaluación de la esta unidad respondiendo
en sus cuadernos de forma ordenada
y recurriendo a sus apuntes cuando
sea necesario.
Promueva un ambiente positivo al interior del aula mediante el
desarrollo de la motivación y el interés por el aprendizaje. Para ello,
puede guiar la revisión de la resolución de las actividades propuestas
en la evauación con el fin de observar diferentes estrategias y
analizarlas en conjunto con el curso.
Planificación
págs. 206 y 207
Clase 112
1. Interpreta la información entregada en el siguiente gráfico y luego responde.
En el gráfico se muestran los resultados de una encuesta realizada a un grupo de estudiantes
acerca de la cantidad de hermanos que tienen.
Cantidad de hermanos de un grupo
de estudiantes
Cantidad de
hermanos
Cantidad
de
estudiantes
5
15
20
35
30
25
10
0
15
33
1 2
20
3
26
0
a. ¿A cuántos estudiantes se encuestó?
b. ¿Cuántos estudiantes tienen 2 hermanos?
c. ¿Qué porcentaje de los estudiantes tiene
menos de 2 hermanos?
2. El gráfico circular corresponde a las preferencias de un grupo de 150 estudiantes,
¿cuántos no prefieren el fútbol?
Deportes preferidos
Fútbol
Natación
Tenis
Vóleibol
Básquetbol
Deportes
30%
12%
14%
24%
20%
3. Analiza la situación y luego responde.
Los siguientes datos corresponden a las estaturas en centímetros de los participantes
de un torneo de karate.
145 - 155 - 168 - 178 - 170 - 170 - 168 - 170 - 158 - 168 - 158 - 188 - 190 - 168 - 165 - 159
172 - 145 - 188 - 185 - 156 - 195 - 188 - 175 - 162 - 145 - 154 - 175 - 164 - 160 - 178 - 184
182 - 175 - 169 - 167 - 170 - 175 - 168 - 176 - 174 - 150 - 175 - 148 - 167 - 164 - 169 - 174
a. ¿Cuál es el valor del percentil 70?
b. ¿Cuál es el valor de Q3? ¿Cuál es su interpretación?
c. Si se considera en una de las competencias al 25% de los competidores de menor estatura,
¿hasta qué estatura se podría participar en esta categoría?
d. Construye un diagrama de cajón con los datos.
e. Si con el 35% de los que tienen mayor estatura se realizará una competencia especial,
¿sobre qué estatura se elegirá a los participantes?
Evaluación final
| Unidad 4
206
4
5
6
7
•
•
CL0000000001018 MA

Unidad
4
Antes de finalizar la clase, otorgue unos
minutos para que los estudiantes puedan
compartir sus respuestas a las preguntas
de reflexión y las dificultades respecto de
los contenidos de esta unidad.
Promueva la participación de todos los
estudiantes en un clima de respeto.
Cierre 15 minutos
Finalice la clase preguntando a sus
estudiantes cómo se pueden conectar los
contenidos aprendidos en esta unidad con
los contenidos de las unidades anteriores.
Invite a sus estudiantes a responder en su cuaderno las preguntas de
reflexión para luego compartirlas con sus compañeros en una instancia
de discusión plenaria. Se sugiere desarrollar esta clase como
páginas 132 y 133.
Planificación
Clase 113
Solucionario
2/17/2019 9:39:19 AM
4. Las patentes de automóviles constan de 4 letras y 2 dígitos. Considera que las condiciones
que se deben cumplir en cada patente son las siguientes:
• No se pueden utilizar vocales.
• No se pueden utilizar las letras M, N, Ñ ni Q.
• El primer número no puede ser cero.
a. Determina una expresión para calcular cuántas patentes distintas se pueden construir.
b. ¿Cuántas patentes terminan con un dígito impar?
c. ¿Cuántas patentes tienen todas sus letras iguales?
5. Un 4° medio está confeccionando un polerón que puede ser de color rojo, verde o azul.
Puede también tener o no tener gorro y puede ser con cierre o sin cierre. ¿Cuántos diseños
distintos de polerón hay?
6. Se escriben los dígitos 2, 5, 3, 6, 7 y 9, cada uno en una tarjeta. ¿Cuál es la probabilidad
de que al ordenarlas una al lado de la otra se forme un número impar?
7 6 2 5 3
9
7. Un grupo musical compuesto por 4 mujeres y 3 hombres se sacará una foto para la cual
sus integrantes se dispondrán al azar uno al lado del otro. ¿Cuál es la probabilidad de
que al ordenarse queden todos los hombres juntos y todas las mujeres juntas?
Ejemplo
M M M M H H H
• ¿Crees que debes repasar algún contenido?, ¿por qué?
• ¿Pudiste solucionar las dificultades que hayas tenido en el desarrollo de la unidad?
Páginas132y133.
4
Unidad
Evaluación final | 207
387

Propósito
En esta clase se realizará una síntesis con
los conocimientos más importantes de
las lecciones de la Unidad 4.
Sintetizar y repasar los conocimientos
adquiridos en la Unidad 4.
Inicio 15 minutos
Invite a sus estudiantes a revisar en sus
cuadernos los contenidos estudiados en
esta unidad, para que participen del diseño
de la síntesis de la Unidad 4.
Pida a sus estudiantes que desarrollen los
desafíos propuestos en parejas, anotando
Planificación
Para el desarrollo de estos desafíos es fundamental que los estudiantes
demuestren interés y perseverancia en la resolución de problemas,
y que respeten las opiniones de sus pares.
Para esto, promueva un ambiente de respeto y confianza en el curso,
valorando la diversidad de estrategias e ideas que surjan de
sus estudiantes.
págs. 208 y 209
Clase 114
Estadística
Lección 1
1. Analiza cada variable e indica qué gráfico crees que es el más adecuado para representarla.
Justifica tu respuesta.
a. Temperaturas registradas cada 1 hora durante un día en una ciudad.
b. Resultados de las elecciones de presidente de curso en el 8° básico de un colegio.
c. Estatura de los estudiantes de 8° básico de la región de Arica y Parinacota.
2. Los siguientes datos corresponden a las edades de los participantes de un taller de pintura
de la comuna.
Calcula e interpreta los valores
de Q1, Q2, P70 y P90.
16 - 16 - 23 - 37 - 18 - 16 - 18 - 21 - 32 - 41 - 27 - 37 - 33
21 - 19 - 26 - 35 - 40 - 31 - 23 - 16 - 30 - 24 - 36 - 34
3. En el diagrama de cajón se representa la distribución de las distancias de un puerto
a las localidades cercanas a él.
40
20 60 90
Kilómetros
a. ¿Cuál es la distancia de la ciudad que se encuentra más cerca del puerto?
b. ¿Cuál es el valor del tercer cuartil? ¿Cuál es su interpretación?
Los gráficos permiten representar los datos para comparar las frecuencias de los valores,
analizar cómo se comporta una variable y comunicar dicha información.
• Los gráficos de barras se utilizan para comparar las frecuencias de variables cualitativas
o cuantitativas.
• Los histogramas son gráficos formados por barras contiguas, en que cada una representa
un intervalo de valores. Sirve para expresar información sobre datos que están agrupados.
• Los gráficos de líneas permiten representar variables cuantitativas que varían en el tiempo.
• Los gráficos circulares se emplean para mostrar información que se expresa en
porcentajes o razones respecto de un total, que se representa por el círculo completo.
– Si resulta un número entero, Qk es igual al promedio entre el dato que se ubica en
esa posición y el dato siguiente.
– Si resulta un numero decimal, Qk es igual al dato que ocupa la posición; [n • k
]+ 1
4
.
Para calcular el percentil P_k se deben ordenar los n
datos en forma creciente y calcular (n∙k)/100.
• Si resulta un numero entero, P_k es igual al promedio
entre el dato que se ubica en esa posición y el dato
siguiente.
• Si resulta un numero decimal, P_k es igual al dato que
ocupa la posición [(n∙k)/100]+1
• Un diagrama de cajón es una representación gráfica
que permite visualizar algunas características de la
Las medidas de posición dividen una distribución ordenada en grupos con la misma
cantidad de datos.
• Para calcular el cuartil Qk se deben ordenar los n datos en forma creciente y calcular
n • k
4
.
Síntesisy Repaso
| Unidad 4
208
1
2
3
CL0000000001018 MA

Unidad
4
Invite a algunos estudiantes a presentar sus
respuestas en la pizarra. Motive al resto de
los estudiantes a analizar estas respuestas,
corrigiendo posibles errores cometidos y
compartiendo sus propias dificultades.
Cierre 15 minutos
Finalice la clase orientando a aquellos
estudiantes que presentaron dificultades
o cometieron errores durante el desarrollo
de los ejercicios de repaso.
Solucionario
Puede profundizar el trabajo desarrollado en la unidad mediante las
actividades propuestas en los siguientes links:
2/17/2019 9:39:20 AM
Probabilidad
Lección 2
1. Un juego consiste en lanzar un dado de seis caras. Si se obtiene un número par, se lanza otra
vez el dado. Si se obtiene un número impar, se lanza dos veces una moneda. Si se obtienen
dos caras al lanzar las monedas, se lanza nuevamente un dado.
a. Construye un diagrama de árbol que represente la situación.
b. ¿Cuántas combinaciones posibles se pueden conseguir?
2. Los cinco finalistas de un torneo internacional de golf son España, México, Portugal,
Uruguay y Japón.
a. ¿De cuántas maneras es posible premiar al primer, segundo y tercer lugar?
b. Si el primer lugar lo ganó Portugal y el segundo, México, ¿cuántas maneras
hay de otorgar el tercer lugar entre los países restantes?
3. En el diagrama se elige un camino para ir desde A
hasta H . ¿Cuál es la probabilidad de pasar por E ?
• El principio multiplicativo es una técnica de conteo en la que, si un conjunto está
compuesto por n1 elementos, otro conjunto por n2 elementos, y así sucesivamente con k
conjuntos diferentes, entonces la cantidad de maneras de combinar los elementos de
los conjuntos es:
n1 • n2 • … • nk
• El diagrama de árbol es una representación gráfica que permite mostrar los resultados
posibles al aplicar el principio multiplicativo.
• Si en un experimento aleatorio todos los resultados posibles son equiprobables, entonces
se puede calcular la probabilidad de ocurrencia mediante la regla de Laplace.
• La regla de Laplace establece que la probabilidad de ocurrencia de un suceso A es
el cociente entre la cantidad de casos favorables y la cantidad de casos posibles.
P(A) = cantidad de casos favorables = #A
cantidad de casos posibles #Ω
A
E
H
D
G
F
I J
B C
4
Unidad
209
Síntesis y Repaso |
389

Página 175
• Cuando su rendimiento en función de alguna variable es
mejor que la de otro.
• Se pueden documentar los tiempos de carrera de
competidores de una carrera o los tiempos para un solo
deportista y así ver su evolución. Se pueden tener estadísticas
de los goles convertidos por los jugadores de fútbol en un
determinado torneo o temporada.
• Resouesta a cargo del estudiante.
1. {(c, c); (c, s); (s, c); (s, s)}
2. La probabilidad es 1
8
.
3. La probabilidad de obtener menos de 4 puntos al lanzar
un dado es de 3
6
.
4. a. ¿Cuántas veces juegas fútbol a la semana?
Cantidad de días f
0 1
1 6
2 3
3 5
4 5
5 3
6 1
7 1
Total 25
b. En promedio los niños y niñas juegan 3 veces
a la semana fútbol.
Página 176
Estadística
Lección 1
Representaciones gráficas
• A la falta de tiempo libre, o a la necesidad de realizar otras
actividades.
Página 180
Actividades
1. a. Gráfico circular porque es más fácil representar
porcentajes en él.
b. Gráfico de línea o de barra porque representan de mejor
forma variables cualitativas o cuantitativas.
c. Gráfico de línea porque es una variable numérica que
varía en el tiempo.
d. Gráfico de barra porque representan de mejor forma
variables cualitativas o cuantitativas.
e. Gráfico circular porque es más fácil representar
porcentajes en este tipo de grafico.
f. Gráfico circular porque es más fácil representar
porcentajes en este tipo de grafico.
2. a. 9 estudiantes tienen como mascota un gato
o un roedor.
b. 55 jóvenes prefieren voleibol.
165 el tenis o el atletismo.
Fueron encuestados 550 jóvenes.
c. El intervalo de 31 a 44 años presenta la mayor frecuencia.
El intervalo de 70 a 83 años presenta la menor frecuencia.
Se recaudaron $672 500 por las entradas.
Asistieron 86 personas de las cuales 48 eran menores de
44 años.
Página 181
3. a. La semejanza es que ambos utilizan barras para
representar la frecuencia, la diferencia es que los
histogramas son utilizados para intervalos y los gráficos
de barra para variables cualitativas o cuantitativas que no
estén en intervalos.
b. Ambos gráficos representan los mismos tipos de variables,
la única diferencia entre ellos es la representación gráfica
(líneas contra barras) y que el grafico de líneas tiene un
uso para visualizar tendencias.
c. Cuando la información es de carácter porcentual.
4. a.
Actividad preferida
Actividad preferida
Actividad f
Salir con amigos 30
Practicar un deporte 15
Ver películas 45
Usar el computador 60
Total 150
Salir con amigos
Practicar un deporte
Ver películas
Usar el computador
Actividad
30%
10%
40%
20%

Unidad
4
391
b.
Actividades realizadas por estudiantes
Número de estudiantes
20
40
60
80
Salir con
amigos
Practicar
un deporte
Ver películas Usar el
computador
0
c. 45 estudiantes prefieren salir con amigos o practicar un
deporte. Es cierto que no alcanzan a ser un tercio del total
de encuestados porque un tercio equivale a 33,3%.
d. Es verdad, debido a que en conjunto suman un 70%
de los encuestados.
5.
Juguetes vendidos por mes
20
40
60
80
100
Enero Febrero Marzo Abril Mayo
0
Número de juguetes vendidos
Juguetes vendidos por mes
10
20
30
40
50
60
70
80
Enero Febrero Marzo Abril Mayo
0
Número de juguetes vendidos
Página 182
Medidas de posición
• Es un deporte con varias modalidades en el cual se utilizan
distintos tipos de bicicletas.
• El menor dato es 160 y el mayor 172.
{(160, 160, 160, 162); (162, 162, 164, 164); (164, 166,
168, 168); (168, 170, 170, 172)}
Página 186
Actividades
1. a. Q1 = 5, Q2 = 7; Q3 = 10
b. Q1 = 7,5; Q2 = 20; P50 = 20
c. P20 = 52, P50 = 56; P80 = 62
d. P10 = 2,3; Q3 = 7,875; P75 = 7,875
e. P10 = 10,4; Q3 = 21; P35 = 15,45
f. Q1 = 100; P12 = 100; P92 = 110
Página 187
2. a. Q1 = 3; Q2 = 4; P50 = 4; Q3 = 4
P75 = 4; P80 = 4; P99 = 4
b. Q1 = 90; Q2 = 95; Q3 = 105
P10 = 88; P60 = 100; P90 = 110
3. a. El valor del primer cuartil de los datos es 170,5
y el del tercero es 216,5.
b. 11 alumnos se ubican bajo el segundo cuartil y tienen
entre 1 y 2 hermanos.
c. 4 estudiantes se ubican sobre el percentil 80 y su estatura
debe ser mayor a 1,68.
4. Actividad en clases.
5. No, debido a que el percentil 50 corresponde a tres mascotas,
por lo que se puede afirmar que el 50% de los estudiantes
tienen 3 mascotas o menos.
Página 188
6. a. El presupuesto asignado era de $21 800.
b. El P15.
c. Corresponde al valor asignado, sobre el cual el 85% de
los mensajeros gastaron más dinero en el combustible.
7. El percentil 80 corresponde a 89,5 y esto significa que
el 20% de los cultivos demoraron más de 89,5 minutos
en reproducirse, o que el 80% se demoró menos de
89,5 minutos.
8. a. Q1 = 43; Me = 48
Q3 = 63; Ric = 22
Mín. = 23, Máx. = 68
b. Q1 = 38; Me = 53
Q3 = 63; Ric = 25
Mín. = 33, Máx. = 73
c. Q1 = 28; Me = 43
Q3 = 68; Ric = 40
Mín. = 23, Máx. = 68
9.
72
71
70 73 74 76 78
75 77 79 80

Página 190
1. a.
¿Cuál es el destino?
Ciudad de destino f f (%)
San Pablo 18 37,5
Madrid 6 12,5
Barcelona 15 31,25
París 9 18,75
Total 48 100
b. El gráfico 1 es el que representa correctamente los datos
de la tabla 1.
c. No, porque los pasajeros que van a Madrid y Barcelona
son solo un 43,75%.
d.
Destino de los pasajeros
5
10
15
20
San Pablo Madrid Barcelona Paris
0
Número de pasajeros
Página 191
2. a. Los cuartiles son Q1 = 4; Q2 = 6; Q3 = 7.
b.
4
3
2 5 6 8
7 9
c. Cuatro personas, que son las que obtuvieron más de
7 puntos.
d. Diez personas podrían rendir el test nuevamente.
3.
30
20
10 40 50 60 70
4.
3
2
1 4 5 6 7
Página 192
Probabilidades
Lección 1
Principio multiplicativo
• Deben jugar 3 partidos.
• Tienen una probabilidad de 1
8
.
Página 195
Actividades
1. a. Sí se puede aplicar. Pueden llegar de 243 formas.
b. No se aplica el principio multiplicativo.
c. Los resultados posibles se pueden calcular mediante
el principio multiplicativo. Se pueden obtener 1 296
resultados diferentes.
d. Se puede calcular mediante el principio multiplicativo.
Se pueden ubicar de 12 maneras diferentes.
e. Se puede calcular mediante el principio multiplicativo.
Se pueden tener 32 resultados diferentes.
f. Se puede calcular mediante el principio multiplicativo.
Se pueden tener 24 resultados diferentes.
2. a.
Hamburguesa
Mayonesa
Salsa
Puré
Ensalada
Puré
Ensalada
Lomo
Mayonesa
Salsa
Puré
Ensalada
Puré
Ensalada
Pollo
Mayonesa
Salsa
Puré
Ensalada
Puré
Ensalada
b. 6 de los menús tendrán puré.
c. 3 de los menús tendrán mayonesa y puré.
3. Hay 8 combinaciones posibles.
Masculino
A
B
AB
O
Femenino
A
B
AB
O

Unidad
4
393
b. Hay 18 combinaciones posibles.
Grande
Naranja
Mango
Manzana
Amarillo
Amarillo
Amarillo
Rojo
Rojo
Rojo
Verde
Verde
Verde
Pequeño
Naranja
Mango
Manzana
Amarillo
Amarillo
Amarillo
Rojo
Rojo
Rojo
Verde
Verde
Verde
c. Hay 6 combinaciones posibles.
Azul
Roja
Negra
Violeta
Verde
Roja
Negra
Violeta
Página 196
4. Hay solo 6 posibilidades porque una vez ingresado un sobre
a un buzón solo quedan dos para repartir entre los otros
dos buzones.
Buzón Celeste
Carta Celeste
Buzón Rojo
Carta Roja
BuzónVerde
CartaVerde
Buzón Rojo
CartaVerde
BuzónVerde
Carta Roja
Buzón Celeste
Carta Roja
Buzón Rojo
Carta Celeste
BuzónVerde
CartaVerde
Buzón Rojo
CartaVerde
BuzónVerde
Carta Celeste
Buzón Celeste
CartaVerde
Buzón Rojo
Carta Celeste
BuzónVerde
Carta Roja
Buzón Rojo
Carta Roja
BuzónVerde
Carta Celeste
5. a. {(R, A); (R, V); (R, B); (A, R); (A, V); (A, B); (B1, A); (B1, R); (B1, B);
(B2, R); (B2, V); (B2, A)}
b. Respuesta variada. A continuación se muestra un ejemplo.
Una persona tiene una camisa roja, una azul y dos blancas,
y también tiene pantalones azules, rojos, blancos y verdes.
Si la persona no puede usar el mismo color de camisa y
pantalón, excepto si es la primera camisa blanca, la cual
sí puede utilizar con el pantalón blanco, pero no puede
usarla con el pantalón verde, ¿cuál es la cantidad de
combinaciones que tiene para vestirse?
6. Andrés puede estar 24 meses sin repetir su clave de cuenta
de ahorros.
7. a. Se pueden formar 5 040 mensajes diferentes.
b. 120 mensajes pueden cumplir con esa configuración.
c. Se pueden formar 840 mensajes.
d. Se pueden formar 343 mensajes.
Página 197
8. a.
Fabián
Diego
Boris
Mauricio
Boris Mauricio
Mauricio Boris
Diego Mauricio
Mauricio Diego
Diego Boris
Boris Diego
Diego
Fabián
Boris
Mauricio
Boris Mauricio
Mauricio Boris
Mauricio Fabián
Fabián Mauricio
Boris Fabián
Fabián Boris
Boris
Diego
Fabián
Mauricio
Fabián Mauricio
Mauricio Fabián
Diego Mauricio
Mauricio Diego
Fabián Diego
Diego Fabián
Mauricio
Diego
Fabián
Boris
Fabián Boris
Boris Fabián
Diego Boris
Boris Diego
Fabián Diego
Diego Fabián

b. Se pueden ubicar de 24 maneras diferentes.
c. Se pueden ordenar de 6 maneras diferentes.
d. Está en lo correcto, dado que de las dos formas quedan
libres solo dos puestos para realizar las combinaciones.
9. a. Se pueden realizar 10 caminos.
b. 7 movimientos parten por la derecha.
c. 5 movimientos terminan hacia arriba.
Página 198
Cálculo de probabilidades
• Un cincuenta por ciento.
• Otro día es el fútbol.
Página 201
Actividades
1. a. Los casos favorables son 10: el 2, 3, 5, 7, 11, 13, 17, 19, 23 y
29.
b. Los casos favorables son 3: la e, i y o.
c. Los casos favorables son 3: el 4, 8 y 12.
2. a. 1
4
b. 1
2
c. 1
4
3. a. 1
4
b. 1
13
c. 12
13
d. 1
2
4. {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
a. De una sola forma.
b. La probabilidad es de 1
36
.
5. C A B D
6. a. 1
8
b. 1
64
c. 1
4
Página 202
7. a. La probabilidad es de 1
64
.
8
.
c. Eduardo: 2, 3, 5, 7, 11, 13, 17 y 19 Mario: 4, 8 y 12.
Claramente no tienen la misma probabilidad de ganar.
d. La probabilidad de un suceso es 1 cuando es un evento
seguro, es decir, cuando el suceso es equivalente al
espacio muestral. La probabilidad de un suceso es 0
cuando es un evento imposible, es decir, no pertenece
al espacio muestral.
Un suceso no puede tener una probabilidad de 1,5,
ya que la certeza es máxima cuando es 1.
e. Ambos tienen la misma probabilidad de ganar ya que el
espacio muestral se compone por cuatro elementos {(c, c);
(c, s); (s, c); (s, s)}.
8. a. 1
3
b. 1
3
c. 1
3
d. 2
3
Página 203
Respuesta variada. A continuación se muestra un ejemplo.
1.
Número 1 2 3 4 5 6
Frecuencia 2 3 4 3 4 4
a. La frecuencia relativa de 3 es 0,2. La probabilidad de
obtener 3 en un dado es de 0,16. Se relacionan en que al
aumentar el número de lanzamientos, se obtendrá una
frecuencia relativa cada vez mas cercana a su valor teórico.
b. El espacio muestral es Ω = {1, 2, 3, 4, 5, 6}. Los resultados en
la práctica no son equiprobables. Esto es debido a que se
tiene un número bajo de experimentos.
c. Al aumentar los experimentos, las frecuencias relativas se
acercan a sus valores teóricos.

Unidad
4
395
Página 204
1. a.
C
C
S
C
S
C
S
S
C
S
C
S
C
S
b.
1
1 2 3 5
4 6
2
1 2 3 5
4 6
3
1 2 3 5
4 6
4
1 2 3 5
4 6
5
1 2 3 5
4 6
6
1 2 3 5
4 6
c.
C
1 2 3 5
4 6
S
1 2 3 5
4 6
d.
M
M
M
F
F
M
F
M
F
M
F
M
F
M
F
F
M
M
F
F
M
F
M
F
M
F
M
F
M
F
e.
H1
C1 C2 C3 C5
C4
H2
C1 C2 C3 C5
C4
H3
C1 C2 C3 C5
C4
f.
E1
F1 F2 F3 F5
F4 F6
E2
F1 F2 F3 F5
F4 F6
E3
F1 F2 F3 F5
F4 F6
2. a. Una persona tiene un pañuelo azul y rojo y dos pares de
guantes, amarillos y cafés. ¿De cuántas formas se puede
vestir?
b. En una clase de baile hay dos hombres y tres mujeres. ¿De
cuántas formas se pueden formar parejas de un hombre
con una mujer?
c. Karla tiene una falda y un pantalón, una blusa y una polera
y unas zapatillas y unas sandalias. ¿De cuántas formas se
puede vestir Karla?
36
.
6
.
c. La probabilidad es de 1
6
.
d. La probabilidad es de 1
6
.
e. La probabilidad es de 11
12
.
f. La probabilidad es 0.

Página 205
32
.
16
.
c. La probabilidad es de 31
32
.
d. La probabilidad es de 13
16
.
e. La probabilidad es de 5
16
.
f. La probabilidad es de 5
16
.
5. a. Se pueden formar 60 números diferentes.
5
.
6. Conviene elegir el recipiente B.
7. a. Respuesta a cargo del estudiante.
b. Se pueden tener 24 formas de menú.
Página 206
Evaluación final
1. a. Se encuestaron 94 canciones.
b. 20 estudiantes tienen 2 hermanos.
c. Aproximadamente el 51,06% de los estudiantes tiene
menos de 2 hermanos.
2. 105 estudiantes no prefieren el fútbol.
3. a. El percentil 70 es 175.
b. El Q3 = 175, lo cual quiere decir que el 75% de los datos
son menores o iguales que 175.
c. Se podría participar hasta 161 cm.
d.
140 150 160 170 180 190
e. Los participantes deben medir 174 o más.
Página 207
4. a. 18 • 18 • 18 • 18 • 9 • 10 = 9 447 840 patentes diferentes.
b. 18 • 18 • 18 • 18 • 9 • 5 = 4 723 920 patentes terminan con
un dígito impar.
c. 18 • 9 • 10 = 1 620 patentes tienen todas sus letras iguales.
5. Hay 12 posibles diseños del polerón.
6. La probabilidad es 3
5
.
7. La probabilidad es de 144
5 040
.
Página 208
Síntesis y Repaso
Lección 1 Estadística
1. a. Gráfico de líneas para poder ver tendencias de
la temperatura.
b. Gráfico de barras debido a que son variables cualitativas.
c. Un histograma, dado que las estaturas pueden ser muy
variables y son más apreciables por intervalos.
2. Q1 = 19; Q2 = 26; P70 = 33 y P90 = 37
3. a. La distancia de la ciudad más cercana del puerto está
a 34 km.
b. El tercer cuartil corresponde a 56 km, lo cual significa que
el 75% de las ciudades se encuentran a menos de 56 km.
Página 209
Lección 2 Probabilidad
1. a.
1
(C,C) (C,S) (S,C) (S,S)
2
1 2 3 5
4 6
1 2 3 5
4 6
3
(C,C) (C,S) (S,C) (S,S)
4
1 2 3 5
4 6
1 2 3 5
4 6
5
(C,C) (C,S) (S,C) (S,S)
6
1 2 3 5
4 6
1 2 3 5
4 6
b. Son 45 combinaciones diferentes.
2. a. Se puede otorgar de 60 formas diferentes.
b. Se puede otorgar de 3 maneras diferentes.
3. La probabilidad de pasar por E es 2
3
.

Unidad
4
397

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
176
a
181
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
15
y
16
de
las
Bases
Curriculares.
Representaciones
gráficas
1.
En
una
empresa,
para
preparar
la
fiesta
de
Navidad
se
les
pregunta
a
sus
trabajadores
cuántos
hijos
tienen.
¿Cuántos
hijos
tiene?
5
10
15
20
2
4
6
0
Cantidad
de
hijos
Frecuencia
a.
¿Cuál
es
la
cantidad
de
hijos
más
frecuente
entre
los
trabajadores?
b.
¿Cuántos
trabajadores
tienen
2
o
más
hijos?
c.
¿Qué
porcentaje
de
trabajadores
tiene
a
lo
más
4
hijos?
d.
¿Cuántos
trabajadores
tiene
la
empresa?
e.
¿Cuál
es
la
cantidad
de
hijos
menos
frecuente
entre
los
trabajadores?
Marca
la
opción
correcta.
2.
¿Para
cuál
de
los
siguientes
datos
el
gráfico
de
línea
no
es
el
más
apropiado?
A.
Cantidad
de
alumnos
que
se
inscriben
cada
mes
del
año
en
un
curso
de
manejo.
B.
Número
de
personas
que
mueren
por
cierta
enfermedad
entre
los
años
2006
y
2014.
C.
Porcentaje
de
alumnos
con
promedio
y
sin
promedio
bajo
5
en
un
curso.
D.
Cantidad
de
accidentes
de
tránsito
por
mes
del
año.
Unidad
4
•
El
deporte
Estadística
Lección
1
110
|
Unidad
4
110
CL0000000001052
110
12/17/2019
9:46:04
AM
3.
En
el
gráfico
se
muestran
las
ventas
realizadas
en
una
casa
comercial.
¿Qué
se
puede
concluir
del
gráfico?
Ventas
del
primer
semestre
100
000
300
000
200
000
400
000
800
000
700
000
600
000
500
000
Febrero
Marzo
Abril
Mayo
Junio
Julio
Enero
0
Mes
Pesos
($)
A.
Las
ventas
mejoraron
en
febrero.
B.
Las
ventas
comenzaron
a
subir
en
marzo.
C.
Las
ventas
serán
mejores
en
agosto.
D.
En
febrero
no
hubo
ventas.
Considera
la
siguiente
información
y
responde
los
ítems
4,
5
y
6.
El
siguiente
gráfico
muestra
las
preferencias
en
un
grupo
de
150
estudiantes
de
su
deporte
favorito.
Fútbol
Vóleibol
Natación
Básquetbol
Tenis
Deportes
Deportes
preferidos
20%
14%
24%
12%
30%
4.
¿Cuántos
estudiantes
prefieren
el
básquetbol?
A.
36
estudiantes.
B.
21
estudiantes.
C.
45
estudiantes.
D.
30
estudiantes.
5.
¿Cuántos
estudiantes
prefieren
la
natación
y
el
vóleibol?
A.
21
estudiantes.
B.
41
estudiantes.
C.
51
estudiantes.
D.
61
estudiantes.
6.
¿Cuál
afirmación
es
falsa?
A.
La
mayor
preferencia
es
el
fútbol.
B.
Al
básquetbol
lo
prefieren
más
estudiantes
que
a
la
natación.
C.
La
menor
preferencia
tiene
un
14
%.
D.
Al
vóleibol
lo
prefieren
menos
estudiantes
que
al
básquetbol.
4
Unidad
111
111
Lección
1
•
Estadística
|
CL0000000001052
111
12/17/2019
9:46:04
AM
Estadística
Lección
1
4
Unidad
398
Cuaderno
de
Actividades
•
Unidad
4
De
0
a
2.
15
trabajadores.
66,67 %
30
Entre
2
y
4.
Orientaciones y solucionario Cuaderno de Actividades

Unidad
4
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
176
a
181
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
15
y
16
de
las
Bases
Curriculares.
7.
Las
calificaciones
obtenidas
por
los
estudiantes
de
un
octavo
básico
se
representaron
en
el
siguiente
histograma.
Calificaciones
del
curso
1
3
2
4
5
1,0
2,0
3,0
4,0
5,0
6,0
7,0
0
Calificación
obtenida
Cantidad
de
estudiantes
¿Cuántos
estudiantes
obtuvieron
calificación
superior
o
igual
a
4,0?
A.
5
estudiantes.
B.
10
estudiantes.
C.
14
estudiantes.
D.
18
estudiantes.
8.
En
el
siguiente
gráfico
se
muestran
los
medios
de
transporte
que
utilizan
los
estudiantes
para
ir
al
colegio.
¿Cuál
de
las
siguientes
afirmaciones
es
correcta?
Bus
Auto
A
pie
Bicicleta
Transporte
Transporte
al
colegio
10%
30%
40%
20%
A.
El
porcentaje
de
estudiantes
que
no
utilizan
la
bicicleta
para
ir
al
colegio
es
de
un
60
%.
B.
La
mayoría
de
los
alumnos
llegan
al
colegio
a
pie.
C.
Un
20
%
de
los
estudiantes
se
va
en
bicicleta
al
colegio.
D.
Más
de
la
mitad
de
los
alumnos
se
van
al
colegio
en
automóvil
o
en
bus.
Estadística
Lección
1
112
|
Unidad
4
CL0000000001052
112
12/17/2019
9:46:04
AM
9.
Observa
el
gráfico
en
el
que
se
muestra
la
relación
entre
la
hora
y
la
temperatura
en
una
ciudad.
Temperatura
en
un
día
de
otoño
5
15
10
20
25
7:00
8:00
9:00
11:00
10:00
12:00
13:00
14:00
15:00
17:00
16:00
18:00
19:00
0
Hora
°C
¿Cuál
de
las
siguientes
conclusiones
no
se
puede
obtener
del
gráfico?
A.
La
temperatura
más
baja
se
presentó
a
las
7:00
horas.
B.
Durante
el
día
la
temperatura
presentó
una
amplitud
térmica
de
15
ºC.
C.
La
temperatura
fue
aumentando
con
cada
hora
del
día.
D.
El
mayor
cambio
de
temperatura
se
observó
entre
las
9
y
las
10,
y
entre
las
18
y
las
19
horas.
10.
Pedro,
Juan
y
Diego
están
en
un
tratamiento
por
sobrepeso.
¿Cuál
de
las
siguientes
opciones
representaría
mejor
la
variación
del
peso
de
cada
uno
en
los
seis
meses
de
tratamiento?
A.
Gráfico
de
barras.
B.
Gráfico
de
líneas.
C.
Gráfico
circular.
D.
Histograma.
11.
En
el
siguiente
gráfico
se
muestra
la
cantidad
de
hermanos
que
tienen
los
estudiantes
de
8º básico.
¿Cuántos
tienen
tres
hermanos?
Un
hermano
Dos
hermanos
Tres
hermanos
Cuatro
hermanos
Total:
60
estudiantes
¿Cuántos
hermanos
tienes?
30%
40%
10%
20%
A.
6
estudiantes.
B.
12
estudiantes.
C.
18
estudiantes.
D.
24
estudiantes.
4
Unidad
113
Lección
1
•
Estadística
|
CL0000000001052
113
12/17/2019
9:46:04
AM
Cuaderno
de
Actividades
•
Unidad
4
399
8

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
182
a
189
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
15
y
16
de
las
Bases
Curriculares.
Medidas
de
posición
1.
Para
adecuar
las
actividades
de
su
clase,
el
profesor
del
curso
electivo
Gimnasia
recopiló
los
datos
de
la
masa
corporal
y
la
estatura
de
sus
estudiantes.
Los
resultados
se
muestran
a continuación.
54
-
56
-
67
-
65
-
87
-
48
-
66
56
-
55
-
58
-
47
-
61
-
48
-
78
59
-
49
-
65
-
49
-
49
-
51
-
58
Masa
corporal
(kg)
Estatura
(cm)
157
-
155
-
167
-
172
-
171
-
167
-
160
160
-
162
-
169
-
149
-
162
-
150
-
170
163
-
152
-
155
-
147
-
156
-
161
-
162
a.
Calcula
las
medidas
en
cada
caso
y
completa
la
tabla.
Masa
corporal
(kg)
Estatura
(cm)
Media
Mediana
Moda
Q
1
Q
3
b.
¿Cuántos
alumnos
están
por
encima
de
la
masa
corporal
promedio?
c.
¿Cuántos
alumnos
están
por
debajo
del
promedio
de
estatura?
d.
Escribe
dos
conclusiones
a
partir
de
los
resultados
obtenidos
para
la
masa
corporal.
e.
Escribe
dos
conclusiones
a
partir
de
los
resultados
obtenidos
para
la
estatura.
Estadística
Lección
1
114
|
Unidad
4
CL0000000001052
114
12/17/2019
9:46:04
AM
2.
Los
siguientes
datos
corresponden
a
la
cantidad
de
trabajadores
que
se
ausentaron
de
una
fábrica
durante
los
últimos
30
días
laborales.
13
-
5
-
13
-
3
-
7
-
10
-
16
-
8
-
6
-
10
-
4
-
6
-
29
-
12
-
9
11
-
7
-
7
-
3
-
11
-
6
-
15
-
10
-
21
-
12
-
11
-
3
-
8
-
20
-
11
a.
Calcula
la
media.
b.
Calcula
la
mediana.
c.
Calcula
la
moda.
d.
Calcula
Q
1
y
Q
3
.
e.
Escribe
dos
conclusiones
a
partir
de
los
resultados
obtenidos
para
la
asistencia
del
personal.
3.
Una
profesora
de
gimnasia
tiene
un
taller
con
un
grupo
de
36 alumnos
y
registró
sus
edades
en
años.
18
-
19
-
16
-
15
-
15
-
17
-
19
-
20
-
17
-
16
-
16
-
17
-
15
-
20
-
17
-
17
-
19
-
18
15
-
17
-
16
-
16
-
17
-
24
-
11
-
17
-
16
-
15
-
17
-
16
-
19
-
16
-
16
-
19
-
17
-
18
a.
¿Cuál
es
la
media
de
las
edades,
en
años,
del
grupo
de
alumnos?
b.
¿Qué
valores
se
encuentran
entre
el
primer
y
segundo
cuartil?,
¿cuántos
son?
Puedes
comprobar
tu
resolución
utilizando
la calculadora
de
cuartiles
del
siguiente
link:
http://www.alcula.com/es/
calculadoras/estadistica/
cuartiles/
4
Unidad
115
Lección
1
•
Estadística
|
CL0000000001052
115
12/17/2019
9:46:04
AM
Estadística
Lección
1
4
Unidad
400
Cuaderno
de
Actividades
•
Unidad
4
58,38
56
49
49
65
160,33
161
162
155
167
8
alumnos.
10
alumnos.
La
mayor
parte
de
los
estudiantes
tienen
una
masa
dde
49
kg.
La
masa
corporal
promedio
es
de
58,38
kg.
La
mayor
parte
de
los
estudiantes
miden
162
cm.
La
estatura
promedio
es
de
160,33
cm.
10,
23
trabajadores.
10
trabajadores.
11
trabajadores.
Q
1
=
6
días,
Q
2
=
12
días.
La
mayor
parte
de
los
días
faltaron
11
trabajadores.
En
promedio
faltaron
10,23.trabajadores.
17,03
meses.
16
y
17
meses.

Unidad
4
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
182
a
189
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
15
y
16
de
las
Bases
Curriculares.
c.
Calcula
P
10
,
P
30
y
P
70
.
d.
Escribe
una
conclusión
a
partir
de
los
resultados
obtenidos.
4.
En
un
estudio
de
la
rapidez
límite,
se
puso
un
dispositivo
en
un
tramo
de
una
carretera
para registrar
la
rapidez
de
los
automóviles
entre
las
8
y
las
9
de
la
mañana.
Las
rapideces
(en
km/h)
registradas
fueron
las
siguientes:
60
-
40
-
90
-
70
-
55
-
65
-
80
-
70
-
65
-
60
-
100
-
65
-
70
-
85
-
60
-
35
75
-
60
-
60
-
65
-
85
-
60
-
60
-
60
-
50
-
55
-
65
-
80
-
85
-
70
-
65
-
85
70
-
65
-
75
-
95
-
80
-
45
-
55
-
65
-
55
-
85
-
80
-
60
-
70
-
40
-
50
-
65
a.
Calcula
Q
1
y
Q
3
.
Interpreta
los
valores
obtenidos
en
el
contexto
de
la
situación.
b.
La
municipalidad
decidió
fijar
como
límite
de
velocidad
un
valor
tal
que
bajo
él
se
encuentre
al
menos
el
65%
de
los
automóviles.
¿Cuál
es
este
valor?
c.
Escribe
una
conclusión
a
partir
de
los
resultados
obtenidos.
5.
Observa
el
siguiente
conjunto
de
valores
que
se
entregaron
como
respuesta
a
la
siguiente
pregunta:
¿qué
edad
tenía
tu
madre
cuando
tú
naciste?
23
-
21
-
34
-
26
-
17
-
22
-
23
-
42
-
36
-
19
-
15
-
24
-
32
-
30
-
34
-
32
-
28
16
-
19
-
21
-
27
-
23
-
28
-
29
-
31
-
33
-
29
-
21
-
17
-
24
-
20
-
25
-
30
-
25
29
-
33
-
15
-
27
-
31
-
19
-
22
-
35
-
39
-
29
-
31
-
22
-
18
-
16
-
19
-
25
a.
Determina
la
media
y
los
cuartiles
para
este
conjunto
de
datos.
b.
Escribe
una
conclusión
a
partir
de
los
resultados
obtenidos.
Estadística
Lección
1
116
|
Unidad
4
CL0000000001052
116
12/17/2019
9:46:04
AM
6.
Un
profesor
asignó
puntajes
a
los
trabajos
de
sus
estudiantes
y
los
resultados
se
muestran
a
continuación:
75
-
85
-
82
-
92
-
80
-
90
-
67
-
60
-
88
-
70
-
89
91
-
96
-
79
-
79
-
99
-
40
-
85
-
90
-
67
-
45
-
60
79
-
82
-
89
-
90
-
77
-
80
-
97
-
76
-
85
-
90
a.
Determina
la
media
y
los
cuartiles
del
grupo.
b.
¿Qué
porcentaje
de
estudiantes
obtuvo
un
puntaje
superior
o
igual
a
70?
Marca
la
opción
correcta
del
ítem
7
y
del
8
a
partir
de
los
siguientes
datos.
Las
edades,
en
años,
de
varios
trabajadores
de
una
empresa
se
registran
a
continuación:
44
-
42
-
48
-
47
-
38
-
35
-
40
-
39
-
38
-
35
-
50
-
40
44
-
35
-
33
-
41
-
32
-
40
-
45
-
37
-
46
-
39
-
43
-
40
48
-
33
-
47
-
49
-
33
-
44
-
51
-
32
-
47
-
55
-
33
7.
¿Cuál
es
la
mediana
del
conjunto
de
datos?
A.
40
años.
B.
41,25
años.
C.
41
años.
D.
42,5
años.
8.
¿Cuál
es
el
primer
cuartil
del
conjunto
de
datos?
A.
35
años.
B.
36,25
años.
C.
43
años.
D.
44,5
años.
4
Unidad
117
Lección
1
•
Estadística
|
CL0000000001052
117
12/17/2019
9:46:04
AM
Cuaderno
de
Actividades
•
Unidad
4
401
0
P
10
=
15;
P
30
=
16;
P
70
=
18
En
promedio
los
bebés
tienen
17,03
meses.
Q
1
=
60
km,
Q
2
=
80
km
70
km.
La
rapidez
del
25 %
de
los
automóviles
es
de
60
km
o
menos.
Q
1
=
21
años,
Q
2
=
25
años,
Q
3
=
31
años.
Promedio:
25,72
años.
Q
1
=
76,
Q
2
=
82,
Q
3
=
90
Promedio:
79,81
81,25 %
En
promedio
sus
madres
tenían
25,72
años
cuando
nacieron.

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
182
a
189
del
Texto
del
Estudiante.
Aborda
los
Objetivos
de
Aprendizaje
15
y
16
de
las
Bases
Curriculares.
9.
Se
preguntó
a
32
niños
de
cuarto
básico
cuántas
horas
dedican
a
ver
televisión
en
un
día
de semana.
Los
resultados
son:
1
-
5
-
5
-
5
-
4
-
5
-
6
-
8
-
4
-
4
-
4
-
6
-
7
-
7
-
4
-
4
5
-
5
-
5
-
3
-
6
-
6
-
4
-
4
-
5
-
3
-
7
-
5
-
3
-
4
-
5
-
7
a.
Calcula
Q
1
,
Q
3
,
Me
y
RIC.
Luego
construye
un
diagrama
de
cajón
a
partir
de
estos
datos.
b.
¿Cuántos
y
cuáles
datos
están
fuera
del
recorrido
intercuartil?
c.
Sin
calcular
el
promedio
de
los
datos,
¿en
qué
lugar
del
diagrama
crees
que
se
ubica?
Justifica
tu
respuesta.
d.
Calcula
el
promedio
de
los
datos
y
ubícalo
en
el
diagrama.
La
ubicación
obtenida,
¿es semejante
a
la
que
tú
creías?
Escribe
una
conclusión.
Estadística
Lección
1
118
|
Unidad
4
CL0000000001052
118
12/17/2019
9:46:04
AM
Marca
la
opción
correcta.
10.
De
acuerdo
al
siguiente
diagrama,
es
correcto
afirmar
que:
30
20
40
50
60
70
80
A.
El
rango
de
los
datos
es
30.
B.
La
mediana
es
55.
C.
Q
1
=
40
D.
P
3
=
70
A
partir
de
la
información,
responde
los
ítems
11
y
12.
Los
siguientes
datos
corresponden
al
tiempo,
en
horas,
que
destina
un
grupo
de
estudiantes
a hacer
deporte
durante
la
semana.
12
-
5
-
10
-
4
-
14
-
12
-
10
-
12
-
15
-
10
12
-
5
-
15
-
8
-
6
-
12
-
10
-
4
-
6
-
8
11.
¿Cuál
es
la
mediana
de
los
datos?
A.
6
horas.
B.
9,5
horas.
C.
10
horas.
D.
12
horas.
12.
¿Cuál
de
los
siguientes
diagramas
de
cajón
representa
la
distribución
de
las
horas
a
la
semana
destinadas
a
hacer
deporte
por
el
grupo
de
estudiantes?
6
4
8
10
12
14
6
4
8
10
12
14
6
4
8
10
12
14
6
4
8
10
12
14
A.
B.
C.
D.
4
Unidad
119
Lección
1
•
Estadística
|
CL0000000001052
119
12/17/2019
9:46:04
AM
Evaluación
Lección
1
4
Unidad
402
Cuaderno
de
Actividades
•
Unidad
4
2
1
3
0
4
5
6
7
8
9
10
Los
menores
a
4
y
mayores
a
6,
estos
abarcan
aproximadamente
la
mitad
de
los
datos.
Entre
4
y
5,
ya
que
la
mediana
se
observa
por
encima
del
4,
que
es
la
mitad
del
gráfico.
5,
ya
que
ese
el
valor
de
la
mediana.
El
promedio
es
4
horas.
Si
es
semejante
o
no,
depende
de
cada
respuesta.

Unidad
4
Orientaciones
de
uso
•
Estas
páginas
comprenden
una
evaluación
formativa
de
la
Lección
1
Estadística.
Aborda
los
Objetivos
de
Aprendizaje
15
y
16
de
las
Bases
Curriculares.
A
partir
de
la
siguiente
información,
responde
de
la
pregunta
1
a
la
6.
Las
edades,
en
años,
de
los
asistentes
a
una
obra
de
teatro
escolar
son:
25
-
18
-
32
-
28
-
20
-
32
-
27
-
28
-
30
-
20
21
-
30
-
17
-
27
-
22
-
30
-
19
-
20
-
23
-
24
¿Cuál
es
el
tercer
cuartil?
1.
¿Cuáles
son
los
datos
suficientes
para
resolver
el
problema?
A.
Las
edades
de
los
asistentes
a
la
obra
de
teatro.
B.
Las
personas
que
tienen
menos
de
25
años.
C.
Las
personas
que
tienen
más
de
25
años.
D.
El
lugar
donde
asistieron
las
personas.
2.
¿Qué
es
lo
que
se
pregunta?
A.
El
valor
de
la
mediana.
B.
El
valor
del
tercer
cuartil.
C.
El
valor
del
primer
cuartil.
D.
El
valor
del
segundo
cuartil.
3.
¿Cuál
es
la
respuesta
al
problema?
A.
27
años.
B.
28
años.
C.
29
años.
D.
30
años.
4.
¿Cuál
es
el
primer
cuartil?
A.
17
años.
B.
20
años.
C.
24
años.
D.
29
años.
5.
¿Cuál
es
el
segundo
cuartil?
A.
24,5
años.
B.
25,5
años.
C.
24
años.
D.
25
años.
6.
¿Cuál
es
el
percentil
60?
A.
20
años.
B.
22
años.
C.
25
años.
D.
27
años.
Evaluación
Lección
1
|
Unidad
4
120
CL0000000001052
120
12/17/2019
9:46:05
AM
•
¿Qué
crees
que
es
lo
más
complejo
de
lo
que
aprendiste
sobre
estadística?
¿Por
qué?
•
¿Para
qué
es
útil
tener
conocimientos
de
estadística?
Explica.
Reflexiona
y
responde
Reflexiona
y
responde
A
partir
de
la
siguiente
información,
marca
la
respuesta
correcta
en
las
preguntas
7
a
la
12.
Los
siguientes
datos
corresponden
a
las
estaturas,
en
centímetros,
de
un
grupo
de estudiantes.
170
-
175
-
160
-
155
-
162
-
170
-
175
-
158
-
164
-
165
-
159
-
160
-
165
-
175
-
170
-
158
155
-
168
-
157
-
166
-
160
-
170
-
155
-
160
-
172
-
164
-
173
-
159
-
174
-
166
-
168
-
156
¿Cuántos
estudiantes
miden
165
cm
o
más?
7.
¿Cuáles
son
los
datos
suficientes
para
resolver
el
problema?
A.
La
cantidad
de
intervalos.
B.
Las
estaturas
de
los
estudiantes.
C.
La
cantidad
de
estudiantes
que
miden
más
de
165
cm.
D.
La
cantidad
de
estudiantes
que
miden
165
cm
o
menos.
8.
¿Qué
es
lo
que
se
pregunta?
A.
La
cantidad
de
estudiantes
que
miden
más
de
165
cm.
B.
La
cantidad
de
estudiantes
que
miden
menos
de
165
cm.
C.
La
cantidad
de
estudiantes
que
miden
165
cm
o
más.
D.
La
cantidad
de
estudiantes
que
miden
165
cm
o
menos.
9.
¿Cuál
es
la
respuesta
al
problema?
A.
6
estudiantes.
B.
16
estudiantes.
C.
22
estudiantes.
D.
32
estudiantes.
10.
¿Cuántos
estudiantes
miden
menos
de 160
cm?
A.
23
estudiantes.
B.
16
estudiantes.
C.
13
estudiantes.
D.
9
estudiantes.
11.
¿Qué
porcentaje
de
estudiantes
mide
menos
de
165
cm?
A.
6%
B.
19%
C.
50%
D.
56%
12.
¿Cuál
de
los
siguientes
intervalos
tiene
menor
frecuencia?
A.
[155,
160[
B.
[160,
165[
C.
[165,
170[
D.
[170,
175]
4
Unidad
121
Evaluación
Lección
1
|
CL0000000001052
121
12/17/2019
9:46:05
AM
Cuaderno
de
Actividades
•
Unidad
4
403
2

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
192
a
197
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
17
de
las
Bases
Curriculares.
Principio
multiplicativo
1.
Resuelve
los
siguientes
problemas.
Comprueba
tus
resultados
con
una
calculadora.
a.
En
una
carrera
de
200
m
participaron
10
atletas.
¿De
cuántas
formas
distintas
podrán
ser premiados
los
tres
primeros
lugares
con
medallas
de
oro,
plata
y
bronce?
b.
Un
ingeniero
de
control
de
calidad
realizará
una
prueba
a
5
artículos
distintos
de
la
línea
de
producción
de
repuestos.
Cada
uno
de
ellos
debe
ser
clasificado
como
aceptable
o
defectuoso.
¿De
cuántas
formas
puede
resultar
la
revisión
de
los
5
artículos?
c.
Una
profesora
de
octavo
básico
debe
decidir
qué
estudiantes
asistirán
a
un
taller
de
computación
un
fin
de
semana.
Si
dispone
de
8
voluntarios
y
tiene
4
cupos
disponibles
para
el
curso,
¿de
cuántas
formas
distintas
puede
elegirlos?
d.
Para
ir
desde
su
casa
a
la
parcela
de
su
abuela,
Patricio
puede
caminar
o
tomar
un
colectivo
que
lo
lleve
al
paradero
de
buses
interurbanos
y
elegir
entre
7
flotas
que
lo
trasladan
a
su
destino.
¿De
cuántas
maneras
puede
realizar
el
trayecto
considerando
que
los
buses
hacen distintos
recorridos
para
llegar
al
mismo
lugar?
e.
En
la
escuela
de
Carlos
los
estudiantes
deben
escoger
cada
semestre,
como
electivos,
una
de
las
3 asignaturas
de
ciencias
básicas,
una
de
las
5
de
literatura
y
uno
de
los
10
talleres
deportivos.
¿De
cuántas
maneras
diferentes
puede
elegir
Carlos
estos
tres
ramos?
Probabilidad
Lección
2
122
|
Unidad
4
CL0000000001052
122
12/17/2019
9:46:05
AM
f.
Una
bicicleta
de
montaña
posee
cambios
de
velocidades.
Para
esto,
tiene
tres
discos
delanteros
y
siete
traseros.
Los
cambios
de
la
bicicleta
son
las
posibles
combinaciones
que
efectúa
la
cadena
entre
los
discos
delanteros
y
los
traseros.
¿Cuántos
cambios
posee
la
bicicleta?
2.
Calcula
la
cantidad
de
combinaciones
posibles
en
cada
una
de
las
siguientes
situaciones.
a.
Para
una
alianza
se
ocupan
banderas
con
3
colores:
blanco,
rojo
y
azul.
¿Cuántas
banderas
diferentes
pueden
elaborarse
con
estos
3
colores
si
se
organizan
formando
tres
líneas
horizontales
o
tres
líneas
verticales
sin
repetir
los
colores?
Represéntalas
mediante
un diagrama.
b.
¿Cuántas
combinaciones
es
posible
elaborar.
Considera
27
letras
utilizando dos letras
diferentes
seguidas
de
tres
dígitos
distintos?
4
Unidad
123
Lección
2
•
Probabilidad
|
CL0000000001052
123
12/17/2019
9:46:05
AM
Probabilidad
Lección
2
4
Unidad
404
Cuaderno
de
Actividades
•
Unidad
4
10
•
9
•
8
=
720
2
•
2
•
2
•
2
•
2
=
32
8
•
7
•
6
•
5
=
1 680
2
•
7
=
14
3
•
5
•
10
=
150
720
formas.
32
formas.
1 680
formas.
14
formas.
150
maneras.
3
•
7
=
21
27
•
26
•
10
•
9
•
8
=
505 440
21
cambios
505 440
combinaciones.
Horizontales
B
R
A
R
B
B
A
A
R
A
A
R
R
B
B
Verticales
B
R
A
R
B
B
A
A
R
A
A
R
R
B
B
12
banderas

Unidad
4
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
192
a
197
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
17
de
las
Bases
Curriculares.
c.
En
una
concesionaria
ofrecen
dos
tipos
de
vehículo:
mecánico
y
automático.
Además,
se
puede
agregar
vidrios
eléctricos,
aire
acondicionado
o
sistema
de
audio.
Hay
en
cinco
colores:
rojo,
gris,
dorado,
verde
y
negro.
¿De
cuántas
maneras
se
puede
escoger
un
vehículo?
Represéntalas mediante un
diagrama
de
árbol.
d.
Daniela
quiere
elegir
entre
4
chaquetas
(blanca,
roja,
verde
y
azul),
3
pantalones
(celeste,
negro
y
verde)
y
2
pares
de
zapatos
(café
y
negro).
¿De
cuántas
formas
distintas
puede
escoger
una
chaqueta,
un
pantalón
y
un
par
de
zapatos?
Representa
las
combinaciones
en un
diagrama
de
árbol.
e.
¿Cuál
es
la
cantidad
de
resultados
posibles
al
lanzar
4
monedas?
Representa
los
resultados
en
un
diagrama
de
árbol.
Probabilidad
Lección
2
124
|
Unidad
4
CL0000000001052
124
12/17/2019
9:46:05
AM
Marca
la
opción
correcta.
3.
Los
resultados
posibles
de
un
experimento
aleatorio
que
consiste
en
lanzar
al
aire
tres
monedas
se
pueden
ver
parcialmente
en
la
tabla
adjunta,
donde
C
corresponde
a
cara
y
S corresponde
a
sello.
¿Cuál
de
las
alternativas
siguientes
muestra
el
o
los
resultados
posibles
que
faltan
en
la
tabla
para
completarla?
Primera
moneda
C
C
C
C
S
S
Segunda
moneda
C
C
S
S
C
S
Tercera
moneda
C
S
C
S
C
S
A.
CSC
B.
SSC
C.
SCS
y
SSC
D.
CSS
y
SSC
4.
Un
grupo
de
tres
niños
y
tres
niñas
se
sientan
en
una
fila
con
seis
sillas.
¿De
cuántas
maneras
se
pueden
sentar
si
debe
haber
un
niño
al
inicio
y
una
niña
al
final?
A.
6
maneras.
B.
12
maneras.
C.
216
maneras.
D.
360
maneras.
5.
De
una
urna
con
bolitas
numeradas
del
0
al
9
se
extraen
tres
bolitas
sin
reposición
para
formar
números
de
3 cifras.
¿Cuántos
números
se
pueden
formar?
A.
360
B.
648
C.
720
D.
900
6.
Cuatro
amigos,
Camilo,
Miguel,
Andrea
y
Tamara,
compraron
entradas
numeradas
para
asistir
a
una
película.
Los
asientos
están
marcados
como
M4,
M5,
M6
y
M7.
¿De
cuántas
maneras
se
pueden
ubicar
los
cuatro
amigos
en
los
asientos?
A.
4
B.
6
C.
12
D.
24
4
Unidad
125
Lección
2
•
Probabilidad
|
CL0000000001052
125
12/17/2019
9:46:05
AM
Cuaderno
de
Actividades
•
Unidad
4
405
4
M
VE
AA
SA
A
VE
AA
SA
R
G
D
V
N
R
G
D
V
N
R
G
D
V
N
R
G
D
V
N
R
G
D
V
N
R
G
D
V
N
B
C
N
V
C
N
C
N
C
N
R
C
N
V
C
N
C
N
C
N
V
C
N
V
C
N
C
N
C
N
A
C
N
V
C
N
C
N
C
N
C
S
C
S
C
C
S
C
S
C
S
C
S
C
S
C
S
C
S
C
C
S
C
S
C
S
C
S
C
S
30
maneras
24
formas
16
resultados

Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
198
a
203
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
17
del
Programa
de
Estudio.
Cálculo
de
probabilidades
1.
En
una
bolsa
con
32
dulces,
8
son
de
guinda,
10
de
piña,
12
de
naranja
y
el
resto
son de manzana.
Si
se
extrae
uno
sin
mirar:
a.
¿Cuál
es
la
probabilidad
de
que
sea
de
manzana?
b.
¿Cuál
es
la
probabilidad
de
que
sea
de
guinda?
c.
¿Cuál
es
la
probabilidad
de
que
sea
de
naranja?
d.
¿Cuál
es
la
probabilidad
de
que
no
sea
de
piña?
2.
Se
lanza
una
moneda
tres
veces.
a.
Anota
todos
los
resultados
que
pueden
ocurrir.
Denota
por
C
las
caras
y
por
S
los
sellos.
b.
Calcula
la
probabilidad
de
cada
suceso.
A:
Que
salga
sello
en
el
primer
lanzamiento.
B:
Que
salga
tres
veces
lo
mismo.
C:
Que
salga
cara
tres
veces.
D:
Que
salga
por
lo
menos
una
cara.
3.
En
una
bolsa
hay
3
papeles
rojos,
4
verdes,
2
amarillos
y
7
azules.
Se
gana
si
al
sacar
un
papel
al
azar
se
obtiene
uno
amarillo,
pero
antes
de
sacar
un
papel
de
la
bolsa
es
posible
realizar
una
de
las
siguientes
acciones:
•
Sacar
un
papel
rojo.
•
Agregar
un
papel
amarillo.
•
Sacar
uno
de
cada
color.
•
Sacar
tres
azules.
•
Sacar
uno
rojo,
uno
verde
y
uno
azul.
¿Qué
conviene
hacer,
entre
estas
opciones,
para
tener
más
probabilidades
de
ganar?
Probabilidad
Lección
2
126
|
Unidad
4
CL0000000001052
126
12/17/2019
9:46:05
AM
4.
Observa
las
siguientes
fichas
de
dominó
¿Cuál
es
la
probabilidad
de
extraer
una
al
azar
y
que
a.
tenga
un
1?
b.
tenga
dos
números
iguales?
c.
tenga
algún
número
par?
d.
tenga
un
múltiplo
de
3?
e.
sume
5?
5.
En
un
restaurante
se
ofrecen
promociones,
conformadas
por
una
comida
y
una
bebida,
que los clientes
pueden
armar
a
su
gusto.
Los
productos
que
se
ofrecen
son:
•
comida:
hamburguesa,
pizza
y
completo.
•
bebida:
jugo,
limonada,
agua
y
gaseosa.
a.
Encuentra
la
cantidad
de
maneras
diferentes
para
armar
las
promociones.
b.
Encuentra
la
probabilidad
de
que
en
una
promoción
se
pida
gaseosa.
c.
Calcula
la
probabilidad
de
que
en
una
promoción
se
pida
hamburguesa
o
pizza.
4
Unidad
127
Lección
2
•
Probabilidad
|
CL0000000001052
127
12/17/2019
9:46:05
AM
Probabilidad
Lección
2
4
Unidad
406
Cuaderno
de
Actividades
•
Unidad
4
1
16
11
16
1
4
3
8
1
2
1
4
1
8
7
8
C
C
C;
C
C
S;
C
S
S;
C
S
C;
S
S
S;
S
S
C;
S
C
C;
S
C
S
3
28
13
28
9
14
1
4
2
3
1
4
1
4
Sacar
3
azules
y
sacar
uno
rojo,
uno
verde
y
uno
amarillo.
Ya
que
en
ambos
se
sacan
12
combos.
tres papelitos
y
la
probilidad
de
sacar
uno
amarillo
es
la
misma
y
la
más
alta.

Unidad
4
Orientaciones
de
uso
•
Práctica
vinculada
con
las
páginas
198
a
203
del
Texto
del
Estudiante.
Aborda
el
Objetivo
de
Aprendizaje
17
de
las
Bases
Curriculares.
6.
Resuelve
los
siguientes
problemas.
a.
Si
se
lanza
un
dado
y
se
suman
los
puntajes
de
todas
las
caras
visibles,
¿cuál
es
la probabilidad
de
que
ese
número
sea
un
múltiplo
de
5?
b.
Noemí
decide
comer
una
fruta
después
de
almuerzo.
Si
tiene
3
manzanas,
2
naranjas
y
4 peras,
¿cuál
es
la
probabilidad
de
que
al
elegirla
al
azar
no
escoja
una
naranja?
c.
Si
por
una
caseta
de
peaje
pasaron
durante
una
hora
45
automóviles,
29
camionetas
y
55 buses,
¿cuál
es
la
probabilidad
de
que
al
elegir
a
uno
de
estos
vehículos
al
azar
sea
una camioneta?
d.
Se
lanzan
cuatro
monedas,
¿cuál
es
la
probabilidad
de
que
se
obtenga
igual
número
de caras
que
de
sellos?
e.
Al
extraer
una
ficha
de
dominó,
¿cuál
es
la
probabilidad
de
que
alguno
de
los
números
sea primo?
f.
En
una
empresa,
en
promedio,
30
de
los
250
artículos
producidos
en
un
mes
presentan
fallas.
¿Cuál
es
la
probabilidad
de
que
en
una
prueba
de
calidad
de
fin
de
mes
se
escoja
un producto
sin
fallas?
Probabilidad
Lección
2
128
|
Unidad
4
CL0000000001052
128
12/17/2019
9:46:05
AM
g.
Se
elige
al
azar
una
bola
numerada
de
una
tómbola
que
tiene
bolas
del
1
al
100.
¿Es
más
probable
que
salga
un
número
primo
o
un
número
par?
h.
En
su
reproductor
musical
Álvaro
tiene
32
canciones
de
rock,
19
de
pop,
7
románticas
y
22 ambientales.
Si
activa
el
sistema
de
reproducción
aleatorio,
¿cuál
es
la
probabilidad
de que
la
primera
canción
que
se
programe
sea
de
pop?
Marca
la
opción
correcta.
7.
¿Cuál
de
los
siguientes
sucesos
es
imposible
al
lanzar
tres
dados
de
seis
caras?
A.
Que
los
puntos
sumen
3.
B.
Que
los
puntos
coincidan.
C.
Que
los
puntos
sean
números
primos.
D.
Que
los
puntos
sumen
menos
que
3.
8.
¿Cuál
de
las
siguientes
afirmaciones
es
falsa
respecto
a
la
probabilidad
de
un
suceso?
A.
Puede
ser
cero.
B.
Puede
representarse
como
porcentaje.
C.
Es
posible
calcularla
a
través
de
un
cociente.
D.
Puede
ser
mayor
que
1
dependiendo
del
número
de
lanzamientos.
9.
Se
elegirá
un
número
entre
los
que
son
pares
y
múltiplos
de
tres
mayores
que
1
y
menores
que
33.
¿Cuál
es
la
probabilidad
de
obtener
un
múltiplo
de
12?
A.
0,2
B.
0,25
C.
0,4
D.
0,5
10.
Martín
ha
juntado
en
una
alcancía
cien
monedas
de
$10,
treinta
de
$50,
cincuenta
y
cinco
de
$100
y
diez
de
$500.
Si
saca
una
moneda
al
azar.
¿Cuál
es,
aproximadamente,
la probabilidad
de
sacar
una
moneda
de
$50?
A.
0,15
B.
0,28
C.
0,6
D.
0,73
4
Unidad
129
Lección
2
•
Probabilidad
|
CL0000000001052
129
12/17/2019
9:46:05
AM
Cuaderno
de
Actividades
•
Unidad
4
407
6
7
36
7
9
29
129
6
=
3
16
8
18
=
9
28
14
220
=
22
250
25
3
+
4
=
7
3
+
4
+
2
=
9
45
+
29
+
55
=
129
250
–
30
=
220
19
80
32
+
19
+
7
+
22
=
80
Un
número
par.
Número
primo
Número
par
25
=
1
100
4
50
=
1
100
2

Orientaciones
de
uso
•
Estas
páginas
comprenden
una
evaluación
formativa
de
la
Lección
2
Probabilidades.
Aborda
el
Objetivo
de
Aprendizaje
17
de
las
Bases
Curriculares.
A
partir
de
la
siguiente
información,
responde
de
la
pregunta
1
a
la
4.
1.
¿Cuáles
son
los
datos
suficientes
para
resolver
el
problema?
A.
La
cantidad
de
menú.
B.
La
cantidad
de
entradas.
C.
La
cantidad
de
platos
de
fondo
y
de
postres.
D.
La
cantidad
de
entradas,
de
platos
de
fondo
y
de
postres.
2.
¿Qué
es
lo
que
se
pregunta?
A.
La
cantidad
de
platos
diferentes.
B.
La
cantidad
de
menús
diferentes.
C.
La
cantidad
de
entradas
y
de
postres.
D.
La
cantidad
de
entradas,
de
platos
de
fondo
y
de
postres.
3.
¿Qué
estrategia
se
utilizó
para
resolver
el
problema?
A.
Ensayo
y
error.
B.
Construir
una
tabla.
C.
Construir
un
diagrama.
D.
Usar
el
principio
multiplicativo.
4.
¿Cuál
es
la
respuesta
al
problema?
A.
48
maneras
distintas.
B.
24
maneras
distintas.
C.
4
maneras
distintas.
D.
3
maneras
distintas.
En
un
restaurante
el
menú
incluye
entrada,
plato
de
fondo
y
postre.
Si
para
elegir
hay
4
tipos
de
entrada,
3
platos
de
fondo
y
4
postres
diferentes,
¿de
cuántas
maneras
distintas
se
puede
armar
el
menú?
Luego
de
elegir
la
estrategia,
el
problema
se
resuelve
de
la siguiente
manera:
Entrada:
4
posibilidades.
Plato
de
fondo:
3
posibilidades.
Postres:
4
posibilidades.
4
•
3
•
4
=
48
Evaluación
Lección
2
|
Unidad
4
130
CL0000000001052
130
12/17/2019
9:46:05
AM
•
¿Qué
estrategias
utilizaste
para
resolver
los
problemas?
¿Crees
que
fueron
útiles?,
¿por
qué?
•
¿En
qué
situaciones
de
la
vida
cotidiana
puedes
aplicar
lo
aprendido
sobre
probabilidades?
Reflexiona
y
responde
Reflexiona
y
responde
A
partir
de
la
siguiente
información,
marca
la
respuesta
correcta
en
las
preguntas
5
a
la
10.
En
una
heladería
se
puede
comprar
un
helado
de
un
sabor
entre
10
disponibles,
agregarle
salsa
de
manjar,
de
chocolate
o
de
frutilla
y
llevarlo
en
cono
de
vainilla
o de
chocolate.
¿De
cuántas
formas
distintas
es
posible
comprar
un
helado?
5.
¿Cuáles
son
los
datos
suficientes
para
resolver
el
problema?
A.
La
cantidad
de
salsas.
B.
La
cantidad
de
sabores
de
helados.
C.
La
cantidad
de
sabores
de
helados
y
de conos.
D.
La
cantidad
de
sabores
de
helados,
de salsas
y
de
conos.
6.
¿Qué
es
lo
que
se
pregunta?
A.
La
cantidad
de
conos
diferentes.
B.
La
cantidad
de
salsas
diferentes.
C.
La
cantidad
de
helados
diferentes
que se pueden
comprar.
D.
La
cantidad
de
sabores
de
helados,
de salsas
y
de
conos.
7.
¿Cuál
es
la
respuesta
al
problema?
A.
30
formas.
B.
60
formas.
C.
90
formas.
D.
120
formas
8.
Si
una
persona
quiere
cono
de
vainilla,
¿de cuántas
formas
distintas
puede
elegir el
helado?
A.
30
formas.
B.
60
formas.
C.
80
formas.
D.
90
formas.
9.
Si
solo
quedaran
8
sabores,
¿de
cuántas
formas
distintas
es
posible
comprar
un helado?
A.
12
formas.
B.
24
formas.
C.
48
formas.
D.
72
formas.
10.
Si
al
finalizar
el
día
quedan
5
sabores
y
solo
salsa
de
frutilla,
¿de
cuántas
formas
distintas
es
posible
comprar
un
helado?
A.
5
formas.
B.
10
formas.
C.
15
formas.
D.
30
formas.
4
Unidad
131
Evaluación
Lección
2
|
CL0000000001052
131
12/17/2019
9:46:06
AM
Evaluación
final
4
Unidad
408
Cuaderno
de
Actividades
•
Unidad
4

Unidad
4
Orientaciones
de
uso
•
Estas
páginas
comprenden
una
evaluación
formativa
de
la
Unidad
4
El deporte.
Aborda
los
Objetivos
de
Aprendizaje
15,
16
y
17
de
las
Bases
Curriculares.
Marca
la
alternativa
correcta.
1.
En
una
encuesta
se
pregunta
a
las
personas
la
cantidad
de
horas
diarias
que
están
conectadas
a
internet.
Las
respuestas
se
registraron
en
la
siguiente
tabla:
¿Cuántas
horas
estás
conectado
a internet?
Cantidad
de
horas
f
1
2
2
3
3
6
4
4
¿Cuál
es
la
mediana
de
los
datos?
A.
3
horas.
B.
4
horas.
C.
5
horas.
D.
6
horas.
2.
¿Cuál
de
las
siguientes
igualdades
es
correcta?
A.
P
25
=
Me
B.
P
25
=
Q
1
C.
P
2
=
Me
D.
P
50
=
Q
3
3.
Se
pregunta
la
edad
a
un
grupo
de
personas
y
se
obtienen
las
siguientes
respuestas:
20
-
22
-
23
-
25
-
30
-
30
-
33
-
35
-
41
-
45
¿Cuál
es
el
primer
cuartil
de
las
edades?
A.
22
años.
B.
23
años.
C.
22,5
años.
D.
30
años.
Evaluación
final
|
Unidad
4
132
CL0000000001052
132
12/17/2019
9:46:06
AM
4.
De
acuerdo
al
siguiente
diagrama,
es
correcto
afirmar
que:
30
20
40
50
60
70
80
A.
El
rango
de
los
datos
es
30.
B.
Q
3
=
70
C.
La
mediana
es
55.
D.
Q
1
=
60
5.
Un
equipo
de
vóleibol
tiene
4
camisetas
diferentes
(una
verde,
otra
roja,
una
amarilla
y otra azul)
y
pantalones
de
color
negro
o
blanco.
¿Cuál
es
la
probabilidad
de
que
en
un partido
vista
con
camiseta
roja
y
pantalón
blanco?
A.
4
8
B.
3
8
C.
2
8
D.
1
8
6.
¿Cuántos
números
de
3
cifras
se
pueden
formar
con
los
dígitos
1,
2,
3,
4,
5
y
6
si
se
eligen
uno
a
uno
y
no
se
pueden
repetir?
A.
120
números.
B.
18
números.
C.
36
números.
D.
216
números.
7.
Con
las
letras
de
la
palabra
AMIGOS
se
quieren
formar
palabras
de
3
letras,
con
sentido
y
sin sentido.
Si
se
eligen
una
a
una
las
letras
y
se
pueden
repetir,
¿cuántas
palabras
se
pueden formar?
A.
18
palabras.
B.
729
palabras.
C.
36
palabras.
D.
216
palabras.
•
¿Qué
contenidos
de
la
unidad
crees
que
debes
repasar?
¿Por
qué?
•
Si
tuvieras
que
explicarle
a
un
familiar
lo
que
aprendiste
en
esta
unidad,
¿cómo
lo
harías?
Reflexiona
y
responde
4
Unidad
Evaluación
final
|
133
CL0000000001052
133
12/17/2019
9:46:06
AM
Cuaderno
de
Actividades
•
Unidad
4
409
8

Material
fotocopiable
1. Los siguientes son los meses en que están
de cumpleaños cada uno de los estudiantes
de un curso.
septiembre - octubre - enero - marzo
diciembre - enero - septiembre - octubre
febrero - marzo - noviembre - septiembre
enero - octubre - noviembre - enero
diciembre - marzo - febrero septiembre - abril
julio - mayo - agosto - enero - febrero
a. Completa la tabla de frecuencias según
los datos presentados.
Mes de cumpleaños de los estudiantes
Mes Frecuencia (f)
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
Octubre
Noviembre
Diciembre
b. ¿Qué tipo de gráfico sería adecuado construir
para esta situación? Justifica.

c. ¿En qué mes hay más estudiantes de cumpleaños?

d. ¿Cuántos estudiantes hay en ese curso?

2. Analiza la siguiente situación. Luego, responde
las preguntas.
En un gimnasio registraron las edades de sus
clientes y estos fueron los datos obtenidos:
23 - 25 - 18 - 18 - 40 - 30 - 29
18 - 21 - 42 - 31 - 35 - 35 - 29
27 - 27 - 31 -18 - 27 - 38
a. ¿Cuál es el menor y el mayor dato de la muestra?

b. ¿Cuál es el valor del cuartil 1?

c. ¿Cuál es el valor del cuartil 3?

d. ¿Cuál es el valor de la mediana?

e. Construye un diagrama de cajón para
esta situación.
Lección 1

Unidad
4
Material
fotocopiable
1. Analiza las siguientes situaciones y calcula en tu cuaderno las medidas de posición solicitadas en
cada caso.
a. La siguiente tabla muestra las horas de estudio
semanal de los estudiantes de un 8° básico
para la asignatura de Matemática.
Horas de
estudio semanal
1 2 3 4 5
Frecuencia (f) 5 7 9 6 8
• Q1 =
• P20 =
• P85 =
• Q2 =
b. Se registraron los gramos al momento de nacer
de los bebés en un día en una clínica.
380 - 295 - 290 - 350 - 358 - 391
305 - 380 - 395 - 348 - 356 - 342
• Q2 =
• P50 =
• P90 =
• Q3 =
c. En una tienda registraron las tallas de los
zapatos de mujer que vendieron en una
semana en la siguiente tabla:
Talla de zapatos 35 36 37 38 39
Frecuencia (f) 12 15 26 29 10
• Q1 =
• P62 =
• P75 =
• Q3 =
d. Se evaluó a 20 estudiantes en velocidad
lectora para saber cuántas palabras leían en
un minuto. Los datos recolectados fueron:
148 - 143 - 149 - 150 - 148 - 145 - 146
153 - 155 - 152 - 150 - 149 - 151 - 147
148 - 149 - 153 - 150 - 151 - 152
• Q1 =
• P81 =
• P30 =
• Q2 =
2. Analiza el siguiente diagrama de cajón y realiza las actividades a. y b..
Dato menor Dato mayor
Q1 Q3
Me
16 15 20 25 30 35 40 45
a. Completa con los valores solicitados.
• Dato menor:
• Dato mayor:
• Q1 =
• Q3 =
• Me =
• Ric =
b. Escribe una situación que pueda modelarse con la información representada en el diagrama de cajón.
Luego, explica el significado de los valores calculados en el ítem a..

411
Lección 1

Material
fotocopiable
1. Viviana siempre prepara el desayuno
considerando lácteos y frutas. Ella realiza el
siguiente diagrama de árbol para ver todas
las posibilidades que puede formar con los
alimentos que tiene.
Leche
Naranja
Pera
Plátano
Durazno
Queso
Naranja
Pera
Plátano
Durazno
Yogur
Naranja
Pera
Plátano
Durazno
a. ¿Cuántas son las posibilidades que tiene
Viviana para armar el desayuno?
b. ¿Cuál es la probabilidad de que Viviana prepare
un desayuno con yogur y naranja?
c. Si Viviana tuviera una fruta más, ¿cuántas serían
las opciones para armar el desayuno?
2. En un juego virtual se solicita a los participantes
crear una contraseña de cuatro letras distintas,
con las letras de la palabra JUEGO.
a. ¿Cuántas contraseñas se pueden crear?
b. ¿Cuál es la probabilidad de que la contraseña
tenga la letra O?
c. ¿La probabilidad de que la contraseña
empiece con una vocal es la misma que la
probabilidad de que la contraseña empiece
con una consonante? Justifica.
3. Se lanza un dado y una moneda a la vez.
a. Dibuja un diagrama de árbol y responde,
¿cuántos casos posibles hay?
b. ¿Cuál es la probabilidad de obtener cara en la
moneda y un número impar en el dado?
Lección 2

Unidad
4
Material
fotocopiable
1. Analiza las siguientes situaciones, aplica el principio multiplicativo y responde las preguntas.
a. ¿Cuántos números enteros diferentes de tres dígitos se pueden formar con los dígitos 1, 2, 3, 4, 5 y 6?
b. En el siguiente esquema se presentan en rojo las diferentes rutas que existen para
llegar de una ciudad a otra. Por ejemplo, para llegar de la ciudad B a la ciudad C
hay 4 posibles rutas. Si se quiere viajar desde la ciudad A a la ciudad D, ¿por cuántas
rutas se podría ir?
c. Se quiere tomar una foto a tres parejas juntas. ¿De cuántas maneras se pueden ubicar si se mezclan
en una fila?
2. Calcula la probabilidad de los siguientes sucesos. Para ello, escribe el espacio muestral (Ω), los casos
favorables (A) y luego aplica la regla de Laplace.
a. En una familia tienen 3 hijos. ¿Cuál es la probabilidad de que haya dos hombres y una mujer?
• Ω = • A =
• Probabilidad =
b. En la vitrina de una tienda hay un pantalón, una camisa y una chaqueta. ¿Cuál es la probabilidad de que
al sacar al azar dos prendas de la vitrina sean una camisa y un pantalón?
• Ω = • A =
• Probabilidad =
B
C
D
A
413
Lección 2

Refuerzo
1. a.
Mes de cumpleaños de los estudiantes
Mes Frecuencia (f)
Enero 5
Febrero 3
Marzo 3
Abril 1
Mayo 1
Junio 0
Julio 1
Agosto 1
Septiembre 4
Octubre 3
Noviembre 2
Diciembre 2
b. Un gráfico de barras, porque la situación tiene variables
cuantitativas y este tipo de gráficos permite comparar
las frecuencias de estas variables.
c. En el mes de enero.
d. En el curso hay 26 estudiantes.
2. a. El menor dato de la muestra es 18 y el mayor es 42.
b. El valor del cuartil 1 es 22.
c. El valor del cuartil 3 es 33.
d. El valor de la mediana es 28
e.
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
Edades de los clientes de un gimnasio
Ampliación
1. a. • Q1 = 2
• P20 = 2
• P85 = 5
• Q2 = 3
b. • Q2 = 353
• P90 = 391
• P50 = 353
• Q3 = 380
c. • Q1 = 36
• P75 = 38
• P62 = 38
• Q3 = 38
d. • Q1 = 148
• P30 = 148
• P81 = 152
• Q2 = 149,5
2. a. • Dato menor: 18
• Dato mayor: 46
• Q1 = 25
• Q3 = 41
• Me
= 32
• Ric = 16
b. Respuesta a cargo del estudiante.
414
Material
fotocopiable

Unidad
4
Material
fotocopiable
Refuerzo
1. a. Tiene 12 posibilidades.
b. La probabilidad es de
1
12
.
c. Serían 15 opciones.
2. a. Se pueden crear 120 contraseñas.
b. La probabilidad es
96
120
.
c. No, porque en la palabra JUEGO hay más vocales,
por lo que la probabilidad es mayor.
3. a.
Cara
1
2
3
4
5
6
Sello
1
2
3
4
5
6
Hay 12 casos posibles.
b. La probabilidad es de
3
12
.
Ampliación
1. Analiza las siguientes situaciones, aplica el principio multiplicativo
y responde las preguntas.
a. 6 • 5 • 4 = 120
Se pueden formar 120 números diferentes.
b. 3 • 4 • 2 = 24
Hay 24 rutas posibles.
c. 6 • 5 • 4• 3 • 2 • 1= 720
Se pueden ubicar de 720 formas distintas.
2. a. • Ω =
{(H; H; H ); (H; H; M); (H; M; H ); (M; H; H ); (H; M; M); (M; H; M);
(M; M; H ); (M; M; M)}
• A = {(H; H; M); (H; M; H ); (M; H; H )}
• La probabilidad es de
3
8
.
b. • Ω = {(P, C); ( P, CH); (C, CH)}
• A ={(P, C)}
• La probabilidad es de
1
3
.
415

Material
fotocopiable
Respecto de la siguiente información, responde
las preguntas 1 a la 3.
Para averiguar la cantidad de horas diarias que los
estudiantes de un colegio destinan a ver televisión
se encuesta a 15 estudiantes por cada curso.
1. ¿Cuál es la población del estudio?
A. Cantidad de horas.
B. 15 estudiantes por curso.
C. Los estudiantes del colegio.
D. Los estudiantes de un curso.
2. ¿Cuál es la muestra seleccionada?
A. 15 estudiantes del colegio.
B. 15 estudiantes de cada curso.
C. Todos los estudiantes del colegio.
D. Cantidad de horas diarias que ven televisión
los estudiantes.
3. ¿Cuál es la variable de estudio?
A. La edad de los estudiantes.
B. El curso de cada estudiante.
C. El tipo de programa que ven los estudiantes.
D. La cantidad de horas diarias que ven
televisión los estudiantes.
En la siguiente tabla se muestra la cantidad de
películas que un grupo de personas vio en el
cine el mes pasado.
Cantidad de películas vistas en el cine
Cantidad de películas f
0 10
1 67
2 51
3 25
4 19
5 8
4. ¿Cuántas personas vieron más de 3 películas en
el cine el mes pasado?
A. 19 personas.
B. 25 personas.
C. 27 personas.
D. 52 personas.
5. ¿Cuántas películas vieron en promedio el mes
pasado en el cine las personas?
A. 2 películas.
B. 3 películas.
C. 4 películas.
D. 5 películas.
6. ¿Cuál es la mediana de los datos?
A. 1 película.
B. 2 películas.
C. 3 películas.
D. 4 películas.

Unidad
4
Material
fotocopiable
7. ¿Cuál es el espacio muestral del experimento aleatorio de lanzar dos monedas?
A. Ω = {C, S}
B. Ω = {(C, C), (S, S)}
C. Ω = {(C, C), (C, S), (S, S)}
D. Ω = {(C, C), (C, S), (S, C), (S, S)}
8. En una caja hay fichas numeradas del 1 al 8 y se extrae una al azar. ¿Cuál es la probabilidad
de obtener el número 5?
A. 0,125
B. 0,25
C. 0,5
D. 0,625
9. ¿Cuál es la probabilidad de obtener menos de 4 puntos al lanzar un dado?
A. 0,1
B. 0,17
C. 0,5
D. 0,67
Resuelve los siguientes problemas.
10. Los siguientes datos corresponden a la cantidad de veces que un grupo de niños y de niñas juegan
fútbol a la semana.
1 - 4 - 3 - 1 - 4 - 1 - 2 - 7 - 5 - 1 - 3 - 1 - 0 - 3 - 2 - 1 - 4 - 3 - 5 - 2 - 3 - 4 - 6 - 4 - 5
a. Representa los datos en una tabla.
b. ¿Cuál es la media aritmética? ¿Cómo interpretas este valor?
11. Se extrae un dulce al azar de una bolsa en la que hay 5 dulces de frutilla, 12 de piña, 8 de plátano,
11 de manzana y 7 de naranja.
a. ¿Cuál es la probabilidad de que el dulce sea de manzana?
b. ¿Cuál es la probabilidad de que el dulce sea de piña o de naranja?
417

1. Selecciona un tipo de gráfico para representar
los datos entregados en cada caso.
a. Opción de un grupo de estudiantes respecto
de la próxima elección de Presidente del
centro de alumnos de un colegio.
Joaquín - Loreto - Camila - Joaquín
Loreto - Camila - Martín - Camila
Camila - Joaquín - Camila - Loreto
Martín - Camila - Loreto - Joaquín
Martín - Camila - Joaquín - Loreto
Joaquín - Camila - Loreto - Camila
Loreto - Loreto - Joaquín - Camila
Martín - Loreto - Camila - Camila
b. Ganancia mensual lograda por una empresa
en millones de pesos.
Ganancia Mensual
Mes
Millones
de pesos
Mes
Millones
de pesos
Enero 25 Julio 50
Febrero 30 Agosto 45
Marzo 40 Septiembre 60
Abril 30 Octubre 40
Mayo 45 Noviembre 50
Junio 40 Diciembre 65
c. Notas obtenidas por un grupo de estudiantes
en una prueba de estadística.
5,8 - 4,5 - 3,2 - 6,4 - 5,5 - 6,1 - 2,5 - 4,6 - 7,0 - 4,5
5,7 - 4,6 - 6,7 - 3,3 - 3,9 - 7,0 - 4,5 - 3,0 - 4,9 - 3,9
4,5 - 2,4 - 2,6 - 4,5 - 6,8 - 5,7 - 5,2 - 6,1 - 6,3 - 7,0
3,6 - 6,4 - 5,8 - 4,7 - 3,2 - 5,6 - 6,2 - 4,6 - 4,8 - 6,0
d. Color preferido por los estudiantes de prekinder.
Rojo - Azul - Amarillo - Azul - Verde
Rosado - Anaranjado - Verde - Rojo - Azul
Morado - Verde - Rojo - Azul - Rojo
Amarillo - Rojo - Blanco - Amarillo
2. Interpreta el siguiente gráfico y responde.
40 %
30 %
10 %
20 %
Un hijo
Dos hijos
Tres hijos
Cuatro hijos
Total: 60 familias
Cantidad de hijos que tienen los padres
de los estudiantes de 8º básico
a. ¿Cuántas familias tienen tres hijos?
b. ¿Cuántas familias tienen más de dos hijos?
3. Los siguientes datos corresponden a las horas
semanales que estudia un grupo de alumnos.
Calcula el cuartil 2 (Q2) y el cuartil 3 (Q3) de
los datos.
4 - 5 - 6 - 2 - 4 - 6 - 10 - 2 - 3 - 2
6 - 7 - 5 - 9 - 4 - 5 - 6 - 7 - 3 - 10
4. Calcula e interpreta los percentiles pedidos
respecto del siguiente grupo de datos.
Minutos de atraso que presenta un grupo de
estudiantes de un colegio durante un día.
2 - 1 - 5 - 3 - 5 - 6 - 10 - 7 - 5 - 8 - 3 - 5 - 20 - 5 - 6 - 15 -
25 - 28 - 2 - 4 - 6 - 18 - 20 - 21 - 15 - 18 - 22
a. P25
b. P12
c. P40
d. P78
e. P80
f. P28
5. Analiza la siguiente situación e interpreta las
medidas de posición pedidas para cada muestra.
Escribe el desarrollo en tu cuaderno.
a. Las siguientes muestras corresponden al
tiempo (en minutos) que tardó en hacer efecto
un medicamento en un grupo de personas.
Mujeres: 24 - 40 - 23 - 34 - 56 - 35 - 43
Hombres: 28 - 45 - 56 - 34 - 23
b. Q1 c. Q2 d. Q3
418
Material
fotocopiable

Unidad
4
Material
fotocopiable
6. Analiza la tabla. Luego complétala, calcula e
interpreta. Escribe el desarrollo en tu cuaderno.
En la siguiente tabla se muestra los tiempos que
demoran los buses de una empresa en completar
su recorrido.
Tiempo de demora de los buses
en completar el recorrido
Minutos 110 125 137 145
f 8 12 15 10
a. ¿Cuál es el valor del percentil 35?
¿Cómo se interpreta?
b. ¿Cuál es el valor del cuartil 2?
¿Cómo se interpreta?
7. Analiza el siguiente gráfico y luego calcula.
Años
Edad de los integrantes de
un taller de cine
Frecuencia
12
0
2
4
6
8
10
12
13 14 15
a. ¿Cuál es el cuartil 3? ¿Cómo se interpreta?
b. ¿Cuántos años tienen a lo más el 25 % de
los integrantes del taller de cine?
8. Analiza el siguiente diagrama de cajón y luego
responde las preguntas.
Notas de un grupo de estudiantes
4,0 4,5 5,0 5,5 6,0 6,5 7,0
Nota
a. ¿Qué nota como mínimo obtuvo el 50 % de
los estudiantes que obtuvieron mejor nota?
b. ¿Qué nota como máximo obtuvo el 25 % de
los estudiantes que obtuvieron peor nota?
A partir de la siguiente información, responde
la preguntas 9 a la 11.
En la tabla se muestra la cantidad de hijos que tienen
los trabajadores de una empresa.
Cantidad de hijos de los trabajadores
de una empresa
Cantidad de hijos 0 1 2 3 4
Cantidad de trabajadores 3 9 4 4 3
9. ¿Qué tipo de gráfico es más adecuado para
representar la situación?
A. Histograma.
B. Gráfico de líneas.
C. Gráfico de barras simples.
D. Gráfico de barras múltiples.
10. ¿Cuál es el valor de Q3?
A. 1 hijo.
B. 2 hijos.
C. 3 hijos.
D. 4 hijos.
11. ¿Cuál de las siguientes afirmaciones corresponde
a la interpretación del percentil 45?
A. El 45 % de los trabajadores tiene a lo más un hijo.
B. El 45 % de los trabajadores tiene a lo menos
un hijo.
C. El 45 % de los trabajadores tiene un hijo.
D. El 45 % de los trabajadores no tiene hijos.
12. El siguiente diagrama representa la distribución
de las estaturas, en metros, de un grupo de niños.
¿Cuál es el valor del recorrido intercuartíl?
Estatura de un grupo de niños
1,5 1,6 1,7 1,8
Metros
A. 0,11 m
B. 1,59 m
C. 1,7 m
D. 3,3 m
419
Lección 1

1. Elabora en tu cuaderno un diagrama de árbol
para representar las siguientes situaciones.
a. Lanzarundadodeseiscarasyluegodosmonedas.
b. Elegir una vocal y un número par mayor que
4 y menor que 11.
c. Lanzar un dado de seis caras. Si se obtiene un
número impar, lanzar una moneda; si se obtiene
un número par, lanzar nuevamente el dado.
2. Calcula la probabilidad de que ocurra cada suceso.
a. Obtener cara al lanzar una moneda.
b. Sacar un as de un mazo de 52 cartas.
c. Sin mirar, sacar un caramelo de frutilla de una
bolsa en la que hay 10 de ese gusto, 15 de piña
y 25 de naranja.
d. Obtener un múltiplo de 3 al sumar los puntos
de 2 dados iguales de seis caras.
3. Se lanzan dos dados, uno rojo y otro azul, y se
suman los puntos obtenidos.
a. ¿Qué probabilidad hay de que sumen 5?
b. ¿Y de que sumen 5 o menos?
c. ¿Cuál es la probabilidad de que sumen más de 5?
d. ¿Qué relación hay entre las probabilidades
obtenidas en los ítems anteriores?
4. En un juego se pueden enviar mensajes usando
estos 4 símbolos:
a. ¿Cuántos mensajes distintos de 3 caracteres
y con posibilidad de repetirlos se pueden
enviar?, ¿y sin repetirlos?
b. ¿Cuántos mensajes distintos de 4 caracteres
y con posibilidad de repetirlos se pueden
enviar?, ¿y sin repetirlos?
5. En una bolsita hay 10 caramelos de chocolate y
5 de frutilla. Si se saca uno sin mirar, ¿cuál es la
probabilidad de que sea de chocolate?
6. Se construirá una bandera con 5 franjas verticales
de los colores rojo, verde, azul, amarillo y negro.
¿Cuántas banderas distintas se pueden formar
si no se pueden repetir los colores?
7. A una empresa llegan 6 postulantes a un trabajo
donde hay 2 puestos distintos en el departamento
de recursos humanos. ¿De cuántas maneras se
pueden otorgar las vacantes?
8. ¿Cuántos números pares hay de 3 cifras?
9. ¿Cuántos números distintos de cuatro cifras se
pueden formar al ordenar uno al lado del otro
los dígitos 2, 4, 5, 6, 7 y 9 sin repetirlos?
10. Se escriben las letras de la palabra HOJA una
en cada una de 4 tarjetas. Si se disponen al azar
una al lado de la otra sobre una mesa, ¿cuántas
palabras distintas, con o sin sentido, se pueden
formar?
H O J A
11. Una familia va al estadio a ver un partido de
fútbol. El papá, la mamá, su hija y sus tres hijos
se ubicarán al azar en la misma fila uno al lado
del otro. ¿Cuál es la probabilidad de que los
hombres queden todos juntos?
12. En una tómbola se disponen 5 bolitas cada una
con uno de los siguientes dígitos sin que se
repitan 7, 2, 4, 6 y 9. Si se extraen una a una las
bolitas y se ubican una al lado de la otra, ¿cuál
es la probabilidad de que el número de 5 cifras
formado sea par?
7
4
9
6
2
420
Material
fotocopiable

Unidad
4
Material
fotocopiable
13. En el colegio de Carlos los estudiantes deben
escoger cada semestre como electivo una de
las 3 asignaturas de ciencias, una de las 5 de
literatura y uno de los 10 talleres deportivos.
¿De cuántas maneras diferentes puede elegir
Carlos estos tres ramos?
14. ¿De cuántas maneras diferentes se puede
pintar el diseño, si cada uno de los 4 triángulos
debe ser de un color distinto y se dispone de
5 colores: rojo, verde, negro, azul y gris?
15. Marcela quiere un helado de limón y para su
hermano uno de frutilla. Los va a sacar sin mirar
de una de dos heladeras, en las que los helados
están mezclados. ¿Qué heladera le conviene
elegir? ¿Por qué?
10 helados
de limón
10 helados
de frutilla
10 Helados
de chocolate
12 helados
de limón
7 helados
de frutilla
11 Helados
de chocolate
Heladera 1 Heladera 2
16. En una ruleta circular de 3 colores, la
probabilidad de obtener rojo es el triple de la
probabilidad de obtener verde, y la probabilidad
de obtener azul es el doble de la probabilidad
de obtener rojo. ¿Cuál es la probabilidad de
obtener rojo?
17. Un equipo de fútbol tiene 3 camisetas (una verde,
otra roja y otra azul) y pantalones de color negro
o blanco. ¿Cuál es la probabilidad de que en el
próximo partido los jugadores vistan camiseta
roja y pantalón blanco?
18. Un grupo de 60 personas, luego de comer,
deciden elegir una opción entre postre y café.
De las mujeres 10 eligieron café, de las 45
personas que eligieron postre 15 son hombres.
En el grupo hay 40 mujeres, entonces si se elige
una persona al azar, ¿cuál es la probabilidad de
que sea hombre y que haya elegido café?
19. En una heladería se puede comprar un helado de
un sabor entre 7 disponibles, agregarle crema o
chocolate y llevarlo en cono o vaso. ¿De cuántas
formas distintas es posible comprar un helado?
A. 7
B. 11
C. 14
D. 28
20. Una persona tiene 3 pantalones, 5 poleras y
2 pares de zapatillas. ¿De cuantas maneras
distintas se puede vestir?
A. 10
B. 15
C. 17
D. 30
21. En el experimento aleatorio de lanzar un dado de
seis caras y una moneda, ¿cuál es la probabilidad
de obtener un número par en el dado y sello en
la moneda?
A.
3
18
B.
3
6
C.
3
9
D.
3
12
22. Se escriben las letras de la palabra PATIO una en
cada una de 5 tarjetas. Si se ordenan al azar, una
al lado de la otra, ¿cuál es la probabilidad de la
palabra formada comience con una vocal?
A.
3
72
B.
3
120
C.
72
120
D.
24
120
421
Lección 2

Material
fotocopiable
1. Analiza el siguiente gráfico y luego responde
en tu cuaderno.
Meses
Ventas realizadas por un vendedor
Millones
de
pesos
Ene Feb Mar Abri Jun
May
0
5
10
15
20
25
a. ¿En qué mes se logró mas ventas?
b. ¿Entre qué meses hubo descenso en sus ventas?
c. ¿Cuánto dinero ha reunido en este primer
semestre?
2. Respecto de los datos responde.
Los siguientes valores corresponden a las cantidad
de personas que atendieron los especialistas de
un centro médico durante una semana.
25 - 30 - 35 - 20 - 35 - 40 - 20 - 15
40 - 25 - 28 - 30 - 40 - 35 - 38 - 25
a. ¿Cuál es el valor del cuartil 2?
b. ¿Cuál es el valor del percentil 35?
¿Cuál es su interpretación
c. ¿Cuál es el valor de P60?
¿Cuál es su interpretación?
3. Construye para cada grupo de datos un
diagrama de cajón.
a. Notas obtenidas por un grupo de estudiantes.
3,5 - 6,2 - 5,8 - 4,5 - 3,1 - 4,6 - 6,7
7,0 - 5,9 - 3,6 - 4,0 - 3,0 - 6,5 - 4,5
b. Masa, en kilógramos, de un grupo de perros.
10 - 15 - 25 - 28 - 5 - 12 - 10 - 14
15 - 10 - 20 - 23 - 14 - 20 - 15 - 10
4. Elabora un diagrama de árbol para representar
las siguientes situaciones y responde
las preguntas.
a. Fernando quiere un helado y le dan a escoger
las siguientes posibilidades para prepararlo:
tamaño grande o pequeño, sabores de frutilla,
de mora o de chocolate y salsa de caramelo,
de frutilla o de manjar. ¿Cuántas posibilidades
le ofrecen en la venta?
b. En un restaurante el menú está dado por
3 platos principales, 2 platos alternativos,
4 postres y 2 bebidas. ¿De cuántas maneras se
puede elegir un menú en dicho restaurante?
5. María José tiene tres carteras: una roja, otra café
y una negra. Además, tiene 4 pares de zapatos:
uno rojo, otro verde, uno negro y uno blanco.
¿De cuántas formas distintas puede combinar
un par de zapatos y una cartera?
6. Respecto del experimento lanzar una moneda
al aire en 3 oportunidades, ¿cuántos son los
elementos del espacio muestral?
7. Un padre va al cine con sus 3 hijos. ¿De cuántas
maneras se pueden ordenar uno al lado del otro
de tal forma que los niños queden todos juntos?
8. Se escriben las letras del nombre MARCOS cada
una en una tarjeta, se mezclan y se ordenan al
azar una al lado de otra en una mesa. ¿Cuál es la
probabilidad de que se forme el nombre MARCOS?
9. Respecto de la pregunta anterior, ¿cuál es la
probabilidad de que la palabra que se forme
comience con una vocal?

Unidad
4
Material
fotocopiable
Respecto de la siguiente información responde
las preguntas 1 y 2.
Inasistencias a clases en una semana
Día Cantidad de inasistencias
Lunes 29
Martes 27
Miércoles 11
Jueves 12
Viernes 17
1. ¿Cuántas fueron las inasistencias en esa semana?
a. 17
b. 27
c. 29
d. 96
2. ¿Qué tipo de gráfico sería más adecuado
utilizar para representar los datos?
A. Histograma.
B. Gráfico circular.
C. Gráfico de barras.
D. Polígono de frecuencias.
3. En el siguiente gráfico circular se muestra
los tipos de películas preferidas por un grupo
de personas.
Tipos de películas preferidas
10 %
17 %
9 %
21 %
20 %
23 % Acción
Aventura
Terror
Comedias
Misterio
Romáticas
¿Qué porcentaje de personas prefieren
las películas de terror?
A. 9 %
B. 17 %
C. 21 %
D. 23 %
4. Los siguientes datos corresponden a las edades
de un grupo de niños que visitó el museo
durante el día sábado.
6 - 7 - 6 - 4 - 5 - 7 - 8 - 5 - 6 - 6 - 4 - 6 - 6
5 - 4 - 5 - 4 - 5 - 6 - 6 - 5 - 4 - 6 - 6 - 5 - 4
¿En cuál de las siguientes tablas se representa
la información anterior?
Niños que visitaron el museo
Edad de niños f
4 6
5 7
6 10
A.
Edad de niños f
4 7
5 6
6 10
B.
Edad de niños f
4 10
5 7
6 6
C.
Edad de niños f
4 10
5 7
6 4
D.
423

Material
fotocopiable
En una reunión se encuestó a los asistentes sobre
la cantidad de personas que viven en sus casas.
Los datos recolectados fueron los siguientes:
5 - 1 - 3 - 5 - 2 - 1 - 3 - 1 - 2 - 1 - 3 - 1
6 - 2 - 4 - 2 - 3 - 5 - 6 - 4 - 4 - 5 - 1 - 3
5. ¿Cuántos encuestados están bajo el cuartil 2?
A. 2
B. 6
C. 12
D. 24
6. ¿Cuál de las siguientes relaciones es verdadera?
A. Q1 = P20
B. Q2 = P25
C. Q3 = P30
D. Q3 = P75
7. ¿Cuál de las siguientes afirmaciones es falsa?
A. Bajo el P50 hay 12 encuestados.
B. Bajo el P75 hay 18 encuestados.
C. Sobre el P50 hay 12 encuestados.
D. Sobre el P75 hay 6 encuestados.
8. ¿Cuál de las siguientes expresiones corresponde
al cálculo del recorrido intercuartil para esta
situación?
A. 4,5 – 1,5 = 3
B. 4 – 1 = 3
C. 3 – 1,5 = 1,5
D. 5 – 2 = 3
9. ¿Cuál de los siguientes diagramas de cajón
representa la situación?
1 2 3 4 5 6
A.
1 2 3 4 5 6
B.
1 2 3 4 5 6
C.
1 2 3 4 5 6
D.
10. ¿Qué significa que un suceso tenga
probabilidad igual a 1?
A. Existe una baja probabilidad de que
el suceso ocurra.
B. No existen probabilidades de que
el suceso ocurra.
C. El suceso siempre ocurre.
D. No se puede determinar la probabilidad
de que el suceso ocurra.
11. Para numerar los estacionamientos de un edificio
se utilizan números de tres cifras utilizando
los dígitos del 0 al 9 y con la condición de que
no se pueden repetir los dígitos. ¿Cuántos
estacionamientos se pueden numerar con
estas condiciones?
A. 27
B. 90
C. 504
D. 720
12. Respecto de la situación planteada en el ítem 10,
¿cuántos números comienzan con el 9?
A. 72
B. 80
C. 90
D. 240
13. En un colegio invitaron a 14 estudiantes de
otros colegios de los cuales 5 son de la misma
región, 3 de Coquimbo, 4 de Valparaíso y el
resto de la Región Metropolitana. Si se elige a
dos estudiantes al azar, ¿qué probabilidad hay
de que sea de la Región Metropolitana?
A.
1
120
B.
2
120
C.
3
120
D.
5
120

Unidad
4
Material
fotocopiable
1. C
2. B
3. D
4. C
5. A
6. B
7. D
8. A
9. C
10. a.
Cantidad de veces que juegan
fútbol a la semana niños y niñas
Cantidad f
0 1
1 6
2 3
3 5
4 5
5 3
6 1
7 1
b. La media aritmética es 3, lo que significa que en promedio los niños y niñas juegan 3 veces fútbol a la semana.
11. a. La probabilidad de que el dulce sea de manzana es de
11
43
.
b. La probabilidad de que el dulce sea de piña o de naranja es de
19
43
.
• Identificar la población, la muestra y la variable en un estudio estadístico.
• Representar datos obtenidos en una muestra y calcular e interpretar las
medidas de tendencia central.
1, 2, 3, 4, 5,
6 y 10
• Describir el espacio muestral de un experimento aleatorio y calcular la
probabilidad de un suceso.
7, 8, 9 y 11
425

Material
fotocopiable
Evaluación proceso Lección 1.
• Mostrar que comprenden las medidas de posición, percentiles y cuartiles:
-
- identificando la población que está sobre o bajo el percentil.
-
- representándolas con diagramas, incluyendo el diagrama de cajón,
-
- utilizándolas para comparar poblaciones.
3, 4, 5, 6,
7, 8, 10, 11
y 12
• Evaluar la forma en que los datos están presentados:
-
- comparando la información de los mismos datos representada en distintos
tipos de gráficos para determinar fortalezas y debilidades de cada uno.
-
- justificando la elección del gráfico para una determinada situación y su
-
- detectando manipulaciones de gráficos para representar datos.
1, 2 y 9
1. a. Gráfico circular.
b. Gráfico de líneas.
c. Gráfico de barras.
d. Gráfico de barras.
2. a. 18 familias.
b. 42 familias.
3. a. Q2 = 3,5 horas.
b. Q3 = 6 horas.
4. a. P25 = 5minutos; el 25 % de los atrasos es menor a 5 minutos.
b. P12 = 3 minutos; el 12 % de los atrasos es inferior a 3 minutos.
c. P40 = 5 minutos; el 40 % de los atrasos es a lo más de 5 minutos.
d. P78 = 20 minutos; el 78 % de los atrasos no superan
los 20 minutos.
e. P80 = 20 minutos; el 80 % de los atrasos no superan los 20
minutos.
f. P28 = 5 minutos; el 28 % de los atrasos es a lo más de 5 minutos.
5. a. Mujeres, Q1 = 24 minutos.
Hombres, Q1 = 23 minutos.
Al comparar los tiempos que demoró el medicamento en hacer
efecto en el 25 % de ambas muestras se puede concluir que hizo
efecto primero en los hombres.
b. Mujeres, Q2 = 35 minutos.
efecto primero en los hombres.
c. Mujeres, Q3 = 43 minutos.
efecto primero en las mujeres.
6. a. P35 = 125 minutos; el 35 % de los buses se demoran menos
de 125 minutos en completar el recorrido.
b. Q2 = 137 minutos; el 50 % de los buses se demoran a lo más
137 minutos en completar el recorrido.
7. a. Q3 = 14 años; el 75 % de los integrantes del taller tiene a lo
más 14 años.
b. El 25 % de los integrantes del taller tienen 12 años.
8. a. Obtuvieron un 5,7 como mínimo.
b. Obtuvieron a lo más un 5,0.
9. C
10. C
11. A
12. A

Unidad
4
Material
fotocopiable
Evaluación proceso Lección 2.
• Aplicar el principio multiplicativo en la resolución de problemas.
• Representar el principio multiplicativo con diagramas de árbol.
1, 4, 6, 7, 8, 9, 10,
13, 14, 19 y 20
• Calcular la probabilidad de un suceso.
2, 3, 5, 11, 12, 15,
16, 17, 18, 21 y 22
1. a.
C C
S
S
S
C
1
C C
S
S
S
C
2
C C
S
S
S
C
3
C C
S
S
S
C
4
C C
S
S
S
C
5
C C
S
S
S
C
6
b.
6 8 10
A
6 8 10
E
6 8 10
I
6 8 10
O
6 8 10
U
c.
S C
1
1 4
2 5
3 6
2
S C
3
1 4
2 5
3 6
4
S C
5
1 4
2 5
3 6
6
2. a.
1
2
= 0,5
b.
4
52
c.
10
50
= 0,2
d.
12
36
3. a.
4
36
b.
10
36
c.
26
36
d. La suma de ambas es 1.
e. La suma más probable es 7 y la probabilidad de obtenerla es
6
36
.
f.
33
36
4. a. Se pueden enviar 64 mensajes si se pueden repetir y
24 sin repetirlos.
b. Se pueden enviar 256 mensajes si se pueden repetir y
24 sin repetirlos.
5. La probabilidad de que sea de chocolate es de
10
15
.
6. Se pueden formar 120 banderas distintas.
7. Las vacantes se pueden otorgar de 30 maneras diferentes.
8. Hay 450 números.
9. Se pueden formar 360 números.
10. Se pueden formar 24 palabras.
11. La probabilidad que la hija quede al medio es
2
6
.
12. La probabilidad de que el número sea par es
72
120
= 0,6.
13. Puede elegir los ramos de 150 formas diferentes.
14. Se puede pintar de 120 maneras diferentes.
15. Le conviene elegir la heladera 1. En ambas heladeras hay la misma
cantidad de helados, pero la heladera 2 tiene más helados de
chocolate, por lo que tiene más probabilidades de sacar el helado
que no quiere.
16. La probabilidad de que sea hombre y haya elegido café es de
5
60
.
17. La probabilidad de que vistan camiseta roja y pantalón blanco
es de
1
6
.
18. La probabilidad de obtener rojo es
3
10
= 0,3.
19. D
20. D
21. C
22. A
427

Material
fotocopiable
Evaluación formativa
1. a. En el mes de junio.
b. Entre marzo y abril. c. Ha reunido $ 105 000 000.
2. a. 30 personas.
b. El 35 % de los especialistas atendió a lo más a 25 personas.
c. El 60 % de los especialistas atendió a lo más a 35 personas.
3. a.
3,0 3,6 4,55 6,2 7,0
Notas obtenidas por un grupo de estudiantes
Nota
b.
3,0 3,6 4,55 6,2 7,0
Masa de un grupo de perros
kg
4. a.
Grande
frutilla manjar
caramelo frutilla manjar
caramelo
frutilla mora chocolate
Pequeño
frutilla manjar
caramelo
frutilla mora chocolate
A Fernando le ofrecen 18 posibilidades de helado.
b.
Principal 1
Postre 1 Postre 2
Bebida 2 Bebida 2
Bebida 1 Bebida 1
Principal 2
Postre 1 Postre 2
Bebida 2 Bebida 2
Bebida 1 Bebida 1
Principal 3
Postre 1 Postre 2
Bebida 2 Bebida 2
Bebida 1 Bebida 1
Se puede elegir un menú de 12 formas diferentes.
5. 12 formas distintas.
6. 8 elementos.
7. De 12 formas.
8. La probabilidad es de
1
720
.
9. La probabilidad es de
240
720
.

Unidad
4
Material
fotocopiable
Evaluación final
1. D
2. C
3. B
4. A
5. B
6. D
7. D
8. A
9. C
10. C
11. D
12. A
13. B
• Evaluar la forma en que los datos están presentados:
-
- comparando la información de los mismos datos representada en distintos
tipos de gráficos para determinar fortalezas y debilidades de cada uno.
-
- justificando la elección del gráfico para una determinada situación y su
-
- detectando manipulaciones de gráficos para representar datos.
1, 2, 3 y 4
• Mostrar que comprenden las medidas de posición, percentiles y cuartiles:
-
- identificando la población que está sobre o bajo el percentil.
-
- representándolas con diagramas, incluyendo el diagrama de cajón,
-
- utilizándolas para comparar poblaciones.
5, 6, 7, 8 y 9
• Explicar el principio combinatorio multiplicativo:
-
- a partir de situaciones concretas.
-
- representándolo con tablas y árboles regulares, de manera manual y/o
con software educativo.
-
- utilizándolo para calcular la probabilidad de un evento compuesto.
10, 11,
12 y 13
429

Bibliografía
• Arenas, F. y equipo (1993). Geometría Elemental. Santiago, Chile: Ediciones Universidad Católica de Chile.
• Brousseau, Guy. Fundamentos y Métodos de la Didáctica de la Matemática. Traducción realizada por Dilma Fregona (FaMAF),
Universidad de Córdoba, y Facundo Ortega, Centro de Estudios Avanzados, UNC, Argentina, 1993.
• Cantoral, R., Montiel, G. (2001) Funciones: Visualización y Pensamiento Matemático. Pearson Educación México.
• Chevallard Y. La transposición didáctica. Del saber sabio al saber enseñado. Aique, Buenos Aires, 1991.
• Chevallard, Y., Bosch, M. y Gascón, J. Estudiar matemáticas. El eslabón perdido entre enseñanza y aprendizaje.
Horsori, Barcelona, 1997.
• Cortes, C. (1994). “Rectas: Software de apoyo al aprendizaje”.
• Memoria de la VIII reunión centroamericana y del Caribe sobre formación de profesores e investigación en matemática educativa.
Costa Rica 1994.
• Coxeter, H.S.M.; Greitzer, S.L. (1967). Geometry Revisited. EEUU: The Mathematical Association of America.
• Dickson, L. Brown, M. y Gibson, O. (1991). El aprendizaje de las Matemáticas. Barcelona, España: Editorial Labor.
• Duval, R., (2004). Semiosis y Pensamiento Humano, Capítulo V. Universidad del Valle, Instituto de Educación y Pedagogía,
Grupo de Educación Matemática. Peter Lang S.A. Editions scientifiques européennes, 1995.
• Duval, R., (1998). Gráficas y ecuaciones: la articulación de dos registros. Traducción del Departamento
de Matemática Educativa del CINVESTAV-IPN, México.
• E.T. Bell. (1948). Los grandes matemáticos. Buenos Aires, Argentina: Editorial Losada S.A.
• Figueroa, L. (2001). Para qué sirve medir. España: Cuadernos de Pedagogía, Nº 302.
• Guedj, D. (1998). El imperio de las cifras y los números. Barcelona, España: Ediciones B S.A.
• Gustafson, D. (1997). Álgebra Intermedia. México: International Thomson Editores.
• Guzmán, I. (2002). Didáctica de la matemática como disciplina experimental. Chile:
Pontificia Universidad Católica de Valparaíso.
• Linares, S. (1988). Fracciones, la relación parte-todo. Madrid, España: Editorial Síntesis.
• Mateos, M. (2001). Metacognición y educación. Buenos Aires, Argentina: Editorial Aique.
• Mena, A. (2002). Elementos de matemática: grupos. Valparaíso: Pontificia Universidad Católica de Valparaíso.
• Novak, J. (1988). Aprendiendo a aprender. Barcelona, España: Ediciones Martínez Roca S.A.
• Ontoria A. (1993). Mapas conceptuales. España: Editorial Nancea, 2ª edición.
• Piaget, J. (1963). Las estructuras matemáticas y las estructuras operatorias de la inteligencia; la enseñanza de las matemáticas.
Madrid: Aguilar.
• Saavedra Gallardo, E. (2005), Contenidos básicos de Estadística y probabilidades, Chile:
Editorial Universidad de Santiago.
• Sternberg, R., Apear-Swerling L. (1996). Enseñar a pensar. España: Aula XXI.
• Stewart, Ian. (1990). Ingeniosos encuentros entre juegos y matemáticas. Barcelona, España: Editorial Gedisa.
• Vygotski, L. (1995). El desarrollo de los procesos psicológicos superiores. Barcelona, España: Editorial Libergraf, S.A.
• Winston H. Elphick D. y Equipo. (2001). 101 Actividades para implementar los Objetivos Fundamentales Transversales. Santiago,
Chile: Lom Ediciones.
430 Bibliografía
CL0000000001141 MATE_8B_GDD_Finales_Tomo_2_5930.indd 430 1/8/2020 12:11:01 PM

Sitios web
• http://www.ugr.es/~jgodino/edumat-maestros/manual/2_Sistemas_numericos.pdf
• http://www.sinewton.org/numeros/numeros/73/Experaula_01.pdf
• http://www.ugr.es/~jgodino/edumat-maestros/manual/2_Sistemas_numericos.pdf
• http://www.sinewton.org/numeros/numeros/33/Articulo03.pdf
• http://descartes.cnice.mec.es/materiales_didacticos/Potencias_mac/indice.htm
• http://nlvm.usu.edu/es/nav/frames_asid_160_g_3_t_1.html?open
• http://www.ugr.es/~jgodino/edumat-maestros/manual/3_Proporcionalidad.pdf
• http://www.sinewton.org/numeros/numeros/77/Apertura.pdf
• http://www.sinewton.org/numeros/numeros/75/Apertura.pdf
• http://nlvm.usu.edu/es/nav/frames_asid_189_g_3_t_2.html
• http://www.sinewton.org/numeros/numeros/82/Enlared_01.pdf
• http://descartes.cnice.mec.es/materiales_didacticos/ecuaciones_primer_grado/indice.htm
• http://descartes.cnice.mec.es/materiales_didacticos/Identificacion_funciones_d3/index.htm
• http://www.educarchile.cl/ech/pro/app/detalle?ID=206998
• http://www.bdigital.unal.edu.co/7739/1/sergioandresmontesalarcon.2012.pdf
• http://tintafresca.com.ar/_docs/Problema7.pdf
• http://www.quadernsdigitals.net/index.php?accionMenu=hemeroteca.DescargaArticuloIU.
Como complemento a los recursos presentes en la Guía Didáctica del Docente, puede utilizar
los recursos existentes en su biblioteca escolar (CRA y digital). Para esto, se le sugiere pedir
asesoría al encargado CRA de su colegio.
431
431
Sitios web

Texto docente 8 básico

Más contenido relacionado

La actualidad más candente

Similar a Texto docente 8 básico

Más de María De Los Angeles

Último

Texto docente 8 básico