VECTORES_RESNICK.pdf

EJERCICIOS DE LA FISICA DE RESNICK
VECTORES: CAPITULO III
Msc. Widmar Aguilar
Mayo 2023
Para que el desplazamiento resultante sea:
a) 7 m
Los vectores deben estar paralelos entre sí y misma dirección
b) 1m
Los vectores deben estar paralelos y opuestos (restándose)
c) 5m
Los vectores deben ser perpendiculares:
⃗ + ⃗ = √9 + 16 = 5 m

Msc. Widmar Aguilar
Mayo 2023
a) ⃗ + ⃗ = ⃗ y a+b=c
Se tienen 2 vectores sumados y se pide que sus magnitudes sumadas sea otro
numero real
Esto se cumple solamente si los vectores son paralelos y tienen la misma dirección
b) ⃗ + ⃗ = ⃗ - ⃗
La ubica opción de que se cumpla la igualdad es que: ⃗ =
⃗ = ⃗
c) ⃗ + ⃗ = ⃗ y + =
Para que se cumpla las condiciones dadas:
Los vectores a y b deben ser perpendiculares

Msc. Widmar Aguilar
Mayo 2023
Usando el AUTOCAD se determina que el desplazamiento es de:
r = 374.28 m
⃗ = 250 55 + 55 + 170
⃗ = 313.39 + 204.78
= √313.39 + 204.78 = 374.36 %
a) ⃗ = 3.1 − 2.4 − 5.2
⃗ = −2.4 − 2.1
r = √2.4 + 2.1 = 3.19 '%

Msc. Widmar Aguilar
Mayo 2023
b)
( = ) *+
,
.-
.+
. = 48.81o
Sur Oeste
/
⃗ = ⃗ + ⃗
Sabemos que, en un triángulo, la suma de dos lados
siempre es mayor que el tercer lado. En el triángulo de arriba,
tenemos:
⃗ + ⃗ < | ⃗| + ⃗
Además, también sabemos que la diferencia de dos lados es menor
que el tercer lado. Entonces, tenemos:
| ⃗| − ⃗ < ⃗ + ⃗
Por tanto:
| ⃗| − ⃗ < ⃗ + ⃗ < | ⃗| + ⃗
Recuerde que el menor valor se obtiene cuando los vectores
son paralelos y direcciones opuestas

Msc. Widmar Aguilar
Mayo 2023
⃗ = 54 + 32 + 27 62 + 62
⃗ = 66.67 + 55.84
|⃗| = √66.67 + 55.84 = 86.96 '%
2
⃗ = ⃗ + ⃗ ; /
⃗ = ⃗ − ⃗
Por teorema de cosenos:
2
⃗ = 2 = √ + + 2 3
2 = √5.2 + 4.3 + 2 ∗ 5.2 ∗ 4.3 125

Msc. Widmar Aguilar
Mayo 2023
2 = √19.88 = 4.46 5
6789
-.:
=
;<=>>
>.
Sen(A = 0.677
A= 42.64
? = 90 − 42.64 = 47.36o
Noreste
/
⃗ = / = √ + + 2 3
R= √5.2 + 4.3 + 2 ∗ 5.2 ∗ 4.3 55
/ = √71.18 = 8.44 5
;<=>>
@.--
=
;<= A
-.:
= 0.417
A = 24.67o
∅ = 90 − = 90 − 24.67
∅ = 65.33 25 C )

Msc. Widmar Aguilar
Mayo 2023
⃗ = ⃗+ + ⃗ + ⃗:
⃗ = 12 + 6 315 + 315 + 3 225 + 225
⃗ = 12j + 4.24i -4.24 j - 2.12 i - 2.12 j
⃗ = 2.12 + 5.64
( = ) *+
,
>.D-
.+
. = 63.4o
Para meter la bola en el primer golpe de debe tener una magnitud de :
= √2.12 + 5.64 = 6 E) , 63.4o
Norte del Este
a)
⃗ = 252 + 252
⃗ = 7.34 252 + 252
⃗ =-2.27 i -6.98 j (u)
b)

Msc. Widmar Aguilar
Mayo 2023
⃗ = F G + H = √25 + 43 = 49.74 5
( = 180 − ) *+ -:
>
= 180 − 59.83
( = 120.17o
⃗ = 13 22 + 22
⃗ = 12.05 + 4.87 %
I
J = 12.05 %
K = 4.87 %

Msc. Widmar Aguilar
Mayo 2023
El vector horizontal en café, representa todos los desplazamientos a lo largo de
X y el vector en amarillo representa los desplazamientos en Y, así:
d = 3.42cos 55+ 3.42 sen 55
d = 1.96+ 2.8
d = 4.76 km
Se tiene que:
⃗+ + ∆⃗ = ⃗
∆⃗ = ⃗ − ⃗+
∆⃗ = 31.4 + 72.6 − 124
∆⃗ = 31.4 − 51.4
( = ) *+
,
:+.-
>+.-
. = 31.42o
∆ = √31.4 + 51.4 = 60.23 M%
∆ = 60.23 '% , 31.42o
NO

Msc. Widmar Aguilar
Mayo 2023

Msc. Widmar Aguilar
Mayo 2023
Se tiene que: l= R3
O = P ∗ 0.45 = 0.45 P %
⃗ = 0.45P + 2/ − 0 + 0
∆⃗ = 1.41 + 2/ = 1.41 + 2 ∗ 0.45
∆⃗ = 1.41 + 0.9 (m)
a) ⃗ = 0 − 12 + 10 − 0 + 14 − 0 '
⃗ = −12 + 10 + 14 ' E)
b) = √12 + 10 + 14

Msc. Widmar Aguilar
Mayo 2023
= 20.97 E)
c) Como la distancia menor es la longitud de la recta que une los puntos
de partida y llegada, no puede existir otra magnitud menor a ella
d) SI LA MOSCA CAMINARA, LA MENOR LONGITUD SERIA:
Q+ = R + +
Q = R + +
Y:

Msc. Widmar Aguilar
Mayo 2023
Q: = R + +
Se tiene:
Q+ = R 10 + 14 + 12 = 26.83
Q = R 12 + 14 + 10 = 27.86
Q: = R 10 + 12 + 14 = 26.08
La menor distancia es; d= 26.08 ft
⃗ + ⃗ = 5 + 3 + −3 + 2
⃗ + ⃗ = 5 − 3 + 3 + 2
⃗ + ⃗ = 2 + 5
( = 3') *+
,
>
. = 68.2o
sobre el eje X
⃗ = 4 − 3 + '
⃗ = − + + 4'
a) ⃗ + ⃗ = 4 − 1 + −3 + 1 + 1 + 4 '
⃗ + ⃗ = 3 − 2 + 5'
b) ⃗ − ⃗ = 4 − 3 + ' – (-i+j+4k)
⃗ − ⃗ = 4 + 1 + −3 − 1 + 1 − 4 '

Msc. Widmar Aguilar
Mayo 2023
⃗ − ⃗ = 5 − 4 − 3'
c.) Si: ⃗ − ⃗ + ⃗ = 0
⃗ = ⃗ − ⃗
⃗ = − ⃗ − ⃗
⃗ = − 5 − 4 − 3'
⃗ = −5 + 4 + 3'
a)
| ⃗| = √3 + 4 = 5 5
( = ) *+
,
:
-
. = − 36.87o
b)
⃗ = √6 + 8 = 10 5
( = ) *+
,
@
D
. = 53.13o
c) ⃗ + ⃗ = 4 − 3 + 6 + 8
⃗ + ⃗ = 10 + 5

Msc. Widmar Aguilar
Mayo 2023
( = ) *+
,
>
+S
. = 26.57o
d) ⃗ − ⃗ = 6 + 8 − 4 − 3
⃗ − ⃗ = 2 + 11
( = ) *+
,
++
. = 79.69o
e) ⃗ − ⃗ = 4 − 3 − 6 + 8
⃗ − ⃗ = −2 − 11
( = ) *+
,
*++
*
. = −79.69o

Msc. Widmar Aguilar
Mayo 2023
a) ⃗ = 1400 + 2100 − 48 '
b)
El hombre regresa por una trayectoria diferente al punto de salida A ( de B a A):
Como vuelve al punto de partida:
∆
⃗ =0

Msc. Widmar Aguilar
Mayo 2023
⃗ = ⃗+ = 4.13 225 + 225
⃗+ = −2.92 − 2.92 %
⃗ = ⃗ = 5.26 i
⃗ = ⃗: = 5.94 cos 26 + 26
⃗: = 5.34 i + 2.6 j
b.) ⃗ = ⃗ + ⃗ + ⃗
⃗ = −2.92 − 2.92 + 5.26 + 5.34 + 2.6
⃗ = 7.68 − 0.32
c) |⃗| = R7.68 + −0.32 = 7.687 %
( = ) *+
,
S.:
W.D@
. = −2.39o
d) −⃗ = −7.68 + 0.32

Msc. Widmar Aguilar
Mayo 2023
∆⃗ = ⃗ − ⃗+
⃗+ = 12000 40 + 40 = 9192.53 + 7713.45
⃗ = 25800 163 + 163 = −24672.66 + 7543.19
∆⃗ = −9192.53 − 24672.66 + −7713.45 + 7543.19
∆⃗ = −33865.19 − 170.26

Msc. Widmar Aguilar
Mayo 2023
De la figura, utilizando el teorema de Pitágoras, se tiene:
= + 3 + 3
= + 2 3 + 3 + 3
= + 2 3 + 3 + 3)
Como: 3 + 3 = 1
= + 2 3 +
= √ + + 2 3
Si: X
⃗ ⊥ 2
⃗ :
2 = X + 2
4 = + 2 ( + + + 2 180 − ( +
180 − ( = − (
4 = + 2 ( + + − 2 ( +
4 = + + +
4 = 2 + 2

Msc. Widmar Aguilar
Mayo 2023
2 = 2
=
a = b
`
a) ⃗ = 0 − + − 0 + − 0 '
⃗ = − + + '
⃗ = − 0 + − 0 + 0 − '
⃗ = + − '

Msc. Widmar Aguilar
Mayo 2023
⃗ = − 0 + 0 − + − 0 '
⃗ = − + '
⃗ = − 0 + − 0 + − 0 '
⃗ = + + '
b)
J = √ + = √2a
) 3 =
G
Z
= √2

Msc. Widmar Aguilar
Mayo 2023
3 = 54.73o
c.) D = √J +
D = F √2 +
D = √2 +
D = √3
El punto de Washington se aprecia en el esquema:

Msc. Widmar Aguilar
Mayo 2023
El punto de Manila se aprecia en el esquema:
Para obtener el vector que sale de O hasta W, se procede de la manera siguientes:

Msc. Widmar Aguilar
Mayo 2023
Sen 39 =
[
]^
; `
H = 6370 ∗ 39 '%
`
H = 4008.77 M%
Cos 39 =
Ga
]^
; `
Ga = 6370 ∗ 39
`
Ga = 4950.42 M%b
De:
sen77=
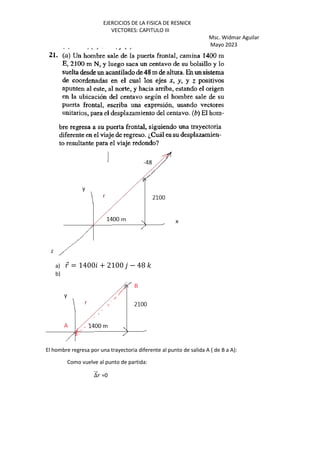
[c
[cd
`
G = `
Ga 77 = 4950.42 ∗ 77
`
G = −4823.54 Km
cos77=
[d
[cd
`
a = `
Ga 77 = 4950.42 ∗ 77
`
a = 1113.6 Km
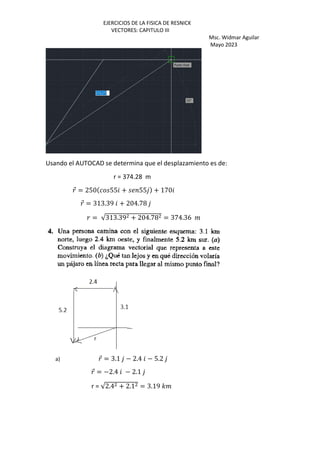
⃗+ = −4823.54 + 4008.77 + 1113.6 '
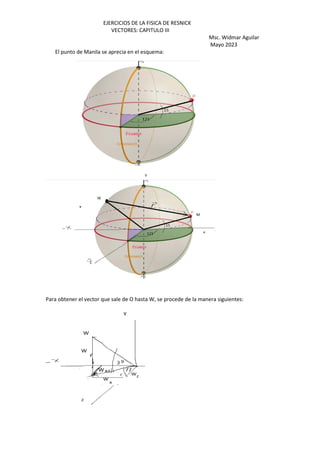
El vector para Manila:

Msc. Widmar Aguilar
Mayo 2023
15 =
e
]
fH = /g 15 = 6370 ∗ 15
fH = 1648.77 M%
15 =
ecd
]
fGa = /g 15 = 6370 ∗ 15
fGa = 6152.95 M%
31 =
ed
ecd
fa = fGa 31 = 6152.95 ∗ 31
fa = − 3169 M%
31 =
ec
fJh
fG = fJh 31 = 6152.95 ∗ 31
fG = 5274.1 M%
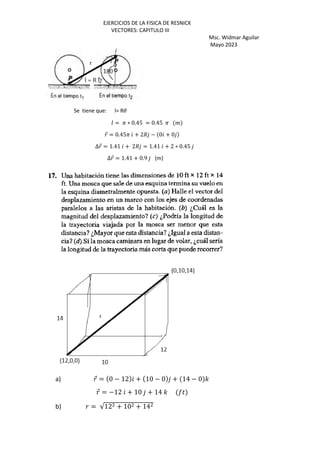
⃗ = 5274.1 + 1648.77 − 3169 '
⃗ = ⃗ − ⃗+
⃗ = 5274.1 + 1648.77 − 3169 ' − −4823.54 + 4008.77 +
1113.6 ')
⃗ = 10097.64 i – 2360 j -4282.6 k (km)
|⃗ | = √10097.64 + 2360 + 4282.6
|⃗ | = 11219. 30 M%

Msc. Widmar Aguilar
Mayo 2023
S= + cos
i
j
+
i
j
+ cos
4P
k
+
4P
k
+ cos
6P
k
+
6
k
+ cos
8P
k
+
8P
k
+ -----
2+ + 2 = + cos
i
j
+
i
j
+ cos
4P
k
+
4P
k
+
cos
6P
k
+
6
k
+ cos
8P
k
+
8P
k
+ -----
2+ = +
2P
k
+ cos4P
k
+ 6P
k
+ 8P
k
+ − − −
2+ = +
2P
k
+ cos4P
k
+ 6P
k
+ 8P
k
+ − − − + k − 1 2P
k
2+
= cos0 +
2P
k
+ cos
4P
k
+
6P
k
+
8P
k
+ − − − + k − 1
2P
k

Msc. Widmar Aguilar
Mayo 2023
De igual forma:
2 =
2P
k
+ sen4P
k
+ 6P
k
+ 8P
k
+ − − −
2 =
2P
k
+ sen4P
k
+ 6P
k
+ 8P
k
+ − − − + k − 1 2P
k
no
A
= 0 +
2P
k
+ sen4P
k
+ 6P
k
+ 8P
k
+ − − − + k − 1 2P
k
Utilizando sumatorias, se tiene:
np
A
= ∑ cos
i=
j
=rj*+
=rS
no
A
= ∑ sen
i=
j
=rj*+
=rS
EN EL CAMPO DE COMPLEJOS:
∑ cos
i=
j
=rj*+
=rS = / ∑ P + P
os
t
=rj*+
=rS
∑ cos
i=
j
=rj*+
=rS = / ∑ P
2
k
=k−1
=0
∑ sen
i=
j
=rj*+
=rS = u%v ∑ P + P
o
t
=
=rj*+
=rS
∑ sen
i=
j
=rj*+
=rS = u%v ∑ wi
os
t
=rj*+
=rS
/ ∑ P
2
k
=k−1
=0 = / ∑ 2P/k
=k−1
=0
S = ao + a1 + ------+ an-1 =
Zy* Zszp{
+*{
= /
1−
2P
k
k−1 2P
k
1−
2P
k
)
= /
1− 2P
1−
2P
k
Se sabe que:

Msc. Widmar Aguilar
Mayo 2023
3 =
<|}*<z|}
w
=
<|}~<z|}
Se tiene:
= /
P
• − P− P €
2
P
k •
− P
k−
P
k‚
2
= /
P
•− − P+ P€
2
P
k•−
− P
k+
P
k‚
2
= /
<|ƒ ;<= i
<
|ƒ
t ;<=
ƒ
t
)
= /
<
|ƒz
|ƒ
t ∗;<= i
;<=
ƒ
t
)
= /
<|ƒ pzp/t ∗;<= i
;<=
ƒ
t
)
= P 1 − 1/k P
P
k
+ i P 1 − 1/k
;<= i
;<=
ƒ
t
Se toma:
P 1 − 1/k P
P
k
Para cualquier valor de N= vectores, se Kene:
2+
= „ cos …
2P
k
†
=rj*+
=rS
= P …1 −
1
k
†
P
,
P
k
.
= 0
Tomando:
P 1 − 1/k
;<= i
;<=
ƒ
t
Para cualquier valor de N= vectores, se Kene:

Msc. Widmar Aguilar
Mayo 2023
no
A
= ∑ sen ,
i=
j
.
=rj*+
=rS = P ,1 −
1
k
.
P
,
P
k
.
= 0
Q
⃗ = 2.6 ' %
a) −Q
⃗ = −2.6 '
Magnitud: d= 2.6 km
Dirección: opuesto a d
b)
‡
⃗
= ?
⃗ = ' ⃗ ; ' O % ) Q O O : paralelos
⃗ = 1
2
Q
⃗ ------- vector mitad
Magnitud: d/2

Msc. Widmar Aguilar
Mayo 2023
Dirección: la misma que d -------son paralelos con misma
dirección
c) -2.5 Q
⃗
Magnitud: 2.5 veces el vector d
Dirección: opuesta al vector d
a) 5 Q
⃗
Magnitud: 5 veces el vector d
Dirección: misma del vector d
Sea: ⃗
⃗ . ⃗ = | ⃗|| ⃗| 3
⃗ . ⃗ = | ⃗|| ⃗| cos 0
⃗ . ⃗ = | ⃗|| ⃗| ; | ⃗| =
⃗ . ⃗ =
⃗ . ⃗ =
b) ⃗ . J ⃗
Sea el productor cruz:

Msc. Widmar Aguilar
Mayo 2023
⃗ J ⃗ = | ⃗|| ⃗| 3 ------x definición
⃗ J ⃗ = 3
⃗ J ⃗ = 0
⃗ J ⃗ = 0 − − − 0 + 0
⃗ = 12 55 + 55 = 6.88 + 9.83
⃗ = 5.8
a) ⃗ . ⃗ = 6.88 5.8 + 9.83 0
⃗ . ⃗ = 39.9 5
⃗ ‰ ⃗ = Š
'
6.88 9.83 0
5.8 0 0
‹
⃗ ‰ ⃗ = −5.8 ∗ 9.83 '
⃗ ‰ ⃗ = -57.014K (u)

Msc. Widmar Aguilar
Mayo 2023
⃗ = 4.5 320 + 320 j
⃗ = 3.45 − 2.89 5
⃗ = 7.3 85 + 85
⃗ = 0.64 + 7.27
a) ⃗ . ⃗ =
⃗ . ⃗ = G G +( H H
⃗ . ⃗ = 3.45 0.64 + −2.89 7.27
⃗ . ⃗ = 2.208 − 21.01 =-18.8 u
b) ⃗ ‰ ⃗ = Š
'
3.45 − 2.89 0
0.64 7.27 0
‹
⃗ ‰ ⃗ = 3.45 ∗ 7.27 + 0.64 ∗ 2.89 '
⃗ ‰ ⃗ = 26.93 ' 5
Sea:
⃗ = G + H + a'
⃗ = G + H + a'
⃗. ⃗ = ( G + H + a' . G + H + a'

Msc. Widmar Aguilar
Mayo 2023
⃗. ⃗ = ( G G . + Œ G H• . + G a . ' +
( H G . + Œ H H• . + Œ H a• . ' +
( a G '. + Œ a H• '. + a a '. '
Donde: i.j =j.i =0
. ' = '. = 0
'. = . ' = 0
. = . = '. ' = 1
⃗. ⃗ = ( G G . + Œ G H• 0 + G a 0 +
( H G 0 + Œ H H• . + Œ H a• 0 +
( a G 0 + Œ a H• 0 + a a '. '
⃗. ⃗ = ( G G . + Œ H H• . + a a '. '
Luego:
⃗. ⃗ = ( G G + Œ H H• + a a
Sea:
⃗ = G + H + a'
⃗ = G + H + a'
⃗ ‰ ⃗ = Ž
'
G H a
G H a
•
Por conceptos de determinantes:

Msc. Widmar Aguilar
Mayo 2023
⃗ ‰ ⃗ = •
H a
H a
• − ‘
G a
G a
‘ + •
G H
G H
• '
⃗ ‰ ⃗ = Œ H a − a H• − G a − a G + Œ G H − H G•'
⃗ ‰ ⃗ = Œ H a − a H• + a G − G a + Œ G H − H G•'
Sea:
⃗ = G + H + a'
⃗ = G + H + a'
⃗ ‰ ⃗ = G x G + G J H + G J a' +
H x J + H J H + H J a'+
a' x J + a' J H + a' J a'
Donde: G x G = G G x i)
Así:
⃗ ‰ ⃗ = G G J +( G H J + G a J' +

Msc. Widmar Aguilar
Mayo 2023
H J J + K K J + K h J')+
a G 'J + ( a H 'J + a a 'J'
Además se cumple:
J = 0 ; J = 0 ; 'J' = 0
J = ' ; J = −'
J ' = − ; 'J =
J' − ; 'J = −
⃗ ‰ ⃗ = G G 0 +( G H ' + G a − +
H J −' + K K 0 + K h )+
a G + ( a H − + a a 0
⃗ ‰ ⃗ = ( G H ' − G a − H J ' + H a +
a G - ( a H
⃗ ‰ ⃗ = [ H a − a K] − [ J h − h J] +[ G H − H J] '
Se aprecia que cada paréntesis tiene cuatro elementos que salen de un
determinante 2 x 2:
•
H a
H a
• = H a − a K
⃗ ‰ ⃗ = •
H a
H a
• − ‘
G a
G a
‘ + •
G H
G H
• '
Los elementos i,j, k forman la primer fila de un determinante de orden 3 x
3, así:
⃗ ‰ ⃗ = Ž
'
G H a
G H a
•

Msc. Widmar Aguilar
Mayo 2023
De: ⃗. ⃗ = ∅
a = √3 + 3 + 3 = 5.196
b = √2 + 1 + 3 = 3.742
(3)(2)+3(1)+3(3) = 5.196*3.742cos ∅
∅ = 0.926
∅ = 22.2o
⃗ = 3 + 3 − 2'
⃗ = − − 4 + 2' ; ⃗ = 2 + 2 + '
a) ⃗. ⃗ J ⃗
⃗ J ⃗ = Š
'
−1 − 4 2
2 2 1
‹
⃗ J ⃗ = ‘
−4 2
2 1
‘ − ‘
−1 2
2 1
‘ + ‘
−1 − 4
2 2
‘ '
⃗ J ⃗ = −4 − 4 − −1 − 4 + −2 + 8 '
⃗ J ⃗ = −8 + 5 + 6'
⃗. Œ ⃗ J ⃗• = 3 −8 + 3 5 + −2 6
⃗. Œ ⃗ J ⃗• = −24 + 15 − 12 − 21

Msc. Widmar Aguilar
Mayo 2023
b) ⃗. ⃗ + ⃗
+ =−1+2 +−4+2 +2+1'
+ = −2 +3 '
⃗. Œ ⃗ + ⃗• = 3 + 3 − 2' . − 2 + 3 '
⃗. Œ ⃗ + ⃗• = 3 1 + 3 −2 + −2 3
⃗. Œ ⃗ + ⃗• = 3 − 6 − 6 = −9
c) ⃗ J ⃗ + ⃗
⃗ + ⃗ = −1 + 2 + −4 + 2 + 2 + 1 '
⃗ + ⃗ = − 2 + 3 '
⃗ JŒ ⃗ + ⃗• = Š
'
3 3 − 2
1 − 2 3
‹
⃗ JŒ ⃗ + ⃗• = ‘
3 − 2
−2 3
‘ − ‘
3 − 2
1 3
‘ + ‘
3 3
1 − 2
‘ '
⃗ JŒ ⃗ + ⃗• = 9 − 4 − 9 + 2 + −6 − 3 '
⃗ JŒ ⃗ + ⃗• = 5 − 11 − 9'
a) ⃗ = 5 + 4 − 6'
⃗ = −2 + 2 + 3' ; ⃗ = 4 + 3 + 2'
⃗ = 5 + 4 − 6' − −2 + 2 + 3' + 4 + 3 + 2'
⃗ = 5+2+4)i +(4-2+3)j + (-6-3+2)
⃗ = 11 + 5 − 7 '

Msc. Widmar Aguilar
Mayo 2023
b)
Cos ( =
{d
{
= −
W
√+ +~ >~-•
= −0.5
( = 1200
c)
⃗ = 5 + 4 − 6'
⃗ = −2 + 2 + 3'
⃗. ⃗ = (
= R5 + 4 + −6 = 8.775
= R −2 + 2 + 3 = 4.123
(5)(-2)+(4)(2)+(-6)(3)= 8.775 ∗ 4.123 (
-20 = 36.179 cos(
( = −0.553
( = 123.56o
`

Msc. Widmar Aguilar
Mayo 2023
Los vectores son:
⃗ = 4 ; ⃗ = 3
⃗ = 5 ( + (
sen3 =
:
>
; 3 = 36.87o
⃗ = 5 216.87 + 216.87
⃗ = −4 − 3
a) ⃗ . ⃗ = 4 0 + 0 3 = 0
b) ⃗ . ⃗ = 4 −4 + 0 −3 = −16
c) ⃗ . ⃗ = 0 −4 + 3 −3 = −9
Los vectores son:
⃗ = 4 ; ⃗ = 3
⃗ = 5 ( + (

Msc. Widmar Aguilar
Mayo 2023
sen3 =
:
>
; 3 = 36.87o
⃗ = 5 216.87 + 216.87
⃗ = −4 − 3
a) ⃗ J ⃗
⃗ J ⃗ = Š
'
4 0 0
0 3 0
‹
⃗ J ⃗ = ‘
4 0
0 3
‘ ' = 12 '
b) ⃗ J ⃗
⃗ J ⃗ = Š
'
4 0 0
−4 − 3 0
‹
⃗ J ⃗ = ‘
4 0
−4 − 3
‘ ' = −12 '
c) ⃗ J ⃗
⃗ J ⃗ = Š
'
0 3 0
−4 − 3 0
‹
⃗ J ⃗ = ‘
0 3
−4 − 3
‘ ' = 12 '

Msc. Widmar Aguilar
Mayo 2023
a) ⃗ . ⃗
`cos 27 =
Zd
Z
; a = 27 = 3.2 27
a = 2.85 5
cos 63 =
Z
Z
; H = 3.2 63
H = 1.453 5
⃗ = 1.453 j + 2.85 k
cos 42 =
–d
–
; a = 42 = 1.4 42
a = 1.04 5
cos48 =
–c
–
; G = 1.4 cos 48
G = 0.94 5
⃗ = 0.94 i + 1.04 k
⃗ . ⃗= (0.94)(0)+1.453(0)+(2.85)(1.04)
⃗ . ⃗ = 2.96 u2
b) ⃗ J ⃗ = Š
'
0 1.453 2.85
0.94 0 1.04
‹
⃗ J ⃗ = = 1.453 1.04 − 0.94 −2.85 − 0.94 ∗ 1.453'
⃗ J ⃗ = = 1.51 + 2.68 − 1.37'
c)
⃗ . ⃗ = (
= √1.453 + 2.85 = 3.2
= √0.94 + 1.04 = 1.4

Msc. Widmar Aguilar
Mayo 2023
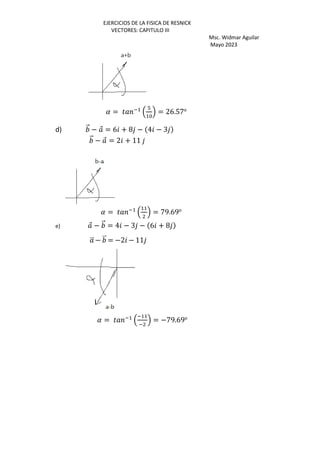
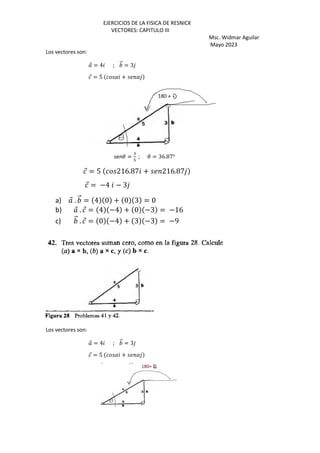
2.96= 3.2*1.4cos(
cos ( = 0.6607
( = 48.64o
⃗. ⃗ = ⃗. ⃗
De: ⃗. ⃗ = 3
⃗. ⃗ = 3 ------------------conmutativa en Reales
Pero: ⃗. ⃗ = 3
Luego:
⃗. ⃗ = ⃗. ⃗
b.) De: ⃗. ⃗ + ⃗ =
= Œ G + H + a'•. G + H + a' + G + H + a'
= Œ G + H + a'•. [ G + G + H + H + a + a ']
Por propiedad del producto escalar:

Msc. Widmar Aguilar
Mayo 2023
= G G + G + HŒ H + H• + a a + a
= G G + G G + H H + H H + a a + a a
Por propiedad conmutativa de la suma:
= G G + H H + a a + G G + H H + a a
Usando la propiedad asociativa de los números reales:
= G G + H H + a a + G G + H H + a a
⃗. ⃗ + —
⃗ = ⃗. ⃗ + ⃗. —
⃗
c.) De: ⃗ J ⃗ + ⃗
⃗ J ⃗ + ⃗ = Ž
'
G H a
G + G H + H a + a
•
⃗ J ⃗ + ⃗ = •
H a
H + H a + a
• − ‘
G a
G + G a + a
‘ +
•
G H
G + G H + H
• '
⃗ J ⃗ + ⃗ = ˜ H a + a − aŒ H + H•™ − [ G a + a −
a G + G ] + ˜ GŒ H + H• − H G + G ™k
⃗ J ⃗ + ⃗ = ˜ H a + H a − a H − a H™ − [ G a + G a − a G −
a G] + ˜ G H + G H − H G − H G™k
⃗ J ⃗ + ⃗ = { ( H a − a H − G a − a G + G H − H G k} +
{( H a − a H − G a − a G + G H − H G k}
Al termino:
H a − a H , Jœ % : •
H a
H a
• , í:
⃗ J ⃗ + ⃗ = {•
H a
H a
• − ‘
G a
G a
‘ + •
G H
G H
• '} +
{‘
H a
H a
‘ − ‘
G a
G a
‘ + ‘
G H
G H
‘ '}

Msc. Widmar Aguilar
Mayo 2023
Donde:
⃗ J ⃗ = •
H a
H a
• − ‘
G a
G a
‘ + •
G H
G H
• '
⃗ J ⃗ = Ž
'
G H a
G H a
•
⃗ J ⃗ = ‘
H a
H a
‘ − ‘
G a
G a
‘ + ‘
G H
G H
‘ '
⃗ J ⃗ = Ž
'
G H a
G H a
•
Por tanto, se tiene:
⃗ Ÿ ⃗ + —
⃗ = ⃗ Ÿ ⃗ + ⃗ Ÿ —
⃗
De: ⃗ J ⃗ = | ⃗ | ⃗ ∅
Del triángulo de la figura:
∅ =
–
; ℎ = ∅ = ⃗ ∅
⃗ J ⃗ = | ⃗ | ⃗ ∅
⃗ J ⃗ = | ⃗ |ℎ
Se sabe que el área de un triángulo es: A= (1/2) a*h
+
⃗ J ⃗ =
+
| ⃗ |ℎ

Msc. Widmar Aguilar
Mayo 2023
=
+
⃗ J ⃗
Se conoce que el área de paralelogramo: A = a*h
∅ =
ℎ
; ℎ = ∅ = ⃗ ∅
⃗ J ⃗ = | ⃗ | ⃗ ∅
⃗ J ⃗ = | ⃗ |ℎ
Por tanto:
A= ⃗ J ⃗

Msc. Widmar Aguilar
Mayo 2023
⃗ . ⃗J ⃗ = | ⃗| ⃗ J ⃗ 3
3 =
Z
; ℎ = 3
⃗ . ⃗J ⃗ = | ⃗| 3 ⃗ J ⃗
⃗ . ⃗J ⃗ = ℎ ⃗ J ⃗
⃗ J ⃗ = –Z;<
⃗ . ⃗J ⃗ = ℎ –Z;<
¢ = ⃗ . ⃗J ⃗
⃗ = G + H = 3.2 + 1.6
⃗ = G + H = 0.5 + 4.5
a) ⃗ . ⃗ = 3

Msc. Widmar Aguilar
Mayo 2023
= √3.2 + 1.6 = 3.58
= √0.5 + 4.5 = 4.53
(3.2)(0.5)+(1.6((4.5)= 3.58*4.53 3
3 = 0.543
3 = 57.14o
b)
⃗ = G + H
⃗ . ⃗ = 0 = 3.2 G + 1.6 H
3.2 G = −1.6 H
H = −2 G
R G + H = 5
G + Œ−2 H• = 25
G + 4 G =25
5 G = 25
G = 5
G = ±2.236
H = −2 G = −4.722
H = −2 G = 4.472
⃗ = G + H
⃗ = 2.236 − 4.472 ; ó
⃗ = −2.236 + 4.472

Msc. Widmar Aguilar
Mayo 2023
5
⃗ = + + '
¤
⃗ = − 0 + − 0 + 0 − 'v
¤
⃗ = + − '
5 = √ + + = √3
¤ = R + + − = √3
5
⃗. ¤
⃗ = 5 ∗ ¤ 3
+ − = √3Œ √3• 3
= 3 3
3 =
+
:
3 = 70.53o
| ⃗| = 3 ; ⃗ = 4 ; |⃗| = 10

Msc. Widmar Aguilar
Mayo 2023
` a) ⃗ = cos0 + 0
⃗ = 3 cos 0 + 3 0 = 3
X= 3 ; y=0
⃗ = cos3 0 + 30
⃗ = 4 cos 30 + 4 30 = 3.46 + 2
J = 3.46 ; K = 2
⃗ = cos 120 + 120
⃗ = 10 cos 120 + 10 120 = −5 + 8.66
J = −5 ; K = 8.66
b.) ⃗ = œ ⃗ + ¥ ⃗
−5 + 8.66 = œ 3 + ¥ 3.46 + 2
−5 + 8.66 = 3œ + 3.46¥ + ¥ 2
Por tanto se tienen las ecuaciones:
I
−5 = 3œ + 3.46¥
8.66 = 2¥
De donde: 8.66 = 2¥
¥ = 4.33
-5= 3p+3.46(4.33)
3p = -19.98
p = - 6.66

Msc. Widmar Aguilar
Mayo 2023
El esquema con la rotación de los ejes:
En XY se tienen vectores i, j
En X’Y’se tienen u,v
|5
⃗| = 1 ; |¤
⃗| = 1 − − − −5 )
Se debe poner u, v en términos de los vectores i, j, así:
¤
⃗ = − ? + ?
5
⃗ = ? + ?
El punto P en XY:
⃗ = G + H
El punto P en X’Y’:
⃗= Gb5 + Hb¤
⃗= G¦ ? + ? + Hb − ? + ?
⃗= G¦ ? + G¦ ? − Hb ? + H¦ ?
⃗= G¦ ? − Hb ? + G¦ ? + H¦ ?
Se tiene:

Msc. Widmar Aguilar
Mayo 2023
G + H = G¦ ? − Hb ? + G¦ ? + H¦ ?
Igualando los términos respectivos:
§
G = G¦ ? − Hb ?
H = G¦ ? + H¦ ?
Ahora; G¦ =
Zc~Z¦;<=¨
©ª;¨
-------(1)
G¦ =
Z*Z¦©ª;¨
;<=¨
-------(2)
Igualando (1) y (2):
Zc~Z¦;<=¨
©ª;¨
=
Z*Z¦©ª;¨
;<=¨
?Œ G + H¦ ?• = ? H − H¦ ?
G ? + H¦ ? = H ? − H¦ ?
H¦ ? + H¦ ? = H ? − G ?
H¦ ? + ? = H ? − G ?
? + ? = 1
H¦ = H ? − G ?
De: H¦ =
*Zc~Zc¦©ª;¨
;<=¨
-------(3)
G¦ =
Z*Zc¦;<=¨
©ª;¨
-------(4)
Igualando (4) y (3):
*Zc~Zc¦©ª;¨
;<=¨
=
Z*Zc¦;<=¨
©ª;¨
? − G + G¦ ? = ? H − G¦ ?
− G ? + G¦ ? = ? H − G¦ ?
G¦ ? + ? = H ? + G ?
G¦ = G ? + H ?

Msc. Widmar Aguilar
Mayo 2023
« J′ = J ? + K ?
H
b
= − J ? + K ?
Este problema es una aplicación de lo obtenido en el problema 51:
a) ⃗ = cos 56 + 56
⃗ = 17 56 + 56
⃗ = 9.5 + 14.09 ; ? = 18
« J′ = J ? + K ?
H
b
= − J ? + K ?
§ J′ = 9.5 18 + 14.09 18
H
b
= −9.5 18 + 14.09 18
§ J′ = 13.39
H
b
= 10.46

Msc. Widmar Aguilar
Mayo 2023
Se conoce que:
⃗ = G + H
⃗ = G + H
⃗ + ⃗ = G + G + Œ H + H•
‘ ⃗ + ⃗ ‘ = F J + J + K + K ----------------------(1)
Además: « J′ = J ? + K ?
H
b
= − J ? + K ?
⃗ = J′ 5 + K′¤

Msc. Widmar Aguilar
Mayo 2023
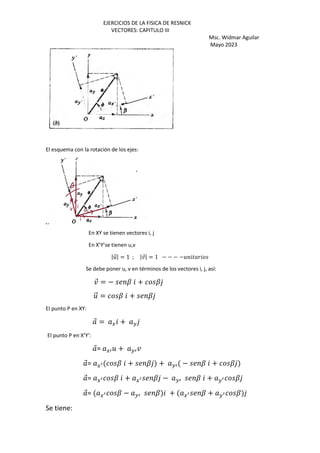
⃗ = Œ J ? + K ?•5 + Œ− J ? + K ?•¤
⃗ = Œ J ? + K ?•5 + Œ− J ? + K ?•¤
⃗ + ⃗ = [ J ? + K ? + G ? + H ?]5 +
[− G ? + H ? − G ? + H ?[¤
⃗ + ⃗ = [ J + J ? + K + K ?]5 +
[ − J − J ? + K + K ?]¤
‘ ⃗ + ⃗ ‘ =
F[ J + J ? + K + K ?] + [− J + J ? + K + K ?]
Donde:
[ J + J ? + K + K ?] =
= [ J + J ?+ K + K ? + 2 J + J ? ∗ K + K ?]
[− J + J ? + K + K ?] =
= [ J + J ?+ K + K ? − 2 J + J ? ∗ K + K ?]
Se tiene:
[ J + J ? + K + K ?] + [− J + J ? + K + K ?]
= [ J + J ?+ K + K ? + 2 J + J ? ∗ K + K ?]+
[ J + J ?+ K + K ? − 2 J + J ? ∗ K + K ?]
= J + J ?+ ? + K + K ? + ?
Finalmente:
‘ ⃗ + ⃗ ‘ = F J + J ? + ? + K + K ? + ?
? + ? = 1
‘ ⃗ + ⃗ ‘ = F J + J + K + K -----------------------(2)
De (1) y (2), se concluye que:
‘ ⃗ + ⃗‘
G
= ‘ ⃗ + ⃗‘
Gb

VECTORES_RESNICK.pdf

Más contenido relacionado

La actualidad más candente

Similar a VECTORES_RESNICK.pdf

Más de Widmar Aguilar González

Último

VECTORES_RESNICK.pdf