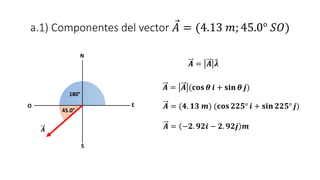
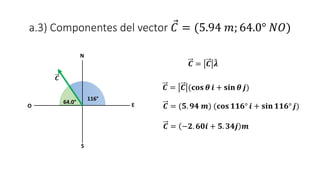
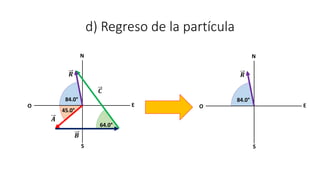
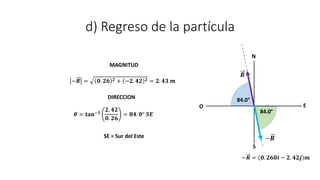
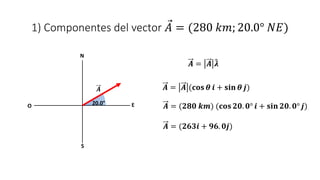
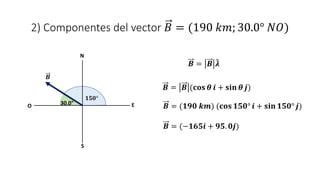
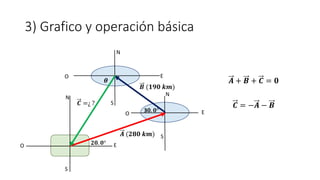
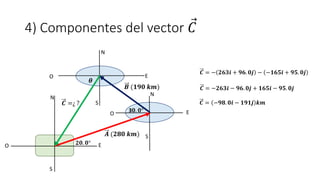
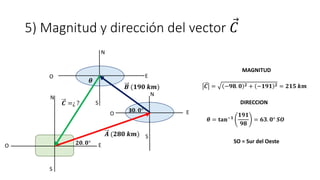
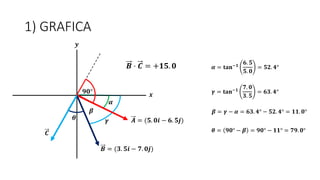
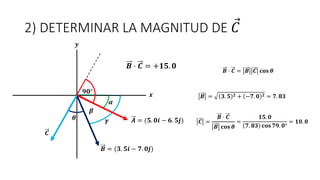
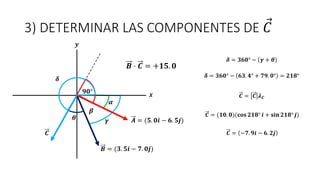
Este documento presenta tres ejemplos de problemas de vectores en física. El primer ejemplo involucra el cálculo del desplazamiento resultante y regreso de una partícula que se mueve en tres etapas. El segundo ejemplo calcula la distancia y dirección entre un lago y una base aérea luego de que un avión vuela entre dos lagos. El tercer ejemplo determina las componentes de un vector perpendicular a dos otros vectores dados su producto escalar.

1. TEMA 5: APLICACIONES
DE VECTORES
UNIDAD 2: VECTORES
FISICA BASICA (05/08/2022)
ING. RODOLFO QUIROA
SEGUNDO SEMESTRE 2022

2. EJEMPLO # 1
Una partícula experimenta tres desplazamientos
sucesivos en un plano, los cuales se describen a
continuación: 4.13 m al Sur del Oeste; 5.26 m al
Este y 5.94 m 64.0° al Norte del Oeste. Elija el
eje “x” apuntando al Este y el eje “y” apuntando
al Norte.
a) Encuentre las componentes de cada
desplazamiento.
b) Encuentre las componentes del
desplazamiento resultante.
c) Encuentre la magnitud y dirección del
desplazamiento resultante.
d) Encuentre el desplazamiento que se
requiere para traer de nuevo a la partícula
al punto de arranque.

3. a.1) Componentes del vector 𝐴 = (4.13 𝑚; 45.0° 𝑆𝑂)
45.0°
𝑨 = 𝑨 𝝀
𝑨 = 𝑨 (𝐜𝐨𝐬 𝜽 𝒊 + 𝐬𝐢𝐧 𝜽 𝒋)
𝑨 = (𝟒. 𝟏𝟑 𝒎) (𝐜𝐨𝐬 𝟐𝟐𝟓° 𝒊 + 𝐬𝐢𝐧 𝟐𝟐𝟓° 𝒋)
𝑨 = −𝟐. 𝟗𝟐𝒊 − 𝟐. 𝟗𝟐𝒋 𝒎
𝑨
N
E
S
O
180°

4. a.2) Componentes del vector 𝐵 = (5.26 𝑚; 𝐸)
0.0°
𝑩 = 𝑩 𝝀
𝑩 = 𝑩 (𝐜𝐨𝐬 𝜽 𝒊 + 𝐬𝐢𝐧 𝜽 𝒋)
𝑩 = (𝟓. 𝟐𝟔 𝒎) (𝐜𝐨𝐬 𝟎. 𝟎° 𝒊 + 𝐬𝐢𝐧 𝟎. 𝟎° 𝒋)
𝑩 = +𝟓. 𝟐𝟔𝒊 𝒎
𝑩
N
E
S
O

5. a.3) Componentes del vector 𝐶 = (5.94 𝑚; 64.0° 𝑁𝑂)
64.0°
𝑪 = 𝑪 𝝀
𝑪 = 𝑪 (𝐜𝐨𝐬 𝜽 𝒊 + 𝐬𝐢𝐧 𝜽 𝒋)
𝑪 = (𝟓. 𝟗𝟒 𝒎) (𝐜𝐨𝐬 𝟏𝟏𝟔° 𝒊 + 𝐬𝐢𝐧 𝟏𝟏𝟔° 𝒋)
𝑪 = −𝟐. 𝟔𝟎𝒊 + 𝟓. 𝟑𝟒𝒋 𝒎
𝑪
N
E
S
O
116°

6. B y C) Desplazamiento resultante
𝑹 = 𝑨 + 𝑩 + 𝑪
𝑹 = −𝟐. 𝟗𝟐𝒊 − 𝟐. 𝟗𝟐𝒋 + 𝟓. 𝟐𝟔𝒊 + −𝟐. 𝟔𝟎𝒊 + 𝟓. 𝟑𝟒𝒋
𝑹 = −𝟐. 𝟗𝟐 + 𝟓. 𝟐𝟔 − 𝟐. 𝟔𝟎 𝒊 + −𝟐. 𝟗𝟐 + 𝟓. 𝟑𝟒 𝒋
𝑹 = −𝟎. 𝟐𝟔𝟎𝒊 + 𝟐. 𝟒𝟐𝒋 𝒎
COMPONENTES
𝑹 = −𝟎. 𝟐𝟔 𝟐 + 𝟐. 𝟒𝟐 𝟐 = 𝟐. 𝟒𝟑 𝒎
𝜽 = 𝐭𝐚𝐧−𝟏
𝟐. 𝟒𝟐
𝟎. 𝟐𝟔
= 𝟖𝟒. 𝟎° 𝑵𝑶
MAGNITUD
DIRECCION
NO = Norte del Oeste

7. d) Regreso de la partícula
45.0°
𝑨
N
E
S
O
𝑩
64.0°
𝑪
𝑹
84.0°
N
E
S
O
𝑹
84.0°

8. d) Regreso de la partícula
N
E
S
O
𝑹
84.0°
−𝑹
84.0°
−𝑹 = 𝟎. 𝟐𝟔 𝟐 + −𝟐. 𝟒𝟐 𝟐 = 𝟐. 𝟒𝟑 𝒎
𝜽 = 𝐭𝐚𝐧−𝟏
𝟐. 𝟒𝟐
𝟎. 𝟐𝟔
= 𝟖𝟒. 𝟎° 𝑺𝑬
MAGNITUD
DIRECCION
SE = Sur del Este
−𝑹 = 𝟎. 𝟐𝟔𝟎𝒊 − 𝟐. 𝟒𝟐𝒋 𝒎

9. EJEMPLO # 2
Un avión vuela desde la base
hacia un lago A que se encuentra
ubicado a 280 km de distancia en
la dirección 20.0° al noreste.
Después de soltar los suministros
vuela a un lago B que esta a 190
km a 30.0° al noroeste del lago A.
Determine la distancia y la
dirección desde el lago B a la base.

10. 1) Componentes del vector 𝐴 = (280 𝑘𝑚; 20.0° 𝑁𝐸)
20.0°
𝑨 = 𝑨 𝝀
𝑨 = 𝑨 (𝐜𝐨𝐬 𝜽 𝒊 + 𝐬𝐢𝐧 𝜽 𝒋)
𝑨 = (𝟐𝟖𝟎 𝒌𝒎) (𝐜𝐨𝐬 𝟐𝟎. 𝟎° 𝒊 + 𝐬𝐢𝐧 𝟐𝟎. 𝟎° 𝒋)
𝑨 = (𝟐𝟔𝟑𝒊 + 𝟗𝟔. 𝟎𝒋)
𝑨
N
E
S
O

11. 2) Componentes del vector 𝐵 = (190 𝑘𝑚; 30.0° 𝑁𝑂)
30.0°
𝑩 = 𝑩 𝝀
𝑩 = 𝑩 (𝐜𝐨𝐬 𝜽 𝒊 + 𝐬𝐢𝐧 𝜽 𝒋)
𝑩 = (𝟏𝟗𝟎 𝒌𝒎) (𝐜𝐨𝐬 𝟏𝟓𝟎° 𝒊 + 𝐬𝐢𝐧 𝟏𝟓𝟎° 𝒋)
𝑩 = (−𝟏𝟔𝟓𝒊 + 𝟗𝟓. 𝟎𝒋)
𝑩
N
E
S
O
𝟏𝟓𝟎°

12. 3) Grafico y operación básica
S
S
S
E
E
E
O
O
O
N
N
N
𝑪 =¿ ?
𝑩 (𝟏𝟗𝟎 𝒌𝒎)
𝑨 (𝟐𝟖𝟎 𝒌𝒎)
3𝟎. 𝟎°
𝟐𝟎. 𝟎°
𝜽 𝑨 + 𝑩 + 𝑪 = 𝟎
𝑪 = −𝑨 − 𝑩

13. 4) Componentes del vector 𝐶
𝑪 = − 𝟐𝟔𝟑𝒊 + 𝟗𝟔. 𝟎𝒋 − −𝟏𝟔𝟓𝒊 + 𝟗𝟓. 𝟎𝒋
𝑪 = −𝟐𝟔𝟑𝒊 − 𝟗𝟔. 𝟎𝒋 + 𝟏𝟔𝟓𝒊 − 𝟗𝟓. 𝟎𝒋
𝑪 = −𝟗𝟖. 𝟎𝒊 − 𝟏𝟗𝟏𝒋 𝒌𝒎
S
S
S
E
E
E
O
O
O
N
N
N
𝑪 =¿ ?
𝑩 (𝟏𝟗𝟎 𝒌𝒎)
𝑨 (𝟐𝟖𝟎 𝒌𝒎)
3𝟎. 𝟎°
𝟐𝟎. 𝟎°
𝜽

14. 5) Magnitud y dirección del vector 𝐶
𝑪 = −𝟗𝟖. 𝟎 𝟐 + −𝟏𝟗𝟏 𝟐 = 𝟐𝟏𝟓 𝒌𝒎
𝜽 = 𝐭𝐚𝐧−𝟏
𝟏𝟗𝟏
𝟗𝟖
= 𝟔𝟑. 𝟎° 𝑺𝑶
MAGNITUD
DIRECCION
S
S
S
E
E
E
O
O
O
N
N
N
𝑪 =¿ ?
𝑩 (𝟏𝟗𝟎 𝒌𝒎)
𝑨 (𝟐𝟖𝟎 𝒌𝒎)
3𝟎. 𝟎°
𝟐𝟎. 𝟎°
𝜽
SO = Sur del Oeste

15. EJEMPLO # 3
Considere los siguientes vectores:
𝐴 = (5.0𝑖 − 6.5𝑗) 𝑦 𝐵 = (3.5𝑖 − 7.0𝑗)
Un tercer vector 𝐶 esta en el plano
“x-y” y es perpendicular a 𝐴 y el
producto escalar de 𝐶 𝑐𝑜𝑛 𝐵 es
+15.0 Con esta información,
obtenga las componentes del vector
𝐶.

16. 1) GRAFICA
𝑩 ⋅ 𝑪 = +𝟏𝟓. 𝟎
𝒚
𝒙
𝑨 = (𝟓. 𝟎𝒊 − 𝟔. 𝟓𝒋)
𝑪
𝑩 = (𝟑. 𝟓𝒊 − 𝟕. 𝟎𝒋)
𝜽
𝟗𝟎°
𝜷
𝜶
𝜸
𝜶 = 𝐭𝐚𝐧−𝟏
𝟔. 𝟓
𝟓. 𝟎
= 𝟓𝟐. 𝟒°
𝜸 = 𝐭𝐚𝐧−𝟏
𝟕. 𝟎
𝟑. 𝟓
= 𝟔𝟑. 𝟒°
𝜷 = 𝜸 − 𝜶 = 𝟔𝟑. 𝟒° − 𝟓𝟐. 𝟒° = 𝟏𝟏. 𝟎°
𝜽 = 𝟗𝟎° − 𝜷 = 𝟗𝟎° − 𝟏𝟏° = 𝟕𝟗. 𝟎°

17. 2) DETERMINAR LA MAGNITUD DE 𝐶
𝑩 ⋅ 𝑪 = 𝑩 𝑪 𝐜𝐨𝐬 𝜽
𝑩 = 𝟑. 𝟓 𝟐 + −𝟕. 𝟎 𝟐 = 𝟕. 𝟖𝟑
𝑪 =
𝑩 ⋅ 𝑪
𝑩 𝐜𝐨𝐬 𝜽
=
𝟏𝟓. 𝟎
𝟕. 𝟖𝟑 𝐜𝐨𝐬 𝟕𝟗. 𝟎°
= 𝟏𝟎. 𝟎
𝑩 ⋅ 𝑪 = +𝟏𝟓. 𝟎
𝒚
𝒙
𝑨 = (𝟓. 𝟎𝒊 − 𝟔. 𝟓𝒋)
𝑪
𝑩 = (𝟑. 𝟓𝒊 − 𝟕. 𝟎𝒋)
𝜽
𝟗𝟎°
𝜷
𝜶
𝜸

18. 3) DETERMINAR LAS COMPONENTES DE 𝐶
𝜹
𝜹 = 𝟑𝟔𝟎° − 𝜸 + 𝜽
𝑪 = 𝑪 𝝀𝑪
𝑪 = (𝟏𝟎. 𝟎)(𝐜𝐨𝐬 𝟐𝟏𝟖° 𝒊 + 𝐬𝐢𝐧 𝟐𝟏𝟖° 𝒋)
𝑪 = −𝟕. 𝟗𝒊 − 𝟔. 𝟐𝒋
𝑩 ⋅ 𝑪 = +𝟏𝟓. 𝟎
𝒚
𝒙
𝑨 = (𝟓. 𝟎𝒊 − 𝟔. 𝟓𝒋)
𝑪
𝑩 = (𝟑. 𝟓𝒊 − 𝟕. 𝟎𝒋)
𝜽
𝟗𝟎°
𝜷
𝜶
𝜸
𝜹 = 𝟑𝟔𝟎° − 𝟔𝟑. 𝟒° + 𝟕𝟗. 𝟎° = 𝟐𝟏𝟖°

19. Repaso de Conceptos
• Realiza la lectura del capitulo 1 del libro de texto, de las paginas 1 a la
24.
• De la tarea # 1, elabora los ejercicios 1.60, 1.64, 1.69 y 1.75 de las
paginas 30 y 31 del libro de texto.
• FECHA DE ENTREGA DE LA TAREA # 1: VIERNES 12 DE AGOSTO DE
2022