El documento presenta dos problemas de mecánica vectorial. El primero involucra tres cables (A, B y C) que sostienen una columna, donde se pide hallar la magnitud de la fuerza en el cable A dado que la suma total de las fuerzas es 400 kN. El segundo problema consiste en (a) hallar el ángulo entre dos vectores dados y (b) calcular el producto vectorial de los mismos vectores.

1. Universidad Fermín Toro
Facultad de Mantenimiento Mecánico
Mecánica Estática
Actividad N° 01
1.- Los Cables A, B y C ayudan a soportar una columna de una estructura. Las
Magnitudes de las Fuerzas ejercidas por los Cables son iguales AF = BF = CF
La Magnitud de la Suma Vectorial de las tres Fuerzas es de 400 kN ¿Que valor
tiene AF ?
Solución:
La resultante o suma vectorial de los tres vectores en los cables que sostienen la estructura
se obtiene en la forma:
𝐹⃗ = 𝐹⃗𝐴 + 𝐹⃗𝐵 + 𝐹⃗𝐶
En donde:
10m
A B C
3m 3m 3m

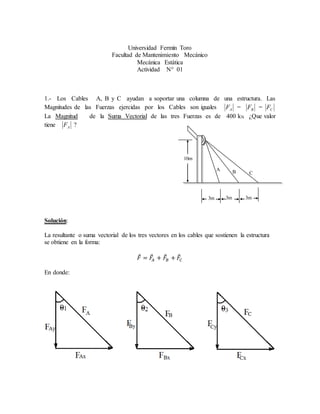
2. 𝐹⃗𝐴 = 𝐹𝐴 𝑠𝑒𝑛𝜃1 𝑖 − 𝐹𝐴 𝑐𝑜𝑠𝜃1 𝑗 ; 𝐹⃗𝐵 = 𝐹𝐵 𝑠𝑒𝑛𝜃2 𝑖 − 𝐹𝐵 𝑐𝑜𝑠𝜃2 𝑗 ; 𝐹⃗𝐶 = 𝐹𝐶 𝑠𝑒𝑛𝜃3 𝑖 − 𝐹𝐶 𝑐𝑜𝑠𝜃3 𝑗
Luego:
𝐹⃗ = ( 𝐹𝐴 𝑠𝑒𝑛𝜃1 + 𝐹𝐵 𝑠𝑒𝑛𝜃2 + 𝐹𝐶 𝑠𝑒𝑛𝜃3) 𝑖 − ( 𝐹𝐴 𝑐𝑜𝑠𝜃1 + 𝐹𝐵 𝑐𝑜𝑠𝜃2 + 𝐹𝐶 𝑐𝑜𝑠𝜃3 ) 𝑗
Además se sabe que
𝐹𝐴 = 𝐹𝐵 = 𝐹𝐶
Entonces:
𝐹⃗ = 𝐹𝐴 [( 𝑠𝑒𝑛𝜃1 + 𝑠𝑒𝑛𝜃2 + 𝑠𝑒𝑛𝜃3)i- ( 𝑐𝑜𝑠𝜃1 + 𝑐𝑜𝑠𝜃2 + 𝑐𝑜𝑠𝜃3)j]
La magnitud de F es por lo tanto:
𝐹 = 𝐹𝐴 √( 𝑠𝑒𝑛𝜃1 + 𝑠𝑒𝑛𝜃2 + 𝑠𝑒𝑛𝜃3)2 + ( 𝑐𝑜𝑠𝜃1 + 𝑐𝑜𝑠𝜃2 + 𝑐𝑜𝑠𝜃3 )2 (1)
Por otro lado:
𝑡𝑎𝑛𝜃1 =
3
10
; 𝜃1 = 16,7°; 𝑡𝑎𝑛𝜃2 =
6
10
; 𝜃2 = 30,96°; 𝑡𝑎𝑛𝜃3 =
9
10
; 𝜃3 = 41,99°

3. Sustituyendo los valores de los ángulos en la ecuación 1 y resolviendo la raíz nos queda que
𝐹 = 2,951𝐹𝐴 → 𝐹𝐴 =
𝐹
2,951
=
400
2,951
→ 𝐹𝐴 = 135,55 𝐾𝑁
2.- a) Ejercicio Hallar el ángulo formado por los vectores
A = 2ˆı + 3ˆj − ˆk, B = 5ˆı −3ˆj + 2ˆk.
Solución:
El producto escalar de los vectores A y B viene dado por:
𝐴⃗ ∙ 𝐵⃗⃗ = 𝐴𝐵𝑐𝑜𝑠𝜃 → 𝜃 = 𝑐𝑜𝑠−1
(
𝐴⃗ ∙ 𝐵⃗⃗
𝐴𝐵
)
En donde 𝜃 es el ángulo formado por los vectores A y B.
Entonces:
𝐴⃗ ∙ 𝐵⃗⃗ = (2)(5) + (3)(−3)+ (−1)(2) = 10 − 9 − 2 = −1
𝐴 = √(2)2 + (3)2 + (−1)2 = √14; 𝐵 = √(5)2 + (−3)2 + (2)2 = √38
𝜃 = 𝑐𝑜𝑠−1
(
−1
√14√38
) 𝜃 = 92,48°

4. b) Hallar el Producto Vectorial
A = 2ˆı + 3ˆj − ˆk, B = 5ˆı −3ˆj + 2ˆk
Solución:
El producto vectorial de los vectores A y B, se obtiene en la forma:
𝐴⃗ 𝑥𝐵⃗⃗ = |
𝑖 𝑗 𝑘
2 3 −1
5 −3 2
|
𝑖 𝑗
2 3
5 −3
= 6𝑖 − 5𝑗 − 6𝑘 − (15𝑘 + 3𝑖 + 4𝑗)
𝐴⃗ 𝑥𝐵⃗⃗ = 3𝑖 − 9𝑗 − 21𝑘