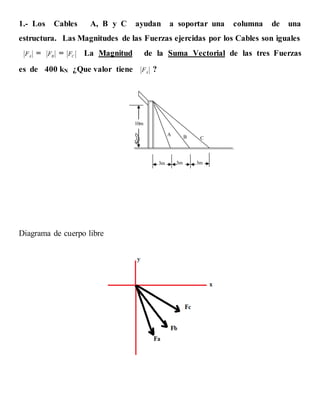
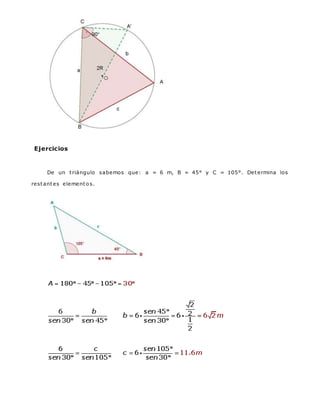
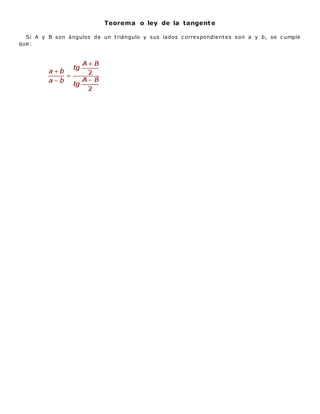El documento presenta dos ejercicios de mecánica estática. El primero involucra tres cables (A, B, C) que sostienen una columna, donde la fuerza de cada cable es igual a 135.5 kN. El segundo ejercicio involucra hallar el ángulo entre dos vectores y calcular su producto vectorial.

1. Universidad Fermín Toro
Vice Rectorado Académico
Facultad de Ingeniería
Tarea 1
Mecanica Estatica
Integrante:
• RieraRafael C.I:18.925.921
Cabudare,12/05/2016

2. 1.- Los Cables A, B y C ayudan a soportar una columna de una
estructura. Las Magnitudes de las Fuerzas ejercidas por los Cables son iguales
AF = BF = CF La Magnitud de la Suma Vectorial de las tres Fuerzas
es de 400 kN ¿Que valor tiene AF ?
Diagrama de cuerpo libre
10m
A B C
3m 3m 3m

3. Descomposición de fuerzas
Para 𝐹𝑎
ℎ = √102 + 32 = √109
𝐹𝑎𝑥 = | 𝐹𝑎| ∗ 𝑠𝑒𝑛( 𝛼) = | 𝐹𝑎| ∗
3
√109
=
3
√109
| 𝐹𝑎|
𝐹𝑎𝑦 = −| 𝐹𝑎| ∗ 𝑐𝑜𝑠( 𝛼) = −| 𝐹𝑎| ∗
10
√109
= −
10
√109
| 𝐹𝑎|
Para 𝐹𝑏
ℎ = √102 + 62 = √136
𝐹𝑏𝑥 = | 𝐹𝑏| ∗ 𝑠𝑒𝑛( 𝛼) = | 𝐹𝑎| ∗
6
√136
=
6
√136
| 𝐹𝑎|
𝐹𝑏𝑦 = −| 𝐹𝑏| ∗ 𝑐𝑜𝑠( 𝛼) = −| 𝐹𝑎| ∗
10
√136
= −
10
√136
| 𝐹𝑎|

4. Para 𝐹𝑐
ℎ = √102 + 92 = √181
𝐹𝑐𝑥 = | 𝐹𝑐| ∗ 𝑠𝑒𝑛( 𝛼) = | 𝐹𝑎| ∗
9
√181
=
9
√181
| 𝐹𝑎|
𝐹𝑐𝑦 = −| 𝐹𝑐| ∗ 𝑐𝑜𝑠( 𝛼) = −| 𝐹𝑎| ∗
10
√181
= −
10
√181
| 𝐹𝑎|
Sumatoria de fuerzas
𝑅 𝑥 = 𝐹𝑎𝑥 + 𝐹𝑏𝑥 + 𝐹𝑐𝑥
𝑅 𝑥 =
3
√109
| 𝐹𝑎| +
6
√136
| 𝐹𝑎| +
9
√181
| 𝐹𝑎| = 1.471| 𝐹𝑎|
𝑅 𝑦 = 𝐹𝑎𝑦 + 𝐹𝑏𝑦 + 𝐹𝑐𝑦
𝑅 𝑦 = −
10
√109
| 𝐹𝑎| −
10
√136
| 𝐹𝑎| −
10
√181
| 𝐹𝑎| = −2.559| 𝐹𝑎|
Modulo de fuerza resultante
| 𝑅| = √𝑅 𝑥
2
+ 𝑅 𝑦
2
400𝑘𝑁 = √(1.471| 𝐹𝑎|)2 + (−2.559| 𝐹𝑎|)2
400𝑘𝑁 = √2.164(| 𝐹𝑎|)2 + 6.548(| 𝐹𝑎|)2

5. 400𝑘𝑁 = √8.712(| 𝐹𝑎|)2
400𝑘𝑁 = √8.712√(| 𝐹𝑎|)2
400𝑘𝑁 = 2.952| 𝐹𝑎|
| 𝐹𝑎| =
400𝑘𝑁
2.952
| 𝐹𝑎| = 135.501𝑘𝑁
2.- a) Ejercicio Hallar el ángulo formado por los vectores
A = 2ˆı + 3ˆj − ˆk, B = 5ˆı −3ˆj + 2ˆk.
Modulo de los vectores
| 𝐴̅| = √(2)2 + (3)2 + (−1)2 = √4 + 9 + 1 = √14
| 𝐵̅| = √(5)2 + (−3)2 + (2)2 = √25 + 9 + 4 = √38
Multiplicación escalar entre los vectores
𝐴̅ ∗ 𝐵̅ = (2𝑖 + 3𝑗 − 𝑘) ∗ (5𝑖 − 3𝑗 + 2𝑘)
𝐴̅ ∗ 𝐵̅ = 2 ∗ 5 + 3 ∗ (−3) + (−1) ∗ 2
𝐴̅ ∗ 𝐵̅ = 10 − 9 − 2
𝐴̅ ∗ 𝐵̅ = −1
Angulo entre los vectores
𝜃 = cos−1 (
𝐴̅ ∗ 𝐵̅
| 𝐴̅| ∗ | 𝐵̅|
)
𝜃 = cos−1 (
−1
√14 ∗ √38
)
𝜃 = cos−1 (
−1
√532
)
𝜃 = 92.48°

6. b) Hallar el Producto Vectorial
A = 2ˆı + 3ˆj − ˆk, B = 5ˆı −3ˆj + 2ˆk
𝐴̅ 𝑥 𝐵̅ = |
𝑖 𝑗 𝑘
2 3 −1
5 −3 2
|
𝐴̅ 𝑥 𝐵̅ = | 3 −1
−3 2
| 𝒊 − |2 −1
5 2
| 𝒋 + |2 3
5 −3
| 𝒌
𝐴̅ 𝑥 𝐵̅ = (3 ∗ 2 − (−3) ∗ (−1))𝒊 − (2 ∗ 2 − 5 ∗ (−1))𝒋 + (2 ∗ (−3) − 5 ∗ 3))𝒌
𝐴̅ 𝑥 𝐵̅ = (6 − 3)𝒊 − (4 + 5)𝒋 + (−6 − 15))𝒌
𝐴̅ 𝑥 𝐵̅ = 3𝒊 − 9𝒋 − 21))𝒌
Operaciones básicas entre vectores
La suma de vectores
La resta de vectores
El producto escalar o producto punto
El producto vectorial

7. La suma de vectores
Sean los vectores
la suma se define como
La resta de vectores
El producto escalar o producto punto
donde para este producto hay que considerar la siguiente convención
En principio podemos observar que bajo esta definición el producto escalar entre dos vectores se
realiza como si estuviéramos multiplicando dos polinomios

8. El producto vectorial
Una operación de gran utilidad dentro de algunas áreas de ciencias e ingenierías. El producto
vectorial permite encontrar un vector perpendicular a los dos vectores
involucrados:
ahora las restricciones son presentadas como sigue:
aplicando esto tendremos:
Esta expresión vectorial se puede también se puede expresar mediante el siguiente determinante:

9. Producto de vectores por escalares
Cuando un vector es multiplicado por una cantidad escalar lo que se modifica es la magnitud del
vector, haciéndolo más grande o mas pequeño.
Por ejemplo, si este es el vector A:
dos veces el vector, 2A tendríamos:
únicamente aumento de tamaño. Por el contrario, si multiplicamos por un escalar r<1, donde r es el
escalar, tendríamos un vector mas pequeño, por ejemplo si multiplicamos por r = 1/2
Teorema o ley del seno
Los lados de un triángulo son proporcionales a los senos de los
ángulos opuestos.

10. Ejercicios
De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Determina los
restantes elemento s.

11. Hallar el radio del c írc ulo c irc unsc rito en un triángulo, donde A = 45°, B =
72° y a=20m.
Teorema o ley del coseno
En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados
de los otros dos menos el doble producto del producto de ambos por el coseno
del ángulo que forman.
Ejemplos
Las diagonales de un paralelogramo miden 10 c m y 12 c m, y el ángulo que
forman es de 48° 15'. Calc ular los lados.

12. El radio de una c irc unferenc ia mide 25 m. Calc ula el ángulo que formarán
las tangentes a dic ha c irc unferenc ia, trazadas por los extremos de una c uerda de
longitud 36 m.

13. Teorema o ley de la tangente
Si A y B son ángulos de un triángulo y sus lados c orrespondientes son a y b, se c umple
que: