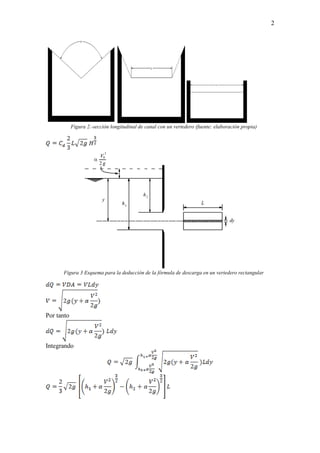
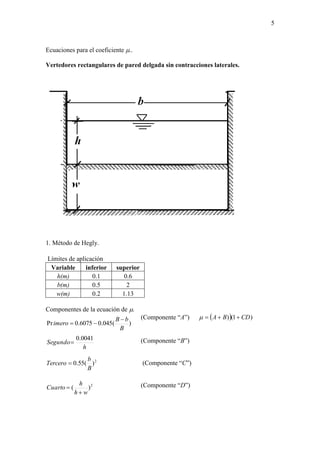
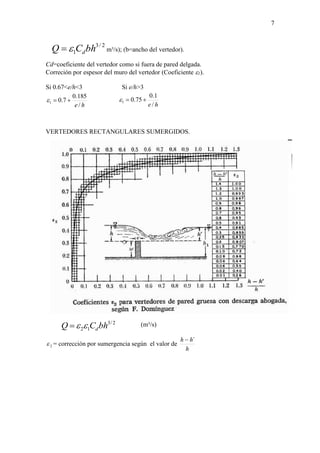
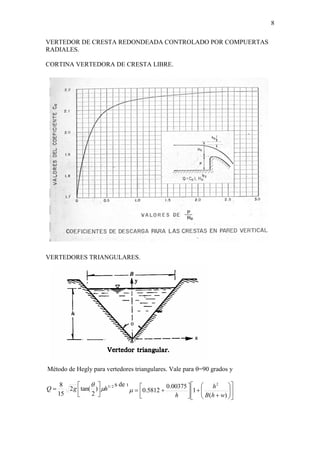
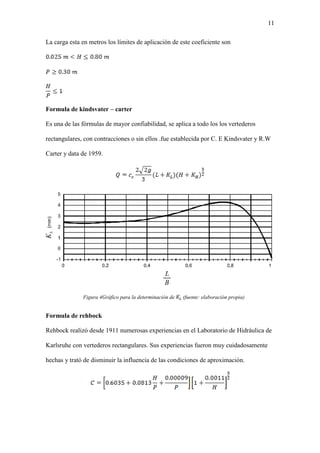
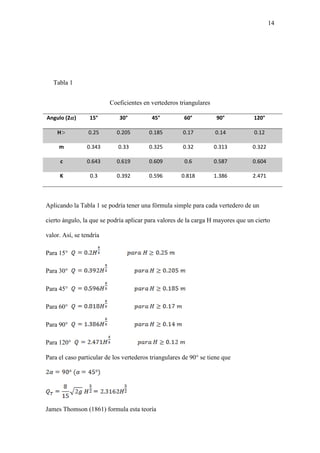
Este documento describe diferentes tipos de vertederos utilizados para medir y controlar el flujo de agua en canales abiertos. Explica las fórmulas para calcular el caudal a través de vertederos rectangulares, triangulares y trapezoidales, incluyendo factores como la geometría, carga de agua y coeficientes de descarga. También cubre métodos para vertederos de pared gruesa, sumergidos y controlados por compuertas. El documento proporciona una referencia detallada de las fórmulas y mé

1. 1
I.-VERTEDEROS
1.1.- CONCEPTO:
(Sanchez Delgado , 2014) Define: “Los vertederos son diapositivas ampliamente
utilizados en la medición de flujo de canales abiertos, también se utiliza para elevar el
nivel de agua. Estos pueden clasificarse en vertederos de pared gruesa y vertederos de
pared delegada”. (pag.131)
1.1.1.-Vertederos de cresta delgada
Un vertedero es una barra colocada en un canal para que el fluido se mantenga detrás
del vertedero y después caiga atreves de una ranura cortada en la cara de vertedero .las
geometrías de los vertederos más comunes son la rectangular, triangular y trapzoidal.la
descarga sobre el vertedero depende de las dimensiones de la ranura y la carga H del
fluido.
FORMULAS
a).-vertedero de sección rectangular
(Rocha Felices, 2007) “La ecuación de descarga de un vertedero de ranura rectangular
sin contracción lateral es:
Figura 1vertdero de sección rectangular, triangular y trapezoidal (fuente: elaboración propia)

2. 2
Figura 2.-sección longitudinal de canal con un vertedero (fuente: elaboración propia)
Figura 3 Esquema para la deducción de la fórmula de descarga en un vertedero rectangular
Por tanto
Integrando

3. 3
El coeficiente de descarga se obtiene experimentalmente
Si tuviésemos un vertedero en el que la velocidad de aproximación fuese tan pequeña
que pudiese despreciarse entonces para v=0 se obtiene la descarga teórica.
La descarga real se obtiene aplicando un coeficiente de descarga c y se llega a
” pag.478
COMPUERTAS PLANAS RECTANGULARES
(Maximo Villon, 2007)
Descarga libre. Se dá si
m³/s
b=ancho de la compuerta (m); a=abertura de la compuerta (m).
Ecuaciones para el coeficiente de descarga Cd.
12gybaCQ d
1
0.0516
dC 0.5316
y
a
 
  
 
1.72
31 yy
0.81
a a
 
  
 

4. 4
S Si y1/a<10
Cd=0.6 Si y1/a>10
Descarga ahogada. Se dá si
72.1
31
81.0 






a
y
a
y
Ecuación para Cd.
VERTEDORES RECTANGULARES DE PARED DELGADA.
(m³/s); b=ancho del vertedor (m).
g
v
hH
2
2
1

12gybaCQ d
1 1
3 c
y y
Φ ,Ψ
y C a
 
   1211
2
A
 
2
22 1
112 






A


1
3A
 
3
211
2/1
2
A
AAACc
Cd


62.0CC
2/3
bHCQ d
 952.22
3
2
 gCd

5. 5
Ecuaciones para el coeficiente ..
Vertedores rectangulares de pared delgada sin contracciones laterales.
1. Método de Hegly.
Límites de aplicación
Variable inferior superior
h(m) 0.1 0.6
b(m) 0.5 2
w(m) 0.2 1.13
Componentes de la ecuación de.
(Componente “A”)   )1() CDBA 
(Componente “B”)
(Componente “C”)
(Componente “D”)
)(045.06075.0Pr
B
bB
imero


h
Segundo
0041.0

2
)(55.0
B
b
Tercero 
2
)(
wh
h
Cuarto



6. 6
2. Método de Rehbock (Vertedores sin contracciones laterales)
Límites de aplicación (primeras restricciones)
Variable inferior superior
h(m) 0.01 0.8
b(m) 0.3
w(m) 0.06
h/w 1
AB
Vertedores rectangulares de pared delgada con contracciones laterales
3.- Método de Hamilton-Smith
Límites de aplicación (primeras restricciones)
Variable inferior superior
h(m) 0.075 0.6
b(m) 0.3
w(m) 0.3
Límites de aplicación (segundo grupo de restricciones)
VERTEDORES RECTANGULARES DE PARED GRUESA. Cuando e/h> 0.67
)
0011.0
(0813.06035.0
w
h
A


2/3
0011.0
1 






h
B
2
w
h  )2( hBb  50.0
b
h







B
b
10
1616.0

7. 7
( m³/s); (b=ancho del vertedor).
Cd=coeficiente del vertedor como si fuera de pared delgada.
Correción por espesor del muro del vertedor (Coeficiente 1).
Si 0.67<e/h<3 Si e/h>3
VERTEDORES RECTANGULARES SUMERGIDOS.
(m³/s)
2 = corrección por sumergencia según el valor de
h
hh ´
2/3
1 bhCQ d
he/
185.0
7.01 
he/
1.0
75.01 
2/3
12 bhCQ d

8. 8
VERTEDOR DE CRESTA REDONDEADA CONTROLADO POR COMPUERTAS
RADIALES.
CORTINA VERTEDORA DE CRESTA LIBRE.
VERTEDORES TRIANGULARES.
Método de Hegly para vertedores triangulares. Vale para =90 grados y
0.10 m<h<0.50 m y valores de w pequeñas.2/5
)
2
tan(2
15
8
hgQ 





 

















)(
1
00375.0
5812.0
2
whB
h
h


9. 9
Método de Gourley y Crimp.
Formula de Francis
James B. Francis realizó más de 80 experimentos, entre 1848 y 1852, en vertederos
Rectangulares en pared delgada con el objetivo de encontrar una expresión para el
coeficiente de descarga.
Francis realizó sus experiencias en Lowell, Massachusetts, dentro de determinadas
condiciones, las que constituyen los límites de aplicación del coeficiente de descarga
que obtuvo.
La fórmula obtenida por Francis considera la velocidad de aproximación 0 V y la
posibilidad de contracciones laterales.
La fórmula de Francis es:
Si, además, no hubiese contracciones laterales, entonces n=o y la formula de Francis
quedaría reducido a
48.2
2
tan32.1 hQ 






10. 10
Formula de bazin
En la que B es el ancho del canal.
Si el vertedero fuese sin contracciones, entonces B=L y el coeficiente de descarga seria:
Formula de la sociedad suiza de ingenieros y arquitectos
En este formula hay 2 coeficientes, según que haya contracciones o no.
El coeficiente c para un vertedero con contracciones es:
B es el ancho del canal
Los límites de aplicación de esta fórmula para coeficiente de descarga en vertederos
rectangulares con contracciones cero.
El coeficiente de descarga c para un vertedero sin contracciones

11. 11
La carga esta en metros los límites de aplicación de este coeficiente son
Formula de kindsvater – carter
Es una de las fórmulas de mayor confiabilidad, se aplica a todo los los vertederos
rectangulares, con contracciones o sin ellos .fue establecida por C. E Kindsvater y R.W
Carter y data de 1959.
Figura 4Gráfico para la determinación de (fuente: elaboración propia)
Formula de rehbock
Rehbock realizó desde 1911 numerosas experiencias en el Laboratorio de Hidráulica de
Karlsruhe con vertederos rectangulares. Sus experiencias fueron muy cuidadosamente
hechas y trató de disminuir la influencia de las condiciones de aproximación.

12. 12
Donde H, P están en metros el coeficiente C se aplica a la ecuación y se recomienda
usar la fórmula para cargas comprendidas entre 0.025 m y 0.60 m.
Vertederos triangulares
Considerando a esta franja como un orificio y despreciando la velocidad de
aproximación se obtiene el caudal.
Integrando
Pero

13. 13
La fórmula de descarga para un vertedero triangular de un Angulo dado y para
coeficiente C constante puede expresarse así:
Otra forma de calcular la descarga atreves de un vertedero triangular verticalmente
simétrico es considerar que la ecuación de uno de los dos lados del triángulo es:
De donde, el caudal es:
Para cada Angulo del vertedero y para cada valor de la carga se obtienen el coeficiente
m:

14. 14
Tabla 1
Coeficientes en vertederos triangulares
Angulo (2 ) 15° 30° 45° 60° 90° 120°
H 0.25 0.205 0.185 0.17 0.14 0.12
m 0.343 0.33 0.325 0.32 0.313 0.322
c 0.643 0.619 0.609 0.6 0.587 0.604
K 0.3 0.392 0.596 0.818 1.386 2.471
Aplicando la Tabla 1 se podría tener una fórmula simple para cada vertedero de un
cierto ángulo, la que se podría aplicar para valores de la carga H mayores que un cierto
valor. Así, se tendría
Para 15°
Para 30°
Para 45°
Para 60°
Para 90°
Para 120°
Para el caso particular de los vertederos triangulares de 90° se tiene que
James Thomson (1861) formula esta teoría

15. 15
Que es la conocida formula de Thomson para vertederos de 90° H esta en metros y el
caudal Q en m3/s
A partir de las mediciones de Thomson y Barr M A Barnes presento la siguiente
formula
Que es equivalente a la de Thomson y para la cual su autor señala que el error es
inferior a 1/5 de 1 %.
Vertederos trapeciales. Vertedero tipo Cipolletti
Figura 5seccion trapezoidal (fuente: elaboración propia)
Vertedero de cipolleti

16. 16
Vertederos en pared gruesa

17. 17
Bibliografía
Maximo Villon, B. (2007). Hidraulica de canales. Lima-Peru: Villon.
Rocha Felices, A. (2007). Hidraulica de tuberias y canales. Lima Peru: Derechos
Reservados.
Sanchez Delgado , M. A. (2014). Hidraulica de canales abiertos teoria y problemas.
Lima: Fondo editorial UNALM.