Actividad 2 parte 2
•Descargar como ODT, PDF•
0 recomendaciones•745 vistas
El valor absoluto representa el valor de un número real independientemente de su signo y se utiliza para medir distancias. La función valor absoluto toma siempre valores positivos en su rango e incluye al cero. La función valor absoluto tiene un eje de simetría vertical y su forma depende de si el término independiente "a" es positivo o negativo. El valor absoluto se usa en aplicaciones como medir rangos de gasto de energía, distancias de viajes, intervalos de temperatura, y capacidad auditiva humana.
Denunciar
Compartir
Denunciar
Compartir
Más contenido relacionado
La actualidad más candente
La actualidad más candente (20)
Aplicación e importancia de las funciones trigonométricas e hiperbólicas y s...

Aplicación e importancia de las funciones trigonométricas e hiperbólicas y s...
Destacado
Destacado (20)
Tendencias%20 emergentes%20extraídas%20del%20ii%20world%20café[1]![Tendencias%20 emergentes%20extraídas%20del%20ii%20world%20café[1]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Tendencias%20 emergentes%20extraídas%20del%20ii%20world%20café[1]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Tendencias%20 emergentes%20extraídas%20del%20ii%20world%20café[1]
Guide%20 utilisateur%20de%20shadowprotect v9-20111129-0911[1]![Guide%20 utilisateur%20de%20shadowprotect v9-20111129-0911[1]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Guide%20 utilisateur%20de%20shadowprotect v9-20111129-0911[1]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Guide%20 utilisateur%20de%20shadowprotect v9-20111129-0911[1]
Autoroutes de la Mer, Rapport d\'Henri de Richemont

Autoroutes de la Mer, Rapport d\'Henri de Richemont
Les festivals musicaux et les réseaux sociaux en 2013

Les festivals musicaux et les réseaux sociaux en 2013
Similar a Actividad 2 parte 2
Similar a Actividad 2 parte 2 (20)
Trabajo de Matematica II Universidad Fermin Toro UFT

Trabajo de Matematica II Universidad Fermin Toro UFT
Límites derivadas e integrales y análisis matemático.pptx

Límites derivadas e integrales y análisis matemático.pptx
Más de Sofia Torres
Más de Sofia Torres (15)
Último
Último (20)
Novena de Pentecostés con textos de san Juan Eudes

Novena de Pentecostés con textos de san Juan Eudes
🦄💫4° SEM32 WORD PLANEACIÓN PROYECTOS DARUKEL 23-24.docx

🦄💫4° SEM32 WORD PLANEACIÓN PROYECTOS DARUKEL 23-24.docx
RESOLUCIÓN VICEMINISTERIAL 00048 - 2024 EVALUACION

RESOLUCIÓN VICEMINISTERIAL 00048 - 2024 EVALUACION
ACERTIJO LA RUTA DEL MARATÓN OLÍMPICO DEL NÚMERO PI EN PARÍS. Por JAVIER SOL...

ACERTIJO LA RUTA DEL MARATÓN OLÍMPICO DEL NÚMERO PI EN PARÍS. Por JAVIER SOL...
Tema 10. Dinámica y funciones de la Atmosfera 2024

Tema 10. Dinámica y funciones de la Atmosfera 2024
ACRÓNIMO DE PARÍS PARA SU OLIMPIADA 2024. Por JAVIER SOLIS NOYOLA

ACRÓNIMO DE PARÍS PARA SU OLIMPIADA 2024. Por JAVIER SOLIS NOYOLA
Factores que intervienen en la Administración por Valores.pdf

Factores que intervienen en la Administración por Valores.pdf
Prueba de evaluación Geografía e Historia Comunidad de Madrid 4ºESO

Prueba de evaluación Geografía e Historia Comunidad de Madrid 4ºESO
Actividad 2 parte 2
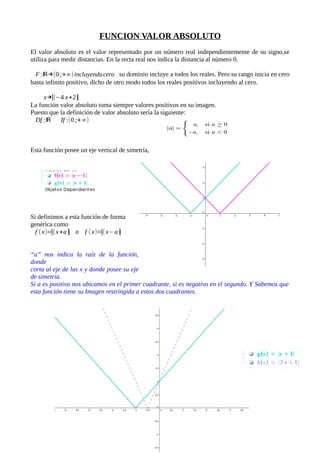
- 1. FUNCION VALOR ABSOLUTO El valor absoluto es el valor representado por un número real independientemente de su signo,se utiliza para medir distancias. En la recta real nos indica la distancia al número 0. F:ℝ→(0;+∞)incluyendocero su dominio incluye a todos los reales. Pero su rango inicia en cero hasta infinito positivo, dicho de otro modo todos los reales positivos incluyendo al cero. x→|(−4 x+2)| La función valor absoluto toma siempre valores positivos en su imagen. Puesto que la definición de valor absoluto sería la siguiente: Df :ℝ If :(0;+∞) Esta función posee un eje vertical de simetría, Si definimos a esta función de forma genérica como f (x)=|(x+a)| o f (x)=|(x−a)| “a” nos indica la raíz de la función, donde corta al eje de las x y donde posee su eje de simetría. Si a es positivo nos ubicamos en el primer cuadrante, si es negativo en el segundo. Y Sabemos que esta función tiene su Imagen restringida a estos dos cuadrantes.
- 2. Vemos aquí que si el coeficiente de x es distinto de 1 la apertura de los brazos de esta función cambia. Ahora la raíz es el punto ½, por simple operación algebraica de despejar x. Por otra parte notamos que los brazos se cierran. Vemos aquí una función módulo compuesta con una función cuadrática, o polinómica de segundo grado. Vemos que cuando “c”( de la forma genérica ax ²+bx+c ) es negativo y asume valores negativos, éstos en la función módulo se reflejan hacia los dos primeros cuadrantes. O “hacia arriba” del eje de las x. La parte punteada muestra la porción de la función cuadrática y la función de verde muestra la función cuadrática combinada con la función módulo. Esa parte punteada es reflejada hacia arriba, y como vemos el vértice que en la cuadrática original era negativo, ahora es positivo- Video de cómo graficar una función valor absoluto que contiene a una función cuadrática Aplicaciones del valor absoluto en la vida real • Rango en que varia el número de kilovatios del gasto mensual en una vivienda si queremos saber una distancia a recorrer en un viaje sin importar el punto de partida, si vamos a cierto punto o nos devolvemos para hallar los km que recorre el automóvil.
- 3. • Si queremos hallar el intervalo de una temperatura. entre cuantos grados centígrados se derrite cierto objeto. • Capacidad que tiene el oído humano en resistir un ruido sin ser perturbado ni afectado. • A todo lo anterior agregaría que el conocimiento de este concepto es muy importante para entender el concepto fundamental de límite, ya sea de funciones o de sucesiones y que nos permite hacer el paso al infinito.
