Clases COMIPEMS.pptx

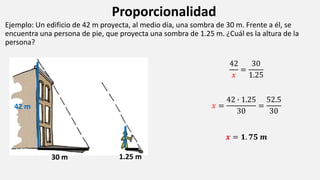
Proporcionalidad
Ejemplo: Un edificio de 42 m proyecta, al medio día, una sombra de 30 m. Frente a él, se
encuentra una persona de pie, que proyecta una sombra de 1.25 m. ¿Cuál es la altura de la
persona?
42
𝑥
=
30
1.25
𝑥 =
42 ∙ 1.25
30
=
52.5
30
𝒙 = 𝟏. 𝟕𝟓 𝒎
42 m
30 m 1.25 m

Proporcionalidad
Ejemplo: Calcula la altura del edificio con base en el siguiente dibujo:
𝑥
5
=
270
6
𝑥 =
270 ∙ 5
6
=
1,350
6
𝒙 = 𝟐𝟐𝟓 𝒎

Proporcionalidad
Ejemplo: Calcula la altura de la luminaria con base en el siguiente dibujo:
𝑥
1.7
=
60
8
𝑥 =
60 ∙ 1.7
8
=
102
8
𝒙 = 𝟏𝟐. 𝟕𝟓 𝒎
1.70 m

Proporcionalidad
Ejemplo. Calcula el ancho del río con base en el siguiente esquema:
𝑥
10.4
=
75.1
20.8
𝑥 =
75.1 ∙ 10.4
20.8
=
781.04
20.8
𝒙 = 𝟑𝟕. 𝟓𝟓 𝒎

Funciones trigonométricas
𝑠𝑒𝑛 =
𝑐𝑜
ℎ
𝑐𝑜𝑠 =
𝑐𝑎
ℎ
𝑡𝑎𝑛 =
𝑐𝑜
𝑐𝑎
Hipotenusa: Lado
opuesto al ángulo
recto. Es el de
mayor longitud.
Cateto opuesto:
Lado opuesto al
ángulo de
referencia.
Cateto adyacente: Lado forma parte del
ángulo de referencia y del ángulo recto.
𝒉
𝒄𝒐
𝒄𝒂

𝑠𝑒𝑛 =
𝑐𝑜
ℎ
𝑐𝑜𝑠 =
𝑐𝑎
ℎ
Hipotenusa: Lado
opuesto al ángulo
recto. Es el de
mayor longitud.
Cateto opuesto:
Lado opuesto al
ángulo de
referencia.
Cateto adyacente: Lado forma parte del
ángulo de referencia y del ángulo recto.
𝒉
𝒄𝒐
𝒄𝒂
Inversa:
𝑐𝑠𝑐 =
ℎ
𝑐𝑜
𝑡𝑎𝑛 =
𝑐𝑜
𝑐𝑎
Inversa:
𝑐𝑜𝑡 =
𝑐𝑎
𝑐𝑜
Inversa:
𝑠𝑒𝑐 =
ℎ
𝑐𝑎

¿Para qué me sirven las funciones trigonométricas?
Como estas funciones relacionan los lados con los ángulos en
un triángulo rectángulo, tienen la utilidad para encontrar
valores faltantes de ángulos o de algún lado.
Con el hecho de tan sólo conocer el valor de uno de los
ángulos no rectos del triángulo y el valor de un lado,
podemos encontrar todos los valores faltantes tanto de lados
como de ángulos.
Además, cuando se requiera calcular un ángulo, se puede
calcular la función inversa de una función trigonométrica.

Ejemplo. Calcula el valor de los lados y ángulos faltantes del siguiente triángulo rectángulo.
𝜃 = 180° − 90° − 57°
𝜽 = 𝟑𝟑°
𝑠𝑒𝑛 33° =
𝑏
25 𝑐𝑚
𝑏 = 𝑠𝑒𝑛(33°)(25 𝑐𝑚)
𝑏 = 0.54 25 𝑐𝑚
𝒃 = 𝟏𝟑. 𝟔𝟏 𝒄𝒎
𝑐𝑜𝑠 33° =
𝑎
25 𝑐𝑚
𝑏 = 𝑐𝑜𝑠(33°)(25 𝑐𝑚)
𝑏 = 0.83 25 𝑐𝑚
𝒃 = 𝟐𝟎. 𝟗𝟔 𝒄𝒎
57°
𝑎
𝑏
𝜃

Ejemplo. Calcula el valor del ángulo y del lado que se indican.
𝑐𝑜𝑠 𝜃 =
9
16
𝜃 = arccos
9
16
𝜽 = 𝟓𝟓. 𝟕𝟕°
𝑠𝑒𝑛 55.77° =
𝑏
16 𝑐𝑚
𝑏 = 𝑠𝑒𝑛 55.77° (16 𝑐𝑚)
𝑏 = 0.82 16 𝑐𝑚
𝒃 = 𝟏𝟑. 𝟐𝟐𝒄𝒎
9 𝑐𝑚
𝑏
𝜃
16 𝑐𝑚

Ejemplo. Calcula el valor de los lados faltantes.
𝑐𝑜𝑠 45° =
5.5𝑐𝑚
ℎ
ℎ =
5.5𝑐𝑚
cos(45°)
ℎ =
5.5𝑐𝑚
0.70
𝒉 = 𝟕. 𝟕𝟕 𝒄𝒎
𝑡𝑎𝑛 45° =
𝑏
5.5 𝑐𝑚
𝑏 = 𝑡𝑎𝑛 45° (5.5 𝑐𝑚)
𝑏 = 1 16 𝑐𝑚
𝒃 = 𝟏𝟔 𝒄𝒎
5.5 𝑐𝑚
𝑏
45°
ℎ

Ejercicios.
3. En un triángulo rectángulo donde el cos 𝛼 es 4/5, ¿cuánto mide el cateto opuesto?
𝑎2 = 𝑐2 − 𝑏2
𝑎2
= 52
− 42
𝑎2 = 25 − 16
𝑎2 = 9
𝑎 = 9
𝒂 = 𝟑
5
4
𝛼

Ejercicios.
1. En un triángulo rectángulo, uno de los ángulos agudos mide 𝛼 y su cateto adyacente mide n.
¿Cuál es el área del triángulo?
𝐴 =
𝑏 ∙ ℎ
2
𝐴 =
𝑛 ∙ 𝑛 𝑡𝑎𝑛(𝛼)
2
𝑨 =
𝒏𝟐 𝒕𝒂𝒏(𝜶)
𝟐
𝑡𝑎𝑛 𝛼 =
ℎ
𝑛
ℎ = 𝑛 𝑡𝑎𝑛(𝛼)
ℎ
𝑛
𝛼

Ejercicios.
2. En la sig. figura, el área del cuadrado grande es de 36 𝑐𝑚2. Calcula el área sombreada.
𝐴𝑐𝑖𝑟𝑐𝑢𝑙𝑜 = 𝜋𝑟2
𝐴𝑐𝑖𝑟𝑐𝑢𝑙𝑜 𝑝𝑒𝑞𝑢𝑒ñ𝑜 = (3.1416)(1)2
𝐴𝑐𝑖𝑟𝑐𝑢𝑙𝑜 𝑝𝑒𝑞𝑢𝑒ñ𝑜 = 3.1416 𝑐𝑚2
𝐴𝑐𝑖𝑟𝑐𝑢𝑙𝑜 𝑔𝑟𝑎𝑛𝑑𝑒 = (3.1416)(2)2
𝐴𝑐𝑖𝑟𝑐𝑢𝑙𝑜 𝑔𝑟𝑎𝑛𝑑𝑒 = 12.5664 𝑐𝑚2
𝑨𝒔𝒐𝒎𝒃𝒓𝒆𝒂𝒅𝒂 = 𝟏𝟓. 𝟕𝟎𝟔 𝒄𝒎𝟐
2 cm

Ejercicios.
7. En una escuela se destinó un área triangular para espacio de recreación de 33 m cada lado.
Al centro de esta área, se asigna un triángulo semejante que se ocupará para consumir
alimentos, donde la longitud de sus lados es de 2/3 partes de los lados correspondientes del
espacio de recreación. ¿Cuánto medirá el perímetro del área de consumo?
Cada lado mide
2
3
33 𝑚
22 𝑚
𝑃 = 22 + 22 + 22
𝑷 = 𝟔𝟔𝒎
33 cm 33 cm
33 cm
22 cm 22 cm
22 cm

Ejercicios.
12. Si se quiere calcular el área total del rombo, ¿qué ecuación se debe resolver?
𝐴 =
𝐷 ∙ 𝑑
2
𝐴 =
(4𝑥 + 1)(2𝑥 + 2)
2
𝐴 =
8𝑥2 + 8𝑥 + 2𝑥 + 2
2
𝐴 =
8𝑥2
+ 10𝑥 + 2
2
𝑨 = 𝟒𝒙𝟐 + 𝟓𝒙 + 𝟏

Ejercicios.
21. Calcula el área del siguiente trapecio.
𝐴 =
𝐵 + 𝑏 ∙ ℎ
2
𝐴 =
(9𝑐𝑚 + 5𝑐𝑚)(4𝑐𝑚)
2
𝐴 =
(14 𝑐𝑚)(4𝑐𝑚)
2
𝐴 =
56𝑐𝑚2
2
𝑨 = 𝟐𝟖𝒄𝒎𝟐
9 cm

Ejercicios.
26. Dado el siguiente triángulo, ¿cuál es su área?
3 cm
5 𝑐𝑚
3 𝑐𝑚
𝛼
𝑎2 = 𝑐2 − 𝑏2
𝑎2
= 25 − 9
𝑎2 = 16
𝑎 = 16
𝒂 = 𝟒
Por ende, la base del
triángulo original mide 8 cm.
𝐴 =
𝑏 ∙ ℎ
2
𝐴 =
(8 𝑐𝑚)(3 𝑐𝑚)
2
𝑨 = 𝟏𝟐 𝒄𝒎𝟐

Ejercicios.
30. En la figura, ABCD es un cuadrado de lado 8 cm. Calcula el perímetro y área de la figura
sombreada.
𝐴𝑐𝑖𝑟𝑐𝑢𝑙𝑜 = 𝜋𝑟2
𝐴𝑐𝑖𝑟𝑐𝑢𝑙𝑜 = (3.1416)(4)2
𝐴𝑐𝑖𝑟𝑐𝑢𝑙𝑜 = (3.1416)(16)
𝐴𝑐𝑖𝑟𝑐𝑢𝑙𝑜 = 50.2656 𝑐𝑚2
𝐴𝑐𝑢𝑎𝑑𝑟𝑎𝑑𝑜 = 𝑙2
𝐴𝑐𝑢𝑎𝑑𝑟𝑎𝑑𝑜 = 64 𝑐𝑚2
𝐴 = 𝐴𝑐𝑢𝑎𝑑𝑟𝑎𝑑𝑜 − 𝐴𝑐𝑖𝑟𝑐𝑢𝑙𝑜
𝑨 = 𝟏𝟑. 𝟕𝟑 𝒄𝒎𝟐
8 cm

Ejercicios.
38. Determina la expresión que contiene el área de un rectángulo cuyo ancho es de 8 unidades
menos que su largo.
𝐴 = 𝑏ℎ
𝐴 = 𝑥(𝑥 − 8)
𝑨 = 𝒙𝟐 − 𝟖𝒙 x
x-8

Ejercicios.
39. Se tiene un cilindro en el que el diámetro de la base es de 10 cm y la altura es de 200 mm.
¿Cuál es su volumen?
𝑉 = 𝜋𝑟2
ℎ
= 3.1416 5𝑐𝑚 2 (20 𝑐𝑚)
= (3.1416)(25𝑐𝑚2)(20 𝑐𝑚)
𝑽 = 𝟏, 𝟓𝟕𝟎. 𝟖 𝒄𝒎𝟑

Ejercicios.
6. Las ruedas de la bicicleta de Valeria tienen 30 cm de radio. ¿Qué distancia recorre cuando
las ruedas giran exactamente 10 vueltas?
𝑃 = 𝜋𝑑
= (3.1416)(60 𝑐𝑚)
= 188.496 𝑐𝑚
Ahora, multiplicamos lo anterior por 10, para
obtener la distancia recorrida en las 10
vueltas.
= 𝟏, 𝟖𝟖𝟒. 𝟗𝟔 𝒄𝒎

Ejercicios.
Ustedes realizarán los siguientes ejercicios (a partir de la pág. 35):
5
9
10
13
14
18
24
25
29

Ejercicios.
5. Se desea producir un envase para puré de tomate. Si el envase muestra tiene 6 cm de ancho,
6 cm de largo y 6 cm de altura, ¿qué cantidad de material se utilizará para construir el envase?

Ejercicios.
9. En un triángulo rectángulo, el 𝑠𝑒𝑛 𝛼=3/5. ¿A cuánto equivale la 𝑡𝑎𝑛 𝛼?
10. ¿Cuál es el área de un pentágono regular de 10 cm de lado cuyo apotema mide 8.88 cm?

Ejercicios.
13. Dentro de un libro de recortables, Dante encontró uno que constaba de un muñeco hecho
de varias figuras: un círculo, un cuadrado, dos rectángulos y dos triángulos. Dante lo recortó y
lo pegó en su cuaderno. ¿Qué área de la hoja de su cuaderno ocupó?
14. Ahora, Dante quiere hacer el muñeco en 3D. Para ello, la cabeza es una esfera, el torso es
un cubo, las manos un paralelepípedo (con altura de 2 cm) y los pies una pirámide de base
cuadrada. ¿Cuál es el volumen del muñeco?

Ejercicios.
18. Si un reloj marca las 3:00, ¿cuál es el área del sector menor si el minutero mide 12 cm?
24. Si el coseno de un ángulo es 4/5, ¿cuál es el valor de la secante para el mismo ángulo?

Ejercicios.
25. Si se sabe que el valor del seno es de 4/7 y del coseno es de 6/7, ¿cuánto valen la tangente
y la cosecante?
29. Dado el triángulo que se encuentra a continuación, determina el valor del ángulo A.

Ejemplo. Encuentra el valor del ángulo theta.
𝑠𝑒𝑛 𝜃 =
12
13
𝑐𝑜𝑠 𝜃 =
5
13
𝑡𝑎𝑛 𝜃 =
12
5
5
12
𝜃
𝜃 = 𝑎𝑟𝑐𝑠𝑒𝑛
12
13
= 67.38°
𝜃 = 𝑎𝑟𝑐𝑐𝑜𝑠
5
13
= 67.38°
𝜃 = 𝑎𝑟𝑐𝑡𝑎𝑛
12
5
= 67.38°

Ejemplo. Relaciona cada razón con su respectiva función trigonométrica.
𝑠𝑒𝑛 𝛼
𝑐𝑜𝑠 𝛼
𝑡𝑎𝑛 𝛼
𝑐𝑠𝑐 𝛼
𝑠𝑒𝑐 𝛼
𝑐𝑜𝑡 𝛼
5
12
𝛼
13
12
5
12
5
13
12
5

Ejemplo. Relaciona cada razón con su respectiva función trigonométrica para cada ángulo.
𝑠𝑒𝑛 𝛼
𝑐𝑜𝑠 𝛼
𝑡𝑎𝑛 𝛼
𝑐𝑠𝑐 𝛼
𝑠𝑒𝑐 𝛼
𝑐𝑜𝑡 𝛼
7
24
𝛼
25
24
7
24
24
25
7
25
𝜃
𝑠𝑒𝑛 𝜃
𝑐𝑜𝑠 𝜃
𝑡𝑎𝑛 𝜃
𝑐𝑠𝑐 𝜃
𝑠𝑒𝑐 𝜃
𝑐𝑜𝑡 𝜃

Ejemplo. Calcula el volumen de la siguiente caja.
𝑉 = 𝑙 ∙ 𝑎 ∙ ℎ
= (50 𝑐𝑚)(25 𝑐𝑚)(20 𝑐𝑚)
= 𝟐𝟓, 𝟎𝟎𝟎 𝒄𝒎𝟑
Volumen
20 cm

Ejemplo. Calcula el volumen de la siguiente caja.
𝑉 = 𝜋 ∙ 𝑟2
∙ ℎ
= 3.1416 3 𝑐𝑚 2(15 𝑐𝑚)
= 3.1416 (9 𝑐𝑚2
)(15 𝑐𝑚)
= 𝟒𝟐𝟒. 𝟏𝟏𝟔 𝒄𝒎𝟑
Volumen
3 cm
15 cm

Ejemplo. Calcula el volumen del siguiente prisma triangular.
𝑉 = 𝐴𝑏𝑎𝑠𝑒 ∙ ℎ
𝐴𝑏𝑎𝑠𝑒 =
(5𝑐𝑚)(4𝑐𝑚)
2
= 10𝑐𝑚2
𝑉 = (10 𝑐𝑚2) ∙ (8 𝑐𝑚)
= 𝟖𝟎 𝒄𝒎𝟑
Volumen
8 cm

Representa el
reparto
equitativo, el
equilibrio.
Medidas de
tendencia central
Mediana
Es la cifra que se
encuentra la misma
distancia de los
números que lo
generan.
Si no hay
elementos que
se repiten, no
existe la moda.
Media o
promedio
Es el valor que se
encuentra en la
posición central en
un conjunto de
datos ordenados.
1. Sumamos todos
los datos.
2. El resultado lo
dividimos entre la
cantidad de datos.
Si la cantidad de
datos es par, la
mediana se
obtiene calculando
el promedio de los
datos centrales.
Es el valor que
más se repite
en un conjunto
de datos.
Moda

Ejercicios.
Calcula la media, mediana y moda de las calificaciones obtenidas en matemáticas en un grupo:
8, 7, 10, 9, 9, 7, 6, 9, 8, 10, 9, 6
Media:
8+7+10+9+9+7+6+9+8+10+9+6
12
=
98
12
= 𝟖. 𝟏𝟔
Mediana: 6, 6, 7, 7, 8, 8, 9, 9, 9, 9, 10, 10
=
8 + 9
2
=
17
2
= 𝟖. 𝟓
Moda: 𝟗

Ejemplo: Calcula la media, mediana y moda de las edades de un grupo de amigos.
21, 27, 21, 23, 25, 27, 24, 27, 25
Media:
21 + 27 + 21 + 23 + 25 + 27 + 24 + 27 + 25
9
=
220
9
= 𝟐𝟒. 𝟒𝟒
Mediana:
21, 21, 23, 24, 25, 25, 27, 27, 27
= 𝟐𝟓
Moda: 𝟐𝟕
Ejemplos

Ejercicios.
17. ¿En cuál de los siguientes casos la media, la mediana y la moda no coinciden?
a. Cuando todos los datos son los mismos
10, 10, 10, 10, 10
Media:
10+10+10+10+10
5
=
50
5
= 10
Mediana: 10
Moda: 10
b. Cuando sólo se tiene un dato.
8
Media:
8
1
= 8
Mediana: 8
Moda: 8

Ejercicios.
17. ¿En cuál de los siguientes casos la media, la mediana y la moda no coinciden?
c. Cuando se tiene un caso impar de datos y
éstos son consecutivos.
5, 6, 7, 8, 9
Media:
5+6+7+8+9
5
=
35
5
= 7
Mediana: 7
Moda: −

Representación gráfica de datos
Para poder visualizar de una mejor forma las estadísticas de los datos y su comportamiento, se
utilizan algunos tipos de gráficas de datos, en las cuales, se representa la distribución de la
frecuencia de datos, es decir, del número de veces que se tiene ese dato o cifra, atendiendo a
un atributo o carácter cualitativo.
Algunos de los tipos de gráficas que se tienen son:
- Gráficas de barras.
- Histogramas.
- Polígonos de frecuencias.
- Polígonos circulares.

Antes de realizar un gráfico, es conveniente primeramente registrarlos en una tabla de
frecuencia, que es una tabla que registra todos los datos a partir de su frecuencia.
Ejemplo: Si en una encuesta se tiene que 3 personas escuchan radio, 5 ven televisión y 4 leen
libros, su tabla de frecuencia es la siguiente:
Preferencia Frecuencia
Escucha radio 3
Ve TV 5
Lee libros 4
= 12

Gráfica de barras.
Para trazarlas, se delinea un plano cartesiano, donde el eje X contendrá el tipo de dato
numérico o de atributo, mientras que en el eje Y se indicará la frecuencia de ella.

Polígono de frecuencias.
Es un tipo de gráfica basado en el histograma que consiste en unir los puntos de mayor altura
de cada una de las columnas o barras, para así, sólo representar la frecuencia con que se
presentan los datos recolectados.

Gráfica circular.
También conocida como gráfica de pastel, es un recurso estadístico que se utiliza para
representar porcentajes y proporciones de un dato dentro del conjunto total de ellos en un
área circular.
Para obtener el área de cada sector
circular y el ángulo que ocupa en el
círculo, se ocupa la siguiente
fórmula:
° =
360°
𝑇𝑜𝑡𝑎𝑙 𝐷𝑎𝑡𝑜𝑠
× 𝐹𝑟𝑒𝑐𝑢𝑒𝑛𝑐𝑖𝑎

Ejemplo: Se encuestó a 100 personas sobre su deporte preferido y estos fueron los resultados:
Deporte preferido Frecuencia
Fútbol americano 27
Basquetbol 15
Tenis 13
Fútbol 39
Béisbol 4
Voleibol 2
= 100

Basquetbol 15
Tenis 13
Fútbol 39
Béisbol 4
Voleibol 2
= 100
0
5
10
15
20
25
30
35
40
FRECUENCIA
DEPORTE
Fútbol americano Basquetbol Tenis Fútbol Béisbol Voleibol

0
5
10
15
20
25
30
35
40
45
Fútbol americano Basquetbol Tenis Fútbol Béisbol Voleibol
FRECUENCIA
DEPORTE
Basquetbol 15
Tenis 13
Fútbol 39
Béisbol 4
Voleibol 2
= 100

Deporte
preferido
Frecuencia Porcentaje Ángulo
Fútbol
americano
27 27% 97.2°
Basquetbol 15 15% 54°
Tenis 13 13% 46.8°
Fútbol 39 39% 140.4°
Béisbol 4 4% 14.4°
Voleibol 2 2% 7.2°
= 100 = 100% = 360°
27%
15%
13%
39%
4%
2%
Fútbol americano
Basquetbol
Tenis
Fútbol
Béisbol
Voleibol

También podemos combinar gráficas dentro de un mismo plano, con el fin de visualizar de
mejor manera una comparación entre datos.

Ejemplo: La siguiente tabla contiene la preferencia por los candidatos en las pasadas
elecciones.
Candidato Ene 18 Feb 18 Mar 18 Abr 18 May 18 Jun 18
José Antonio
Meade
15 17 18 17 19 18
Ricardo
Anaya
37 35 33 31 29 27
AMLO 42 43 46 50 50 52
El Bronco 6 5 3 2 2 3
= 100% = 100% = 100% = 100% = 100% = 100%
0
10
20
30
40
50
ene-18 feb-18 mar-18 abr-18 may-18 jun-18
José Antonio Meade Ricardo Anaya AMLO El Bronco

Ejemplo: La siguiente tabla contiene los puntos de audiencia que tuvieron ciertos programas
de TV.
Programa Ene 20 Feb 20 Mar 20 Abr 20 May 20
Exatlón 17 15 15 10 12
Novela 8 8 10 11 12
Noticiero 14 14 13 14 15
Malcolm 12 13 16 15 16
0
2
4
6
8
10
12
14
16
18
ene-20 feb-20 mar-20 abr-20 may-20
Exatlón Novela Noticiero Malcolm

Probabilidad
La probabilidad es la posibilidad que existe de que un evento, es decir, el grado de
certidumbre de que dicho suceso se lleve a cabo.
La fórmula que permite calcular la probabilidad de un evento es:
𝑃 𝐸𝑣𝑒𝑛𝑡𝑜 =
𝑁ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑐𝑎𝑠𝑜𝑠 𝑓𝑎𝑣𝑜𝑟𝑎𝑏𝑙𝑒𝑠
𝑁ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑐𝑎𝑠𝑜𝑠 𝑡𝑜𝑡𝑎𝑙𝑒𝑠
× 100%
De esta forma, la probabilidad puede tomar valores de entre 0 y 1 (0% y 100%).

Ejercicios.
En una bolsa, hay 8 canicas verdes, 6 canicas azules, 2 canicas blancas, 6 canijas rojas y 5
canicas moradas. Si se extrae una canica al azar, ¿cuál es la probabilidad de que…
Salga una canica que no sea verde ni
azul.
Salga una canica blanca o azul.
Salga una canica café.
Salga una canica blanca.
𝑷 𝒏𝒊 𝒗𝒆𝒓𝒅𝒆 𝒏𝒊 𝒂𝒛𝒖𝒍 =
𝟏𝟑
𝟐𝟕
= 𝟎. 𝟒𝟖𝟏𝟒 = 𝟒𝟖. 𝟏𝟒%
𝑷 𝒃𝒍𝒂𝒏𝒄𝒂 𝒐 𝒂𝒛𝒖𝒍 =
𝟖
𝟐𝟕
= 𝟎. 𝟐𝟗𝟔𝟐 = 𝟐𝟗. 𝟔𝟐%
𝑷 𝒄𝒂𝒇𝒆 =
𝟎
𝟐𝟕
= 𝟎 = 𝟎%
𝑷 𝒃𝒍𝒂𝒏𝒄𝒂 =
𝟐
𝟐𝟕
= 𝟎. 𝟎𝟕𝟒𝟎 = 𝟕. 𝟒𝟎%

Ejercicios.
Se lanzan 3 monedas. ¿Cuál es la probabilidad de que…
En las 3 monedas
salga águila.
Salga una vez sol.
Salga al menos
dos veces águila.
Una cara salga dos
veces.
𝑷 𝟑 𝒂𝒈𝒖𝒊𝒍𝒂𝒔 =
𝟏
𝟖
= 𝟎. 𝟏𝟐𝟓 = 𝟏𝟐. 𝟓%
𝑷 𝟏 𝒔𝒐𝒍 =
𝟑
𝟖
= 𝟎. 𝟑𝟕𝟓 = 𝟑𝟕. 𝟓%
𝑷 𝟐 𝒐 𝟑 𝒂𝒈𝒖𝒊𝒍𝒂𝒔 =
𝟒
𝟖
= 𝟎. 𝟓 = 𝟓𝟎%
𝑷 𝟐 𝒂𝒈𝒖𝒊𝒍𝒂𝒔 𝒐 𝒔𝒐𝒍𝒆𝒔 =
𝟔
𝟖
= 𝟎. 𝟕𝟓 = 𝟕𝟓%
Moneda
1
Moneda
2
Moneda
3
𝐴 𝐴 𝐴
𝐴 𝐴 S
𝐴 S 𝐴
𝐴 S S
S 𝐴 𝐴
S 𝐴 S
S S 𝐴
S S S

Ejercicios.
1. Una empresa de investigación privada encuestó a 200 familias, de las cuales 32 dijeron tener
un hijo, 55 dos hijos, 58 tres hijos, 25 cuatro hijos y 30 cinco o más hijos. ¿Cuál es la
probabilidad de que una familia escogida de la encuesta al azar tenga a lo más tres hijos?
Familias con un hijo: 32
Familias con dos hijos: 55
Familias con 3 hijos: 58
𝑃 𝑎 𝑙𝑜 𝑚á𝑠 3 ℎ𝑖𝑗𝑜𝑠 =
145
200
𝑃 𝑎 𝑙𝑜 𝑚á𝑠 3 ℎ𝑖𝑗𝑜𝑠 = 0.725
𝑷 𝒂 𝒍𝒐 𝒎𝒂𝒔 𝟑 𝒉𝒊𝒋𝒐𝒔 = 𝟕𝟐. 𝟓%

Ejercicios.
6. En una encuesta a un grupo de 100 personas, se les pregunta si les gusta leer y ver TV: Los
resultados indican que a 40 personas leer y ver TV, a 35 personas les gusta leer y a 25 personas
les gusta ver TV. Si se elige al azar a una de esas personas, ¿cuál es la probabilidad de que no le
guste ver TV?
40 personas leen Y VEN TV.
35 personas sólo leen.
25 personas sólo ven TV.
𝑃 𝑁𝑜 𝑔𝑢𝑠𝑡𝑒 𝑣𝑒𝑟 𝑇𝑉 =
35
100
𝑃 𝑁𝑜 𝑔𝑢𝑠𝑡𝑒 𝑣𝑒𝑟 𝑇𝑉 = 0.35
𝑷 𝑵𝒐 𝒈𝒖𝒔𝒕𝒆 𝒗𝒆𝒓 𝑻𝑽 = 𝟑𝟓%

Ejercicios.
8. En un centro de salud se lleva el control de nivel de colesterol en 90 pacientes adultos, como
se muestra a continuación. Si se elige al azar a una de estas personas para que continúe con
sus estudios, ¿qué probabilidad hay de que esa persona tenga el colesterol normal?
𝑃 𝑐𝑜𝑙𝑒𝑠𝑡𝑒𝑟𝑜𝑙 𝑛𝑜𝑟𝑚𝑎𝑙 =
50
90
𝑃 𝑐𝑜𝑙𝑒𝑠𝑡𝑒𝑟𝑜𝑙 𝑛𝑜𝑟𝑚𝑎𝑙 = 0.55
𝑷 𝒄𝒐𝒍𝒆𝒔𝒕𝒆𝒓𝒐𝒍 𝒏𝒐𝒓𝒎𝒂𝒍 = 𝟓𝟓. 𝟓%

Ejercicios.
10. Se tienen 2 dados comunes y se lanzan al mismo tiempo. ¿Cuál es la probabilidad de que la
suma de las caras que hayan salido sea un número primo?
𝑃 𝑆𝑢𝑚𝑎 𝑠𝑒𝑎 𝑝𝑟𝑖𝑚𝑜 =
15
36
𝑃 𝑆𝑢𝑚𝑎 𝑠𝑒𝑎 𝑝𝑟𝑖𝑚𝑜 = 0.416
𝑷 𝑺𝒖𝒎𝒂 𝒔𝒆𝒂 𝒑𝒓𝒊𝒎𝒐 = 𝟒𝟏. 𝟔%
Dado 1/Dado 2 1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12

Ejercicios.
12. Mario compró un boleto de un sorteo de lotería. El sorteo consiste en elegir 4 números de
entre 0 y 20, los cuales se pueden repetir. Si eligió los números 7, 17, 1 y 20, ¿cuál es la
probabilidad de ganar?
𝑃 𝐺𝑎𝑛𝑎𝑟 =
1
21 ∙ 21 ∙ 21 ∙ 21
1
194,481
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
𝑃 𝐺𝑎𝑛𝑎𝑟 = 0.00000514
𝑷 𝑮𝒂𝒏𝒂𝒓 = 𝟎. 𝟎𝟎𝟎𝟓𝟏𝟒%

Ejercicios.
13. Mario compra un boleto de otro sorteo, en el cual tiene que elegir 5 números de entre 1 y
15, los cuales no se pueden repetir. Si compró el boleto con los números 7, 1, 15, 10 y 11, ¿cuál
es la probabilidad de ganar? ¿en cuál de los dos sorteos tiene más probabilidad de ganar?
1
15 ∙ 14 ∙ 13 ∙ 12 ∙ 11
1
360,360
𝑃 𝐺𝑎𝑛𝑎𝑟 = 0.00000277
𝑷 𝑮𝒂𝒏𝒂𝒓 = 𝟎. 𝟎𝟎𝟎𝟐𝟕𝟕%
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 2 3 4 5 6 8 9 10 11 12 13 14 15
2 3 4 5 6 8 9 10 11 12 13 14 15
2 3 4 5 6 8 9 10 11 12 13 14
2 3 4 5 6 8 9 11 12 13 14

Ejercicios.
14. En una baraja inglesa, ¿cuál es la probabilidad de obtener un rey de tréboles, una reina de
corazones o una carta de tréboles?
𝑃 𝑐𝑢𝑎𝑙𝑞. 𝑐𝑎𝑟𝑡𝑎
=
14
52
𝑃 𝑐𝑢𝑎𝑙𝑞. 𝑐𝑎𝑟𝑡𝑎
= 0.269
𝑷 𝒄𝒖𝒂𝒍𝒒. 𝒄𝒂𝒓𝒕𝒂
= 𝟐𝟔. 𝟗%

Ejercicios.
20. En una bolsa, tenemos pelotas, donde cada una tiene uno de los dígitos entre 0 y 5. ¿Cuál
es la probabilidad de que, al sacar las pelotas, se forme el número 52?
𝑃 𝑛ú𝑚𝑒𝑟𝑜 52 =
1
6 ∙ 5
𝑃 𝑛ú𝑚𝑒𝑟𝑜 52 =
1
30
𝑃 𝑛ú𝑚𝑒𝑟𝑜 52 = 0.0333
𝑷 𝒏𝒖𝒎𝒆𝒓𝒐 𝟓𝟐 = 𝟑. 𝟑𝟑%
0 1 2 3 4 5
0 1 2 3 4

Ejercicios.
Ustedes realizarán los siguientes ejercicios (a partir de la pág. 43):
2
3
4
5
11
15
16
18
19
21
22

Ejercicios.
2. Determina la probabilidad de que al lanzar un dado caiga un número par.
3. Una caja contiene 3 plumones rojos, 5 verdes y 4 azules. La probabilidad de sacar un crayón
rojo es…

Ejercicios.
4. Las calificaciones que obtuvieron 10 alumnos en su examen bimestral de matemáticas son:
9, 5, 9, 6, 5, 6, 7, 6, 9 y 6. La moda de esta muestra es…
5. El juego de dominó contiene 28 fichas. ¿Cuál es la probabilidad de extraer al azar una ficha
con el mismo número de puntos en ambos lados?

Ejercicios.
11. Se sabe que las estaturas de los alumnos de un salón de secundaria son las siguientes (en
cm): 152, 160, 155, 154, 157, 159, 161, 159, 160, 158, 150, 162, 155, 152, 155, 153, 160, 151,
155 y 159. Calcula la media, mediana y moda de estos datos.
15. Se van a lanzar 3 monedas al aire en tiempos distintos. ¿Cuál de las siguientes
probabilidades es la menor?
a. Al menos dos monedas caigan sol.
b. Exactamente 2 monedas caigan águila
c. Las primeras dos monedas caigan caras distintas.
d. No más de una moneda caiga águila.

Ejercicios.
18. Dentro de una lista aleatoria de música, se sabe que se tienen 9 canciones de rock
progresivo, 15 de metal, 8 de grunge, 15 de rock alternativo, 13 de blues y 12 de rock & roll.
¿Cuál es la probabilidad de que al elegir una canción no sea ni de grunge ni de blues? ¿Y cuál
es la probabilidad de que una canción sea de algún tipo de rock?
19. Previo a la katafixia de Chabelo, un concursante tiene que extraer una ficha, la cual puede
contener un número de entre el 1 y el 20. ¿Cuál es la probabilidad de que saque una ficha con
un múltiplo de 4?

Ejercicios.
21. Sabemos que en un grupo de inglés, hay 6 alumnos de 1ro. A, 4 de 1ro. B, 11 de 2do. A y 9
de 2do. B. ¿Cuál es la probabilidad de que si sacamos a un alumno del salón al azar sea de 1ro.
de secundaria?

Mínimo Común Múltiplo y Máximo Común Divisor
El mínimo común múltiplo (mcm) es el entero más pequeño que es múltiplo de los números
dados. Se ocupa en problemas donde, dados los datos, …
- … “vuelven a coincidir”
- … “se repiten”
- … “¿cuándo volverán a encontrarse?”
- … “vuelva a suceder”
- … “lo más próximo”
Es decir, se debe calcular un número más alto que los dados en el problema.

El máximo común divisor (MCD) es el mayor entero que divide a los números dados. Se ocupa
en problemas donde, dados los datos, …
- … “lo más grande posibles”
- … “dividir” “cortar” “repartir”
- … “segmentos/pedazos lo más grande posibles”
- … “envasar” “empaquetar”
- … “lo mayor posible”
Es decir, se debe calcular un número menor que los dados en el problema.

Ejemplo. Tres trabajadores de una empresa reciben un sueldo en tiempos distinto. A uno de
ellos le pagan cada 7 días, a otro le pagan cada 10 días, mientras que al último le pagan cada
15 días. ¿Cada cuántos días coinciden?
Se utiliza el mínimo común múltiplo, que es 2 × 3 × 5 × 7 = 𝟐𝟏𝟎.
7 10 15 2
7 5 15 3
7 5 5 5
7 1 1 7
1 1 1

Ejemplo. Un carpintero tiene tres tablas: una de 24, otra de 36 cm y la última de 20 cm. Las
desea cortar de tal manera que los pedazos sean lo más grande posibles. ¿Cuál debe ser la
medida de cada pedazo de madera?
Se utiliza el máximo común divisor, que es 2 × 2 = 𝟒.
24 36 20 2
12 18 10 2
6 9 5 2
3 9 5 3
1 3 5 3
1 1 5 5
1 1 1
24 2
12 2
6 2
3 3
1
36 2
18 2
9 3
3 3
1
20 2
10 2
5 5
1

Ejemplo. En una joyería, un trabajador cuenta con 96 brillantes rojos, 144 verdes y 72 brillantes
blancos para elaborar collares. Si necesita elaborarlos del mismo color y del mismo tamaño, de
tal manera que tenga la mayor cantidad posible de brillantes, ¿de cuántos debe constar cada
collar?
Se utiliza el máximo común divisor, que es 2 × 2 × 2 × 3 = 𝟐𝟒.
96 144 72 2
48 72 36 2
24 36 18 2
12 18 9 2
6 9 9 2
3 9 9 3
1 3 3 3
1 1 1
96 2
48 2
24 2
12 2
6 2
3 3
1
144 2
72 2
36 2
18 2
9 3
3 3
1
72 2
36 2
18 2
9 3
3 3
1

Ejemplo. Sabemos que 3 hospitales reciben la visita del supervisor en distinto periodo de
tiempo. Uno es visitado cada 6 días, otro cada 9 días y el tercero es visitado cada 12 días.
¿Cada cuántos días son visitados los 3 hospitales en el mismo día?
Se utiliza el mínimo común múltiplo, que es 2 × 2 × 3 × 3 = 𝟑𝟔.
6 9 12 2
3 9 6 2
3 9 3 3
1 3 1 3
1 1 1

Jerarquía de operaciones
1. Paréntesis.
I. Paréntesis ( )
II. Corchetes [ ]
III. Llaves { }
2. Exponentes y raíces
3. Multiplicaciones y divisiones
4. Sumas y restas

Ejemplo.
3 + 5 ∙ 7 − 82
= 3 + 5 ∙ 7 − 64
= 3 + 35 − 64
= −𝟐𝟒
Ejemplo.
10 − 5 − 6 − (−3)2
= 10 − −1 − (9)
= 10 + 1 − 9
= 𝟐

Ejemplo.
5 + [8 −2 + 4 ] ÷ {9 − (8 − 2)}
= 5 + [8 2 ] ÷ {9 − (6)}
= 5 + [16] ÷ {3}
= 21 ÷ {3}
= 𝟕
Ejemplo.
−4 − [ 5 − 8 + 1] {6 + −2 3}
= −4 − [−3 + 1] {6 + (−8)}
= −4 − [−2] {−2}
= −4 + 2 {−2}
= −2 {−2}
= 𝟒

Proporcionalidad
La proporción se presenta cuando existe una relación entre dos variables o datos. Aquí se
tienen dos casos:
- Proporción directa: Si una variable aumenta, la otra igual lo hace. Si una disminuye, la otra
igualmente.
- Proporción inversa: Si una variable disminuye, la otra aumenta, o viceversa.
𝐴
𝐵
𝑥
𝐶

Proporcionalidad
¿Cómo planteo y resuelvo una regla de 3?
1. Escribimos las variables y ordenamos los datos, donde el
dato faltante se representa con la letra x.
2. Identificamos el tipo de proporción que es.
3.
- Si es proporción directa, multiplicamos los números cruzados
y luego lo dividimos entre el número que falta.
- Si es proporción inversa, multiplicamos los números en
horizontal y luego lo dividimos entre el número que falta.
𝐴
𝐵
𝑥
𝐶
𝐴
𝐵
𝑥
𝐶

Proporcionalidad
Ejemplo: Con 4 litros de pintura pintamos 100 𝑚2. ¿Cuántos metros cuadrados podemos
cubrir con un bote que contiene 7 litros?
𝑥 =
100 ∙ 7
4
=
700
4
𝒙 = 𝟏𝟕𝟓 𝒎𝟐
Pintura (litros) Metros cuadrados
4 100
7 x

Proporcionalidad
Ejemplo: Entre 6 personas, tardan 4 horas en descargar la mercancía que les llega a una
bodega. Si para la siguiente ocasión, apoyan 8 personas, ¿cuánto tiempo tardarán?
𝑥 =
6 ∙ 4
8
=
24
8
𝒙 = 𝟑 𝒉𝒐𝒓𝒂𝒔
Personas Tiempo (horas)
6 4
8 x

Proporcionalidad
Ejemplo: Un frasco de vitaminas con 280 pastillas cuesta $72.50. ¿Cuánto cuesta un frasco que
tiene 220 pastillas?
𝑥 =
72.5 ∙ 220
280
=
15,950
280
𝒙 = 𝟓𝟔. 𝟗𝟔 𝒑𝒆𝒔𝒐𝒔
Pastillas Precio
280 72.50
220 x

Proporcionalidad
Ejemplo: Sabemos que 2 de cada 9 alumnos no entregan tarea. Si el profesor tiene un total de
82 alumnos, ¿cuántos de ellos sí entregaron tarea?
𝑥 =
82 ∙ 2
9
=
164
9
𝑥 = 18.22 𝑎𝑙𝑢𝑚𝑛𝑜𝑠
Ahora, al total de 82 alumnos, le restamos los 18.22,
para obtener el número de alumnos que sí
entregaron.
𝟔𝟑. 𝟕𝟖 𝒂𝒍𝒖𝒎𝒏𝒐𝒔
Alumnos que no entregan Alumnos en total
2 9
x 82

Proporcionalidad
Ejemplo: Entre 8 personas, tardan 20 días en terminar una obra. Si para la siguiente obra, se
suman 2 trabajadores más, ¿cuánto tiempo se demorarán en la siguiente ocasión?
𝑥 =
8 ∙ 20
10
=
160
10
𝒙 = 𝟏𝟔 𝒅í𝒂𝒔
Personas Tiempo (días)
8 20
10 x

Proporcionalidad
Ejemplo: Encontrar la medida de la base del triángulo pequeño.
𝑥
70
=
8
20
𝑥 =
70 ∙ 8
20
=
560
20
𝒙 = 𝟐𝟖 𝒄𝒎
70 cm

Ejemplo. Durante la Gran Venta Nocturna de Liverpool, una chica compró 3 vestidos en $9,450.
Si recibió un 25% de descuento, ¿de cuánto fue el descuento y cuánto pagó?
Porcentaje
9,450
25
47250
18900
236250
Le descontaron $2,362.50.
A los $9,450 le resto el descuento de
$2,362.50.
Por lo tanto, pagó $7,087.50.

Ejemplo. En un concurso, participan 28 mujeres y representan el 35%. ¿Cuántos concursantes
hay en total?
𝑥 =
28 ∙ 100
35
=
2,800
35
𝒙 = 𝟖𝟎 𝒄𝒐𝒏𝒄𝒖𝒓𝒔𝒂𝒏𝒕𝒆𝒔
Porcentaje
Concursantes Porcentaje
28 35
x 100

• Ejemplo.
7 𝑥 − 3 = 9 𝑥 + 1 − 38
7𝑥 − 21 = 9𝑥 + 9 − 38
7𝑥 − 9𝑥 = +9 − 38 + 21
−2𝑥 = −8
𝑥 =
−8
−2
𝒙 = 𝟒
Ecuaciones de primer grado

• Ejemplo.
7𝑥
8
− 5 =
9𝑥
10
− 8
40
7𝑥
8
− 5 = 40
9𝑥
10
− 8
35𝑥 − 200 = 36𝑥 − 320
35 − 36𝑥 = −320 + 200
−𝑥 = −120
𝒙 = 𝟏𝟐𝟎

• Ejemplo.
𝑥 +
𝑥
2
+
𝑥
3
= 11
6 𝑥 +
𝑥
2
+
𝑥
3
= 6(11)
6𝑥 + 3𝑥 + 2𝑥 = 66
11𝑥 = 66
𝑥 =
66
11
𝒙 = 𝟔

Ángulos
Ejemplo. Indica el valor del ángulo donde se encuentran los demás establecimientos de
acuerdo al ángulo dado.
𝟔𝟖°
𝟔𝟖°
𝟔𝟖°
𝟔𝟖°
𝟏𝟏𝟐°
𝟏𝟏𝟐°
𝟏𝟏𝟐°
𝟏𝟏𝟐°

Ángulos
Ejemplo. ¿Cuánto mide el ángulo x formado por la altura y la diagonal del rectángulo?
Como entre el ángulo x y el ángulo de 14° deben sumar 90°, entonces, 𝒙 = 𝟕𝟔°.
x
14°

Ángulos
Ejemplo. ¿Cuánto mide el ángulo x?
Como entre el ángulo x y el ángulo de 32° deben sumar 180°, entonces, 𝒙 = 𝟏𝟒𝟖°.
x
32°

Ángulos
Ejemplo. ¿Cuánto mide el ángulo x?
Como la suma de los ángulos internos de un triángulo es de 180°, entonces 𝒙 = 𝟕𝟗°.
35°
𝑥
66°

Potencias algebraicas
• Ejemplos.
4𝑥2
𝑦3
𝑧5
9𝑥𝑦2
𝑧7
= 𝟑𝟔𝒙𝟑
𝒚𝟓
𝒛𝟏𝟐
3𝑥4
𝑧2
−7𝑥4
𝑦9
𝑧5
= −𝟐𝟏𝒙𝟖𝒚𝟗𝒛𝟕
4𝑥2
𝑦3
𝑧5 3
= 𝟔𝟒𝒙𝟔
𝒚𝟗
𝒛𝟏𝟓
−2𝑥5
𝑦9
𝑧2 3
= −𝟖𝒙𝟏𝟓𝒚𝟐𝟕𝒛𝟔

Potencias algebraicas
• Ejemplos.
16𝑥4𝑦3𝑧2
4𝑥𝑦9𝑧2
=
𝟒𝒙𝟑
𝒚𝟔
−
25𝑥3𝑦5𝑧6
15𝑥4𝑧2
= −
𝟓𝒚𝟓𝒛𝟒
𝟑𝒙
−5−2
= −
1
52
= −
1
25
−5 −2
=
1
(−5)2
=
1
25

Factorización
Ejemplo.
8𝑥5 + 24𝑥3 − 28𝑥9
= 4𝑥3(2𝑥2 + 6 − 7𝑥6)
Ejemplo.
27𝑥7𝑦 − 18𝑥8𝑦4 − 3𝑥5𝑦3
= 3𝑥5𝑦(9𝑥2 − 6𝑥3𝑦3 − 𝑦2)

Factorización
Ejemplo.
5𝑥9𝑦7 − 7𝑥5 + 2𝑥3𝑦
= 𝑥3(5𝑥6𝑦7 − 7𝑥2 + 2𝑦)

Productos notables
Ejemplo.
5𝑥 + 2𝑦 2
= 5𝑥 2
+ 2 5𝑥 2𝑦 + 2𝑦 2
= 𝟐𝟓𝒙𝟐 + 𝟐𝟎𝒙𝒚 + 𝟒𝒚𝟐
Ejemplo.
5𝑥 − 2𝑦 2
= 5𝑥 2
− 2 5𝑥 2𝑦 + 2𝑦 2
= 𝟐𝟓𝒙𝟐 − 𝟐𝟎𝒙𝒚 + 𝟒𝒚𝟐

Factorización
Ejemplo.
25𝑥2 + 90𝑥𝑦 + 81𝑦2
25𝑥2 81𝑦2
= 5𝑥 + 9𝑦 2
Ejemplo.
25𝑥2 − 90𝑥𝑦 + 81𝑦2
25𝑥2 81𝑦2
= 5𝑥 − 9𝑦 2

Productos notables
Ejemplo.
(3𝑥3 − 6𝑦)(3𝑥3 + 6𝑦)
= 3𝑥3 2
− 6𝑦 2
= 𝟗𝒙𝟔 − 𝟑𝟔𝒚𝟐
Ejemplo.
(7𝑥4 − 𝑦)(7𝑥4 + 𝑦)
= 7𝑥4 2
− 𝑦 2
= 𝟒𝟗𝒙𝟖 − 𝒚𝟐

Factorización
Ejemplo.
100𝑥4 − 4𝑦2
100𝑥4 4𝑦2
= (10𝑥2
− 2𝑦)(10𝑥2
+ 2𝑦)
Ejemplo.
64𝑥8 − 𝑦10
64𝑥8 𝑦10
= (8𝑥4 − 𝑦5)(8𝑥4 + 𝑦5)

Factorización
Ejemplo.
𝑥2 + 8𝑥 + 15
+5 +3 = +15
+5 + 3 = +8
= (𝑥 + 5)(𝑥 + 3)
Ejemplo.
𝑥2 + 7𝑥 − 30
+10 −3 = −30
+10 − 3 = +7
= (𝑥 + 10)(𝑥 − 3)

Factorización
Ejemplo.
𝑥2 − 11𝑥 + 28
−7 −4 = +28
−7 − 4 = −11
= (𝑥 − 7)(𝑥 − 4)
Ejemplo.
𝑥2 − 2𝑥 − 3
−3 (+1) = −3
−3 + 1 = −2
= (𝑥 − 3)(𝑥 + 1)

Multiplicación de polinomios
• Ejemplo.
4𝑥2
+ 3𝑥 𝑥2
− 2𝑥 + 1
= 4𝑥2
𝑥2
− 2𝑥 + 1 + 3𝑥 𝑥2
− 2𝑥 + 1
= 4𝑥4 − 8𝑥3 + 4𝑥2 + 3𝑥3 − 6𝑥2 + 3𝑥
= 4𝑥4 − 5𝑥3 − 2𝑥2 + 3𝑥

Multiplicación de polinomios
• Ejemplo.
5𝑥 − 2 𝑥2
+ 4𝑥 − 2
= 5𝑥 𝑥2
+ 4𝑥 − 2 − 2 𝑥2
+ 4𝑥 − 2
= 5𝑥3 + 20𝑥2 − 10𝑥 − 2𝑥2 − 8𝑥 + 4
= 5𝑥3 + 18𝑥2 − 18𝑥 + 4

División de
polinomios
División de un
polinomio entre un
monomio
División de un
polinomio entre
otro polinomio
Se reparte el
denominador a cada
sumando del
numerador y se
aplican propiedades.
Si se divide entre un
binomio de la forma
𝑥±𝑎.
Si no se divide entre
un binomio de grado
1.
Se aplica algoritmo de
la división para
polinomios.
Se aplica división
sintética.

División de polinomios
• Ejemplo.
32𝑥7
𝑦6
𝑧5
+ 16𝑥5
𝑦7
𝑧3
− 8𝑥3
𝑦6
𝑧3
8𝑥3𝑦6𝑧3
=
32𝑥7
𝑦6
𝑧5
8𝑥3𝑦6𝑧3
+
16𝑥5
𝑦7
𝑧3
8𝑥3𝑦6𝑧3
−
8𝑥3
𝑦6
𝑧3
8𝑥3𝑦6𝑧3
= 𝟒𝒙𝟒
𝒛𝟐
+ 𝟐𝒙𝟐
𝒚 − 𝟏

• Ejemplo.
2𝑥2
𝑥 + 3 2𝑥3 + 7𝑥2 + 2𝑥 − 3
−2𝑥3 − 6𝑥2
𝑥2
+ 2𝑥 − 3

• Ejemplo.
2𝑥2
+ 𝑥
𝑥 + 3 2𝑥3 + 7𝑥2 + 2𝑥 − 3
−2𝑥3 − 6𝑥2
𝑥2
+ 2𝑥 − 3
−𝑥2 − 3𝑥
−𝑥 − 3

• Ejemplo.
2𝑥2
+ 𝑥 − 1
𝑥 + 3 2𝑥3 + 7𝑥2 + 2𝑥 − 3
−2𝑥3 − 6𝑥2
𝑥2
+ 2𝑥 − 3
−𝑥2 − 3𝑥
−𝑥 − 3
+𝑥 + 3
0

• Ejemplo.
3𝑥2
6𝑥 − 2 18𝑥3 − 18𝑥2 + 28𝑥 − 8
−18𝑥3 + 6𝑥2
−12𝑥2
+ 28𝑥 − 8

• Ejemplo.
3𝑥2
− 2𝑥
6𝑥 − 2 18𝑥3 − 18𝑥2 + 28𝑥 − 8
−18𝑥3 + 6𝑥2
−12𝑥2
+ 28𝑥 − 8
12𝑥2 − 4𝑥
24𝑥 − 8

• Ejemplo.
3𝑥2
− 2𝑥 + 4
6𝑥 − 2 18𝑥3 − 18𝑥2 + 28𝑥 − 8
−18𝑥3 + 6𝑥2
−12𝑥2
+ 28𝑥 − 8
12𝑥2 − 4𝑥
24𝑥 − 8
−24𝑥 + 8
0

• Ejemplo.
𝑥
𝑥2 − 1 𝑥3 − 6𝑥2 − 𝑥 + 6
−𝑥3 + 𝑥
−6𝑥2
+ 6

• Ejemplo.
𝑥 − 6
𝑥2 − 1 𝑥3 − 6𝑥2 − 𝑥 + 6
−𝑥3 + 𝑥
−6𝑥2
+ 6
+6𝑥2 − 6
0

• Ejemplo.
2𝑥3−15𝑥+9
𝑥+3
𝑥 + 3 2𝑥3
+ 0𝑥2
− 15𝑥 + 9

• Ejemplo.
2𝑥2
𝑥 + 3 2𝑥3 + 0𝑥2 − 15𝑥 + 9
−2𝑥3 − 6𝑥2
−6𝑥2
− 15𝑥 + 9

• Ejemplo.
2𝑥2
− 6𝑥
𝑥 + 3 2𝑥3 + 0𝑥2 − 15𝑥 + 9
−2𝑥3 − 6𝑥2
−6𝑥2
− 15𝑥 + 9
6𝑥2 + 18𝑥
3𝑥 + 9

• Ejemplo.
2𝑥2
− 6𝑥 + 3
𝑥 + 3 2𝑥3 + 0𝑥2 − 15𝑥 + 9
−2𝑥3 − 6𝑥2
−6𝑥2
− 15𝑥 + 9
6𝑥2 + 18𝑥
3𝑥 + 9
−3𝑥 − 9
0

• Ejemplo.
2𝑥3 − 15𝑥 + 9
𝑥 + 𝟑
𝑥3 𝑥2 𝑥 𝑇. 𝐼.
+2 0 − 15 + 9
−𝟑
+2

• Ejemplo.
2𝑥3 − 15𝑥 + 9
𝑥 + 𝟑
𝑥3 𝑥2 𝑥 𝑇. 𝐼.
+2 0 − 15 + 9
−𝟑 − 6 + 18 − 9
+2 − 6 + 3 0
𝑥2
𝑥 𝑇. 𝐼. 𝑅
= 2𝑥2 − 6𝑥 + 3

• Ejemplo.
3𝑥2 + 25𝑥 − 18
𝑥 + 𝟗
𝑥2 𝑥 𝑇. 𝐼.
+3 + 25 − 18
−𝟗
+3

• Ejemplo.
3𝑥2 + 25𝑥 − 18
𝑥 + 𝟗
𝑥2 𝑥 𝑇. 𝐼.
+3 + 25 − 18
−𝟗 − 27 + 18
+3 − 2 0
𝑥 𝑇. 𝐼. 𝑅
= 3𝑥 − 2

La notación científica se utiliza para expresar cantidades muy grandes o muy pequeñas y
consiste en expresarlas en función de potencias de 10.
Una expresión en notación científica es de la forma:
5.12 × 107
Se desplazará a la derecha si el exponente es positivo y hacia la izquierda si es negativo.
Notación científica
Potencia
de 10
Cantidad de posiciones
que se mueve el punto
decimal.
Cifra
significativa

De notación decimal a notación científica
Cuando son números grandes Cuando son números pequeños
1. Escribimos la primer cifra significativa.
2. Escribimos las siguientes cifras hasta
la última cifra distinta de cero.
3. Colocamos el “x10”.
4. El exponente será la cantidad de
posiciones que debe recorrerse el punto
a la derecha.
1. Escribimos la primer cifra significativa
que sea distinta de cero.
2. Escribimos las cifras restantes.
3. Colocamos el “x10”.
4. El exponente será la cantidad de
posiciones que debe recorrerse el punto
a la izquierda.

Ejemplos:
7,000,000
= 𝟕 × 𝟏𝟎𝟔
1,280,000,000
= 𝟏. 𝟐𝟖 × 𝟏𝟎𝟗
75,070,000,000
= 𝟕. 𝟓𝟎𝟕 × 𝟏𝟎𝟏𝟎
10,905,000,000,000,000
= 𝟏. 𝟎𝟗𝟎𝟓 × 𝟏𝟎𝟏𝟔

Ejemplos:
0.058
= 𝟓. 𝟖 × 𝟏𝟎−𝟐
0.000,008
= 𝟖 × 𝟏𝟎−𝟔
0.901
= 𝟗. 𝟎𝟏 × 𝟏𝟎−𝟏
0.000,000,500,4
= 𝟓. 𝟎𝟎𝟒 × 𝟏𝟎−𝟕

Para convertir de notación decimal a notación científica, seguimos estos pasos:
5.12 × 107
1. Se escriben las cifras que conforman el número en su notación científica.
2. Recorremos el punto decimal la cantidad de posiciones según el exponente del “x 10”,
tomando en cuenta el sentido.
Exponente negativo Exponente positivo

Ejemplos:
9 × 1011
= 𝟗𝟎𝟎, 𝟎𝟎𝟎, 𝟎𝟎𝟎, 𝟎𝟎𝟎
7.02 × 107
= 𝟕𝟎, 𝟐𝟎𝟎, 𝟎𝟎𝟎
5.413 × 103
= 𝟓, 𝟒𝟏𝟑
4.9001 × 1014
= 𝟒𝟗𝟎, 𝟎𝟏𝟎, 𝟎𝟎𝟎, 𝟎𝟎𝟎, 𝟎𝟎𝟎

Ejemplos:
3 × 10−3
= 𝟎. 𝟎𝟎𝟑
4.6 × 10−5
= 𝟎. 𝟎𝟎𝟎, 𝟎𝟒𝟔
6.004 × 10−11
= 𝟎. 𝟎𝟎𝟎, 𝟎𝟎𝟎, 𝟎𝟎𝟎, 𝟎𝟔𝟎, 𝟎𝟒
1.0905 × 10−2
= 𝟎. 𝟎𝟏𝟎, 𝟗𝟎𝟓

Plantear el modelo matemático para resolver un problema consiste en traducir el problema
expresado con palabras en una ecuación algebraica utilizando el lenguaje algebraico. La
solución de la ecuación nos da la respuesta al problema.
Recordemos que el lenguaje algebraico es una forma de traducir por medio de símbolos,
letras y números ciertas expresiones o frases que se pueden modelar matemáticamente. Este
lenguaje nos ayuda a plantear y resolver problemas matemáticos. En él, utilizamos letras para
representar datos que no conocemos.
Problemas de ecuaciones lineales

Ejemplo: El triple de un número es 10 unidades mayor que la mitad del mismo. ¿Cuál es ese
número?
𝟑𝒙 =
𝒙
𝟐
+ 𝟏𝟎
3𝑥 −
𝑥
2
= +10
5𝑥
2
= 10
5𝑥 = 20
𝒙 = 𝟒

Ejemplo: Un número más 14 es igual a 7 veces el mismo número. ¿Cuál es el número?
𝒙 + 𝟏𝟒 = 𝟕𝒙
𝑥 − 7𝑥 = −14
−6𝑥 = −14
𝑥 =
−14
−6
𝒙 =
𝟕
𝟑

Ejemplo: La suma de cuatro números consecutivos es 102. ¿Cuáles son esos números?
𝒙 + 𝒙 + 𝟏 + 𝒙 + 𝟐 + 𝒙 + 𝟑 = 𝟏𝟎𝟐
𝑥 + 𝑥 + 𝑥 + 𝑥 = 102 − 1 − 2 − 3
4𝑥 = 96
𝑥 =
96
4
𝒙 = 𝟐𝟒
Los números consecutivos son:
𝒙 𝟐𝟒
𝒙 + 𝟏 𝟐𝟓
𝒙 + 𝟐 𝟐𝟔
𝒙 + 𝟑 27

Serie 4, pág. 113, ejercicio 4. Repartimos $900 entre 3 personas. La tercera persona recibe $50
menos que la segunda. La segunda recibe $100 más que la primera. ¿Cuánto dinero recibe c/u?
𝒙 + 𝒚 + 𝒛 = 𝟑𝟎𝟎
𝒙 + 𝒙 + 𝟏𝟎𝟎 + 𝒛 = 𝟑𝟎𝟎
𝒙 + 𝒙 + 𝟏𝟎𝟎 + 𝒙 + 𝟓𝟎 = 𝟑𝟎𝟎
𝑥 + 𝑥 + 𝑥 = 300 − 100 − 50
3𝑥 = 150
𝑥 =
150
3
𝒙 = 𝟓𝟎
La primera persona recibió $50.
La segunda persona recibió $150.
La tercera persona recibió $100.

Ejemplo: La edad de Chabelo es 6 veces la edad de Dani más 1 año. ¿Qué edad tiene Chabelo
si se sabe que la suma de las edades de ambos es de 99 años?
𝑪 + 𝑫 = 𝟗𝟗
𝟔𝑫 + 𝟏 + 𝑫 = 𝟗𝟗
6𝐷 + 𝐷 = 99 − 1
7𝐷 = 98
𝐷 =
98
7
𝑫 = 𝟏𝟒
𝐶 + 14 = 99
𝐶 = 99 − 14
𝑪 = 𝟖𝟓
𝐶 = 6 14 + 1
𝐶 = 84 + 1
𝑪 = 𝟖𝟓

Ejemplo: La mitad de los cubos que hay en una caja son azules, la quinta parte son amarillos, la
décima parte son rojos y además hay 40 verdes. ¿Cuántos cubos tiene la caja?
𝒙 el total de cubos en la caja
𝒙 =
𝒙
𝟐
+
𝒙
𝟓
+
𝒙
𝟏𝟎
+ 𝟒𝟎
10 𝑥 −
𝑥
2
−
𝑥
5
−
𝑥
10
= 10(40)
10𝑥 − 5𝑥 − 2𝑥 − 𝑥 = 400
2𝑥 = 400
𝑥 =
400
2
𝒙 = 𝟐𝟎𝟎

Ejemplo: Sabemos que la base de un rectángulo mide el triple de su altura más dos unidades y
que su perímetro es de 36 cm. ¿Cuánto miden su base y su altura?
𝒙 la altura del rectángulo
𝟑𝒙 + 𝟐 + 𝒙 + 𝟑𝒙 + 𝟐 + 𝒙 = 𝟑𝟔
𝟑𝒙 + 𝒙 + 𝟑𝒙 + 𝒙 = 36 − 2 − 2
8𝑥 = 32
𝒙 = 𝟒
La altura mide 4 cm.
La base mide 14 cm.
x
3x+2

Ejemplo: Un lado de un triángulo mide el doble que otro de los lados y el lado restante mide la
suma de los otros dos. Si el perímetro del triángulo es de 120 cm, ¿cuánto mide cada lado?
𝒙 un lado del triángulo
𝒙 + 𝟐𝒙 + 𝒙 + 𝟐𝒙 = 𝟏𝟐𝟎
6𝑥 = 120
𝒙 = 𝟐𝟎
Un lado mide 20 cm.
Otro lado mide 40 cm.
El lado restante mide 60 cm.
x
2x
x+2x

Clases COMIPEMS.pptx

Recomendados

Recomendados

Más contenido relacionado

Similar a Clases COMIPEMS.pptx

Similar a Clases COMIPEMS.pptx (20)

Último

Último (20)

Clases COMIPEMS.pptx