Las derivadas son el resultado de realizar un proceso de diferenciación sobre una función o una expresión. En matemáticas, La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. La derivada es el ritmo de cambio de cualquier función en un determinado instante, pero que también puede representar el ritmo o velocidad de cambio de cualquier cosa.

1. Las Derivadas

2. República Bolivariana De Venezuela
Ministerio El Poder Popular Para La Educación
Instituto Universitario De Tecnología
Antonio José De Sucre
Extensión: Maracaibo
Cátedra: Matemáticas
Alumno: Alejandra Tortolero Brett CI: 28.436.571
Las Derivadas

3. Esquema
Introducción………………………………………………………………1
Capítulo I: Definición…………………………………………………………………...2
Capítulo II: Interpretación geométrica de la Derivada….………………………..…......3
Capítulo III: Historia…………………………………..……………………………......4
Capítulo IV: Aplicación de Derivadas……….…………...……………………………..5
Capítulo V: Propiedades de Derivadas…..………………………………………………6
Capítulo VI: Notaciones de la Derivadas...………………………………………….......7
Capítulo VII: Cálculo de Derivadas……...……………………………………………...8
Capítulo VIII: Formulas de Derivación…..….…………………………………………..9
Capítulo IX: Ejercicios de Derivadas....……………...………………………………....10
Conclusión………………………………………………………………....11

4. Introducción
El deseo de medir y de cuantificar el cambio, la variación, condujo en el siglo XVII
hasta la noción de derivada.
El estudio de las operaciones con derivadas, junto con las integrales, constituye el
cálculo infinitesimal. Los introductores fueron Newton y Leibnitz, de forma
independiente. Los conceptos son difíciles y hasta bien entrado el siglo XIX no se
simplificaron. A ello contribuyó la aparición de una buena notación, que es la que
usaremos. Las aplicaciones prácticas de esta
teoría no dejan de aparecer.
Dentro de las aplicaciones de las derivadas quizás una de las más importantes es la de
conseguir los valores máximos y mínimos de una función. También la derivada es una
herramienta
muy útil para graficar funciones.

5. Capítulo I
Definición
Las derivadas son el resultado de realizar un proceso de diferenciación sobre una
función o una expresión. En matemáticas, La derivada de una función es un concepto
local, es decir, se calcula como el límite de la rapidez de cambio media de la función en
cierto intervalo, cuando el intervalo considerado para la variable independiente se torna
cada vez más pequeño. Por eso se habla del valor de la derivada de una función en un
punto dado. La derivada de un concepto local se calcula como el límite de la rapidez de
cambio media de la función en un cierto intervalo, cuando el intervalo considerado para
la variable independiente se toma cada vez más pequeño. La derivada de una función,
en principio, puede ser calculada de la definición, mediante el cociente de diferencias, y
después calcular su límite. En la práctica, únicamente las derivadas de unas pocas
funciones son conocidas, las derivadas de otras funciones son fáciles de calcular
utilizando reglas para obtener derivadas de funciones más complicadas de otras más
simples.
El valor de la derivada de una función en un punto puede interpretarse
geométricamente, ya que se corresponde con pendiente de la recta tangente a la gráfica
de la función en dicho punto.
La derivada es el ritmo de cambio de cualquier función en un determinado instante,
pero que también puede representar el ritmo o velocidad de cambio de cualquier cosa.

6. El dominio de derivadas. Es posible que la derivada de una función en un punto,
no exista, en cuyo caso decimos que la función no es derivable en ese punto.
Decimos que una función es derivable en un intervalo abierto (x1,x2) de su dominio
si lo es en cada uno de sus puntos. En general el conjunto de puntos donde la función es
derivable constituye su dominio de derivabilidad. Hay que observar que el dominio de
derivabilidad de una función puede no coincidir con el dominio de la función. O dicho
de otra forma, el dominio de la función f(x) puede no coincidir con el dominio de la
función derivada f ´(x).Ejemplo: Consideremos la función valor absoluto de x que
queda definida de la siguiente manera:
La Función derivada Sea f una función continua definida en un dominio A, se
define la función derivada de f en el punto a del conjunto A y se denota por f´(a), al
valor del siguiente límite: Si llamamos h= x-a, también se puede escribir la definición
de la siguiente forma:

7. Si una vez calculada la función derivada, ésta a su vez se puede volver a derivar, esta
función se denomina derivada segunda y se denota por f´´. Si nuevamente se puede
derivar, se obtendría la derivada tercera y así sucesivamente, conociéndose este proceso
por derivadas sucesivas.
También encontramos las derivadas laterales llamadas derivadas por la izquierda:
Análogamente, llamamos derivada por la derecha:
Una función será derivable cuando los límites laterales de la derivada existan y
tengan el mismo valor.

8. Capítulo II
Interpretación geométrica de la
Derivada
Geométricamente, la derivada de una función en un punto dado me da el
pendiente de la recta tangente a en el punto .
Explicación:
La recta dibujada forma un cierto ángulo que llamamos .
Evidentemente, este ángulo estará relacionado con el pendiente de la recta, que hemos
dicho que era el valor de la derivada en el punto de tangencia.
Por lo tanto uno puede concluir en:

9. Geométricamente la derivada se define como la pendiente de la recta tangente a la
curva en un punto previamente establecido. Antes debemos explicar varios conceptos
que estarán aplicados en dicha geometrización:
Recta tangente: Es una recta que tiene solo un punto común con una curva o
función.
La pendiente de la recta: está definida como el cambio o diferencia en el eje
vertical dividido por el respectivo cambio o diferencia en el eje horizontal (relación de
cambio)
Notación:
Recta secante: Es una recta que interseca dos o más puntos de una curva.

10. Capítulo III
Historia
Los problemas típicos que dieron origen al cálculo infinitesimal, comenzaron a
plantearse en la época clásica de la antigua Grecia (siglo III a.c), pero no se encontraron
métodos sistemáticos de resolución hasta veinte siglos después (en el siglo XVII por
obra de Isaac Newton y Gottfried Leibniz).
En lo que atañe a las derivadas existen dos conceptos de tipo geométrico que le
dieron origen:
El problema de la tangente a una curva (Apolonio de Perge)
El Teorema de los extremos: máximos y mínimos (Pierre de Fermat)
En su conjunto dieron origen a lo que modernamente se conoce como cálculo
diferencial.
Siglo XVII
Johannes Kepler y Bonaventura Cavalieri empezaron a andar un camino que llevaría
en medio siglo al descubrimiento del cálculo infinitesimal.
A mediados del siglo XVII, las cantidades infinitesimales fueron cada vez más
usadas para resolver problemas de cálculos de tangentes, áreas, volúmenes; los
primeros darían origen al cálculo diferencial, los otros al integral.
Newton y Leibniz.

11. A finales del siglo XVII sintetizaron en dos conceptos, métodos usados por sus
predecesores los que hoy llamamos «derivadas» e «integrales». Desarrollaron reglas
para manipular las derivadas (reglas de derivación) y mostraron que ambos conceptos
eran inversos (teorema fundamental del cálculo).
Newton desarrolló en Cambridge su propio método para el cálculo de tangentes. En
1665 encontró un algoritmo para derivar funciones algebraicas que coincidía con el
descubierto por Fermat. A finales de 1665 se dedicó a reestructurar las bases de su
cálculo, intentando desligarse de los infinitesimales, e introdujo el concepto de fluxión,
que para él era la velocidad con la que una variable «fluye» (varía) con el tiempo.
Gottfried Leibniz
Fue uno de los grandes pensadores de los siglos XVII y XVIII, y se le reconoce
como "El último genio universal". Realizó profundas e importantes contribuciones en
las áreas de metafísica, epistemología, lógica, filosofía de la religión, así como en la
matemática, física, geología, jurisprudencia e historia. Incluso Denis Diderot, el filósofo
deísta francés del siglo XVIII, cuyas opiniones no podrían estar en mayor oposición a
las de Leibniz
Leibniz, por su parte, formuló y desarrolló el cálculo diferencial en 1675. Fue el
primero en publicar los mismos resultados que Isaac Newton descubriera 10 años antes.
En su investigación conservó un carácter geométrico y trató a la derivada como un
cociente incremental y no como una velocidad, viendo el sentido de su correspondencia
con la pendiente de la recta tangente a la curva en dicho punto. A él se deben los
nombres de: cálculo diferencial y cálculo integral, así como los símbolos de derivada y
el símbolo de la integral.

12. Capítulo IV
Aplicaciones de una derivada
La derivada tiene una gran variedad de aplicaciones además de darnos la pendiente
de la tangente a una curva en un punto. Se puede usar la derivada para estudiar tasas de
variación, valores máximos y mínimos de una función, concavidad y convexidad, etc.
La derivada de una función f en un punto x se denota como f′(x). La función cuyo
valor en cada punto x es esta derivada es la llamada función derivada de f, denotada por
f′. El proceso de encontrar la derivada de una función se denomina diferenciación, y es
una de las herramientas principales en el área de las matemáticas conocida como cálculo
infinitesimal.
Las derivadas encuentran un lugar vital en la ingeniería, física e incluso en los
negocios y la economía, etc. Algunas de las aplicaciones más notables de las derivadas
se explican a continuación:
La derivada nos sirve para encontrar la pendiente de la recta tangente a una gráfica
en un punto x dado.
Algunas de las aplicaciones más notables de las derivadas se explican a continuación:
 Tasa de variación: Esta es la aplicación más utilizada de las derivadas.
Encuentra su aplicación en muchos problemas de la física.
 Punto Crítico: El punto crítico tiene una cantidad vasta de aplicaciones que
incluyen la termodinámica, la física de la materia condensada, etc. Un punto
crítico es aquel donde la derivada de la función es cero,

13.  Determinación de valores mínimos y máximos: A este proceso se le denomina
optimización. Existen una serie de problemas que requieren la determinación de
los valores mínimos y máximos de alguna función tal como la determinación del
menor costo, aproximación del menor tiempo, cálculo de mayor ganancia, etc.
 Método de Newton: Una aplicación digna de notar de las derivadas es el método
de Newton, este es utilizado para rastrear las raíces de una ecuación en una
cascada de etapas para que en cada paso de la solución encontremos una
solución mejor y más adecuada como raíz de la ecuación.
 Aplicaciones en el ámbito del comercio: Existe una gran cantidad de lugares en
el comercio donde las derivadas son requeridas. Dado que el objetivo final del
comercio es el de maximizar las ganancias y minimizar las pérdidas, la teoría de
máximos y mínimos puede utilizarse aquí para evaluar la respuesta correcta y así
aumentar la productividad total del comercio. También resulta conveniente
analizar el costo promedio de un artículo lo que puede ayudar al aumento de la
ganancia.
 Aproximación lineal: En una serie de ramas de la física, como es el caso de la
óptica, la Aproximación lineal juega un papel vital. En este utilizamos una
función lineal con el fin de encontrar la aproximación de cualquier función
general.

14. Capítulo V
Propiedades de una derivada
Las derivadas forman una parte importante del cálculo. En base a su definición está
claro que la salida de la función es una función de la entrada de la función.
Las derivadas tienen algunas propiedades especiales puesto que estas propiedades
resuelven los problemas de una manera mejor y más conveniente, con un mejor enfoque
hacia el tema.
Algunas de las propiedades más importantes son las siguientes:
 Si la función f(x): X → Y es diferenciable en un punto P, entonces se puede
concluir que la función f(x) es continua en el punto p.
 La derivada de la suma de dos funciones es igual a la suma de las derivadas de
las dos funciones tomadas individualmente. La misma regla aplica también para
la resta de dos derivadas. Esta regla es más conocida por el nombre de la regla
de la linealidad.
 La derivada de la multiplicación de una cantidad escalar con una función es
igual a cuando la cantidad escalar se multiplica a la derivada de la misma
función.
 La derivada de un número constante es siempre igual a cero.
 La diferenciación de una variable con respecto a si misma producirá uno.
 La derivada de la multiplicación de dos funciones es lo mismo que sumar la
multiplicación de la primera función con la derivada de la segunda función y la

15. multiplicación de la segunda función con la derivada de la primera función. Esta
regla se conoce más comúnmente con el nombre de la regla del producto.
 La derivada de una variable elevada a una potencia es igual a las veces de la
potencia de la derivada de la misma variable elevada a una potencia reducida por
uno. Esta regla es mejor conocida por el nombre de la regla de la potencia. Es
esencial que n sea un número real para que la propiedad anterior sea cierta.
 La derivada de la división de una función con alguna otra función es lo mismo
que la división de la resta de la multiplicación de la primera función con la
derivada de la segunda función y la multiplicación de la segunda función con la
derivada de la primera función con el cuadrado de la segunda función. Aquí el
valor de la función no debería ser igual a cero. Esta regla se conoce por el
nombre de la regla del cociente.
 La regla de la cadena es una propiedad bastante compleja y se utiliza para
funciones compuestas; es decir una función que es impuesta sobre cualquier otra
función. De dos funciones diferenciables g(x) y f(x) que haya en una función
compuesta h(x) se define como,
h(x) = g(f(x)) = (g 0 f)(x)
 Para la función anterior h(x) la derivada puede ser calculada usando la regla de
la cadena de la siguiente forma,
 La Regla de la cadena sólo puede ser usada cuando existen dependencias en
cadena en una función, en otras palabras, para funciones compuestas. Observe
un ejemplo resuelto con la regla de la potencia,
d(5x4)/dx = 5[d(x4)/dx]
= 5(4x4−1)
= 5(4x3)
= 204x3

16. Ejemplos:

17. Capítulo VI
Las notaciones de Derivadas
La notación de la derivada es la forma en la que expresamos derivadas
matemáticamente. Esto es en contraste del lenguaje natural en el que decimos
simplemente "la derivada de...".
Existen 3 tipos diferentes de notación, creados por diferentes matemáticos. Estos
son:
 Notación de Newton para Derivadas:
En la notación de Newton para la diferenciación se representa la diferenciación
mediante un punto o comilla situado sobre el nombre de la función, y que Newton
denominó fluxion. La notación de Isaac Newton se utiliza fundamentalmente en
mecánica.
Partiendo de una función:
La notación de Newton para la diferenciación respecto al tiempo, era poner un punto
arriba del nombre de la función:

18. Y así sucesivamente.
 Notación de Langrange para Derivadas:
En la notación de Lagrange, la derivada de f se expresa como f′, prime (se
pronuncia "f prima”).
La notación más simple para diferenciación, en uso actual, es debida a Lagrange. Para
identificar las derivadas de en el punto , se escribe:
Para la primera derivada,
Para la segunda derivada,
Para la tercera derivada,
Para la enésima derivada ( ). (También se pueden usar números
romanos).
Para la función derivada de en , se escribe . De modo parecido, para la segunda
derivada de en , se escribe , y así sucesivamente
Esta notación es probablemente la más común cuando se trabaja con funciones de
una variable
 Notaciones de Cauchy y Jacobio o
 Notacion de Leibniz
En la notación de leibniz, la derivada de f se expresa como cuando
tenemos la ecuación , podemos expresar la derivada como . Aquí,
sirve como un operador que indica una deriacion con respecto a x. esta notacion nos

19. permite expresar directamente la derivada de una expresión sin usar una función o una
variable dependiente. Se escribe: la derivada de se expresa como .

20. Capítulo VII
Cálculo de derivadas
Recordamos que, formalmente, la derivada de una función es un límite. Sin embargo,
como la mayoría de las funciones son una composición de funciones más simples,
podemos aplicar reglas para calcular la derivada sin necesidad de límites.
El proceso de cálculo de la derivada de una función se llama diferenciación. Siempre
se deriva o diferencia, se usa mayoritariamente la primera palabra, respecto a una
variable, normalmente x, de forma genérica y una vez que hemos obtenido la derivada
sustituimos en la x el punto donde queremos calcular la derivada, particularizando así el
valor de ésta. La forma de calcular la derivada usando la definición consiste en aplicar
la fórmula de la definición.
Nunca se usa la definición de la derivada de una función para calcular su función
derivada ya que es un proceso largo y demasiado complejo, máxime cuando existe otro
método mucho más rápido y sobre todo menos propenso a cometer errores. Para
calcular la derivada de una función vamos a usar la Tabla de derivadas o Tabla de
fórmulas de derivadas junto con las reglas de derivación.
Reglas de derivación
Sean f(x) y g(x) dos funciones que vamos a denotar por f y g
 Derivada de la suma/resta de dos funciones
La derivada de una suma/resta de dos funciones es la suma/resta de las derivadas de
estas funciones

21.  Derivada del producto de dos funciones
La derivada del producto de dos funciones es igual a la derivada de la primera función
por la segunda sin derivar más la primera sin derivar por la segunda derivada.
 Derivada del cociente de dos funciones
a derivada del cociente de dos funciones es igual a la derivada del numerador por el
denominador sin derivar menos el numerador sin derivar por la derivada del
denominador, todo ello dividido entre el denominador al cuadrado.
 Derivada del producto de una constante a por una función
La derivada de una función por una constante es la deriva de la función por la constante
sin derivar.
Regla de la cadena
Permite derivar una función que es composición de varias funciones.
Matemáticamente se expresa por:
Básicamente, la regla de la cadena se puede resumir como "derivar y multiplicar por
la derivada de lo de dentro"

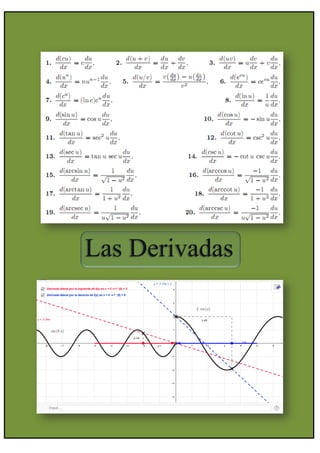
22. Capítulo VIII
Fórmulas de Derivación
Sean a, b, e y k constantes (números reales) y consideremos a: u(x) y v(x) como
funciones.
 Derivada de una constante
 Derivada de x
 Derivada de la función lineal
 Derivada de una potencia
 Derivada de una raíz cuadrada
 Derivada de una raíz

23.  Derivada de una suma
 Derivada de una constante por una función
 Derivada de un producto
 Derivada de una constante partida por una función
 Derivada de un cociente
 Derivada de la función exponencial
 Derivada de la función exponencial de base e

24.  Derivada de un logaritmo
Como , también se puede expresar así:
 Derivada del logaritmo neperiano
 Derivada del seno
 Derivada del coseno
 Derivada de la tangente
 Derivada de la cotangente

25.  Derivada de la secante
 Derivada de la cosecante
 Derivada del arcoseno
 Derivada del arcocoseno
 Derivada del arcotangente
 Derivada del arcocotangente

26.  Derivada del arcosecante
 Derivada del arcocosecante
 Derivada de la función potencial-exponencial
 Regla de la cadena
 Derivadas implícitas

27. Capítulo IX
Ejercicios
Ejercicio 1
Función logarítmica:
Solución:
Derivamos el logaritmo y multiplicamos por la derivada del argumento, que es un
polinomio:
Simplificando,
f′(x)=2(1+4x2)
x(1+2x2)
Ejercicio 2
Función racional:
Aplicamos la regla del cociente:

28. Ejercicio 3
Función con raíz cuadrada:
Podemos escribir la raíz cuadrada como una potencia (de exponente 1/2) para
derivar la raíz como una potencia:
f(x ( )
Calculamos la derivada:
Ejercicio 4
Función con raíces de distintos órdenes y parámetros:

29. Como la función es una suma, su derivada es la suma de las derivadas. Para abreviar,
calculamos las derivadas de cada sumando por separado. Sean las funciones:
√
√
√
√
Las derivadas son:

30. Luego la derivada de la función es
Ejercicio 5
Función con raíz en el denominador:
Derivamos el cociente:
Ejercicio 6
Función logarítmica con cociente de raíces:

31. Antes de aplicar la regla de la cadena, podemos aplicar las propiedades de los
logaritmos para evitar la raíz.
La función queda como:
( )
Aplicando de nuevo las propiedades, podemos evitar la fracción:
Calculamos la derivada:
Operamos para simplificar la expresión (sumando las fracciones):
( )
( )
En el denominador tenemos una suma por diferencia:
( )
Finalmente, simplificamos la fracción aplicando la fórmula fundamental de
trigonometría (x)=1):

32. ( )
( )
Ejercicio 7
Función con logaritmo natural en el denominador:
Tenemos que aplicar la regla del cociente. Observad que el exponente del numerador
está al cuadrado.
Ejercicio 8
Función exponencial:
Recordamos que la derivada de una exponencial es la derivada del exponente
multiplicada por el logaritmo de la base y por la propia función:
Ejercicio 9
Función exponencial:

33. Tenemos de nuevo una exponencial con base distinta de e.
Ejercicio 10
Función cociente con exponenciales:
Ejercicio 11
Función exponencial con tangente:
Recordad que
Se trata de una exponencial cuya base es un parámetro, a, por lo que en su derivada
tendremos el factor ln(a). Además, en el exponente tenemos una función trigonométrica
con otro parámetro, n.

34. Ejercicio 12
Función cociente con seno, logaritmo y raíz quinta:
Hay que tener en cuenta que la raíz no es cuadrada (es de orden 5). Podemos
considerarla como una potencia de exponente 1/5.
Ejercicio 13
Función arcocoseno:

35. La dificultad de esta derivada es conocer la derivada de arcsin(x).
Ejercicio 14
Función con raíz, arcocoseno y parámetro:

36. Ejercicio 15
Función con raíces y logaritmo:
Ejercicio 16
Demostración de la derivada de una función elevada a una función:
Vamos a calcular la derivada de una función elevada a otra función.
Para simplificar, llamaremos y , y a sus derivadas,
y
Por tanto, queremos calcular la derivada de
Aplicamos logaritmos y sus propiedades a la igualdad anterior:

37. Derivamos en la igualdad (derivada del producto y del logaritmo) aplicando la regla de
la cadena:
Aislamos y′ en la expresión anterior:
Por tanto, hemos obtenido una fórmula para calcular y′ en términos de “y” y las
funciones f y g y sus derivadas.
Ejercicio 17
Función exponencial:
Para calcular la derivada de esta función, no podemos aplicar directamente las fórmulas
de la derivada de la exponencial ni de la derivada de una potencia. Sí podemos aplicar la
fórmula calculada en el Ejercicio 16.

38. Ejercicio 18
Función exponencial:
De nuevo, tenemos que emplear la fórmula del Ejercicio 16:
Ejercicio 19
Función exponencial:
Aplicamos la fórmula del Ejercicio 16:

40. Conclusión
La derivada tiene muchas aplicaciones en la vida diaria, con la derivada se puede
calcular: con la derivada implica que se calcula la “razón de cambio” o en palabras más
simples, velocidad. Muchas son las aplicaciones de la derivada en profesiones como la
ingeniería, la economía, la administración etc.
Es Aplicable también en la economía para hallar valores mínimos y máximos. Sirven
para explicar el comportamiento de la curva de una función trigonométrica. Es decir
tiene un número sin fin de aplicaciones en las cuales toma un papel importante.
El propósito principal de un derivado es optimizar los sistemas que se expresan por
las funciones más o menos complejo. Además, es habitual encontrar la derivada de
aplicar los valores máximos y mínimos de ciertas expresiones matemáticas.