Estadística descriptiva de variables y correlación

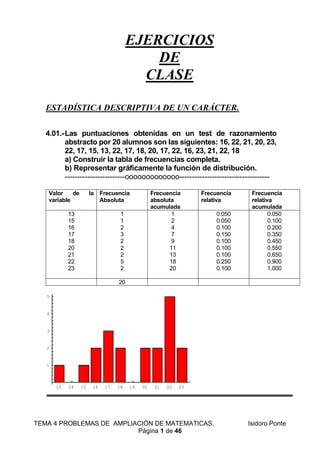
TEMA 4 PROBLEMAS DE AMPLIACIÓN DE MATEMATICAS. Isidoro Ponte
Página 1 de 46
EJERCICIOS
DE
CLASE
ESTADÍSTICA DESCRIPTIVA DE UN CARÁCTER.
4.01.-Las puntuaciones obtenidas en un test de razonamiento
abstracto por 20 alumnos son las siguientes: 16, 22, 21, 20, 23,
22, 17, 15, 13, 22, 17, 18, 20, 17, 22, 16, 23, 21, 22, 18
a) Construir la tabla de frecuencias completa.
b) Representar gráficamente la función de distribución.
------------------------ooooooooooooo------------------------------------
Valor de la
variable
Frecuencia
Absoluta
Frecuencia
absoluta
acumulada
Frecuencia
relativa
Frecuencia
relativa
acumulada
13
15
16
17
18
20
21
22
23
1
1
2
3
2
2
2
5
2
1
2
4
7
9
11
13
18
20
0.050
0.050
0.100
0.150
0.100
0.100
0.100
0.250
0.100
0.050
0.100
0.200
0.350
0.450
0.550
0.650
0.900
1.000
20
13 14 15 16 17 18 19 20 21 22 23
1
2
3
4
5

Página 2 de 46
4.02.-Los jugadores de baloncesto de un equipo se clasifican por altura
según la siguiente tabla
Altura Numero de jugadores
[1,70 – 1,80)
[1,80 – 1,90)
[1,90 – 2,00)
[2,00 – 2,10)
3
4
5
3
a) Formar la tabla de frecuencias completa.
b) Representar gráficamente la función de distribución.
------------------------ooooooooooooo------------------------------------
Alturas Frecuencia
Absoluta
Frecuencia
absoluta
acumulada
Frecuencia
relativa
Frecuencia
relativa
acumulada
[1.70-1.80)
[1.80-1.90)
[1.90-2.00)
[2.00-2.10)
3
4
5
3
3
7
12
15
0.200
0.267
0.333
0.200
0.200
0.467
0.800
1.000
15
4.03.-Según una encuesta realizada en el gremio de libreros, durante el
año 2005 el precio de los libros se distribuyó como indica la tabla
siguiente:
Precio (euros) Numero de libros
Hasta 3
De 3,01 a 5
De 5,01 a 7
De 7,01 a 10
Más de 10
Sin especificar precio
6663
6541
4111
5279
9477
5841
Formar la tabla estadística y representar gráficamente la
distribución mediante el diagrama más adecuado.
1.75 1.85 1.95 2.05
1
2
3
4
5

Página 3 de 46
------------------------ooooooooooooo------------------------------------
Valor de la
variable
Frecuencia
Absoluta
Frecuencia
absoluta
acumulada
Frecuencia
relativa
Frecuencia
relativa
acumulada
[0.00-3.00]
[3.01-5.00]
[5.01-7.00]
[7.01-10.0]
Mas de 10
Sin especificar
6663
6541
4111
5279
9477
5841
6663
13204
17315
22594
32071
37912
0.176
0.173
0.108
0.139
0.250
0.154
0.174
0.348
0.457
0.596
0.846
1.000
37912
4.04.-Las puntuaciones obtenidas en un test de razonamiento
abstracto por 20 alumnos son las siguientes: 16, 22, 21, 20, 23,
22, 17, 15, 13, 22, 17, 18, 20, 17, 22, 16, 23, 21, 22, 18
Halla la media, los cuarteles, el rango y la varianza.
xi fi xi* fi x2
i* fi Fi
13
15
16
17
18
20
21
22
23
1
1
2
3
2
2
2
5
2
13
15
32
51
36
40
42
110
46
169
225
512
867
648
800
882
2420
1058
1
2
4
7 > 5
9
11
13
18 > 15
20
20 385 7581
------------------------ooooooooooooo------------------------------------
NUMERO DE LIBROS VENDIDOS SEGUN EL PRECIO
6663
6541
4111
5279
9477
5841

Página 4 de 46
Media: 25
.
19
20
385
x =
=
Cuartil 1º
: 17
Q
5
4
20
4
N
1 =

=
=
Cuartil 3 : 22
Q
5
1
4
60
4
N
3
3 =

=
=
Rango : 10
13
23 =
−
Varianza: 47
.
8
25
.
19
20
7581
s 2
2
=
−
=
4.05.-Durante el mes de julio, en una determinada ciudad de la costa
levantina se han registrado las siguientes temperaturas máximas:
32, 31, 28, 29, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30,
30, 29, 29, 30, 30, 31, 30, 31, 34, 33, 33
a) Halla la moda, la media y los percentiles de orden 30 y 70.
b) el recorrido y la varianza.
------------------------ooooooooooooo------------------------------------
xi fi xi* fi x2
i* fi Fi
27
28
29
30
31
32
33
34
1
2
6
7
8
3
3
1
27
56
174
210
248
96
99
34
729
1568
5046
6300
7688
3072
3267
1156
1
3
9
16 > 9.3
24 > 21.7
27
30
31
31 944 28826
Moda 31
M0 =
Media: 45
.
30
31
944
x =
=
Percentil de orden 30 : 30
P
3
.
9
100
31
30
100
N
30
30 =

=

=
Percentil de orden 70 : 31
P
7
.
21
100
31
70
100
N
70
70 =

=

=
Recorrido : 7
27
34 =
−
Varianza: 67
.
2
45
.
30
31
28826
s 2
2
=
−
=

Página 5 de 46
4.06.-Se ha aplicado un test de capacidad espacial compuesto por 90
items, a 100 alumnos de 6o
Primaria, habiéndose obtenido los
siguientes resultados:
Número de ítems correcto Numero de alumnos
[0 – 15)
[15 – 30)
[30 - 45)
[45 - 60)
[60 - 75)
[75 – 90)
10
15
25
20
20
10
a) halla la media, la moda y la mediana. Comprobar la relación
empírica entre estos parámetros.
b) Rango y varianza.
------------------------ooooooooooooo------------------------------------
Clases Marcas de clase
xi
fi xi* fi x2
i* fi
[0 – 15)
[15 – 30)
[30 - 45)
[45 - 60)
[60 - 75)
[75 - 90)
7.5
22.5
37.5
52.5
67.5
82.5
10
15
25
20
20
10
75
337.5
937.5
1050
1350
825
562.5
7593.75
35156.25
55125
91125
68062.5
100 4575 257625
Moda 40
5
10
10
15
30
M0 =
+
+
=
Media: 75
.
45
100
4575
x =
=
Mediana: 45
M =
Relación empírica 25
.
2
75
.
5
)
M
x
(
3
M
x 0 

−

− , en este caso la relación
empírica no se cumple por ser la distribución asimétrica.
Rango: 90
0
90 =
−
Varianza: 19
.
483
75
.
45
100
257625
s 2
2
=
−
=
4.07.-Un profesor ha realizado dos tests a un grupo de 40 alumnos,
obteniendo que la media y la desviación típica de los resultados
de primer test son 6 y 1,5, respectivamente. La media y la
desviación típica de los resultados de segundo test son 4 y 0,5,
respectivamente. Un alumno obtuvo un 6 en el primer test y un
5 en el segundo. Comparativamente con el grupo, ¿en cuál
obtuvo mejor puntuación?.
------------------------ooooooooooooo------------------------------------
La primera distribución tiene 5
.
1
s
;
6
x 1
1 =
= .

Página 6 de 46
La segunda distribución tiene 5
.
0
s
;
4
x 1
2 =
= .
Para poder comparar las puntuaciones de ambos tests calcularemos las
puntuaciones típicas:
Primer test : 0
5
.
1
6
6
=
−
Segundo test : 2
.
0
5
.
0
4
5
=
−
Luego comparativamente obtuvo mejor calificación el segundo test.
4.08.-Se ha aplicado un test de agresividad a 40 alumnos de 3o
ESO,
obteniéndose los siguientes resultados:
Puntuaciones Numero de alumnos
[15 – 20)
[20 – 25)
[25 - 30)
[30 - 35)
[35 - 40)
[40 – 45)
[45 – 50)
2
8
13
7
6
3
1
a) Halla la agresividad media por persona.
b) ¿A partir de que puntuación se encontrará el 25% con mayor
agresividad de la clase?
c) Calcular la desviación típica.
------------------------ooooooooooooo------------------------------------
Clases Marcas de clase
xi
fi xi* fi x2
i* fi
[15 – 20)
[20 – 25)
[25 - 30)
[30 - 35)
[35 - 40)
[40 – 45)
[45 – 50)
17.5
22.5
27.5
32.5
37.5
42.5
47.5
2
8
13
7
6
3
1
35
180
357.5
227.5
225
127.5
47.5
612.50
4050
9831.25
7393.75
8437.50
5418.75
2256.25
40 1200 38000
Agresividad media: 30
40
1200
x =
=
Cuartil 3 : 35
Q
30
4
120
4
N
3
3 =

=
=
Desviación típica 07
.
7
30
40
38000
s 2
=
−
=

Página 7 de 46
VARIABLE BIDIMENSIONAL.REGRESIÓN Y CORRELACIÓN.
4.09.-Los gastos de publicidad de una empresa, en miles de euros, y
sus correspondientes ventas en miles de euros
Publicidad Ventas
1
2
3
4
5
6
7
8
15
16
14
17
20
18
18
19
Calcular:
a)Las medias de X e Y.
b)Las varianzas de X e Y.
c)La covarianza de (X,Y).
------------------------ooooooooooooo------------------------------------
xi yi fi xi* fi x2
i* fi yi* fi y2
i* fi xi*yi*fi
1
2
3
4
5
6
7
8
15
16
14
17
20
18
18
19
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
8
1
4
9
16
25
36
49
64
15
16
14
17
20
18
18
19
225
256
196
289
400
324
324
361
15
32
42
68
100
108
126
152
8 36 204 137 2375 643
Media de la variable x: 5
.
4
8
36
x =
= Media de la variable y: 13
.
17
8
137
y =
=
Varianza de x : 25
.
5
5
.
4
8
204
s 2
2
x =
−
=
Varianza de y : 61
.
3
13
.
17
8
2375
s 2
2
y =
−
=
Covarianza de (x,y): 31
.
3
13
.
17
5
,
4
8
643
s y
x =

−
=
4.10.-La evolución del IPC (índice de precios al consumo) y la tasa de
inflación en los primeros meses del año pasado de un estado,
viene reflejada en la siguiente tabla
Meses IPC Tasa de
inflación
Enero
Febrero
0,7
1,1
6
6

Página 8 de 46
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
1,7
2
1,9
1,9
2,9
2,9
3,8
6,3
6,2
5,8
4,9
4,9
4,5
4,4
Calcular: a) la desviación media del IPC y de la tasa de inflación.
b) Las desviaciones típicas.
c) La covarianza. d)El diagrama de dispersión.
------------------------ooooooooooooo------------------------------------
xi yi fi xi* fi x2
i* fi yi* fi y2
i* fi xi*yi*fi
0,7
1,1
1,7
2
1,9
1,9
2,9
2,9
3,8
6
6
6,3
6,2
5,8
4,9
4,9
4,5
4,4
1
1
1
1
1
1
1
1
1
0,7
1,1
1,7
2
1,9
1,9
2,9
2,9
3,8
0.49
1.21
2.89
4
3.61
3.61
8.41
8.41
14.44
6
6
6,3
6,2
5,8
4,9
4,9
4,5
4,4
36
36
39.69
38.44
33.64
24.01
24.01
20.25
19.36
4.2
6.6
10.71
12.4
11.02
9.31
14.21
13.05
16.72
9 18,9 47.07 49 271.4 98.22
Media de IPC: 1
.
2
9
9
.
18
x =
= Media tasa de inflación: 44
.
5
9
49
y =
=
Desviación típica de x : 91
.
0
1
.
2
9
07
.
47
s 2
x =
−
=
Desviación típica de y : 71
.
0
44
.
5
9
4
.
271
s 2
y =
−
=
.
0
44
.
5
1
.
2
9
22
.
98
s y
x −
=

−
=
4.11.-La distribución de recursos hidráulicos naturales de la España
peninsular queda reflejada en la siguiente tabla:
Cuencas
hidrográficas
Totales
(1.000 hm3
/año)
Por habitante y
año (100 m3
)
Norte de España
Duero
Tajo
Guadiana
Guadalquivir
Sur de España
Segura
Júcar
Ebro
Pirineo oriental
43,87
12,17
9,98
4,91
8,23
3,09
1,1
3,97
18,2
2,75
6,57
5,53
1,88
3,07
1,87
1,63
0,84
0,99
6,73
0,5

Página 9 de 46
Calcular: a) las medias y varianzas totales y por habitante.
b)La covarianza de ambas variables.
------------------------ooooooooooooo------------------------------------
xi yi fi xi* fi x2
i* fi yi* fi y2
i* fi xi*yi*fi
43,87
12,17
9,98
4,91
8,23
3,09
1,1
3,97
18,2
2,75
6,57
5,53
1,88
3,07
1,87
1,63
0,84
0,99
6,73
0,5
1
1
1
1
1
1
1
1
1
1
43,87
12,17
9,98
4,91
8,23
3,09
1,1
3,97
18,2
2,75
1924.58
148.11
99.60
24.11
67.73
9.55
1.21
15.76
331.24
7.56
6,57
5,53
1,88
3,07
1,87
1,63
0,84
0,99
6,73
0,5
43.16
30.58
3.53
9.42
3.50
2.66
0.71
0.98
45.29
0.25
288.23
67.30
18.76
15.07
15.39
5.04
0.92
3.93
122.49
1.38
10 108.27 2629.45 29.61 140.09 538.50
Media de x: 83
.
10
10
27
.
108
x =
= Media de y: 96
.
2
10
61
.
29
y =
=
Varianza de x : 72
.
145
83
.
10
10
45
.
2629
s 2
x
2
=
−
=
Varianza de y : 24
.
5
96
.
2
10
09
.
140
s 2
y
2
=
−
=
.
21
96
.
2
83
.
10
10
50
.
538
s y
x =

−
=
4.12.-La extensión en millones de km2
, y la población hace algunos
años, en millones de habitantes de los diez países más extensos
de la Tierra viene dada en la siguiente tabla:
Paises Extensión Población
Antigua URSS
Canadá
China
Estados Unidos
Brasil
Australia
India
Argentina
Sudán
Argelia
22,40
9,97
9,56
9,36
8,51
7,68
3,28
2,76
2,50
2,38
272,31
25,02
1021,63
233,74
129,66
15,17
733,24
28,78
20,80
20,56
Calcular: a) la medias y varianza de la extensión y la población.
b)La covarianza de ambas variables.
------------------------ooooooooooooo------------------------------------
xi yi fi xi* fi x2
i* fi yi* fi y2
i* fi xi*yi*fi
22,40
9,97
9,56
9,36
8,51
272,31
25,02
1021,63
233,74
129,66
1
1
1
1
1
22,40
9,97
9,56
9,36
8,51
501.76
99.40
91.39
87.61
72.42
272,31
25,02
1021,63
233,74
129,66
74152.74
626.00
1043728.00
54634.39
16811.72
6099.74
249.45
9766.78
2187.81
1103.41

Página 10 de 46
7,68
3,28
2,76
2,50
2,38
15,17
733,24
28,78
20,80
20,56
1
1
1
1
1
7,68
3,28
2,76
2,50
2,38
58.98
10.76
7.62
6.25
5.66
15,17
733,24
28,78
20,80
20,56
230.13
537640.90
828.29
432.64
422.71
116.51
2405.03
79.43
52.00
48.93
10 78.40 941.86 2500.91 1729507.00 22109.09
Media de x: 84
.
7
10
4
.
78
x =
= Media de y: 09
.
250
10
91
.
2500
y =
=
Varianza de x : 72
.
32
84
.
7
10
85
.
941
s 2
x
2
=
−
=
Varianza de y : 2
.
110405
09
.
250
10
1729507
s 2
y
2
=
−
=
.
250
09
.
250
84
.
7
10
09
.
22109
s y
x =

−
=
4.13.-Los gastos de publicidad de una empresa, en miles de euros, y
sus correspondientes ventas en miles de euros
Publicidad Ventas
1
2
3
4
5
6
7
8
15
16
14
17
20
18
18
19
Teniendo en cuenta los resultados del ejercicio 9, calcular:
a) el coeficiente de correlación lineal e interpretarlo.
b) decir que tipo de dependencia existe entre las variables X e Y.
------------------------ooooooooooooo------------------------------------
Habíamos obtenido en el problema 4.09 los siguientes datos:
Media de la variable x: 5
.
4
8
36
x =
= Media de la variable y: 13
.
17
8
137
y =
=
Varianza de x : 25
.
5
5
.
4
8
204
s 2
2
x =
−
=  desviación típica de x : 29
.
2
sx =
Varianza de y : 61
.
3
13
.
17
8
2375
s 2
2
y =
−
= desviación típica de y : 9
.
1
sy =
.
3
13
.
17
5
,
4
8
643
s y
x =

−
=
a) el coeficiente de correlación lineal: 76
.
0
9
.
1
29
.
2
31
.
3
r =

= , la correlación
es positiva

Página 11 de 46
b) dependencia aleatoria débil.
4.14.-La evolución del IPC (índice de precios al consumo) y la tasa de
inflación en los primeros meses del año pasado de un estado,
viene reflejada en la siguiente tabla
Meses IPC Tasa de
inflación
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
0,7
1,1
1,7
2
1,9
1,9
2,9
2,9
3,8
6
6
6,3
6,2
5,8
4,9
4,9
4,5
4,4
c) ¿Qué tasa de inflación es razonable esperar en un mes que el
IPC es 4,5?.
------------------------ooooooooooooo------------------------------------
Media de x: 1
.
2
9
9
.
18
x =
= Media de y: 44
.
5
9
49
y =
=
D. típica x : 91
.
0
1
.
2
9
07
.
47
s 2
x =
−
= D. típica y : 71
.
0
44
.
5
9
4
.
271
s 2
y =
−
=
.
0
44
.
5
1
.
2
9
22
.
98
s y
x −
=

−
=
el coeficiente de correlación lineal: 8
.
0
71
.
0
91
.
0
52
.
0
r −
=

−
= , la correlación es
negativa (cuando aumenta x, disminuye y).
las variables están en dependencia aleatoria.
La recta de regresión de y sobre x es : )
1
.
2
x
(
63
.
0
44
.
5
y −
−
=
−
Cuando el IPC es 5
.
4
x = , esperamos que la inflación se de 93
.
3
y = .
4.15.-La distribución de recursos hidráulicos naturales de la España
peninsular queda reflejada en la siguiente tabla:
Cuencas
hidrográficas
Totales
(1.000 hm3
/año)
Por habitante y
año (100 m3
)
Norte de España
Duero
Tajo
Guadiana
43,87
12,17
9,98
4,91
6,57
5,53
1,88
3,07

Página 12 de 46
Guadalquivir
Sur de España
Segura
Júcar
Ebro
Pirineo oriental
8,23
3,09
1,1
3,97
18,2
2,75
1,87
1,63
0,84
0,99
6,73
0,5
------------------------ooooooooooooo------------------------------------
Media de x: 83
.
10
10
27
.
108
x =
= Media de y: 96
.
2
10
61
.
29
y =
=
Varianza de x : 72
.
145
83
.
10
10
45
.
2629
s 2
x
2
=
−
= , desv. típica de x: 07
.
12
sx =
Varianza de y : 24
.
5
96
.
2
10
09
.
140
s 2
y
2
=
−
.
2
sy =
.
21
96
.
2
83
.
10
10
50
.
538
s y
x =

−
=
.
0
29
.
2
07
.
12
79
.
21
r =

= , la correlación es
positiva (cuando aumenta x, aumenta y).
las variables están en dependencia aleatoria no muy fuerte.
4.16.-La extensión en millones de km2
, y la población hace algunos
años, en millones de habitantes de los diez países más extensos
de la Tierra viene dada en la siguiente tabla:
Paises Extensión Población
Antigua URSS
Canadá
China
Estados Unidos
Brasil
Australia
India
Argentina
Sudán
Argelia
22,40
9,97
9,56
9,36
8,51
7,68
3,28
2,76
2,50
2,38
272,31
25,02
1021,63
233,74
129,66
15,17
733,24
28,78
20,80
20,56
------------------------ooooooooooooo------------------------------------
Media de x: 84
.
7
10
4
.
78
x =
= Media de y: 09
.
250
10
91
.
2500
y =
=

Página 13 de 46
Varianza de x : 72
.
32
84
.
7
10
85
.
941
s 2
x
2
=
−
.
5
sx =
Varianza de y : 2
.
110405
09
.
250
10
1729507
s 2
y
2
=
−
= ,
Desviación típica de y: 27
.
332
sy =
.
250
09
.
250
84
.
7
10
09
.
22109
s y
x =

−
=
.
0
27
.
332
72
.
5
2
.
250
r =

= ,
las variables están prácticamente incorreladas.
CÁLCULO DE PROBABILIDADES
4.17.-Se considera el experimento aleatorio que consiste en lanzar un
dado cuyas caras están numeradas del 1 al 6 y anotar el
resultado de la cara superior. Se pide:
a) espacio muestral.
b) suceso “obtener número par”.
c) suceso “obtener número impar”.
d) suceso “obtener múltiplo de 2”.¿Cómo son los sucesos
obtenidos en el apartado b) y d)?.
------------------------ooooooooooooo------------------------------------
a) }
6
,
5
,
4
,
3
,
2
,
1
{
E=
b) }
6
,
4
,
2
{
A=
c) }
5
,
3
,
1
{
B=
d) }
6
,
4
,
2
{
C= . Los sucesos A y C son iguales.
4.18.-Se considera el experimento consistente en lanzar dos monedas
al aire y anotar el resultado de las caras superiores. Se pide:
a) Espacio muestral.
b) espacio de sucesos.
c) suceso “obtener al menos una cara”.
------------------------ooooooooooooo------------------------------------
a) }
XX
,
XC
,
CX
,
CC
{
E=
b) },
XC
,
CX
{
},
XX
,
CC
{
},
XC
,
CC
{
},
CX
,
CC
{
},
XX
{
},
XC
{
},
CX
{
},
CC
{
,
{
S 
=
},
XX
,
XC
,
CX
{
},
XX
,
XC
,
CC
{
},
XX
,
CX
,
CC
{
},
XC
,
CX
,
CC
{
},
XX
,
XC
{
},
XX
,
CX
{
}}
XX
,
XC
,
CX
,
CC
{
c) }
XC
,
CX
,
CC
{
A=

Página 14 de 46
4.19.- En el experimento aleatorio cuyo espacio muestral es
}
6
,
5
,
4
,
3
,
2
,
1
{
=
E se consideran los siguientes sucesos: }
6
,
5
,
2
{
=
A ,
}
5
,
4
,
3
,
1
{
=
B , }
6
,
5
,
4
{
=
C , }
3
{
=
D . Calcula:
a) los sucesos contrarios de cada uno de ellos.
b) B
A , C
A , ( )
C
B
A 
 , B
A , B
A , ( )
C
B
A 
 , ( )
C
B
A 

------------------------ooooooooooooo------------------------------------
a) }
4
,
3
,
1
{
A= , }
6
,
2
{
B= , }
3
,
2
,
1
{
C = , }
6
,
5
,
4
,
2
,
1
{
D=
b) }
6
,
5
,
4
,
3
,
2
,
1
{
B
A =
 , }
6
,
5
{
C
A =
 , ( ) }
6
,
5
,
4
,
3
,
2
,
1
{
C
B
A =

 ,

=
B
A , 
=
B
A , ( ) }
6
,
5
,
3
,
2
,
1
{
C
B
A =

 , ( ) }
6
,
5
,
2
{
C
B
A =


4.20.-Un jugador italiano expresó a Galileo su sorpresa al observar
que al jugar con tres dados, la suma 10 aparecía con más
frecuencia que la suma 9. Según el jugador, ambas sumas tenían
los mismos casos favorables.
Casos favorables al 9: 126, 135,144,225, 234,333
Casos favorables al 10: 136, 145,226,235, 244,334
Galileo comprobó matemáticamente que ambos sucesos no
tenían los mismos casos favorables. Explica por qué y calcula
los casos favorables a cada una de estas sumas.
------------------------ooooooooooooo------------------------------------
Casos favorables al 9
126, 162, 216, 261, 612, 621, 135, 153, 351, 315, 513, 531, 144, 414, 441,
225, 252, 522, 234, 243, 324, 342, 423, 432, 333. Total casos favorables a
la suma nueve = 25
Casos favorables al 10
136, 163, 316, 361, 613, 631, 145, 154, 451, 415, 514, 541, 226, 262, 622,
235, 253, 325, 352, 523, 532, 244, 424, 442, 334, 343, 433. Total casos
favorables a la suma diez = 27
Luego hay más casos favorables a la suma diez que a la suma nueve.
4.21.-¿Puede ser la probabilidad negativa?. Razona la respuesta.
------------------------ooooooooooooo------------------------------------
La probabilidad de un suceso no puede ser negativa, ya que por el primer
axioma de Kolmogoroff se tiene que la probabilidad de un suceso es
positiva o nula.
Por la definición de Laplace tampoco puede ser negativa, ya que es el
cociente entre el número de casos favorables partido por el numero de
casos posibles y como ninguno de los dos es negativos, su cociente
siempre será positivo o nulo.

Página 15 de 46
4.22.-¿Puede ser la probabilidad mayor que 1?. Razona la respuesta.
------------------------ooooooooooooo------------------------------------
La probabilidad de un suceso no puede ser mayor que la unidad.
Por el axioma segundo de Kolmogoroff se tiene que la probabilidad del
suceso cierto es 1, y como cualquier suceso está contenido en el cierto, su
probabilidad será menor o igual a la unidad.
Por la definición de Laplace, como el número de casos favorables siempre
será menor o igual que el de casos posibles, por tanto el cociente será
menor o igual que la unidad.
4,23.-Indica la diferencia entre sucesos independientes y sucesos
incompatibles.
------------------------ooooooooooooo------------------------------------
A y B son independientes ⇔ 𝑃(𝐴 ∩ 𝐵) = 𝑃(𝐴) ⋅ 𝑃(𝐵)
A y B son incompatibles 


 B
A
4.24.-Un dado está trucado, de modo que la probabilidad de obtener
cara es directamente proporcional a los números de estas.
Calcula:
a) la probabilidad de cada una de las caras.
a) la probabilidad de sacar un número par.
------------------------ooooooooooooo------------------------------------
a) sea x la probabilidad de sacar 1, es decir 𝑃(1) = 𝑥, entonces,
𝑃(2) = 2𝑥, 𝑃(3) = 3𝑥, 𝑃(4) = 4𝑥, 𝑃(5) = 5𝑥, 𝑃(6) = 6𝑥,
por ser 6
,
5
,
4
,
3
,
2
,
1 elementos del espacio muestral, la suma de
probabilidades es 1, por tanto
1 = 𝑃(1) + 𝑃(2) + 𝑃(3) + 𝑃(4) + 𝑃(5) + 𝑃(6) = 𝑥 + 2𝑥 + 3𝑥 + 4𝑥 + 5𝑥 +
6𝑥 = 21𝑥 ⇒
21
1
x =
 , por tanto
𝑃(1) =
1
21
, 𝑃(2) =
2
21
, 𝑃(3) =
3
21
, 𝑃(4) =
4
21
, 𝑃(5) =
5
21
, 𝑃(6) =
6
21
b) 𝑃(𝑠𝑎𝑐𝑎𝑟𝑝𝑎𝑟) = 𝑃({2,4,6}) = 𝑃(2) + 𝑃(4) + 𝑃(6) =
2
21
+
4
21
+
6
21
=
4
7
4.25.-Halla la probabilidad de un suceso, sabiendo que la suma de su
cuadrado y la del cuadrado de la probabilidad del suceso
contrario vale 5/9.
------------------------ooooooooooooo------------------------------------
Sea A el suceso y x su probabilidad, es decir , 𝑃(𝐴) = 𝑥 ⇒ 𝑃(𝐴) = 1 − 𝑥
Teniendo en cuenta el enunciado del problema tenemos;

Página 16 de 46
𝑥2
+ (1 − 𝑥)2
=
5
9
⇒ 2𝑥2
− 2𝑥 +
4
9
= 0 ⇒ {
𝑥1 =
2
3
𝑥2 =
1
3
⇒𝑃(𝐴) =
2
3
0 𝑃(𝐴) =
1
3
4.26.-A un congreso de científicos asisten 100 congresistas; de ellos,
80 hablan francés y 40 inglés.¿Cuál es la probabilidad de que
dos congresistas elegidos al azar no puedan entenderse sin
intérpretes?.
------------------------ooooooooooooo------------------------------------
Sean francés
habla
a
congresist
un
F = ,
inglés
habla
a
congresist
un
I =
entonces


−
+
=


−
+
=
 )
I
F
(
Card
40
80
100
)
I
F
(
Card
)
I
(
Card
)
F
(
Card
)
I
F
(
Card
20
)
I
F
(
Card =


Por tanto,
Número de congresistas que hablan sólo francés 60
Número de congresistas que hablan sólo inglés 20
Número de congresistas que hablan francés e inglés 20
Vamos, ahora, a hallar la probabilidad aplicando la regla de Laplace:
Número de casos posibles: las parejas que se pueden formar con los 100
congresistas son: 4950
1
2
99
100
2
100
=


=








Número de casos favorables: como hay 60 que no saben inglés y 20 que
no saben francés, el número de parejas que no se entienden es 60
20
Por tanto la probabilidad de que dos congresistas elegidos al azar no
puedan entenderse sin intérpretes es 𝑃 =
1200
4950
=
8
33
4.27.-Se ha comprobado que en una ciudad están enfermos con
diarrea el 60% de los niños, con sarampión el 50% y el 20% con
ambas enfermedades.
a) calcula la probabilidad de que elegido un niño al azar, esté
enfermo con diarrea o sarampión o ambas enfermedades.
b) en un colegio con 450 niños,¿cuántos cabe esperar que estén
enfermos con diarrea o sarampión?.
------------------------ooooooooooooo------------------------------------
Si designamos por A el suceso “estar enfermo con diarrea” y
B el suceso “estar enfermo con sarampión” tenemos,
𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵) = 0.6 + 0.5 − 0.2 =0.9
𝑛 = 450 ⋅ 𝑃(𝐴 ∪ 𝐵) = 450 ⋅ 0.9 =405 niños.

Página 17 de 46
4.28.-Los números 1, 2, 3, . . . . , n se alinean al azar. Calcular la
probabilidad de que los números 2 y 3 aparezcan seguidos y en
ese orden.
------------------------ooooooooooooo------------------------------------
Casos posibles: son las distintas ordenaciones de n números : !
n
Casos favorables: para que aparezcan el 2 y el 3 seguidos y en ese orden,
consideramos la ordenación 23 como un solo número, y por tanto habrá
( )!
1
n− posibilidades de ordenar los números para que que cumplan la
condición exigida.
𝑃 =
(𝑛 − 1)!
𝑛!
=
1
𝑛
4.29.-Se lanzan tres dados al aire. Calcular la probabilidad de que se
obtenga; a) un 4 en cada dado.
b) suma total de puntos igual a 8.
------------------------ooooooooooooo------------------------------------
a) Sea C el suceso “obtener 4 en el lanzamiento de un dado”, 𝑃(𝐶) =
1
6
por tanto la probabilidad pedida es 𝑃(𝐶) ⋅ 𝑃(𝐶) ⋅ 𝑃(𝐶) =
1
6
⋅
1
6
⋅
1
6
=
1
216
b) casos favorables:
sumar 8 puntos con tres dados puede darse de las siguientes formas:











=
=

=
=

=
=

=
=

=
=

3
!
2
!
3
)
nes
permutacio
(
P
)
2
,
3
,
3
(
3
!
2
!
3
)
nes
permutacio
(
P
)
2
,
2
,
4
(
3
!
3
)
nes
permutacio
(
P
)
1
,
3
,
4
(
6
!
3
)
nes
permutacio
(
P
)
1
,
2
,
5
(
3
!
2
!
3
)
nes
permutacio
(
P
)
1
,
1
,
6
(
2
3
2
3
3
3
2
3
total de casos favorables 21
casos posibles:
los casos son 216
6
VR 3
6
3 =
=
En consecuencia, la probabilidad de obtener una suma total de 8 es
𝑃 =
21
216
=
7
72
4.30.-Un producto está formado por tres partes A, B y C. El proceso
de fabricación es tal que la probabilidad de un defecto en A es
0,03, de un defecto en B es 0,04 y de un defecto en C es 0,08.
¿Cuál es la probabilidad de que el producto no sea defectuoso?
------------------------ooooooooooooo------------------------------------
Para que el producto no sea defectuoso, no puede ser defectuoso ni en A
ni en B ni en C 𝑃(𝑛𝑜𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑜) = (1 − 0.03)(1 − 0.04)(1 − 0.08) =0.856

Página 18 de 46
4.31.-Halla la probabilidad de obtener al menos un 6 doble en n tiradas
de dos dados.
------------------------ooooooooooooo------------------------------------
Sean 1
A el suceso “sacar 6 doble en la primera tirada”
2
A el suceso “sacar 6 doble en la segunda tirada”
……………………………………………………….
n
A el suceso “ sacar 6 doble en la n-ésima tirada”
A el suceso pedido “ sacar al menos un 6 doble en n tiradas”
𝑃(𝐴) = 𝑃(𝐴1 ∪ 𝐴2 ∪ 𝐴3 ∪ ⋅ ⋅ ⋅∪ 𝐴𝑛) = 1 − 𝑃(𝐴1 ∪ 𝐴2 ∪ 𝐴3 ∪ ⋅ ⋅ ⋅∪ 𝐴𝑛) =
= 1 − 𝑃(𝐴1 ∩ 𝐴2 ∩ 𝐴3 ∩ ⋅ ⋅ ⋅∩ 𝐴𝑛) =
∗
1 − 𝑃(𝐴1) ⋅ 𝑃(𝐴2) ⋅ 𝑃(𝐴3) ⋅ ⋅ ⋅ 𝑃(𝐴𝑛) =
∗∗
1 − (𝑃(𝐴1))
𝑛
=
∗∗∗
1 − (
35
36
)
𝑛
* ya que los sucesos son independientes.
** ya que todos los sucesos tienen la misma probabilidad.
*** ya que de los 36 casos que resultan al tirar dos dados sólo el 66 es
favorable, como 1
A es el complementario, su probabilidad es
36
35
.
4.32.-¿Qué es más probable, obtener al menos un 1 en un lanzamiento
de cuatro dados al aire o obtener al menos dos 1 en veinticuatro
tiradas con dos dados?.
------------------------ooooooooooooo------------------------------------
Con ayuda de los sucesos contrarios calculamos cada una de las
probabilidades de obtener
- Al menos un 1 en un lanzamiento de cuatro dados al aire
𝑃(𝐴) = 1 − (
5
6
)
4
=0.5178
-Al menos dos 1 en veinticuatro tiradas con dos dados
𝑃(𝐵) = 1 − (
35
36
)
24
=0.49 , por lo que es más probable el primer caso.
4.33.-Halla la probabilidad de ganar uno o más juegos en una serie de
m
juegos independientes si la probabilidad de ganar uno de ellos
es p. Hallar el valor de p para que esta probabilidad sea de m
2
1
1−
------------------------ooooooooooooo------------------------------------
Sean 1
A el suceso “ganar el primer juego”
2
A el suceso “ganar el segundo juego”
……………………………………………………….

Página 19 de 46
m
A el suceso “ ganar el m-ésimo juego”
A el suceso pedido “ganar uno o mas juegos en una serie de m
juegos independientes”
𝑃(𝐴) = 𝑃(𝐴1 ∪ 𝐴2 ∪ 𝐴3 ∪ ⋅ ⋅ ⋅∪ 𝐴𝑚) = 1 − 𝑃(𝐴1 ∪ 𝐴2 ∪ 𝐴3 ∪ ⋅ ⋅ ⋅∪ 𝐴𝑚) =
= 1 − 𝑃(𝐴1 ∩ 𝐴2 ∩ 𝐴3 ∩ ⋅ ⋅ ⋅∩ 𝐴𝑚) =
∗
1 − 𝑃(𝐴1) ⋅ 𝑃(𝐴2) ⋅ 𝑃(𝐴3) ⋅ ⋅ ⋅ 𝑃(𝐴𝑛) =
∗∗

=
∗∗
1 − (𝑃(𝐴1))
𝑚
=
∗∗∗
1 − (1 − 𝑝)𝑚
* ya que los sucesos son independientes.
** ya que todos los sucesos tienen la misma probabilidad.
Aplicamos ahora la condición 1 − (1 − 𝑝)𝑚
= 1 −
1
2𝑚
⇒ 1 − 𝑝 =
1
2
⇒𝑝 =
1
2
4.34.-La probabilidad de que una persona sea rubia es 0,4 y la
probabilidad de que tenga los ojos negros es 0,3. Calcula las
siguientes probabilidades:
a) que sea rubia y tenga los ojos negros.
b) que sea rubia o tenga los ojos negros.
c) que tres personas sean rubias.
d) que dos personas sean rubias o tengan los ojos negros.
------------------------ooooooooooooo------------------------------------
Si representamos por R el suceso “ser rubio” y N el suceso “tener los
ojos negros
a) 𝑃(𝑅 ∩ 𝑁) = 𝑃(𝑅) ⋅ 𝑃(𝑁) = 0.4 ⋅ 0.3 =0.12
b) 𝑃(𝑅 ∪ 𝑁) = 𝑃(𝑅) + 𝑃(𝑁) − 𝑃(𝑅 ∩ 𝑁) = 0.4 + 0.3 − 0.12 =0.58
c) 𝑃(𝑅 ∩ 𝑅 ∩ 𝑅) = 𝑃(𝑅) ⋅ 𝑃(𝑅) ⋅ 𝑃(𝑅) = 0.4 ⋅ 0.4 ⋅ 0.4 =0.064
d) 𝑃((𝑅 ∩ 𝑅) ∪ (𝑁 ∪ 𝑁)) = 𝑃(𝑅 ∩ 𝑅) + 𝑃(𝑁 ∩ 𝑁) − 𝑃(𝑅 ∩ 𝑅 ∩ 𝑁 ∩ 𝑁) =
= 0. 42
+ 0. 32
− (0. 42
⋅ 0. 32
) =0.2356
4.35.-En un centro escolar, los alumnos de 2do
BAC pueden optar por
cursar, como lengua extranjera, entre inglés o francés. En un
determinado curso, el 90% estudia inglés y el resto francés. El
30% de los que estudian inglés son varones, y de los que
estudian francés son chicos el 40%. Elegido un alumno al azar
¿Cuál es la probabilidad de que sea chica?.
------------------------ooooooooooooo------------------------------------
Sean los sucesos
I =“estudiar inglés” F = “estudiar francés” V = “ser varón”
M =”ser mujer”
Sabemos que
𝑃(𝐼) = 0.9 , 𝑃(𝑉/𝐼) = 0.3 , entonces 𝑃(𝑀/𝐼) = 1 − 0.3 = 0.7
𝑃(𝐹) = 0.1 , 𝑃(𝑉/𝐹) = 0.4 , entonces 𝑃(𝑀/𝐹) = 1 − 0.4 = 0.6
la probabilidad pedida, de que sea chica es:
𝑃((𝑀 ∩ 𝐼) ∪ (𝑀 ∩ 𝐹)) = 𝑃(𝑀 ∩ 𝐼) + 𝑃(𝑀 ∩ 𝐹) = 𝑃(𝐼) ⋅ 𝑃(𝑀/𝐼) + 𝑃(𝐹) ⋅ 𝑃(𝑀/𝐹)
= 0.9 ⋅ 0.7 + 0.1 ⋅ 0.6 =0.69

Página 20 de 46
4.36.-Un alumno de ampliación de matemáticas ha preparado 10
temas de los 14 que consta el programa. Se eligen al azar 3
temas. ¿ Cuál es la probabilidad de que conteste bien a 2, en los
siguientes casos:
a) exactamente 2. b) dos temas al menos?.
------------------------ooooooooooooo------------------------------------
Consideramos el suceso B =” contestar bien a un tema” 𝑃(𝐵) =
10
14
1
B = ”contestar bien al primer tema”
2
B = ”contestar bien al segundo tema”
3
B = ”contestar bien al tercer tema”
a) Sea el suceso C =” contestar bien a exactamente a dos temas”
𝑃(𝐶) = 𝑃[(𝐵1 ∩ 𝐵2 ∩ 𝐵3) ∪ (𝐵1 ∩ 𝐵2 ∩ 𝐵3) ∪ (𝐵1 ∩ 𝐵2 ∩ 𝐵3)] = 3(𝐵1 ∩ 𝐵2 ∩ 𝐵3) =
= 3 ∙ 𝑃(𝐵1) ⋅ 𝑃(𝐵2/𝐵1) ⋅ 𝑃(𝐵3/(𝐵1 ∩ 𝐵2)) = 3
10
14
9
13
4
12
=0.4945
b) Sea el suceso D =” contestar bien al menos a dos temas”
Sea el suceso E =” contestar bien a tres temas”
𝑃(𝐷) = 𝑃(𝐶) + 𝑃(𝐸) = 0.4945 + 𝑃(𝐵1 ∩ 𝐵2 ∩ 𝐵3) = 0.4945 +
10
14
9
13
8
12
=0.8252
4.37.-Un grupo de alumnos de esta asignatura, son 24, tiene la
costumbre de celebrar su cumpleaños invitándose entre si.
Como solo se puede acudir a una fiesta, ¿Cuál es la probabilidad
de no poder asistir a alguna fiesta debido a la coincidencia de
fechas de nacimiento?
------------------------ooooooooooooo------------------------------------
Un año no bisiesto tiene 365 días, la probabilidad de que no coincidan los
cumpleaños de 24 personas es:
𝑃(𝐶1 ∩ 𝐶2 ∩ ⋯ 𝐶𝑛) =
365
365
364
365
⋯
342
365
=0.462
es decir, casi en el 50% de los casos se perderá alguien asistir a alguna
fiesta por coincidir las fechas de nacimiento.
4.38.-Un autobús recorre diariamente el trayecto de ida y vuelta entre
dos ciudades y se sabe por las estadísticas que las
probabilidades de tener un accidente en día con o sin lluvia son
de 0,08 y 0,004 respectivamente. En una semana con solo dos
días lluviosos tuvo un accidente. Calcular la probabilidad de
que el accidente haya sido en un día con lluvia.
------------------------ooooooooooooo------------------------------------
Planteamos gráficamente el problema

Página 21 de 46
Sea los sucesos: E = “conjunto de días”
1
A =”días con lluvia” ,𝑃(𝐴1) =
2
7
, 1
2 A
A = =”días con lluvia” , 𝑃(𝐴2) =
5
7
B =”días con accidente” B =”días sin accidente”
1
A
/
B =” accidente con día de lluvia” , 𝑃(𝐵/𝐴1) = 0.08
2
A
/
B =” accidente con día sin lluvia” , 𝑃(𝐵/𝐴2) = 0.004
1
A
/
B =” sin accidente con día de lluvia” , 𝑃(𝐵/𝐴1) = 0.92
2
A
/
B =” sin accidente con día sin lluvia” , 𝑃(𝐵/𝐴2) = 0.996
Aplicamos la fórmula de Bayes para calcular los resultados pedidos
B
/
A1 =” si ha habido accidente , posibilidad de que haya sido en día de
lluvia”
B
/
A2 =” si ha habido accidente , posibilidad de que haya sido en día que
no llovió”
𝑃(𝐴1/𝐵) =
𝑃(𝐵/𝐴1) ⋅ 𝑃(𝐴1)
𝑃(𝐵/𝐴1) ⋅ 𝑃(𝐴1) + 𝑃(𝐵/𝐴2) ⋅ 𝑃(𝐴2)
=
0.08 ⋅
2
7
0.08 ⋅
2
7
+ 0.004 ⋅
5
7
=
16
18
𝑃(𝐴2/𝐵) =
𝑃(𝐵/𝐴2) ⋅ 𝑃(𝐴2)
𝑃(𝐵/𝐴1) ⋅ 𝑃(𝐴1) + 𝑃(𝐵/𝐴2) ⋅ 𝑃(𝐴2)
=
0.004 ⋅
5
7
0.08 ⋅
2
7
+ 0.004 ⋅
5
7
=
2
18

Página 22 de 46
4.39.-Una empresa automovilística tiene dos factorías: A y B. En la A
tiene el 60% de la producción. El 10% de los vehículos
producidos en la factoría A son furgonetas, en tanto que la mitad
de la producción de la factoría B son furgonetas. Si se compra
una furgoneta, calcula la probabilidad de que se haya fabricado
en la factoría B.
------------------------ooooooooooooo------------------------------------
Planteamos gráficamente el problema
Sea los sucesos: E = “empresa automovilística”
1
A =”producción en factoria A”,𝑃(𝐴1) = 0.6,
1
2 A
A = =” producción en factoria B” , 𝑃(𝐴2) = 0.4
B =”furgoneta” B =”no furgoneta”
1
A
/
B =” siendo producido en A, que sea furgoneta” , 𝑃(𝐵/𝐴1) = 0.1
2
A
/
B =” siendo producido en B, que sea furgoneta” , 𝑃(𝐵/𝐴2) = 0.5
1
A
/
B =” siendo producido en A, que no sea furgoneta” , 𝑃(𝐵/𝐴1) = 0.9
2
A
/
B =” siendo producido en B, que no sea furgoneta”, 𝑃(𝐵/𝐴2) = 0.5
B
/
A1 =” si se compró una furgoneta, posibilidad de que haya sido en la
factoría A”
B
/
A2 =” si se compró una furgoneta, posibilidad de que haya sido en la
factoría B”
𝑃(𝐴1/𝐵) =
𝑃(𝐵/𝐴1) ⋅ 𝑃(𝐴1)
𝑃(𝐵/𝐴1) ⋅ 𝑃(𝐴1) + 𝑃(𝐵/𝐴2) ⋅ 𝑃(𝐴2)
=
0.1 ⋅ 0.6
0.1 ⋅ 0.6 + 0.5 ⋅ 0.4
=
3
13
𝑃(𝐴2/𝐵) =
𝑃(𝐵/𝐴2) ⋅ 𝑃(𝐴2)
𝑃(𝐵/𝐴1) ⋅ 𝑃(𝐴1) + 𝑃(𝐵/𝐴2) ⋅ 𝑃(𝐴2)
=
0.5 ⋅ 0.4
0.1 ⋅ 0.6 + 0.5 ⋅ 0.4
=
10
13
4.40.-Dos expertos, E y F, realizan peritaciones para una cierta
compañía de seguros. La probabilidad de que una peritación
haya sido realizada por E es 0.55 y por F es 0.45. Si una
peritación ha sido realizada por E, la probabilidad de que de
lugar al pago de indemnización es 0.98 y si ha sido realizada por

Página 23 de 46
F es 0.90 . Un siniestro ha supuesto a la compañía el pago de
una indemnización. Hallar la probabilidad de que la peritación
haya sido realizada por F.
------------------------ooooooooooooo------------------------------------
Sea los sucesos:
E =”indemnización hecha por el experto E”,𝑃(𝐸) = 0.55,
E
F = =” indemnización hecha por el experto F” , 𝑃(𝐹) = 0.45
I = “pagar indemnización”
I =”no pagar indemnización”
E
/
I =” siendo peritado por E, pago de indemnización” , 𝑃(𝐼/𝐸) = 0.98
E
/
I =”siendo peritado por E, no pago de indemnización”, 𝑃(𝐼/𝐸) = 0.02
F
/
I =” siendo peritado por F, pago de indemnización” , 𝑃(𝐼/𝐹) = 0.9
E
/
I =”siendo peritado por F, no pago de indemnización”, 𝑃(𝐼/𝐹) = 0.1
I
/
F =” si se pagó indemnización, posibilidad de que haya sido peritado
por F”
𝑃(𝐹/𝐼) =
𝑃(𝐼/𝐹) ⋅ 𝑃(𝐹)
𝑃(𝐼/𝐹) ⋅ 𝑃(𝐹) + 𝑃(𝐼/𝐸) ⋅ 𝑃(𝐸)
=
0.9 ⋅ 0.45
0.9 ⋅ 0.45 + 0.98 ⋅ 0.55
=0.429
4.41.-En un colegio el 4% de los chicos y el 1% de las chicas miden
más de 180 cm. de estatura. Además el 60% de los estudiantes
son chicas. Si se selecciona al azar un estudiante y es mas alto
de 180 cm. ¿ Cuál es la probabilidad de que el estudiante sea
chica?
------------------------ooooooooooooo------------------------------------
Sea los sucesos:
E =”ser chico”,𝑃(𝐸) = 0.4,
E
F = =”ser chica” , 𝑃(𝐹) = 0.6
I = “medir mas de 180 cms.”
I =” no medir 180 cms.”
E
/
I =” siendo chico, medir mas de 180 cms.” , 𝑃(𝐼/𝐸) = 0.04
E
/
I =” siendo chico, no medir 180 cms.”, 𝑃(𝐼/𝐸) = 0.96
F
/
I =” siendo chica, medir mas de 180 cms.” , 𝑃(𝐼/𝐹) = 0.01
E
/
I =” siendo chica, no medir 180 cms”, 𝑃(𝐼/𝐹) = 0.99
I
/
F =” si midió más de 180 cms., posibilidad de que el estudiante sea
chica”
𝑃(𝐹/𝐼) =
𝑃(𝐼/𝐹) ⋅ 𝑃(𝐹)
𝑃(𝐼/𝐹) ⋅ 𝑃(𝐹) + 𝑃(𝐼/𝐸) ⋅ 𝑃(𝐸)
=
0.01 ⋅ 0.6
0.01 ⋅ 0.6 + 0.04 ⋅ 0.4
=0.2727

Página 24 de 46
DISTRIBUCIONES DISCRETAS.
4.42.-Sea el experimento aleatorio que consiste en el lanzamiento de
tres monedas al aire y anotar el número de caras obtenidas. Se
pide:
a) función de probabilidad y su representación.
b) función de distribución y su representación.
c) media y varianza de la distribución.
d) Sea X a variable que expresa el número de caras obtenidas,
halla 𝑷(𝟏 < 𝑿 < 𝟑).
------------------------ooooooooooooo------------------------------------
a)
x1 p1
0
1
2
3
1/8
3/8
3/8
1/8
b)

















=
x
3
1
3
x
2
8
7
2
x
1
8
4
1
x
0
8
1
0
x
0
)
x
(
F
xi fi xi* fi x2
i x2
i* fi
0
1
2
3
1/8
4/8
3/8
1/8
0
3/8
6/8
3/8
0
1
4
9
0
3/8
12/8
9/8
12/8 24/8
c) Media: 5
.
1
8
/
12 =
=
 Varianza: 𝜎2
= 24/8 − 1. 52
= 0.75
d) 𝑃(1 < 𝑋 < 3) = 𝑃(𝑋 = 2) = 3/8 =0.375
4.43.-Sea X una variable aleatoria discreta cuya función de
probabilidad es :
X 0 1 2 3 4 5
p 0,1 0,2 0,1 0,4 0,1 0,1
a) Calcula y representa gráficamente la función de distribución.
0 1 2 3 4
0.05
0.1
0.15
0.2
0.25
0.3
0.35
-2
2
4
6
0.2
0.4
0.6
1

Página 25 de 46
b)Calcula las siguientes probabilidades: 𝑷(𝑿 ≤ 𝟒, 𝟓) , 𝑷(𝑿 ≥ 𝟑) y
𝑷(𝟑 ≤ 𝑿 < 𝟒, 𝟓).
------------------------ooooooooooooo------------------------------------
a)























=
x
5
1
5
x
4
9
.
0
4
x
3
8
.
0
3
x
2
4
.
0
2
x
1
3
.
0
1
x
0
1
.
0
0
x
0
)
x
(
F
b) 𝑃(𝑋 ≤ 4,5) = 𝐹(4.5) =0.9
𝑃(𝑋 ≥ 3) = 1 − 𝑃(𝑋 < 3) = 1 − 0,4 =0.6
𝑃(3 ≤ 𝑋 < 4,5) = 𝑃(𝑋 = 3) + 𝑃(𝑋 = 4) = 0.4 + 0.1 =0.5
4.44.-Sea X una variable aleatoria discreta cuya función de
probabilidad viene dada por: 𝑷(𝑿 = 𝒓) =
𝟏
𝟖
, (𝒓 = 𝟐, 𝟑, . . . . , 𝟗). Se
pide que halles:
a) representación de la función de probabilidad.
b) la función de distribución y su representación.
c) la media y la desviación típica.
d)las siguientes probabilidades: 𝑷(𝑿 ≥ 𝟔) , 𝑷(𝟒 < 𝑿 < 𝟕) y
𝑷(𝑿 < −𝟑)
------------------------ooooooooooooo------------------------------------
a)
b)
-2 2 4 6
0.2
0.4
0.6
0.8
1
0 1 2 3 4 5 6 7 8 9 10 11
0.02
0.04
0.06
0.08
0.1
0.12

Página 26 de 46































=
x
9
1
9
x
8
8
/
7
8
x
7
8
/
6
7
x
6
8
/
5
6
x
5
8
/
4
5
x
4
8
/
3
4
x
3
8
/
2
3
x
2
8
/
1
2
x
0
)
x
(
F
c)
xi pi xi* pi x2
i x2
i* pi
2
3
4
5
6
7
8
9
1/8
1/8
1/8
1/8
1/8
1/8
1/8
1/8
2/8
3/8
4/8
5/8
6/8
7/8
8/8
9/8
4
9
16
25
36
49
64
81
4/8
9/8
16/8
25/8
36/8
49/8
64/8
81/8
44/8 284/8
Media: 𝜇 = 44/8 = 5.5 Desviación típica: 𝜎 = √284/8 − 5. 52 = 2.29
d) 𝑃(𝑋 ≥ 6) = 𝑃(𝑋 = 6) + 𝑃(𝑋 = 7) + 𝑃(𝑋 = 8) + 𝑃(𝑋 = 9) = 1/8 + 1/8 +
+1/8 + 1/8 =0.5
𝑃(4 < 𝑋 < 7) = 𝑃(𝑋 = 5) + 𝑃(𝑋 = 6) = 1/8 + 1/8 =0.25
𝑃(𝑋 < −3) =0
4.45.-La opinión que tiene la población sobre terapia de grupo es
favorable en el 45% de los casos, y desfavorable el resto.
Elegidos cinco individuos al azar, calcula:
a) probabilidad de que solo dos la consideren favorable.
b) probabilidad de que mas de dos la consideren favorable.
c) sobre una población de 1.000 individuos, ¿cuántos la
consideran desfavorable?.
------------------------ooooooooooooo------------------------------------
Sean los sucesos A=”opinión favorable”,𝑝 = 𝑃(𝐴) = 0.45,
A=” opinión no favorable” , 𝑞 = 𝑃(𝐴) = 0.55
Si representamos por X la variable que expresa el número de individuos
de la muestra que tiene opinión favorable, en una probabilidad binomial
resulta:
a) 𝑃(𝑋 = 2) = (
5
2
) 0.452
⋅ 0.558
=0.3369
b)𝑃(𝑋 > 2) = 1 − 𝑃(𝑋 = 0) − 𝑃(𝑋 = 1) − 𝑃(𝑋 = 2) = 1 − 0.0503 −
0.2059 − 0.3369 =0.4069
c) 1000 ⋅ 𝑝 = 1000 ⋅ 0.45 =450 individuos la consideran desfavorable.
-2 2 4 6 8 10 12
0.2
0.4
0.6
0.8
1

Página 27 de 46
4.46.-Se lanza una moneda 100 veces. Halla la probabilidad de :
a) obtener a lo sumo 40 caras.
b) obtener más de 40 caras.
------------------------ooooooooooooo------------------------------------
En principio se trata de una distribución binomial )
2
1
,
100
(
B ; como
5
50
2
1
100
p
n 
=

=
 y 5
50
2
1
100
q
n 
=

=

Aplicando el teorema de Moivre se puede aproximar mediante una
)
,
(
N 
 siendo 50
p
n =

=
 y 5
q
p
.
n =

=

a)𝑃(𝑋 ≤ 40.5) = 𝑃 (𝑍 ≤
40.5−50
5
) = 𝑃(𝑍 ≤ −1.9) = 1 − (𝑍 ≤ 1.9) = 1 −
0.9713 =0.0287
b) 𝑃(𝑋 > 40.5) = 1 − 𝑃(𝑋 ≤ 4.5) = 1 − 0.0287 = 0.97113
DISTRIBUCIONES CONTINUAS.
4.47.-Dada la función de densidad de una variable aleatoria continua,
definida por:











=
x
si
x
si
x
s
co
x
si
x
f
2
0
2
0
0
0
)
(

 halla la función de
distribución.
------------------------ooooooooooooo------------------------------------
La función de distribución viene dada por la siguiente expresión:
𝐹(𝑥) = 𝑃(𝑋 ≤ 𝑥) = ∫ 𝑓(𝑥)𝑑𝑥
𝑥
−∞
. Por tanto:
Si 0
dx
0
)
x
(
F
0
)
x
(
f
0
x
x
=
=

=

  
−
Si x
sen
dx
x
cos
dx
0
)
x
(
F
x
cos
)
x
(
f
2
x
0
x
0
0
=
+
=

=


 
 
−

Si   1
x
sen
dx
0
dx
x
cos
dx
0
)
x
(
F
0
)
x
(
f
2
x 2
0
x
2
2
0
0
=
=
+
=

=

 

 
−




En resumen,











=
x
2
si
1
2
x
0
si
x
sen
0
x
si
0
)
x
(
F



Página 28 de 46
4.48.-Un almacén de camisas ha determinado que el cuello de los
varones adultos se distribuye normalmente con media de 38 cm.
Y desviación típica 1,5 cm. Con el fin de poder preparar la
producción de la próxima temporada y teniendo en cuenta que
su producción está en 10.000 camisas, ¿cuántas camisas de los
números 35, 36, 37, 38 y 39 tendrán que fabricar?.
------------------------ooooooooooooo------------------------------------
𝑃(34.5 < 𝑋 ≤ 35.5) = 𝑃 (
34.5 − 38
1.5
< 𝑍 ≤
35.5 − 38
1.5
) = 𝑃(−2.33 < 𝑍 ≤ −1.66) =
= 𝑃(𝑍 ≤ 2.33) − 𝑃(𝑍 ≤ 1.66) = 0.9901 − 0.9515 = 0.0386 ⇒ 10000 ⋅ 0.0386 =
= 386
386 camisas del número 35 tendrán que fabricar.
𝑃(35.5 < 𝑋 ≤ 36.5) = 𝑃 (
35.5−38
1.5
< 𝑍 ≤
36.5−38
1.5
) = 𝑃(−1.66 < 𝑍 ≤ −1) =
𝑃(𝑍 ≤ 1.66) − 𝑃(𝑍 < 1) = 0.9515 − 0.8413 = 0.1102 ⇒ 10000 ⋅ 0.1102 =
= 1102
𝑃(36.5 < 𝑋 ≤ 37.5) = 𝑃 (
36.5−38
1.5
< 𝑍 ≤
37.5−38
1.5
) = 𝑃(−1 < 𝑍 ≤ −0.33) =
𝑃(𝑍 ≤ 1) − 𝑃(𝑍 ≤ 0.33) = 0.8413 − 0.6293 = 0.2120 ⇒ 10000 ⋅ 0.2120 =
2120
𝑃(37.5 < 𝑋 ≤ 38.5) = 𝑃 (
37.5 − 38
1.5
< 𝑍 ≤
38.5 − 38
1.5
) = 𝑃(−0.33 < 𝑍 ≤ 0.33) =
= 2[𝑃(𝑍 ≤ 0.33)−0.5] = 2(0.6293 − 0.5) = 0.2586 ⇒ 10000 ⋅ 0.2586 = 2586
𝑃(38.5 < 𝑋 ≤ 39.5) = 𝑃 (
38.5 − 38
1.5
< 𝑍 ≤
39.5 − 38
1.5
) = 𝑃(0.33 < 𝑍 ≤ 1) =
𝑝(𝑍 ≤ 1) − 𝑝(𝑍 ≤ 0.33) = 0.8413 − 0.6293 = 0.2120 ⇒ 10000 ⋅ 0.2120=
= 2120
4.49.-En una distribución N(0,1) , ¿entre qué valores está el 94% de
los valores centrales?.
------------------------ooooooooooooo------------------------------------
𝑃(−𝑧 ≤ 𝑍 ≤ 𝑧) = 0.94
𝑃(−𝑧 ≤ 𝑍 ≤ 𝑧) = 𝑃(𝑍 ≤ 𝑧) − 𝑃(𝑍 ≤ −𝑧) = 𝑃(𝑍 ≤ 𝑧) − (1 − 𝑃(𝑍 ≤ 𝑧)) =
= 2𝑃(𝑍 ≤ 𝑧) − 1 = 0.94 ⇒ 𝑃(𝑍 ≤ 𝑧) = 0.97 ⇒ 𝑧 = 1.88
Por tanto, el 9% de los individuos esté en el intervalo (−1.86,1.86)
INFERENCIA ESTADISTICA.

Página 29 de 46
EJERCICIOS
DE
EXÁMENES
ESTADÍSTICA DESCRIPTIVA DE UN CARÁCTER.
VARIABLE BIDIMENSIONAL.REGRESIÓN Y CORRELACIÓN.
EX4B.01-Se han observado durante un mes determinado, el gasto en
el teléfono móvil y el ingreso total en seis familias, expresando
en euros. Han sido:
Gasto móvil
(euros)
Ingreso total
(miles de euros)
Familia 1
Familia 2
Familia 3
Familia 4
Familia 5
Familia 6
2
3
6
9
10
11
4
6
8
10
12
20
Calcular:
a)La covarianza entre el gasto y el ingreso. A la vista de este
resultado, ¿Se puede afirmar que las variables sean
dependientes o independientes?
b) Para estas seis familias ¿Qué variable se distribuye de forma
más homogénea, el gasto en móvil o en los ingresos totales?
------------------------ooooooooooooo------------------------------------
Ingreso
total
xi
Gasto
móvil
yi
𝒙𝒊
𝟐
𝒚𝒊
𝟐 𝒙𝒊𝒚𝒊
4
6
8
10
12
20
2
3
6
9
10
11
16
36
64
100
144
400
4
9
36
81
100
121
8
18
48
90
120
220
60 41 760 351 504
Media de la variable x: 𝑥 =
60
6
= 10 Media de la variable y: 𝑦 =
41
6
= 6.83

Página 30 de 46
Varianza de x : 𝑠𝑥
2
=
760
6
− 102
= 26.67
Varianza de y : 𝑠𝑦
2
=
351
6
− 6.832
= 11.85
Covarianza de (x,y): 𝑠𝑥𝑦 =
504
6
− 10 ⋅ 6.83 = 15.7
b) Media de y: 𝑦 =
41
6
= 6.83 , 𝑠𝑦 = √11,85 = 3.44 𝐶𝑉
𝑦 =
𝑠𝑦
𝑦
= 0,5037
(50,37% de dispersión)
Media de x: 𝑥 =
60
6
= 10 , 𝑠𝑥 = √26,67 = 5.16 𝐶𝑉
𝑥 =
𝑠𝑥
𝑥
= 0,516
(51,6% de dispersión)
Se distribuye más homogénea el ingreso total de las familias
CÁLCULO DE PROBABILIDADES
EX4C.01-Se lanza una moneda al aire. Si se cale cara, se echan 𝑎 bolas
a una urna y si sale cruz 2𝑎 bolas blancas. Igual procedimiento
se sigue con una segunda tirada, poniendo 𝑏 bolas negras si
sale cara y 2𝑏 negras si sale cruz. De la urna compuesta así se
toma una bola al azar. ¿Cuál es la probabilidad de que salga
negra?
------------------------ooooooooooooo------------------------------------
Sean:
𝐴11 suceso de que salgan: cara-cara
𝐴12 suceso de que salgan: cara-cruz
𝐴21 suceso de que salgan: cruz-cara
𝐴22 suceso de que salgan: cruz-cruz
𝐵 suceso de obtener bola negra en la extracción
𝑃 (𝐵
𝐴𝑖𝑗
⁄ ) =
𝑏𝑗
𝑎𝑖+𝑏𝑗
; 𝑖 = 1,2 , 𝑗 = 1,2 y 𝑃(𝐴𝑖𝑗) =
1
4
La probabilidad total es:
𝑃(𝐵) = 𝑃 (𝐵
𝐴11
⁄ ) 𝑃(𝐴11) + 𝑃 (𝐵
𝐴12
⁄ ) 𝑃(𝐴12) + 𝑃 (𝐵
𝐴21
⁄ ) 𝑃(𝐴21) + 𝑃 (𝐵
𝐴22
⁄ ) 𝑃(𝐴22) =
=
1
4
(
𝑏
𝑎 + 𝑏
+
𝑏
2𝑎 + 𝑏
+
2𝑏
𝑎 + 2𝑏
+
2𝑏
2𝑎 + 2𝑏
) =
𝑏
2𝑎 + 2𝑏
+
4𝑏2
+ 5𝑎𝑏
8𝑎2 + 8𝑏2 + 20𝑎𝑏
EX4C.02-Tenemos seis cajas que contienen 12 tornillos buenos y
defectuosos. Una caja contiene 8 buenos y 4 defectuosos, dos
cajas 6 buenos y 6 defectuosos y tres cajas 4 buenos y 8
defectuosos.
Se elije una caja al azar y se extraen 3 tornillos, sin
reemplazamiento, de dicha caja; de estos resultan ser 2 buenos
y 𝟏 defectuoso. ¿Cuál es la probabilidad de que la caja elegida
contenga 6 buenos y 6 defectuosos?

Página 31 de 46
------------------------ooooooooooooo------------------------------------
Sean:
𝐴1 suceso de que la caja elegida tenga 8 buenos y 4 defectuosos.
𝐵 suceso de que al extraer tres resulten 2 buenos y 1 defectuosos.
La probabilidad pedida será:
𝑃 (
𝐴2
𝐵
⁄ ) =
𝑃(𝐵
𝐴2
⁄ )𝑃(𝐴2)
𝑃(𝐵
𝐴1
⁄ )𝑃(𝐴1)+𝑃(𝐵
𝐴2
⁄ )𝑃(𝐴2)+𝑃(𝐵
𝐴3
⁄ )𝑃(𝐴3)
y :
𝑃(𝐴1) =
1
6
, 𝑃(𝐴1) =
2
6
, 𝑃(𝐴1) =
3
6
Además:
𝑃 (𝐵
𝐴1
⁄ ) =
(8
2)(4
1)
(12
3 )
=
28∙4
220
=
112
220
, 𝑃 (𝐵
𝐴2
⁄ ) =
(6
2)(6
1)
(12
3 )
=
15∙6
220
=
90
220
𝑃 (𝐵
𝐴3
⁄ ) =
(4
2
)(8
1
)
(12
3
)
=
6 ∙ 8
220
=
48
220
Sustituyendo:
𝑃 (
𝐴2
𝐵
⁄ ) =
90
220
∙
2
6
112
220
∙
1
6
+
90
220
∙
2
6
+
48
220
∙
3
6
=
180
436
= 0.4128
EX4C.03-Si 10 bolas indistinguibles se distribuyen entre 7 cajas de
modo que todas las distribuciones son igualmente probables.
Calcula la probabilidad de:
i) que una determinada caja contenga 3 bolas.
ii) que todas las cajas estén ocupadas.
iii) que exactamente 5 cajas estén vacías.
------------------------ooooooooooooo------------------------------------
Las formas de colocar las 10 bolas en 7 cajas, son las combinaciones
con repetición 𝑅𝐶7,10 = (10+7−1
10
) = (16
10
) es la asignación de las bolas a
las cajas.
i) Las 6 restantes cajas han de tener las 7 bolas, para que quede una
caja con 3 bolas , entonces 𝑃 =
𝑅𝐶6,7
𝑅𝐶7,10
=
(12
7 )
(16
10)
=
792
8008
=0.989
ii) cada caja ha de tener 1 bola y las otras 3 las repartimos entre las 7
cajas, entonces 𝑃 =
𝑅𝐶3,7
𝑅𝐶7,10
=
(9
7)
(16
10)
=
36
8008
=0.0044
iii) las 10 bolas tienen que estar en 5 cajas , y 0 bolas en 2 cajas, por
tanto, distribución de las 7 cajas de 5 en 5, por combinaciones de 10
bolas en 2 cajas, entonces 𝑃 =
𝐶7,5𝑅𝐶2,10
𝑅𝐶7,10
=
(7
5)(11
10)
(16
10)
=
21∙11
8008
=0.0288

Página 32 de 46
EX4C.04- i) una urna contiene 𝑎 bolas blancas y 𝑏 negras. Una persona
saca 𝑘 bolas. ¿Cuál es la probabilidad de que sean 𝑥 blancas y
𝑘 − 𝑥 negras?
ii) ¿Cuál es la probabilidad de torpedear un barco, sabiendo que
sólo pueden lanzarse 3 torpedos y que la probabilidad de hacer
blanco con cada uno de ellos es 0,20?
------------------------ooooooooooooo------------------------------------
i) los casos posibles al sacar 𝑘 bolas de una urna que contiene 𝑎 + 𝑏
son: (𝑎+𝑏
𝑘
)
los casos favorables teniendo que sacar 𝑥 blancas y 𝑘 − 𝑥 negras son:
(
𝑎
𝑥
) (
𝑏
𝑘 − 𝑥
)
Por tanto, la probabilidad pedida es:
(𝑎
𝑥)( 𝑏
𝑘−𝑥)
(𝑎+𝑏
𝑘 )
ii) Pasando al suceso complementario (no hacer blanco con ningún
torpedo).
La probabilidad de no hacer blanco con un torpedo es 0,8 ,y la de no
hacerlo con ninguno de los 3, por ser independientes es 0,83
.Entonces
la probabilidad de destruir el barco es 1 − 0,83
Planteamos el problema matemáticamente:
Llamamos 𝐴1, 𝐴2 , 𝐴3 A los sucesos independientes “destruir el barco con
el primer torpedo , segundo torpedo , tercer torpedo”
𝑃(𝐴1 ∪ 𝐴2 ∪ 𝐴3) = 1 − 𝑃(𝐴1
̅̅̅ ∩ 𝐴2
̅̅̅ ∩ 𝐴3
̅̅̅̅) = 1 − 𝑃(𝐴1
̅̅̅)3
= 1 − 0,83
=0,488
EX4C.05- i) Un cirujano se especializa en cirugías estéticas. Entre sus
pacientes, el 20 por 100 se realizan correcciones faciales, el 35
por 100 implantes mamarios y el restante en otras cirugías
correctivas. Se sabe, además, que son de género masculino el
25 por 100 de los que se realizan correcciones faciales , 15 por
100 implantes mamarios y 40 por 100 otras cirugías correctivas.
Si se selecciona un paciente al azar
a) calcula la probabilidad de que sea de género masculino.
b) si resulta que es de género masculino halla la probabilidad
de que se haya realizado una cirugía de implantes mamarios.
------------------------ooooooooooooo------------------------------------
Se definen los sucesos:
Suceso 𝐹: pacientes que se realizan cirugías faciales.
suceso 𝑀: pacientes que se realizan implantes mamarios.
suceso 𝑂 : pacientes que se realizan otras cirugías correctivas.
suceso 𝐻 : pacientes de género masculino.
a) La probabilidad de que sea de género masculino se refiere a un
problema de probabilidad total , ya que es el suceso condicionado y
las cirugías, los condicionantes. Dicho valor será:

Página 33 de 46
𝑃(𝐻) = 𝑃(𝐹) ∙ 𝑃(𝐻
𝐹
⁄ ) + 𝑃(𝑀) ∙ 𝑃(𝐻
𝑀
⁄ ) + 𝑃(𝑂) ∙ 𝑃(𝐻
𝑂
⁄ ) =
= 0.20 ∙ 0.25 + 0.35 ∙ 0.15 + 0.45 ∙ 0.40 =0,2825
b) como el suceso condicionado ha ocurrido entonces se aplica el
Teorema de Bayes, luego, el valor de la probabilidad será:
𝑃(𝐻) =
𝑃(𝑀) ∙ 𝑃(𝐻
𝑀
⁄ )
𝑃(𝐹) ∙ 𝑃(𝐻
𝐹
⁄ ) + 𝑃(𝑀) ∙ 𝑃(𝐻
𝑀
⁄ ) + 𝑃(𝑂) ∙ 𝑃(𝐻
𝑂
⁄ )
=
0,0525
0,2825
=0,1858
EX4C.06- Una urna A contiene 4 bolas blancas y 7 negras. Otra urna
B contiene 8 blancas y 3 negras
a) Se extraen 3 bolas, sin reemplazamiento, de la urna B. ¿Cuál
es la probabilidad de que sean las 3blancas
b)de la urna A se pasa una bola tomada al azar a la urna B sin
mirar. Después se saca una bola de la urna B
i) ¿Probabilidad de que la bola traída de B sea blanca?
ii) La bola extraída de B resultó ser blanca.¿ Probabilidad de
que la bola pasada de la urna A la B fuese negra?
------------------------ooooooooooooo------------------------------------
a) sin reemplazamiento, las 3 sean blancas:
𝑃(𝑙𝑎𝑠 3 𝑏𝑙𝑎𝑛𝑐𝑎𝑠) = 𝑃(𝐵1 ∩ 𝐵2 ∩ 𝐵3) = 𝑃(𝐵1) ∙ 𝑃 (
𝐵2
𝐵1
⁄ ) ∙ 𝑃 (
𝐵3
𝐵1 ∩ 𝐵2
⁄ ) =
=
8
11
∙
7
10
∙
6
9
=0,339
b)i) 𝑃(𝐵) = 𝑃(𝐵
𝐵𝐵
⁄ ) ∙ 𝑃(𝐵𝐵) + 𝑃(𝐵
𝐵𝑁
⁄ ) ∙ 𝑃(𝐵𝑁) =
9
12
∙
4
11
+
8
12
∙
7
11
=0,696
b)ii) 𝑃(𝐵𝑁
𝐵
⁄ ) =
𝑃(𝐵𝑁∩𝐵)
𝑃(𝐵)
=
𝑃(𝐵
𝐵𝑁
⁄ )∙𝑃(𝐵𝑁)
𝑃(𝐵)
=
8
12
∙
7
11
0,696
=0,609
EX4C.07-De las personas que han seguido las sesiones diarias dobles
de partidos de fútbol por televisión (primer partido a las 16:00
y segundo a las 20:00) de la primera fase (dieciseisavos y
octavos de final) del campeonato europeo de fútbol, se sabe
que al 70% les ha gustado el primer partido; al 30% le ha
gustado el primero pero no el segundo; al 20%les ha gustado
el segundo, pero no el primero. Elegimos una persona al azar,
al finalizar una de las sesiones diarias dobles de futbol. Calcula
la probabilidad de los siguientes sucesos:
i) le haya gustado sólo uno de los partidos.
ii) le hayan gustado los dos partidos.
iii) no le haya gustado el segundo partido, si se sabe que el
primero no le gustó.
iv) le haya gustado el segundo partido.
------------------------ooooooooooooo------------------------------------
i)𝑃((𝐴 ∩ 𝐵
̅) ∪ (𝐴̅ ∩ 𝐵)) = 𝑃(𝐴 ∩ 𝐵
̅) + 𝑃(𝐴̅ ∩ 𝐵) − 𝑃((𝐴 ∩ 𝐵
̅) ∪ (𝐴̅ ∩ 𝐵)) =
𝑃(𝐴 ∩ 𝐵
̅) + 𝑃(𝐴̅ ∩ 𝐵) − 𝑃(∅) = 0,3 + 0,2 =0,5

Página 34 de 46
ii) 𝑃(𝐴 ∩ 𝐵) = 𝑃(𝐵 ∩ 𝐴) = 𝑃(𝐵
𝐴
⁄ ) ∙ 𝑃(𝐴) =
4
7
∙ 0,7 =0,4 , pues:
𝑃(𝐵
𝐴
⁄ ) = 1 − 𝑃 (𝐵
̅
𝐴
⁄ ) = 1 −
𝑃(𝐴 ∩ 𝐵
̅)
𝑃(𝐴)
= 1 −
0,3
0,7
=
4
7
iii) 𝑃 (𝐵
̅
𝐴̅
⁄ ) = 1 − 𝑃 (𝐵
𝐴̅
⁄ ) = 1 − 0,66 =0,33 , pues:
𝑃 (𝐵
𝐴̅
⁄ ) =
𝑃(𝐵 ∩ 𝐴̅)
𝑃(𝐴̅)
=
0,2
0.3
= 0,66
iv)𝑃(𝐵) = 𝑃(𝐵
𝐴
⁄ ) ∙ 𝑃(𝐴) + 𝑃 (𝐵
𝐴̅
⁄ ) ∙ 𝑃(𝐴̅) =
4
7
∙ 0,7 +
2
3
∙ 0,3 =0,6
EX4C.08-a) Halla la probabilidad de ganar uno o más juegos en una
serie de 4 juegos independientes, siendo 𝑞 la probabilidad de
ganar en uno de ellos. Expresa el resultado en función de 𝑞.
b) halla el valor de 𝑞 para que esta probabilidad sea
80
81
.
------------------------ooooooooooooo------------------------------------
a) Sean:
𝐴1 suceso de “ganar el primer juego”.
𝐴2 suceso de “ganar el segundo juego”.
𝐴3 suceso de “ganar el tercer juego”.
𝐴4 suceso de “ganar el cuarto juego”.
𝐴 suceso pedido, es decir, “ganar uno o más juegos en una serie de
4 juegos independientes”
𝑃(𝐴) = 𝑃(𝐴1 ∪ 𝐴2 ∪ 𝐴3 ∪ 𝐴4) = 1 − 𝑃(𝐴1 ∪ 𝐴2 ∪ 𝐴3 ∪ 𝐴4
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅) =
= 1 − 𝑃(𝐴1
̅̅̅ ∩ 𝐴2
̅̅̅ ∩ 𝐴3
̅̅̅ ∩ 𝐴4
̅̅̅) = 1 − 𝑃(𝐴1
̅̅̅) ∙ 𝑃(𝐴2
̅̅̅) ∙ 𝑃(𝐴3
̅̅̅) ∙ 𝑃(𝐴4
̅̅̅) =
⏟
𝑡𝑜𝑑𝑜𝑠 𝑚𝑖𝑠𝑚𝑎
𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑑𝑎𝑑
= 1 − (𝑃(𝐴1
̅̅̅))
4
= 1 − (1 − 𝑃(𝐴1))
4
=1 − (1 − 𝑞)4
b) Aplicamos 1 − (1 − 𝑞)4
=
80
81
= 1 −
1
81
⇒ (1 − 𝑞)4
=
1
81
= (
1
3
)
4
⇒
⇒ 1 − 𝑞 =
1
3
⇒𝑞 =
2
3
EX4C.09-a) Halla la probabilidad de ganar uno o más juegos en una
serie de 5 juegos independientes, siendo 𝑞 la probabilidad de
ganar en uno de ellos. Expresa el resultado en función de 𝑞.
b) halla el valor de 𝑞 para que esta probabilidad sea
242
243
.
------------------------ooooooooooooo------------------------------------
a) Sean:
𝐴1 suceso de “ganar el primer juego”.
𝐴2 suceso de “ganar el segundo juego”.
𝐴3 suceso de “ganar el tercer juego”.
𝐴4 suceso de “ganar el cuarto juego”.
𝐴5 suceso de “ganar el quinto juego”.

Página 35 de 46
𝐴 suceso pedido, es decir, “ganar uno o más juegos en una serie de
5 juegos independientes”
𝑃(𝐴) = 𝑃(𝐴1 ∪ 𝐴2 ∪ 𝐴3 ∪ 𝐴4 ∪ 𝐴5) = 1 − 𝑃(𝐴1 ∪ 𝐴2 ∪ 𝐴3 ∪ 𝐴4 ∪ 𝐴5
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅) =
1 − 𝑃(𝐴1
̅̅̅ ∩ 𝐴2
̅̅̅ ∩ 𝐴3
̅̅̅ ∩ 𝐴4
̅̅̅ ∩ 𝐴5
̅̅̅) = 1 − 𝑃(𝐴1
̅̅̅) ∙ 𝑃(𝐴2
̅̅̅) ∙ 𝑃(𝐴3
̅̅̅) ∙ 𝑃(𝐴4
̅̅̅) ∙ 𝑃(𝐴5
̅̅̅) =
⏟
𝑡𝑜𝑑𝑜𝑠 𝑚𝑖𝑠
𝑝𝑟𝑜𝑏𝑎𝑏
= 1 − (𝑃(𝐴1
̅̅̅))
5
= 1 − (1 − 𝑃(𝐴1))
5
=1 − (1 − 𝑞)5
b) Aplicamos 1 − (1 − 𝑞)5
=
242
243
= 1 −
1
243
⇒ (1 − 𝑞)5
=
1
243
= (
1
3
)
5
⇒
⇒ 1 − 𝑞 =
1
3
⇒𝑞 =
2
3
EX4C.10-Una encuesta sobre 500 estudiantes de una o más
asignaturas de álgebra física y estadística durante el primer
semestre reveló los siguientes números de estudiantes en las
asignaturas indicadas :
álgebra : 329 álgebra y física: 83
física: 186 álgebra y estadística: 217
estadística: 295 física y estadística: 63 .
Cuántos estudiantes estaban estudiando:
a) las 3 asignaturas
b) álgebra, pero no estadística
c) física, pero no álgebra
d) estadística, pero no física
------------------------ooooooooooooo------------------------------------
a) Sean:
𝐴 suceso “estudiantes que estudian álgebra ”.
𝐹 suceso “estudiantes que estudian física ”.
𝐸 suceso “estudiantes que estudian estadística ”.
𝐴𝐹 suceso “estudiantes que estudian álgebra y física ”.
𝐴𝐸 suceso “estudiantes que estudian álgebra y estadística ”.
𝐹𝐸 suceso “estudiantes que estudian física y estadística ”.
𝐴𝐹𝐸 suceso “estudiantes que estudian las tres”.
a) Tenemos:
(𝐴 + 𝐹 + 𝐸) = (𝐴) + (𝐹) + (𝐸) −
−(𝐴𝐹) − (𝐴𝐸) − (𝐹𝐸) + (𝐴𝐹𝐸) =
500 = 329 + 186 + 295 − 83 − 63 −
−217 + (𝐴𝐹𝐸) ⇒ (𝐴𝐹𝐸) = 53
Por tanto,
53 alumnos estudian las tres
b) Observando la gráfica comprobamos que los estudiantes de álgebra
,pero no estadística son : (𝐴) − (𝐴𝐸) = 329 − 217 = 112
Estudian álgebra, pero no estadística 112 estudiantes

Página 36 de 46
c) Observando la gráfica comprobamos que los estudiantes de física
pero no álgebra , son : (𝐹) − (𝐴𝐹) = 186 − 83 = 103
Estudian física, pero no álgebra 103 estudiantes
d) Observando la gráfica comprobamos que los estudiantes de
estadística pero no física, son : (𝐸) − (𝐹𝐸) = 295 − 63 = 232
Estudian estadística pero no física, 232 estudiantes
EX4C.11-En una fábrica se embalan(en cajas) galletas en 4 cadenas
de montaje: A1, A2, A3 y A4. El 35% de la producción total se
embala en la cadena A1 y el 20%, 24% y 21% en A2, A3 y A4
respectivamente. Los datos indican que no se embalan
correctamente un porcentaje pequeño de las cajas; el 1 por 100
de A1, el 3 por 100 de A2, el 2,5 por 100 de A3 y el 2 por 100 de
a 4.
a)¿Cuál es la probabilidad de que una caja elegida al azar de la
producción total sea defectuosa?.
b) Supongamos que descubrimos que una caja es defectuosa.
Calcula la probabilidad de que la caja provenga de la cadena
A1.
------------------------ooooooooooooo------------------------------------
a) Se trata de una probabilidad total.
𝐷 suceso “caja defectuosa”.
𝑃(𝐷) = 𝑃 (𝐷
𝐴1
⁄ ) ∙ 𝑃(𝐴1) + 𝑃 (𝐷
𝐴2
⁄ ) ∙ 𝑃(𝐴2) + 𝑃 (𝐷
𝐴3
⁄ ) ∙ 𝑃(𝐴3) + 𝑃 (𝐷
𝐴4
⁄ ) ∙ 𝑃(𝐴4) =
= 0,01 ∙ 0,35 + 0,03 ∙ 0,20 + 0,25 ∙ 0,24 + 0,02 ∙ 0,21 =0,0197
b) 𝑃 (
𝐴1
𝐷
⁄ ) =
𝑃(𝐷
𝐴1
⁄ )∙𝑃(𝐴1)
𝑃(𝐷)
=
0,01∙0,35
0,0197
=0,1777
EX4C.12- En una empresa informática se sabe por experiencias
pasadas, que la probabilidad de que una fuente de alimentación
se encuentre defectuosa es del 2%. La probabilidad de que un
control diagnostique un fallo en una fuente defectuosa es del
88% y de que la diagnostique en una fuente no defectuosa es
del 6%.
i) ¿Cuál es la probabilidad de que se le diagnostique un fallo a
una fuente?
ii) ¿Cuál es la probabilidad de que a una fuente que no se le
diagnostique un fallo, se defectuosa?
iii) Los sucesos “diagnosticar un fallo” y “ser defectuosa” ¿son
compatibles?.¿son independientes?
------------------------ooooooooooooo------------------------------------
i) Sean:
𝐹 suceso “diagnosticar fallo en una fuente ”.
𝐷 suceso “fuente defectuosa”.
𝑃(𝐹) = 𝑃(𝐹
𝐷
⁄ ) ∙ 𝑃(𝐷) + 𝑃 (𝐹
𝐷
̅
⁄ ) ∙ 𝑃(𝐷
̅) = 0,88 ∙ 0,02 + 0,06 ∙ 0,98 =0,0764

Página 37 de 46
ii) 𝑃 (𝐷
𝐹
̅
⁄ ) =
𝑃(𝐷∩𝐹
̅)
𝑃(𝐹
̅)
=
𝑃(𝐹
̅
𝐷
⁄ )∙𝑃(𝐷)
𝑃(𝐹
̅)
=
0,12∙0,02
1−0,0764
=0,0026
iii) 𝐹 y 𝐷 son compatibles , pues:
𝑃(𝐹 ∩ 𝐷) = 𝑃(𝐹
𝐷
⁄ ) ∙ 𝑃(𝐷) = 0,88 ∙ 0,02 ≠ 0 → compatibles
𝐹 y 𝐷 no son independientes , pues:
𝑃(𝐹) = 0,0764 ≠ 0,88 = 𝑃(𝐹
𝐷
⁄ ) , la ocurrencia de 𝐷 favorece la de 𝐹,
DISTRIBUCIONES DISCRETAS.
EX4D.01- ¿Qué es más fácil ganar a un jugador con probabilidad 0,5
de ganar una partida:
i) 3 partidas de 4 ó 5 partidas de 8?
ii) no más de n partidas de 2n+1 partidas ó mas de n partidas
de 2n+1 partidas?
------------------------ooooooooooooo------------------------------------
Se trata de una distribución discreta de tipo binomial:
Una variable aleatoria 𝑋 sigue una distribución binomial de parámetros
𝑛 ∈ ℕ y 𝑝 ∈ (0,1) , se denota 𝑋 ∼ 𝐵(𝑛, 𝑝), si describe el número de éxitos
en 𝑛 realizados independientes de un experimento que tiene de
probabilidad de éxito 𝑝 (probabilidad de fracaso 1 − 𝑝). Puede tomar
cualquier valor en {0,1,2, ⋯ , 𝑛}
Si 𝑘 ∈ {0,1,2, ⋯ , 𝑛}, se cumple que
𝑃(𝑥 = 𝑘) = (
𝑛
𝑘
) 𝑝𝑘(1 − 𝑝)𝑛−𝑘
i) Probabilidad de ganar 3 de 4
𝑃3,4 = (
4
3
) 0,53(1 − 0,5)1
= 4 ∙
1
16
= 0,25
Probabilidad de ganar 5 de 8
𝑃5,8 = (
8
5
) 0,53(1 − 0,5)5
= 56 ∙
1
256
= 0,2188
Es más fácil ganar 3 de 4, que 5 de 8
ii) Igualmente probables
EX4D.02- Calcula:
a) La probabilidad de obtener exactamente 2 caras en 6
lanzamientos de una moneda al aire.
b) La probabilidad de obtener al menos 4 caras en 6
lanzamientos de una moneda al aire.
------------------------ooooooooooooo------------------------------------

Página 38 de 46
probabilidad de éxito 𝑝 (probabilidad de fracaso 1 − 𝑝). Puede tomar
𝑃(𝑥 = 𝑘) = (
𝑛
𝑘
) 𝑝𝑘(1 − 𝑝)𝑛−𝑘
a) Probabilidad de obtener 2 caras en 6 lanzamientos
𝑃2,6 = (
6
2
) 0,52(1 − 0,5)4
= 15 ∙
1
64
=0,23437
b) Probabilidad de obtener al menos 4 caras en 6 lanzamientos
𝑃≥4,6 = 𝑃4,6 + 𝑃5,6 + 𝑃6,6 = (
6
4
) 0,54(1 − 0,5)2
+ (
6
5
) 0,55(0,5)1
+ (
6
6
) 0,56(0,5)0
=
=15 ∙
1
64
+ 6 ∙
1
64
+ 1 ∙
1
64
=
22
64
=0,34375
EX4D.03- De una urna con 4 bolas blancas y 3 negras se extraen
sucesivamente 3 bolas, que se vuelven a introducir en ella
después de cada extracción. Dada la variable aleatoria “número
de bolas blancas extraídas”, halla la media y la desviación
típica.
Lo mismo para “número de bolas negras extraídas”.
------------------------ooooooooooooo------------------------------------
probabilidad de éxito 𝑝 (probabilidad de fracaso 𝑞 = 1 − 𝑝). Puede tomar
𝑃(𝑥 = 𝑘) = (
𝑛
𝑘
) 𝑝𝑘(1 − 𝑝)𝑛−𝑘
además:
La media es 𝜇 = 𝑛 ∙ 𝑝 , la desviación típica es 𝜎 = √𝑛 ∙ 𝑝 ∙ 𝑞
Para la variable aleatoria “número de bolas blancas extraídas”
𝑛 = 3 , 𝑝 =
4
7
obtenemos
Media 𝜇 = 𝑛 ∙ 𝑝 = 3 ∙
4
7
=
12
7
=1,714 , desviación típica 𝜎 = √𝑛 ∙ 𝑝 ∙ 𝑞 =0,86
Para la variable aleatoria “número de bolas negras extraídas”
𝑛 = 3 , 𝑝 =
3
7
obtenemos
Media 𝜇 = 𝑛 ∙ 𝑝 = 3 ∙
3
7
=
9
7
=1,285 , desviación típica 𝜎 = √𝑛 ∙ 𝑝 ∙ 𝑞 =0,86
EX4D.04- Si el 20 por 100 de los cerrojos producidos por una máquina
son defectuosos. Determinar la probabilidad de que 4 cerrojos
elegidos al azar sean:
a) un cerrojo defectuoso

Página 39 de 46
b) todos sean válidos
c) 2 defectuosos
d) como máximo 2 defectuosos
------------------------ooooooooooooo------------------------------------
𝑃(𝑥 = 𝑘) = (
𝑛
𝑘
) 𝑝𝑘(1 − 𝑝)𝑛−𝑘
además:
a)𝑃(1 𝑐𝑒𝑟𝑟𝑜𝑗𝑜 𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑜) = (
4
1
) 0,21
0,83
=0,4096
b) 𝑃(0 𝑐𝑒𝑟𝑟𝑜𝑗𝑜 𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑜) = (
4
0
) 0,20
0,84
=0,4096
c) 𝑃(2 𝑐𝑒𝑟𝑟𝑜𝑗𝑜𝑠 𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑜𝑠) = (
4
2
) 0,22
0,82
=0,1536
d) 𝑃(𝑎 𝑙𝑜 𝑠𝑢𝑚𝑜 2 𝑐𝑒𝑟𝑟𝑜𝑗𝑜𝑠 𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑜𝑠) = 𝑃(2 𝑐𝑒𝑟𝑟𝑜𝑗𝑜 𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑜) +
+𝑃(1 𝑐𝑒𝑟𝑟𝑜𝑗𝑜 𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑜) + 𝑃(0 𝑐𝑒𝑟𝑟𝑜𝑗𝑜 𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑜) =0,9728
EX4D.05- Un 10 por 100 de los utensilios producidos en un cierto
proceso de fabricación resultan ser defectuosos. Halla la
probabilidad de que de una muestra de 10 utensilios elegidos al
azar sean exactamente 2 los defectuosos
a) mediante distribución binomial
b) la aproximación de Poisson a la distribución binomial
------------------------ooooooooooooo------------------------------------
𝑃(𝑥 = 𝑘) = (
𝑛
𝑘
) 𝑝𝑘(1 − 𝑝)𝑛−𝑘
además:
a)𝑃(2 𝑢𝑡𝑒𝑛𝑠𝑖𝑙𝑖𝑜𝑠 𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑜𝑠) = (
10
2
) 0,12
0,98
=0,1937
b) dada una distribución binomial 𝑋 ∼ 𝐵(𝑛, 𝑝) ∼ 𝐵(10,0.1) , si se verifica que
{
𝑛 > 30 𝑦 𝑝 < 0,1
ó
𝑛 ∙ 𝑝 ≤ 5
la distribución binomial puede aproximarse por una
distribución de Poisson de parámetro 𝜆 = 𝑛 ∙ 𝑝 = 10 ∙ 0,1 = 1
Una variable aleatoria 𝑋 sigue una distribución de Poisson de
parámetro 𝜆, se denota 𝑋 ∼ 𝑃(𝜆), si describe el número de eventos

Página 40 de 46
ocurridos independientemente y a velocidad constante o con intensidad
constante en un tiempo o región fija. Puede tomar cualquier valor en
{0,1,2, ⋯ }
Si 𝑘 ∈ {0,1,2, ⋯, se cumple que
𝑃(𝑥 = 𝑘) =
𝜆𝑘
𝑘!
𝑒−𝜆
En este caso:
𝑃(2 𝑢𝑡𝑒𝑛𝑠𝑖𝑙𝑖𝑜𝑠 𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑜𝑠) = 𝑃(𝑥 = 2) =
12
2!
𝑒−1
=0,1839
EX4D.06- Un puerto del Caribe que sufre tormentas tropicales afirma,
que en una proporción de 3 de cada 100 atraques en el puerto
no se efectúa el día asignado por culpa de las tormentas.
Para contrastar esa información se eligen al azar 5 atraques de
barcos. ¿Cuál es la probabilidad de los siguientes sucesos:
a) todos los barcos atraquen en el puerto el día asignado.
b) al menos dos no puedan hacerlo el día asignado.
c) ¿cuál es el número medio de atraques, cada año, de barcos
que lo hacen en el día asignado si llegan cada año 135 barcos?.
------------------------ooooooooooooo------------------------------------
𝑃(𝑥 = 𝑘) = (
𝑛
𝑘
) 𝑝𝑘(1 − 𝑝)𝑛−𝑘
además: 𝑛 = 100 , 𝑝 = 0,97
acertar= atracar el día asignado
a)𝑃(5 𝑎𝑐𝑖𝑒𝑟𝑡𝑜𝑠) = (
5
5
) 0,975
0,030
=0,8587
b) 𝑃(𝑎𝑙 𝑚𝑒𝑛𝑜𝑠 2 𝑛𝑜 𝑎𝑐𝑖𝑒𝑟𝑡𝑒𝑛) = 1 − [𝑃(𝑛𝑜 𝑎𝑐𝑖𝑒𝑟𝑡𝑒𝑛 0) − 𝑃(𝑛𝑜 𝑎𝑐𝑖𝑒𝑟𝑡𝑒𝑛 1)]
= 1 − [𝑃(𝑎𝑡𝑟𝑎𝑞𝑢𝑒𝑛 𝑏𝑖𝑒𝑛 5) − 𝑃(𝑎𝑡𝑟𝑎𝑞𝑢𝑒𝑛 𝑏𝑖𝑒𝑛 4)] =
= 1 − [(
5
5
) 0,975
0,030
+ (
5
4
) 0,974
0,031
] = 1 − [0,8587 + 0,1328] =0,00847
c) número de éxitos en el año: 𝜇 = 𝑛 ∙ 𝑝 = 135 ∙ 0,97 =130
EX4D.07- Tenemos una moneda trucada con probabilidad de que
salga cruz es 0,4.
a) si lanzamos la moneda 3 veces. ¿Cuál es la probabilidad de
que salga exactamente una cruz?.
b) Halla la probabilidad de que la primera cruz salga en la tercera
vez que lanzamos la moneda.
------------------------ooooooooooooo------------------------------------
a) Se trata de una distribución discreta de tipo binomial:

Página 41 de 46
𝑃(𝑥 = 𝑘) = (
𝑛
𝑘
) 𝑝𝑘(1 − 𝑝)𝑛−𝑘
además: 𝑛 = 3 , 𝑝 = 0,4
acertar= que salga cruz
𝑃(1 𝑎𝑐𝑖𝑒𝑟𝑡𝑜𝑠) = 𝑃(𝑥 = 1) = (
3
1
) 0,41
0,62
=0,432
b) Se trata de una distribución discreta de tipo geométrica (Pascal):
Una variable aleatoria 𝑋 sigue una distribución geométrica de
parámetro 𝑝 ∈ (0,1) , se denota 𝑋 ∼ 𝐺𝑐(𝑝), si describe el número de
realizaciones independientes de un experimento necesarias hasta
obtener el primer éxito, siendo 𝑝 la probabilidad de éxito en una
realización del experimento (probabilidad de fracaso 𝑞 = 1 − 𝑝). Puede
tomar cualquier valor en {0,1,2, ⋯ }
Si 𝑘 ∈ {0,1,2, ⋯ }, se cumple que
𝑃(𝑥 = 𝑘) = (1 − 𝑝)𝑘−1
𝑝 además: , 𝑝 = 0,4 , 𝑘 = 3
En este caso: 𝑃(𝑥 = 3) = (1 − 0,4)3−1
∙ 0,4 =0,144
EX4D.08- El 2% de los libros encuadernados en cierto taller tiene una
encuadernación defectuosa. Calcula la probabilidad para
obtener 5 libros con encuadernación defectuosa de un total de
500 libros.
------------------------ooooooooooooo------------------------------------
{0,1,2, ⋯ }
Si 𝑘 ∈ {0,1,2, ⋯ } número de ocurrencias, se cumple que
𝑃(𝑥 = 𝑘) =
𝜆𝑘
𝑘!
𝑒−𝜆
En este caso 𝑘 = 5
El parámetro 𝜆 es el valor esperado de libros defectuosos, es decir, el
2% de 400, por tanto 𝜆 = 8
Entonces 𝑃(𝑥 = 5) =
85
5!
𝑒−8
=
10.99243939
120
=0,0916
EX4D.09- Supongamos que el número de mensajes de entrada a una
emisora de radio en un intervalo de tiempo 𝒕 sigue una
distribución de Poisson con parámetro 𝟎, 𝟑 ∙ 𝒕 . Calcula las
probabilidades de los siguientes sucesos:

Página 42 de 46
i) Lleguen exactamente 4 mensajes en un período de 10
segundos.
ii) El número de mensajes que lleguen en 5 segundos esté entre
3 y 5.
------------------------ooooooooooooo------------------------------------
{0,1,2, ⋯ }
𝑃(𝑥 = 𝑘) =
𝜆𝑘
𝑘!
𝑒−𝜆
i) En este caso 𝑡 = 10 , entonces el parámetro 𝜆 es 𝜆 = 0,3 ∙ 10 = 3
34
4!
𝑒−3
=0,168
ii) En este caso 𝑡 = 5 , entonces el parámetro 𝜆 es 𝜆 = 0,3 ∙ 5 = 1,5
Entonces me piden 𝑃(3 ≤ 𝑥 ≤ 5) = 𝑃(𝑥 = 3) + 𝑃(𝑥 = 4) + 𝑃(𝑥 = 5) =
=
1,53
3!
𝑒−1,5
+
1,54
4!
𝑒−1,5
+
1,55
5!
𝑒−1,5
=0,1869
EX4D.10- Supongamos que el número de mensajes de entrada a una
emisora de tv en un intervalo de tiempo 𝒕 sigue una distribución
de Poisson con parámetro 𝟎, 𝟒 ∙ 𝒕 . Calcula las probabilidades de
los siguientes sucesos:
i) Lleguen exactamente 3 mensajes en un período de 15
segundos.
ii) El número de mensajes que lleguen en 6 segundos esté entre
2 y 4 (ambos incluidos).
------------------------ooooooooooooo------------------------------------
{0,1,2, ⋯ }
𝑃(𝑥 = 𝑘) =
𝜆𝑘
𝑘!
𝑒−𝜆
i) En este caso 𝑡 = 15 , entonces el parámetro 𝜆 es 𝜆 = 0,4 ∙ 15 = 6
63
3!
𝑒−6
=0,0892
ii) En este caso 𝑡 = 6 , entonces el parámetro 𝜆 es 𝜆 = 0,4 ∙ 6 = 2,4
Entonces me piden 𝑃(2 ≤ 𝑥 ≤ 4) = 𝑃(𝑥 = 2) + 𝑃(𝑥 = 3) + 𝑃(𝑥 = 4) =
=
2,42
2!
𝑒−2,4
+
2,43
3!
𝑒−2,4
+
2,44
4!
𝑒−2,4
=0,5957

Página 43 de 46
EX4D.11- Se sabe que la probabilidad de que un niño expuesto a una
enfermedad contagiosa la contraiga es de 0,6. Calcula la
probabilidad de que el quinto niño estudiado sea el tercero en
contraer la enfermedad.
------------------------ooooooooooooo------------------------------------
Podemos enfocar el problema como una binomial negativa de
parámetros k = 5, r=3 y p=0,6
Una variable aleatoria 𝑋 sigue una distribución binomial negativa
de parámetros 𝑟 ∈ ℕ y 𝑝 ∈ (0,1), se denota 𝑋 ∼ 𝐵𝑁(𝑟, 𝑝), si es una
secuencia infinita de intentos de tipo Bernouilli en los que:
Cada secuencia es independiente de las otras.
En cada intento sólo son posibles 2 resultados(éxito 𝑝 ó fracaso 1 − 𝑝).
La probabilidad de éxito es constante en cada secuencia 𝑝.
Los intentos continúan hasta que se consigan 𝑟 éxitos.
(La distribución geométrica es el caso particular de la binomial negativa
cuando 𝑟 = 1)
Si llamamos 𝑥 = "𝑛º 𝑑𝑒 𝑒𝑥𝑝𝑒𝑟𝑖𝑚𝑒𝑛𝑡𝑜𝑠 𝑟𝑒𝑎𝑙𝑖𝑧𝑎𝑑𝑜𝑠 ℎ𝑎𝑠𝑡𝑎 𝑜𝑏𝑡𝑒𝑛𝑒𝑟 𝑒𝑙 𝑟 −
é𝑠𝑖𝑚𝑜 𝑒𝑥𝑖𝑡𝑜"
𝑃(𝑥 = 𝑘) = (
𝑟 + 𝑘 − 1
𝑟 − 1
) 𝑝𝑟(1 − 𝑝)𝑘
La media es 𝜇 =
𝑟(1−𝑝)
𝑝
, la desviación típica es 𝜎 = √
𝑟(1−𝑝)
𝑝2
en este caso 𝑘 = 5 , 𝑟 = 3 ,𝑝 =
6
10
𝑃(𝑥 = 5) = (
3 + 5 − 1
3 − 1
) (
6
10
)
3
(
4
10
)
5
= (
7
2
) (
6
10
)
3
(
4
10
)
5
=0.04645
EX4D.12- Supongamos la extracción aleatoria de 8 elementos de un
conjunto formado por 40 elementos totales (cartas baraja
española) de los cuales 10 son del tipo A (salir oro) y 30 son del
tipo complementario (no salir oro).
Si realizamos las extracciones sin devolver los elementos
extraídos y llamamos X al número de elementos del tipo A (oros
obtenidos) que extraemos en las 8 cartas.
Calcular la probabilidad de obtener 4 oros.
------------------------ooooooooooooo------------------------------------
Podemos enfocar el problema usando la distribución
hipergeométrica.
La distribución hipergeométrica es especialmente útil en todos aquellos
casos en los que se extraigan muestras o se realicen experiencias
repetidas sin devolución del elemento extraído o sin retornar a la
situación experimental inicial.
Es una distribución fundamental en el estudio de muestras pequeñas
de poblaciones pequeñas y en el cálculo de probabilidades de juegos

Página 44 de 46
de azar. Tiene grandes aplicaciones en el control de calidad para
procesos experimentales en los que no es posible retornar a la situación
de partida.
Las consideraciones a tener en cuenta en una distribución
hipergeométrica:
El proceso consta de 𝑛 pruebas, separadas o separables de entre un
conjunto de 𝑁 pruebas posibles.
Cada una de las pruebas puede dar únicamente dos resultados
mutuamente excluyentes.
El número de individuos que presentan la característica 𝐴 (éxito) es 𝑘.
En la primera prueba las probabilidades son: 𝑃(𝐴) = 𝑝 y 𝑃(𝐴) = 1 − 𝑝
En estas condiciones, se define la variable aleatoria 𝑋 =
“𝑛º 𝑑𝑒 é𝑥𝑖𝑡𝑜𝑠 𝑜𝑏𝑡𝑒𝑛𝑖𝑑𝑜𝑠”. La función de probabilidad de esta variable
sería:
Se representa 𝐻 (𝑁, 𝑛,
𝐷
𝑁
) siendo 𝑁 = tamaño de la población,
𝑛 = tamaño de la muestra
𝑘 = 𝑛º 𝑑𝑒 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢𝑜𝑠 𝑞𝑢𝑒..
𝑥 = 𝑣𝑎𝑙𝑜𝑟 𝑞𝑢𝑒 𝑡𝑜𝑚𝑎 𝑙𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒
𝑃(𝑋 = 𝑥) =
(
𝑘
𝑥
) ∙ (
𝑁 − 𝑘
𝑛 − 𝑥
)
(
𝑁
𝑛
)
La media es 𝜇 = 𝑛 ∙ 𝑝 , la desviación típica es 𝜎 = √𝑛 ∙ 𝑝 ∙ 𝑞 ∙
𝑁−𝑛
𝑁−1
Cuando 𝑁 es muy grande, como criterio se suele considerar 𝑁 > 10𝑛, la
distribución hipergeométrica se puede aproximar por la binomial 𝐵( 𝑛, 𝑝 )
con 𝑝 = 𝑘/𝑁.
En este ejercicio:
X seguirá una distribución hipergeométrica de parámetros 40,8,10/40
La probabilidad de obtener 4 oros:
𝑃(𝑋 = 4) =
(
10
4
) ∙ (
30
4
)
(
40
8
)
=0,08
EX4D.12- De cada 20 piezas fabricadas por una máquina, hay 2 que
son defectuosas. Para realizar un control de calidad, se
observan 15 elementos y se rechaza el lote si hay alguna que
sea defectuoso. Calcula la probabilidad de que el lote sea
rechazado.
------------------------ooooooooooooo------------------------------------
Podemos enfocar el problema usando la distribución
hipergeométrica.
𝑁 = 20 , 𝑛 = 15 , 𝑋 = 𝑛º 𝑝𝑖𝑒𝑧𝑎𝑠 𝑑𝑒𝑓𝑒𝑐𝑡𝑢𝑜𝑠𝑎𝑠 𝑑𝑒 𝑙𝑎𝑠 15 𝑒𝑠𝑐𝑜𝑔𝑖𝑑𝑎𝑠

Página 45 de 46
𝑃(𝑋 ≥ 1) = 1 − 𝑃(𝑋 < 1) = 1 − 𝑃(𝑋 = 0) = 1 −
(
2
0
) ∙ (
20 − 2
15
)
(
20
15
)
=0,947
DISTRIBUCIONES CONTINUAS.
EX4E.01- Se estima que el tiempo en horas que se necesita para
memorizar un tema de Historia de la Filosofía es una variable
aleatoria normal, cuya media y varianza se desconocen.
Calcular la media y la desviación típica de esta distribución si
se sabe que las tres cuartas partes de las estudiantes necesitan
más de 3 horas y que el 5% necesita más de 6 horas para
memorizarlo.
------------------------ooooooooooooo------------------------------------S
Se trata de una distribución normal o gaussiana 𝑁(𝜇, 𝜎).
Una variable aleatoria 𝑋 sigue una distribución normal de media 𝜇
y desviación típica 𝜎 y se denota 𝑋~𝑁(𝜇, 𝜎) si toma valores en toda la
recta real, según la función de densidad: 𝑓𝑋(𝑥) =
1
𝜎√2𝜋
𝑒
−
(𝑥−𝜇)2
2𝜎2
No podemos dar de forma explícita ninguna primitiva de esta función,
por lo tanto la función de distribución sólo podemos describirla como:
𝐹𝑋(𝑥) = ∫ 𝑓𝑋(𝑡)𝑑𝑡 = ∫
1
𝜎√2𝜋
𝑒
−
(𝑡−𝜇)2
2𝜎2
𝑑𝑡 =.
𝑥
−∞
.
𝑥
−∞
Llamamos normal tipificada o estándar a la normal media 0 y
desviación típica 1 , 𝑁(0,1).
Si 𝑋~𝑁(𝜇, 𝜎) , entonces la variable aleatoria 𝑍 =
𝑋−𝜇
𝜎
~𝑁(0,1)
Para hacer cálculos usamos la tabla de la normal tipificada.
Sea 𝑋: variable aleatoria “tiempo, en horas, necesario para memorizar
un tema de Historia de la Filosofía”
La distribución de la variable𝑋 es 𝑁(𝜇, 𝜎), siendo ambos parámetros
desconocidos.
Las tres cuartas partes de las estudiantes necesitan más de 3 horas →
𝑃(𝑋 > 3) = 0,75
El 5% necesita más de 6 horas → 𝑃(𝑋 > 6) = 0,05
Tipificamos ambas expresiones:
𝑃(𝑋 > 3) = 0,75 → 𝑃 (𝑍 >
3−𝜇
𝜎
) = 0,75 ⇒ 𝑃 (𝑍 ⩽
3−𝜇
𝜎
) = 1 − 0,75 = 0,25
𝑃(𝑋 > 6) = 0,05 → 𝑃(𝑍 >
6−𝜇
𝜎
) = 0,05 ⇒ 𝑃(𝑍 ⩽
6−𝜇
𝜎
) = 1 − 0,05 = 0,95
Buscamos en la tabla 𝑁(0, 1) los valores hallados:

Página 46 de 46
0,25 no está en la tabla equivale a 0,75 → 0,75 está entre 0,7486 y 0,7517
→ le corresponde −0,675 (hay que cambiar el signo)
0,95 está entre 0,9495 y 0,9505 → le corresponde 1,645
- Resolviendo el sistema:
𝑃(𝑍 ⩽
3−𝜇
𝜎
) = 0,25 ⇒
3−𝜇
𝜎
= −0,675
𝑃(𝑍 ⩽
6−𝜇
𝜎
) = 0,95 ⇒
6−𝜇
𝜎
= 1,645 →
𝜇 = 3 + 0,675𝜎 = 6 − 1,645𝜎
De donde obtenemos 𝜇 = 3,8728 y σ =1,2931
INFERENCIA ESTADISTICA.

Estadística descriptiva de variables y correlación

Recomendados

Recomendados

Más contenido relacionado

Similar a Estadística descriptiva de variables y correlación

Similar a Estadística descriptiva de variables y correlación (20)

Más de AngelCasodelaVega

Más de AngelCasodelaVega (7)

Último

Último (20)

Estadística descriptiva de variables y correlación