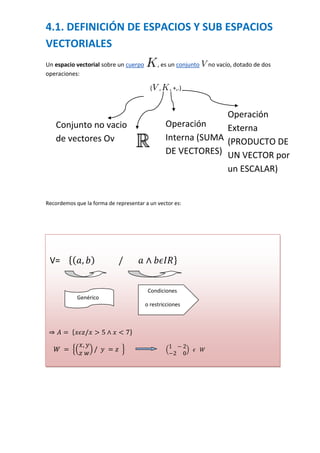
1. 4.1. DEFINICIÓN DE ESPACIOS Y SUB ESPACIOS
VECTORIALES
Un espacio vectorial sobre un cuerpo , es un conjunto no vacío, dotado de dos
operaciones:
( , , +,.)
Operación
Conjunto no vacio Operación Externa
de vectores Ov Interna (SUMA (PRODUCTO DE
DE VECTORES) UN VECTOR por
un ESCALAR)
Recordemos que la forma de representar a un vector es:
V=
Condiciones
Genérico
o restricciones

2. OPERACIÓN INTERNA OPERACIÓN EXTERNA
Suma de Vectores Multiplicación de un escalar por un Vector
α=3
Espacios Vectoriales Comunes
(V,K,+,*) GENÉRICO EJEMPLO
a + bx 3-x 0 + 0x
( a, b ) ( 2 ,5) ( 0, 0 )
( a, b , c ) ( 4 , -6 , 2 ) ( 0, 0 , 0 )
Un espacio vectorial (V), definido sobre un cuerpo k (en general ) es un conjunto
; sobre el que hay definidas dos operaciones:
1. Suma:
Verificando las siguientes propiedades:
(a) Conmutativa:
(b) Asociativa: .
(c) Elemento neutro
(d) Elemento opuesto:

3. 2. Producto por un escalar:
Verificando las siguientes propiedades:
(a)
(b)
(c)
(d)
Los elementos de un espacio vectorial se llaman vectores.
Un espacio vectorial real es un espacio vectorial sobre el cuerpo R de los números reales.
SUBESPACIO VECTORIAL
Se llama subespacio vectorial (S) de un espacio vectorial V a cualquier subconjunto no
vacío, tal que que es espacio vectorial con las mismas operaciones definidas
sobre V.
Caracterización de subespacios vectoriales
Si V es un espacio vectorial , entonces:
CONDICIONES PARA QUE SE CUMPLA UN ESPACIO VECTORIAL
a)
b)
c)

4. Ejemplo:
Demostrar si W es subespacio vectorial:
a)
1.
2.
b)
1.
COMBINACIÓN LINEAL
Sea , un conjunto de vectores de un e.v. V, un vector u de V es una
combinación lineal de los vectores de B, sí se puede escribir lo siguiente:

5. Ejemplo1:
¿ Es combinación lineal de ?
Ejemplo2:
¿ Es combinación lineal de ?
Ejemplo3:
¿ Es combinación lineal de ?

6. CAPSULA LINEAL ( )
Gráficamente se lo representa así:
Sea , un conjunto de vectores de un e.v. V. El conjunto S
genera a V, o V es generado por S, si todo vector u es de V una combinación lineal
de los vectores de S, es decir:
PASOS PARA OBTENER UNA CAPSULA LINEAL ALGÚN CONJUNTO S
Ejemplo:
Encontrar la capsula de
1. Escribimos la definición:
2. Escribimos la formula genéricamente
3. Obtenemos un sistema de ecuaciones

7. 4. Expresamos matricialmente la expresión anterior
5. Aplicamos Gauss-Jordán para encontrar la restricción en este caso
6. Como tenemos que no existe solución obtenemos la siguiente capsula
CONJUNTO GENERADOR
S genera a W, donde S es el conjunto generador
PASOS PARA HALLAR S QUE GENERA A W
1. Hallar las restricciones
2. Remplazar las restricciones
3. Contar el numero de variables
4. Descomponer el vector de acuerdo al números de variables
5. Extraer los escalares
6. Escribir el conjunto generador
Ejemplo 1:

8. Ejemplo 2:
DEPENDENCIA E INDEPENDENCIA LINEAL
En álgebra lineal, un conjunto de vectores es linealmente independiente si ninguno de
ellos puede ser escrito con una combinación lineal de los restantes. Por ejemplo, en R3,
los vectores (1, 0, 0), (0, 1, 0) y (0, 0, 1) son linealmente independientes, mientras que
(2, −1, 1), (1, 0, 1) y (3, −1, 2) no lo son, ya que el tercero es la suma de los dos primeros.
Un conjunto de vectores es linealmente dependiente si alguno de los vectores puede ser
escrito con una combinación lineal de los restantes.
Un conjunto es LI si ninguno de sus vectores es combinación lineal de los otros.
Un conjunto es LD si alguno de sus vectores es combinación lineal de los otros.
PASOS PARA PROBAR SI ES L.I. O L.D.
1. Se tiene que hacer la combinación lineal nula.
2. Obtener el sistema homogéneo
3. Resolver el sistema de ecuaciones homogéneo por Gauss o Gauss-Jordán

9. Ejemplo 1:
Verificar si S es LD
Ejemplo 2:
Verificar si S es LI

10. BASE
Sea (V, k, +,*)un e.v y
S es base de V si:
a) S es L.I.
b) S genera Av
PASOS PARA HALLAR UNA BASE
a) Hallar el conjunto generador
b) Probar que es L.I.
DIMENSIÓN DE V
DEFINICIÓN: es el número de vectores de S
EJEMPLO:
Encontrar una base del s.e.v W.
a) Hallar el conjunto generador
b) Probar que S es L.I.

11. EJEMPLO:
Encontrar una base del s.e.v W.
Hallar el conjunto generado
Probar que S es L.I.
Teorema 11(libro de trabajo)
Dim (V)= n =# de vectores de S
S es la base de V si tiene n vectores LI
Teorema 12(libro de trabajo)
Dim (V)= n =# de vectores de S
S es la base de V si tiene n vectores que generan a V
Teorema:
Para que sea base debe cumplir 2 de las tres condiciones:

12. Ejemplo:
Demostrar que S es una base de W:
Dim(R3)= 3 =# de vectores de S
S genera a W
Encontrar la dimensión de S con W:
Dim( )= 2 =# de vectores de S
Teorema
Dim (s.e.v) = dim (e.v) - # restricciones
Dim(W) = Dim(V) - # restricciones

13. Ejemplos:
COMO COMPLETAR UNA BASE
Ejemplo:
Completar la base S para llegar al e.v V=R3.
1. Tenemos la base S pero podemos observar que para que se cumpla que sea base de R 3
tienen que haber tres vectores en la base, por lo que aumentamos un vector a la base S
que no cumpla la restricción y lo ponemos seguido a los que ya teníamos.
El vector no cumple que y=x+z
2. Ahora tenemos que es de dimensión tres por lo tanto tenemos la primera condición
para que sea base de R3.
Dim(S’)=3

14. 3. Ahora demostramos si es LI para completar una base de R3.