Este documento presenta una historia general de la topografía desde sus orígenes en Egipto hasta la topografía moderna. Comienza describiendo cómo los egipcios utilizaban "topógrafos" para restablecer los límites de tierras después de las inundaciones anuales del Nilo. Luego discute las contribuciones de los griegos, romanos, árabes y europeos a lo largo de los siglos, incluidos los primeros instrumentos topográficos. Finalmente, describe el rápido desarrollo de la topografía en los siglos XVIII















































![TOPOGRAFIA
GEODESIA Y TOPOGRAFÍA – I CICLO
ESCUELA TECNICA SUPERIOR – UNIDAD OPERATIVA 56
ING. H. MIGUEL BAZÁN CENTURIÓN
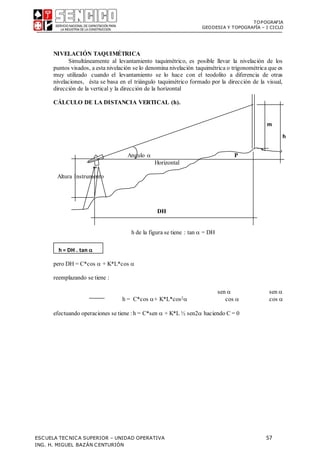
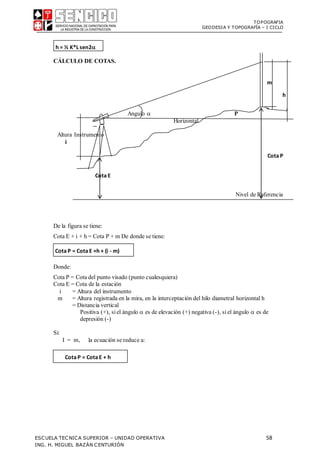
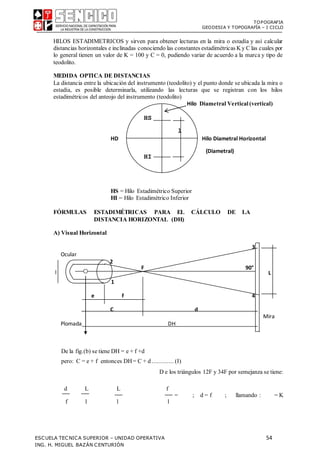
De acuerdo a la figura se tiene:
D = C + k*L'
pero: L' = L*cos()
además DH = D*cos ; pero: D = C + K*L' DH = [C + K(L*cos)] cos
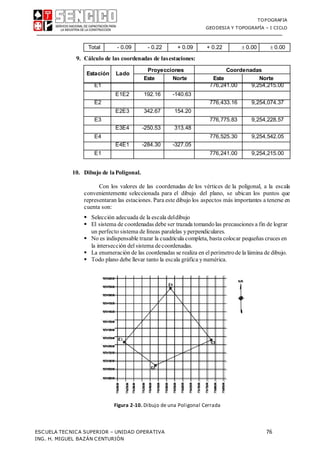
efectuando operaciones se tiene:
DH = C*cos + KL(cos)2
Que representa la fórmula generalde la estadía, porque si = 0 se obtiene la fórmula
básica, y haciendo C = 0 se tiene :
DH = KL(cos)2](https://image.slidesharecdn.com/001-210706144427/85/001-separata-curso-topografia-SENCICO-Cajamarca-53-320.jpg)