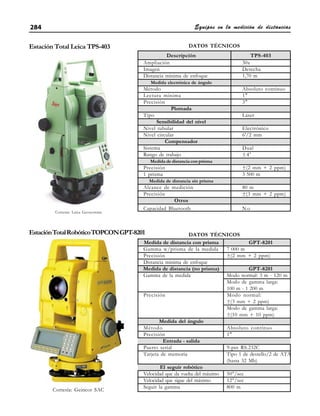
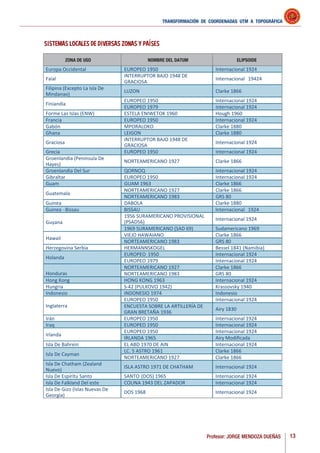
Este documento presenta información general sobre técnicas topográficas modernas. Explica conceptos clave como la planimetría, altimetría y topografía integral. También describe brevemente la historia de la topografía y los instrumentos topográficos importantes como el teodolito y la estación total. Finalmente, destaca la importancia de los puntos de control en la topografía para determinar la posición de otros puntos.

1. Técnicas Modernas
JORGE MENDOZA DUEÑAS

2. CLASE 1

3. Generalidades
7
7
7
7
7
Concepto de topografía
Es una rama de la ingeniería que se propone determinar la posición relativa de los puntos, mediante
la recopilación y procesamiento de las informaciones de las partes físicas del geoide, considerando
hipotéticamente, que la superficie terrestre de observación es una superficie plana horizontal. En
términos simples: La topografía se encarga de realizar mediciones en una porción de tierra relativa-
mente pequeña. Las informaciones se obtienen de instituciones especializadas en cartografía y/o a
través de las mediciones realizadas sobre el terreno (“levantamiento”), complementando esta infor-
mación con la aplicación de elementales procedimientos matemáticos.
En realidad la existencia de la topografía obedece a varias razones, a continuación citaremos algunas
de ellas.
Con ayuda de la topografía, es posible representar en un plano una o varias estructuras artificiales de acuerdo a una
escala establecida.
La Topografía se encarga de representar en un plano, una porción de tierra relativamente pequeña de acuerdo a una
escala determinada.

4. Generalidades
8
8
8
8
8
Con la topografía podemos determinar la posición de un punto sobre la superficie de la tierra, respecto a un sistema de
coordenadas.
Apoyándonos en la topografía podemos replantear un punto desde un plano en el terreno.
Gracias a la topografía se puede realizar el trazo de los ejes de una futura construcción.

5. Generalidades
9
9
9
9
9
BREVE RESEÑA HISTÓRICA
Ciertamente la topografía no apareció como ciencia ni como ingeniería, ni siquiera con el nombre
que hoy conocemos “topografía”, sino más bien surgió como consecuencia de la necesidad de nues-
tros antepasados de realizar mediciones sobre la superficie de la tierra.
Es fácil entender entonces que la medición de la tierra, sobre el globo terráqueo apareció cuando el
hombre pasó de un sistema de vida errante a sedentario; paralelo a ello también evolucionó el proce-
so biológico y mental del ser humano, así como su ambición de extender sus propiedades de tierra.
Es por ello que la propia necesidad obligó al hombre a tomar medidas sobre porciones de tierra
¿Pero medidas respecto a que unidades? Cuenta la historia, que fueron los egipcios y babilónicos los
primeros en medir distancias, tomando como unidades las partes de sus cuerpos, como el codo, el pie,
el pulgar, la cuarta, etc.
Como es de suponer cada parte del cuerpo de una persona difiere de las demás, así por ejemplo, el
codo de un individuo puede ser más grande o más pequeño que otro, fue entonces que se optó por
homogenizar el codo (por ejemplo); Allá por el año 3 000 a.c. en Egipto se acordó tomar un codo
patrón de aproximadamente 52,3 cm; fue así que en adelante aparecieron diversas unidades conven-
cionales que rigieron a la vez en varias ciudades.
Por otro lado no se puede negar que los griegos dieron un gran aporte a la geometría (palabra que
en ese entonces significaba: medida de la tierra) así podemos citar a Tales de Mileto, Pitágoras,
Arquímedes, Euclides, entre otros; tal es así que Eratóstenes, 220 a.c. calculó la circunferencia
media de la Tierra (40 000 km).
Años atrás la civilización suponía que la Tierra era una superficie plana, sin embargo esta hipótesis
empezaba a desvanecerse al ver desaparecer los, barcos cuando se alejaban al navegar y entonces el criterio
lógico asociado con la matemática hacia suponer que en realidad la Tierra era curva y no plana.
Acriteriodelosautores,lagranrevolucióndelaerapasadafueconlaaparicióndelaDIOPTRÍA,enelsiglo
II a.c. que en términos simples podemos afirmar que viene a ser el teodolito de hoy en día sin la vista
telescópica, este mismo principio se continúa usando en la actualidad con el eclímetro; la descripción
detalladadelmencionadoinstrumentoaparecióenlaobratitulada:Dioptría, escritaporHeróndeAlejandría.
Ese mismo siglo apareció el astrolabio, gracias al ingenio de Hiparco.
Desde el nacimiento de Cristo hasta la aparición de Galileo, La Topografía no tuvo aporte poderoso
excepto por la invención de la brújula por parte de los chinos en el año 1 100 d.c.
El escaso avance de la topografía en dicha época se debió a las ideas radicales de la Iglesia Católica de
sentenciar y ejecutar a aquellos hombres que contradijeran los principios del filósofo Aristóteles y
seguidores.
Fue en 1 609 que se produce la segunda revolución de la Topografía con la aparición del TELESCOPIO,
graciasalagenialidaddeGalileo; talesasíqueen1720JonathanSissonconstruyeelprimerTEODOLITO,
posteriormente aparece la plancheta, el nivel, etc.
Desde entonces hasta fines de la segunda guerra mundial, el estudio de la topografía quedó prácticamen-
te paralizada.
El uso del radar en la segunda guerra mundial, trajo consigo la solución de un gran problema: La
medición de distancias(con ayuda de ondas electromagnéticas).
Fue así que a mediados del siglo pasado, se dió inicio a la tercera revolución y hoy por hoy tanto nosotros
como de ustedes tenemos la suerte de estar inmersos dentro de esta gran revolución tecnológica.

6. Generalidades
10
10
10
10
10
Losequiposymétodosdelasegundarevolución,continúanusándosemasivamentedadoquelosprincipios
nocambian,sinembargoseestánconvirtiendoentecnologíadeprocesolentoycostoso.
Ennuestrosdías,losequiposymétodosparalatopografíaestánprogresandonotoriamente;losequiposde
mediciónelectrónica,lafotogrametríaaérea,lossensoresremotos,lasobservacionessatelitales,lamediciónde
distanciasconrayos,laestacióntotal,elniveldeautonivelación,lacomputadora,lossoftwares,lasmáquinas
ploteadoras,etc.hacenposiblelaobtencióndeunagrancantidaddedatosenuncortotiempo.
Sin embargo ello no significa que los principios y conceptos que rigen la disciplina clásica entren al recuer-
do, sino más bien servirán como base o cimiento para poder comprender y optimizar los equipos y
metodologías en el desarrollo de la topografía.
INSTRUMENTOS IMPORTANTES EN LA TOPOGRAFÍA
La cinta métrica La calculadora La libreta de campo El equialtímetro
La brújula El teodolito El jalón La mira
El eclímetro La estación total El criterio humano

7. Generalidades
11
11
11
11
11
La pintura La radio
El cordel
La comba
La plomada La estaca de madera
o fierro
INSTRUMENTOS COMPLEMENTARIOS EN LA TOPOGRAFÍA
DIVISIÓN BÁSICA DE LA TOPOGRAFÍA
Para el mejor desarrollo de la topografía, ésta se divide en tres partes:
A) PLANIMETRÍA
Se encarga de representar gráficamente una porción de tierra, sin tener en cuenta los desniveles
o diferentes alturas que pueda tener el mencionado terreno.
Para esto es importante proyectar a la horizontal todas las longitudes inclinadas que hayan de
intervenir en la determinación del plano.

8. Generalidades
12
12
12
12
12
B) ALTIMETRÍA
Se encarga de representar gráficamente las diferentes altitudes de los puntos de la superficie
terrestre respecto a una superficie de referencia.
C) TOPOGRAFÍA INTEGRAL
Se encarga de representar gráficamente los diferentes puntos sobre la superficie terrestre, teniendo
presente su posición planimétrica y su altitud.
IMPORTANCIA DE LA TOPOGRAFÍA EN LA INGENIERÍA
La importancia de la topografía,radica en que éste interviene en todas las etapas de la ingeniería. Es fácil
entender que la realización de una obra civil pasa por varias etapas; sin embargo dos de ellas tienen
relación directa con la topografía, estas son:
A) ESTUDIO
Llamado también proyecto; realizado por el ingeniero consultor o empresa consultora. Consiste
en llevar a cabo los planos y el expediente técnico de una futura obra.
Obviamente para ello, lo primero que debe hacer el ingeniero es representar en un plano el
terreno o porción de tierra donde se va a proyectar la futura obra; ello significa el apoyo obliga-
torio de la topografía.
De un plano topográfico preciso y una correcta representación de los linderos, es posible proyectar
una adecuada obra.

9. 13
Consiste en realizar el proceso constructivo de la obra de acuerdo al plano elaborado por el consultor.
Es el proceso por el cual se realiza un conjunto de operaciones y métodos para representar gráficamente en
unplanounaporcióndetierra,ubicandolaposicióndesuspuntosnaturalesy/oartificialesmásimportantes.

10. 14
14
14
14
14
2017

11. Generalidades
15
15
15
15
15
CLASES DE LEVANTAMIENTOS TOPOGRÁFICOS MÁS COMUNES
Cuadro Esquemático: Etapas de un levantamiento topográfico
Cuadro Esquemático: Etapas de un levantamiento topográfico
A) Levantamientos catastrales
Son los que se realizan con el objeto de definir y fijar los límites de áreas y propiedades, como
también para la identificación de estos límites.

12. 16

13. Generalidades
17
17
17
17
17
B) EL TOPÓGRAFO
Es el técnico que ejecuta los trabajos de campo dirigido a su vez por un ingeniero topógrafo.
Lógicamente un buen topógrafo también debe cumplir ciertos requisitos, así tenemos:
• Debe ser una persona honesta y honrada, debe ser el personal de confianza del ingeniero.
• Debe tener facilidad en el manejo de personal de campo.
• Debe tener conocimientos de álgebra, geometría y trigonometría, sobre todo debe tener amplio
criterio.
• Debe estar en constante actualización.
• Debe ser cauteloso y muy celoso con los equipos topográficos.
• Debe ser leal.
C) LOS EQUIPOS TOPOGRÁFICOS
Se puede lograr un excelente levantamiento topográfico, siempre y cuando se cumpla con tener:
Un eficiente ingeniero, un buen topógrafo y equipos topográficos en aceptables condiciones.
Es obvio suponer que para obtener un levantamiento topográfico de alta precisión se requiere
de equipos de alta tecnología.
Sin embargo puede usarse equipos topográficos tradicionales para trabajos de precisión, siempre
y cuando estos se encuentren en perfecto estado, para ello será necesario un adecuado y periódi-
co mantenimiento de los aparatos.
Por tal motivo, el topógrafo antes de iniciar el trabajo de campo, deberá comprobar el perfecto
estado del equipo a usar.
EL PUNTO DE CONTROL EN LA TOPOGRAFÍA
Punto de control o punto topográfico, es aquel punto a partir del cual se realiza las mediciones
lineales y/o angulares.
En ocasiones estos puntos sirven de referencia para definir la dirección de un alineamiento.
Los puntos topográficos se dividen en dos:
A) Puntos topográficos permamentes.- Son puntos de referencia fijos, creados antes y al margen del
levantamiento topográfico, así tenemos por ejemplo: Los faros, las astas de las plazas, las antenas,
los pararrayos, los hitos, etc.
B) Puntos topográficos temporales.- Son puntos creados especialmente para la realización de un
proyecto, generalmente estos puntos deben desaparecer finalizado el levantamiento.
Estos puntos se marcan con estacas de madera o fierro y se recomienda pintarlas para poder
ubicarlas fácilmente, asi mismo, éstas deben estar referidos a una estructura cercana.

14. Generalidades
18
18
18
18
18
IMPORTANCIA DE LOS PUNTOS TOPOGRÁFICOS
En matemática cuando se quiere determinar la po-
sición de un punto, basta ubicar sus coordenadas
respecto a un origen.
Ahora, bien, es posible ubicar un sub-sistema de
coordenadas; así.
En topografía cada punto topográfico representa el origen de un sub-sistema de coordenadas y gracias
a él se podrá determinar la posición de otros puntos.
La posición del punto “A” es: (x,y) La posición del punto P se puede de-
terminar gracias al subsistema (x' – y')
Gracias al punto topográfico “A”, se podrá determinar la posición de los puntos 1,2,3 y 4.

15. 19
Fig. c : Con los ángulos planos se hace uso de la trigometría
plana.
Fig. d : Con los ángulos esféricos se hace uso de la trigo-
nometría esférica.
La topografía tiene la aplicación en una porción pequeña de tierra, vale decir en un plano.
EXTENSIÓN DEL USO DE LA TOPOGRAFÍA

16. 20
hectómetro
decámetro
Hm
Dm
100
10
hectómetro cuadrado
decámetro cuadrado
Hm
Dm

17. 21
Una escala de 1/1000, nos indica que 1 metro en plano representa 1000 metros en
el Terreno y 3 cm en el plano representa 30 metros en el terreno.
30
m
3
cm
Terreno Plano

18. 22


19. 23
LÍMITE DE APRECIACIÓN GRÁFICA
Método Práctico
=
=
ESCALA LÍMITE DE APRECIACIÓN GRÁFICA
1 / 50 50 x 0,2 / 1 000 = 0,01 m = 1 cm
1 / 100 100 x 0,2 / 1 000 = 0,02 m = 2 cm
1 / 200 200 x 0,2 / 1 000 = 0,04 m = 4 cm
1 / 500 500 x 0,2 / 1 000 = 0,10 m = 10 cm
1 / 1 000 1 000 x 0,2 / 1 000 = 0,20 = 20 cm
1 / 2 000 2 000 x 0,2 / 1 000 = 0,40 = 40 cm
1 / 5 000 5 000 x 0,2 / 1 000 = 1,00 m
1 / 10 000 10 000 x 0,2 / 1 000 = 2,00 m
1/20 000 20 000 x 0,2/1000 = 4,00 m
1/50 000 50 000 x 0,2/1000 = 10,00 m
1/100 000 100 000 x 0,2/1000 = 20,00 m

20. Teoría de observaciones
24
24
24
24
24
En el gráfico:
Coordenada de A = (3; 3)
Coordenada de B = (6; 2)
En el gráfico:
Coordenada de A = (2,4; 30°)
Coordenada de B = (3,6; 52°)
SISTEMA DE COORDENADAS
Sistema que nos permite indicar la posición relativa de un punto de la superficie terrestre y
pueden ser ortogonales (rectangulares), polares, entre otros.
A) Coordenadas ortogonales
Las coordenadas ortogonales de un punto corresponden a las distancias perpendiculares entre éste y
dos ejes perpendiculares entre si . El eje “Y”, hacia el norte (hacia arriba) es positivo; hacia el sur (hacia
abajo) es negativo; el eje “X”, hacia el oriente (hacia la derecha) es positivo, hacia el occidente (hacia
la izquierda) es negativo; los cuadrantes se numeran en el sentido de las manecillas del reloj (sentido
horario).
B) Coordenadas Polares
Las coordenadas polares de un punto están definidas por la distancia radial y el ángulo de dirección (θ),
medidos desde el punto inicial (punto polar) y la línea de recta fija que es la dirección de partida (eje
polar) en el sentido de la rotación de las agujas del reloj (sentido horario).

21. 25
N
Norte
Contenido
Gráfico
Localización
Leyenda Membrete
Cuadro de
datos Técnicos
Sistema y
tipo de
proyección
cartográfica
Escala
Gráfica
N
Norte
Contenido
Gráfico
Localización
Leyenda
Membrete
Cuadro de
datos Técnicos
Escala
Gráfica
Sistema y tipo de
proyección cartográfica
Mostrando otro formato de plano
Componentes de un Plano Topográfico
Un plano puede tener diversos componentes, sin embrago los más importantes se mues-
tran a continuación.

22. 26
A
efectos
de
ilustrar
nuestros
formatos
presentamos
a
continuación
un
ejemplo.
Esacala gráfica 1/200

23. CLASE 2

24. Medición de distancias
229
229
229
229
229
Hace algunos años, medir la distancia entre dos puntos, era labor de especialistas, dado su
característica tediosa en cuanto al proceso de medición.
Generalmente el topógrafo realizaba la medición tan sólo de algunas distancias, dejando el
saldo al cálculo trigonométrico.
Hoy en día, la tecnología nos ofrece equipos sofisticados y métodos muy simples tanto así que
solo basta oprimir un botón para medir la distancia requerida y en cuestión de segundos obtener
digitalmente el resultado buscado.
En topografía, las distancias que se miden corresponden a líneas rectas, no obstante que la
superficie terrestre no es plana.
Si consideramos a la Tierra como una esfera; la longitud tomada en cuenta
en esta rama es ab, la cual pertenece a una superficie plana imaginaria; sin
embargo la medida real que debería ser considerada es AB.
¿Es preciso realizar alguna corrección?
Dado que la diferencia e = ab – AB, es insignificante para las distancias que se suelen medir en
topografía; no es necesario efectuar corrección alguna.
En realidad el valor de “e” se puede calcular con la siguiente expresión:
( )
=
3
2
AB
e
12R

25. Medición de distancias
234
Si consideramos el radio de la Tierra R ; 6 370 km:
Distancia AB (km) e (mm)
1 0,01
5 0,26
10 2,05
15 6,93
20 16,43
25 32,09
30 55,45
Del gráfico se observa que el error e, crece lentamente hasta d = 15 km, con lo cual la
diferencia “e” es aproximadamente 7 mm y por tanto el error relativo de 1/ 2 140 000,
considerada de muy elevada precisión. No obstante, los equipos topográficos actuales
tienen un alcance mucho menor a 10 km lo cual induce a despreciar la influencia de la
esfericidad terrestre en la medición de distancias.
Reducción de la distancia medida al nivel medio del mar
En la actualidad es característica común en las cartas, referenciar las distancias al nivel medio.
del mar.
Así pues, si se mide una distancia de 6 000,00 m en un lugar donde la altitud es 4 500 m.s.n.m.;
la distancia referida en la carta tendrá que ser: 5 996,71 m. Viceversa; si tenemos según carta,
una distancia de 8 200 m y se quiere replantear, en un lugar donde la altitud es 2 000 m.s.n.m.;
la distancia a replantear es: 8 202,57 m.
 
= ×  
+
 
M
R
D D
R H

26. Medición de distancias
235
TIPOS DE DISTANCIAS
1. La distancia inclinada.- Es la longitud de la línea recta que une dos puntos del terreno.
2. Distancia topográfica.- Es la longitud de la proyección de la distancia inclinada sobre la
horizontal; se le llama también distancia reducida al horizonte.
ALINEAMIENTO
Es la línea resultante de la intersección del terreno con un plano vertical que pasa por dos puntos
establecidos.

27. Medición de distancias
236
Procedimientos para realizar alineamientos en el campo
1. Alineación entre dos puntos A y B visibles entre sí usando jalones
– Se instala un jalón en posición vertical en cada punto A y B. La vista del observador en A debe
apuntar hacia B; lo cual se consigue cuando éste confunde los jalones con uno solo (el de “A”).
– Con ayuda de un tercer jalón se ubica en un punto tal como “1” con la condición que el
observador ubicado detrás del jalón en “A” tan solo vea uno solo.
El punto 1, se encuentra en el alineamiento AB.

28. Medición de distancias
237
2. Alineación entre dos puntos A y B visibles entre sí, usando teodolito y jalón
– Se instala el teodolito en uno de los puntos y el jalón en el otro; dirigir la visual hacia la parte
inferior del jalón, para luego bloquear el movimiento de la alidada.
– Se traslada el jalón hacía un punto tal como 1; con la condición que el eje de colimación del
teodolito contenga al jalón (no se debe girar la alidada).
El punto 1, se encuentra en el alineamiento AB.

29. Medición de distancias
238
MEDIDA DE DISTANCIAS
1. Medición a pasos
La distancia entre dos puntos correspondientes a un terreno plano se mide aproximada-
mente mediante el número de pasos normales que realiza una persona entre ellos.
Este método se utiliza para verificar o comprobar aproximadamente las mediciones de ma-
yor precisión o también para reconocimiento de terrenos y levantamientos preliminares.
Si la persona efectuó 80 pasos en su recorrido de A y B; podemos afirmar que la distancia AB es 80 pasos
respecto a dicho individuo.
En la práctica es usual convertir el número de pasos a unidades convencionales; para tal efecto es
imprescindible conocer la longitud promedio del paso de la persona que va a medir la distancia.
Determinación de la longitud promedio de un paso
A este proceso se le llama cartaboneo de paso; el procedimiento es el siguiente:
– Se elige un terreno aproximadamente horizontal.
– Se localiza dos puntos de longitud conocida (L).
– Se recorre con pasos normales ida y vuelta la longitud L.
– Sumar el número total de pasos.
 
=  
°
 
paso
2L
L
N total de pasos
dAB = (N° pasos)×(longitud de cada paso)

30. Medición de distancias
239
Ilustración
2. Medición con cinta
Se puede aplicar en levantamientos de detalles así como en redes de apoyo; para este último caso,
es conveniente usar por lo menos cintas de acero y con metodologías apropiadas y rigurosas.
A continuación se explican los métodos más importantes.
A) Cuando la superficie es plana
A-1) Sobre una losa o pavimento.- Para medir AB; se realiza medidas parciales de longi-
tud estándar, tal como 20 metros.
Es conveniente conservar apoyada la cinta sobre la losa y hacer coincidir la marca de
los 20 metros en el punto de partida (para cada tramo parcial) manteniendo la alinea-
ción correcta y la tensión más o menos constante y apropiada; cada puesta de cinta se
marca con pintura.
– En un terreno con pendiente, los pasos son en promedio más cortos cuando se sube y
más largos cuando se baja; por tanto se recomienda que el topógrafo realice el
cartaboneo de su paso en pendientes, tanto de subida como de bajada.
– Existe un instrumento que cuenta el número de pasos que recorre una persona (podó-
metro), ésta se instala al estilo llavero en una de las piernas de la persona; no obstan-
te no es imprescindible su uso.
Observaciones

31. Medición de distancias
240
Se recomienda repetir la operación por lo menos dos veces por cada tramo.
Para mayor precisión y no obstante que la losa es aproximadamente plana, se debe
llevar a cabo una nivelación geométrica entre A y B para luego proyectar la longitud
total medida sobre la horizontal real.
A-2) Sobre Terreno Natural.- El procedimiento es similar al anterior con la diferencia que
en cada puesta de cinta se coloca una estaca de madera realizando sobre la misma una
marca con pintura o similar.

32. Medición de distancias
241
B-2) Cuando la pendiente del terreno es mayor del 5%.- Cuando el terreno es muy
inclinado, cada puesta de cinta deberá ser tal que el relieve de la superficie lo permi-
ta pero conservando siempre la longitud estándar (en nuestro caso 20 m) y por
supuesto la horizontalidad de la cinta.
B) Cuando la superficie es inclinada
B-1) Cuando la pendiente del terreno es menor del 5%.- La medida se debe iniciar en el
punto más elevado, para que así, el operador pueda presionar la marca de la longitud
estándar (en este caso 20 m) sobre la estaca. En el otro extremo (marca del cero), el
operador se ayudará de una plomada y siguiendo las recomendaciones de los casos
anteriores, se monumenta una estaca realizando en ella una marca con pintura o
similar. Es importante conservar la estandarización de cada medida parcial así como
la horizontalidad de la cinta con ayuda de un nivel de mano.

33. Medición de distancias
242
B-3) Cuando el terreno es irregular o cubierto con vegetación.- Se aplica casi el mismo procedi-
miento que en los casos anteriores, pero empleando plomadas en embos extremos de la cinta.
3. Medición con estadía
Consiste en medir distancias geométricas usando los hilos estadimétricos del teodolito
conjuntamente con una mira.
El principio se basa en la proporción que guarda la separación de los hilos estadimétricos y
la longitud del eje de colimación respectiva.
4. Medición electrónica de distancia (MED)
Este método mide directamente la distancia que hay entre dos puntos, gracias a la propaga-
ción de la energía electromagnética (ida y vuelta) desde su punto de emisión hasta un
receptor ubicado en otra posición.
El principio inicial se basa en la ley correspondiente al movimiento rectilíneo uniforme.

34. Medición de distancias
243
2d = vt
Donde:
d : Distancia entre A y B.
v : Velocidad de luz.
t : Tiempo que emplea el rayo en el tramo
de ida y vuelta.
Explicación del fenómeno Físico
De la expresión: 2d = vt
d : Es la distancia por calcular.
v : Velocidad de la onda portadora que viene estar dada por el valor de la velocidad de la luz,
ya que las ondas emitidas son electromagnéticas; no es difícil enetender que dicha veloci-
dad varía con las condiciones atmosféricas (presión y temperatura); sin embargo, esto no
es problema, dado que se pueden realizar las correcciones respectivas (dato).
t : Tiempo que demora la onda en recorrer la distancia 2d, ello significa la presencia de un
reloj de alta precisión capaz de medir tiempos muy pequeños, lo cual implicaría un costo
muy alto en el equipo, sin embargo es posible medir dicho tiempo.
En la actualidad los equipos que usan MED, emplean el mismo principio (ondas
electromagnéticas) pero miden el desfase final o fracción de onda repitiéndose esta
operación para ondas de diferentes frecuencias (menor a mayor); obteniendo como
resultado la distancia buscada.
Los detalles respectivos se analizarán en la pág. 265
5. Sistema de posicionamiento global (GPS)
El GPS; nos determina las coordenadas geodésicas y planas de acuerdo al sistema de refe-
rencia elegido de un punto de la superficie terrestre.
El principio se basa en el método de Pothenot y la ley del movimiento rectilíneo uniforme,
gracias a los satélites artificiales que circulan nuestra atmósfera.
Teniendo dos puntos sobre la superficie terrestre y determinando sus coordenadas bajo el
mismo sistema referencial, es simple calcular la distancia de cuadrícula entre ellos y por
ende la distancia topográfica.
No obstante su alta precisión, el elevado costo que implica su uso hace que hoy en día
todavía la estación total sea el preferido de los topógrafos.

35. Medición de distancias
244
Precisión en la medición de distancias
Geodesta de la Universidad Nacional de Ingeniería,
haciendo uso del GPS diferencial.
La distancia planimétrica entre A y B se calcula gracias a las
coordenadas de cada una.
A pasos.
Método Precisión relativa Uso Instrumento
1/100 a 1/200 Reconocimiento, levantamientos a escala pequeña,
comprobación de mediciones de mayor precisión.
Podómetro.
Estadía.
Medición ordina-
ria con cinta.
Medición preci-
sa con cinta.
Medición electró-
nica de distancia.
1/300 a 1/1 000
1/3 000 a 1/5 000
1/1 000 a 1/30 00
±(10 mm + 10 ppm) a
±(0,2 mm + 0,2 ppm)
±(10 mm + 10 ppm) a
±(3 mm + 0,01 ppm)
Levantamiento de detalles, comprobación de
mediciones de mayor precisión.
Poligonales para levantamientos de terrenos y le-
vantamientos topográficos de control de ruta y cons-
trucción.
Poligonales de levantamientos en ciudades, líneas
de base para triangulación de baja precisión y le-
vantamientos de construcción que requieren alta
precisión.
Se emplea en todo tipo de levantamientos desde
taquimetría, poligonales de precisión, medición de
deformaciones, replanteos de precisión hasta en re-
des geodésicas básicas.
Redes de alta precisión, medición de control
geodinámico, geodesia de alta precisión.
Teodolito y mira.
Cinta de acero, estacas
y plomadas.
Sistema de posicio-
namiento global.
Cinta de acero calibra-
da, temómetro, dina-
mómetro, nivel de
mano y plomada.
Distanciómetros o es-
tación total y prisma.
Receptor GPS dife-
rencial.

36. Medición de distancias
245
TRABAJOS ELEMENTALES CON JALONES Y CINTA
1. Levantar una perpendicular a un alineamiento
1° Paso.- Sobre el alineamiento AB se fija un punto “a” distante 3 metros de “b”.

37. Medición de distancias
246
2° Paso.- Con centro en “b”, se traza un arco de 4 metros de radio.
3° Paso.- Con centro en “a”, se traza un arco de 5 metros de radio, interceptando al primero
en el punto “C”.

38. Medición de distancias
247
4° Paso.- La perpendicular buscada pasa por la línea cb .
2. Bajar una perpendicular a un alineamiento

39. Medición de distancias
248
1° Paso.- Con centro en “C” se traza un arco, lo suficiente grande como para bisecar la cuerda AB.
2° Paso.- Se ubica el punto medio de la recta 1 2
d d (D). La perpendicular buscada pasa por la línea CD.

40. Medición de distancias
249
3. Trazar desde un punto dado, una paralela a un alineamiento.
1° Paso.- Desde el punto “C”, se baja una perpendicular al alineamiento AB; para luego medir
la longitud “l”.

41. Medición de distancias
250
2° Paso.- Desde un punto del alineamiento AB, se levanta una perpendicular al mismo; luego
se ubica un punto “D” a una distancia “l” del mencionado alineamiento.
3° Paso.- La paralela buscada es la línea recta que pasa por CD.

42. Medición de distancias
251
4. Alinear dos puntos no visibles entre sí
Sean A y B puntos pertenecintes a un alineamiento que nos interesa trazar; sin embargo
entre ellos se presenta un obstáculo que impide la visibilidad mútua.
1° Paso.- Se traza una línea auxiliar fuera del obstáculo.

43. Medición de distancias
252
2° Paso.- Se baja una perpendicular desde el punto “B” a la línea auxiliar para luego medir la
longitud BB' y AB'
3° Paso.- Sobre el alineamieto AB', se ubica un punto C' para luego medir la longitud AC '.
=
C 'C AC '
B' B AB'
Aplicando el teorema de Thales, se calcula la distancia C'C

44. Medición de distancias
253
4° Paso.- Desde C' se levanta una perpendicular a la línea AB’ hasta ubicar con la cinta el punto C.
5° Paso.- Se repite el 3° y 4° paso tantas veces como sea necesario, ubicando los puntos D, E, F, etc.
La línea recta que une A, B, C, D, E. F; será el alineamiento buscado.

45. Medición de distancias
254
5. Prolongar un alineamiento a través de un obstáculo
Dado AB; se quiere prolongar dicho alineamiento a través del obstáculo.
1° Paso.- Por “A” se levanta una perpendicular AC de longitud conveniente.

46. Medición de distancias
255
2° Paso.- Por “C” se levanta una perpendicular CD, y por “D” otra perpendicular DE, tal
que DE = CA
3° Paso.- Por “E” se levanta una perpendicular EF, el cual será la prolongación de AB.

47. Medición de distancias
256
6. Intersección de alineamientos
El ayudante (oscuro) provisto de un jalón debe moverse en la dirección del alineamiento
AC hasta que el operador ubicado en B lo ubique simultáneamente. El punto visible para
ambos operadores es la intersección buscada.
7. Medir la distancia entre dos puntos accesibles con interferencia de
obstáculo
Se quiere medir la distancia entre dos puntos A y B separados por un obstáculo intermedio.

48. Medición de distancias
257
1° Paso.- Se elige un punto “C” accesible desde A y desde B; luego se prolonga la alineación
BC y AC (fig. a).
2° Paso.- Se ubica un punto “b” tal que BC = Cb; de igual modo se fija “a” con la condición
que AC = Ca. La distancia ab es la longitud buscada dado que AB = ab (fig. b).
8. Medir la distancia entre dos puntos, siendo uno de ellos inaccesible
Se quiere medir AB, siendo el punto “B” inaccesible.
Fig. a Fig. b

49. Medición de distancias
258
1° Paso.- Se alinea AB; desde el punto “A” se levanta una perpendicular al alineamiento y se
fija un punto C lo más lejos posible de “A”.
2° Paso.- Se alinea CB; desde el punto “C” se levanta una perpendicular al alineamiento y se
fija un punto D en la línea AB.
3° Paso.- Se mide la distancia AD y AC ; finalmente se calcula AB con la siguiente fórmula:
=
2
AC
AB
AD

50. Medición de distancias
259
9. Medir la distancia entre dos puntos inaccesibles
Se quiere medir la distancia entre A y B, siendo estos inaccesibles.
1° Paso.- Se elige un punto “C” con la condición que desde él sean visibles A y B. Desde
dicho punto se calcula L1
y L2
aplicando el método anterior (distancia entre dos puntos,
siendo uno de ellos inaccesible).

51. Equipos en la medición de distancias
260
3° Paso.- Aplicando el teo-
rema de Thales, se calcula la
distancia Cb (y)
=
2 1
y x
L L
 
=  
 
2
1
L
y x
L
4° Paso.- Sobre el alineamiento CB, se replantea el punto “b”.
2° Paso.- Sobre el alineamiento AC , se ubica un punto “a”, lo
más lejos posible de “C”, para luego medir aC (x).
5° Paso.- Se procede a me-
dir la longitud ab y se calcula
AB con la siguiente expresión.
 
=  
 
ab
AB AC
x

52. Equipos en la medición de distancias
257
257
257
257
257
CINTAS DE MEDICIÓN
No obstante la masificación del uso de equipos: MED; las cintas están en vigencia; no con la
importancia de hace algunos años, pero nadie puede negar que todo topográfo cuenta en su
equipaje con una cinta de medición.
Se encuentra en el mercado tanto en el Sistema Métrico como en el Ingles, sin embargo es
preciso acotar la tendencia universal del uso del primer sistema mencionado.
Respecto al material, se pueden presentar cintas de fibra de vidrio, de lona, de acero y de invar.
Posición cero
Existen tres formas diferentes de parte del fabricante en ubicar el cero:
El cero comienza aproximadamen-
te a 10 cm. del extremo de la cinta.
El cero comienza en el extremo
de la cinta.
El cero comienza en el extremo
del collarín de la cinta.
Reglamentación técnica según la Comunidad Europea
En Europa toda cinta debe cumplir con las normas de la Comunidad Europea (CE) y en tal
sentido debe tener grabado datos obligatorios tal como se muestra a continuación.
Clase Longitud en metros / tolerancia en mm
de precisión 1 2 3 5 8 10 20 30 50 100
I ±0,2 ±0,3 ±0,4 ±0,6 ±0,9 ±1,1 ±2,1 ±3,1 ±5,1 ±11,0
II ±0,5 ±0,7 ±0,9 ±1,3 ±1,9 ±2,3 ±4,3 ±6,3 ±10,3 ±20,3
III ±1,0 ±1,4 ±1,8 ±2,6 ±3,8 ±4,6 ±8,6 ±12,6 ±20,6 ±40,6

53. Equipos en la medición de distancias
262
Cinta de fibra de vidrio
Está constituida por millares de filamentos ex-
traídos de la fibra de vidrio, recubierto con
cloruro de polivinilo (PVC).
Es ligera, flexible y resistente al estiramiento
proveniente generalmente del cambio de tem-
peratura y/o humedad.
Tiene la ventaja de ser un material no conduc-
tor de la electricidad.
Se usa generalmente para mediciones cortas,
así como en levantamientos de detalles.
La foto muestra una cinta de fibra de vidrio de 30 metros
de longitud grabada por ambos lados.
Uno de los lados posee graduaciones correspondien-
tes al Sistema Métrico. La cinta total está dividida en
metros; cada metro en centímetros (100 cm); cada
centímetro en 5 partes de 2 mm cada uno.
El otro lado posee graduaciones correspondientes al Siste-
ma Ingles. La cinta total está dividida en pies (100 pies); cada
pie en pulgadas y cada pulgada compuesta en 8 partes.
Cinta de fibra de vidrio de 100 pies de longitud, graba-
da por ambos lados. Por un lado grabado en pies,
decimos de pie, en ths y 100 ths.
Por el otro lado en pies, pulgada y 8 ths.
Fuente: Forestry Suppliers, INC.
Cinta de fibra de vidrio de 100 pies de longitud, graba-
da por un lado (en pie y pulgadas).
Fuente: Forestry Suppliers, INC.

54. Equipos en la medición de distancias
263
Cinta de tela o lona
Está compuesto por un tejido impermeable
que lleva entrelazadas hilos de bronce o co-
bre en sentido longitudinal con el fin de
darle consistencia e impedir su alargamien-
to excesivo; por tal motivo se debe evitar el
uso de cintas simples de lona. Por ser un
material conductor de la electricidad no se
recomienda su uso cerca de dispositivos
eléctricos y/o campos electromagnéticos.
Es recomendarle verificar su longitud, usando como patrón una cinta de acero, dado que
producto del uso, la cinta de lona generalmente se estira.
La foto muestra una cinta de lona de 20 metros de
longitud grabada por ambos lados
Cinta de acero
Usualmente se emplean (aunque han sido desplazadas por los equipos MED) en levantamientos
importantes tales como redes de apoyo.
Comercialmente en el sistema métrico se venden en longitudes de 50 y 100 m; aunque las cintas
mayores a 50 metros son poco manejables y se rompen con facilidad.
La mayor parte (sistema métrico)
vienen graduadas en metros, decí-
metros, centímetros, con el primer
decímetro dividido en milímetros.
Las cintas totalmente graduadas en
milímetros son muchos más cos-
tosos que las ordinarias.
Es recomendable verificar su lon-
gitud, usando como patrón una cin-
ta de invar. ó equipos: MED. Por
ser un buen conductor de la electri-
cidad, se debe restringir su uso cer-
ca de dispositivos eléctricos y/o
campos electromagnéticos.
Uno de los lados posee graduaciones correspondien-
tes al Sistema Métrico. La cinta total está dividida en
metros y cada metro en centímetros.
El otro posee graduaciones correspondientes al Siste-
ma Ingles. La cinta total está dividida en pies; cada pie
en pulgadas y cada pulgada en 4 partes.
La foto muestra una cinta de acero de 30 metros de longitud, grabada por
un solo lado.

55. Equipos en la medición de distancias
264
La Cinta invar
Está compuesta por una aleación: 65% de niquel y 35% de acero.
Su coeficiente de dilatación térmica: 0,5×10
-6
es tan pequeño
que puede considerarse despreciable.
Este coeficiente en promedio es del orden de 1/30 del co-
rrespondiente al acero comercial.
El invar es un metal suave, por lo que se puede doblar o
romper fácilmente, por tal razón debe manipularse con mu-
cho cuidado. Se emplea (mejor dicho, se empleaba, dado
que ha sido relegado por los equipos MED) en levantamien-
tos geodésicos de alta precisión. El costo de una cinta invar.
es 10 veces mayor que una cinta de acero.
Por ser un buen conductor de la electricidad, se debe res-
tringir su uso cerca de dispositivos eléctricos y/o campos electromagnéticos.
Algunas firmas europeas las fabricaban tal que los extremos de la cinta en una longitud de
11 cm poseían escalas graduadas de mm en mm.
Respecto a la cinta de la fotografía anterior, podemos mencionar:
- Las graduaciones corresponden al sistema métrico.
- El trazo que indica el cero, se ubica a 10 cm del extremo de la cinta.
- La cinta de 30 metros está dividida en metros, y el metro en centímetros.
- En los 10 primeros centímetros, cada centímetro está dividido en milímetros.
Cuando se desarrolla la cinta se debe transportar en alto y con toda su longitud
extendida mientras se avanza. No se debe permitir nunca que se golpee ó
friccione contra el suelo u otro objeto. Fuente: C&GS Season’s Report Hodeson

56. Equipos en la medición de distancias
265
Errores en las medidas con cinta de acero
1. Cinta de longitud errada
La longitud de la cinta no tiene exactamente la indicada.
El error se determina, gracias a la ayuda de otros métodos e instrumentos más precisos.
El error puede ser positivo o negativo.
2. Alineamiento imperfecto
Se presenta cuando el ayudante delantero no conserva el alineamiento, y realiza las marcas
en uno u otro lado.
Si bien es cierto, este error no puede ser eliminado; si es posible reducirlo a límites aceptables.
El error resultante siempre es positivo.
3. Cinta no horizontal
Es muy difícil apreciar a simple vista la horizontalidad de una cinta, pero con la práctica se
consigue hacerlo con mucha precisión, y si el caso lo requiere, se puede utilizar un nivel de mano.
4. Cinta floja o torcida
Este error se presenta cuando se realizan mediciones en terrenos cubiertos por vegeta-
ción alta o cuando soplan fuertes vientos.
Si se presenta vegetación alta, realizar cortes para obtener senderos que determinen los
alineamientos perfectos.
Si se presentan vientos fuertes, esperar que los vientos se calmen o colocar pantallas
para reducir al máximo el movimiento de la cinta.
5. Defectos de observación
El error por observación y marca es aproximadamente 2 mm por medida; el error total no
tiene mayormente influencia por ser compensable.
6. Cambio de temperatura
Las cintas de acero, comúnmente se dilatan o contraen por efectos del cambio de temperatura.
El error tiene gran importancia cuando se mide con tiempo demasiado caluroso o
extremadamente frío. Los errores que se cometen por cambio de temperatura pueden
ser positivos o negativos.
7. Tensión de cintas variables
La cinta por ser elástica, sufre un estiramiento cuando es sometido a una tensión, modifi-
cando así su longitud real.
Este error se puede controlar mediante el dinamómetro dado que pertenece a la familia de
los errores sistemáticos.

57. Equipos en la medición de distancias
266
8. Cinta con catenaria
Cuando la cinta no se encuentra apoyada en toda su longitud sino únicamente entre los
extremos, toma una curva debido a su peso que se le denomina catenaria.
Este tipo de error sistemático es fácilmente calculable.
Corrección de la medida con cinta graduada
1. Corrección por estándar
Consiste en determinar la verdadera longitud de la cinta a usar, comparándola con una
longitud patrón, a la temperatura y tensión especificada en la cinta de acero.
Esta operación se realiza generalmente en cintas reparadas.
Las comparaciones se realizan en instituciones acreditadas para tal efecto a cambio de una
retribución económica; el resultado final está representado por un certificado de calibración.
Tener presente: Ln : Longitud nominal o grabada en la cinta.
Lv : Longitud verdadera de la cinta.
CE : Corrección por estándar = Lv – Ln
Ejemplo
Según un certificado de calibración se tiene: Ln = 30,000 m; Lv = 30,008 m. Con dicha cinta se
mide una longitud, obteniéndose como resultado 16,250 m.
Para determinar la longitud verdadera de dicha medición basta realizar un regla de tres simple:
 
= ×
 
 
30, 008
x 16, 250
30, 000
2. Corrección por temperatura
Cuando la temperatura ambiente es mayor o menor que la especificada en la cinta, se produce una
dilatación o contracción; el valor algebraico de la corrección se determina con la siguiente expresión:
CT = L0 ⋅ α (TF – T0)
CT : Corrección por temperatura.
L0 : Longitud medida en cada cintada.
α : Coeficiente de dilatación lineal de la cinta.
TF : Temperatura ambiente.
T0 : Temperatura según especificaciones.
Ln Lv
30 m 30,008 m
16,250 m x Longitud verdadera = 16,254 m

58. Equipos en la medición de distancias
267
Ejemplo
Sí tenemos una cinta de acero con las siguien-
tes especificaciones de fabricación:
Longitud = 50 m
Temperatura = 20° C
Tensión = 5 kg
α = 1,2×10
–5
°C
–1
y se mide una longitud obteniendo 34,632 m como
resultado, siendo la temperatura ambiente 15° C;
la corrección será:
C
T
= 34,632×1,2×10
–5
(15 – 20)
C
T
= –0,002 m
Finalmente la longitud verdadera:
L = 34,632 + (–0,002) = 34,630 m
Nótese que el signo de la corrección proviene
directamente de la fórmula (puede ser positiva o
negativa).
3. Corrección por horizontalidad
La medida de una longitud se expresa siempre en función de una distancia horizontal.
Si la diferencia de altura entre dos puntos es h, y la distancia medida corresponde a la
distancia inclinada L, la distancia reducida al horizontal “D” se puede obtener con ayuda de
la siguiente expresión.
D = L + Ch
Donde:
−
=
2
h
h
C
2L
Ch : Corrección por horizontalidad
Ejemplo
Sí la longitud de una distancia inclinada es 27,30 m y la diferencia de nivel entre sus extremos es
2,00 m se tendrá:
D = 27,30 +
( )
( )
 
−
 
 
 
2
2
2 27,30
⇒ D = 27,23 m
4. Corrección por tensión
Cuando la tensión con que se aplica a la cinta es mayor o menor que la indicada en las
especificaciones, la cinta se alarga o se acorta.
La corrección, se puede calcular con la siguiente expresión.
( )
−
= ⋅
⋅
0
p
P P
C L
A E

59. Equipos en la medición de distancias
268
Cp = Corrección por tensión.
P = Tensión aplicada.
P0 = Tensión según especificaciones.
L = Longitud de la cintada.
A = Área de la sección transversal de la cinta.
E = Módulo de elasticidad del metal.
Ejemplo
Se cuenta con una cinta de acero, cuyas especi-
ficaciones se muestran a continuación:
A = 2 mm
2
E = 2×10
6
kg/cm
2
P0 = 5 kg
L = 50 m
W = 0,020 kg/m (peso por metro lineal)
Sí se ha medido una longitud, obteniéndose
27,212 m aplicando una tensión de 8 kg, la
corrección por tensión será:
( )
( ) ( )
−
−
= ⋅
× ⋅ ×
p 2 6
8 5
C 27, 212
2 10 2 10
Cp = 0,002 m
Por tanto la longitud corregida será
Lc = 27,212 + 0,002
Lc = 27,214 m
Nótese que el signo de la corrección obedece
al valor algebraico proveniente de la fórmula.
5. Corrección por catenaría
Cuando la cinta es suspendida sólo en sus extremos, toma la forma de catenaria debido al
peso de la misma.
Su corrección se determina mediante la siguiente expresión.
( )
−
=
2 3
2
W L
Cc
24 P
W : Peso de la cinta por metro lineal
L : Longitud medida entre apoyos
P : Tensión aplicada
Ejemplo
Si se utiliza la cinta del ejemplo anterior y se mide cierta longitud apoyada sólo en sus extremos
con una tensión de 8 kg obteniendo como resultado L = 42,367 m
Se tendrá: ( ) ( )
( )
−
= = −
2 3
2
0, 020 42,367
Cc 0, 020
24 8
Por tanto la longitud corregida será: Lc = 42,367 + (–0,020) = 42,347 m
Nóte Ud. que el signo de la corrección es siempre negativa.

60. Equipos en la medición de distancias
269
EL DISTANCIÓMETRO
Es un instrumento que se utiliza en la medición
de distancias haciendo uso del MED.
Comúnmente estos equipos van montados en un
teodolito, mientras que en el extremo por medir
se ubica un reflector (prisma), es posible obviar el
uso de estos prismas, siempre y cuando la superfi-
cie reflectante sea de color claro para que así la
reflexión no se vea afectada; sin embargo no se
puede esperar una precisión igual o mejor que el
medido con prisma. Es importante resaltar que
entre distanciómetro y prisma (en el recorrido de la onda) no debe existir obstáculo alguno tales
como hojas o ramas de árboles, dado que la onda en su recorrido se refleja en el primer cuerpo
que encuentra mostrando por ende una distancia falsa.
Distanciómetro a punto de ser instalado sobre
un teodolito óptico mecánico.
Distanciómetros montados en diversos tipos de
teodolitos.
Distanciómetro en operación.
Análisis de la onda portadora
En realidad la distancia entre dos puntos se puede calcular teniendo como unidad de medida la longitud
de onda (λ).

61. Equipos en la medición de distancias
270
En el caso del distanciómetro:
El distanciómetro emite ondas
de una frecuencia determinada
y por tanto de longitud de onda
λ conocida, ésta llega al prisma,
se refleja y regresa al
distanciómetro donde auto-
máticamente se detiene la emi-
sión de dicho tipo de ondas.
La longitud L:
λ +
=
n x
L
2
n : Número de ondas
x : Fraccióndeλ
Según la ley del movimiento rectilíneo uniforme: L = (C)⋅(t)
Donde: L : Longitud recorrida por la onda
C : Velocidad de la onda electromagnética
t : El Tiempo transcurrido en el viaje de la onda
Para efectos de evitar el uso de un reloj atómico, se puede expresar el tiempo
∆θ ∆θ
= =
ω π
t
2 f
∆θ
 
= ⋅ 
π
 
L C
2 f
∆θ : Ángulo de fase
f : Frecuencia de transmisión de la onda
De lo analizado, es fácil deducir que sí tenemos conocido el ángulo de fase, podemos calcular el
desplazamiento L, dado que la frecuencia de la onda se supone conocida.
En el siguiente gráfico:
L = 2λ + x
x : Fracción de λ

62. Equipos en la medición de distancias
271
Cuando la onda viaja λ, el ángulo de fase medido por el distanciómetro será 0°, de igual modo
cuando la onda viaja 2λ, 3λ, 4λ, nλ, el equipo siempre medirá un ángulo de fase 0°; sin
embargo, siempre existirá una fracción de λ(x) al cual le corresponderá un ángulo de fase θ que
por medio de un detector de fase elctrónico convierte dicho ángulo en un número, éste es
enviado a un microprocesador interno donde dicho valor es convertido en distancia.
Así por ejemplo: Sí el ángulo de fase es θ = 65°.
Para una frecuencia de 10
7
Hz y una longitud de onda λ = 10 m; la porción “x” será:
( )
θ °
   
= ⋅λ = ⋅
   
° °
   
65
x 10
360 360
⇒ x = 1,8 m
En conclusión, los distanciómetros detectan directamente la fracción de longitud de onda (x), pero no
cuentan los ciclos completos por los que ha pasado la energía que regresa después de su doble recorrido.
Sin embargo este problema se soluciona con la emisión de ondas de diferentes frecuencias.
Al respecto creemos conveniente presentar el espectro electromagnético.
Espectro electromagnético
Por su frecuencia (Hz) Por su longitud de onda (m)

63. Equipos en la medición de distancias
272
Espectro electromagnético es el conjunto de ondas electromagnéticas que se encuentran ordenados de
acuerdo a su frecuencia (f) y longitud de onda (λ), si bien todas las ondas electromagnéticas son iguales
por su naturaleza, los efectos que ocasionan no son siempre las mismas, razón por la cual a cada grupo
de ondas electromagnéticas que dan lugar a efectos similares se les ha asignado un nombre.
La luz visible forma parte del espectro electromagnético, teniendo como límites el violeta de 4 100 A°
y el rayo de 7 000 A°.
Para nuestro estudio:
– Frecuencia baja:Ondas de radio, 10
4
a 10
6
Hz con λ desde 10
4
a 10
2
m
– Frecuencia mediana: Ondas de radio FM y microondas, 107
a 1012
Hz con λ desde 101
a 10–3
m.
– Frecuencia alta: Rayos infrarrojos, 10
13
a 10
14
Hz con λ desde 10
–4
a 10
–5
m.
En realidad un distanciómetro emite varias ondas de diferentes frecuencias (empezando por las
ondas de frecuencia baja), este proceso es controlado totalmente por un procesador interno el cual es
capaz incluso de corregir el error por presión y temperatura en tiempo real.
La onda de frecuencia alta, se usa para obtener los dígitos de alta precisión, mientras que las ondas de
frecuencia media o baja se emplean para obtener los dígitos medianos o gruesos respectivamente.
Supongamos que se midió una longitud y se obtuvo como resultado (en la pantalla digital)
346,431 m; la medición respectiva pudo haberse realizado del siguiente modo:
– Primero: El distanciómetro emitió una onda de λ = 1 000 m, con lo que se obtuvo un desfase
346,1 m; de donde se rescata la cifra más significativa (3).
– Segundo: El distanciómetro emitió otra onda, ahora de λ = 100 m, con lo cual se obtuvo un
desfase 46,2 m; de donde se rescata la cifra más significativa (4).
– Tercero: El distanciómetro emitió una tercera onda, ahora de λ = 10,000 m, con lo cual se
obtuvo un desfase 6,431 m; de donde se rescatan todos los dígitos.
Finalmente el resultado final está compuesto por la unión de todas las cifras más significativas;
en nuestro caso: 346,431 m
Los rayos infrarrojos tienen la ventaja de poder modular directamente la frecuencia; sin embar-
go tienen la desventaja que su alcance está restringido a unos cuantos kilómetros, por ello en
algunos casos se usan rayos láser, los cuales son capaces incluso de realizar mediciones en plena
noche. Mientras que las ondas de rayo infrarrojo tienen un alcance de hasta 7 km, las ondas de
rayos láser pueden alcanzar distancias de hasta 60 km.

64. Equipos en la medición de distancias
273
Errores en la medición electrónica de distancia
- Partes por millón (ppm)
Expresa la precisión o error relativo de una medición.
±1 ppm = ±
1 mm
1 km
; significa que por cada kilómetro de distancia puede existir un error de
±1 mm.
• Para ±1 ppm; el error relativo será:
ER =
1 mm
1 km
=
1 mm
1 000 000 mm
=
 
 
 
1
1 000 000 mm
1 mm
ER =
1
1 000 000
• Para ±5 ppm; el error relativo será:
ER =
5 mm
1 km
=
5 mm
1 000 000 mm
=
 
 
 
1
1 000 000 mm
5 mm
ER =
1
200 000
• Deducimos que ±1 ppm es más preciso respecto a ±5 ppm.
- Análisis General
Según la clasificación de errores visto en el capítulo teoría de observaciones, éstas se divi-
den en: propios, sistemáticos y accidentales.
Si los valores medidos son almacenados en una libreta electrónica tal como sucede en una
estación total, la probabilidad de la existencia de errores propio es casi nula; motivo por el
cual tan sólo se toma en cuenta los otros dos tipos de errores.
- Análisis de los errores sistemáticos
Sabemos que éstos generalmente aparecen debido a la influencia de agentes externos tales
como la presión atmosférica, temperatura, humedad etc. En distanciómetros electroópticos
y láser, los dos primeros tienen mayor incidencia; no obstante que éstos afectan nuestros
resultados, es posible su corrección mediante leyes matemáticas.
El valor de las correcciones atmosféricas es obtenido fácilmente con el siguiente Nomograma,
para una húmedad relativa de aire de 60%.

65. Equipos en la medición de distancias
274
Nomograma: Presión atmosférica – ppm
Ejemplo de aplicación
Se ha medido una distancia, obteniéndose como resultado 537,26 m; sí en el momento de la medi-
ción, la temperatura es 26° C y la presión atmósferica 500 mm Hg; calcular la medida corregida.
• La distancia corregida:
d = 537,26 m + 102,4
mm
km
×0,53726 km
d = 537,26 m + 55 mm ⇒ d = 537,32 m
Solución:
• Según el nomograma:
Para T = 26 °C y
Presión = 500 mm Hg = 666,61 mb
Se obtiene +102,4 ppm
Las líneas horizontales representan la temperatura y las verticales la presión atmosférica; las líneas diagonales representan
el valor de la corrección en ppm. Con una temperatura de 15°C y una presión de 1 atmósfera (760 mm Hg ó 1 013,25 mb)
se obtendrá cero ppm.

66. Equipos en la medición de distancias
275
En la actualidad, la mayor parte de los distanciómetros se encuentran integradas en la estacio-
nes totales; y en ellos se presentan dos opciones para para definir la correción atmosférica: una
manera es medir en campo las lecturas de temperatura y presión para luego introducir los
valores al equipo, éste calcula el ppm; otra forma es digitar el valor de la corrección directamen-
te al instrumento, para lo cual será necesario hacer uso del nomograma.
Después de haber sido ingresado el ppm correspondiente, las distancias medidas con posterio-
ridad se autocorregirán automáticamente, dándonos distancias corregidas.
Relación: Altitud – presión atmosférica
Altura sobre el nivel Presión atmosférica Altura sobre el nivel Presión atmosférica
del mar en metros mmHg mbar del mar en metros mmHg mbar
0 760 1 013,25 2 500 560 746,61
100 751 1 001,25 2 600 553 737,27
200 742 989,25 2 700 546 727,94
300 733 977,25 2 800 539 718,61
400 725 966,59 2 900 532 709,28
500 716 954,59 3 000 526 701,28
600 707 942,59 3 100 519 691,94
700 699 931,92 3 200 512 682,61
800 690 919,92 3 300 506 674,61
900 682 909,26 3 400 500 666,61
1 000 674 898,59 3 500 493 657,28
1 100 666 887,93 3 600 487 649,28
1 200 658 877,26 3 700 481 641,28
1 300 650 866,60 3 800 474 631,95
1 400 642 855,93 3 900 468 623,95
1 500 634 845,26 4 000 462 615,95
1 600 626 834,60 4 100 456 607,95
1 700 618 823,93 4 200 450 599,95
1 800 611 814,60 4 300 444 591,95
1 900 604 805,27 4 400 439 585,29
2 000 596 794,60 4 500 433 577,29
2 100 589 785,27 4 600 427 569,29
2 200 581 774,60 4 700 422 562,62
2 300 574 765,27 4 800 416 554,62
2 400 567 755,94 4 900 410 546,62
2 500 560 746,61 5 000 405 539,96
- Análisis de los errores accidentales
Los errores accidentales en estos equipos suelen expresarse con una desviación estándar
mediante la siguiente expresión:
E = ±(a + b⋅D)

67. Equipos en la medición de distancias
276
Donde:
a : Es un valor constante en mm.
b : Es un valor proporcional a la distancia medida; se expresa en ppm (partes por millón).
D : Distancia medida en km.
Numéricamente se puede expresar un error como:
E = ±(3 mm + 3 ppm)
En este caso para 500 metros de distancia se tendrá:
E = ±(3 mm + 3
mm
km
×0,5 km) = ±(3 mm + 1,5 mm)
E = ± +
2 2
3 (1,5) = 3,4 mm (error más probable)
Traducido a error relativo:
Error relativo = ;
1 1
500 000 147 000
3, 4
En distancias cortas, el error constante se hace importante; mientras que en distancias largas el
error variable es considerable.
La precisión de un distanciómetro está definido por el error accidental; así un
distanciómetro de ±(1 mm + 1 ppm), constituye un equipo de alta precisión.
La mayor parte poseen un error de ±(3 mm + 3 ppm); no obstante también se puede encontrar
equipos de ±(5 mm + 5 ppm); los cuales siguen siendo de precisión respetable, muestra de ello
es que para una distancia de 1 km se obtiene un error relativo de 1 / 141 000
Prisma
Es aquel instrumento constituido básicamente por
un cristal de varias caras planas donde llegan los
rayos del distanciómetro, para luego reflejarse en
la misma dirección pero en sentido contrario.
Generalmente los fabricantes usan un prisma de
vidrio en forma de cubo truncado por uno de los
vértices y formado por tres espejos internos.

68. Equipos en la medición de distancias
277
En planta:
La capacidad de medida se incrementa cuando se utiliza una batería de prismas.
No todos los distanciómetros tienen el mismo alcance; no obstante, para efectos de ejemplo, se
mostrará el correspondiente a uno específico.
Condiciones
1 Prisma 3 Prismas
Atmosféricas
1 1 500 m 2 000 m
2 5 000 m 7 000 m
3 > 5 000 m > 9 000 m
1 : Muy brumoso, visibilidad 5 km o mucho sol con
fuerte centelleo por el calor.
2 : Poco brumoso, visibilidad 20 km o parcialmente
soleado y poco centelleo de aire.
3 : Cubierto, sin bruma, visibilidad 40 km, sin cente-
lleo del aire.
Sistema de prismas (Fuente: Topcon)
Existe la posibilidad de variar la composición de los juegos de acuerdo con sus necesidades.
Bastón-2
(no se usa con 9 prismas)
Prisma-2
Bastón-2
Adaptador-A
Porta prisma
Porta prisma
1 prisma
Porta prisma-2
Un sólo prisma
Porta prisma-2
Tres prismas
Porta prisma-1
Tres prismas
Porta prisma-2
9 prismas
Adaptador para
base nivelante-2
Adaptador para
base nivelante S-2
Bastón Adaptador-F2 Base nivelante con plomada
Base nivelante

69. Equipos en la medición de distancias
278
Correcciones instrumentales en la medición de distancias
Puede cambiar la combinación de acuerdo a sus necesidades
Utilice los juegos de prismas después de ponerlos a la misma altura que el instrumento. Para ajustar la altura de los
juegos de prismas, cambie la posición de los 4 tornillos de fijación.
1. Constante del instrumento (K)
Se le llama también constante aditiva y viene
a ser la distancia existente entre la vertical
que pasa por el punto de estación y su similar
que pasa por el centro de emisión de ondas.
En la mayoría de los equipos, la constante K
es del orden de 1 mm si es que lo hubiese.
Comúnmente el valor de dicha constante lo
ingresa el fabricante, por lo que el usuario
no tiene necesidad de digitarlo en el equipo.
Sin embargo, es preciso comprobar la vera-
cidad de dicho valor y en el caso extremo
ajustarla.
Unidad para colocar 1 prisma Unidad para colocar 3 prismas Unidad para colocar 9 prismas

70. Equipos en la medición de distancias
279
Comprobación y ajuste de la constante del instrumento (Fuente: Topcon)
Generalmente, la constante del instrumento no debe presentar discrepancias. Se recomien-
da efectuar la medición comparándola con una distancia de la que ya se conozca su longitud
exacta. Si no dispone de un lugar con dichas características, establezca una base de 20 m (al
adquirir el instrumento) y compare los datos medidos con el instrumento recién adquirido.
En ambos casos, tenga en cuenta que la precisión de la comprobación estará determinada
por el desplazamiento de la posición del instrumento sobre el punto, el prisma, la precisión
de la línea de base, la calidad de la colimación, la corrección atmosférica y la corrección de
la refracción y curvatura terrestre. Por favor, téngalo en cuenta.
Además cuando sitúe la base en un edificio, recuerde que las diferencias de temperatura
afectan notablemente.
Si el resultado es igual o superior a 5 mm, puede seguir el procedimiento mostrado a
continuación para modificar la constante del instrumento.
a. Determine un punto C sobre una línea recta AB, prácticamente horizontal y de 100 m de
longitud, Mida las líneas rectas AB, AC, BC.
Nótese que “b”, no se encuentra en la dirección de la distancia buscada.
a + b + c = 2t
b. Calcule la constante del instrumento repitiendo varias veces la operación arriba indicada.
Constante del instrumento = AC + BC – AB
c. Mida de nuevo la base calibrada y compare los resultados.
2. Constante del prisma (k)
Para efectos de realizar una explicación didáctica, citaremos a continuación algunos
conceptos fundamentales.
A) Recorrido de la onda dentro del prisma.- El recorrido del rayo dentro del prisma está
determinado por la siguiente expresión:

71. Equipos en la medición de distancias
280
B) Equivalente del viaje en el aire de la onda dentro del prisma.- Es posible reemplazar el
recorrido de la onda dentro del prisma por su equivalente en el aire.
La zona sombreada representa el supuesto prisma de aire; el rayo incide, llega al punto “D”
y se refleja recorriendo en su trayectoria de ida y vuelta: 2(1,517 t).
C) Constante del prisma (k).- Es la excentricidad o distancia que hay entre el punto de re-
flexión “D” y el punto de estación del porta prisma.
Generalmente los fabricantes prefieren usar prismas de constante k = 0; sin embargo las
hay en el mercado, diferentes medidas: –30 mm; +30 mm; +17,5 mm; +34,5 mm; etc.
El signo depende de la posición del punto de estación.
El signo y valor se deben ingresar al equipo antes de dar inicio al trabajo.
Comprobación de la constante del prisma
Se repite la operación pero reemplazando el
prisma por una placa reflectante (k = 0).
La diferencia: d1 – d2; viene a ser aproximada-
mente el valor de la constante k.
Se elige dos puntos A y B separados una dis-
tancia corta (puede ser aproximadamente 20
m) y en lo posible plano.
Se estaciona el distanciómetro en A y el prisma en
B, para luego medir la distancia; obteniendo d1.

72. Equipos en la medición de distancias
281
LIBRETA ELECTRÓNICA
Llamada también colectora de datos; generalmen-
te va conectada a un teodolito electrónico y/o un
distanciómetro; puede registrar automáticamente
los valores medidos correspondientes a los pun-
tos previamente codificados en dicha colectora.
Con ello se obvia la tradicional libreta de campo
y se anulan los posibles errores que se puedan
cometer en dicho proceso.
En el post-proceso, es posible conectar dicha
colectora a una computadora, con lo cual se consi-
gue ingresar los datos de campo en forma automá-
tica a un software preferido por el usuario. Como
verá Ud. no es necesario escribir los datos en el
campo, ni mucho menos copiar a la computadora
para realizar el cálculo respectivo.
Sin embargo es necesario resaltar que la codifica-
ción realizada en la colectora de datos obedece a algún croquis realizado por el operador en el
campo, dibujo que será una herramienta imprescindible en la transferencia y cálculo de datos.
En la actualidad las Libretas Electrónicas o colectoras de datos no sólo puedan registrar
datos de campo, sino también pueden realizar cálculos básicos tales como las correcciones
de distancia, la reducción de distancia al horizonte e incluso la determinación de las coor-
denadas de los puntos topográficos.
Para ello el operador introduce los códigos de los puntos topográficos en la libreta electrónica, dicha
colectora almacena las medidas tomadas con un archivo previamente establecido para luego calcu-
lar los parámetros básicos y almacenarlos con el mismo archivo pero con diferente extensión.
ESTACIÓN TOTAL
Es aquel instrumento topográfico constituido por un teodolito electrónico unido solidariamente
con un distanciómetro, estos a su vez llevan en su interior una libreta electrónica y un microprocesador,
el cual le permite registrar los datos de campo, obviando la libreta tradicional, así como compensar
y procesar los datos obtenidos para registrarlos en un archivo de su memoria.
La estación total nos permite obtener trabajos de alta precisión y un gran ahorro de tiempo; no
obstante es preciso aceptar que la presencia de este equipo no cambia en absoluto los principios
básicos de la topografía.

73. Equipos en la medición de distancias
282
Con la estación total, podemos medir ángulos horizontales y verticales así como distancias
inclinadas; su procesador interno le permite calcular y mostrarnos inmediatamente la proyec-
ción horizontal y vertical de la distancia medida, así como las coordenadas de los puntos
medidos, dependiendo del caso.
La estación total permite medir y calcular la altura de ciertas estructura así como replantear
puntos en el terreno con gran precisión.

74. 283
USB, luego copiarlo a una computadora, o caso
inverso, los datos de un proyecto ubicados en una
memoria USB pueden ser transferidos a la estación
total para el posterior replanteo de los puntos.

75. Equipos en la medición de distancias
284
Cortesía: Leica Geosystems
Estación Total Leica TPS-403
Descripción TPS-403
Ampliación 30x
Imagen Derecha
Distancia mínima de enfoque 1,70 m
Medida electrónica de ángulo
Método Absoluto contínuo
Lectura mínima 1"
Precisión 3"
Plomada
Tipo Láser
Sensibilidad del nivel
Nivel tubular Electrónico
Nivel circular 6'/2 mm
Compensador
Sistema Dual
Rango de trabajo ±4'
Medida de distancia con prisma
Precisión ±(2 mm + 2 ppm)
1 prisma 3 500 m
Medida de distancia sin prisma
Alcance de medición 80 m
Precisión ±(3 mm + 2 ppm)
Otros
Capacidad Bluetooth No
DATOS TÉCNICOS
EstaciónTotalRobóticoTOPCONGPT-8201 DATOS TÉCNICOS
Medida de distancia con prisma GPT-8201
Gamma w/prisma de la medida 7 000 m
Precisión ±(2 mm + 2 ppm)
Distancia mínima de enfoque
Medida de distancia (no prisma) GPT-8201
Gamma de la medida Modo normal: 3 m - 120 m
Modo de gamma larga:
100 m - 1 200 m
Precisión Modo normal:
±(3 mm + 2 ppm)
Modo de gamma larga:
±(10 mm + 10 ppm)
Medida del ángulo
Método Absoluto contínuo
Precisión 1"
Entrada - salida
Puerto serial 9-pin RS.232C
Tarjeta de memoria Tipo 1 de destello/2 de ATA
(hasta 32 Mb)
El seguir robótico
Velocidad que da vuelta del máximo 50°/sec
Velocidad que sigue del máximo 12°/sec
Seguir la gamma 800 m
Cortesía: Geincor SAC

76. Equipos en la medición de distancias
285
CONTROLADOR DE CAMPO
Con la aparición de la estación total, se pronosticaba el fin de la colectora de datos portátil, dado
que la estación la incluía dentro de su propio sistema.
Sin embargo con la miniaturización de los circuitos integrados, dichas colectoras han recobrado im-
portancia, pues hoy se presentan como potentes computadoras que almacenan, procesan datos, reciben
y proporcionan información via tarjetas, cables, ondas, etc.; por tal razón muchos los llaman controladores
de campo, pues incluso el topógrafo puede manejar la estación total o cualquier equipo topográfico
digital desde el controlador, siempre y cuando ambos se encuentren conectados.
Esto significa que para efectos de realizar la transferencia de información, ya no es necesario
llevar el equipo al lugar de transmisión, pues ello se limita solo el traslado del controlador.
Incluso, hoy en día muchos se inclinan por usar el sistema bluetooth.
Bluetooth proporciona una vía de interconexión inalámbrica entre diversos aparatos que tengan
dentro de sí esta tecnología, usando por supuesto una conexión segura de radio de muy corto alcance.
El alcance que logran tener estos dispositivos es de 10 metros. Para mejorar la comunicación es
recomendable que nada físico (como una pared) se interponga.
Manejo de la estación total mediante un controlador
de campo, haciendo uso del sistema Bluetooth.
Cortesía: Geincor SAC
Manejo de la estación total mediante un controlador
de campo, haciendo uso de un cable de conexión.
Cortesía: Geincor SAC

77. Equipos en la medición de distancias
286
Descripción Topcon FC-100 Topcon FC-2000 Trimble TS C2
Microprocesador IntelPXA255Z-scale IntelPXA255Z-scale IntelPX270X-scale
VelocidaddelCPU 400MHz 400MHz 520MHz
Sistemaoperativo WindowsCE.NET WindowsCE.NET WindowsMobileparaPockerPC
Memoria 64MbSDRAM 64MbSDRAM 128MbSDRAM
Tarjetadedatos 1Compactflash CompactFlashextraíble 1Compactflash(CF)tipoI
1SDMediacard 1Compactflash(CF)tipoII
Tarjetadememoriasecuredata(SD)
CapacidadBluetooth Si Si Si
Pantalla 320×240QVGA 320×240QVGA 320×240QVGA
Serial Puerto serial RC 232C (9 pines) Puerto serial RS 232 (9 pines) Puerto serial RS 232C (9 pines)
USB USB USB
PuertoserialRS232(6pines) PuertodealimentacióndeDC
Temperaturadeoperación –20 °C a + 50 °C –20 °C a + 60 °C –20 °C a + 60 °C
Operacióndebatería 20 hr 6 hr 30 hr
Dimensiones 182×103×583mm 255×130×61.5mm 266×131×48mm
Peso 580g(conbatería) 800g(conbatería) 950g(conbatería)
Controlador Topcon FC-100
Controlador Topcon FC-200
Cortesía: Geincor SAC
Cortesía: Geincor SAC
Controlador Trimble TS C2

78. Equipos en la medición de distancias
287
CINTA LÁSER
Es un dispositivo pariente del distanciómetro. El objetivo de este pequeño equipo, es medir distan-
cias en los interiores y exteriores adyacentes de las estructuras, con ayuda de los rayos láser que se
emiten de él.
La cinta láser contiene un pequeño microprocesador capaz de realizar cáculos simples, tales
como áreas, volúmenes, hipotenusas, etc. E incluso algunos modelos pueden almacenar los datos
obtenidos en el campo para luego tranferirlos al disco duro de una computadora.
Este diminuto pero potente equipo obedeciendo a la tendencia de la miniaturización, se convierte en
un elemento preciso, fiable, manuable y permite medir distancias con precisión milimétrica con tan
sólo una persona.
Su tamaño es muy similar al de un teléfono celular.
Las características más importantes de los modelos LEICA DISTO, se muestran a continuación:
DATOS TÉCNICOS PLUS A5 A3
Precisión ±1,5 mm ±2 mm ±3 mm
Alcance 0,20 m a 200 m 0,05 m a 200 m 0,05 m a 100 m
Bluetooth Sí No No
Fuente: Leica Geosystems

79. Redes de apoyo planimétricos
288
Medición de superficies rápida y sencilla
Fuente: Leica Geosystems
Medición de alturas: tan fácil como apretar un botón
Fuente: Leica Geosystems
Medición de volúmenes: pemite cacular el volumen
de una habitación o la superficie de paredes y techos
con sólo pulsar un botón.
Fuente: Leica Geosystems
Medición indirecta de alturas: la función Pitágoras per-
mite medir la altura de fachadas.
Fuente: Leica Geosystems

80. Teoría de observaciones
25
25
25
25
25
INTRODUCCIÓN
Las operaciones topográficas, se realizan fundamentalmente para determinar mediciones ya sean lineales
y/o angulares. Estas mediciones se efectúan bajo el control de la vista humana u observación, que
evidentemente, como cualquiera de los demás sentidos, tiene un límite de percepción, más allá del cual
no se aprecian perfectamente las magnitudes que se observan, originando una observación aproximada
de la medida, sin embargo mediante la estadística inductiva o inferencia se logra establecer ciertos límites
detolerancia,esdecirelgradodeprecisióndelaobservaciónquesemanifiestacualitativaycuantitativamente
a través de ese error de apreciación.
1. Clases de medición
A) Medición directa
Es aquella en la cual se obtienen la medida
“exacta” mediante un proceso visual, a partir
de una simple comparación con la uni-
dad patrón.
B) Medición indirecta
Es aquella medida que se obtiene mediante
ciertos aparatos o cálculos matemáticos ya que
se hace imposible medirla mediante un
proceso visual simple.
Unidad patrón: 1 metro
Ejemplo ilustrativo; Magnitud: Longitud Ejemplo ilustrativo:
En la figura, es fácil notar que la longitud AB mide
3 veces un metro: 3 metros (medición directa).
Fórmula: A = (largo)(ancho) = (3 m) (2 m)
A = 6 m
2
Se recurrió al uso de una fórmula matemática.
Se quiere medir el área del rectángulo.

81. Teoría de observaciones
2. Errores en la medición
La medición es una actividad que lo ejecuta el hombre provisto o no de un instrumento especiali-
zado para dicho efecto.
En toda medición hay que admitir, que por más calibrado que se encuentre el instrumento a usar,
siempre el resultado obtenido estará afectado de cierto error; ahora, en el supuesto de que existiendo
un aparato perfecto cuyos resultados cifrados coincidieran matemáticamente con la realidad física,
nunca llegaríamos a dicho valor, debido a la imposibilidad humana de apuntar al punto preciso o
de leer exactamente una escala.
A) Valor verdadero
Esaquelvalorquenotieneningunaclasedeerror.Noobstanteesprecisoanotarqueelverdaderovalorno
seconoceniseconocerájamás.
B) Error
Es la incerteza en la determinación del resultado de una medición.
C) Exactitud
Es el grado de aproximación a la verdad o grado de perfección a la que hay que procurar llegar.
Un instrumento inexacto nos entrega resultados sesgados o desplazados.
D) Precisión
Es el grado de perfección de los instrumentos y/o procedimientos aplicados. La precisión de un
instrumento está determinado por la mínima división de la misma (sensibilidad).
Ejemplo
– un cronómetro es más preciso que un reloj de pared.
– una balanza de joyería es más preciso que una de camiones pesados.
La sensibilidad o precisión con que se fabrican los aparatos de medida dependen de los fines a los que se
destina. No tendría sentido fabricar una balanza que aprecie el miligramo para usarla como balanza para
camiones.
28

82. Teoría de observaciones
29
Ilustración: Exactitud - precisión
Los valores medidos son:
• Poco precisos
• Pocos exactos
Los valores medidos son:
• Poco precisos
• Más exactos
Los valores medidos son:
• Muy precisos
• Pocos exactos
Los valores medidos son:
• Muy precisos
• Muy exactos
3. Causa de los errores
A) Naturales
Son aquellos errores ocasionados por las variaciones meteorológicas (lluvia, viento, temperatura,
humedad, etc.). Ver fig. a.
B) Instrumentales
Son aquellos que se presentan debido a la imperfección de los instrumentos de medición (fig. b).
C) Personales
Son aquellos ocasionados debido a las limitaciones de los sentidos humanos en las observaciones
(vista, tacto, etc). Ver fig. c.
4.- Clases de errores
A) Propios
Son aquellos que provienen del descuido, torpeza o distracción del observador, éstas no entran
en el análisis de la teoría de errores.
Fig. b: Las agujas de un cronómetro
son susceptibles al retraso o adelanto
debido al mecanismo del mismo instru-
mento, luego se cometerá un error de
medición.
Fig. c: La vista de una persona puede
no permitir observar correctamente
las agujas de un reloj, se cometerá
entonces un error personal en la me-
dida del tiempo.
Fig. a: Al medir la longitud entre dos
puntos, en días calurosos, la cinta mé-
trica se dilata debido a la fuerte tem-
peratura, luego se cometerá un error
de medición.
Es posible que el operador lea en la cinta métrica
15,40 metros y al momento de anotar escriba por
descuido L = 154 metros.

83. Teoría de observaciones
30
Probabilidad
Es la relación que define el número de veces que un resultado debe
ocurrir respecto al número total de posibilidades.
En el ejemplo de la figura se observa que el círculo está dividido
en 10 triángulos; El color negro tendrá entonces una probabili-
dad de dos a diez (2/10) de ser el ganador en el juego de la ruleta,
el plomo: 3/10 y el blanco 5/10 como se aprecia.
Para analizar la teoría de probabilidades en la topografía se
tomará un ejemplo ilustrativo, con el cual se explicará los
conceptos fundamentales así como su respectivo significado.
TEORÍA DE PROBABILIDADES
Son entes matemáticos que sirven para aproximar una cantidad a un rango permisible (de los errores
accidentales); en esta teoría se supone que:
• Los errores pequeños son más frecuentes que los grandes.
• No se cometen errores muy grandes.
• Los errores pueden ser positivos o negativos.
• El verdadero valor de una cantidad es la media de un número infinito de observaciones análogas.
B) Sistemáticos
Son aquellos que aparecen debido a una imperfección de los aparatos utilizados; así como también a
la influencia de agentes externos como viento,calor humedad, etc.
Estos errores obedecen siempre a una ley matemática o física, por lo cual es posible su corrección.
Suponga Ud. que se quiere medir la longi-
tud AB, pero al usar la cinta métrica, ésta
se pandea como se muestra, la lectura que
se toma en estas condiciones no será la
verdadera, habrá que corregir.
L = L' – corrección
2
W L
Corrección =
24 F
En este caso la corrección se determina mediante la siguiente fórmula:
Donde:
W, L y T son parámetros conocidos.
C) Accidentales o fortuitos
Son aquellos que se presentan debido a causas ajenas a la pericia del observador, y al que no puede
aplicarse corrección alguna, sin embargo estos errores suelen obedecer a as leyes de las
probabilidades; por tal motivo se recomienda tomar varias lecturas de una misma medición
pues generalmente estas suelen ser diferentes.

84. Teoría de observaciones
31
Ejemplo ilustrativo
Se ha medido la longitud en milímetros que exis-
te entre dos puntos, para ello se han realizado 100
mediciones, los valores que se presentan carecen
de errores sistemáticos. La tabla muestra los va-
lores medidos y el número de veces.
Valor medido (mm) Número de veces
692,00 1
693,00 1
694,00 1
694,20 1
695,00 1
695,20 2
695,70 2
696,00 3
696,80 2
697,00 4
697,40 2
697,90 2
698,00 5
698,20 4
698,70 3
699,00 6
699,10 3
699,60 2
700,00 10
700,40 2
700,70 2
701,00 8
701,30 2
701,90 3
702,00 5
702,20 3
702,80 4
703,00 4
704,00 4
704,40 1
704,70 1
705,00 2
706,00 2
707,00 1
708,00 1
La media aritmética X; será:
X = 700,00 mm
Calculando la desviación entre cada valor y la
media:
Xi (mm) Número de veces Vi (mm)
692,00 1 –8,00
693,00 1 –7,00
694,00 1 –6,00
694,20 1 –5,80
695,00 1 –5,00
695,20 2 –4,80
695,70 2 –4,30
696,00 3 –4,00
696,80 2 –3,20
697,00 4 –3,00
697,40 2 –2,60
697,90 2 –2,10
698,00 5 –2,00
698,20 4 –1,80
698,70 3 –1,30
699,00 6 –1,00
699,10 3 –0,90
699,60 2 –0,40
700,00 10 0,00
700,40 2 0,40
700,70 2 0,70
701,00 8 1,00
701,30 2 1,30
701,90 3 1,90
702,00 5 2,00
702,20 3 2,20
702,80 4 2,80
703,00 4 3,00
704,00 4 4,00
704,40 1 4,40
704,70 1 4,70
705,00 2 5,00
706,00 2 6,00
707,00 1 7,00
708,00 1 8,00
V = X – X
i i

85. Teoría de observaciones
32
Llamaremos “marca de clase” a la mínima di-
visión constante que puede variar en todas las
mediciones; en nuestro caso “1 milímetro”
Tabulando y teniendo presente:
f = Frecuencia absoluta
f = Número de desviaciones en el intervalo
Se presenta a continuación al histograma de fre-
cuencias absolutas que viene a ser la representa-
ción discreta de la frecuencia con que se repiten las
desviaciones en cada intervalo de marca de clase.
Intervalo del histograma (mm) Frecuencia absoluta
–8,5 a –7,5 1
–7,5 a –6,5 1
–6,5 a –5,5 2
–5,5 a –4,5 3
–4,5 a –3,5 5
–3,5 a –2,5 8
–2,5 a –1,5 11
–1,5 a –0,5 12
–0,5 a +0,5 14
+0,5 a +1,5 12
+1,5 a +2,5 11
+2,5 a +3,5 8
+3,5 a +4,5 5
+4,5 a +5,5 3
+5,5 a +6,5 2
+6,5 a +7,5 1
+7,5 a +8,5 1
Si se unen mediante líneas rectas los puntos su-
periores centrales de las barras del histograma,
se obtendrá el “polígono de frecuencia”
Si se aumentara el número de mediciones tanto
como se quisiera y se ajusta aún más la preci-
sión, se obtendría una marca de clase bastante
pequeña al punto que el polígono de frecuencia
pasaría a ser una línea contínua curva, simétrica
respecto al centro y en forma de campana.
Se observará en la curva la existencia de dos
puntos de inflexión (cambio de concavidad).
Matemáticamente es posible representar dicha curva
mediante modelos probabilísticos de variable aleatoria
contínua; el más usado es el Modelo Normal Estándar.

86. Teoría de observaciones
33
En la curva típica de probabilidad se ubican dos puntos de inflexión cuyas abcisas correspondien-
tes toman el nombre de: Desviación Típica o Estándar (σ)
Observaciones de igual precisión
Se considera que las observaciones son tomadas en idénticas condiciones, vale decir con los
mismos instrumentos, la misma brigada, las mismas condiciones climatológicas, etc.
A) Media (X )
Es el valor que tiende a situarse en el centro del conjunto de datos ordenados según su magnitud.
Es la media aritmética de un conjunto de datos.
X X X ... + X
1 2 3 n
X =
n
+ + +
B) Desviación (Vi)
Se le llama también error aparente de una medición, es la diferencia entre la media y el valor
correspondiente a una medición.
En realidad la desviación es el error aproximado para cada medición, dado que no se conoce el
verdadero valor.
V = X – X
i i
C) Error medio cuadrático de una observación (Desviación típica o estándar): σ
σ
σ
σ
σ
Corresponde al valor del error del punto de inflexión de la curva típica de probabilidad.
En el caso de nuestro ejemplo ilustrativo (pag. 29)
X = 700,00
Veáse ejemplo ilustrativo (pag. 29)
El área achurada indica que entre los límites –σ y +σ se puede esperar que estos errores
ocurran el 68,27% de veces.
Como se aprecia, el área encerrada por la curva de
probabilidad limitado por los valores de la desvia-
ción típica (σ) corresponde al 68,27% del área total
bajo la misma curva.

87. Teoría de observaciones
34
Matemáticamente:
σ : Desviación típica o estándar
V : Desviación de cada medición
n : Número de mediciones
Estadísticamente, la primera expresión (2 ≤ n ≤ 30) es porque el valor resultante representa
un mejor estimador de la desviación típica de una población de la que se ha tomado una
muestra. Prácticamente si n = 30, no hay diferencia entre las dos expresiones.
Σ
σ ±
2
V
=
n
2 ≤ n ≤ 30 n > 30
Σ
σ ±
2
V
=
n – 1
n = Σ = 100 Σ = 930,14
Xi (mm) Número de veces Vi (mm) V
2
Σ
Σ
Σ
Σ
ΣV
2
692,00 1 –8,00 64,00 64,00
693,00 1 –7,00 49,00 49,00
694,00 1 –6,00 36,00 36,00
694,20 1 –5,80 33,64 33,64
695,00 1 –5,00 25,00 25,00
695,20 2 –4,80 23,04 46,08
695,70 2 –4,30 18,49 36,98
696,00 3 –4,00 16,00 48,00
696,80 2 –3,20 10,24 20,48
697,00 4 –3,00 9,00 36,00
697,40 2 –2,60 6,76 13,52
697,90 2 –2,10 4,41 8,82
698,00 5 –2,00 4,00 20,00
698,20 4 –1,80 3,24 12,96
698,70 3 –1,30 1,69 5,07
699,00 6 –1,00 1,00 6,00
699,10 3 –0,90 0,81 2,43
699,60 2 –0,40 0,16 0,32
700,00 10 0,00 0,00 0,00
700,40 2 0,40 0,16 0,32
700,70 2 0,70 0,49 0,98
701,00 8 1,00 1,00 8,00
701,30 2 1,30 1,69 3,38
701,90 3 1,90 3,61 10,83
702,00 5 2,00 4,00 20,00
702,20 3 2,20 4,84 14,52
702,80 4 2,80 7,84 31,36
703,00 4 3,00 9,00 36,00
704,00 4 4,00 16,00 64,00
704,40 1 4,40 19,36 19,36
704,70 1 4,70 22,09 22,09
705,00 2 5,00 25,00 50,00
706,00 2 6,00 36,00 72,00
707,00 1 7,00 49,00 49,00
708,00 1 8,00 64,00 64,00
Analizando el ejemplo ilustrativo de la página 31

88. Teoría de observaciones
35
Dado que n = 100 > 30
2
V 930,14
=
n 100
Σ
σ ± = ± ⇒ σ = ±3,05 mm
Este valor significa que de las 100 mediciones tomadas es probable que 68 de ellas queden
dentro de los límites de error [–3,05 mm; +3,05 mm].
Veamos la tabla, para un intervalo de error [–3,50 mm; +3,50 mm], tenemos 76 mediciones
que caen dentro de dicho rango (analice Ud. en el intervalo [–3,05 mm; +3,05 mm]).
Intervalo del histograma Frecuencia absoluta
(mm)
–8,5 a –7,5 1
–7,5 a –6,5 1
–6,5 a –5,5 2
–5,5 a –4,5 3
–4,5 a –3,5 5
–3,5 a –2,5 8
–2,5 a –1,5 11
–1,5 a –0,5 12
–0,5 a +0,5 14
–0,5 a +1,5 12
+1,5 a +2,5 11
+2,5 a +3,5 8
+3,5 a +4,5 5
+4,5 a +5,5 3
+5,5 a +6,5 2
+6,5 a +7,5 1
+7,5 a +8,5 1











76 mediciones
D) Error probable de una observación (E50)
Es aquel intervalo, dentro de cuyos límites exis-
te la probabilidad de que el 50% del total de
mediciones integren dicho rango.
En la actualidad se usa poco este error.
± σ
50
E = 0, 6745
σ : Desviación típica o estándar
En el ejemplo ilustrativo:
± σ ±
50
E = 0,6745 = 0,6745( 3, 05)
±
50
E = 2, 06 mm
Este valor significa que de las 100 mediciones tomadas, es probable que 50 de ellas queden
dentro de los límites de error [–2,06 mm; +2,06 mm].

89. Teoría de observaciones
36
E) Ecuación general del índice de precisión
La probabilidad de un error de cualquier porcentaje de probabilidad se determina por la siguien-
te expresión:
= σ
p
E K
Ep : Porcentaje de error
K : Factor numérico que corresponde al porcentaje de error
σ : Desviación típica o estándar
Expresiones usuales en topografía: E90 = 1.6449 σ
E95 = 1.9599 σ
E99,73 = 3 σ
Comúnmente en topografía se usa con mayor frecuencia: E95, en nuestro ejemplo ilustrativo:
E95 = 1,9599 (±3,05)
E95 = ± 5,98 mm
Este valor significa que de las 100 mediciones tomadas es probable que 95 de ellas queden
dentro de los límites de error [–5,98 mm; +5,98 mm].
Por otro lado es preciso anotar que la curva de probabilidad en el eje de las X es una asíntota, luego;
no se puede evaluar el error de 100%, razón por la cual debe considerarse que estas tres expresio-
nes (E90; E95; E99,73) nos dan los valores máximos que se presentan en la práctica. Errores mayores
que ±3σ ya no se consideran errores accidentales sino equivocaciones.
F) Error de la media (Em)
Está visto que la media, también está sujeto a error.
Error de la media a cualquier porcentaje de probabilidad es aquel intervalo (–Em; +Em) dentro de
cuyos límites puede caer el verdadero error accidental de la media con una probabilidad de p%.
Ep
Em
n
=
=
+ + + +
1 2 3 n
x x x ... x
X
n
Si hacemos: E = Ep
2 2
E nE
suma p
=
E n E
suma p
= ...(2)
(2) en (1): =
p
m
E
E
n
...demostrado
Demostración:
Luego:
Esuma
Em
n
= ...(1)
Pero: 2 2
E E
suma = Σ

90. Teoría de observaciones
37
En el ejemplo ilustrativo (si p = 95%)
E
95
= ±5,98 mm
= ⇒ = ±
95
m m
E
E E 0,60 mm
100
G) Valor más probable (V.M.P.)
Es aquel valor que se acerca más al verdadero valor pero que no lo es. Comúnmente se
considera a la media como el valor más probable de varias mediciones.
V.M.P. = X
En el ejemplo ilustrativo: V.M.P. = 700,00 mm; como quiera que el V.M.P. nunca será el
valor verdadero, se deduce que existirá un error y que dicho valor exacto estará ubicado
dentro del rango de ciertos limites: [V.M.P. –Em; V.M.P. +Em] con una probabilidad de
p%. En el ejemplo ilustrativo, el valor verdadero estará contenido en el rango de [700 –
0,60 ; 700 + 0,60], lo que es [–699,40 mm ; 700,60 mm] con una probabilidad del 95%.
PROBLEMAS DE APLICACIÓN
1. Se midió una base cinco veces, obteniéndose:
115,334 m; 115,326 m; 115,315 m; 115,336 m;
115,335 m. Calcular el error probable de una
observación con el 95% de probabilidad de
que sea cierto.
Solución
Número Valor (m) Vi Vi
2
1 115,334 0,005 2,5×10-5
2 115,326 -0,003 0,9×10-5
3 115,315 -0,014 19,6×10-5
4 115,336 0,007 4,9×10-5
5 115,335 0,006 3,6×10-5
X = 115,329 ΣVi
2
= 31,5×10
-5
Σ ×
± = ±
×
σ
σ
2 -5
i
-3
V 31,5 10
=
4
= 8,874 10 m
n – 1
El error probable de una observación con el
95% de probabilidad de que sea cierto es:
E95= 1,9599σ = 1,9599(±8,874×10
-3
)
E95= ±0,017 m
Nótese que ningún valor referente a V so-
brepasa el correspondiente a 3σ = 0,027, con
el cual no hay motivo de depuración.
2. Se ha efectuado la medición de una distan-
cia y los resultados obtenidos son:
1° Medición: 800, 213 m
2° Medición: 800,220 m
3° Medición: 800,603 m
4° Medición: 800,218 m
Se pide calcular el verdadero valor con una
probabilidad del 50%

91. Teoría de observaciones
38
Solución
En primer lugar, si analizamos el valor de
cada medición, respecto a los demás, será fá-
cil detectar que la tercera medición tiene un
valor muy lejano a las otras, lo cual hace de-
ducir que en el proceso de medición se debió
cometer un error propio(en la 3° medición),
por tal motivo no se tomará en cuenta en los
cálculos.
Luego: 1° Medición: 800,213 m
2° Medición: 800,220 m
3° Medición: 800,218 m
• n = 3
800, 213 800, 220 800, 218
X =
3
+ +
2 400, 651
X =
3
X = 800, 217 m
• Tabulando
Medida (m) V = X – X
i i V2
800,213 –0,004 16×10
-6
800,220 +0,003 9×10
-6
800,218 +0,001 1×10-6
ΣV
2
= 26×10
-6
Σ ×
± = ±
±
σ
σ
2 -6
i
V 26 10
=
= 0, 0036 m
n – 1 3 – 1
Nótese que ningún valor referente a V, so-
brepasa el correspondiente a 3σ = ±0,011,
con lo cual no hay motivo de depuración.
• El error de una observación para una pro-
babilidad de 50%.
E = ±0,6745σ =±0,0024 m
• El error de la media para una probabilidad
de 50%.
Em =
E
3
= ±0,0014 m
• El verdadero valor está comprendido en el
siguiente intervalo:
L = 800,217 m ± 0,0014 m
3. Se presentan una serie de n Lecturas de
estadal (mira); que se tomaron con un nivel
en condiciones idénticas. Responder si el
valor 2,260 está dentro del intervalo co-
rrespondiente al 50% de probabilidad si:
L1 = 2,250 m ; L4 = 2,257 m ; L7 = 2,250 m
L2 = 2,253 m ; L5 = 2,259 m ; L8 = 2,260 m
L3 = 2,258 m ; L6 = 2,251 m
Solución
Analizando la totalidad de mediciones:
Número L Vi Vi
2
1 2,25 –0,005 2,5×10
-5
2 2,253 –0,002 0,4×10
-5
3 2,258 +0,003 0,9×10-5
4 2,257 +0,002 0,4×10
-5
5 2,259 +0,004 1,6×10
-5
6 2,251 –0,004 1,6×10-5
7 2,250 –0,005 2,5×10
-5
8 2,260 +0,005 2,5×10-5
L = 2,255 m ΣV
2
= 12,4×10
-5

92. Teoría de observaciones
39
2 -5
i
V 12, 4 10
=
= 0, 0042
n – 1 7
Σ ×
± = ±
±
σ
σ
Vmax = 3σ = ±0,013
La varianza de ninguna medición sobrepasa
el máximo, por lo cual no hay motivo de de-
puración de valores:
E50 = 0,6745σ = ±0,003 m
El verdadero valor con el 50% de probabili-
dad está dentro del siguiente intervalo:
L = L ± E50
L = 2,255 ± 0,003 = [2,252; 2,258] m
El valor 2,260 no está dentro del intervalo
correspondiente al 50% de probabilidad.
4. Se llevó a cabo una nivelaciónentre los puntos
A, B y C. Realizados por los grupos 1, 2 y 3
obteniéndoselossiguientesdatos,(enmetros).
Grupo 01
Pto V(atrás) V(adelante) Cota D(m)
A 0,251 100,00
1 1,424 2,423 50,00
B 0,923 1,212 40,10
2 1,726 0,632 48,30
A 0,08 31,80
Pto V(atrás) V(adelante) Cota D(m)
B 1,22
1 2,42 1,22 35,10
2 1,824 0,472 44,20
C 0,223 0,414 50,70
3 0,523 1,425 34,60
4 1,032 2,453 48,90
B 1,248 46,50
Grupo02
Pto V(atrás) V(adelante) Cota D(m)
A 0,257
1 0,832 1,070 20,00
2 1,253 1,724 30,00
3 2,426 1,232 40,00
4 2,102 0,342 40,00
5 1,834 0,723 35,00
C 0,264 2,200 20,00
6 0,102 2,432 30,00
7 1,234 1,263 45,00
8 2,620 1,264 70,00
A 0,660 30,00
Grupo03
• Las cotas de B y C son:
Cota B = 98,051 ; Cota C = 101,400
Dicho grupo también midió el ángulo ver-
tical que forma el horizonte con la línea
recta que une B y C.
Obteniéndose: θ = 01° 30' 20"
θ = 01° 30' 45"
θ = 01° 30' 40"
Se pide: El valor más probable de la dis-
tancia topográfica.

93. Teoría de observaciones
40
Solución
• Analizando la nivelación del grupo 01
Pto V(atrás) V(adelante) Cota Ci Cota Compensada
A 0,251 100,251 100,00
1 1,424 99,252 2,423 97,828 0,001 97,829
B 0,923 98,963 1,212 98,040 0,002 98,042
2 1,746 100,077 0,632 98,331 0,002 98,333
A 0,08 99,997 0,003 100,00
Cota B = 98,042
Pto V(atrás) V(adelante) Cota Ci Cota Compensada
B 1,22 99,262 98,042
1 2,42 100,462 1,22 98,042 -0.001 98,041
2 1,824 101,814 0,472 99,99 -0.003 99,987
C 0,223 101,623 0,414 101,40 -0.005 101,395
3 0,523 100,721 1,425 100,198 -0.006 100,192
4 1,032 99,3 2,453 98,268 -0.008 98,26
B 1,248 98,052 -0.01 98,042
Cota C = 101,395
• Analizando la nivelación del grupo 02
Pto V(atrás) V(adelante) Cota Ci Cota Compensada
A 0,257 100,257 100,00 100,000
1 0,832 100,019 1,070 99,187 -0.001 99,186
2 1,253 99,548 1,724 98,295 -0.002 98,293
3 2,426 100,742 1,232 98,316 -0.003 98,313
4 2,102 102,502 0,342 100,400 -0.005 100,395
5 1,834 103,613 0,723 101,779 -0.006 101,773
C 0,264 101,677 2,200 101,413 -0,007 101,406
6 0,102 99,347 2,432 99,245 -0,008 99,237
7 1,234 99,318 1,263 98,084 -0,010 98,074
8 2,620 100,674 1,264 98,054 -0,013 98,041
A 0,660 100,014 -0,014 100,000
Cota C = 101,406

94. Teoría de observaciones
41
• Analizando la nivelación del grupo 03
Por dato: Cota B = 98,051
Cota C = 101,400
• Calculando el valor más probable: Cota B;
Cota C
Cota B = = 98,047
Cota C =
Cota C = 101,400
• Calculando el valor más probable del án-
gulo de elevación:
θ =
θ = 01° 30' 35"
• Procediendo a calcular el V.M.P. de la dis-
tancia topográfica BC (D)
∆h = Cota C – Cota B
∆h = 3,353 m
D = ∆h ctg θ = (3,353) ctg(01° 30' 35")
D = 127,221 m
5. Tres alumnos A, B y C; integrantes del gru-
po #3 del curso de topografía, tienen que
medir una longitud muy extensa, turnán-
dose por tramos, el alumno A mide el 40%
de la longitud equivocándose 1 cm por cada
50 metros; el alumno B hace el 30% pero se
equivoca 1 cm por cada 10 m y C que mide
el tramo final se equivoca 1 cm por cada 20
metros. Si el profesor del curso mide con
estación total cada tramo que le correspon-
de a cada alumno y se dá cuenta que hubo
un error de 1 cm. ¿Cuál es el alumno más
probable de cometer el error?
Solución
A1 = A mide la longitud ç P(A) = 0,40
A2 = B mide la longitud ç P(B) = 0,30
A3 = C mide la longitud ç P(C) = 0,30
E: se equivocó al medir:
Según los datos: P(E/A1) = 1/50
P(E/A2) = 1/10
P(E/A3) = 1/20
Se pide: P(Ak/E) = ? ; k = 1; 2; 3 ....
Como: P(E) = ΣP(Ai)P(E/Ai)
P(E)=P(A1)P(E/A1)+P(A2)P(E/A2)+P(A3)P(E/A3)
P(E)=(0,40)(1/50)+(0,30)(1/10)+(0,30)(1/20)
P(E) = 0,053
P(A1/E) = = 0,151
P(A2/E) = = 0,566
P(A3/E) = = 0,283
El más probable de cometer el error es el
integrante B debido a que su probabili-
dad es mayor que el resto.
3 3
P(A )P(E/A ) (0,30)(1/20)
=
P(E) 0,053
101, 395 + 101, 406 + 101, 400
3
2 2
P(A )P(E/A ) (0,30)(1/10)
=
P(E) 0,053
98, 042 + 98, 051
2
1 1
P(A )P(E/A ) (0,40)(1/50)
=
P(E) 0, 053
01°30'20"+ 01°30'45"+ 01°30'40"
3

95. Teoría de observaciones
42
Observaciones de diferente precisión
En algunas ocasiones, la medida de una magnitud se realiza en diferentes días, con diversos equipos e
incluso con cambio de operadores (en el peor de los casos); cada uno de ellos constituye una circunstan-
cia particular. Cada circunstancia tiene cierta precisión el cual se puede cuantificar mediante el peso.
Peso
Es un parámetro que mide el grado de precisión que debe aplicarse a cada una de las observaciones.
• El peso puede estar dado por el número de mediciones de cada observación.
Ejemplo de aplicación:
Observación A Observación C
120° 30' 16" 120° 30' 36"
120° 30' 40" 120° 30' 10"
120° 30' 40"
Observación B 120° 30' 38"
120° 30' 22"
120° 30' 32" ⇒ θ2 = 120° 30' 22" (Peso = 3)
120° 30' 12"
• El peso puede estar dado por el error probable de cada observación.
= =
2 2 2
P E P E P E
1 1 2 2 3 3
Ejemplo de aplicación:
Observación A :120° 30' 28" ± 10"
Observación B :120° 30' 22" ± 5"
Observación C :120° 30' 31" ± 2"
= =
1 2 3
2 2 2
P (10) P (5) P (2)
Haciendo P1 = 1
Se tiene: P1 = 1 ; P2 = 4 ; P3 = 25
De lo cual se deduce que la observación C tiene mayor precisión.
A) Media ponderada ( )
La media ponderada de varias observaciones de diferente precisión, está determinada por la
siguiente expresión.
⇒ θ1 = 120° 30' 28" (Peso = 2)
⇒ θ3 = 120° 30' 21" (Peso = 4)
+ + +
+ + +
1 1 2 2 3 3 n n
1 2 3 n
P X P X P X ... + P X
X =
P P P ... + P
X

96. Teoría de observaciones
43
B) Error probable de la media (Em)
Es aquel intervalo [–Em ; +Em], dentro de cuyos límites puede caer el verdadero error
accidental de la media con una probabilidad de p%.
2
m
(PV )
E K
( P)(n – 1)
Σ
= ±
Σ
Em : Error de la media para p%
K : Factor número que corresponde al porcentaje de error
P : Peso
V : Desviación
n : Número de observaciones
Obteniendo: p = 50% ⇒ K = 0,6745
p = 90% ⇒ K = 1,6449
p = 95% ⇒ K = 1,9599
C) Valor más probable (V.M.P.)
Comúnmente se considera a la media como el valor más probable.
V.M.P. = X
Errores en las operaciones matemáticas
Hasta el momento se han analizado los errores accidentales para una operación simple.
Sin embargo existen ocasiones en las cuales es necesario realizar una operación compuesta; así
por ejemplo, supongamos que se desea medir la distancia que hay entre dos puntos del orden de
100 metros, con una cinta métrica de 20 metros; en este caso el valor final vendrá afectado de un
error que será la resultante de los errores de las mediciones elementales.
A) Error de una suma
L = L1 + L2 + L3
= ± + +
2 2 2
suma 1 2 3
E E E E

97. 44
=
± +
=
∂ ∂
=
± × + ×
∂ ∂
= =

98. Teoría de observaciones
45
1. Determine el error probable de una línea
de longitud de masa igual a 3 500 m. Sí el
error probable al medir la longitud de una
cinta de 35 m es de ±0,02 m.
Solución
• El error de la suma de una serie de cantidades:
= ± + +
= ±
!
2 2 2
S
n
S
E E E ... + E
E E n
• Elnúmerodeobservaciones:
3 500
n = =100
35
• El error probable:
S
S
E 0, 02 100
E 0, 2 m
= ±
= ±
2. Se ha realizado observaciones, midiendo tres
ángulos formados alrededor de un punto
“O” en las mismas condiciones con el si-
guiente resultado:
X1 ± E1 = 150° 20' 30 ± 05
X2 ± E2 = 140° 30' 35 ± 03
X3 ± E3 = 069° 09' 30 ± 01
Determinar los valores más probables de di-
chos ángulos.
Solución
• Dado que los ángulos están formados alre-
dedor de un punto:
ΣX = 360° ............ (teórico)
En nuestro caso:
ΣX = 360° 00' 35
Ecierre= +35
PROBLEMAS DE APLICACIÓN
Luego: C1 + C2 + C3 = 35
• Distribución del error:
3
1 2
2 2 2
1 2 3
3
1 2
2 2 2
C
C C
= =
E E E
C
C C
= =
5 3 1
Si: C3 = 1 ç C2 = 9 ; C1 = 25
• Finalmente:
X1 = 150° 20' 30 – 25 ç X1 = 150° 20' 05
X2 = 140° 30' 35 – 09 ç X2 = 140° 30' 26
X3 = 069° 09' 30 – 01 ç X3 = 069° 09' 29
3. Corregir cada uno de los ángulos
Solución
• Σ θ = 180° 00' 14 ⇒ Ecierre = +14
C1 + C2 + C3 = 14 ...(a)
• 3
1 2
2 2 2
C
C C
2 4 6
= =
3
2
1
C
C
C
4 9
= = ...(b)
• De (a) y (b): C1 = 1 ; C2 = 4 ; C3 = 9
• Ángulos corregidos
X
1 = 42° 20' 10 – 1 ⇒ X
1 =42°20'09±02
X
2 = 83° 16' 12 – 4 ⇒ X
2 =83°16'08±04
X
3 = 54° 23' 52 – 9 ⇒ X
3 =54°23'43±06

99. Teoría de observaciones
46
4. Se ha realizado la medición de una línea
de ferrocarril, empleando diferentes equi-
pos, obteniéndose los siguientes resulta-
dos de campo (en metros).
X1 ± E1 = 1000,10 ± 0,01
X2 ± E2 = 1000,20 ± 0,02
X3 ± E3 = 1000,30 ± 0,03
Calcular el valor más probable de la línea
medida.
Solución
• Calculando el peso en cada caso:
2 2 2
2 2 3 3
P E = P E = P E
P1(0,01)
2
= P2(0,02)
2
= P3(0,03)
2
Si hacemos: P1 = 1
Se tendrá: P2= 1/4 ; P3 = 1/9
• El valor más probable es el media ponderada:
1 2 2 3 3
2 3
P X P X P X
X =
P P P
+ +
+ +
1 1
(1)(100,10) (100, 20) (100, 30)
4 9
X =
4 9
   
+ +
   
   
+ +
X = 100,135 m
5. Se ha realizado una nivelación entre P y Q
siguiendo tres recorridos diferentes como
muestra la tabla.
Recorrido Longitud (km) Cota Q
Primero 10 164,321 m
Segundo 25 164,300 m
Tercero 80 164,242 m
Calcular el verdadero valor referido a la
cota del punto “Q”
Solución
En una nivelación, a mayor longitud en el reco-
rrido del itinerario, mayor será el error probable
de la media y por tanto menor su peso. Como
quiera que en topografía se trabaja con incre-
mentosodecrementoslineales;seconcluyeque
el peso de un itinerario será inversamente pro-
porcional a la longitud recorrida:
P1 =
10
; P2 =
25
; P3 =
80
1 2 2 3 3
2 3
P X P X P X
X =
P P P
+ +
+ +
1 1 1
(164,321) (164,300) (164,242)
10 25 80
X=
10 25 80
     
+ +
     
     
+ +
X = 164, 309 m
Además:
X(m) Peso V V2
PV2
164,321 1/10 0,012 1,44×10-4
1,44×10-5
164,300 1/25 –0,009 0,81×10-4
0,32×10-5
164,242 1/80 –0,067 44,89×10-4
5,61×10-5
ΣPV2
= 7,37×10-5
Σ ×
± =
Σ
±
σ
σ
2 -5
V 7, 37 10
=
= 0, 0155 m
P
( P)(n – 1) (0,1525)(3 – 1)
Se quiere el error para k = 50% de probabilidad
E= kσ =0,6745×0,0155
E50 = 0,0105 m
Luego el error de la media para k = 50%
de probabilidad:
50
m
E
E 0, 006 m
3
= =

100. Teoría de observaciones
47
El verdadero valor se encuentra en el si-
guiente intervalo:
X : (164,309 ± 0,006) m
6. Determinar el verdadero valor de la superfi-
cie del sector circular medido, sabiendo que
el radio es de 120,80 m ± 0,05 m; el ángulo
observado es 11° 15' ± 05'.
Sugerencia: 1 minuto = 0,0003 rad.
Solución
r = 120,80 m ± 0,05 m
θ = 11° 15' ± 05'
A = ?
A =
1
2
br
A =
1
2
(θ×r)r
A =
1
2
θ×r
2
=
360
π
θ×r
2
• Calculandoelvalormásprobabledelasuperficie:
π 2
A = (11° 15')(120,80)
360
A = 1432,63 m2
• Calculando el error probable:
2 2
r
A A
r
E E E
θ
θ
∂ ∂
   
= × + ×
   
∂ ∂
   
θ
θ⋅ θ⋅
θ
   
∂ π ∂ π
   
= × + ×
   
   
∂ ∂
   
   
H
2 2
2 2
r r
r
E E E
360 360
[ ]
2 2
2
r
E E 2r E
360
θ θ×
π
 
 
= × + × × 
 
 
H
[ ]
×
π
 
 
= × + × × × 
 
 
2 2
2
120,8 120,8
E (5 0,0003) 11°15' 2 0,05
360
E = 1,20 m
2
• El verdadero valor estará comprendido en
el siguiente rango:
A = 1 432,63 m2
± 1,20 m2
7. Se ha medido una distancia inclinada entre dos
puntos dando una longitud de 400 m, habién-
dose usado una cinta de 25 m con un error por
cintada de ±0,01 m y el ángulo vertical con res-
pecto al horizonte igual a 7° 15' ± 03'. Hallar el
verdadero valor de la distancia horizontal.
Solución
• Analizando la longitud de media.
L
Total
= 8(25) = 400 m
2 2 2
8 veces
Error probable (0,01) (0,01) ... +(0,01)
= + +
!
2
Error probable 8(0, 01) 0, 028 m
= =
L : 400 m ± 0,028 m
• Analizando el triángulo rectángulo generado:
L = 400 m ±
}
EL
0, 028
θ = 7° 15' ± {
E
3'
θ
D =L cos θ
D = 400 cos 7° 15' ⇒ D = 396,802 m
Calculando el error probable:
2 2
L
D D
L
E E Eθ
θ
∂ ∂
   
= × + ×
   
∂ ∂
   
[ ]
2 2
L
cos –sen
E E L Eθ
θ θ
= × + × ×
 
 
[ ]
 
π
 
= × + × ×
 
 
 
 
2
2
cos –sen
E 7°15' 0,028 7°15' 400 0°3'
180°
E = ±0,052 m

101. Teoría de observaciones
48
• El verdadero valor correspondiente a la
distancia horizontal se encuentra:
D = 396,802 m ± 0,052 m
8. Calcular el verdadero valor de la longi-
tud AC con una probabilidad del 90%;
máxima tolerancia = 0,010 m.
• Longitud AB
1° observación 2° observación
20,253 m 20,255 m
20,242 m 20,239 m
20,261 m
• Longitud BC
1° observación 2° observación 3° observación
16,232 m 16,241 m 16,239 m
16,234 m 16,222 m
Solución
• Analizando la longitud AB
1° observación
L = 20,252; P = 3
Medición (m) V
20,253 +0,001
20,242 –0,001
20,261 +0,009
2° observación
L = 20,247; P = 2
Medición (m) V
20,255 +0,008
20,242 –0,008
Li Pi PL V V2
PV2
20,252 3 60,756 +0,002 4×10
–6
12×10
–6
20,247 2 40,494 –0,003 9×10–6
18×10–6
Σ 5 101,250 +0,002 4×10–6
30×10–6
PL 101, 25
L
P
Σ
= =
Σ
L 20, 250 ; n 2
= =
Nótese: i
V = L – L
Calculando:
Em para 90% de probabilidad
2
m
(PV )
E 1, 6449
( P)(n – 1)
Σ
= ±
Σ
–6
m
30 ×10
E 1,6449 0, 004 m
5(2 – 1)
= ± = ±
AB = 20,250 m ± 0,004 m
• Analizando la longitud BC
1° observación
L = 16,233 m; P = 2
Medición (m) V
16,232 –0,001
16,234 +0,001
2° observación
L = 16,238 m; P = 2
Medición (m) V
16,241 +0,003
16,23 –0,003
3° observación
L = 16,239 m; P = 1
Medición (m) V
16,239 0,000

102. Teoría de observaciones
49
PL 81,181
L
P 5
Σ
= =
Σ
= =
L 16,236 m; n 3
• Calculando: Em para 90% de probabilidad
2
m
(PV )
E 1, 6449
( P)(n – 1)
Σ
= ±
Σ
–6
m
34,8 ×10
E 1, 6449 0, 003 m
5(3 – 1)
= ± = ±
BC = 16,236 m ± 0,003 m
• Analizando la longitud AC
AC = AB + BC = 20,250 + 16,236
AC = 36,486 m
• Calculando el error de la media con una probabilidad del 90%.
= ± + = ± +
2 2 2 2
suma 1 2
E E E (0,004) (0,003)
suma
E 0, 005 m
= ±
El verdadero valor de la longitud AC con una probabilidad del 90% se encontrará en el
siguiente rango:
[36,486 m ± 0,005 m] = [36,481; 36,491] m
Li Pi PL V V2
PV2
16,233 2 32,466 –3,2×10
–3
10,24×10
–6
20,48×10
–6
16,238 2 32,476 +1,8×10–3
3,24×10–6
6,48×10–6
16,239 1 16,239 +2,8×10
–3
7,84×10
–6
7,84×10
–6
Σ 5 81,189 +0,002 4×10–6
34,8×10–6

103. Equipos básicos de altimetría
50
9. Dos brigadas han medido una misma longitud obteniéndo en metros los siguientes resultados.
Solución:
• Con la brigada 1: X 225,29
=
Valor = −
i i
V X X Vi
2
225,25 –0,04 0,0016
225,32 0,03 0,0009
225,30 0,01 0.0001
225,35 0,06 0,003
225,27 –0,02 0,0004
225,28 –0,01 0,0001
225,28 –0,01 0,0001
Σ 1 577,05 0,0068
2
1
V
3,4 cm
7 1
Σ
σ = ± = ±
−
3σ = ±10,2 cm
Dado que ningún valor sobrepasa el máximo
error: 3σ, no hay lugar a depuración.
• Con la brigada 2: X 225,29
=
Dado que ningún valor sobrepasa el máximo
error: 3σ, no hay lugar a depuración.
– Comparando σ: llegamos a la conclusión que
la brigada 2 es más fiable que la 1; dado que:
σ2 σ1.
Ilustrando:
Valor = −
i i
V X X Vi
2
225,26 –0,03 0,0009
225,26 –0,03 0,0009
225,30 0,01 0.0001
225,30 0,01 0,0001
225,32 0,03 0,0009
225,27 –0,02 0,0004
225,27 –0,02 0,0004
225,29 0 0
225,29 0 0
225,29 0 0
225,34 0,05 0,0025
Σ 2 478,19 0,0062
3σ = ±7,5 cm
2
2
V
2,49 cm
11 1
Σ
σ = ± = ±
−
Brigada 1 225,25 225,32 225,30 225,35 225,27 225,28 225,28 225,28
Brigada 2 225,26 225,26 225,30 225,30 225,32 225,27 225,27 225,29 225,29 225,29 225,34
¿Cuál de las dos brigadas tiene resultados más fiables?

104. CLASE 3

105. El teodolito
135
135
135
135
135
Es un aparato que posee múltiples usos en topografía, se usa principalmente para medir ángulos
horizontales y verticales, alineación de puntos en un plano horizontal o vertical, así como medida
aproximada de distancias por medio del principio de estadia.
EJES PRINCIPALES DE UN TEODOLITO
Eje principal.- Es la línea imaginaria alrededor del cual gira la alidada, además de pasar por el centro del
limbo horizontal.
Eje horizontal.- Es la línea imaginaria alrededor del cual gira el anteojo, además de pasar por el centro
del limbo vertical.
Eje de colimación.- Es la línea que une el cruce de los hilos del retículo con el centro óptico del
objetivo.

106. El teodolito
140
COMPONENTES CLÁSICOS DE UN TEODOLITO
A) Base
Constituida por:
(1) Una plataforma que involucra los tornillos nivelantes.
(2) El limbo horizontal, que contiene el transportador respectivo, el cual puede girar respecto al eje
principal,sinembargodichomovimientopuedeserbloqueadoporeltornillodefijacióndelabase.
B) Alidada
Constituida por:
(3) UnaestructuraenformadeYquevamontadasobrelabaseypuedegirarrespectoalejeprincipal,sin
embargo dicho movimiento puede ser bloqueado por el tornillo de fijación de la alidada.
(4) El anteojo (telescopio) que puede girar respecto al eje horizontal; dicho movimiento puede ser
bloqueado por el tornillo de fijación del anteojo.

107. El teodolito
141
(5) El limbo vertical, que contiene al respectivo transportador, cuyo centro coincide con el eje
horizontal del anteojo.
OBJETIVO FUNDAMENTAL DE UN TEODOLITO
La medición de ángulos es la tarea más importante que se realiza con un teodolito; para dicho efecto se
utilizan los llamados “limbos”, que son placas circulares de vidrio de algunos milímetros de espesor en
cuya superficie llevan grabados trazos o líneas muy finas que definen la graduación del transportador y
por ende del instrumento.
Generalmente un teodolito lleva dos limbos: vertical y horizontal.

108. El teodolito
142
ORGANIZACIÓN DE LOS LIMBOS
Creemos conveniente hacer público la
explicación que realiza El Ing. Carlos
Basadre. Un teodolito es un goniómetro
que está compuesto de una base T pro-
vista de tres tornillos nivelantes que lle-
va sobre una columna C un círculo o lim-
bo graduado H destinado a la lectura de
los ángulos acimutales. Alrededor del eje
YOY concéntrico con ese círculo giran
dos montantes o soporte sobre los cuales
reposan un anteojo LL y un círculo V. El
eje YY se llama eje vertical del teodolito,
el eje XX se llama eje horizontal. Para la
lectura de ángulos acimutales las mon-
tantes arrastran consigo la alidada hori-
zontal que lleva dos puntos de referencia
diametralmente opuestos RR1 (índices)
que pueden ser dos verniers o dos mi-
croscopios que permiten apreciar una
cierta subdivisión de la graduación del
limbo H. Para leer ángulos verticales ó
cenitales el anteojo LL gira alrededor del
eje XX, llevando en su movimiento una
segunda alidada SS, en la cual por medio
de verniers o de microscopio puede tam-
bién apreciarse una cierta subdivisión del
círculo V.
Errores debido a los limbos
A) Falta de uniformidad de las divisiones
Generalmente por muy eficiente que sea la fabricación de estos limbos, la distancia angular entre
cada división no es exactamente igual.
Se reduce el error aplicando el método de reiteración.
B) Desviación de índices
Los índices de la alidada no están rigurosamente en los extremos opuestos de un diámetro. Dicha
desviación es siempre constante para cualquier lectura (fig. a).
Se reduce el error tomando lecturas en los ìndices supuestamente opuestos, para luego calcular la
media.

109. El teodolito
143
C) Error de Excentricidad
El centro del círculo no coincide con el centro de rotación de la alidada (fig. b).
Este error es variable según la dirección de la visual, el error se puede eliminar empleando el mismo
método que en el caso de desviación de índices.
Ejemplo:
Desde una estación se ha visado un punto y se han tomado lecturas diametralmente opuestas:
12 10' 20
° y 192 10' 00
° ; determinar la lectura libre de errores por desviación de índices y por
excentricidad.
Solución:
Lectura corregida =
(12 10' 20 192 10' 00) 180
2
° + ° − °
Lectura corregida = 12 10' 10
°
MICRÓMETRO
Consiste en un microscopio cuyo objetivo es de observar ampliada las graduaciones del limbo a leer; la
mayoría lleva consigo una escala graduada que se superpone a la imagen que se recibe del limbo.
La graduación del microscopio coincide con la del limbo.
Tipos de micrómetros
A) De observación directa
Constituido solamente de un microscopio que permite leer directamente los trazos del limbo.
121° 40' 372
g
60
c
Fig. a Fig. b

110. El teodolito
144
B) Micrómetro de estima o escala
Consiste en un microscopio provisto de una escala cuya extensión es igual a una división del limbo.
C) Micrómetro óptico de estima
La alidada está provista del eje L1L2 que divide
al limbo en dos partes iguales, dicho eje, en la
práctica cumple la función de índice en cada
extremo.
La lectura buscada es T1 + a1.
El sistema óptico traladada el lado opues-
to T2 + a2 a una posición tangente a la
primera (fig. a).
Las fig (b) y fig (c), muestra la imagen que el
micrómetro ofrece al observador.
La lectura final es T1 más la semisuma de a1 y
a2, es decir
+
 
+
 
 
1 2
1
a a
T
2
.
Como se verá este método duplica la aprecia-
ción y anula los errores tanto de índice como
de excentricidad.
32° 46' 143,12
g
= 143
g
12
c
232° 12' 40
Fig. a

111. El teodolito
145
D) Micrómetro óptico de coincidencia
Es una especie de versión mejorada del micrómetro óptico de estima.
Consiste en usar el sistema de placas de vidrio plano paralelos.
El proceso es el siguiente:
1° Se realiza la lectura preliminar empleando el método de micrómetro óptico de estima.
2° Con ayuda del tornillo micrómetrico se desplazan opticamente y en sentido contrario
ambas imágenes hasta conseguir la coincidencia de los trazos de ambos semicírculos;
este desplazamiento es medido por el tambor ubicado adyacentemente, el cual indica
la lectura adicional gracias a la coincidencia y no a la estima.
+
° + = °
;
1 2
a a 90'
90'
63 63 45'
2
+
+ =
; c
1 2
c
g g c
a a 70
70
82 82 35
2
+
°
°
°
63 40'
8
0 00, 0
000 0 ,
' 38
63 48' 3
0
0 8, 0
Lectura final:
Lectura estimada:
63° 45'
Fig. b Fig. c

112. El teodolito
146
E) Micrómetro encuadrado
El índice de la alidada está constituida por una “doble línea”. Una vez bloqueada la alidada y obtenida
la lecturaestimada(fig.d yfig.e) ;conayudadeltornillomicrométricoserealizalacoincidenciaentreel
índice de la alidada y uno de los trazos del círculo (solo es posible la coincidencia a una línea); el
desplazamiento angular realizado para el encuadre es medido en el tambor micrométrico.
Ejemplo 2
Ilustración del fenómeno fisíco
27° 23' 40
364
g
76
c
ç
ç
Fig. d
Fig. e
Ejemplo 1

113. El teodolito
147
Ejemplo 3
Existen micrómetros donde el índice de la alidada está constituida por una sola línea
mientras que las graduaciones por dos.
Observación
Ejemplo 4
PUESTA EN ESTACIÓN DEL TEODOLITO
214 20'
5' 37,5
2
37,5
2
14 25' 37,5
14 0
° +
°
°
g C
C CC
g C C
g
C
15 60
11
37,
76
15 71
1
76
5
+
1° Se sueltan los tornillos de las patas del trípode; para luego juntar estas últimas tal como se
muestra, (fig. a) hasta que la superficie de la plataforma coincida aproximadamente con la
quijada del operador, en dicha posición se ajustan los tornillos antes mencionados.
2° Se extienden las patas del trípode sobre el punto topográfico tratando de colocar la plataforma de
éste en posición aproximadamente horizontal (fig. b).
3° Se instala el teodolito en el trípode con ayuda del tornillo de sujeción (fig. c).
Fig. a Fig. b Fig. c

114. El teodolito
148
4° Se realiza la coincidencia aproximada del eje vertical respecto al punto topográfico.
5° Llevar a cabo el centrado exacto del eje vertical respecto al punto topográfico.
Para ello existen dos métodos:
A) Soltar ligeramente el tornillo de sujeción para luego desplazar el teodolito respecto al trípode lo
necesario hasta hacer coincidir el eje vertical con el punto topográfico.
Mover el equipo respecto a una de las patas hasta que
el punto topográfico se encuentre muy cerca del eje
vertical.
Se recomienda al operador, colocar uno de sus pies
adyacentes al monumento para que la ubicación del
mismo se realice en menos tiempo.

115. El teodolito
149
B) Con ayuda de los tornillos nivelantes se consigue el centrado exacto.
6° Se realiza el calado del nivel esférico (nivelación aproximada del limbo horizontal) con
ayuda de las patas del trípode.
Se aproxima la burbuja al centro
del círculo. Esta operación se eje-
cuta aflojando el tornillo de la pata
que más se acerque a la dirección
radial de la burbuja, para luego
cambiar la longitud de la misma
según la posición de la burbuja.
Con el operador en la siguiente
pata, se repite el proceso anterior.
Se recomienda hacer uso de tan
solo dos patas.

116. El teodolito
150
7° Se lleva a cabo el centrado del nivel tubular (nivelación precisa del limbo horizontal) con
ayuda de los tornillos nivelantes.
Girar la alidada
aproximadamente
90° (100g
) respecto a
la posición inicial,
con ello la burbuja
volverá a descen-
trarse; coger el tercer
tornillo nivelante
hasta calar completa-
mente la burbuja.
8° Verificar la posición del punto topográfico en la plomada óptica; si el eje vertical se encuentra en
coincidencia con el punto en cuestión, la puesta en estación a culminado, de lo contrario es
necesario realizar la corrección haciendo uso del 5° paso (caso A).
Se ubica la línea rec-
ta que une dos tor-
nillos nivelantes cua-
lesquiera paralela al
eje longitudinal del
nivel tubular, para
luego girar simultá-
neamente ambos
tornillos ya sea hacía
afuera o hacía aden-
tro hasta centrar la
burbuja.
Final
Final
Inicial
Inicial

117. El teodolito
151
CLASIFICACIÓN DE LOS TEODOLITOS SEGÚN EL MÉTODO
PARA MEDIR ÁNGULOS HORIZONTALES
1. Teodolitos repetidores
Están constituidos por doble eje.
– El eje de rotación de la base; alrededor del cual puede girar la estructura que contiene al
transportador horizontal conjuntamente con éste.
Para bloquear dicho movimiento, basta ajustar el tornillo de fijación de la base.
Para activar el movimiento lento de la base, primero se ajusta el tornillo de fijación respectivo
para luego girar el tornillo tangencial correspondiente.
– El eje de rotación de la alidada, alrededor del cual puede girar la alidada.
Para bloquear el movimiento de rotación de la misma, basta ajustar el tornillo de fijación de
la alidada.
Para activar el movimiento lento, primero se ajusta el tornillo de fijación de la alidada para luego
girar el tornillo tangencial correspondiente.
Estos teodolitos han sido creados para poder aplicar en el campo el método de repetición
(ver pag. 195).

118. El teodolito
152
El Teodolito Repetidor

119. El teodolito
153
Medición de un ángulo horizontal
Para medir el ángulo horizontal ABC, se realiza la siguiente operación.
1° Se estaciona el teodolito sobre el punto “B”.
2° Determinación del 0° 0' 00.
– Con ayuda del tornillo micrométrico se
colocalaescalamicrométricaencero.
– Se bloquea el tornillo de fijación de la base y
se suelta el tornillo de fijación de la alidada.
– Se coloca aproximadamente en cero la
lectura del transportador horizontal;
esto se consigue con el movimiento gi-
ratorio de la alidada.

120. El teodolito
154
– Se lleva exactamente a cero la lectura del
transportador horizontal; para ello se re-
curre al movimiento de la tangencial de
la alidada bloqueando previamente el
respectivo tornillo de sujeción.
3° Traslado del 0° 0' 00 a la dirección BA.
– Se bloquea el tornillo de fijación de la alida-
da y se suelta el tornillo de fijación de la
base.
– Se dirige la visual aproximadamente
hasta el punto A.
– Con ayuda de la tangencial de la base,
se realiza la ubicación exacta del men-
cionado punto, bloqueando previamen-
te el respectivo tornillo de sujeción.
– Dado que la alidada está sujeta a la base; el
ángulo 0° 0' 00 permanecerá congelado.
Base suelta y alidada ajustada

121. El teodolito
155
4° Medición del ángulo ABC.
– Se bloquea el tornillo de fijación de la base y se suelta el tornillo de fijación de la alidada.
– Se dirige la visual aproximadamente hacía el punto C (fig. a); con ayuda de la tangencial
de la alidada, se realiza la ubicación exacta del mencionado punto (fig. b), bloqueando
previamente el respectivo tornillo de sujeción.
5° Se lee el ángulo
Base ajustada y alidada suelta.
45° 40' 40
Fig. a Fig. b

122. El teodolito
156
2. Teodolitos reiteradotes
Se les llaman también direccionales; el transportador horizontal se encuentra fijo a la “base
inmóvil”. Dicho círculo solo puede ser girado por acción del tornillo del transportador horizontal.
Están constituidos por un eje:
– El eje de rotación de la alidada; alrededor del cual puede girar la alidada.
Para bloquear el movimiento de rotación de la misma, basta ajustar el tornillo de fijación de la
alidada.
Para activar el movimiento lento, primero se ajusta el tornillo de fijación de la alidada
para luego girar el tornillo tangencial correspondiente.

123. El teodolito
157
El Teodolito Reiterador

124. El teodolito
158
Medición de un ángulo horizontal
Para medir el ángulo horizontal ABC, se realiza la siguiente operación.
1° Se estaciona el teodolito en el punto “B”
2° Determinación de la dirección BA.
Se dirige la visual aproximadamente hacía el punto “A” (fig. a); con ayuda de la tangencial de la
alidada, se realiza la ubicación exacta del mencionado punto, bloqueando previamente el
respectivo tornillo de sujeción (fig. b).
Fig. a
Fig. b

125. El teodolito
159
3° Determinación aproximada del ángulo de
partida en la dirección BA
– Con ayuda del tornillo micrométrico se
colocalaescalamicrométricaencero.
– Mediante el tornillo del transporta-
dor horizontal, intentar la coinciden-
cia entre el ángulo de partida (ejem-
plo 0° 0' 00) con el índice.
En la práctica esta operación es muy
tediosa por lo que se recomienda
aproximar lo mejor que se pueda al
ángulo de partida.
– Mediante el tornillo micrométrico, hacer
coincidir el cero del transportador con el
índice; el desplazamiento realizado será
reflejado en la escala micrométrica.
En nuestro ejemplo el ángulo de partida
es: 0° 24' 20.
4° Medición del ángulo ABC
Se suelta el bloqueo de la alidada y se dirige la
visual aproximadamente hacía el punto C (fig.
c); con ayuda de la tangencial de la alidada, se
realiza la ubicación exacta del mencionado
punto (fig. d), bloqueando previamente el res-
pectivo tornillo de sujeción.
5° Se lee el ángulo
El ángulo ABC quedará definido por la
diferencia entre la lectura final y el án-
gulo de partida.
Fig. c
Fig. d

126. El teodolito
160
ÁNGULOS VERTICALES CON EL TEODOLITO
La medida de ángulos verticales se lleva a cabo, gracias a la acción conjunta del limbo vertical (eclímetro)
y el anteojo (telescopio).
De acuerdo a la posición del cero del círculo vertical, existen varios tipos de teodolitos; los más usados
son los cenitales a los cuales haremos referencia.
Los pasos a seguir para medir un ángulo vertical son:
1° Se estaciona el teodolito sobre el punto topográfico.
2° Se ubica el punto por medir con el anteojo en posición direc-
ta (limbo vertical a la izquierda del operador), para luego
calar el nivel tubular del eclímetro; este último se realiza
con el fin de colocar el círculo vertical en posición correcta.
El nivel tubular del eclímetro se
cala con el tornillo del nivel tubular
eclimetral.
Anteojo en posición directo
Ángulo vertical = α
Ubicación del punto por medir

127. El teodolito
161
3° Se ubica el punto por medir con el anteojo en posición inverso (limbo vertical a la derecha
del operador); para luego calar nuevamente el nivel tubular del eclímetro y tomar lectura.
4° El ángulo vertical final se calcula mediante el promedio de los dos ángulo:
Ángulo vertical =
( ) ( )
α + ° − β α + − β
g
360 400
=
2 2
Nótese que teóricamente: α + β = 360° = 400
g
Observaciones
– Para cada lectura del ángulo vertical es imprescindible centrar la burbuja del nivel
tubular eclímetral.
– Se recomienda medir el ángulo vertical con las dos posiciones del anteojo (directo e inver-
tido)paraeliminaroreducirelerrorporíndicedellimborespectivo.
Anteojo en posición invertido
Ángulo vertical = β
Invertir el anteojo Girar la alidada hasta ubicar el punto buscado

128. El teodolito
162
Compensador automático del eje vertical
Los teodolitos modernos cuentan con un compensador automático de verticalidad (controlado por la
gravedad) que coloca en posición correcta la escala vertical cuando el instrumento está totalmente nivela-
do; es decir, muestran la lectura del círculo vertical referido a la dirección de la gravedad, sin importar las
pequeñas inclinaciones del eje principal del equipo.
Los teodolitos más precisos cuentan con un compensador de doble eje que garantiza la lectura
no solo de los ángulos verticales, sino también de los horizontales.
Las pequeñas inclinaciones del eje principal son corregidas automáticamente por medio de un prisma de péndulo
que está incluido en el haz de rayos luminosos de lectura del círculo vertical. El péndulo está colgado en cintas de
bronce especialmente fabricadas para protegerlo de las sacudidas. la amplitud de sus oscilaciones es de 5 minutos
de arco, en promedio.

129. El teodolito
163
Teodolito con compensador automático y con micrométro
de estima o escala.
Teodolito con compensador automático y con mi-
crómetro óptico de coincidencia.
MICRÓMETRO MICRÓMETRO

130. El teodolito
164
AJUSTES Y COMPROBACIONES DEL TEODOLITO
En el proceso de medición es importante contar con equipos calibrados para dicho efecto.
Esto significa que todo equipo debe estar en constante mantenimiento, sin embargo los desgastes de
piezas móviles, no pueden mantenerse de manera permanente, conveniendo que sean ajustables por el
propio operador. Los ajustes del instrumento deben comprobarse con frecuencia durante el trabajo, no
mereciendo veracidad una operación topográfica en la que se haya empleado instrumentos que no están
debidamente comprobados.
Todo ajuste consta de dos partes: La prueba para determinar el error, y la corrección para eliminarlo.
Cuando todos los ajustes necesitan corrección solo se llega a un buen resultado final repitiendo dos
o más veces, sucesivamente, todos los ajustes. Esto se debe a que el ajuste de una de las partes puede
afectar en algo la de otra, de manera que el trabajo final en la corrección de un instrumento es comprobar
sucesivamente la exactitud de todos los ajustes.
La mayor parte de veces los ajustes se hacen moviendo por medio de una barrita de acero (puede
reemplazarse en caso necesario por una aguja de acero de las que se emplean para tejer hilo, partida por la
mitad), tornillos de cabeza cilíndrica provistos de huecos, dentro de los cuales penetra la barrita y hace el
efecto de palanca, los ajustes resultarán más permanentes si los tornillos que sirven para realizarlos
permanecen en contacto perfecto con las superficies sobre las cuales actúan; por lo que conviene “apretar”
los tornillos un poco con la barra de acero, digamos haciéndolos girar 20° después de que están en contacto
Teodolito con compensador automático y con micrémetro encuadrado.
MICRÓMETRO

131. El teodolito
165
con esas superficies; hay que considerar sin embargo que no debe emplearse sino una presión moderada
a fin de no malograr el hilo del tornillo, que es de metal relativamente blando (bronce).
Es preciso confesar que esta introducción referida a los ajustes del teodolito, pertenece al Inge-
niero Carlos Basadre.
Principales ajustes
1. Coincidencia del eje principal con la vertical.
Comprobación
Cuando la burbuja del nivel tubular o tórica de la alidada está totalmente
calada. el eje principal debe coincidir con la vertical.
Instalado el equipo, se lleva el eje del nivel tubular, paralelo a
la línea que une dos tornillos nivelantes; en caso de producir-
se una descorrección, usar los dos tornillos mencionados.
Se gira la alidada 180°
Si la burbuja se desplaza concluimos que el equipo está
descorregido, de lo contrario se encuentra ajustado

132. El teodolito
166
Corrección
Corregir la mitad del desfase con
ayuda de los tornillos nivelantes.
La otra mitad se corrige con los
tornillos de ajuste del nivel.
A continuación girar la alidada 90°; cualquier desviación de la burbuja, se elimina con el tercer
tornillo nivelante. La operación total se repite hasta que la burbuja permanezca centrada para
cualquier posición del eje del nivel tubular.
Tomar la lectura del arco desfasado.
2. Eliminar o evitar el paralaje de los hilos del retículo.
La comprobación y/o ajuste por paralaje es completamente personal y depende de las características
ópticas del operador.
Un teodolito ajustado para una persona, se presenta cuando el plano del
retículo coíncide con el plano de la imagen del objeto: A'B'

133. El teodolito
167
Comprobación
Se dirige el anteojo hacia una parte del cielo y se regula el ocular hasta ver con toda nitidez los hilos del retículo.
Corrección
Se corrige moviendo ligeramente el ocular y si fuera necesario el enfoque hasta conseguir que
no exista paralaje. cada observador tiene que realizar la corrección del paralaje.
Se dirige el anteojo hacia un objetivo y se regula la imagen con el tornillo o abrazadera de enfoque hasta que el objeto se vea
con toda claridad.
Instrumento descorregido: cuando al mover rápidamente
el ojo hacia arriba y hacia abajo, detrás del ocular, se
desplaza también la imagen observada con respecto al
centro del retículo.
Instrumento ajustado: cuando al mover rápidamente el ojo
hacia arriba y hacia abajo, detrás del ocular, la imagen se
mantiene invariable con respecto al centro del retículo.

134. El teodolito
168
3. El eje de colimación debe ser perpendicular al eje horizontal.
Instrumento ajustado: θ = 90°
Instrumento descorregido: El hilo vertical del retículo
no coincide con el eje de simetría por lo que θ ≠ 90°
Seinstalaelteodolitoenunazonaestratégicamenteplanaydeun
radio aproximado de 100 metros destinado a zona de trabajo.
Comprobación
Se invierte el anteojo, y sin desplazar el eje de colima-
ción se ubica el jalón en un punto “B” con las mismas
características que “A”.
Con el anteojo en posición directo se ubica un jalón
ubicado a una distancia de 80 a 100 m.
A continuación se gira la alidada hasta ubicar aproxima-
damente el jalón en A. Con ayuda de los tornillos
tangenciales se ubica el jalón con precisión.

135. El teodolito
169
Corrección
Se invierte el anteojo retomando nuevamente la posición
directa; si el hilo vertical del retículo no coíncide con el
jalón, nos encontramos frente a un teodolito descorregido.
Se instala un jalón en la dirección del eje de colima-
ción de tal modo que BP = CP; a continuación se mide
la distancia horizontal entre B y C.
4. El eje horizontal debe ser perpendicular a la dirección de la gravedad.
Con ayuda de dos tornillos opuestos de ajuste del
retículo, se dirige la visual hasta un punto D; donde
BD = 1/4 BC (en la línea BC).
Se repite la operación tantas veces como sea necesario
hasta encontrar el ajuste correcto.
Fig. a : Instalado el teodolito y con anteojo directo se
dirige la visual hacia un punto “A” previamente marca-
do; a continuación, sin girar la alidada, se baja dicha
visual marcando un punto tal como “1”.
Fig. b : Sin cambiar de estación pero con anteojo inver-
tido se repite la operación de la fig (a). Si los puntos 2 y 1
coinciden, nos encontramos ante un instrumento ajusta-
do; de lo contrario el equipo está descorregido.

136. El teodolito
170
Corrección:
5. El hilo vertical del retículo debe coincidir con la dirección de la gravedad
(a): Instrumento ajustado
(b): Instrumento descorregido, dado que el hilo vertical no coincide con el cordel de la plomada.
Corrección:
Con ayuda de dos tornillos consecutivos se gira el retículo hasta hacer coincidir el “hilo vertical” con el cordel de
la plomada.
Se desplaza el centro filar de retículo hasta el punto A
gracias a los tornillos del eje horizontal; a partir de en-
tonces tendremos el equipo ajustado.
Sin cambiar de estación y con anteojo directo se ubica
el punto medio entre 1 y 2; B. Sin girar la alidada se
levanta la visual hasta que el hilo horizontal contenga al
punto A; llamaremos A' al centro filar.

137. El teodolito
171
6. La suma de las lecturas de un ángulo vertical medido en las dos posiciones del círculo debe
dar exactamente 360° (400
g
).
Comprobación
Estacionado el equipo, se ubica un punto en las
posiciones directa e inversa del círculo vertical.
Antes de efectuar las lecturas mencionadas, debe
centrarse el nivel tubular del eclímetro con el tor-
nillo respectivo.
La diferencia de la suma de las dos lecturas con-
tra 360° o 400g
respectivamente, representa el
doble del desajuste, del nivel del limbo verti-
cal, es decir, lo que se llama “error de índice”.
Ejemplo sexagesimal:
A. directo : 80° 18' 36
A. inverso : 279° 41' 36
SUMA : 360° 00' 12
2×Error : +12 (doble error de índice)
Error de índice : +06
Corrección por aplicar a cada lectura del círculo: –6
Corrección
Sin cambiar de estación el equipo, se vuelve a ubicar el
mismo punto con el anteojo en posición directo, obte-
niendo la misma lectura anterior.
Con ayuda del tornillo micrométrico se reduce (en
nuestro caso 6) el error de índice; obteniendo: 8' 30
en el micrométro, pero desajustando la lectura del
limbo vertical.

138. El teodolito
172
7. Ajuste correcto de la plomada óptica
Comprobación
Al girar el aparato alrededor de su eje vertical, el centro del retículo no debe salir de la marca del suelo.
Con ayuda del tornillo del nivel tubular eclímetral se rea-
liza la coincidencia del índice con los 80° 10'; regresando
así a la lectura corregida: 80° 18' 30; sin embargo el res-
pectivo nivel tubular habrá sufrido cierta descorrección.
El centrado del nivel tubular del eclímetro se realiza me-
diante el tornillo de ajuste respectivo.
Terminada la rectificación se recomienda efectuar una
medición de comprobación.
Corrección
Instalado el teodolito; girese 180° o 200
g
alrede-
dor del eje vertical. Si el centro del retículo ha
salido de la marca en el suelo, corrígase la mi-
tad de la distancia con la ayuda de los tornillos
de ajuste del retículo de la plomada óptica.

139. El teodolito
173
REGLA DE BESSEL
Consiste en medir un ángulo acimutal o vertical con anteojo directo e inverso, para luego
calcular el promedio de ambas lecturas; esta regla se utiliza para incrementar la precisión, así
como para controlar los errores angulares debido a desajustes y falta de calibración.
Ejemplo 1:
Se mide el ángulo acimutal BAC; obteniéndose
los siguentes datos de campo; calcular el ángulo
buscado.
Explicación esquemática del trabajo de
campo
1° Visando el punto B.
• Cálculo para el anteojo directo:
Ángulo BAC = 26° 32' – 0° 00'
Ángulo BAC = 26° 32'
• Cáculo para el anteojo invertido:
Ángulo BAC = 206° 31' – 180° 01'
Ángulo BAC = 26° 30'
• Ángulo promedio:
Ángulo BAC =
° + °
26 32' 26 30'
2
Ángulo BAC = 26° 31'
El mismo resultado se puede obtener con
la siguiente tabla:
Visando el punto “B” con anteojo directo; el índice R1
marca 0° 00' 00
Se invierte el anteojo, mientras tanto la lectura del índi-
ce R
1
no ha cambiado
Punto Lecturas acimutales
Visado Anteojo directo (A.D.) Anteojo invertido (A.I.)
B 0° 0' 180° 01'
C 26° 32' 206° 31'
Punto Lecturas acimutales
Visado A.D. A.I. Promedio Ángulo
B 0° 0' 180° 01' 0° 0',5 26° 31'
C 26° 32' 206° 31' 26° 31',5
Lectura = 0° 0' 00
Lectura = 0° 0' 00

140. El teodolito
174
Se gira la alidada en sentido horario hasta ubicar con la
visual el punto B. La lectura del índice R1
es 180° 01'
2. Visando el punto C.
Se gira la alidada en sentido horario hasta ubicar con la
visual el punto C. La lectura del índice R1
es 206° 31'.
Visando el punto “C” con anteojo directo; el índice R1
marca 26° 32'
Se invierte el anteojo, mientras tanto la lectura del índi-
ce R
1
no ha cambiado
Ejemplo 2
Utilizando un teodolito cenital se mide el ángu-
lo vertical para el punto P; obteniéndose el si-
guiente dato de campo; calcular la lectura final.
• Ángulo final = [42° 27' + (360° – 317° 31')]/ 2
Ángulo final = 42° 28'
Explicación esquemática del trabajo de campo
1. Visando el punto “P” con anteojo directo.
Visando el punto “P” con anteojo directo; el índice S1
marca 42° 27'
Lectura = 180° 01'
Punto Lectura Vertical
Visado Anteojo directo (A.D.) Anteojo invertido (A.I.)
P 42° 27' 317° 31'
Lectura = 42° 27'
Lectura = 26° 32'
Lectura = 26° 32'
Lectura = 206° 31'

141. El teodolito
175
EL TEODOLITO ELECTRÓNICO
Permite obtener el valor de la medida angular en una pantalla digital de cristal cuarzo.
A diferencia de los teodolitos ópticos mecánicos, estos poseen limbos codificados acompañados de un
sensor electrónico que permite convertir los valores analógicos en digitales.
En la actualidad existen dos sistemas de lecturas.
A) El sistema incremental
Consiste en medir la diferencia angular entre dos alineamientos, de manera que cuando
se coloque el 0° 00' 00 (si se desease) en un alineamiento, estará realmente marcando una
lectura aleatoria, al girar la alidada solidaria al limbo hasta ubicar el alineamiento busca-
do, el valor angular se habrá incrementado, sin embargo el sensor electrónico nos dará
como medida, la diferencia de lecturas.
El limbo de cristal que poseen estos aparatos están codificados mediante franjas transparentes y
oscuras, cuando gira el limbo, la luz atraviesa las zonas claras produciéndose un tren de ondas que
son contados por el fotosensor.
En realidad estos teodolitos al igual que los òpticos mecánicos también poseen una escala
adicional siempre compuesta por zonas claras y oscuras que permiten dar mayor precisión
a las lecturas.
Se invierte el anteojo, moviéndose solidario con éste el
índice S
1
Se gira la alidada acimutalmente al igual que el anteojo
respecto al eje horizontal hasta ubicar el punto P. La
lectura del índice S
1
es 317° 31'

142. El teodolito
176
Ilustración del principio físico
El sistema consiste en utilizar las dos rejillas de la escala codificada (el cual es un plato circular
completo paralelo al limbo codificado). Debido a que estos se encuentran desfasadas 90°, los
impulsos producidos aparecen con ese desfase, de tal manera que si la lectura correspondiente
a un período es de veinte segundos, al contar los impulsos producidos por la utilización conjun-
ta de las rejillas estos apreceran cada cinco segundos.
B) El sistema absoluto
Está basado en un limbo codificado, pero con un cero absoluto definido en alguna posición del
disco, de modo que cuando se ordene colocar el 0° 00' 00 en alguna dirección, el limbo girará
hasta ubicar dicho valor en el alineamiento establecido. Actualmente existen dos tipos del presen-
te sistema.
B-1) Sistema estático
Toma el nombre de estático (se le llama también contínuo), porque el fotosensor
permanece inmóvil, mientras el limbo gira solidariamente con la alidada. Al igual
que el teodolito óptico mecánico, estos también llevan consigo un micrómetro pero
electrónico que permite obtener valores finales de minutos y segundos.

143. El teodolito
177
Ilustración del principio físico
Con esto, los sensores del tipo óptico ofrecen una salida de señal codificados digitalmente.
B-2) Sistema dinámico
Consiste en un limbo similar al del sistema incremental (franjas transparentes y
oscuras), este posee dos fotosensores, uno que es fijo y establece el origen de la lectura,
mientras que el otro es móvil y gira junto con la alidada.
La codificación se fundamenta en el sis-
tema de códigos binarios.
Fuente: M. Angeles Hernandez Caro - Emilio Mata de Castro
GRAY (Binario)
Franja de codificación
Número digital G3 G2 G1 G0
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111

144. El teodolito
178
En realidad el limbo está compuesto de 2048 franjas iguales (1024 oscuras y 1024
transparentes) tanto las franjas oscuras y transparentes, pasan por delante de los
fotosensores, de tal manera que, cuando la luz emitida por el diodo emisor es refleja-
da por una franja transparente hacia el fotosensor receptor, éste genera una señal que
es transmitida a un circuito digital encargado de procesarla, mostrando en la pantalla el
valor de la lectura angular.
Es decir, la medida de un ángulo proviene de la exploración de todos los trazos del
limbo, eliminando así los probables errores por graduación y excentricidad.
°
φ =
360
1 024
El ángulo medido: {
φ = φ + ∆φ
!
o
Medición
Medición
precisa
aproximada
n
n = # de períodos (entero)
 
∆φ = φ
 
 
o
o
T
T
= desfase (se determina por comparación).
To = Período correspondiente al paso de una graduación
T = Tiempo total
Explicación
Los dos mediciones a realizar, número de intervalos de graduación φ0 y fracciones de éste, se harán
al mismo tiempo pero de manera independiente.
` Medición aproximada
Para contar el número de intervalos (φ0) comprendicos entre las cabezas lectoras (foto
sensores) CE y CM, se graba en el disco giratorio una marca de referencia, de tal modo
que, cuando esta marca pasa frente a un cabezal, se acciona un dispositivo que contará el
número de intervalos que pasa frente a la cabeza hasta que la marca de referencia pase al
otro cabezal, momento en el que se detendrá la cuenta y procesará la información.
` Medición precisa
Al tiempo que se realiza la cuenta de intervalos de graduación, se mide el desfase entre
las señales generadas por las cabezas lectoras, realizado en función de una medición de
tiempo.
Una vez procesadas las dos mediciones, se muestra el valor de la lectura a través de una
pantalla o se registra.

145. El teodolito
179
Teodolito electrónico TOPCON DT-101
Teodolito electrónico LEICA TC105
Descripción DT-101
Ampliación 30x
Imagen Derecha
Constante de estadía o aditiva 0
Constante diastimométrica de estadía 100
Distancia mínima de enfoque 0,9 m
Medida electrónica de ángulo
Método Incremental
Lectura mínima 1
Precisión 2
Plomada
Tipo Óptico
Sensibilidad del nivel
Nivel tubular 30/2 mm
Nivel circular 10'/2 mm
Compensador
Sistema Vertical automático
Rango de trabajo ±3'
DATOS TÉCNICOS
Descripción TC105
Ampliación 30x
Imagen Derecha
Constante de estadía o aditiva 0
Constante diastimométrica de estadía 100
Distancia mínima de enfoque 1,6 m
Medida electrónica de ángulo
Método Absoluto contínuo
Lectura mínima 1
Precisión 5
Plomada
Tipo Laser
Sensibilidad del nivel
Nivel tubular Electrónico
Nivel circular 6'/2 mm
Compensador
Sistema Vertical automático
Rango de trabajo ±4'
DATOS TÉCNICOS
Cortesía: Geincor SAC
Cortesía: Leica Geosystems

146. Medida de ángulos y direcciones
180
Teodolito electrónico SOKIA DT210
Teodolito electrónico PENTAX ETH-105A
Descripción DT210
Ampliación 30x
Imagen Derecha
Constante de estadía o aditiva 0
Constante diastimométrica de estadía 100
Distancia mínima de enfoque 0,9 m
Medida electrónica de ángulo
Método Absoluto contínuo
Lectura mínima 1
Precisión 2
Plomada
Tipo Óptico
Sensibilidad del nivel
Nivel tubular 20/2 mm
Nivel circular 10'/2 mm
Compensador
Sistema Dual automático
Rango de trabajo ±3'
DATOS TÉCNICOS
Descripción ETH-105A
Ampliación 30x
Imagen Derecha
Constante de estadía o aditiva 0
Constante diastimométrica de estadía 100
Distancia mínima de enfoque 0,85 m
Medida electrónica de ángulo
Método Incremental
Lectura mínima 5
Precisión 5
Plomada
Tipo Óptico
Sensibilidad del nivel
Nivel tubular 40/2 mm
Nivel circular 8'/2 mm
Compensador
Sistema Vertical automático
Rango de trabajo ±3'
DATOS TÉCNICOS

147. Medida de ángulos y direcciones
177
177
177
177
177
MEDIDA DE ÁNGULOS
Comúnmente los ángulos que se utilizan en topografía son de dos tipos: Horizontales y
verticales.
Sistema de unidades
A) Sistema sexagesimal
Resulta de dividir la circunferencia en 360 partes iguales llamados grados sexagesimales.
1 vuelta = 360° = 360 grados sexagesimales
1° = 60' = 60 minutos sexagesimales
1' = 60 = 60 segundos sexagesimales
B) Sistema centesimal
Resulta de dividir la circunferencia en 400 partes iguales llamados grados centesimales.
1 vuelta = 400g
= 400 grados centesimales
1 g
= 100m
= 100c
= 100 minutos centesimales
1 m
= 100S
= 100cc
= 100 segundos centesimales
C) Sistema milesimal
Resulta de dividir la circunferencia en 6 400 partes iguales llamados grados milesimales o
milésimas artilleras.
1 vuelta = 6 400∞
= 6 400 grados milesimales

148. Medida de ángulos y direcciones
182
D) Sistema radial
Un radián es la medida del ángulo central que subtiende en cualquier circunferencia un arco de
longitud igual al radio.
1 vuelta = 2π radianes
Relación entre los cuatro sistemas
1 vuelta = 360° = 400
g
= 6400
∞
= 2π rad
ÁNGULOS HORIZONTALES
Ángulo horizontal es la abertura formada por dos líneas que parten de un mismo punto,
proyectadas en un mismo plano horizontal.
Clase de ángulos horizontales
A) Ángulos a la derecha
Para la presente explicación se tendrá en consideración lo siguiente.
A : Punto topográfico antecesor.
B : Punto topográfico de estación.
C : Punto topográfico posterior.
El ángulo horizontal AOB, es la abertura radial respecto al punto “O” proyectado en un plano horizontal.

149. Medida de ángulos y direcciones
183
El ángulo a la derecha se caracteriza por medirse en el sentido de las agujas del reloj
(horario) partiendo del alineamiento que une el punto de estación (B) con el antecesor (A)
hasta llegar al alineamiento que une el punto de estación (B) con el posterior (C).
B) Ángulos de deflexión
Ángulo de deflexión en un punto de estación o vértice es el que se genera por la prolonga-
ción del alineamiento anterior con el siguiente.
– Si el sentido del ángulo es horario, se denota con la letra “D” y se le asume signo positivo.
– Si el sentido del ángulo es antihorario se denota con la letra “I” y se le asume signo negativo.
ÁNGULO VERTICAL
Es el ángulo que forma la línea vertical con la línea de referencia.
A continuación definiremos dos elementos importantes.
La figura muestra que la vertical correspondiente al punto “A”
tiene un Cenit y un Nadir.
Cenit (z)
Es aquel punto de encuentro entre la
vertical superior de un observador y
el infinito.
Nadir (n)
Es aquel punto de encuentro entre la
vertical inferior de un observador y el
infinito.

150. 184
Fig. b
θ
Fig. a
Azimut
Azimut

151. Medida de ángulos y direcciones
185
Rumbo
Es el ángulo horizontal agudo formado por el Norte o Sur y la línea de referencia. Se le llama
también rumbo directo.
Rumbo PA = N α E
Rumbo PB = S θ E
Rumbo PC = S γ W
Rumbo PD = N β W
Rumbo Inverso
Es el rumbo del sentido opuesto al alineamiento inicial, vale decir tomando como estación el
segundo punto de dicha línea.
Al rumbo N θ E de la línea de referencia AB, se le
llama rumbo directo de AB.
Al rumbo S α W de la línea BA (estación en B), se le
llama rumbo inverso de AB.
Conceptos Fundamentales
Eje polar geográfico
Es aquella línea recta que pasa por el centro de la Tierra y entorno a la cual esta última realiza su
movimiento de rotación (fig. a). Esta línea corta a la superficie terrestre en dos puntos: Polo Norte
Geográfico (PNG) y Polo Sur Geográfico (PSG).
Ecuador terrestre
Es aquel círculo máximo perpendicular al eje polar geográfico; dicho plano divide a la Tierra en dos
zonas: Hemisferio Norte y Hemisferio Sur (fig. a).

152. Medida de ángulos y direcciones
186
Magnetismo terrestre
La Tierra se comporta como un imán gigante. Cuando se cuelga una barra de imán de su
punto medio, ésta se orienta “aproximadamente” en la dirección del polo norte – sur geográ-
fico de la Tierra. La parte del imán que se dirige hacía el polo norte geográfico (PNG)
recibe el nombre de polo norte (N) y la parte que se dirige hacía el polo sur geográfico (PSG)
se llama polo sur (S), como la Tierra es considerado como un imán, entonces ésta tiene sus
polos norte y sur magnéticos, que son diferentes a sus polos norte y sur geográficos (fig. b).
En adelante por convención, se denotará Polo Norte Magnetico Terrestre al cual apunta al
norte del imán: PNM y al opuesto PSM.
Observación
Fig. a Fig. b

153. Medida de ángulos y direcciones
187
Meridianos
Meridiano geográfico (M.G.)
El M.G. de un punto de la superficie de la Tierra, es el círculo máximo que pasa por dicho punto y por
los polos Norte y Sur de la Tierra (fig. c).
Meridiana geográfica
Es la línea recta orientado tangente al meridiano geográfico en el punto en cuestión y que
pertenece al plano horizontal del lugar (N-S). Fig. d
Meridiano magnético (M.M.)
El M.M. de un punto de la superficie de la Tierra, es el círculo máximo que pasa por dicho punto
y por los polos Norte y Sur magnético de la Tierra, El M.M. que pasa por un punto varía con el
tiempo debido al cambio contínuo de posición de los polos (fig. e).
Meridiana magnética
Es la línea recta orientada tangente al meridiano magnético en el punto en cuestión y que pertenece al
plano horizontal del lugar (N-S). Fig. f
La meridiana magnética también cambia con el tiempo.
Fig. c Fig. d
Fig. e Fig. f

154. Medida de ángulos y direcciones
188
Declinación magnética (δ
δ
δ
δ
δ)
Es el ángulo horizontal que forman las meridianas geográfica y magnética en un punto.
La declinación magnética es diferente para cada lugar de la Tierra y variable respecto al tiempo
en un mismo punto debido al cambio contínuo de la meridiana magnética.
Los puntos de la superficie terrestre que tienen igual declinación magnética forman una línea
que toma el nombre de Isógona.
En un mismo punto, “δ” puede variar de Este
a Oeste.
∆δ = Variación de la declinación.
∆δ(+): Cuando crece al Este respecto al N.G.
∆δ(–) : Cuando crece al Oeste respecto al N.G.
La declinación Este se considera positiva y la Oeste negativa.
Meridiano de cuadrícula
Es aquella línea recta (eje Y) proveniente de la proyección transversal mercator universal:
UTM que es un sistema de coordenadas planas proveniente de la proyección ortogonal del
elipsoide de referencia sobre dicho plano.
El cilindro transversal es la tangente al elipsoide a lo largo del meridiano central del huso que se toma
como meridiano origen.

155. Medida de ángulos y direcciones
189
Convergencia de meridianos (ω
ω
ω
ω
ω)
Es el ángulo plano que forma la meridina geo-
gráfica con la de cuadrícula en un punto.
ω, es positiva cuando el norte de cuadrícula
está al Este del norte geográfico y negativa
cuando está al oeste.
PROYECCIÓN TRANSVERSAL MERCATOR UNIVERSAL
Al desarrollar el cilindro transversal, se generan líneas rectas perpendiculares a la línea ecuatorial limitadas hasta los
80° de latitud norte y sur. Dichas líneas rectas toman el nombre de meridiano de cuadrícula. Convencionalmente
se ha dividido el elipsoide en sesenta zonas de seis grados cada uno.
En el meridiano de origen y en la línea ecuatorial coinciden el norte geográfico con el de
cuadrícula.
Observación
Convergencia magnética (D)
Se le llama también desviación magnética.
Es el ángulo formado por la dirección norte magnético con la dirección norte de cuadrícula.
Es positiva al este del norte de cuadrícula y negativa al oeste del mismo.
∆D = Variación de la convergencia magnética.
∆D(+) : Cuando crece al Este respecto al N.C.
∆D(–) : Cuando crece al Oeste respecto al N.C.
La variación para la declinación magnética es igual al de la convergencia magnética para
un mismo intervalo de tiempo.
Observación

156. Medida de ángulos y direcciones
190
VARIACIÓN DE LA DECLINACIÓN MAGNÉTICA
La declinación magnética es variable con el espacio y el tiempo, en tal sentido podemos clasifi-
car dicha variación en periódica y geográfica.
A) Variaciones periódicas
Para un mismo lugar, la declinación varía contínuamente con el transcurso del tiempo;
estos se dividen en:
A-1) Variación secular
Es la más importante entre todas las variaciones periódicas; la declinación varía a lo
largo de los siglos y no existe en la actualidad un modelo matemático que calcule con
exactitud el valor de dicho cambio.
Según estudios científicos, esta variación se genera debido a la rotación de eje magné-
tico alrededor del geográfico en un período irregular promedio de 700 años.
Hoy en día se suele publicar en la zona inferior de las cartas la declinación del centro
de la hoja con la fecha de observación; así mismo se consigna el cambio promedio
anual (que viene a ser el cambio promedio de la variación secular para un año).
Estos datos nos permite actualizar la declinación desde la fecha de observación hasta
la presente; sin embargo debemos tener cuidado de apoyarnos en planos no muy
antiguos para asumir un incremento o decremento líneal.
A manera de ilustración se presentan los valores medios anuales de declinación toma-
dos en el observatorio magnético de Teoloyucan–México desde el año 1941 al 1993.
AÑO δ
δ
δ
δ
δ
1914 08° 49',6
1915 –
1916 08° 59',7
1917 09° 05',0
1918 09° 06',6
1919 09° 07',7
1920 09° 09',6
1921 09° 11',9
1922 09° 11',2
1923 09° 13',4
1924 09° 14',0
1925 09° 14',7
1926 09° 18',2
1927 09° 19',9
1928 09° 20',8
1929 09° 23',5
1930 09° 25',5
1931 09° 29',2
1932 09° 30',6
1933 09° 33',8
AÑO δ
δ
δ
δ
δ
1934 09° 36',1
1935 09° 37',5
1936 09° 39',0
1937 09° 39',4
1938 09° 40',0
1939 09° 40',7
1940 09° 41',8
1941 09° 40',9
1942 09° 41',5
1943 09° 39',5
1944 09° 38',5
1945 09° 39',1
1946 09° 37',0
1947 09° 37',2
1948 09° 28',4
1949 09° 25',0
1950 09° 21',6
1951 09° 18',7
1952 09° 15',7
1953 09° 14',6
AÑO δ
δ
δ
δ
δ
1954 09° 14',3
1955 09° 10',7
1956 09° 10',6
1957 09° 07',0
1958 09° 06',1
1959 09° 05',2
1960 09° 02',5
1961 08° 59',5
1962 08° 53',5
1963 08° 45',8
1964 08° 47',5
1965 08° 43',6
1966 08° 37',6
1967 08° 32',4
1968 08° 30',0
1969 08° 24',9
1970 08° 18',6
1971 08° 13',2
1972 08° 09',6
1973 08° 07',2
AÑO δ
δ
δ
δ
δ
1974 08° 03',0
1975 07° 55',4
1976 07° 47',5
1977 07° 39',1
1978 07° 33',7
1979 07° 36',4
1980 07° 41',4
1981 07° 43',0
1982 07° 35',0
1983 07° 32',4
1984 07° 30',3
1985 07° 18',8
1986 07° 25',8
1987 07° 22',9
1988 07° 19',9
1989 07° 20',0
1990 07° 15',7
1991 07° 11',7
1992 07° 07',0
1993 07° 03',4

157. Medida de ángulos y direcciones
191
VARIACIÓN SECULAR DE LA DECLINACIÓN (1914-1993)
EN EL OBSERVATORIO MAGNÉTICO DE TEOLOYUCAN – MÉXICO
A continuación se muestra un ejemplo de la
presentación de los datos concernientes a de-
clinación magnética consignado en las cartas,
ubicadas comúnmente en la zona inferior de la
hoja y correspondiente al centro de la misma.
Si quisieramos determinar la declinación
magnética para el 1 de Julio del 2005, ten-
dremos que sumar algebraicamente la varia-
ción secular para dicho tiempo.
∆t = (1 Julio 2005) – (1 de Enero 1982)
∆t = 23,5 años
δ
01/07/05
= δ
01/01/82
+
{
∆δ
δ
01/07/05
= (–3° 37') + (23,5)(–7',6)
δ
01/07/05
= (–3° 37') + − °
!
02 58'
δ
01/07/05
= – 06° 35'
Note Ud. que en veintitrés años y medio la
declinación magnética aumentó en promedio
02° 58'; sin embargo es posible obtener una
declinación actual mejor ajustada, trabajan-
do con un plano actualizado.
variación
secular
variación
secular
Generalmente los planos cartográficos nos dan
tres datos en tres sistemas; sexagesimal,
centesimal y milesimal; en el Perú, comúnmen-
te se utiliza el primero.
Como se aprecia; tenemos la declinación mag-
nética para el 1 de enero de 1982:
δ = –3° 37'
Convergencia de cuadrícula
ω = –2° 09' (–2g
38c
)(–38∞
)
Declinación magnética para
el 1 de enero de 1982
δ = –3° 37'(–4g
03c
)(–65∞
)
Variación anual de la decli-
nación
∆δ = –7',6 (–14
c
)(–2
∞
,2)

158. Medida de ángulos y direcciones
192
A-2) Variación anual
La declinación magnética varía a lo largo del año debido a la variación del campo
magnético terrestre a través del tiempo, como consecuencia de la interacción entre la
Tierra y los cuerpos celestes más cercanos a ella.
Como quiera que esta oscilación periódica es pequeña respecto a la precisión de la
brújula, en la práctica comúnmente se ignora.
A-3) Variación diaria
La declinación oscila desde la salida hasta la puesta del Sol una amplitud promedio
de 20 minutos sexagesimales.
La variación diaria es máxima en los meses de verano y mínima en invierno.
En nuestro país la hora más conveniente para trabajar es en promedio a las 10 horas
(tiempo universal).
A continuación se presenta la variación diaria de la declinación registrada en el
observatorio de Jicamarca – Perú, mediante un magnetómetro (28-05-2006).
MAGNETOGRAMA DE UN DÍA TRANQUILO JICAMARCA-PERÚ
(FUENTE: INSTITUTO GEOFÍSICO DEL PERÚ).
B) Variaciones geográficas
Para cada punto sobre la superficie de la
Tierra, la declinación es diferente.
Las líneas Isogónicas son aquellas que
unen puntos que tienen igual declinación.
La línea agónica es aquella que une
puntos cuya declinación es cero; esto
significa que en dichos puntos la meri-
diana magnética y geográfica se con-
funden en una línea.
El mapa que muestra las líneas
isogónicas y agónicas toma el nombre
mapa magnético o isogónico. MAPA ISOGÓNICO 1976
Polo Norte Magnético
Polo Sur Magnético

159. Medida de ángulos y direcciones
193
Si no existiesen las variaciones perió-
dicas o similares; dicho mapa sería
invariable en el tiempo; sin embargo
es preciso actualizar constantemen-
te este documento dado la variación
periódica contínua; por tal razón se
suele consignar la fecha de publica-
ción en todo mapa magnético.
La variación de la declinación por kiló-
metro es en promedios de 25 segundos
sexagesimales por lo que puede consi-
derarse constante para un radio de has-
ta 25 km dada la apreciación de la brújula.
Fenómenos que afectan la declinación magnética
En algunos casos, la aguja de la brújula no se orienta en la dirección de la meridiana magnética
como es de esperar; es más, hay ocasiones en que para una misma estación la aguja se orienta en
diferentes direcciones para cada observación; esto se debe específicamente a dos factores:
A) Atracción local
Debido a la presencia de cuerpos magnéticos y/o ondas electromagnéticas que perturban el
campo magnético terrestre y por ende la aguja de la brújula.
Son casos típicos, la presencia de vetas de minas cercanas a la zona del levantamiento; la cercanía
de objetos metálicos y/o artefactos que emitan ondas electromagnéticas (radios, telefonos,
computadoras, etc.), la presencia de líneas de alta tensión.
En general a exepción de las zonas mineras, la atracción local se puede evitar, prescindiendo de
los objetos metálicos y/o artefactos que emitan ondas electromagnéticas.
Una de las formas de verificar la presencia o ausencia de este fenómeno, es midiendo el rumbo directo e
inverso de una línea; si la diferencia es sustancial (grados), estaremos en un caso típico de atracción local.
ESTADOS UNIDOS MEXICANOS
MAPA ISOGÓNICO 1995
MAGNETOGRAMA DE UN DÍA TEMPESTUOSO
JICAMARCA – PERÚ (FUENTE: INSTITUTO GEOFÍSICO DEL PERÚ)
B) Fenómenos accidentales
La declinación en un estación pue-
de cambiar temporalmente debi-
do a la presencia de tormentas mag-
néticas, auroras boreales, manchas
solares. Su duración no es mayor
de un día y su amplitud puede ser
muy variable e importante.
Se recomienda no usar brújula
en dichos días.

160. Medida de ángulos y direcciones
194
Ejemplos de aplicación
Ejemplo 1
Si la declinación en un lugar para 1990 era 1°
23' W y decrece 8',5 anualmente; obtener la
declinación para el 1 de Julio del 2 004.
Solución:
Dado que la declina-
ción para 1 990 es al
Oeste y su variación
anual decrece, se de-
duce que esta última
está dirigida al Este.
Con lo cual:
• δ
01/07/04
= δ
01/01/90
+ ∆δ
δ
01/07/04
= –1° 23' + t(0° 8',5) ...... (1)
• Calculando t:
t = (1/07/04) – (01/01/90) = 14,5 años
• t en (1)
δ
01/07/04
= –1° 23' + (14,5)(0° 8',5)
δ
01/07/04
= +0° 40'
ó δ
01/07/04
= 0° 40' E
Graficando:
Ejemplo 2
Según una carta publicada el 1 de enero de
1 960, se tienen los siguientes datos para el
centro de la hoja:
δ = 0° 32' E
D = 0° 50' E
Variación anual = – 6'
Se pide:
A) La convergencia magnética para el 30 de
Septiembre del año 2 000
B) La declinación magnética para el 30 de Sep-
tiembre del año 2 000
C) La convergencia de meridianos para el 01
de enero de 1 960
D) La convergencia de meridianos para el 30 de
Septiembre del año 2 000
Solución:
A) D
30/09/00
= ?
• Calculando el tiempo
t = (30/09/00) – (01/01/60)
t = 40,75 años
• D
30/09/00
= D
1/01/60
+ ∆D
D
30/09/00
= +0° 50' + t(–0° 06')
D
30/09/00
= +0° 50' + 40,75(–0° 06')
D
30/09/00
= –03° 14'
ó D
30/09/00
= 03° 14' W

161. Medida de ángulos y direcciones
195
B) δ30/09/00
= ?
• t = 40,75 años
• δ30/09/00
= δ1/01/60
+ ∆δ
δ30/09/00
= +0° 32' + t(–0° 06')
δ30/09/00
= +0° 32' + 40,75(–0° 06')
δ30/09/00
= –03° 32'
ó δ30/09/00
= 03° 32' W
Graficando:
Graficando:
C) ω
01/01/60
= ?
Del gráfico: ω = –18'
El signo negativo indica que la meridiana de
cuadrícula está ubicada al Oeste de la meridia-
na geográfica.
D) ω
30/09/00
= ?
Ubicando la con-
vergencia magné-
tica (D) y la decli-
nación magnética
para el 01/01/60
Ubicando la con-
vergencia magné-
tica (D) y la decli-
nación magnética
para el 30/09/00
Del gráfico: ω = –18'
Ejemplo 3
Según la carta editada el 1 de enero de 1995; se
tienen los siguientes datos:
δ = 3° 46' E
D = 3° 00' E
Variación anual = – 8'
Se pide:
A) La convergencia magnética para el 09 de
agosto de 1999
B) La declinación magnética para el 09 de
agosto de 1999
C) La convergencia de meridianos para di-
cho lugar.
Laconvergenciademeridianosparaunmis-
mo lugar es constante, dado que es
indenpendiente del tiempo.
Estosedebeaquelameridianageográficay
decuadrículasonfijosrespectoaltiempo.
Observación

162. Medida de ángulos y direcciones
196
Solución:
A) D09/08/99
= ?
• Calculando el tiempo
t = (09/08/99) – (01/01/95)
t = 4,6 años
• Calculando ∆D
∆D = t(–0° 08') = (4,6)(–0° 08')
∆D = –37'
• D09/08/99
= D01/01/95
+ ∆D
D09/08/99
= +3° 00' + (–0° 37')
D09/08/99
= +02° 23'
ó D09/08/99
= 02° 23' E
Graficando:
B) δ
09/08/99
= ?
• ∆δ = –37'
• δ
09/08/99
= δ
01/01/95
+ ∆δ
δ
09/08/99
= +03° 46' + t(–0° 37')
δ
09/08/99
= +03° 09'
ó δ
09/08/99
= 03° 09' E
Graficando:
C) ω = ?
Analizando las
meridianas para
el 01/01/95
De donde: ω = +46'

163. Medida de ángulos y direcciones
197
INCLINACIÓN MAGNÉTICA ( i )
Es el ángulo plano vertical que forma la brújula (cuando está suspendida de su centro de gravedad) y el
plano horizontal respectivo.
Análisis de la inclinación magnética
– Cuando la brújula se sitúa en el punto A(Ecuador); los polos magnéticos se encuentran ubicados
simétricamente respecto a la brújula; por tal motivo ésta no sufre desviación vertical alguna (i = 0).
– Cuando la brújula se sitúa en el punto B; el polo norte de la brújula, se ve atraído con
mayor intensidad por el polo norte magnético de la Tierra; sucediendo lo contarrio en el
otro extremo, por tal razón la brújula se inclina hacía la zona de mayor atracción, gene-
rando así la inclinación magnética.
– Cuando la brújula se sitúa en el punto C (polo norte magnético); la inclinación magnética se hace 90°.
– Cuando la brújula se sitúa en el punto D; el polo sur de la brújula se ve atraído con
mayor intensidad por el polo sur magnético de la Tierra; sucediendo lo contrario en el
otro extremo; por tal razón la brújula se inclina hacía la zona de mayor atracción
generando así la inclinación magnética.
– Cuando la brújula se sitúa en el punto E (polo sur magnético); la inclinación magnética se hace 90°.
– Las líneas sobre la Tierra que unen puntos de igual inclinación magnética toman el nombre
de Isoclinas.
Preguntas y Respuestas
¿Cómo se determina en el campo, la dirección de la meridiana magnética en un punto?
Comúnmente se determina con ayuda de la brújula, dado que ésta es sensible a la acción del
campo magnético terrestre.
No olvidarse de tomar la precaución necesaria para evitar la acción de la atracción local y posibles
fenómenos accidentales.
¿Cómo se determina en el campo, la dirección de la meridiana geográfica en un punto?
El método más recomendable es el de visaciones al sol.

164. Medida de ángulos y direcciones
198
¿Cómo se determina en el campo, la dirección de la meridiana de cuadrícula en un punto?
1° Caso: Teniendo como datos la dirección de la meridiana geográfica y la convergen-
cia de meridianos.
Sólo tendremos que estacionarnos con el teodolito en el punto en cuestón, alinear la visual
al norte geográfico, por último girar la alidada (en sentido antihorario) según el valor y
signo de la convergencia. El alineamiento final de la visual indicará el norte de cuadrícula.
2° Caso: Teniendo como datos las coordenadas del punto en cuestón así como también la de otro
punto visible desde la primera (ambas en coordenadas UTM bajo el mismo datum).
Al conocer las coordenadas de ambos puntos es posible calcular el acimut de
cuadrícula de la línea que las une.
Ya en el campo, se hace estación en el punto en cuestión, se dirige la visual hacía el
segundo punto; por último se gira la alidada en sentido antihorario según el valor
del acimut de cuadrícula. El alineamiento final de la visual indicará el norte de
cuadrícula.
¿Cómo se determina la convergencia de meridianos en cada lugar?
Para dicho efecto, es imprescindible conocer las coordenadas planimétricas del punto
de estación. Con dichos datos, es posible calcular “ω” según fórmulas establecidas,
tablas o softwares.
¿Cómo se determina la declinación y la inclina-
ción magnética para una fecha específica en una
estación geomagnética?
Los registros de campo se realizan en una caseta
antimagnética con ayuda de un instrumento llama-
do magnetómetro; los datos son procesados y se
obtienen así los valores medios horarios, diarios,
mensuales y anuales, así como la variación anual
de los elementos magnéticos y la elaboración de
boletines anuales geomagnéticos.
Cada observatorio funciona de manera automática,
lo cual permite disponer de datos todo el año.
¿En el Perú – Cuantos observatorios geomagnéticos
existen?
El Instituto Geofísico del Perú (I.G.P.) es la entidad
en nuestro país que se encarga de registrar y procesar
dichos valores, para lo cual cuenta con observatorios
fijos en Ancón, Huancayo, Cañete y Piura.
MAGNETÓMETRO
Fuente: Instituto Geofísico del Perú

165. Medida de ángulos y direcciones
199
MÉTODOS PARA MEDIR ÁNGULOS HORIZONTALES
1. Método del ángulo simple
Consiste en cuantificar la diferencia angular entre el alineamiento inicial y final.
El ángulo horizontal obtenido también toma el nombre de ángulo acimutal en virtud al
acimut de las visuales inicial y final respecto a un Norte arbitrario.
El ángulo ABC se determina mediante la diferencia
angular “β – α”
Es común asignar al alineamiento inicial el valor 0° 00' 00,
de modo que el ángulo ABC queda determinado con la
lectura final “θ”.
2. Método de repetición
Consiste en medir un ángulo repetidas veces pero de forma acumulada.
Con este método se puede obtener el valor de un ángulo con mayor precisión que la del instrumen-
to con sólo hacer cero en el alineamiento inicial y tomar la lectura final de la enésima repetición.
El procedimiento general se explica a continuación:
Primer paso
Se hace 0° 00' 00 en el primer alineamiento
(BA) para luego aplicar el método del án-
gulo simple.
Segundo paso
Se traslada la lectura obtenida en el pri-
mer paso (α) al alineamiento de partida
(BA), a continuación se aplica nuevamen-
te el método del ángulo simple.
Siguiente paso
Se repite el segundo paso tantas veces
como se quiera, obteniendo una lectu-
ra final; para calcular el ángulo busca-
do, basta dividir la lectura final entre el
número de repeticiones (n).
=
Lectura final
Ángulo
n

166. Medida de ángulos y direcciones
200
Análisis numérico
Supongamos que idealmente conocemos el verdadero valor de un ángulo (63° 06' 07). Sin
embargo cierta persona que desconoce dicho valor se atreve a medir aplicando el método
de repetición con un teodolito de 20 de precisión.
Obviamente, con dicho equipo y con el método del ángulo simple nunca llegará a obtener
la precisión de unidades de segundo; en el mejor de los casos podrá estimar la mitad de la
graduación; es decir 10.
Veamos lo que sucede con el método de repetición
• Cuando n = 1
Si el operador quisiera anotar el ángulo,
éste sería 63° 06'; sin embargo en realidad
no está tomando en cuenta el ángulo e1
Con el método de repetición, el valor de
e1
se irá acumulando.
63° 06' + e
1
• Cuando n = 2
• Cuando n = 4
2(63° 06') + (e
1
+ e
2
)
• Cuando n = 3
3(63° 06') + (e
1
+ e
2
+ e
3
)
4(63° 06') + (e
1
+ e
2
+ e
3
+ e
4
)
Es fácil entender que para el operador, la
lectura final es: 4(63° 06') + 30; pues la mí-
nima graduación del equipo es 20 y por tan-
to la estimación 10.

167. Medida de ángulos y direcciones
201
Lectura final = 4(63° 06') + 30 = 252° 24' 30
°
= = °
252 24' 30
Ángulo 63 06' 7,5
4
Si el teodolito fuese de las caracterísiticas que se indica en el cuadro (a) de la pág. 431, el
error máximo accidental usando miras de poligonación sería ±5; por lo cual no tiene
sentido expresar el ángulo en décimas de segundo.
Por tanto, redondeando a unidades de segundo:
Ángulo (V.M.P.) = 63° 06' 08
Observaciones
A) No es recomendable aplicar el método de repetición más de cuatro veces para un mismo
ángulo, pues si bien es cierto, este método aumenta la precisión (disminuye el error); ésta
no prospera o en el mejor de los casos se hace muy lenta para n 4; lo cual implica trabajar
demasiado por una infima mejora de precisión.
B) Cuando la distancia de las visuales son cortas (por ejemplo 100 metros) y se hace uso de
jalones; no tiene sentido aplicar el método de repeticion, dado que la precisión no mejora
para dicho efecto.
En caso sea necesario trabajar con visuales cortas, se recomienda utilizar miras de poligonación
o en el peor de los casos, usar jalones pero con la visual dirigida a la base de éstos.
C) Para teodolitos de precisión 1 segundo, no es tan ventajosos usar este método, a pesar de
tener visuales largas.
En todo caso, a modo de verificación es aceptable su uso.
D) Se recomienda emplear las dos posiciones del anteojo (directo e invertido) en iguales cantidades.
A continuación se muestra un ejemplo esquemático de la medida de un ángulo aplicando
el presente método con cuatro repeticiones.
Tener presente que en cada repetición es preciso seguir los pasos explicados en la pág. 149
referidos al teodolito repetidor.

168. Medida de ángulos y direcciones
202
En el presente caso; n = 4
θ ±
= 4
4 e
Ángulo
4
E) La lectura del círculo en la primera visual (AB) no tiene que ser necesariamente cero; no
obstante se acostumbra hacerlo por la sencillez del cálculo.
Ejemplo 1
Observe Ud. que:
• Sólo se toma la lectura para la primera y últi-
ma repetición.
• La lectura correspondiente a la primera
repetición, si bien no es imprescindible,
es útil para efectos de comprobación.
• Se asume igual cantidad de posiciones di-
rectas e invertidas, respecto al anteojo.
Estación PV N Anteojo Lectura Ángulo
B 0 D 0° 00' 00
A C 1 D 63° 06' 00 63° 06' 08
C 4 I 252° 24' 30
Ejemplo 2
Note Ud. la importancia que merece la lectura
correspondiente a la primera repetición, pues
sin ésta sería imposible determinar el ángulo
buscado, dado que el teodolito óptico mecáni-
co no acumula el número de vueltas completas.
Con ayuda de la primera lectura se puede
estimar el orden de la lectura correspondien-
te a la última repetición, en nuestro caso:
6(132° 05' 20) = 792° 32' 00; la cual supera
las dos vueltas que no ha guardado el equipo;
por tanto:
° + °
=
2(360 ) 72 32' 30
Ángulo
6
Ángulo = 132° 05' 25
Estación PV N Anteojo Lectura Ángulo
B 0 D 0° 00' 00
A C 1 D 132° 05' 20 132° 05' 25
C 6 I 72° 32' 30
Modelo de libreta de campo
Un modelo práctico es el que se muestra a
continuación:
PV = Puntos visados
N = Número de repeticiones

169. Medida de ángulos y direcciones
203
3. Método de reiteración
Consiste en medir un ángulo varias veces, tomando como origen diversos puntos del
transportador.
Cada medida recibe el nombre de reiteración, serie o set.
El procedimiento general, se explica a continuación.
Primer paso:
Se determina los ángulos de partida apoyán-
dose en la siguiente expresión:
=
°
01 vuelta
Incremento
N de series
Para grados sexagesimales:
°
=
°
360
Incremento
N de series
A continuación y a modo de ejemplo numéri-
co, se tomará como número de series: 4; por lo
que el incremento será 90°, luego:
Serie Ángulo de partida
1° 0° 00' 00
2° 90° 00' 00
3° 180° 00' 00
4° 270° 00' 00
Segundo paso
Se hace 0° 00' 00 en el primer alineamiento para
luego aplicar el método del ángulo simple.
Tercer paso
Se visa el primer alineamiento, tomando como
origen 90° 00' 00, para luego aplicar el méto-
do del ángulo simple.
Cuarto paso
Se visa el primer alineamiento, tomando como
origen 180° 00' 00, para luego aplicar el méto-
do del ángulo simple.
Quinto paso
Se visa el primer alineamiento, tomando como
origen 270° 00' 00, para luego aplicar el méto-
do del ángulo simple.

170. Medida de ángulos y direcciones
204
Sexto paso
El ángulo buscado será el promedio de las cua-
tro series.
Serie Ángulo
1° 60° 00' 06
2° 60° 00' 00
3° 60° 00' 12
4° 60° 00' 12
Promedio 60° 00' 07,5
Si el teodolito fuese de las características que se
indica en el cuadro (b) de la pág. 435, el error máxi-
mo accidental usando jalones sería ±7; por lo cual
no tiene sentido expresar el ángulo en décimas de
segundo, si el error es de unidades de segundo. Por
tanto, redondeando a unidades de segundo:
Ángulo (V.M.P.) = 60° 00' 08
Observaciones
A) En caso sea necesario trabajar con visuales cortas, se recomienda utilizar miras de poligonación
o en el peor de los casos, usar jalones pero con la visual dirigida a la base de éstos.
Serie Ángulo de partida Ángulo de partida
teórico en campo (tentativo)
1° 0° 00' 00 0° 02' 10
2° 90° 00' 00 90° 00' 40
3° 180° 00' 00 180° 04' 30
4° 270° 00' 00 270° 00' 50
C) Este método es conveniente cuando hay que medir ángulos alrededor de un mismo punto.
B) En la práctica, se hace tedioso intentar la
coincidencia del primer alineamiento con
un ángulo de partida específico, por tal
motivo se recomienda instalar dicho án-
gulo de manera aproximada.
D) El número de series a usar depende de los requerimientos y calidad de trabajo.
E) Se recomienda emplear las dos posiciones del anteojo (directo e invertido) en iguales cantidades.

171. Medida de ángulos y direcciones
205
Modelo libreta de campo
Ejemplo 1
Observe Ud. que:
– Se han tomado cuatro series.
– El método aplicado es igual, tanto para el
anteojo en posición directa como invertido.
Lectura Lectura reducida Promedio Promedio
Estación PV Directa Inversa Directa Inversa Serie Estación
B 0° 00' 06 180° 00' 19 0° 00' 00 0° 00' 00
C 173° 06' 06 353° 06' 22 173° 06' 00 173° 06' 03 173° 06' 02 173° 06' 05
B 90° 00' 22 270° 00' 29 0° 00' 00 0° 00' 00
C 263° 06' 34 83° 06' 38 173° 06' 12 173° 06' 09 173° 06' 10
A
B 180° 00' 39 0° 00' 42 0° 00' 00 0° 00' 00
C 353° 06' 45 173° 06' 42 173° 06' 06 173° 06' 00 173° 06' 03
B 270° 00' 20 90° 00' 16 0° 00' 00 0° 00' 00
C 83° 06' 22 263° 06' 22 173° 06' 02 173° 06' 06 173° 06' 04
Ejemplo 2
Lectura Lectura reducida Promedio Promedio
Estación PV Directa Inversa Directa Inversa Serie Estación
B 0° 00' 06 180° 00' 19 0° 00' 00 0° 00' 00
C 173° 06' 06 353° 06' 22 173° 06' 00 173° 06' 03 173° 06' 02 173° 06' 05
D 188° 16' 05 08° 16' 12 188° 15' 59 188° 15' 53 188° 15' 56 188° 15' 52
E 272° 35' 09 92° 35' 20 272° 35' 03 272° 35' 01 272° 35' 02 272° 35' 02
B 90° 00' 22 270° 00' 29 0° 00' 00 0° 00' 00
C 263° 06' 34 83° 06' 38 173° 06' 12 173° 06' 09 173° 06' 10
D 278° 16' 06 98° 16' 16 188° 15' 44 188° 15' 47 188° 15' 46
A E 02° 35' 28 182° 35' 32 272° 35' 06 272° 35' 03 272° 35' 04
B 180° 00' 39 0° 00' 42 0° 00' 00 0° 00' 00
C 353° 06' 45 173° 06' 42 173° 06' 06 173° 06' 00 173° 06' 03
D 08° 16' 29 188° 16' 37 188° 15' 50 188° 15' 55 188° 15' 52
E 92° 35' 31 272° 35' 45 272° 34' 52 272° 35' 03 272° 34' 58
B 270° 00' 20 90° 00' 16 0° 00' 00 0° 00' 00
C 83° 06' 22 263° 06' 22 173° 06' 02 173° 06' 06 173° 06' 04
D 98° 16' 16 278° 16' 11 188° 15' 56 188° 15' 55 188° 15' 56
E 182° 35' 27 02° 35' 16 272° 35' 07 272° 35' 00 272° 35' 04

172. Medida de ángulos y direcciones
206
Note Ud.:
– La ventaja del método de reiteración, cuan-
do hay varios ángulos alrededor de un
mismo punto.
Ventajas y desventajas
Aumenta la precisión de la medida.
MÉTODO VENTAJAS DESVENTAJAS
Cuando el número de repeticiones es
mayor de cuatro, el incremento de precisión
se hace lento.
El error accidental es más preciso que el obte-
nido por el método de reiteración.
Aumenta la precisión de la medida.
Reduce o compensa el error por graduación
del limbo, así como los errores del índice y
excentricidad.
Cuanto más series se realicen más confiable
será el ángulo, dado que la compensación del
error por graduación del limbo se optimiza.
Tan sólo utiliza dos lecturas (partida y final),
por lo que un error en cualquiera de las lecturas
inválida el trabajo realizado en dicho ángulo.
Acumulación del error por graduación del
limbo.
El error accidental es ligeramente mayor que
el de repetición.
REPETICIÓN
REITERACIÓN
Conclusión
– El método por reiteración tiene más ventajas que el de repetición.
– El método de repetición se utiliza en levantamiento de 3° y 4° así como en poligonales.
– El método de reiteración se utiliza en levantamientos geodésicos de 1° y 2° orden.
– Los fabricantes producen equipos repetidores de 5, 10, 20, 30 1', etc.
– Los fabricantes producen equipos reiteradores, en su mayoría menores o iguales a 1,
debido principalmente a la compensación del error por graduación.

173. 207
 
= + − °
 
= + + °
 
= ° + ° − °
RELACIÓN ENTRE EL ÁNGULO ACIMUTAL Y EL AZIMUT DE LOS LADOS QUE LA
COMPONEN
azimut
azimut
azimut
azimut
azimut
azimut

174. Medida de ángulos y direcciones
208
Solución:
• Regla práctica:
°
= ° + ° + °
$
%
180
BC
Z 52 10' 44 12' 180
ZBC = 276° 22'
1. Determinar la suma de los ángulos de
deflexión de una poligonal cerrada.
Solución:
PROBLEMAS DE APLICACIÓN
Del gráfico:
E = (180° – ˆ
1) + (180° – ˆ
2) + (180° – ˆ
3) +
............ + (180° – ˆ
n)
E = 180°×n – (ˆ
1 + ˆ
2 + ˆ
3 + . + ˆ
n)
E = 180°×n – 180°(n – 2) ⇒ E = 360°
2. Determinar los ángulos de deflexión de B,
C, D y E.
Solución:
• Graficando los rumbos.
• Deduciendo las deflexiones:
°
−
ˆ
1
8
0
1
° − ˆ
180 2
° − ˆ
180 3
°
−
ˆ
1
8
0
4
° − ˆ
180 n
ˆ
1
ˆ
2 ˆ
3
ˆ
4
ˆ
n

175. Medida de ángulos y direcciones
209
3. Calcular el ángulo promedio en cada vértice, así como el error de cierre angular.
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 243° 37' 06 333° 38' 56 63° 38' 41 153° 38' 43
AI 63° 39' 18 153° 38' 54 243° 38' 10 333° 38' 30
Promedio
ÁNGULO D
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 261° 57' 30 351° 57' 44,5 81° 57' 43 171° 57' 27,5
AI 81° 57' 26 171° 57' 58 261° 57' 44 351° 57' 25,5
Promedio
ÁNGULO C
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 205° 40' 24 295° 41' 02 25° 40' 49 115° 41' 05
AI 25° 40' 16 115° 41' 10 205° 40' 53,5 295° 41' 24
Promedio
ÁNGULO E
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 202° 31' 03 292° 31' 00 22° 31' 7,5 112° 31' 26
AI 22° 30' 49 112° 30' 55 202° 31' 00 292° 31' 25
Promedio
ÁNGULO B
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 271° 47' 22 1° 47' 16 91° 47' 20 181° 47' 26
AI 91° 47' 21 181° 47' 11 271° 47' 22 1° 47' 26
Promedio
ÁNGULO F
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 254° 24' 22 344° 24' 25,5 74° 24' 16 164° 24' 41
AI 74° 24' 22 164° 24' 17 254° 24' 14 344° 24' 41,5
Promedio
ÁNGULO A
Precisión del teodolito = 5
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 243° 37' 06 333° 38' 56 63° 38' 41 153° 38' 43
AI 63° 39' 18 153° 38' 54 243° 38' 10 333° 38' 30
Promedio
ÁNGULO D
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 261° 57' 30 351° 57' 44,5 81° 57' 43 171° 57' 27,5
AI 81° 57' 26 171° 57' 58 261° 57' 44 351° 57' 25,5
Promedio
ÁNGULO C
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 205° 40' 24 295° 41' 02 25° 40' 49 115° 41' 05
AI 25° 40' 16 115° 41' 10 205° 40' 53,5 295° 41' 24
Promedio
ÁNGULO E
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 202° 31' 03 292° 31' 00 22° 31' 7,5 112° 31' 26
AI 22° 30' 49 112° 30' 55 202° 31' 00 292° 31' 25
Promedio
ÁNGULO B
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 271° 47' 22 1° 47' 16 91° 47' 20 181° 47' 26
AI 91° 47' 21 181° 47' 11 271° 47' 22 1° 47' 26
Promedio
ÁNGULO F

176. Medida de ángulos y direcciones
210
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
A D 243° 37' 06 333° 38' 56 63° 38' 41 153° 38' 43
AI 63° 39' 18 153° 38' 54 243° 38' 10 333° 38' 30
Promedio 243° 38' 12 243° 38' 55 243° 38' 25,5 243° 38' 36,5 243° 38' 32,3
ÁNGULO D
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
AD 261° 57' 30 351° 57' 44,5 81° 57' 43 171° 57' 27,5
AI 81° 57' 26 171° 57' 58 261° 57' 44 351° 57' 25,5
Promedio 261° 57' 28 261° 57' 51,3 261° 57' 43,5 261° 57' 26,5 261° 57' 37,3
ÁNGULO C
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
A D 205° 40' 24 295° 41' 02 25° 40' 49 115° 41' 05
AI 25° 40' 16 115° 41' 10 205° 40' 53,5 295° 41' 24
Promedio 205° 40' 20 205° 41' 06 205° 40' 51,2 205° 41' 14,5 205° 40' 52,9
ÁNGULO E
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
A D 202° 31' 03 292° 31' 00 22° 31' 7,5 112° 31' 26
AI 22° 30' 49 112° 30' 55 202° 31' 00 292° 31' 25
Promedio 202° 30' 56 202° 30' 57,5 202° 31' 03,8 202° 31' 25,5 202° 31' 05,7
ÁNGULO B
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
A D 271° 47' 22 1° 47' 16 91° 47' 20 181° 47' 26
AI 91° 47' 21 181° 47' 11 271° 47' 22 1° 47' 26
Promedio 271° 47' 21,5 271° 47' 13,5 271° 47' 21 271° 47' 26 271° 47' 20,5
ÁNGULO F
Posición
1era. 2da. 3era. 4ta.
Serie (0°) Serie (90°) Serie (180°) Serie (270°)
Promedio
A D 254° 24' 22 344° 24' 25,5 74° 24' 16 164° 24' 41
AI 74° 24' 22 164° 24' 17 254° 24' 14 344° 24' 41,5
Promedio 254° 24' 22 254° 24' 21,2 254° 24' 15 254° 24' 41,2 254° 24' 24,9
ÁNGULO A
Solución:

177. Medida de ángulos y direcciones
211
• Cálculo del error de cierre.
Σ ángulos = 1 439° 59' 53
Error = –7
• Error máximo permitido.
Emáx = ±5 n = ±5 6 = ±12,3
Dado que error = 7 12,3
Se dá por aceptado el trabajo.
4. Se realizó el levantamiento topográfi-
co de una poligonal cerrada utilizándo-
se una brújula cuyos datos son los si-
guientes:
Estación PV Rumbo D Rumbo I d (m)
A E N 28° 00' W S 28° 30' E 106,3
B A N 30° 40' E S 30° 40' W 56,4
C B N 84° 30' W S 83° 50' E 84,2
D C S 02° 15' E N 02° 00' W 65,8
E D ESTE 96,9
Calcular el ángulo interno D y el rumbo CD.
Solución:
• Calculando el promedio del rumbo directo e
inverso.
Estación PV Rumbo promedio
A E N 28° 15' W
B A N 30° 40' E
C B N 84° 40' W
D C S 02° 7',5 E
E D ESTE
• Graficando
Del croquis:
ˆ
A = 238° 55'
ˆ
B = 64° 40'
ˆ
C = 82° 32' 30
ˆ
D = 92° 07' 30
ˆ
E = 61° 45'
Σ = 540° 00' 00
Luego: ˆ
D = 92° 07' 30
RCD = N 2° 07' 30 W
5. Dado la siguiente poligonal:
Se desea determinar el rumbo de la línea
ED, sabiendo que: ZBA = 280° 30' 20
Solución:
• Expresando los datos en función del mé-
todo de ángulos a la derecha:

178. Medida de ángulos y direcciones
212
• Cálculo del acimut ZAB.
ZAB = ZBA – 180°
ZAB = 100° 30' 20
• Cálculo de cada acimut:
– ZBC = (ZAB + 103° 20' 11) – 180°
ZBC = 23° 50' 31
– ZCD = (ZBC + 249° 22' 48) – 180°
ZCD = 93° 13' 19
– ZDE = (ZCD + 150° 40' 12) – 180°
ZDE = 63° 53' 31
• Cáculo del acimut ZED
ZED = ZDE + 180° = 243° 53' 31
• El rumbo de la línea ED
Rumbo ED: S 63° 53' 31 W
6. Determinar el ángulo BOC de la poligonal
ABCDE, si se conoce ZCE = 245° 25' y
A(3266; 4965), B(3822; 4849), D(3123; 5446).
Solución:
• Analizando el acimut ZBD
ZBD = 310° 29' 59,5
• Analizando el acimut ZCE
• Analizando la dirección BD y CE

179. Medida de ángulos y direcciones
213
(ZBD + θ) ± 180° = ZCE
(310° 29' 59,5 + θ) – 180° = 245° 25'
θ = 114° 55' 0,5
• Finalmente: µ
BOC = 180° – θ
µ
BOC = 65° 04' 59,5
7. Se hizo un levantamiento en enero de 1994,
época en la cual la declinación magnética era
8° 40' E en esa zona y se encontró que el rum-
bo magnético de una línea era N 25° 45' E.
Determinar el rumbo magnético que se ne-
cesita en enero del 2010 para replantear la
línea, sabiendo que la declinación magné-
tica para entonces es 2° 15' W.
Solución:
Ilustrando el enunciado:
8. Nuestro amigo Armando tiene su domici-
lio en Comandante Jiménez, punto “A”
Magdalena; ver plano. Se pide el acimut
magnético para el 01 de enero de 1 990 así
como para el 2 004 de la misma fecha.
Declinación magnética aproximada para el 1 de enero
de 1990 para toda la hoja varía anualmente 10',5 Oeste.
ZAB (magnético) = ?
Solución:
Cálculo del acimut de cuadrícula de la línea AB.
∆
=
∆
AB
x
Z arctan
y
 
−
=  
−
 
AB
275 925 275 857
Z arctan
8 662 635 8 662 500
ZAB = 26° 44' 4,4
N 36° 40' E
Plano del 1 de enero de 1 990; Sistema UTM WGS84
Graficando el
acimut de cua-
drículaABpara
1990

180. La brújula
214
El acimut magnético de AB para el 01 de
enero de 1990
ZAB = (0° 22' + 26° 44' 4,4) – 1° 45'
ZAB = 25° 21' 4,4
• Calculando la declinación magnética
para el 1 de Enero del 2 004:
Datos del plano: δ(01/01/90) = 1° 45'
∆δ = –10',5
δ(01/01/2004) = δ(01/01/90) + t(∆δ)
t = 2 004 – 1 990 = 14 años
δ(01/01/2004) = 1° 45' + 14(–0° 10',5)
δ(01/01/2004) = –0° 42'
• Graficando
9. El rumbo a AB tomado con una brújula en
enero de 1 981 fue de S 0° 50' E. ¿Cuál es el
rumbo verdadero y el rumbo magnético que
tendrá que tomarse en enero del 2 007 para
poder replantear dicha dirección AB?.
La declinación magnética aproximada en
1 981 fue de 3° 51' E y la variación magné-
tica anual 5',5 Oeste.
Solución:
Del gráfico; el acimut magnético de AB
para el 01 de Enero 2 004:
ZAB = 0° 42' + 0° 22’ + 26° 44' 4,4
ZAB = 27° 48' 4,4
Tanto el norte de cuadrícula como el nor-
te geográfico permanecen invariables a
través del tiempo.
Recordar
• Del enunciado:
t = 26 años
Declinación magnética para 1 981
• Del gráfico, el rumbo magnético de AB
para enero del 2007: S 01° 33' W
• El rumbo verdadero no varía; del gráfico;
el rumbo de AB:
S (01° 28' + 01° 33') W = S 03° 01' W
ó S (03° 51' – 0° 50’) W = S 03° 01' W
• δ(01/2007) = δ(01/1981) + ∆δ
δ(01/2007) = 03° 51' + t(–0° 5',5)
δ(01/2007) = 01° 28' ó 01° 28' E
Graficando

181. La brújula
211
211
211
211
211
Es aquel instrumento que se utiliza para determinar la meridiana magnética que pasa por
un punto. Está constituida por una caja metálica no magnética en cuyo interior se aloja una
aguja imantada apoyada en su centro de gravedad sobre un pivote, el cual a su vez se ubica
en el centro de un limbo graduado (transportador).
Se suele adicionar a la aguja magnética un contrapeso que anule el efecto de la inclinación
magnética; en lugares ubicados en el hemisferio norte, el contrapeso se coloca en el lado sur
de la aguja, mientras en el hemisferio sur (caso Perú), el contrapeso se instala en el lado
norte de la aguja.
Generalmente la graduación del transportador es al grado y algunos al medio grado, lo cual nos permite
tomar lecturas con apreciación de quince minutos (15').
En la actualidad existen brújulas que determinan el rumbo y otros el acimut de una línea de referencia.
Para determinar la dirección de una línea, se gira la brújula hasta hacer coincidir la línea N-
S del transportador con la línea de referencia.
Generalmente las
brújulas que de-
terminan el rum-
bo de una línea
de referencia, po-
seen los puntos
cardinales E y W
intercambiadas
con el fin de ofre-
cer una lectura
directa; en la figu-
ra, el rumbo de la
línea de referen-
cia es S 51° W.

182. La brújula
216
CLASES DE BRÚJULAS
A) La Brújula de topógrafo
Este tipo de instrumento va montado sobre un trípode y en algunos modelos sobre un
bastón.
No obstante su eficiencia, hoy en día tiene poca divulgación debido a que su uso se inclina
más como un taquímetro que como brújula, con lo cual no cumple su objetivo original.
El procedimiento de uso es como sigue:
El eje de colimación del telescopio siempre coincide con la línea
N – S del transportador.
Generalmente
las brújulas aci-
mutales poseen
graduaciones de
0° a 360° en el
transportador,
muchos de ellos
en sentido anti-
horario, con el
fin de ofrecer
una lectura di-
recta; en la figu-
ra el acimut de
la línea de refe-
rencia es 238°.

183. La brújula
217
– Se desea determinar el acimut AB
B) Brújula declinatoria
La aguja magnética puede estar dentro de una caja rectangular o cilíndrica; en las prime-
ras se utilizan generalmente en conjunto con la plancheta o para trazar el norte magnético
en un croquis determinado.
Las brújulas declinatorias cilíndricas van montadas comúnmente sobre un teodolito.
Brújula declinatoria rectangular.
Se instala la brújula en el punto A, se dirige la visual hacía B (para mayor precisión hacer uso de la tangencial).
La lectura en la brújula será el acimut buscado; hay brújulas que llevan consigo un Nonio
con lo cual se consigue mayor precisión; en nuestro caso el acimut de la línea AB es 191°.
Brújula declinatoria circular.

184. La brújula
218
El procedimiento para hacer uso de la brújula declinatoria circular es el siguiente:
– Se desea determinar el acimut AB
Se instala el teodolito en el punto A; se
coloca la brújula sobre el primero.
Se suelta el bloqueo de la alidada del teodolito, colocando el ojo en
el ocular de la brújula se gira la alidada hasta hacer coincidir el Norte
de la aguja Magnética con el cero de la graduación circular de la
brújula; para mayor precisión se puede hacer uso del tornillo tangencial
de la alidada del teodolito.
En estas condiciones se habrá conseguido orientar el eje de colimación del teodolito en la dirección del norte magnético.

185. La brújula
219
Para medir el acimut AB, sólo tenemos que soltar el bloqueo de la alidada y girarla en sentido horario hasta ubicar
el jalón en el punto “B”.
El desplazamiento angular medido en el teodolito será el acimut AB buscado.
C) Brújula de bolsillo
Su determinación está basada en el tamaño de la misma; los más conocidos son las de tipo
Brunton. Sus elementos principales se muestran a continuación.

186. La brújula
220
Método para medir el acimut o rumbo de una línea de referencia con la brúju-
la de bolsillo
Método 1. Se desea determinar el acimut AB
Se sostiene la brújula a la altura de la cintura sobre el punto A; se abre la tapa (espejo) hacía el
operador aproximadamente 45°; se orienta el visor grande perpendicular a la caja de la brújula. Se
procede a girar la brújula horizontalmente hasta que: visor grande, línea central del espejo y jalón (ó
similar) ubicado en “B” se encuentren alineadas.
1. Espejo.
2. Visor pequeño: forma parte del dispositivo de puntería.
3. Visor grande: forma parte del dispositivo de puntería
4. Ventana de espejo.
5. Línea central del espejo.
6. Escala circular de la brújula.
7. Nivel circular.
8. Nivel tubular.
9. Graduación del clinómetro:
10. Clinómetro: mide la pendiente de un plano.
11. Vernier para ángulos verticales.
12. Botón de bloqueo: permite bloquear la aguja magnética.
13. Mando de ajuste para escala circular de la brújula:
permite orientar el transportador circular para cada
método de medición usual.
14. Dispositivo para hacer uso del clinómetro: permite
medir la pendiente de un plano cuando el nivel
tubular se encuentra centrado.
15. Caja.
16. Aguja magnética.

187. La brújula
221
La última opera-
ción (alineamien-
to); se consigue,
cuando el opera-
dor mientras está
mirando hacía aba-
jo en el espejo, ve
la línea central de
éste que biseca
simétricamente el
visor grande y el ja-
lón respectivo; en
estas condiciones
se debe centrar la
caja con ayuda del
nivel circular, una
vez que la aguja
magnética quede
estabilizada se blo-
quea la misma. En
nuestro caso el aci-
mut AB es 240°.
Método 2. Se desea determinar el acimut AB.
Se sostiene la brújula a la altura de ojo sobre el punto “A”; se abre el visor grande hacía el operador, vertical o
ligeramente fuera de la caja.

188. La brújula
222
Se procede a girar la brújula horizontalmente hasta que: visor grande, visor pequeño y jalón (ó
similar) que pase por “B” se encuentren alineados; esto se consigue cuando el operador ve a través
del visor grande y pequeño el jalón en B. En estas condiciones se debe centrar la caja con ayuda del
nivel circular, una vez que la aguja magnética se estabilice, se procede a bloquear la misma.
Si buscamos mayor precisión, vea a través del visor grande y la ventana del espejo (línea central)
el jalón en B. En estas condiciones se debe centrar la caja con ayuda del nivel circular, una vez
que la aguja magnética quede estabilizada, se bloquea la misma.

189. La brújula
Se instala un teodolito en el punto A.
Método 3. Se desea determinar el acimut AB con ayuda de la brújula de bolsillo y un teodolito.
Si la brújula es acimutal, tendremos como lectura el acimut inverso de AB; en nuestro caso: 57°
Luego el acimut AB será: 180° + 57° = 237°
223

190. La brújula
224
Se abre la tapa de la brújula con el visor delantero
dirigido al punto B, luego se hace coincidir la zona
lateral plana de la brújula con la zona plana lateral del
teodolito, de tal forma que la línea N – S de la escala
circular de la brújula sea paralela al eje de colimación
del teodolito.
Con la posición anterior, proceda a soltar el bloqueo de la
alidada del teodolito para luego girarla horizontalmente
hasta que aproximadamente el norte de la aguja magnética
coincida con el norte de la escala circular de la brújula; para
afinar la precisión, se hace uso del tornillo tangencial de la
alidada del teodolito (no olvidar de nivelar la brújula).
En estas condiciones se habrá conseguido orientar el eje de colimación del teodolito en la dirección del norte magnético.
Como quiera que el eje de colimación está dirigido hacía el norte magnético; para medir el acimut AB, solo
tenemos que soltar el bloqueo de la alidada y girarla en sentido horario hasta ubicar el jalón en el punto B. El
desplazamiento será el acimut AB buscado.

191. La brújula
225
USO DE LA BRÚJULA EN LA GEOLOGÍA
Para definir la orientación de un plano en estudio (estrato, falla, diaclasa) en el terreno, se hace
uso del rumbo, buzamiento y dirección de inclinación.
Rumbo
Es la dirección del plano en estudio
respecto a la meridiana magnética.
Buzamiento
Es el ángulo entre el plano en estu-
dio y un plano horizontal.
Dirección de inclinación
Es la dirección de la proyección
horizontal de la línea de máxi-
ma pendiente.
La Brújula Freiberger
Esta brújula posibilita me-
dir la dirección y el ángulo
de buzamiento de estratos
rocosos o de yacimientos en
un sola operación, así como
determinar el rumbo y bu-
zamiento de elementos es-
tructurales planos y lineales
(planos de estratificación,
esquistosidad y de fisura,
ejes de plegado y direccio-
nes de lineaciones).
El transportador circular de
la brújula es orientable, para
cada método de medición
usual.

192. La brújula
226
3. Graduación del clinómetro: mide la pendiente de
un plano.
4. Escala circular vertical: mide el buzamiento.
5. Nivel tubular de burbuja de aire.
6. Nivel esférico de burbuja de aire.
7. Muesca (forma parte del dispositivo de puntería)
8. Caja.
9. Tecla de bloqueo: permite bloquear ó desbloquear la
aguja magnética.
10. Escala circular de la brújula.
11. Aguja magnética.
12. Clinómetro: mide la pendiente de un plano.
13. Mirilla para nivel tubular de burbuja de aire.
14. Dispositivo para el bloqueo del clinómetro.
15. Mando de ajuste para escala circular de la brújula: per-
mite orientar el transportador circular para cada mé-
todo de medición usual.
Pasos para medir la dirección del plano y ángulo de buzamiento
1. Girar la escala circular de la brújula (15) en sentido antihorario 90°. De este modo consegui-
remos medir directamente la dirección del plano (ZAB).
Posición final
Posición inicial
2. Colocar la brújula en la posición mostrada; tomar las lecturas respectivas, no sin antes
asegurarse de calar el nivel esférico.
De la ilustración: Acimut del plano: ZAB = 70°
Ángulo de buzamiento: α = 55°
1. Espejo.
2. Punto de mira (forma parte del dispositivo de
puntería).

193. La brújula
227
3. Para otro valor de ángulo de buzamiento:
De la ilustración: Acimut del plano: ZAB = 70°
Ángulo de buzamiento: β = 75°

194. La brújula
228
Pasos para medir la dirección de la inclinación y ángulo de buzamiento
1. Comprobar la posición normal de la escala circular de la brújula.
2. Colocar la brújula en la posición mostrada; tomar las lecturas respectivas, no sin antes
asegurarse de calar el nivel esférico.
De la ilustración: Dirección de inclinación. ZBC = 204°
Ángulo de buzamiento: α = 55°

195. La brújula
229
3. Para otro valor de ángulo de buzamiento.
De la ilustración: Dirección de inclinación. ZDE = 200°
Ángulo de buzamiento: β = 55°
Medición de pendientes con ayuda del clinómetro
Para aplicar este método, es preciso apoyar el lado adjunto a la burbuja de aire sobre el plano
cuya pendiente se requiere medir.
El ángulo buscado lo determinará el clinómetro, debido a su posición vertical por efecto de
la gravedad.
Este tipo de medir pendientes dá lugar a un manejo cómodo y rápido de la brújula con una
sola mano al realizar mediciones estáticas de fisuras.
Merced al borde de aplicación alargado al abrir la cubierta, se aumenta la precisión de las
mediciones.
Antes de proceder a la medición hay que desbloquear el clinómetro (14).

196. La brújula
230
La Brújula Brunton
Esta brújula también permite medir la dirección y el ángulo de buzamiento de estratos rocosos
o de yacimientos; a diferencia de la brújula Freiberger, la brújula Brunton necesita dos operacio-
nes independientes entre sí para medir el rumbo y buzamiento (uno cada uno).
Medición de la dirección de un plano o estrato rocoso
Colocar el eje longitudinal de la brújula, paralelo a la dirección del estrato rocoso como
muestra la ilustración. Tomar la lectura respectiva, no sin antes asegurarse de centrar el nivel
circular (ver fig. a).
Medición del ángulo de buzamiento de un estrato rocoso
Se instala la brújula de canto, además de guardar el paralelismo entre su eje longitudinal y la
línea de máxima pendiente del plano. Se procede a centrar el nivel tubular; por último se toma
la lectura en el clinómetro (ver fig. b)
Lectura: –48°
Lectura: 43°

197. La brújula
231
Lectura: –31° = 149° ≅ – 60%
LEVANTAMIENTO CON BRÚJULA
El levantamiento con brújula de bolsillo sirve para reconocimiento o levantamiento preliminar.
El ángulo BAC no se mide directamente, sino se calcula a partir de una o diferencia de rumbos o acimuts.
Fig. a
Fig. b
Lectura: ZAB = 263°

198. Medición de distancias
232
Ilustración
1° Paso.- Se estaciona la brújula en el punto “1” y se dá lectura al rumbo 1-2 (lectura directa).
2° Paso.- Se estaciona la brújula en el punto “2” y se dá lectura al rumbo 2-1 (lectura inversa).
Libreta de campo
Estación PV Rumbo D Rumbo I Rumbo promedio
1 2 N 30° 30' E S 30° W N 30° 15' E
2 S 54° E N 53° 30' W S 53° 45' E
1 N 70° W S 70° E N 70° W

199. CLASE 4

200. Redes de apoyo planimétricos
285
285
285
285
285
Cuando se proyecta realizar un le-
vantamiento topográfico plani-
métrico, es imprescindible ceñirse
a una metodología apropiada, es así
que antes de tomar medidas sobre
la estructura materia del trabajo, es
preciso ubicar puntos estratégicos
en el terreno, los cuales servirán de
apoyo primario en el levantamien-
to final; la o las figuras geométricas
que se forman al generar los men-
cionados puntos toman el nombre
de redes de apoyo.
Los puntos que conforman una red
de apoyo toman el nombre de pun-
tos de control.
En rigor, las redes de apoyo son fi-
guras geométricas enlazadas entre
sí, distribuidas en una superficie de
terreno, su objetivo es servirnos de
apoyo para realizar un levantamien-
to topográfico.
El cerco perimétrico que se muestra, puede ser levantado completa-
mente desde el punto “o”; esto significa que la red de apoyo está
constituida tan solo por un solo punto (“o”).
Las estructuras pueden ser levantadas gracias a los puntos que consti-
tuyen el triángulo mostrado, la red de apoyo es un triángulo.

201. Redes de apoyo planimétricos
290
A continuación se ilustra la manera como se emplea los puntos de control en un levantamien-
to topográfico.
Para poder determinar la posición de un punto tal
como “A”, es necesario apoyarse en un sistema de
coordenadas.
Teniendo presente la figura anterior, es posible deter-
minar las coordenadas de los vértices de una figura
geométrica (puntos de control).
Con ayuda de los puntos de control, podremos calcular las coordenadas de puntos estraté-
gicos de diversas estructuras naturales y/o artificiales que conforman la zona a levantar.
En una estructura longitu-
dinal como es el caso de
una carretera, los puntos
de apoyo obedecen aproxi-
madamente la geometría
lineal de la vía. En este caso
la red de apoyo está cons-
tituida por un conjunto de
líneas quebradas.

202. Redes de apoyo planimétricos
291
MÉTODOS PLANIMÉTRICOS CON CINTA MÉTRICA Y
TEODOLITO
Para efectuar un buen levantamiento, es imprescindible conocer el objetivo del trabajo final, ello
permitirá definir la precisión que se necesita y por ende el método y los equipos mejores apropia-
dos para el caso, pues no se trata de utilizar un teodolito (por ejemplo) de 01 segundo de precisión
con dieciséis series en la medición angular para efectos de un anteproyecto vial.
No obstante cualquiera sea el caso, el rendimiento y criterio humano debe estar siempre en su
más alto nivel.
Existen tres métodos básicos que permiten determinar una red de apoyo:
A. Método de radiación
B. Método de intersección de visuales.
C. Método de la poligonal
C.1. Poligonal cerrada.
– Poligonal cerrada de circuito cerrado
– Poligonal cerrada completamente ligada en sus dos extremos.
C.2. Poligonal abierta.
A. Método de radiación
Consiste en una red de apoyo constituida por un solo punto de control, obviamente de
coordenadas conocidas.
Para aplicar el método, se recomienda seguir los siguientes pasos:
– ubicar en planta los puntos por levantar.

203. Redes de apoyo planimétricos
292
– Elegir el punto de control;
teóricamente deberá ser
el centro de la figura
geométrica por levantar,
comúnmente esto se hace
imposible, no obstante
hay que acercarse a dicho
objetivo; otro requisito
para la elección de dicho
punto es la total visibili-
dad desde el punto de
control respecto a todos
los puntos por levantar.
– Determinar alguna de
las meridianas (magné-
tica, geográfica o de
cuadrícula) en el punto
de control.
– Con ayuda del teodolito y con el eje de colimación coincidente con la meridiana respectiva,
se miden los acimut de las líneas radiales (fig. a). Es importante que una vez medido el
último acimut (en nuestro ejemplo; ZA5), se dirija la visual hacia el primer punto para
chequear el error de cierre angular, el cual no deberá ser mayor que la precisión del teodolito.
Fig. a Fig. b

204. Redes de apoyo planimétricos
293
– Por último se miden las distancias radiales con la mayor precisión posible haciendo
uso de una cinta métrica.
– El cálculo respectivo se explicará mediante un ejemplo numérico.
De la fig. b: ∆x = dA3⋅Sen ZA3
∆y = dA3⋅Cos ZA3
Ejemplo de aplicación
Sabiendo que las coordenadas del punto “A” son A = (60; 90) metros y la precisión del teodolito
20 segundos. Calcular las coordenadas de 1; 2; 3; 4 y 5, teniendo en cuenta como datos de campo:
Solución:
• Verificando el error de cierre angular Ec:
ZA1 = 20° 30' 10 ...................... (partida)
ZA1 = 20° 30' 20 ...................... (llegada)
Ec = 20° 30' 20 – 20° 30' 10
Ec = 10 20 ........................(conforme)
• Calculando las coordenadas parciales ∆x y ∆y.
Última medición angular
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
A1 20°30'10 85,61 29,98 80,19
A2 82°45'30 72,56 71,98 9,15
A3 148°25'40 98,74 51,70 –84,13
A4 240°10'20 55,80 –48,41 –27,76
A5 305°20'30 67,36 –54,95 38,96
• Coordenadas absolutas
Punto E = 60 + ∆x N = 90 + ∆y
1 89,98 170,19
2 131,98 99,15
3 111,70 5,87
4 11,59 62,24
5 5,05 128,96

205. Redes de apoyo planimétricos
294
b. Método de intersección de visuales
Consiste en una red de apoyo constituida por dos estaciones, desde las cuales se pueden ver
el conjunto de puntos que se desea localizar; la línea que une estas dos estaciones se le
conoce como base y debe ser medido con la mayor precisión posible.
Es imprescindible conocer las coordenadas de uno de los puntos en mención.
Este método se aplica cuando no es posible medir las distancias radiales al intentar ejecutar
el método de radiación.
Para aplicar el método se recomienda seguir los siguientes pasos:
– Ubicar en planta los puntos por levantar así como las estaciones A y B; se recomienda que
la línea AB se encuentre aproximadamente centrado respecto a los puntos por localizar.
– Tanto desde A como de B, la visibilidad debe ser total respecto a los puntos por locali-
zar, incluyéndose entre ambas mútuamente.

206. Redes de apoyo planimétricos
295
– Determinar alguna de las meridianas (magnética, geográfica o de cuadrícula) en el punto A.
– Con ayuda del teodolito y con el eje de colimación coincidente con la meridiana respectiva, se
miden los acimuts de las líneas radiales, incluyendo la correspondiente a la línea AB (ver fig. a).
– Haciendo estación en el otro punto (B), se ubica el 0° 00' 00 en dirección a A, para
luego medir los ángulos en dirección a cada punto desconocido (ver fig. b).
– Por último, se mide la base AB con la mayor precisión posible, haciendo uso de la cinta métrica.
– Para efectos de cálculo, se forman triángulos, teniendo como lado común la base AB (ver fig. c).
Fig. a Fig. b

207. Redes de apoyo planimétricos
296
AB1
– Haciendo el uso de la ley de senos, se calcula los lados A1, A2, A3, A4, A5, (fig. d).
• Ley de senos: • En forma general:
 
=  
θ
 
1
Sen AB1
A1 AB
Sen
 
=  
θ
 
i
Sen ABi
Ai AB
Sen
– Finalmente, el problema se convierte en un clásico método de radiación respecto al punto “A”.
θ1 =
 
° − − +
 
AB A1
180 Z Z AB1
Fig. c Fig. d
Fig. e

208. Redes de apoyo planimétricos
297
Ejemplo de aplicación
Según la figura (a y b), se ha medido la base AB
obteniéndose como resultado 10,00 metros; si
los datos acimutales de campo son los que se
muestran; calcular las coordenadas de 1; 2; 3; 4
y 5; sabiendo que A = (20,0; 30,0) metros.
Solución:
• Calculando
Punto lado Z
S ABn (interno)
1 A1 15° 18' 30 83° 20' 40
2 A2 92° 35' 20 162° 43' 20
3 A3 158° 25' 10 100° 49' 20
4 A4 193° 12' 40 54° 34' 30
5 A5 267° 53' 10 06° 54' 50
AB 100° 40' 40
Punto lado ZAB – ZAi θi Ai (m)
1 A1 85° 22' 10 11° 17' 10 50,75
2 A2 08° 05' 20 09° 11' 20 18,60
3 A3 57° 44' 30 21° 26' 10 26,88
4 A4 92° 32' 00 32° 53' 30 15,01
5 A5 167° 12' 30 05° 52' 40 11,75
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
A1 15°18'30 50,75 13,40 48,95
A2 92°35'20 18,60 18,58 –0,84
A3 158°25'10 26,88 9,89 –25,00
A4 193°12'40 15,01 –3,43 –14,61
A5 267°53'10 11,75 –11,74 –0,43
Punto E = 20 + ∆x N = 30 + ∆y
1 33,40 78,95
2 38,58 29,16
3 29,89 5,00
4 16,57 15,39
5 8,26 29,57
Nótese que:
θi =
 
° − − +
 
AB Ai
180 Z Z ABi
• Aplicando el método de radiación respec-
to al punto A:
• Finalmente:
C. Método de la poligonal
Se caracteriza por estar constituida por un conjunto de líneas consecutivas; el trabajo de campo
se reduce en medir ángulos acimutales y longitudes de los lados formados.
Existen dos tipos: cerrada y abierta.
C.1. Poligonal cerrada
C.1.1 poligonal cerrada de circuito cerrado.- Consiste en un conjunto de líneas consecutivas, en
donde el punto de partida coincide con el de llegada; este tipo de poligonal permite verificar la
precisión del trabajo, dado que es posible la comprobación y posterior corrección de los ángu-
los y longitudes medidos.
En la actualidad es el método con mejor aceptación por parte de ingenieros y topógrafos.
Para aplicar el método se recomienda seguir los siguientes pasos:
hay que tener mucho cuidado en la elec-
ción de los puntos A y B, pues en trabajos
de cierta importancia, los ángulos internos
que conforman los triángulos deben estar
comprendidos entre 30º y 150º
Observación

209. Redes de apoyo planimétricos
298
– Ubicar y monumentar los puntos de control (vértices de la poligonal).
– Los puntos deben ser intervisibles.
No deben existir obstáculos que impidan la total visibilidad entre puntos adyacentes.
La ubicación de los puntos de control es consecuencia del plan de trabajo así
como del reconocimiento de terreno. La poligonal no necesariamente debe rodear
las estructuras por levantar.

210. 299
azimut
azimut
,
azimut
azimut

211. Redes de apoyo planimétricos
300
– Con ayuda del teodolito, medir los ángulos acimutales de los vértices de la poligonal;
para dicho efecto es casi común el uso del método de ángulos a la derecha.
Cuando el recorrido del circuito es antihorario, los
ángulos medidos serán los internos.
Cuando el recorrido del circuito es horario, los ángu-
los medidos serán los externos
– Por último, se mide los lados de la poligonal con la mejor precisión posible. Si bien es cierto
estamos presentando los métodos empleando teodolito y cinta métrica, hay que advertir, que
hoy en día casi todas las longitudes se miden con MED (medición electrónica de distancias).
Es propicio recordar que cada ángulo deberá medirse varias veces, según la
precisión buscada. En cada vértice el número de veces medido con anteojo
en posición directa debe ser igual al número de veces en posición inversa.

212. Redes de apoyo planimétricos
301
Proceso de gabinete
1. Análisis del cierre angular.- Se denomina así a la diferencia entre la suma teórica y su
similar procedente de la medición.
Teóricamente: Σ Ss interiores= 180°(n - 2)
Σ Ss exteriores= 180°(n+ 2)
Si; Ec = Error de cierre angular.
El máximo Ec permitido: Ec=± R n R: Mínima división limbo acimutal
n: Número de vértices
– Si el error de cierre angular, supera el máxi-
mo permitido, es necesario regresar al
campo y medir nuevamente los ángulos,
dado que es casi seguro que se han come-
tido una o varias equivocaciones.
Sin embargo, es posible que la equivoca-
ción mayor se encuentre concentrada en
un solo ángulo, por tal razón se recomien-
da dibujar a escala las longitudes y direc-
ciones de los lados de la poligonal.
– Si el error de cierre angular, es me-
nor que el máximo permitido, se pro-
cede a compensar dicho valor entre
todas. Generalmente la totalidad de
los ángulos de una poligonal se mi-
den con la misma precisión, es por tal motivo que casi siempre se acostumbra a
repartir el error en cantidades iguales para cada ángulo. No obstante el método de
mínimos cuadrados es el mejor ajuste angular
con ayuda de los ángulos
compensados, se procede a ejecutar la regla práctica para este efecto.
°
= + − °
64
74
8
S
180
BC AB
Z Z B 180
°
= + + °
64
74
8
S
180
BC AB
Z Z B 180
Tener presente el uso del método de ángulos a la derecha para la aplicación de esta regla.
La perpendicular bisectriz de la línea AA' indica el
ángulo equivocado, el cual deberá ser sometido a una
nueva medición.
n = Número de vértices
2. Cálculo de la azimut de los lados de la poligonal.-

213. Redes de apoyo planimétricos
302
3.- Cálculo de coordenadas parciales.- Se procede a descomponer cada lado de la
poligonal, tanto en el eje x (este) como en el eje y (norte).
En nuestro ejemplo:
En el grafico, se aprecia la descomposición de los lados AB y CD.
Por otro lado, hay que advertir que es necesario obedecer el orden
del recorrido del circuito ABCDE .
4.- Cálculo del error de cierre lineal.- Se observa el siguiente gráfico, no será difícil
entender que teóricamente tanto “A” como “A' ” deben coincidir en el primer punto; sin
embargo en la práctica esto no sucede dado que AA' casi siempre es diferente de cero y su
valor viene hacer el llamado error de cierre lineal.
∆x = d⋅
⋅
⋅
⋅
⋅sen Z ∆y = d⋅cos Z
Si se ha cometido una equivocación en la medición de distancias de los lados de la poligonal, hay que sospechar
del lado “paralelo” a la línea AA'; en nuestro ejemplo: CD.
εx = Σ∆x
εy = Σ∆y
( ) ( )
ε = ε + ε
2 2
x y
5.- Cálculo del error relativo (E
R
).- Este parámetro, nos permite evaluar la precisión o
calidad de la poligonal.
( )
=
ε
R
1
E
Perímetro de poligonal
Conocido el error de cierre lineal; es inmediato el cálculo del error relativo y su compara-
ción con la siguiente clasificación:

214. 303
ε
ε
ε ε
ε
∆ ∆
∆ ∆
∆ ∆
=
− ×
=
− ×

215. Redes de apoyo planimétricos
304
Ejemplo ilustrativo 1
Determine las coordenadas de los puntos B; C; D y E, sabiendo que el teodolito con el cual se trabajó tiene
una precisión de cinco segundos, A = (100 000; 100 000) m.
ZAB = 137°03’46’’
Nota
El Error relativo no deberá ser
mayor de 1/10 000
Punto Ángulo promedio
medido
L(m) Lado
A 146°01’55’’ 108,805 AB
B 36°26’12’’ 96,753 BC
C 155°38’15’’ 106,709 CD
D 74°01’52’’ 31,858 DE
E 127°51’53’’ 85,912 EA
S 540°00’07’’
Punto Ángulo medido C Ángulo compensado
A 146°01’55’’ -1’’ 146°01’54’’
B 36°26’12’’ -1’’ 36°26’11’’
C 155°38’15’’ -2’’ 155°38’13’’
D 74°01’52’’ -1’’ 74°01’51’’
E 127°51’53’’ -2’’ 127°51’51’’
S 540°00’07’’ -7’’ 540°00’00’’
Solución:
u Análisis de cierre angular:
Teóricamente; el error máximo permitido:
ZAB = 137°03’46’’
Comparando: EC = 07’’ 11,8’’
Lo cual indica que la medición angular es aceptable.
u Compensación de ángulos:
A continuación procedemos a repartir el “exceso angular” en cada valor medido.
Una opción podría ser distribuir:
Lo cual significa restar a cada ángulo 1,4 . Otra opción es el uso de tan solo números enteros, la
desición queda a criterioo del Ingeniero,
En nuestro caso:

216. Redes de apoyo planimétricos
305
u Calculando del azimut de los lados de la poligonal,
w
w
w
w
w
u Comprobando:
u Cálculo de las coordenadas parciales:
Lado Z d(m) Dx = dsen Z Dy = dcos Z
AB 137°03’46’’ 108,805 74,118 -79,656
BC 353°29’57’’ 96,753 -10,954 96,131
CD 329°08’10’’ 106,709 -54,742 91,598
DE 223°10’01’’ 31,858 -21,795 -23,236
EA 171°01’52’’ 85,912 13,394 -81.862
S P = 430,037 ex = 0,021 ey = -0,025
u Cálculo de error de cierre lineal:
u Cálculo del error relativo:
Ü
Ü

217. Redes de apoyo planimétricos
306
Dado que (1/13 000) (1/10 000); se da por aceptado el trabajo de campo.
u Compensación de errores lineales:
- yB = 100,000 + (-79,650) = 20,350
yC = 20,350 + 96,137 = 116,487
yD = 116,487 + 91,604 = 208,091
yE = 208,091 + (23,234) = 184,857
Lado L(m) Cx Cy
AB 108,805 -0,005 0,006
BC 96,753 -0,005 0,006
CD 106,709 -0,005 0,006
DE 31,858 -0,002 0,002
EA 85,912 -0,004 0,005
Lado Dx Dy E(m) N(m) Punto
AB 74,113 -79,650 100,000 100,000 A
BC -10,959 96,137 174,113 20,350 B
CD -54,747 91,604 163,154 116,487 C
DE -21,797 -23,234 108,407 208,091 D
EA 13,390 -84,857 86,610 184,857 E
Punto lado Ángulo Distancia (n) Este (m) Norte (m)
A AB 146°01’46’’ 108,797 100,000 100,000
B BC 36°26’04’’ 96,760 174,113 20,350
C CD 155°38’19’’ 106,717 163,154 116,487
D DE 74°02’13’’ 31,858 198,407 208,091
E EA 127°51’38’’ 85,907 86,610 184,857
Lado
Coordenadas parciales Compensación
Coordenadas parciales
compensadas
Dx Dy Cx Cy Dx Dy
AB 74,118 -79,656 -0,005 0,006 74,113 -79,650
BC -10,954 96,131 -0,005 0,006 -10,959 96,137
CD -54,742 91,598 -0,005 0,006 -54,747 91,604
DE -21,795 -23,236 -0,002 0,002 -21,797 -23,234
EA 13,394 -84,862 -0,004 0,005 13,390 -84,857
S +0,021 -0,025 -0,021 +0,025 0,000 0,000
u Compensando las coordenadas parciales:
u Cálculo de coordenadas absolutas:
- xB = 100,000 + 74,113 = 174,113
xC = 174,113 + (-10,959) = 163,154
xD = 163,154 + (-54,747) = 108,407
xE = 108,407 + (-21,797) = 86,610
Recordar que la medición de
ángulos internos proviene de una
poligonal antihoraria, presentamos
a continuación otro formato, no
obstante obedecer al mismo
sistema de cálculos.
Tener presente que los ángulos finales de cada vértice y las distancias finales entre ellos, cambian en virtud
a la compensación lineal y obtención de coordenadas parciales compensadas; en nuestro caso:
Explicando
-
-

218. 307
NORTE ESTE NORTE ESTE NORTE ESTE NORTE ESTE
A B 146⁰01'55 -1 146⁰01'54 137⁰03'46 108.805 -79.656 74.118 0.006 -0.005 -79.650 74.113 100 100
B C 36⁰26'12 -1 36⁰26'11 353⁰29'57 96.753 96.131 -10.954 0.006 -0.005 96.137 -10.959 20.350 174.113
C D 155⁰38'15 -2 155⁰38'13 329⁰08'10 106.709 91.598 -54.742 0.006 -0.005 91.604 -54.747 116.487 163.154
D E 74⁰01'52 -1 74⁰01'51 223⁰10'01 31.858 -23.236 -21.795 0.002 -0.002 -23.234 -21.797 208.091 108.407
E A 127⁰51'53 -2 127⁰51'51 171⁰01'52 85.912 -84.862 13.394 0.005 -0.004 -84.857 13.390 184.857 86.610
∑ 540⁰00'07 - 7 540⁰00'00 430.037 -0.025 0.021 0.025 -0.021 0.000 0.000
EST - P.V.
PROYECCIONES
PROYECCIONES
COMPENSADAS
COORDENADAS
ABSOLUTAS
ÁNGULO
INTERNO
OBSERVADO
COMPENSACIÓN
ÁNGULO
INTERNO
COMPENSADO
COMPENSACIÓN
AZIMUT

219. 308
PUNTO DE CONTROL PLANIMÉTRICO
ENERO -2017
1 / 2500
P-01
LIMA
LAMINA
LIMA
PROYECTO
PERIMÉTRICO
ESPECIALIDAD
PROPIETARIO
UBICACION
PROFESIONAL
ESCALA
CADISTA.
DTO.
PROV.
DPTO.
JUAN PEREZ RODRIGUEZ
CERCADO
Calle
POLIGONAL LIBRO
CONTENIDO
PLANTA
Juan C. Gonzales
POLIGONAL
PTO LADO ÁNGULO DISTANCIA (m) ESTE (m) NORTE (m)
A AB 146°01'46 108,797 100,000 100,000
B BC 36°26'04 96,760 174,113 20,350
C CD 155°38'19 106,717 163,154 116,487
D DE 74°02'13 31,858 108,407 208,091
E EA 127°51'38 85,907 86,610 184,857
Graficando:

220. 309
2
Determinar las coordenadas de los puntos B; C; D y E, sabiendo que el teodolito con el cual se
trabaja tiene una precisión de cinco segundos.
Además:
Pto. Ángulo promedio medido L (m) Lado
A 192°11’04’’ 98,353 AB
B 274°59’07’’ 306,45 BC
C 268°24’50’’ 76,223 CD
D 253°01’30’’ 293,180 DE
E 271°23’36’’ 74,866 EA
Pto. Este (m) Norte (m)
A 276952,651 8670505,707
P 276955,857 8670423,375
87°49’30’’
C D
E
A
B
P

221. 310
Solución:
Conociendo las coordenadas de los puntos A y P procedemos a cacular el azimut AP.
ZAP = 177°46’12’’
Graficando: N
E
P
A
B
87°49’30’’
ZAP = 177°46’12’’
ZAB = 265°35’42’’
En adelante, el problema se resuelve adoptando el mismo procedimiento del ejemplo anterior.
Análisis de cierre angular
Según el cuadro:
ΣÁNGULOS = 1260°00’07’’
Luego EC = +7’’
EC EMAX (medición angular aceptable)
Error de cierre lineal (ver cuadro)
Error relativo
Perímetro = 849,072 m (ver cuadro)
Dado que ER
(Poligonal aceptable)
ε
ε
ε
ε
ε

222. 311
NORTE ESTE NORTE ESTE NORTE ESTE NORTE ESTE
A B 192⁰11'04 - 1.4 192⁰11'2,6 265⁰35'42 98.353 -7.554 -98.063 0.002 -0.001 -7.552 -98.064 8670505.707 276952.651
B C 274⁰59'07 - 1.4 274⁰59'5,6 0⁰34'47.6 306.45 306.434 3.102 0.005 -0.004 306.439 3.098 8670498.155 276854.587
C D 268⁰24'50 - 1.4 268⁰24'48,6 88⁰59'36.2 76.223 1.339 76.211 0.001 -0.001 1.340 76.210 8670804.594 276857.685
D E 253⁰01'30 - 1.4 253⁰01'28,6 162⁰01'4.8 293.18 -278.859 90.51 0.005 -0.003 -278.854 90.507 8670805.934 276933.895
E A 271⁰23'36 - 1.4 271⁰23'34,6 253⁰24'39.4 74.866 -21.375 -71.75 0.001 -0.001 -21.374 -71.751 8670527.081 277024.402
∑ 1260⁰00'07 - 7 1260⁰00'00 849.072 -0.015 0.01 0.015 -0.010 0.000 0.000
EST - P.V.
PROYECCIONES
PROYECCIONES
COMPENSADAS
COORDENADAS
ABSOLUTAS
ÁNGULO
EXTERNO
OBSERVADO
COMPENSACIÓN
ÁNGULO
EXTERNO
COMPENSADO
COMPENSACIÓN
AZIMUT

223. 312
PTO LADO ÁNGULO DISTANCIA (m) ESTE (m) NORTE (m)
A AB 167°48'55 98,355 276952.651 8670505.707
B BC 85°01'01 306,455 276854.587 8670498.155
C CD 91°35'12 76,222 276857.685 8670804.594
D DE 106°58'28 293,173 276933.895 8670805.934
E EA 88°36'24 74,867 277024.402 8670527.081
PUNTO DE CONTROL PLANIMÉTRICO
ENERO -2017
1 / 4000
P-01
LIMA
LAMINA
LIMA
PROYECTO
PERIMÉTRICO
ESPECIALIDAD
PROPIETARIO
UBICACION
PROFESIONAL
ESCALA
CADISTA.
DTO.
PROV.
DPTO.
AURELIO QUIROZ
CERCADO
Calle
POLIGONAL LIBRO
CONTENIDO
PLANTA
Juan C. Gonzales
POLIGONAL

224. Redes de apoyo planimétricos
313
C1.2 poligonal cerrada completamente ligada en sus dos extremos.- Consiste en un conjunto
de líneas consecutivas en la que se conocen las coordenadas de los puntos inicial y final, así
como las orientaciones de las alineaciones de partida y de llegada, siendo posible efectuar los
controles de cierre angular y lineal.
La estación de llegada debe tener una exactitud de posición igual o mayor que la del punto de partida.
Este método se usa generalmente en proyectos o estructuras longitudinales, tales como carrete-
ras, canales, ferrocarriles, etc.
El procedimiento para resolver este tipo de poligonales, es muy similar al método anterior, por
tal motivo su explicación se expondrá mediante un ejemplo numérico.
Ejemplo de aplicación
Determinar las coordenadas de los puntos R; T; U; V, sabiendo que el teodolito con el cual se
trabajó, tiene una precisión de veinte segundos; la poligonal citada servirá de apoyo para el
levantamiento de un camino rural donde el error relativo no debe ser mayor que 1/5000.
Lado Distancia (m)
SR 52,503
RT 63,806
TU 75,704
UV 42,600
VM 48,322
Solución:
• Cálculo del acimut de los lados.
S = (200,000 ; 200,000) m
M = (362,940 ; 194,231) m
Para efectos de calcular el
acimut por el método ya
conocido es preciso cono-
cer los ángulos a la derecha
en lugar de deflexiones.
Transformando:

225. Redes de apoyo planimétricos
314
°
= ° + ° − °
64444
4
744444
8
180
RT
Z 350 30' 00 320 10' 20 180
ZRT = 130° 40' 20
°
= ° + ° − °
64444
4
744444
8
180
TU
Z 130 40' 20 106 39' 20 180
ZTU = 57° 19' 40
°
= ° + ° − °
64444
74444
8
180
UV
Z 57 19' 40 229 30' 30 180
ZUV = 106° 50' 10
°
= ° + ° − °
64444
4
74444
4
8
180
VM
Z 106 50' 10 230 20' 10 180
ZVM = 157° 10' 20
°
= ° + ° − °
64444
4
74444
4
8
180
MN
Z 157 10' 20 127 35' 00 180
ZMN = 104° 45' 20
• Analizando el cierre angular (Ec):
– Ec = ZMN (calculado) – ZMN (medido)
Ec = 104° 45' 20 – 104° 44' 50
Ec = 0° 0' 30 (exceso).
– El error máximo permitido:
Ecmax = ±20 n = ±20 5
Ecmax ≅ ±45
Comparando: Ec = 30 45
Lo cual indica que la medición angular es
aceptable.
Nótese que n es el numero de vértices: n = 5
• Compensación de ángulos:
cierre
E 30
C 6
n 5
= = =
Lo cual significa, restar a cada ángulo 6
Punto Ángulo medido C Ángulo compensado
R 320° 10' 20 -6 320° 10' 14
T 106° 39' 20 -6 106° 39' 14
U 229° 30' 30 -6 229° 30' 24
V 230° 20' 10 -6 230° 20' 04
M 127° 35' 00 -6 127° 34' 54
• Recálculo del acimut de los lados:
Punto Ángulo compensado Acimut Lado
S 350° 30' 00 SR
R 320° 10' 14 130° 40' 14 R T
T 106° 39' 14 57° 19' 28 T U
U 229° 30' 24 106° 49' 52 U V
V 230° 20' 04 157° 09' 56 VM
M 127° 34' 54 104° 44' 50 M N
Vera Ud. que el acimut ZMN calculado
coincide con el medido.
• Cálculo de las coordenadas parciales.
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
SR 350°30'00 52,503 –8,665 51,783
RT 130°40'14 63,806 48,395 –41,583
TU 57°19'28 75,704 63,723 40,871
UV 106°49'52 42,600 40,775 –12,335
VM 157°09'56 48,322 18,752 –44,535
MN 104°44'50
Σ p=282,935
Lado ∆x ∆y E(m) N(m) Punto
SR –8,665 51,783 200,000 200,000 S
R T 48,395 –41,583 191,335 251,783 R
T U 63,723 40,871 239,730 210,200 T
U V 40,775 –12,335 303,453 251,071 U
VM 18,752 –44,535 344,228 238,736 V
M N 362,980 194,201 M
• Cálculo de coordenadas absolutas.
S = (200,00 ; 200,00)

226. 315
ε
= −
ε
ε
= −
ε
( ) ( )
ε = ± ε + ε
ε
= =
   
   
ε
   
( )
ε
=
− × =
− ×
× ×
( )
ε −
=
− × =
− ×
× ×
∆ ∆
∆ ∆
Σ

227. 316
NORTE ESTE NORTE ESTE NORTE ESTE NORTE ESTE NORTE ESTE NORTE ESTE
SR 350⁰30'00 350⁰30'00 52.503 51.783 -8.665 200.000 200.000 0.006 -0.007 51.789 -8.672 200.000 200.000
RT 320⁰10'20 130⁰40'20 - 6 320⁰10'14 130⁰40'14 63.806 -41.58 48.395 251.783 191.335 0.007 -0.009 -41.576 48.386 251.789 191.328
TU 106⁰39'20 57⁰19'40 - 6 106⁰39'14 57⁰19'28 75.704 40.87 63.723 210.200 239.730 0.008 -0.011 40.879 63.712 210.212 239.714
UV 229⁰30'30 106⁰50'10 - 6 229⁰30'24 106⁰49'52 42.600 -12.34 40.775 251.071 303.453 0.005 -0.006 -12.330 40.769 251.091 303.426
VM 230⁰20'10 157⁰10'20 - 6 230⁰20'04 157⁰09'56 48.322 -44.54 18.752 238.736 344.228 0.005 -0.007 -44.530 18.745 238.761 344.195
MN 127⁰35'00 104⁰45'20 104⁰44'50 - 6 127⁰34'54 104⁰44'50 194.201 362.980 194.231 362.940 194.231 362.940
Error +30 +00 282.935 -0.030 0.040
0.030 -0.040
PROYECCIONES
COMPENSADAS
COORDENADAS
ABSOLUTAS
EST - P.V.
PROYECCIONES
COORDENADAS
MEDIDAS
AZIMUT
MEDIDO
COMPENSACIÓN
ÁNGULO
A LA
DERECHA
COMPENSADO
AZIMUT
COMPENSADO
COMPENSACIÓN
ÁNGULO
A LA
DERECHA
PRE
COORDENADAS
ABSOLUTAS
AZIMUT
CALCULADO

228. 317
Ejemplo de aplicación 2
Determinar las coordenadas de los puntos A, B, C, D y E, sabiendo que la estación total con la
cual se trabajó, tiene una precisión de cinco segundos. Error relativo tolerable: 1/10 000.
Puntos de control
Teniendo como información las coordenadas de
los puntos de control, es posible calcular los
azimuts PQ y RS.
Solución:
Est. - PV Ángulo Distancia
P - Q
Q - A 222°53’37’’ 39,992
A - B 125°49’02’’ 507,894
B - C 242°53’24’’ 1487,535
C - D 191°31’39’’ 548,826
D - E 189°20’26’’ 405,318
E - R 173°31’13’’ 252,490
R - S 118°58’42’’
Pto. E N
P 596918,958 8523715,259
Q 597951,333 8523648,917
R 599730,308 8521329,633
S 600579,897 8521200,437
Análisis de cierre angular
Tenemos siete ángulos: n = 7
Lado Azimut
P - Q 93°40’36,69’’
R - S 98°38’47,96’’
Según el cuadro: EC = 6,11’’
EC EMAX (medición angular aceptable)
Error de cierre lineal (ver cuadro)
ε = 0,173 m
Error relativo
Perímetro = 3242,055 (ver cuadro)
Dado que ER (Poligonal aceptable)
P
Q
A
B
C
D
E
R S
,
ε
ε
ε
ε

229. 318
PTO
NORTE ESTE NORTE ESTE NORTE ESTE NORTE ESTE NORTE ESTE NORTE ESTE
PQ 93⁰40'36.69 93⁰40'36.69 93⁰40'36.69
QA 222⁰53'37 136⁰34'13.6 + 1.18 222⁰53'38.18 136⁰34'14.8
39.992
-29.043 27.493 8523648.917 597951.333 8523648.917 597951.333 -0.001 -0.002 -29.044 27.491 8523648.917 597951.333
Q
AB 125⁰49'02 82⁰23'15.69 + 1.18 125⁰49'3.18 82⁰23'18.05
507.894
67.275 503.419 8523619.874 597978.826 -0.016 -0.021 67.259 503.398 8523619.873 597978.824
A
BC 242⁰53'24 145⁰16'39.6 + 1.19 242⁰53'25.19 145⁰16'43.2
1487.535
-1222.653 847.279 8523687.149 598482.245 -0.048 -0.063 -1222.701 847.216 8523687.131 598482.222
B
CD 191⁰31'39 156⁰48'18.6 + 1.18 191⁰31'40.18 156⁰48'23.4
548.826
-504.470 216.148 8522464.496 599329.524 -0.018 -0.023 -504.488 216.125 8522464.430 599329.438
C
DE 189⁰20'26 166⁰08'44.69 + 1.18 189⁰20'27.18 166⁰08'50.6
405.318
-393.529 97.043 8521960.026 599545.672 -0.013 -0.017 -393.542 97.026 8521959.942 599545.563
D
ER 173⁰31'13 159⁰39'57.6 + 1.18 173⁰31'14.18 159⁰40'4.78
252.490
-236.759 87.73 8521566.497 599642.715 -0.008 -0.011 -236.767 87.719 8521566.400 599642.589
E
RS 118⁰58'42 98⁰38'39.69 98⁰38'47.96 + 1.18 118⁰58'43.18 98⁰38'47.96 8521329.738 599730.445 8521329.633 599730.308 8521329.633 599730.308
R
Error -8.27 +00 3,242.055 0.105 0.137
-0.105 -0.137
PROYECCIONES
COMPENSADAS
COORDENADAS ABSOLUTAS
EST - P.V.
PROYECCIONES COORDENADAS MEDIDAS
AZIMUT
MEDIDO
COMPENSACIÓN
ÁNGULO
A LA
DERECHA
COMPENSADO
AZIMUT
COMPENSAD0
COMPENSACIÓN
ÁNGULO
A LA
DERECHA
DISTANCIA
HORIZONTAL
PRE COORDENADAS
ABSOLUTAS
AZIMUT
CALCULADO

230. 319
8523000
8522000
8521000
587000
598000
599000
600000
P
Q
B
A
C
D
E
R
S
N

231. Redes de apoyo planimétricos
320
C.2. Poligonal abierta
Consiste en un conjunto de lineas consecutivas, en el cual el punto de partida y llegada
son diferentes.
La particularidad de este método radica en que el punto final no posee coordenadas
conocidas; por tal razón no es posible establecer el control de cierre lineal.
En ocasiones tampoco es conocida la orientación del último lado, no obstante, es reco-
mendable medir el acimut de dicho lado, para obtener así, por los menos el error angular
y ser sometido al ajuste respectivo.
Como un medio de verificación, se recomienda repetir las mediciones y cálculos, sin
embargo debe tratar de evitarse el empleo de este método.
Ejemplo de aplicación
Determinar las coordenadas de los puntos B, C, D y E, sabiendo que el teodolito con el cual se
trabajó tiene una precisión de veinte segundos.
Solución:
• Cálculo del acimut de los lados.
Lado Distancia (m)
AB 20,250
BC 32,260
CD 17,420
DE 25,240
A = (100,000 ; 100,000) m
Para efectos de calcular
el acimut por el méto-
do ya conocido, es pre-
ciso conocer los ángu-
los a la derecha en lu-
gar de deflexiones.
Transformando:

232. Redes de apoyo planimétricos
321
• Analizando el cierre angular (Ec):
– Ec = ZDE (calculado) – ZDE (medido)
Ec = 57° 49' 10 – 57° 49' 40
Ec = –0° 00' 30 (Defecto)
– El error máximo permitido:
Ecmax = ±20 n = ±20 3
Ecmax ≅ ±35
Comparando: Ec = 30 35
Lo cual indica que la medición angular es
aceptable.
• Compensación de ángulos:
cierre
E 30
C 10
n 3
−
= = = −
Lo cual significa, sumar a cada ángulo 10
Lado Acimut
AB 40° 30' 10
BC 122° 50' 40
CD 45° 23' 00
DE 57° 49' 10 • Recálculo del acimut de los lados
Punto Ángulo medido C Ángulo compensado
B 262° 20' 30 +10 262° 20' 40
C 102° 32' 20 +10 102° 32' 30
D 192° 26' 10 +10 192° 26' 20
Punto Ángulo compensado Acimut Lado
A 40° 30' 10 AB
B 262° 20' 40 122° 50' 50 BC
C 102° 32' 30 45° 23' 20 CD
D 192° 26' 20 57° 49' 40 DE
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
AB 40°30'10 20,250 13,152 15,398
BC 122°50'50 32,260 27,102 –17,498
CD 45°23'20 17,420 12,401 12,234
DE 57°49'40 25,240 21,364 13,439
Lado ∆x ∆y E(m) N(m) Punto
AB 13,152 15,398 100,000 100,000 A
BC 27,102 –17,498 113,152 115,398 B
CD 12,401 12,234 140,254 97,900 C
DE 21,364 13,439 152,655 110,134 D
174,019 123,573 E
Vera Ud. que el acimut ZDE calculado,
coincide con el medido.
• Cálculo de las coordenadas parciales.
• Cálculo de coordenadas absolutas.
A = (100,000 ; 100,000) m
• Graficando:

233. Redes de apoyo planimétricos
322
Preguntas y respuestas
Si para efectos de levantar una poligonal cerrada de circuito cerrado, se cuenta tan solo
con las coordenadas del punto inicial mas no con el acimut de referencia. ¿Se puede
asumir un acimut arbitrario para no retrazar el trabajo?
La respuesta es SI.
Fig. 1: Suponga Ud. que se tiene una poligonal en la cual se conoce tanto las coordenadas del
punto de partida como el acimut del primer lado. (ZAB = 30°).
Fig. 2: Si Ud. no conoce dicho acimut, puede asumir un valor arbitrario, por ejemplo 50°, para
luego levantar la poligonal, incluso el relleno topográfico y realizar los cálculos respectivos,
obteniendo un gráfico como el que se muestra.
Fig. 3: Posteriormente, determine el acimut real de la línea AB, en el presente caso 30°. Para
orientar poligonal y relleno en la dirección verdadera, tan solo habrá que rotar todo el
sistema un ángulo de 50° – 30° = 20° en sentido antihorario.
Fig. 1: Después de concluído el
cálculo, los puntos de la poligonal
y relleno quedarán en su posición
real por tanto las direcciones de sus
lados también lo serán.
Fig. 2: Después de concluído el cál-
culo, los lados de la poligonal y relle-
no quedarán rotados respecto al pun-
to A. Por tanto los puntos estarán ubi-
cados en posiciones no reales.
Fig. 3: Los puntos de la poligonal
y relleno se ubican en su posi-
ción real al rotar el sistema un án-
gulo de: 50° – 30° = 20° respecto al
punto A.
Si para efectos de levantar una poligonal cerrada de circuito cerrado, no se cuenta con las
coordenadas del punto inicial ni con el acimut de referencia. ¿Se puede levantar una
poligonal y luego el relleno? - el trabajo es tan solo de interés del propietario.
La respuesta es SI; dado que la geometría de la poligonal es independiente de las coordenadas
del punto de partida así como del acimut respectivo.
Si bien es cierto, la poligonal con coordenadas relativa no estará enlazado a una red oficial; los
detalles levantados (edificaciones, vías, terreno natural, etc.), estarán relacionados entre sí tal
como lo están en el terreno, a una escala elegida.

234. Redes de apoyo planimétricos
323
Este tipo de trabajo se suele usar, generalmente cuando el levantamiento es de interés tan solo del
propietario, para efectos de ampliación, remodelación mantenimiento o cambios varios en el terreno.
Generalmente un plano definitivo casi siempre a de pasar por algún organismo público (muni-
cipalidad, registros públicos, etc.) en donde los ingenieros concatenarán dicho plano con las
cartas oficiales, para lo cual el sistema de referencia debe ser el mismo.
En una poligonal cerrada ligada en sus dos extremos: Si los puntos inicial y final, están
ligados a una red nacional. ¿ Las distancias medidas en dicha poligonal se enlazarán direc-
tamente a dichos puntos?
La respuesta es NO, pues antes es necesario realizar dos ajustes importantes:
– Reducir las longitudes medidas a su equivalente en el nivel medio del mar.
– Las distancias que han sido sometidas al primer ajuste, (distancia topográficas) deben ser
transformadas a distancias de cuadrícula.
Con estos dos ajustes, recién es aceptable enlazar las distancias obtenidas con la red nacional.
En cualquier tipo de poligonal ¿cuántas veces deben ser medidos los ángulos acimutales
en cada vértice?
Dependiendo de la precisión buscada, se deben medir varias veces y aplicando la regla de Bessel
(anteojo directo e invertido).
¿ Cómo se obtienen las coordenadas absolutas de los puntos inicial y final en una poligonal?.
Al respecto, existen varias metodologías:
– Cuando el punto de partida pertenece a una red geodésica.

235. 324

236. Redes de apoyo planimétricos
325
• Ilustrando:
Dado que se conocen las coordenadas de
P, así como A, B, C, D y E; es posible
calcular las distancias radiales así como
los acimuts respectivos.
• Analizando PA
( ) ( )
= − + − =
2 2
d 150 78 70 125 90,60
−
=
−
PA
150 78
Z arctg
70 125
ZPA = 127° 22' 32,9
• Finalmente:
Estación Punto Acimut d(m)
A 127° 22' 32,90 90,600
B 221° 18' 58,40 77,314
P C 310° 16' 44,20 50,938
D 18° 09' 07,32 31,893
E 85° 15' 39,69 54,202
2. En el levantamiento de los linderos de un
predio, se omitieron dos medidas que pre-
sentaron dificultades poco comunes en
el campo; esto se ilustra en la siguiente
tabla de campo.
Es importante en el proceso de cálculo del
acimut, comparar las posibles soluciones
con el gráfico y escoger el valor adecuado.
Observación
Línea Distancia (m) Rumbo
CD 952,60 N 80° 15' E
DE 844,10 S 87° 37' E
EF 397,00 S 17° 15' W
FC ? ?
Solución:
• Cálculo de las coordenadas parciales de cada
lado.
Lado Acimut Dist.(m) ∆x ∆y
CD 80°15' 952,60 938,84 161,32
DE 92°23' 844,10 843,37 –35,10
EF 197°15' 397,00 –117,73 –379,14
FC Z d dSen Z dCos Z
Σ εx εy
• εx = 938,84 + 843,37 – 117,73 + dSen Z = 0
dSen Z = –1 664,48 ...................(1)
• εy = 161,32 – 35,10 - 379,14 + dCos Z = 0
dCos Z = 252,92 ...................... (2)
• De (1) y (2)
ZFC = 278° 38'
ó Rumbo(FC) = N 81° 22' W
d = 1 683,59 m
Calcule los datos faltantes:

237. Redes de apoyo planimétricos
326
3. Se realizó un levantamiento topográfico
por el método de intersección de visua-
les, la libreta de campo es la que se mues-
tra, si A(100,00 ; 100,00); determinar las
coordenadas absolutas de los otros vérti-
ces (teodolito con aproximación a 20).
AB = 32,65 m
Estación “A” Acimut
B 156° 48' 50
1 56° 43' 10
2 108° 25' 50
3 141° 17' 20
4 189° 53' 30
5 234° 29' 20
6 306° 58' 30
Estación “B” S Horizontal
A 0° 00' 00
1 33° 14' 20
2 81° 32' 10
3 133° 46' 40
4 240° 33' 40
5 314° 40' 30
6 348° 21' 50
Punto lado Z $
S ABn (interno)
1 A1 56° 43' 10 33° 14' 20
2 A2 108° 25' 50 81° 32' 10
3 A3 141° 17' 20 133° 46' 40
4 A4 189° 53' 30 119° 26' 20
5 A5 234° 29' 20 45° 19' 30
6 A6 306° 58' 30 11° 39' 10
Punto lado |ZAB – ZAi| θi Ai (m)
1 A1 100° 05' 40 46° 40' 00 24,60
2 A2 48° 23' 00 50° 04' 50 42,11
3 A3 15° 31' 30 30° 41' 50 46,18
4 A4 33° 04' 40 27° 29' 00 61,66
5 A5 77° 40' 30 57° 00' 00 27,68
6 A6 150° 09' 40 18° 12' 10 21,08
Solución:
Nótese: θi = 180° –
 
− +
 
AB Ai
Z Z ABi
• Aplicando el mètodo de radiación respec-
to al punto “A”.
• Finalmente
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
A1 56°43'10 24,60 20,57 13,50
A2 108°25'50 42,11 39,95 –13,31
A3 141°17'20 46,18 28,88 –36,04
A4 189°53'30 61,61 –10,58 –60,69
A5 234°29'20 27,68 –22,53 –16,08
A6 306°58'30 21,08 –16,84 12,68
Punto E = 100 + ∆x N = 100 + ∆y
1 120,57 113,50
2 139,95 86,69
3 128,88 63,96
4 89,42 39,31
5 77,47 83,92
6 83,16 112,68
4. Calcular las coordenadas totales del polígono
ABCDE, calculado a partir de una base medi-
da y cuya base es el lado AB y mide 111,803 m.
Coordenada A = (250,00 ; 200,00) m.
Estación “A” Acimut
B 153° 26' 06
C 213° 41' 24
D 255° 57' 50
E 281° 18' 36
Estación “B” S Horizontal
A 0° 00' 00
C 278° 07' 48
D 307° 52' 30
E 329° 35' 20

238. Redes de apoyo planimétricos
327
Solución:
Punto Lado |ZAB – ZAi| θi Ai (m)
C AC 60° 15' 18 37° 52' 30 180,277
D AD 102° 31' 44 25° 20' 46 206,155
E AE 127° 52' 30 21° 42' 50 152,971
Nótese: θi = 180° – $
 
− +
 
AB Ai
Z Z ABi
• Aplicando el método de radiación respec-
to al punto “A”.
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
AB 153°26'06 111,803 50,000 –100,000
A C 213°41'24 180,277 –100,000 –150,000
AD 255°57'50 206,155 –200,000 –50,000
AE 281°18'36 152,971 –150,000 30,000
Punto E = 250,000 + ∆x N = 200,000 + ∆y
A 250,000 200,000
B 300,000 100,000
C 150,000 50,000
50,000 150,000
E 100,000 170,000
• Finalmente:
Punto Lado Z
5 ABn (interno)
C AC 213° 41' 24 81° 52' 12
D AD 255° 57' 50 52° 07' 30
E AE 281° 18' 36 30° 24' 40
5. Se ha realizado un levantamiento
planimétrico con una estación total,
obteniéndose los siguiente datos de campo:
Posición Pto/dirección Áng. Acimutal DH
Espalda NM 0° 00' 05 ----------
Frente B 125° 10' 30 50,432
Posición Punto Áng. Acimutal DH
Espalda A 0° 00' 00 50,432
Frente C 287° 43' 42 43,780
Posición Punto Áng. Acimutal DH
Espalda B 0° 00' 00 43,780
Frente A 300° 36' 46 55,816
Posición Punto Áng. Acimutal DH
Espalda C 0° 00' 00 55,816
Frente B 311° 39' 32 50,432
Estación A
Estación B
Estación C
Estación A
Se pide calcular las coordenadas de los
puntos B y C.
Sabiendo: A = (500,000 ; 500,000) m
Solución:
• Graficando el croquis del polígono
– Σ ángulos externos:
Σ = 311° 39' 32 + 287° 43' 42 + 300° 36' 46
Σ = 900° 00' 00
Lo cual significa que no es necesario la
compensación
– ZAB = 125° 10' 30
– ZBC = (125° 10' 30 + 287° 43' 42) – 180°
ZBC = 232° 54' 12
– ZCA = (232° 54' 12 + 300° 36' 46) – 180°
ZCA = 353° 30' 58

239. Redes de apoyo planimétricos
328
• Cálculo de las coordenadas
Lado ∆x ∆y E(m) N(m) Punto
AB 41,223 –29,053 500,000 500,000 A
BC –34,920 –26,406 470,947 541,223 B
C A –6,303 55,459 444,541 506,303 C
Σ 0,000 0,000 500,000 500,000 A
Nótese que no ha sido necesario realizar la com-
pensación lineal, dado que tanto, εx y εy son nulos.
6. Se realiza el levantamiento topográfico de una
polígonal cerrada con ayuda de una estación
total; se muestra el croquis respectivo.
Coordenadas de A = (100,00 ; 100,00) m
Libreta de campo:
Estación Pto. visado Áng. horizontal DH(m)
P 20° 30' 10
A
B 152° 20' 50 24,304
A 19° 16' 45 24,304
B
C 242° 23' 08 37,883
B 119° 49' 30 37,883
C
A 103° 11' 43 58,047
C 190° 46' 36 58,047
D
B 164° 17' 58 24,304
Se pide determinar:
– El acimut de cada lado de la poligonal.
– Las coordenadas planimétricas de B y C.
– El error angular.
– El error relativo planimétrico.
Precisión angular de la estación total = 5
Solución:
• Resumen de la libreta de campo
ZAB = 152° 20' 50
– Nótese:
333° 31' 22 = (164° 17' 58 + 360°) – 190° 46' 36
223° 06' 23 = 242° 23' 08 – 19° 16' 45
343° 22' 13 = (103° 11' 43 + 360°) – 119° 49' 30
– Dato: ZAB = 152° 20' 50
• Cálculo del error angular (Ec)
Σ ang. horizontal = 899° 59' 58
Σ Teórica = 180°(n + 2) = 180°(3 + 2) = 900°
Ec = 899° 59' 58 – 900° = –2
Emáx = ±5 n = ±5 3 = ±8,7
Comparando: Ec = 2 8,7
Lo cual indica que la medición angular
es aceptable.
Estación Áng. Horizontal d(m) Lado
A 333° 31' 22 24,304 AB
B 223° 06' 23 37,883 BC
C 343° 22' 13 58,050 CA
Σ 899° 59' 58

240. Redes de apoyo planimétricos
329
• Compensación de ángulos:
cierre
E 2
C 0 ,7
n 3
−
= = −
;
Lo cual significa que debemos incremen-
tar a dos ángulos el valor de 0,7, y mien-
tras que al tercero tan sólo 0,6; para que
la suma de Ci resulte exactamente 2.
• Acimut de cada lado:
Punto lado 5 Horizontal Z
A AB 333° 31' 22 152° 20' 50
B BC 223° 06' 23,7 195° 27' 13,7
C C A 343° 22' 13,6 358° 49' 27,3
Σ 900° 00' 00
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
AB 152°20'50 24,304 11,280 –21,528
BC 195°27'13,7 37,883 –10,094 –36,513
CA 358°49'27,3 58,050 –1,191 58,038
Σ p=120,237 εx = –0,005 εy = –0,003
• Coordenadas parciales:
• Error de cierre lineal:
( ) ( )
ε = + =
2 2
0, 005 0, 003 0, 006 m
• Cálculo del error relativo planimétrico:
= =
   
   
ε
   
R
1 1
E
Perímetro 120,237
0,006
;
R
1
E
20 000
• Compensación de errores lineales:
( )
ε −
= − × = − ×
x
x
0, 005
C L L
p 120, 237
Cx = 4,158×10–5
m
( )
ε −
= − × = − ×
y
y
0, 003
C L L
p 120, 237
Cy = 2,495×10–5
m
Lado L(m) Cx C y
AB 24,304 0,001 0,001
BC 37,883 0,002 0,001
C A 58,050 0,002 0,001
Σ 0,005 0,003
Coord. parciales comp. Coord. absolutas
Lado ∆x ∆y E(m) N(m) Punto
AB 11,281 –21,527 100,000 100,000 A
BC –10,092 –36,512 111,281 78,473 B
C A –1,189 58,039 101,189 41,961 C
Coordenadas parciales compensadas
Lado ∆x + Cx ∆y + Cy
AB 11,281 –21,527
BC –10,092 –36,512
C A –1,189 58,039
Σ 0,000 0,000
• Compensando:
• Cálculo de las coordenadas absolutas
planimétricas:
7. Se tiene un terreno de vértices ABCDEQ. Al
realizarse el levantamiento perimetral por el
método de la polígonal cerrada, se descubre
que es imposible estacionar el teodolito en el
punto Q, por lo cual se decide hacer el levan-
tamiento del polígono ABCDEF.
Si QF = 30,32 m; se pide:
A) El error relativo de la poligonal
ABCDEF.
B) El perímetro del terreno (ABCDEQ).

241. Redes de apoyo planimétricos
330
Datos de campo:
ZAB = 143° 28' 52,5
Punto A. Directo A. Inverso d(m) Lado
A 90° 14' 20 360° 57' 34 83,52 AB
B 153° 20' 13 613° 20' 40 63,49 BC
C 68° 23' 48 273° 35' 00 57,41 CD
D 204° 13' 35 816° 54' 04 87,55 DE
E 58° 19' 50 233° 18' 54 110,11 EF
F 145° 28' 40 581° 54' 13 55,59 FA
Precisión angular del teodolito = 5
Solución:
• Análisis del ángulo acimutal medido en
cada vértice: Observando los datos de cam-
po, deducimos que los valores correspon-
dientes al anteojo invertido son cuatro ve-
ces al tomado con anteojo directo, de lo
cual se concluye que la repetición de cada
ángulo es de cuatro veces, luego:
Pto. 5 Promedio 5 Compensado d(m) Lado
A 90° 14' 23,5 90° 14' 22,5 83,52 AB
B 153° 20' 10 153° 20' 09 63,49 BC
C 68° 23' 45 68° 23' 44 57,41 CD
D 204° 13' 31 204° 13' 30 87,55 DE
E 58° 19' 43,5 58° 19' 42,5 110,11 EF
F 145° 28' 33,25 145° 28' 32 55,59 FA
Σ 720° 00' 6,25 0° 00' 00 457,67
• Cálculo del error angular (Ec)
Σ ang. horizontal = 720° 00' 6,25
Σ Teórica = 180°(n – 2) = 180°(6 – 2) = 720°
Ec = 720° 00' 6,25 – 720° = 6,25
Emáx = ±5 n = ±5 6 = ±12,2
Comparando: Ec = 6,25 12,2
Lo cual indica que la medición angular es aceptable.
• Compensación de ángulos:
cierre
E 12 , 2
C 1, 042
n 6
= = ;
No obstante, nosotros optaremos por restar a
cada ángulo 1, a exepción de “F” al cual se le
sustrae 1,25. La decisión la toma Ud.
• Coordenadas parciales
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
AB 143°28'52,5 83,52 49,70 –67,12
BC 116°49'01,5 63,49 56,66 –28,64
CD 5°12'45,5 57,41 5,22 57,17
DE 29°26'15,5 87,55 43,03 76,25
EF 267°45'58 110,11 –110,03 –4,29
FA 233°14'30 55,59 –44,54 –33,27
Σ p=457,67 εx = 0,04 εy = 0,10
• Error de cierre lineal:
( ) ( )
ε = + =
2 2
0, 04 0,10 0,11 m
• Cálculo del error relativo planimétrico:
= =
   
   
ε
   
R
1 1
E
Perímetro 457,67
0,11
=
R
1
E
4 160

242. Redes de apoyo planimétricos
331
• Coordenadas parciales compensadas:
Lado Cx C y ∆x + Cx ∆y + Cy d(m)
AB –0,01 –0,02 49,69 –67,14 83,53
BC –0,01 –0,02 56,65 –28,66 63,49
CD 0,00 –0,01 5,22 57,16 57,40
DE –0,01 –0,02 43,02 76,23 87,53
EF –0,01 –0,02 –110,04 –4,31 110,12
FA 0,00 –0,01 –44,54 –33,28 55,60
Nótese: ( ) ( )
= ∆ + + ∆ +
2 2
x y
d x C y C ; di-
cho valor difiere ligeramente del medido en
campo, como es de esperar.
• Analizando el triángulo AQF
( ) ( ) ( )( )
= + − °
2 2
AQ 55,60 20,32 2 55,60 20,32 Cos34 31' 28
AQ = 40,53 m
• El perímetro del terreno (ABCDEQ)
p = AB + BC + CD + DE + EF + FQ + QA
p = 83,53 + 63,49 + 57,40 + 87,53 + 110,12 +
20,32 + 40,53
p = 462,92 m
8. Se desea levantar la piscina en planta,
para lo cual se cuenta con la poligonal
cerrada A, 1, 2, 3, 4, 5, 6; sin embargo es
imposible dicho objetivo desde dicha
poligonal, por lo que se decide ubicar
un punto de control auxiliar “P”.
Determinar las coordenadas absolutas
del punto P.
Datos de la poligonal abierta:
Punto S Medido d(m) Lado
A AB
B 250° 20' 10 121,432 BC
C 72° 13' 40 77,456 CD
D 284° 20' 50 37,125 DE
E 293° 57' 30 93,233 EF
F 42° 16' 20 150,601 FG
G
Coordenadas Absolutas:
A = (101,532 ; 209,410) m
B = (176,314 ; 317,642) m
Acimut medido en campo:
ZFG = 77° 47' 26,9

243. Redes de apoyo planimétricos
332
Datos del triángulo G1P:
Lado Z D(m)
G-1 105° 23' 19 32,010
1-2 50° 54' 09 30,280
2-3 347° 00' 49 102,460
3-4 302° 47' 35 55,420
4-5 212° 25' 16 38,650
5-6 161° 31' 41 113,610
Punto Ángulo
G 299° 59' 30
1 300° 00' 00
P 300° 00' 00
Solución:
• Solucionando la poligonal abierta, con el obje-
tivo de calcular las coordenadas del punto “G”.
• Calculando el acimut de cada lado:
Punto Ángulo Acimut Lado
A 34° 38' 31,9 AB
B 250° 20' 10 104° 58' 41,9 BC
C 72° 13' 40 357° 12' 21,9 CD
D 284° 20' 50 101° 33' 11,9 DE
E 293° 57' 30 215° 30' 41,9 EF
F 42° 16' 20 77° 47' 1,9 FG
G
• Analizando el error de cierre angular:
ZFG (medido) = 77° 47' 26,9
ZFG (calculado) = 77° 47'
Error angular = 77° 47' 1,9 – 77° 47' 26,9
Error angular = –25
• Compensación angular:
Dado que el error se presenta por defecto,
habrá que agregar a cada ángulo:
= =
25
Compensación 5
5
Con lo cual se obtiene:
Punto Ángulo Acimut Lado
A 34° 38' 31,9 AB
B 250° 20' 15 104° 58' 46,9 BC
C 72° 13' 45 357° 12' 31,9 CD
D 284° 20' 55 101° 33' 26,9 DE
E 293° 57' 35 215° 31' 01,9 EF
F 42° 16' 25 77° 47' 26,9 FG
G
• Cálculo de las coordenadas de los puntos
de control.
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
AB 34°38'31,9 131,554 74,782 108,232
BC 104°58'46,9 121,432 117,305 –31,387
CD 357°12'31,9 77,456 –3,772 77,364
DE 101°33'26,9 37,125 36,372 –7,438
EF 215°31'01,9 93,233 –54,164 –75,886
FG 77°47'26,9 150,601 147,195 31,849
Lado ∆x ∆y E(m) N(m) Punto
AB 74,782 108,232 101,532 209,410 A
BC 117,305 –31,387 176,314 317,642 B
CD –3,772 77,364 293,619 286,255 C
DE 36,372 –7,438 289,847 363,619 D
EF –54,164 –75,886 326,219 356,181 E
FG 147,195 31,849 272,055 280,295 F
419,250 312,144 G
Datos de la poligonal cerrada:

244. Redes de apoyo planimétricos
333
• Solucionando la poligonal cerrada, con el
objetivo de calcular las coordenadas del
punto “1”.
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
G-1 105°23'19 32,010 30,862 –8,494
1-2 50°54'09 30,280 23,499 19,096
2-3 347°00'49 102,460 –23,025 99,839
3-4 302°47'35 55,420 –46,588 30,016
4-5 212°25'16 38,650 –20,722 –32,626
5-G 161°31'41 113,610 35,996 –107,757
Σ p=372,430 εx = 0,022 εy = 0,074
Lado Cx C y ∆x + Cx ∆y + Cy
G-1 –0,002 –0,006 30,860 –8,500
1-2 –0,002 –0,006 23,497 19,090
2-3 –0,006 –0,020 –23,031 99,819
3-4 –0,002 –0,011 –46,590 30,005
4-5 –0,003 –0,008 –20,725 –32,634
5-G –0,007 –0,023 35,989 –107,780
Coord. parciales comp. Coord. absolutas
Lado ∆x ∆y E(m) N(m) Punto
G-1 30,860 –8,500 419,250 312,144 G
1-2 23,497 19,090 450,110 303,644 1
2-3 –23,031 99,819 473,607 322,734 2
3-4 –46,590 30,005 450,576 422,553 3
4-5 –20,725 –32,634 403,986 452,558 4
5-G 35,989 –107,780 383,261 419,924 5
Error de cierre lineal:
( ) ( )
ε = + =
2 2
0, 022 0, 074 0, 077 m
Cálculo del error relativo planimétrico:
( )
= =
ε
R
1 1
E
372, 430
Perímetro
0, 077
=
R
1
E
4 800
• Analizando el triángulo G1P: El acimut G1,
se calcula gracias a las coordenadas de G y 1
• Coordenadas de “P”
Conociendo G = (419,250 ; 312,144) m
E = 419,250 + 32,009Sen 165° 24' 18,3
E = 427,316 m
N = 312,144 + 32,009Cos 165° 24' 18,3
N = 281,168 m
Por tanto:
P = (427,316 ; 281,168) m
Compensando ángulos:

245. Redes de apoyo planimétricos
334
9. Se desea realizar una red de apoyo, teniendo
como control, las estacas: A, B, C, D y E;
para lo cual se usa el método de radiación,
obteniéndose la siguiente libreta de campo.
Estación P (N = 100 ; E = 100)
Línea Distancia (m) Acimut
PA 67,32 235° 26' 10
PB 36,30 310° 40' 32
PC 48,43 30° 12' 10
PD 56,37 110° 38' 05
Como quiera que no se pudo visar el punto
E, se hizo estación en A y en D, obteniéndose:
Estación en A: S PAE = 40° 20' 20
Estación en D: S PDE = 51° 27' 30
Se pide calcular las coordenadas de los
puntos A, B, C, D y E.
Solución:
• Aplicando el método de radiación respec-
to al punto P.
Lado Z d (m) ∆x = dsen Z ∆y = dcos Z
PA 235°26'10 67,32 –55,44 –38,19
PB 310°40'32 36,30 –27,53 23,66
PC 30°12'10 48,43 24,36 41,86
PD 110°38'05 56,37 52,75 –19,87
Punto E = 100,00 + ∆x N = 100,00 + ∆y
A 44,56 61,81
B 72,47 123,66
C 124,36 141,86
D 152,75 80,13
• Analizando la posición del punto “E”
– = = °
−
PD
52, 75
Z arctg 110 38' 25,8
19,87
–
−
= = °
−
PA
55, 44
Z arctg 235 26' 19, 9
38,19
P = ZPA – ZPD = 124° 47' 54,1
– µ
E = 360° – ( µ
A + µ
D +
P)
µ
E = 143° 24' 15,9
– α + β = 143° 24' 15,9 ............... (1)
– =
° α
L 67,32
Sen 40 20' 20 Sen
=
α
43,577
L
Sen
.................................. (2)
– =
° β
L 56,37
Sen 51 27' 30 Sen
=
β
44, 09
L
Sen
.................................... (3)

246. Redes de apoyo planimétricos
335
– De (1), (2) y (3)
β = 72° 42' 57,28
L = 46,18 m
– θ = 180° – (51° 27' 30 + β)
θ = 55° 49' 32,72
– ZPE = ZPD + θ = 166° 27' 37,7
– Coordenadas parciales de “E”
∆x = L⋅Sen ZPE = 10,81 m
∆y = L⋅Cos ZPE = –44,90 m
– Coordenadas absolutas de “E”
N = 100,00 + (–44,90) = 55,10 m
E = 100,00 + 10,81 = 110,81 m
• Finalmente:
Punto Norte(m) Este(m)
A 61,81 44,56
B 123,66 72,47
C 141,86 124,36
D 80,13 152,75
E 55,10 110,81
10. Se tiene el siguiente registro de campo de
una poligonal ABCDE.
Punto lado Ss Internos Acimut d (m)
A AB 100° 26' 00 158° 49' 44 75,84
B BC 120° 23' 05 78,03
C CD 85° 44' 40 103,62
D DE 89° 27' 00 71,97
E EA 143° 59' 45 48,68
– Calcular las coordenadas absolutas de la
poligonal si: A(59,00 ; 130,00) m
– Calcular las coordenadas absolutas de un
punto K de tal modo que CK divide al
polígono en dos áreas iguales. K pertene-
ce al perímetro del polígono.
Solución:
• Σ ángulos internos = 540° 00' 30
Error de cierre angular = +30
−
= = −
30
Compensación angular 6
5
• Compensando los ángulos y desarrollando:
Punto lado Ángulo Z
A AB 100° 25' 54 158° 49' 44
B BC 120° 22' 59 99° 12' 43
C CD 85° 44' 34 4° 57' 17
D DE 89° 26' 54 274° 24' 11
E EA 143° 59' 39 238° 23' 50
Lado d (m) ∆x = dsen Z ∆y = dcos Z
AB 75,84 27,39 –70,72
BC 78,03 77,02 –12,49
CD 103,62 8,95 103,23
DE 71,97 –71,76 5,53
EA 48,68 –41,46 –25,51
Σ 378,14 0,14 0,04
– Error de cierre lineal:
( ) ( )
= + =
2 2
Ec 0,14 0, 04 0,146 m
– Cálculo del error relativo planimétrico:
= =
   
   
   
R
1 1
E
Perímetro 378,14
Ec 0,146
=
R
1
E
2 590

247. Redes de apoyo planimétricos
336
• Compensando las coordenadas parciales:
–
ε
= − × = − ×
x
x
0,14
C L L
p 378,14
Cx = 3,70×10–4
×L
–
ε
= − × = − ×
y
y
0, 04
C L L
p 378,14
Cy = 1,06×10–4
×L
Lado L(m) Cx C y
AB 75,84 –0,03 –0,01
BC 78,03 –0,03 –0,01
CD 103,62 –0,04 –0,01
DE 71,97 –0,02 –0,01
EA 48,68 –0,02 0,00
Coord. parciales comp. Coord. absolutas
Lado ∆x ∆y E(m) N(m) Punto
AB 27,36 –70,73 59,00 130,000
BC 76,99 –12,50 86,36 59,27 B
CD 8,91 103,22 163,35 46,77 C
DE –71,78 5,52 172,26 149,99 D
EA –41,48 –25,51 100,48 155,51 E
Coordenadas parciales compensadas
Lado ∆x + Cx ∆y + Cy
AB 27,36 –70,73
BC 76,99 –12,50
CD 8,91 103,22
DE –71,78 5,52
EA –41,48 –25,51
• Calculando las coordenadas del punto K.
Teniendo presente que el área de un trián-
gulo se puede calcular del siguiente modo:
( )( ) β
= 1 2
L L Sen
2
( )( ) °
=
1
75,84 78, 00 Sen 120 22' 59
2
A1 = 2 551,55
( )( ) °
=
2
n 133, 48 Sen 70 10' 0,34
2
A2 = 62,78×n
( )( ) °
=
3
m 125,61 Sen 88 25' 28,13
2
A3 = 62,78×m
• En nuestro caso:

248. Taquimetría
337
( )( ) °
=
4
103,60 71, 99 Sen 89 26' 54
A
2
A4 = 3 728,91
– Condición del problema:
A1 + A2 = A3 + A4
2 551,55 + 62,78×n = 62,78×m + 3 728,91
n – m = 18,75 ................................ (1)
– Del gráfico:
AE = n + m
n + m = 48,70 ............................. (2)
– De (1) y (2)
n = 33,73
m = 14,98
– Analizando el punto “K”.
–
−
=
−
y 130 25,51
x 59 41, 48
y = 0,615x + 93,715 .................... (3)
– ( ) ( ) ( )
− + − =
2
2 2
x 59 y 130 33, 73 ...... (4)
– De (3) y (4)
K = (x ; y) = (87,75 ; 147,68) m

249. CLASE 5

250. Taquimetría
335
335
335
335
335
Es un procedimiento de medida rápida que permite obtener prácticamente de manera simultá-
nea pero de forma indirecta la distancia horizontal y desnivel entre dos puntos. Se utiliza en
trabajos de poca precisión tales como:
– En la determinación de puntos estratégicos de detalles o rellenos topográficos.
– En levantamientos de curvas de nivel.
– En la comprobación de mediciones de mayor precisión.
– En trabajos preliminares.
Existen diversos equipos para la aplicación de este método (taquimétrico), sin embargo en la
actualidad los preferidos son: El teodolito con la mira parlante así como la estación total y por
último el GPS navegador e incluso diferencial.
MÉTODOS MÁS USADOS EN TAQUIMETRÍA
1. Método estadimétrico
El principio se fundamenta en la determinación de la distancia horizontal entre dos puntos (D),
aprovechando la semejanza de triángulos que se presenta.
Si “O” es el ocular de un observador y
asumimos conocido los elementos del
instrumento “P” e “i” así como la lon-
gitud m; geométricamente se tiene:
D m
P i
=
De donde:
P
D m
i
 
=  
 

251. Taquimetría
340
Dado que “P” e “i” son elementos fijos del instrumento y por tanto constantes, podemos
hacer; K = (P/i), luego:
D = K×m
Concluyendo que la distancia “D” es proporcional a la distancia vertical “m”.
Los puntos 1 ; 2 y 1' ; 2', toman el nombre de extremos estadimétricos.
Hilos estadimétricos
Se presentan generalmente en los telescopios de equipos
topográficos tal como el teodolito.
Estos hilos son líneas muy finas paralelas y simétricos res-
pecto al hilo horizontal del retículo.
Estas líneas generalmente (en los equipos modernos) se mon-
tan en la misma retícula y en el mismo plano que la cruz filar;
de manera que la distancia entre ellos es constante.
A) Para visuales horizontales
Consiste en hacer uso de los hilos estadimétricos del teodolito conjuntamente con las
graduaciones de una mira parlante en posición vertical.
D = (Lectura hilo superior – Lectura hilo inferior)×100
Demostración
– Principio de óptica geométrica.

252. Taquimetría
341
Telescopio de enfoque interior.
– En el caso del teodolito y la mira.
Semejanza de triángulos:
 
=  
 
f
d m
i
Pero: f = Distancia focal (constante)
i = Distancia entre los hilos estadimétricos (constante)
Si hacemos:
 
=  
 
f
K
i
= Constante diastimométrica
d = K×m
Del gráfico: D = (c + f) + d
D = C + K×m
Constante de estadía o aditiva (C): C = c + f ; es un valor que depende de la fabricación del
telescopio; su valor generalmente aparece en la caja del instrumento.
Telescopio de enfoque exterior.
C ; 30 cm C ; 0

253. Taquimetría
342
Comúnmente, los teodolitos usan este último tipo de telescopio (C ; 0).
Constante Diastimométrica (K).- También depende de la fabricación; si la distancia entre los hilos
estadimétricos es grande, K es relativamente pequeño y por tanto más preciso (K = 100 ; 200 ; 300).
Generalmente K = 100
Finalmente: D = C + K×m = 0 + 100×m
D = (Lectura hilo superior – Lectura hilo inferior)×100 .............. Demostrado
Ejemplo
Lo que se muestra en la figura, corresponde a la imagen de una mira vertical que observa un
operador al ver por el ocular de un teodolito.
Si teodolito y mira se encuentran sobre un mismo plano horizontal; la distancia entre ellos
será: D = (1,69 – 1,31)×100
D = 38,00 metros
B) Para visuales inclinadas
El eje de colimación del tele-
scopio forma un ángulo α con
la horizontal y los hilos esta-
dimétricos cortan a la mira
vertical en A y B cuya longi-
tud es “m”; si A'B' = m'
m' = m⋅cos α

254. Taquimetría
343
Distancia Geométrica (G)
G = 100⋅m⋅cos α
Del Gráfico: G = C + d = C + K⋅m'
G = C + K⋅m⋅cos α
Para telescopios de enfoque interno: C = 0
G = K⋅m⋅cos α
Para teodolitos con K = 100
G = 100⋅m⋅cos α ............... Demostrado
Proyección Horizontal.- Del triángulo sombreado.
DH = G⋅cos α
DH = (100⋅m⋅cos α)(cos α)
DH = 100⋅m⋅cos
2
α
Proyección Vertical.- Del triángulo sombreado.
DV = G⋅sen α
DV = (100⋅m⋅cos α)(sen α)
DV =
1
2
(100⋅m)sen 2α
Errores y precisiones planimétricos en el método estadimétrico
A. Error propio
Debido a la enorme cantidad de medidas que se forman con el presente método, es usual
caer en errores propios; para tratar de evitarlos se recomienda tomar como lectura adicio-
nal, el hilo central horizontal.
El promedio de las lecturas de los hilos estadimétricos debe ser igual a la lectura del
hilo central, aunque ello solo es válido para visuales horizontales, también es aceptable
su aplicación para visuales inclinadas, dado que la diferencia es imperceptible.
B. Errores sistemáticos
La refracción atmosférica en la zona inferior de la mira puede darnos lecturas falsas (menor
de la real), es por ello que se debe tratar en lo posible de no tomar lecturas casi al pie de la mira.
C. Errores accidentales
C.1 Error por falta de verticalidad de la mira.- Cuando la mira está provista de un nivel esférico,
este tipo de error es fácilmente controlable; sin embargo cuando no lo tiene, la inclinación de ésta
se hace común y fácilmente puede llegar a 2° o incluso 3° (grados sexagesimales); no obstante; para
terrenos planos es despreciable el error cometido.
No sucede lo mismo en terrenos ondulados o de pendientes pronunciadas, dado que a mayor
inclinación de la visual respecto al horizonte, mucho más grande será el error producido por falta de
verticalidad de la mira; es por ello que es importante el uso de miras provistas del nivel esférico. En
la práctica es poco común el uso de estos tipos de miras, pues requieren de cuidado y cierta destreza
para calar la burbuja del nivel.

255. Taquimetría
344
Si se realiza estación en el punto “A” para
luego dirigir la visual hacia la mira situada
en “B” (la cual tiene una inclinación “δ”
respecto a la vertical), la lectura que se to-
mará será m' en lugar de m que sería la
correcta.
Si bien es cierto, el error que se comete será
la distancia P'P, es lícito considerar dicho
error como la diferencia: m' – m, dado la
magnitud diminuta de la inclinación δ.
Si: EP = Error máximo por falta de verticalidad de la mira
EP = ±m'
( )
α + δ
 
−
 
α
 
Cos
1
Cos
Demostración:
En el triángulo sombreado (BPP'):
– β = 180° – δ – (90° + α) = 90° – (α + δ)
–
( )
=
° + α β
m ' m
Sen 90 Sen
( )
( )
( )
° − α + δ
  α + δ
 
= =
° + α α
Sen 90 Cos
m
m' Sen 90 Cos
( )
α + δ − α
−
=
α
Cos Cos
m m '
m Cos
–EP = m'
( )
α + δ
 
−
 
α
 
Cos
1
Cos
EP = –m'
( )
α + δ
 
−
 
α
 
Cos
1
Cos
...Demostrado
Analizando la expresión:
– Cuando δ = 0°: para cualquier ángulo ver-
tical, no existe error alguno, dado que no
hay inclinación de la mira.
δ = 0°
EP(metros)
α m' = 1,5 m' = 2,5
0° 0 0
10° 0 0
20° 0 0
30° 0 0
δ = 1°
EP(metros)
α m' = 1,5 m' = 2,5
0° 0,000 0,0004
10° 0,005 0,0080
20° 0,010 0,0160
30° 0,015 0,0260
– Cuando:

256. Taquimetría
345
δ = 2°
EP(metros)
α m' = 1,5 m' = 2,5
0° 0,001 0,002
10° 0,010 0,017
20° 0,020 0,033
30° 0,031 0,052
δ = 3°
EP(metros)
α m' = 1,5 m' = 2,5
0° 0,002 0,003
10° 0,016 0,026
20° 0,031 0,051
30° 0,047 0,079
Ahora bien; dado que se toman dos lecturas estadimétricas (hilo superior e inferior), el error
probable de la diferencia de hilos será:
( ) ( )
= ± +
2
2
P PS PI
E E E
EP = Error total por falta de verticalidad de la mira.
EPS = Error del hilo superior.
EPI = Error del hilo inferior.
C.2. Error por Lectura.- En el método estadimétrico, la distancia máxima entre equipo y mira
queda limitado hasta apreciar como mínimo la mitad de la menor división de la mira; así
tenemos en promedio (cuando la mínima división de la mira es de 1 cm).
Aumento del telescopio = 20x ............................................Dmáx = 150 m
Aumento del telescopio = 30x ............................................Dmáx = 200 m
Analizando cuando A = 30x; recordemos que la apreciación se considera como la mitad de
la mínima división de la regla (en nuestro caso 0,5×0,01 m = 0,005 m).
El error máximo que se puede cometer por lectura corresponde a los 2/3 de la apreciación:
(2/3)(0,005 m) = 0,0033 m
Como quiera que para calcular “m” es imprescindible tomar dos lecturas estadimétricas (supe-
rior e inferior), por teoría de observaciones, el error máximo probable de la diferencia de ambas
lecturas será: Em = ( ) ( )
± +
2 2
0, 0033 0, 0033 = ±0,0047 m
Si utilizamos un teodolito de constante K = 100, el error en la medida de distancia geométrica de 200 metros
será: ±100×0,0047 m = ±0,47 m
En conclusión, si ER = Error relativo:
– Cuando A = 30x
=
R
0,47 m
E
200 m
⇒ ;
R
1
E
430
– Cuando A = 20x
=
R
0,47 m
E
150 m
⇒ ;
R
1
E
320

257. Taquimetría
346
C.3 Error total accidental de la distancia geométrica.- El error total probable de la distancia
geométrica, se podrá determinar mediante la siguiente expresión:
( ) ( )
= ± +
2 2
P Lectura
E E E
Análisis
Aunque la proporción que se presenta a continuación es aproximada, es útil para deducir la
escala mínima que debemos usar en el plano.
Si el aumento A = 30x
Como quiera que la apreciación gráfica de una persona en promedio es de 0,2 mm; si la escala del plano
a dibujar fuese 1/1 000; longitudes en el terreno menores a 20 cm no tienen representación en el plano.
Es por ello que si las visuales no superan los 100 metros de distancia, es aceptable la aplicación
del presente método para trabajos cuya escala de representación sea menor a 1/1 000.
Ejemplo
Se mide la distancia geométrica entre dos puntos con un teodolito de aumento A = 30x; sì el
ángulo de elevación de la visual es 30° y la inclinación de la mira respecto a la vertical es 2°.
Calcular el error probable accidental total.
Lectura hilo superior = 2,5 m
Lectura hilo inferior = 1,5 m
Solución:
– Cálculo del error por falta de verticalidad de la mira.
Si m' = 2,5 metros ⇒ E = ±0,052 m
m' = 1 ,5 metros ⇒ E = ±0,031 m
( ) ( )
= ± +
2 2
P
E 0, 052 0, 031
EP = ±0,061 m
Distancia Error
Geométrica (m) Accidental (m)
200 0,500
100 0,250
50 0,125
10 0,025

258. Taquimetría
347
B) Para visuales inclinadas
El eje de colimación del telescopio forma un ángulo α con la horizontal.
El equipo mide la distancia geométrica “G” e inmediatamente procesa y calcula la distancia
“DH” así como el desnivel “DV”.
– Cálculo del error por lectura.
D = 100⋅m⋅Cos α = 100(2,5 – 1,5)Cos 20° ⇒ D = 93,97 m
Si Para D = 200 m; el error máximo por lectura es ±0,47 m.
Para D = 93,97 m podemos estimar dicho error en ±0,219 m.
– Error total accidental.
( ) ( )
= ± +
2 2
Total
E 0, 061 0, 219 ⇒ ETotal = ±0,227 m
2. Método de la estación total
El principio se fundamenta en la medición electrónica de distancias (MED), el sistema
electrónico en la medición de ángulos y el manejo digital de la información.
Dada la elevada cantidad de puntos que son materia de medición con este método, se recomien-
da hacer uso del MED en modo rápido, pues pese a ello la precisión obtenida seguirá siendo
elevada; así por ejemplo si Ud. elige trabajar con un equipo en modo rápido cuya precisión es
±(10 mm + 10 ppm) (precisión baja respecto a estaciones totales), para 1 km de distancia
horizontal, el probable error es de 20 mm; en otros términos: 1/50 000 de error relativo.
A) Para visuales horizontales
La distancia “D” es medida y leída directamente en la pantalla digital.

259. 348
α
α
3 km.

260. Taquimetría
349
A) Método estadimétrico
A.1) Cuando la lectura del hilo horizontal del retículo es igual a la altura instrumental.- El
método consiste en hacer estación en un punto de cota conocida, para luego medir la altura instrumen-
tal; mientras que el ayudante coloca la mira vertical en un punto “B” cuya cota se desea conocer. Luego
el operador dirige la visual hacia la mira hasta tomar como lectura la altura instrumental.
Cuando la lectura en la mira es igual, a la altura instrumental, el eje de colimación del teodolito se hace paralelo
a la línea recta AB, formándose así dos triángulos iguales.
Si Cota “A” = conocida ⇒ Cota “B” = Cota “A” + DV
Donde: DV = 100(Lectura hilo superior – Lectura hilo inferior)
α
Sen 2
2
Ejemplo
Se estaciona un teodolito en un punto “A” donde la cota es 100 metros; obteniendo una altura
instrumental de 1,50 metros.
Asimismo se coloca una mira en el punto “B” obteniendo como medidas estadimétricas:
Lectura hilo superior (H.S.) = 1,94 m
Lectura hilo inferior (H.I.) = 1,06 m

261. Taquimetría
350
– Según los datos:
DV = 100×(HS – HI)×
α
Sen 2
2
DV = 100×(1,94 – 1,06)× ( )
× °
Sen 2 28 30' 10
2
⇒ DV = 36,90 m
– Cálculo de la cota de “B”
Cota “B” = Cota “A” + DV = 100,000 + 36,90 ⇒ Cota “B” = 136,90 m
En la práctica, el topógráfo prefiere usar siempre esta metodología, dado que tan sólo
tiene que ocuparse de anotar los datos estadimétricos así como el ángulo vertical, siem-
pre y cuando la lectura en la mira coincida con el de la altura instrumental.
Es preciso recordar que la nivelación trigonométrica se aplica intensamente y la ventaja se
manifiesta en el gabinete al usar tan solo una “fórmula” para el cálculo de las cotas de
todos ellos.
Observación
A.2.) Cuando la lectura del hilo horizontal del retículo no es igual a la altura instrumental.-
Existen casos en las que se hace imposible aplicar la metodología anterior, como es el
caso de la siguiente ilustración.
El muro impide la visibilidad de la mira para una lectu-
ra igual a la altura instrumental.
En tal circunstancia es apropiado ubicar la visual en la mira con una lectura conveniente y
diferente de la altura instrumental.
La cota del punto visado, se puede obtener con ayuda de la siguiente expresión:
Cota “B” = Cota “A” + DV + (h – H)
Se ha girado verticalmente el anteojo, obteniendo una
lectura en la mira diferente a la altura instrumental.

262. Taquimetría
351
Demostración:
Si Cota “A” = conocida
DV = 100(HS – HI)×
α
Sen 2
2
Del gráfico:
Cota “A” + h + DV = Cota “B” + H
Cota “B” = Cota “A” + DV + (h – H)
Nótese que si h = H
Cota “B” = Cota “A” + DV
B) Método de la estación total
Consiste en ubicar la estación total en un punto de cota conocida, para luego medir la altura
instrumental, mientras que el ayudante acoloca el portaprisma vertical en un punto “B”
cuya cota se desea conocer (previamente se debe medir la altura del mismo).
Finalmente el operador realiza la medición electrónica respectiva.
Si Cota “A” = conocida: Cota “B” = Cota “A” + DV + (h – H)
Donde: DV = G⋅Sen α
¿Cómo elegir la altura del prisma?
En realidad no existe una regla para tal efecto; lo que si hay que tomar en cuenta es que general-
mente se levantan muchos puntos y es conveniente ingresar al equipo la altura del prisma tan
solo en la primera medida y por ende no cambiar la altura del mismo.
No obstante se recomienda que la altura del prisma sea lo menos posible para reducir el posible
error de verticalidad.

263. Taquimetría
352
Errores en la nivelación trigonométrica
A) Error propio
Para reducir la presencia de estos tipos de errores se recomienda tomar como lectura
adicional el hilo central horizontal.
B) Errores sistemáticos
Los más importantes son: por refracción y curvatura terrestre; la combinación de éstos
toma el nombre de error por nivel aparente.
Corrección por nivel aparente.- Al igual que en una nivelación geométrica, cuando las distan-
cias son considerables; el error por curvatura terrestre así como de refracción se hacen impor-
tantes; la suma algebraica de estos dos tipos de errores, toma el nombre de error aparente.
Si: ec = Error por curvatura terrestre.
er = Error por refracción atmosférica.
C = Corrección por nivel aparente.
DH = Distancia horizontal entre los puntos.
K = Coeficiente de refracción (varía desde 0,07 hasta 0,20)
R = radio terrestre.
C = ec + er =
( ) ( )
 
− ×
+  
 
2 2
H H
D D K
2R R
C =
( ) ( )
− ⋅
2 2
H H
D D
K
2R R
Del gráfico:
Cota “B” = Cota “A” + h + C + (DV – H)
Cota “B” = Cota “A” + DV + (h – H) + C
lustrando:

264. Taquimetría
353
En una nivelación trigonométrica es común utilizar visuales de grandes distancias (mayores de 1 km),
por tal razón se hace prácticamente obligatorio considerar la corrección por nivel aparente.
A continuación, mostraremos las correcciones para algunas distancias horizontales cuando K = (1/14)
C =
( )
⋅
2
H
D
6
14 R
- El valor del coeficiente de refracción K, se pue-
de determinar en el campo mediante nivela-
ción trigonométrica desde un punto “A” res-
pecto a B1 y B2.
- En la actualidad existen equipos digitales que corrigen automáticamente el error por
nivel aparente.
Observaciones
Ejemplo
Con ayuda de una estación total, se mide la distancia entre los puntos A y B, obteniendo una
longitud horizontal de 2 000 metros; si el ángulo vertical respecto a la horizontal es 26° 32' 14;
calcular la cota del punto “B”, sabiendo que la cota de “A” es 346,203 m.
Altura instrumental = 1,478 m
Altura de prisma = 1,75 m
Solución:
– Del triángulo: DV = 998,786 m – Datos: Cota “A” = 346,203 m
h = 1,478 m
H = 1,75 m
Cota “B” = Cota “A” + DV + (h – H) + C
Cota “B” = 346,203 + 998,786 + (–0,272) + 0,269
Cota “B” = 1 344, 986 m
– Cáculo de C:
C =
( )  
⋅ =  
 
2 2
H
2
D
6 6 (2 000)
14 R 14 (6 370 000)
DH C(m) DH C(m)
500 0,017 4 500 1,362
1 000 0,067 5 000 1,682
1 500 0,151 5 500 2,035
2 000 0,269 6 000 2,422
2 500 0,421 6 500 2,843
3 000 0,601 7 000 3,297
4 000 1,076 7 500 3,784

265. Taquimetría
354
C) Errores accidentales
En una nivelación trigonométrica, se dan tres importantes tipos de errores, estos son:
C.1. Error de altura instrumental.- Comúnmente dicha longitud es medida con cinta métrica, no
obstante el cuidado que se tenga, siempre se cometerá un pequeño error, el cual influirá en los
cáculos altimétricos.
Comúnmente se toma como 1 cm el máximo error accidental.
En la actualidad existen equipos digitales con plomada láser; en un futuro cercano será de
práctica masiva el uso de esta plomada en la medida de la altuta instrumental reduciendo así el
posible error a unos cuantos milímetros.
Actualmente: EI(máx) ; 1 cm
C.2. Error por falta de verticalidad de la mira o portaprisma.- La explicación es la misma que
la expuesta en la pág 339 correspondiente a errores planimétricos.
Sin embargo es preciso acotar que se va a tomar como error vertical; la diferencia m' – m (igual
que para distancias planimétricas), maximizando el error en estudio.
– Cuando δ = 0° : Para cualquier ángulo vertical, no existe error alguno, dado que no hay
inclinación de la mira o portaprisma.
– Cuando δ = 1° : Este es el caso desfavorable de un portaprisma; si el ángulo vertical “α” es
30° y la altura del bastón fuese 2,5 metros; el error máximo sería 2,6 cm.
En una nivelación geométrica α = 0°; si m' = 1,5 metros, el error probable máximo es
0,0002 m (prácticamente cero).
– Cuando δ = 2° ó 3°: Estos casos se presentan en una nivelación estadimétrica cuando se
usan miras sin nivel circular.
Nótese que el error puede llegar a 8 cm cuando la inclinación de la mira se hace 3°.
Hay que tener presente:
– Cuando se usa estación total y prisma; el error por falta de verticalidad del portaprisma se
calcula con la siguiente expresión:
EP = –m'
( )
α + δ
 
−
 
α
 
cos
1
cos
– Cuando se usa teodolito y mira (método estadimétrico se toman dos lecturas hilo superior
e inferior), luego el error probable de la diferencia de los hilos será:
( ) ( )
= ± +
2
2
P PS PI
E E E
EP = Error total por falta de verticalidad de la mira.
EPS = Error en el hilo superior.
EPI = Error en el hilo inferior.

266. Taquimetría
355
C.3. Error del cálculo trigonométrico con estación total.- El cateto “V” es susceptible a
errores accidentales.
Del Triángulo: V = G⋅sen α
dV = G⋅cos α dα + sen α⋅dG
Asimilando errores a elementos diferenciales:
( ) ( ) ( ) ( )
α
= ± ⋅ α + α
2 2
2
2
T G
E G cos E sen E
Donde: G = Distancia geométrica.
α = Ángulo vertical.
Eα = Error accidental angular vertical (ver pag. 425).
EG = Error accidental de la distancia G (ver pag. 426).
ET = Error trigonométrico probable.
Según cálculos realizados por el Autor, el error máximo promedio que afecta al cateto “V”, asumien-
do que la inclinación máxima del portaprisma es 1°, se comporta según las tablas que se muestran:
Es importante anotar que este tipo de error se hace prácticamente independiente del ángulo
vertical α con el uso de la estación total.
C.4. Error del cálculo trigonométrico con el método estadimétrico.- El cateto “V” es obtenido
gracias a un cálculo trigonométrico, por lo que es susceptible a errores accidentales.
ESTACIÓN TOTAL
Precisión angular = 5
M.E.D. : ±(3 mm + 1 ppm)
A = 30x
S = 20/2 mm
G(m) ET(m)
50 0,010
100 0,010
500 0,014
1 000 0,017
2 000 0,029
3 000 0,044
4 000 0,058
5 000 0,700
10 000 0,140
ESTACIÓN TOTAL
Precisión angular = 5
M.E.D. : ±(5 mm + 3 ppm)
A = 30x
S = 20/2 mm
G(m) ET(m)
50 0,010
100 0,010
500 0,014
1 000 0,017
2 000 0,030
3 000 0,044
4 000 0,058
5 000 0,070
10 000 0,140
ESTACIÓN TOTAL
Precisión angular = 20
M.E.D. : ±(5 mm + 3 ppm)
A = 30x
S = 20/2 mm
G(m) ET(m)
50 0,010
100 0,010
500 0,025
1 000 0,046
2 000 0,090
3 000 0,140
4 000 0,180
5 000 0,220
10 000 0,450

267. Taquimetría
356
Para el tipo de equipos considerados en este libro:
V =
1
2
(100⋅m)sen 2α
dV = 100⋅m⋅cos 2α.dα + 50.sen 2α.dm
Asimilando errores a elementos diferenciales:
( ) ( ) ( ) ( )
α
= ± ⋅ ⋅ α + α
2 2 2
2
2 2
T m
E 10 m cos 2 E (50) sen 2 E
Donde: α = Ángulo vertical.
m = (Lectura hilo superior – Lectura hilo inferior)
Eα = Error accidental angular vertical (ver pag. 425).
Em = Error accidental de “m” (ver pag. 341).
ET = Error del cálculo trigonométrico.
Para un teodolito de aumento A = 30x; Em = ±0,0047 m (pag. 341 - error por lectura)
Utilizando la expresión en los siguientes casos:
Teodolito óptico mecánico
Precisión angular = 60
A = 30x
S = 30/2 mm
Mínima división de la mira = 1 cm
α=0° α=10° α=20° α=30°
G(m) ET(m) ET(m) ET(m) ET(m)
200 0,040 0,090 0,150 0,200
Teodolito electrónico
Precisión angular = 5
A = 30x
S = 20/2 mm
Mínima división de la mira = 1 cm
α=0° α=10° α=20° α=30°
G(m) ET(m) ET(m) ET(m) ET(m)
200 0,003 0,080 0,150 0,200
Teodolito óptico mecánico
Precisión angular = 20
A = 30x
S = 30/2 mm
Mínima división de la mira = 1 cm
α=0° α=10° α=20° α=30°
G(m) ET(m) ET(m) ET(m) ET(m)
200 0,016 0,080 0,150 0,200
C.5. Error total altimétrico accidental.- El error máximo altimétrico, se podrá determinar
mediante la siguiente expresión:
( ) ( ) ( )
= ± + +
2 2 2
I P T
E E E E
Ejemplo1
Determinar el error total altimétrico probable que se puede cometer con un teodolito òptico
mecánico y una mira de graduación mínima 1 cm; para los siguientes casos (para una sola visual):

268. Taquimetría
357
A) Cuando la mira se encuentra totalmente en
posición vertical y el ángulo vertical α es de
10°.
Distancia geométrica = 200 metros.
• Error instrumental: EI = ±1 cm
• Error por falta de verticalidad de la mira: EP
Si δ = 0°; entonces EP
= 0
• Error del cálculo trigonométrico: ET
Si α = 10° ⇒ ET = ±0,08 m
• ( ) ( ) ( )
= ± + +
2 2
2
E 1 0 8
E = ±8,01 cm
B) Cuando la mira se encuentra inclinada 2°
respecto a la vertical y la visual corta a la
mira en 1,5 metros; siendo el ángulo verti-
cal α = 10°
Distancia geométrica = 200 metros.
• G = 100⋅m⋅cos α
200 = 100⋅m⋅cos 10°
m = 2,03 metros
Dato: Lectura hilo central = 1,5 m
Luego:
• Error instrumental: EI = ±1 cm
• Error por falta de verticalidad de la mira: EP
EP = ±m'
( )
α + δ
 
−
 
α
 
cos
1
cos
EPS = ±2,53
( )
° + °
 
−
 
°
 
cos 10 2
1
cos 10
Luego: EPS = ±0,017 m
EPI = ±0,5
( )
° + °
 
−
 
°
 
cos 10 2
1
cos 10
Luego: EPI = ±0,003 m
( ) ( )
= ± +
2 2
P
E 0, 017 0, 003
Luego: EP = ±0,017 m
• Error del cálculo trigonométrico.
Si α = 10° ⇒ ET = ±0,08 m
• Error total probable:
( ) ( ) ( )
= ± + +
2 2
2
E 1 1, 7 8
E = ±8,24 cm
C) Cuando la mira se encuentra inclinada
2° respecto a la vertical y la visual cor-
ta a la mira en 1,90 metros; siendo el
ángulo vertical α = 30°.
Distancia geométrica = 200 metros
• G = 100⋅m⋅cos α
200 = 100⋅m⋅cos 30°
m = 2,31 metros
Dato: Lectura hilo central = 1,90 m
Luego:
• Error instrumental: EI = ±1 cm

269. Taquimetría
358
• Error por falta de verticalidad de la mira: EP
- EPS = ±3,055
( )
° + °
 
−
 
°
 
cos 30 2
1
cos 30
Luego: EPS = ±0,063 m
- EPI = ±0,745
( )
° + °
 
−
 
°
 
cos 30 2
1
cos 30
Luego: EPI = ±0,016 m
( ) ( )
= ± +
2 2
P
E 0, 063 0, 016
Luego: EP = ±0,065 m
• Error del cálculo trigonométrico.
Si α = 30° ⇒ ET = ±0,20 m
• Error total probable:
( ) ( ) ( )
= ± + +
2 2
2
E 1 6,5 20
E = ±21,05 cm
Ejemplo2
Determinar el error total altimétrico proba-
ble que se puede cometer con una estación
total para los siguientes casos (para una visual).
A) Estación total:
– Precisión angular = 5
– M.E.D.: ±(3 mm + 1 ppm)
– A = 30x
– S = 20/2 mm
Cuando el portaprisma se encuentra totalmen-
te en posición vertical y el ángulo α es de 10°:
Altura de portaprisma = 1,5 metros
Distancia geométrica = 500 m
• Error instrumental: EI = ±1 cm
• Error por falta de verticalidad del
portaprisma: EP
δ = ° 

α = ° 

= 
0
10
m' 1,5 metros
E
P
= 0,0 m
Es decir, no hay inclinación del portaprisma.
• Error del cálculo trigonométrico.
G = 500 m ⇒ ET = 0,007 m
• ( ) ( ) ( )
= ± + +
2
2
2
E 1 0 0, 7
E = ±1,22 cm
B) Estación total:
– Precisión angular = 20
– M.E.D.: ±(5 mm + 3 ppm)
– A = 30x
– S = 20/2 mm
Cuando el portaprisma se encuentra inclinada
1° respecto a la vertical y el ángulo α es de 10°:
Altura de portaprisma = 2,5 metros
Distancia geométrica = 500 m
• Error instrumental: EI = ±1 cm
• Error por falta de verticalidad del
portaprisma: E
P
δ = ° 

α = ° 

= 
1
10
m' 2,5 metros
EP
= 0,008 m

270. Taquimetría
359
• Error del cálculo trigonométrico.
G = 500 m ⇒ ET = 0,024 m
• ( ) ( ) ( )
= ± + +
2 2
2
E 1 0,8 2, 4
E = ±2,72 cm
C) Estación total:
– Precisión angular = 20
– M.E.D.: ±(5 mm + 3 ppm)
– A = 30x
– S = 20/2 mm
Cuando el portaprisma se encuentra inclinada
1° respecto a la vertical y el ángulo α es de 30°:
Altura de portaprisma = 2,5 metros
Distancia geométrica = 500 m
• Error instrumental: EI = ±1 cm
2. Relleno Topográfico
El relleno topográfico consiste en determinar puntos en el terreno dentro y/o fuera de una
poligonal o red de apoyo; para con ello representar en un plano los detalles artificiales y
naturales de la superficie en estudio.
Existen dos tipos de detalles: Artificiales; que son estructuras hechas por las manos del
hombre, tales como carreteras, caminos, edificaciones, puentes, postes, buzones, etc. y
Naturales; que vienen a ser estructuras generadas por la evolución geológica de la corteza
terrestre tales como ríos, cerros, quebradas, etc.
El método más usado para tal efecto es el de radiación, dado que hay que determinar
alrededor de cada vértice de la poligonal todos los puntos notables que definan los detalles
del terreno. Los errores que existan en la posición de los puntos de la red de apoyo, se se
reflejarán en los detalles; por tal razón es recomendable verificar y ajustar la poligonal así
como el circuito altimétrico antes de iniciar el relleno topográfico.
En el campo se usa con la misma importancia el método taquimétrico como la medición
con cinta métrica, aplicando simultáneamente el levantamiento planimétrico y altimétrico.
Téngase presente que el producto final de un plano, está constituido por los detalles
topográficos, por tal razón dicha tarea debe encomendarse a personal calificado y experi-
mentado, pues los errores que se cometan en esta actividad serán fácilmente detectados por
cualquier individuo que conozca la zona de trabajo.
Comparando el ejemplo 1 y 2, no es difícil
entender,queconelusodelaestacióntotal,
se puede esperar errores pequeños respecto
almétodoestadimétrico,noobstante dicha
precisión es lejanamente comparable con
unanivelacióngeométrica.
Observación
• Error por falta de verticalidad del
portaprisma: EP
δ = ° 

α = ° 

= 
1
30
m' 2,5 metros
E
P
= 0,026 m
• Error del cálculo trigonométrico.
G = 500 m ⇒ ET = 0,024 m
• ( ) ( ) ( )
= ± + +
2 2
2
E 1 2,6 2, 4
E = ±3,68 cm

271. Taquimetría
360
A continuación explicaremoslos dos métodos más usados en relleno topográfico:
A) Método Estadimétrico
Procedimiento
1° Elección de la red de apoyo o poligonal.-La elección y análisis de la red de apoyo, se estudió
en la pág. 285
Ejemplo de aplicación
Poligonal
Punto Este(m) Norte(m) Cota(m)
A 100,000 700,000 500,000
B 399,042 886,458 523,231
C 755,130 657,915 510,610
D 545,100 174,860 530,420
193,234 199,104 521,232
2° Determinación del croquis de los detalles a levantar.- Se dibuja insitu la geometría y posi-
ción aproximada de los detalles naturales y artificiales (dicho gráfico se debe plasmar en la
libreta de campo).
Esta operación involucra
la detonación de los pun-
tos a levantar (asignación
de nombres a los puntos
de relleno).
Es recomendable que esta
actividad sea encabezado
por un topógrafo de com-
probada experiencia,
dado que la presencia de
dicha persona tanto en el
campo como en el gabi-
nete será vital para la re-
solución de problemas.

272. Taquimetría
361
3° Se determina la mínima longitud a tomar en cuenta en el campo.- Para ello es preciso la
escala a la cual se representará el levantamiento en el plano.
Si la escala elegida es 1/E, es aceptable la siguiente expresión: L = 0,0002×E
Donde: L = Mínima longitud a tomar en cuenta en el campo; tener presente que el valor
obtenido está expresado en metros; si por ejemplo E = 10 000; la mínima longitud L será 2 m.
4° Relleno desde el primer punto de control.
– Se hace estación en un punto de la poligonal.
– Se dirige la visual hacia uno de los puntos vecinos de la poligonal.
– Se hace 0° 00' 00 en dicha dirección.
– Se suelta el bloqueo de la alidada y se dirige la visual hacia el primer punto a levantar, se
toman como datos: el
ángulo acimutal, verti-
cal y la lectura del hilo
superior e inferior. (es
conveniente que la lec-
tura del hilo horizontal
del retículo sea igual a
la altura instrumental).
El ángulo acimutal se
mide hacia la derecha.
– Se suelta el bloqueo de
la alidada y se dirige la
visual hacia el segundo
punto a rellenar, toman-
do como datos los mis-
mos parámetros que el punto antecesor.
La misma operación se realiza con los demás puntos por levantar desde la misma estación.
Modelo de libreta de campo
Proyecto : ..................................................................... Operador : ........................................................................
Lugar : ...................................................................... Instrumento: ......................................................................
Fecha : ......................................................................
Ángulo Vertical Hilo
Estación P.V. 5 H 5 V α Estadimétrico(m) DH(m) DV(m) Cota(m)
A 100,00
B 0° 00' 00
A1 39° 23' 21 85° 19' 40 2,30
=1,41 m 0,66
A2 76° 28' 42 85° 41' 30 2,62
0,34

273. Taquimetría
362
5 H : Ángulo acimutal.
: Altura del instrumento en el punto de estación.
P.V. : Punto visado.
5 V : Ángulo vertical cenital o nadiral.
α : Ángulo vertical respecto al horizonte.
5° Se repite el cuarto paso en cada punto de control.
Ángulo Vertical Hilo
Estación P.V. 5 H 5 V α Estadimétrico(m) DH(m) DV(m) Cota(m)
A 500,00
B 0° 00' 00
A1 39° 23' 21 85° 19' 40 2,30
=1,48 m 0,66
A2 76° 28' 42 85° 41' 30 2,62
0,34
B 523,231
C 0° 00' 00
B1 25° 25' 42 85° 39' 50 2,77
=1,52 m 0,27
B2 298° 39' 04 85° 07' 40 2,27
0,77
C 510,610
D 0° 00' 00
C1 12° 01' 03 84° 53' 35 2,70
=1,50 m 0,30
C2 33° 16' 26 84° 24' 50 2,35
0,65
D 530,420
E 0° 00' 00
D1 26° 01' 11 83° 49' 50 2,43
=1,45 m 0,47
D2 53° 54' 55 83° 40' 00 2,29
0,60
E 521,232
A 0° 00' 00
E1 282° 26' 28 81° 36' 48 2,60
=1,54 m 0,49
E2 323° 03' 59 81° 29' 20 1,73
1,35
E3 331° 41' 31 80° 59' 50 2,50
0,58

274. Taquimetría
363
6° Paralelo al levantamiento taquimétrico, se puede asignar otra brigada que se encargue de
tomar las medidas con cinta métrica; sin embargo el croquis a usar debe tener las mismas
denotaciones que las usadas en taquimetría.

275. Taquimetría
364
7° Trabajo de gabinete: Se realiza el cálculo respectivo:
Ángulo Vertical Hilo
Estación P.V. 5 H 5 V α Estadimétrico(m) DH(m) DV(m) Cota(m)
A 500,000
B 0° 00' 00
A1 39° 23' 21 85° 19' 40 04° 40' 20 2,30 162,912 13,314 513,314
=1,48 m 0,66
A2 76° 28' 42 85° 41' 30 04° 18' 30 2,62 226,713 17,080 517,080
0,34
B 523,231
C 0° 00' 00
B1 25° 25' 42 85° 39' 50 04° 20' 10 2,77 248,571 18,848 542,079
=1,52 m 0,27
B2 298° 39' 04 85° 07' 40 04° 52' 20 2,27 148,918 12,694 535,925
0,77
C 510,610
0° 00' 00
C1 12° 01' 03 84° 53' 35 05° 06' 25 2,70 238,010 21,279 531,889
=1,50 m 0,30
C2 33° 16' 26 84° 24' 50 05° 35' 10 2,35 168,389 16,470 527,080
0,65
530,420
E 0° 00' 00
D1 26° 01' 11 83° 49' 50 06° 10' 10 2,43 193,736 20,942 551,362
=1,45 m 0,47
D2 53° 54' 55 83° 40' 00 06° 20' 00 2,29 166,943 18,529 548,949
0,60
E 521,232
A 0° 00' 00
E1 282° 26' 28 81° 36' 48 08° 23' 12 2,60 206,511 30,446 551,678
=1,54 m 0,49
E2 323° 03' 59 81° 29' 20 08° 30' 40 1,73 37,168 5,562 526,794
1,35
E3 331° 41' 31 80° 59' 50 09° 00' 10 2,50 187,300 29,674 550,906
0,58

276. Taquimetría
365
8° Con ayuda de la poligonal y el cuadro adjunto se lleva a cabo la ubicación gráfica de los
puntos levantados taquimétricamente, gracias al método gráfico de coordenadas polares.
Estación P.V. 5 DH(m)
A
B 0° 00' 00
A1 39° 23' 21 162,912
A2 76° 28' 42 226,713
B
C 0° 00' 00
B1 25° 25' 42 248,571
B2 298° 39' 04 148,918
C
D 0° 00' 00
C1 12° 01' 03 238,010
C2 33° 16' 26 168,389
D
E 0° 00' 00
D1 26° 01' 11 193,736
D2 53° 54' 55 166,943
E
A 0° 00' 00
E1 282° 26' 28 206,511
E2 323° 03' 59 37,168
E3 331° 41' 31 187,300
9° En el gráfico anterior, se realiza el dibujo de los detalles apoyándose en el croquis existente.
En nuestro ejemplo.

277. Taquimetría
366
10° El plano final queda determinado con la representación de los detalles, según las exigencias
pertinentes (nombre, medidas, cotas, etc)
En nuestro ejemplo.
- Es recomendable realizar primero el levantamiento de la red de apoyo o poligonal,
para luego hacer lo propio con el relleno topográfico. Esto nos dá la opción de
verificar y ajustar la red.
En la práctica, la mayoría opta por realizar las dos actividades paralelamente.
- Si bien es cierto que no se deben tomar medidas en el terreno menor que la longitud
mínima establecido por la escala del plano (percepción óptica de 2 mm); la excep-
ción se dá cuando dichas longitudes corresponden a estructuras independientes,
tales como postes, buzones, puentes, árboles, etc. y su representación estará estable-
cida por un punto cuya simbología será parte integrante de la leyenda.
- Los bancos de nivel pueden o no ser vértices de la poligonal; sin embargo es impor-
tante que las cotas de dichos vértices sean producto de una nivelación geométrica.
- No existe una regla que establezca las dimensiones de las cuadrículas, no obstante
es costumbre trazarlos cada 10 cm en el plano. Así por ejemplo en un plano de
escala 1/2000. la malla de la cuadrícula equivale a 200 metros en el terreno.
Observaciones

278. 367
B. Método de la Estación Total.
B.1. Método del ángulo y distancia.- Consiste en anotar y/o guardar como información los ángulos
y distancias medidas en el campo.
Procedimiento:
1. Elección de la Red de Apoyo o poligonal.- La elección de la red de apoyo, se estudió en la Pag. 289
2° Determinación del croquis de los detalles a levantar.- Se dibuja in situ la geometría y posición
aproximada de los detalles naturales y artificiales (dicho gráfico se debe plasmar en la libreta de
campo).
Esta operación involucra la denotación de los puntos a levantar (asignación de nombres a los puntos
de relleno).
Es recomendable que esta actividad sea encabezada por un topógrafo de comprobada experiencia,
dado que la presencia de dicha persona tanto en el campo como en el gabinete será vital para la resolu-
ción de problemas.

279. 368
3° Se determina la mínima longitud a tomar en cuenta en el campo.- Para ello es preciso la escala a
la cual se representará el levantamiento en el plano.
Si la escala elegida es 1 / E .es aceptable la siguiente expresión L = 0,0002xE
Donde: L = Mínima longitud a tomar en cuenta en el campo,; tener presente que el valor obtenido está
expresado en metros; si por ejemplo E = 10 000;la mínima longitud L será 2 m.
4° Relleno desde el primer punto de control.
- Se hace estación en un punto de la
poligonal.
- Se dirige la visual hacia uno de los
puntos vecinos de la poligonal.
- Se hace 0°00’00’’ en dicha dirección.
- Se suelta el bloqueo de la alidada y se
dirige la visual hacia el primer punto a
levantar, se toman como datos:
. El ángulo horizontal
. Las distancias DH y DV
- Se suelta el bloque de la alidada y se
dirige la visual hacia el segundo punto a
rellenar, tomando como datos, los
mismos parámetros que el punto antece-
sor.
- La misma operación se realiza con los
demás puntos por levantar desde la
misma estación.
Estación
Proyecto : .........................................
Lugar : .........................................
Fecha : .........................................
Operador : .........................................
Instrumento : .........................................
A
= 1,41 m A1
A2
B 0°00’00’’
39°23’21’’ 162.912
226.713
500.000
13.314
17.080
76°28’42’’
Cota
DH
(m) DV
(m)
Punto visado Ang. horizontal

280. 369
Estación Punto visado Ang. horizontal DH(m) DV(m) Cota (m)
A 500.000
B 0°00’00’’
A1 39°23’21’’ 162,912 13,314
A2 76°28’42’’ 226,713 17,080
B 523,231
C 0°00’00’’
B1 25°25’42’’ 248,571 18,848
B2 298°39’04’’ 148,918 12,694
C 510,610
D 0°00’00’’
C1 12°01’03’’ 238,010 21,279
C2 33°16’26’’ 168,389 16,470
D 530,420
E 0°00’00’’
D1 26°01’11’’ 193,736 20,942
D2 53°54’55’’ 166,943 18,529
E 521,232
A 0°00’00’’
E1 282°26’28’’ 206,511 30,446
E2 323°03’59’’ 37,168 5,562
E3 331°41’31’’ 187,300 29,674
= 1,41
= 1,506
= 1,602
= 1,398
= 1,427

281. 370
6° Paralelo al levantamiento taquimétrico, se puede asignar otra brigada que se encargue de tomar las
medidas con cinta métrica; sin embargo el croquis a usar debe tener las mismas denotaciones que las
usadas en taquimetría.

282. 371
7° Trabajo de gabinete
Generar la grilla (sistema de coordenadas rectangulares), de acuerdo a la escala elegida.

283. 372
Se representa gráficamente la poligonal respectiva.
PUNTO ESTE NORTE COTA
A 100.000 700.000 500.000
B 399.042 886.458 523.231
C 755.130 657.915 510.610
D 545.100 174.860 530.420
E 193.234 199.104 521.232
A
B
C
D
E

284. 373
Se ubican gráficamente los puntos a rellenar, con ayuda de los ángulos horizontales y distancias respectivas.
A
B
C
D
E
A1
A2
B1
B2
C1
C2
D1
D2
E1
E2
E3
ESTACIÓN P.V. ANG. HOR. DH
A
B 0°00'00
A1 39°23'21 162.912
A2 76°28'42 226.713
B
C 0°00'00
B1 25°25'42 248.571
B2 298°39'04 148.918
C
D 0°00'00
C1 12°01'03 238.010
C2 33°16'26 168.389
D
E 0°00'00
D1 26°01'11 193.736
D2 53°54'55 166.943
E
A 0°00'00
E1 282°26'28 206.511
E2 323°03'59 37.168
E3 331°41'31 187.300

285. 374
Se borra u oculta los trazos realizados.
A
B
C
D
E
A1
A2
B1
B2
C1
C2
D1
D2
E1
E2
E3

286. 375
Se procede a unir los puntos pertenecientes al relleno, de acuerdo al croquis realizado.
A
B
C
D
E
A1
A2
B1
B2
C1
C2
D1
E1
E2
E3
D2

287. 376
Ocultando la poligonal obtenemos el plano final.
ESTRUCTURA 2
PABELLON P
PABELLON
A
ESTRUCTURA
1
PABELLÓN
C

288. B.2. Método de coordenadas.- Consiste en anotar y/o guardar en la memoria del equipo las coordenadas
de los puntos rellenados
Procedimiento:
1. Elección de la Red de Apoyo o poligonal.- La elección de la red de apoyo, se estudió en la Pag. 289
377
2° Determinación del croquis de los detalles a levantar.- Se dibuja in situ la geometría y posición
aproximada de los detalles naturales y artificiales (dicho gráfico se debe plasmar en la libreta de
campo).
Esta operación involucra la denotación de los puntos a levantar (asignación de nombres a los puntos
de relleno).
Es recomendable que esta actividad sea encabezada por un topógrafo de comprobada experiencia,
dado que la presencia de dicha persona tanto en el campo como en el gabinete será vital para la resolu-
ción de problemas.

289. 3° Se determina la mínima longitud a tomar en cuenta en el campo.- Para ello es precio la escala a
la cual se representará el levantamiento en el plano,
Si la escala elegida es 1/E, aceptable la siguiente expresión: L = 0,0002 x E, donde: L = Mínima
longitud a tomar en cuenta en el campo; tener presente que el valor obtenido está expresado en
metros; si por ejemplo E = 10 000; la mínima longitud L será 2 m.
4° Relleno desde el primer punto de control.-
- Se hace estación en un punto de la poligonal.
- Se ingresa al menú particular del equipo que se está utilizando.
- Se dirige la visual hacia uno de los puntos vecinos de la poligonal (espalda).
- Se suelta el bloqueo de la alidada y se dirige la visual hacia el primer punto a levantar, para luego
medir y guardar las coordenadas de dicho punto.
- Se suelta el bloqueo de la alidada y se dirige la visual hacia el segundo punto a rellenar, tomando
como datos, los mismos parámetros que el punto antecesor. La misma operación se realiza con las
demás puntos por levantar desde la misma estación.
5° Trabajo de gabinete.- Se realiza la transferencia de información de la estación total a la computado-
ra, obteniendo como resultado final, las coordenadas de los puntos levantados.
378
A
B
C
D
E
A1
A2
B1
B2
C1
C2
D1
D2
E1
E2
E3
Posteriormente se siguen los mismos pasos descritos en el método

290. CLASE 6

291. 3
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
SUPERFICIE TOPOGRÁFICA :
Es el relieve terrestre, con sus montañas, valles y otras formas terrestres continentales y marítimos.
GEOIDE:
Se define como la superficie equipotencial del campo gravitacional terrestre que coincide con las aguas del mar en
su estado normal de equilibrio.
CONCEPTOS FUNDAMENTALES
Es necesario mencionar que el geoide,
por tener una figura irregular, no es ex-
presable matemáticamente.

292. 4
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Notas adicionales sobre el elipsoide:
El elipsoide de revolución se forma tomando una elipse y girándola sobre su eje menor.
A
x
z
B
F1
F2
P1
P2
P
O a
b
Ahora podemos definir algunos parámetros fundamentales de esta elipse.
Achatamiento: .........................
Primera excentricidad: .............‚
Segunda excentricidad: .............ƒ
A continuación citaremos algunos de los elipsoides usados:
ELIPSOIDE
Parámetro Hayford WGS84
a 6 378 388.000 m 6 378 137.000 m
b 6 356 911.946 m 6356 752.314 m
e2 0.006 722 67 0.006 694 38
e’2 0.006 768 17 0.006 739 497
ELIPSOIDE DE REVOLUCIÓN:
Es un volumen geométrico que proviene de una elipse que gira alrededor de su eje menor
b
a
b
a
Elipse Elipsoide
Eje de rotación

293. 5
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
El elipsoide, en la geodesia aparece debido a la necesidad de expresar matemáticamente la superficie de la tierra,
pues ya sabemos que el geoide carece de dicha facultad; así pues el elipsoide es el cuerpo geométrico que se apro-
xima en mayor medida a la forma real de la TIERRA.
Geoide Elipsoide
ALTURA ORTOMÉTRICA ( H )
Es la separación vertical entre el geoide y la superficie topográfica
ALTURA ELIPSOIDAL ( h )
Es la separación vertical entre el elipsoide y la superficie topográfica .
ONDULACIÓN GEOIDAL (N)
Es la diferencia vertical entre la altura ortométrica y la elipsoidal
Elipsoide
Superficie topográfica
Geoide
N
H h

294. 6
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
DESVIACIÓN DE LA VERTICAL:
Se le llama también desviación astrogeodésica y viene a estar dado por el ángulo formado entre la normal al geoide
(vertical local) y la normal al elipsoide en un punto.
LÍNEA DE VISTA
NIVELADA
SUPERFICIE
TOPOGRÁFICA
ELIPSOIDE
GEOIDE
NORMAL AL
ELIPSOIDE
NORMAL AL
GEOIDE
DESVIACIÓN DE LA
VERTICAL
PUNTO DATUM:
Llamado también punto fundamental o punto origen. Es aquel punto donde se hace coincidir la vertical al geoide
con la normal al elipsoide (desviación de la vertical igual cero).
PERPENDICULAR AL GEOIDE
NORMAL AL ELIPSOIDE
ELIPSOIDE
GEOIDE
SUPERFICIE TOPOGRÁFICA
PUNTO DATUM

295. 7
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
La posición de un punto puede quedar definido dependiendo del tipo de sistema elegido, así como de los objetivos
que se persigue, en tal sentido distinguiremos dos sistemas genéricos.
£ El sistema de referencia terrestre; el cual se considera fijo a la tierra y se utiliza para determinar las coordenadas
de puntos sobre la superficie terrestre o sus proximidades, tal como los satélites artificiales que distan en prome-
dio 20000 Km.
£ El sistema de referencia espacial; tal como su nombre lo indica, se encuentra fijo al espacio, lo cual lo convierte en
un sistema inercial (libre de aceleración) donde los cálculos Newtonianos son totalmente permitidos, este sistema
es el apropiado para analizar el movimiento de cuerpos externos a la tierra, tales como los planetas, estrellas, etc.
1. Sistema de Referencia terrestre
A) Sistema Astronómico Local.
Un punto P; queda definido respecto a los ejes x; y; z;.
Eje “Z”: sentido contrario al vector gravedad en “p”
Eje “Y”: tangente a la superficie equipotencial que pasa por “p” y en la dirección norte.
Eje “X”: tangente a la superficie equipotencial que pasa por “p” y en la dirección este.
SISTEMA DE REFERENCIA
P
y(Norte)
x(Este)
z
g
Este sistema es válido solo para zonas muy limitadas, los ejes de coordenadas obedecen a direcciones diferentes
para cada punto de estación; por tanto no es válido para efectuar un levantamiento de coordenadas, dado que
es único para cada punto, constituye más bien un sistema instrumental para referir las observaciones.
3
2
4
x’
y’
A
En topografía es aceptable incrementos de coordenadas para cada punto y tratarlos conjuntamente, como si
estuvieran en el mismo sistema de referencia; sin embargo para cálculos geodésicos no es válido.

296. 8
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
B) sistema Geodésico Local.
El sistema geodésico local, está compuesto por:
£ Un elipsoide de referencia.
£ Un punto datum.
Punto datum
Elipsoide
Geoide
Inmediaciones del
punto datum
Generalmente el elipsoide elegido se adapta muy bien al geoide en las inmediaciones del punto datum, pero
a medida que nos alejamos, su adaptación se desvanece.
Perpendicular
Perpendicular
Punto datum
Elipsoide
Geoide
Latitud
astronómica
Latitud
geodésica
al elipsoide
Eje de rotación
Centro de la tierra
Centro del elipsoide
de la tierra
Eje del
elipsoide
al geoide
è La latitud y longitud astronómica, toman los mismos valores que la latitud y longitud geodésica en el
punto datum.
è Generalmente el elipsoide de referencia casi nunca se encuentra centrado y su eje no es coincidente con
el eje de rotación de la tierra.

297. 9
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Desventajas del Sistema Local:
è Este sistema es enteramente planimétrico, no es tridimensional; las cotas altimétricas se desarrollan a partir de
otros caminos.
è Las zonas limítrofes sufren confusiones en sus redes geodésicas, dado que comúnmente se presentan diferencias
inaceptables.
è Los elementos de los diversos datum no guardan relación.
Sistemas Locales antes de la Segunda Guerra Mundial:
Antes de 1940, cada país técnicamente avanzado había desarrollado su propio sistema en base a sus conveniencias
económicas y militares, normalmente no había sistemas comunes (si existían éstas eran escasas) dado que ello era
contrario a los intereses militares de cada país.
Algunos sistemas locales de hoy:
è El Datum Norteamericano: referido al elipsoide 1866 de Clarke, el origen es rancho inmóvil de Meades; el
sistema incorpora Canadá, México, Estados Unidos de Norteamerica, asimismo contempla parte de América
Central.
è El Datum Europeo: referido al elipsoide Internacional (Hayford), el origen está situado en Potsdam – Alemania,
este Datum se conoce con el nombre ED50 (Datum Europeo 1950); El origen actual está ubicado en Munich y
se llama ED-70 (Datum Europeo 1979 ó Datum Munich).
La figura muestra la cantidad de sistemas geográficos locales en Asia Suroriental; si bien es cierto cada sistema era
de mucha utilidad para su respectivo país o región, éstos se veían impotentes al no poder determinar las coordena-
das de puntos vecinos o por lo menos limítrofes respecto a su sistema.

298. 10
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
è El Datum Cabo: Referido al Elipsoide modificado en 1880 de Clarke y tiene su punto de origen en el FF-Elsfon-
tein, cerca de Elizabeth Portuario. Este Datum fue basado en el trabajo de los astrónomos de H.: Sir Thomas
Maclear (1833- 1870) y sir David Gill (1879 – 1907).
è El Datum Geodetic Australiano 1984 (AGD84): Se basa en el elipsoide nacional australiano a = 6378 160.00 m
y f = 1/298,25.
El origen es la estación Geodetic de Ichnston.
è El Datum Bogotá: Tiene su punto de partida en el observatorio astronómico de Botogá y está referido al elipsoi-
de internacional (Hayford).
è El Datum Campo Inchauspe: Tiene su origen en el punto astronómico Inchauspe, cerca de la ciudad de Pehua-
jó en la provincia de Buenos Aires, Argentina. El elipsoide asociado fue el internacional (Hayford).
è El Datum Provisional Sudamericano 1956 (PSAD-56): Tiene su punto de partida en la Canoa –Venezuela con
el elipsoide internacional (Hayford).
è El Datum Sudamericano 1969 (SAD69): Tiene su origen en Chua – Brasil (Lat. 19° 45’, Long. 48° 06’) y está
referido al elipsoide sudamericano 1969.
Eje de
la Tierra
D
a
t
u
m
E
u
r
o
p
e
o
Datum
Norteamericano
Centro de
la Tierra
Geoide
Elipsoide Internacional
Elipsoide Clarke
è Se piensa que la mejor solución era escoger el Datum de un área y ajustar todos los sistemas locales a él.
è Mientras que en cada caso el elipsoide elegido es un ajuste adecuado en el área de origen, ni uno ni otro
proporciona un buen ajuste para la tierra entera.

299. 11
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
SISTEMAS DE LOCALES DE DIVERSAS ZONAS Y PAÍSES
Argentina
CAMPO INCHAUSPE 1969 Internacional 1924
1969 SUDAMERICANO (SAD69) Sudamericano 1969
Afganistán HERAT DEL NORTE Internacional 1924
África Del Sur CABO Clarke 1880
Alaska (Excepto Las Islas De
Aleutian)
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Albania S-42 (PULKOVO 1942) Krassovsky 1940
Alberta
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Alemania (antes de 1990) EUROPEO 1950 Internacional 1924
Antartida
ISLA DEL ENGAÑO Clarke 1880
ÁREA ASTRO DEL CAMPO Internacional 1924
Antigua, Islas De Sotovento ISLA ASTRO 1943 DE ANTIGUA Clarke 1880
Arabia Saudita
NAHRWAN Clarke 1880
EUROPEO 1950 Internacional 1924
EL ABD 1970 DE AIN Internacional 1924
Argelia
VOIROL 1874 Clarke 1880
SÁHARA DEL NORTE 1959 Clarke 1880
VOIROL 1960 Clarke 1880
Australia
1968 GEODETIC AUSTRALIANO Nacional Australiano
1984 GEODETIC AUSTRALIANO Nacional Australiano
Austria
EUROPEO 1950 Internacional 1924
EUROPEO 1979 Internacional 1924
Bahamas (Excepto La Isla Del
Salvador Del San)
NORTEAMERICANO 1927 Clarke 1866
Bahrein EL ABD 1970 DE AIN Internacional 1924
Baltra 1969 SUDAMERICANO (SAD 69) Sudamericano 1969
Bangladesh INDIO EVEREST (La India 1956)
Barbados NORTEAMERICANO 1927 Clarke 1866
Barbuda NORTEAMERICANO 1927 Clarke 1866
Belice
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Belgica EUROPEO 1950 Internacional 1924
Bolivia
1956 SUDAMERICANO PROVISIONAL
(FSAS 56)
Internacional 1924
1969 SUDAMERICANO (SAD69) Sudamericano 1963
Bosnia HERMANNSKOGEL Bessel 1841
ZONA DE USO ELIPSOIDE
NOMBRE DEL DATUM
Botswana ARCO 1950 Clarke 1880
Brasil
CORREGO ALEGRE Internacional 1924
1969 SUDAMERICNAO (SAD 69) Sudamericana 1969
Brunei y Malasia de Este
(Sarwak y Sabah)
TIMBALAI 1948 Everest (Sabah Sarawak)
Burkina Faso
ADINDAN Clarke 1880
PUNTO 58 Clarke 1880
Burundi ARCO 1950 Clarke 1880
Camerún
ADINDAN Clarke 1880
NINNA Clarke 1880
Canadá NORTEAMERICANO 1983 GRS 80
Canadá del este (Terranova,
Brunswich nuevo, Nueva
Escocia y Quebec)
NORTEAMERICANO 1983 GRS 80
NORTEAMERICANO 1927 Clarke 1866
Canarias PICO DE LAS NIEVES Internacional 1924

300. 12
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
SISTEMAS LOCALES DE DIVERSAS ZONAS Y PAÍSES
Cerdeña
ROMA 1940 Internacional 1924
EUROPEO 1950 Internacional 1924
Colombia
OBSERVATORIO DE BOGOTÁ Internacional 1924
1956 SUDAMERICANO PROVISIONAL
(PSAD56)
Internacional 1924
1969 SUDAMERICANO (SAD 69) Sudamericano 1969
Colombia Británico NORTEAMERICANO 1927 Clarke 1866
Congo POINTE NOIRE 1948 Clarke 1880
Conus
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Corea Del Sur TOKIO Bessel 1841
Costa Rica
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Croatía HERMANNSKOGEL Bessel 1841 (Namiibia)
Cuba NORTEAMERICANO 1927 Clarke 1866
Checoslovaquia
S-42 (PLKOVO 1942) Krassovsky 1940
S-jtsk Bessel 1841
Chile 1969 SUDAMERICANO (SAD 69) Sudamericano 1969
Chile – Chile meridional
(cerca de 43º S)
1956 SUDAMERICANO PROVISIONAL
(PSAD56)
Internacional 1924
Chile – Chile norteño (cerca
de 19° S)
1956 SUDAMERICANO PROVISIONAL
(PSAD56)
Internacional 1924
Chile meridional (cerca de 53°S) CHILENO DEL SUR PROVISIONAL 1963 Internacional 1924
Chipre EUROPEO 1950 Internacional 1924
Da Cunha (TDC) de Tristan TRISTAN ASTRO 1968 Internacional 1924
Diego García ISTS 073 ASTRO 1969 Internacional 1924
Dinamarca EUROPEO 1950 Internacional 1924
ELIPSOIDE
NOMBRE DEL DATUM
ZONA DE USO
Djiboui FARO DE AYABELLE Clarke 1880
Ecuador
1956 SUDAMERICANO PROVISIONAL
(PSAD 56)
Internacional 1924
Ecuador (Excepto Las Islas De
las Islas Galápagos).
1969 SUDAMERICANO (SAD69) Sudamericano 1969
Egipto
VIEJO EGIPCIO 1907 Helmert 1906
EUROPEO 1950 Internacional 1924
El Salvador
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Emiratos Árabes Unidos NAHRWAN Clarke 1880
Eritrea (Etiopia) MASSAWA Bessel 1841
Escocia
EUROPEO 1950 Internacional 1924
ENCUESTA SOBRE LA ARTILLERIA DE
GRAN BRETAÑA 1936
Airy 1830
Eslovenia HERMANNSKOGEL Bessel 1841 (namibia)
España
EUROPEO 1950 Internacional 1924
EUROPEO 1979 Internacional 1924
Estados Unidos Del Este
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
ESTADOS Unidos Occidentales
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Estonia
ESTONIA: SISTEMA COORDINADO
1937
Bessel 1841
Etiopia ADINDAN Ckarje 1779

301. 13
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
SISTEMAS LOCALES DE DIVERSAS ZONAS Y PAÍSES
Europa Occidental EUROPEO 1950 Internacional 1924
Faial
INTERRUPTOR BAJO 1948 DE
GRACIOSA
Internacional 19424
Filipina (Excepto La Isla De
Mindanao)
LUZON Clarke 1866
Finiandia
EUROPEO 1950 Internacional 1924
EUROPEO 1979 Internacional 1924
Forme Las Islas (ENW) ESTELA ENIWETOK 1960 Hough 1960
Francia EUROPEO 1950 Internacional 1924
Gabón MPORALOKO Clarke 1880
Ghana LEIGON Clarke 1880
Graciosa
INTERRUPTOR BAJO 1948 DE
GRACIOSA
Internacional 1924
Grecia EUROPEO 1950 Internacional 1924
Groenlandia (Península De
Hayes)
NORTEAMERICANO 1927 Clarke 1866
Groenlandia Del Sur QORNOQ Internacional 1924
Gibraltar EUROPEO 1950 Internacional 1924
Guam GUAM 1963 Clarke 1866
Guatemala
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Guinea DABOLA Clarke 1880
ELIPSOIDE
NOMBRE DEL DATUM
ZONA DE USO
Guinea -Bissau BISSAU Internacional 1924
Guyana
1956 SURAMERICANO PROVISIONAL
(PSAD56)
Internacional 1924
1969 SURAMERICANO (SAD 69) Sudamericano 1969
Hawail
VIEJO HAWAIANO Clarke 1866
NORTEAMERICANO 1983 GRS 80
Herzegovina Serbia HERMANNSKOGEL Bessel 1841 (Namibia)
Holanda
EUROPEO 1950 Internacional 1924
EUROPEO 1979 Internacional 1924
Honduras
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Hong Kong HONG KONG 1963 Internacional 1924
Hungria S-42 (PULKOVO 1942) Krassovsky 1940
Indonesio INDONESIO 1974 Indonesio
Inglaterra
EUROPEO 1950 Internacional 1924
ENCUESTA SOBRE LA ARTILLERÍA DE
GRAN BRETAÑA 1936
Airy 1830
Irán EUROPEO 1950 Internacional 1924
Iraq EUROPEO 1950 Internacional 1924
Irlanda
EUROPEO 1950 Internacional 1924
IRLANDA 1965 Airy Modificada
Isla De Bahrein EL ABD 1970 DE AIN Internacional 1924
Isla De Cayman
LC. 5 ASTRO 1961 Clarke 1866
NORTEAMERICANO 1927 Clarke 1866
Isla De Chatham (Zealand
Nuevo)
ISLA ASTRO 1971 DE CHATHAM Internacional 1924
Isla De Espíritu Santo SANTO (DOS) 1965 Internacional 1924
Isla De Falkland Del este COLINA 1943 DEL ZAPADOR Internacional 1924
Isla De Gizo (Islas Nuevas De
Georgia)
DOS 1968 Internacional 1924

302. 14
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
SISTEMAS LOCALES DE DIVERSAS ZONAS Y PAÍSES
Isla De Gusalcanal GUX 1 ASTRO Internacional 1924
Isla De Johnston ISLA 1961 DE JOHNSTON Internacional 1924
Isla De Kerguelen ISLA 1949 DE KERGUELEN Internacional 1924
Isla De la Ascensión ISLA 1958 DE LA ASCENSIÓN Internacional 1924
Isla de los Turcos NORTEAMERICANO 1927 Clarke 1866
Isla De Mahe MAHE 1971 Clarke 1880
Isla De Marcus ESTACIÓN ASTRONÓMICA 1952 Internacional 1924
Isla De Masirah (Omán) NAHRWAN Clarke 1880
Isla De Pascua ISLA 1967 DE PASCUA Internacional 1924
Isla De Pitcaim PITCAIRN ASTRO 1967 Internacional 1924
Isla De Tem ISLA DE ASTRO TERN (FRIG) 1961 Internacional 1924
Isla Del Engaño ISLA DEL ENGAÑO Clarke 1880
ELIPSOIDE
NOMBRE DEL DATUM
ZONA DE USO
Isla del hombre
ENCUESTA SOBRE LA ARTILLERÍA DE
GRAN GRAN BRETAÑA 1936
Airy 1830
Isla Del Salvador Del San NORTEAMERICANO 1927 Clarke 1866
Isla Del Sur De Georgia ISTS 061 ASTRO 1968 Internacional 1924
Islas de Virginia PUERTO RICO Clarke 1866
Islandia HJORSEY 1955 Internacional 1924
Islas De Aleutian NORTEAMERICANO 1983 GRS 80
Islas de Aleutian – a este de
180° W
NORTEAMERICANO 1927 Clarke 1866
Islas de Aleutian al oeste de
180° W
NORTEAMERICANO 1927 Clarke 1866
Islas De América Samoa AMÉRICA SAMOA 1962 Clarke 1866
Islas de Bangka y de Belitung
(Indonesia)
BUKIT RIMPAH Bessel 1841
Islas De Bermudas BERMUDAS 1957 Clarke 1866
Islas de Carolina KUSAIE ASTRO 1951 Internacional 1924
Islas De Cocos ANA 1 ASTRO 1965 Nacional australiano
Islas de Corvo y de Flores
(Azores)
OBSERVATORIO METEOROLÓGICO
1939
Internacional 1924
Islas de Efate y de Erromango BELLEVUE (IGNICIÓN) Internacional 1924
Islas de Escocia y de Shetland
ENCUESTA SOBRE LA ARTILLERÍA DE
GRAN GRAN BRETAÑA 1936
Airy 1830
Islas De las Islas Galápagos 1969 SUDAMERICANO (SAD 69) Sudamericano 1963
Islas de Jamaica NORTEAMERICANO 1927 Clarke 1866
Islas De Mascarene REUNIÓN Internacional 1924
Islas De Phoenix CANTÒN ASTRO 1966 Internacional 1924
Islas De Santa Maria (Azores) SAO BRAZ. Internacional 1924
Islas de Shetland
EUROPEO 1950 Internacional 1924
ENCUESTA SOBRE LA ARTILLERÍA DE
GRAN GRAN BRETAÑA 1936
Airy 1830
Islas de Sotavento
ISLA ASTRO 1943 DE ANTIGUA Clarke 1880
FORTALEZA THOMAS 1955 Clarke 1880
ISLA ASTRO 1958 DE MONTSERRAT Clarke 1880
Islas de Terceira
INTERRUPTOR BAJO 1948 DE
GRACIOSA
Internacional 1924
Islas De Viti Levu (Las Islas Fiji)
(Mvs)
VITI LEVU 1916 Clarke 1880
Islas Del Salvamento SELVAGEM GRANDE 1938 Internacional 1924
Isla Graciosa
INTERRUPTOR BAJO 1948 DE
GRACIOSA
Internacional 1924

303. 15
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
SISTEMAS LOCALES DE DIVERSAS ZONAS Y PAÍSES
Isla Faial
INTERRUPTOR BAJO 1948 DE
GRACIOSA
Internacional 1924
Islas Situado a mitad del
camino
ASTRO SITUADO A MITAD DEL
CAMINO 1961
Internacional 1924
Israel EUROPEO 1950 Internacional 1924
Italia EUROPEO 1950 Internacional 1924
Iwo Jima FARO “E” 1945 DE ASTRO Internacional 1924
Jamaica NORTEAMERICANO 1927 Clarke 1866
Japón TOKIO Bessel 1841
Jordania EUROPEO 1950 Internacional 1924
ELIPSOIDE
NOMBRE DEL DATUM
ZONA DE USO
Kalimantan (Indonesia) GUNUNG SEGARA Bessel 1541
Kauai
VIEJO HAWAIANO Clarke 1866
NORTEAMERICANO 1983 GRS 80
Kazakhstan S-42 (PULKOVO 1942) Krassovsky 1940
Neia ARCO 1960 Clarke 1880
Kuwait EUROPEO 1950 Internacional 1924
La India INDIO Everest (La India 1956)
Latvia S-42 (PULKOVO 1942) Krassovsky 1940
Lesotho ARCO 1950 Clarke 1880
Libano EUROPEO 1950 Internacional 1924
Liberia LIBERIA 1964 Clarke 1880
Luxemburgo EUROPEO 1950 Internacional 1924
Magadascar (Tan)
OBSERVATORIO 1925 DE
ANTANANARIVO
Internacional 1924
Malasia KETAU 1948 Everest (Malay y Cantan)
Maldivas GAN 1970 Internacional 1924
Malawi ARCO 1950 Clarke 1880
Malol ADINDAN Clarke 1880
Malta EUROPEO 1950 Internacional 1924
Manitoba
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Marruecos MERCHICH Clarke 1880
Maui
VIEJO HAWAIANO Clarke 1866
NORTEAMERICANO 1983 GRS 80
México
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Micronesia KUSAIE 1951 Internacional 1924
Mindanao LUZON Clarke 1866
Montserrat ISLA ASTRO 1958 DE MONTSERRAT Clarke 1880
Namibia SCHWARZECK Bessel 1841 (Namibia)
Nepal INDIO Everest (La India 1956)
Nevis FORTALEZA THOMAS 1955 Clarke 1880
Nicaragua
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Nigeria PUNTO 58 Clarke 1880
Nigeria MINNA Clarke 1880
Noruega
EUROPEO 1950 Internacional 1924
EUROPEO 1979 Internacional 1924
Nueva Zelandia DATO GEODETIC 1949 Internacional 1924

304. 16
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
SISTEMAS LOCALES DE DIVERSAS ZONAS Y PAÍSES
Oahu
VIEJO HAWAIANO Clarke 1866
NORTEAMERICANO 1983 GRS 80
Okinawa TOKIO Bessel 1841
Omán OMÁN Clarke 1880
Ontario
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
País de Gales
ENCUESTA SOBRE LA ARTILLERÍA DE
GRAN GRAN BRETAÑA 1936
Airy 1830
Países Bajos EUROPEO 1979 Internacional 1924
Paquistán INDIO Everest (La India 1956)
Paraguay
CHUA ASTRO Internacional 1924
1969 SUDAMERICANO (SAD 69) Sudamericano 1969
Perú
1956 SUDAMERICANO PROVISIONAL
(PSAD 56)
Internacional 1924
1969 SUDAMERICANO (SAD 69) Sudamericano 1969
Pico
INTERRUPTOR BAJO 1948 DE
GRACIOSA
Internacional 1924
Polonia S-42 (PULKOVO 1942) Krassovsky 1940
Porto Santo e islas de Madeira PORTO SANTO 1936 Clarke 1880
Portugal EUROPEO 1950 Internacional 1924
Puerto Rico PUERTO RICO Clarke 1866
Qatar NACIONAL DE QATAR Internacional 1924
República dominicana
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
República de Maldives GAN 1979 Internacional 1924
Rumania S-42 (PULKOVO 1942) Krassovsky 1940
Rusia S-42 (PULKOVO 1942) Krassovsky 1940
Sao Jorge
INTERRUPTOR BAJO 1948 DE
GRACIOSA
Internacional 1924
Sao Miguel SAO BRAZ Internacional 1924
St. Kitts FORTALEZA THOMAS 1955 Clarke 1880
Senegal ADINDAN Clarke 1880
Sicilia (Italia) EUROPEO 1950 Internacional 1924
Sierra Leone 1960 SIERRA LEONE 1960 Clarke 1880
Singapur ASIA DEL SUR Fischer Modificado 1960
Singapur del Oeste KERTAU 1948 Everest (Malay y Cantan)
Siria
EUROPEO 1950 Internacional 1924
EUROPEO 1979 Internacional 1924
Singapur del Oeste KERTAU 1948 Everest (Malay y Cantan)
Singapur ASIA DEL SUR Fisher Modificado 1960
Somalia AFGDOYE Krassvsky 1940
Sri Lanka KANDAWALA Everest (La India 1830)
ELIPSOIDE
NOMBRE DEL DATUM
ZONA DE USO
St, Isla De Helena DOS 71/4 DE ASTRO Internacional 1924
Sudán ADINDAN Clarke 1880
Suecia
EUROPEO 1950 Internacional 1924
EUROPEO 1979 Internacional 1924
Suiza
EUROPEO 1950 Internacional 1924
EUROPEO 1979 Internacional 1924
Sumatra (Indonesia) DJAKARTA (BATAVIA) Bessel 1841
Suriname (ZAN) ZANDERIJ Internacional 1924
Swazilandia ARCO 1950 Clarke 1880
Tailandia
INDIO 1954 Everest (La India 1830)
INDIO 1975 Everest (La India 1830)

305. 17
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
C) Sistema Astronómico Global
Esta constituido por un sistema cartesiano tridimensional, el cual cumple con las siguientes características :
SISTEMAS LOCALES DE DIVERSAS ZONAS Y PAÍSES
Taiwán Hu-tzu-shan Internacional 1924
Tanzania ARCO 1960 Clarke 1880
Tasmania
1966 GEODETIC AUSTRALIANO Nacional Australiano
1984 GEODETIC AUSTRALIANO Nacional Australiano
Territorios y Saskatchewan Del
Noroeste
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Trinidad y Trinidad y Tobago
NAPARIMA, BWI Internacional 1924
1969 SUDAMERICANO (SAD 69) Sudamericano 1969
Túnez
CARTHAGE Clarke 1880
EUROPEO 1950 Internacional 1924
Uruguay (YAC) YACARE Internacional 1924
Venezuela
1956 SUDAMERICANO PROVISIONAL
(PSAD 56)
Internacional 1924
1969 SUDAMERICANO (SAD 56) Sudamericano 1969
Vietnam INDIO 1960 Everest (La India 1830)
Yukon
NORTEAMERICANO 1927 Clarke 1866
NORTEAMERICANO 1983 GRS 80
Yugoslavia (antes de 1990) HERMANNSKOGEL Bessel 1841
Zake ARCO 1950 Clarke 1880
Zambia ARCO 1950 Clarke 1880
Zimbabwe ARCO 1950 Clarke 1880
Zona del Canal NORTEAMERICANO 1927 Clarke 1866
ELIPSOIDE
NOMBRE DEL DATUM
ZONA DE USO
Centro de masa
El origen es el centro de masa de la totalidad de la tierra, incluyendo los océanos y la atmósfera
(geocentro).

306. 18
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Eje de rotación
Terrestre
Z
PN
PS
El eje “z”, pasa por el eje de rotación de la tierra.
El Ecuador es un plano perpendicular al eje de rotación y divide a la tierra en dos zonas :
Hemisferio Norte y Sur
HEMISFERIO SUR
HEMISFERIO NORTE
Z
PN Plano Ecuatorial
PS

307. 19
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
â La posición de un punto queda determinada con las coordenadas cartesianas x; y; z.
â La posición de un punto queda determinada con las coordenadas astronómicas geográficas:
f; l; w.
OBSERVACIONES
La intersección del meridiano internacional de referencia y el Ecuador (A), forma con el punto “o”,
el eje “x”.
El eje “Y” se forma en el Ecuador y parte del punto “O” perpendicular al eje “X” obedeciendo la regla de
la mano derecha.
Meridiano
Internacional
de referencia
(Greenwich)
X
A
O
Z
PS
ECUADOR
x
z
PS
ECUADOR
Elipsoide de
Referencia
y
PN

308. 20
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Ÿ Meridiano astronómico de un punto P .
Es aquel plano paralelo al eje de rotación de la tierra que contiene al vector gravedad que pasa por dicho punto.
Ÿ Latitud astronómica (f) .
Es el ángulo medido en el plano del meridiano astronómico que forman la tangente a la dirección de la línea de
la plomada en “p” y el plano del Ecuador. ( 0° ≤ f ≤ 90° ). f(+) ® Norte
Ÿ Longitud astronómica (l) .
Es el ángulo diedro medido en el plano del Ecuador. Parte del meridiano de Greenwich hacia el este de él, hasta
llegar al meridiano que contiene al punto P
. ( 0° ≤ l ≤ 360° ). l(+) ® Este.
Ÿ Potencial gravitatorio (w) .
Está definido por la superficie equipotencial que pasa por el punto “P”
Meridiano
de
Greenwich
x
z
y
g
P
Eje de rotación
de la tierra
Vertical Astronómica
que pasa por P.
Superficie
equipotencial que
pasa por P (WP
).
Línea de
λ = constante
λ
φ
W
B
W
A
ECUADOR
Las coordenadas f y l; se pueden determinar de forma absoluta mediante observaciones astronómicas; mien-
tras que el campo gravitatorio W no se puede determinar de forma absoluta; pero si la diferencia de potencial
respecto al geoide, empleando para ello la altura ortométrica.
Sin embargo, las observaciones más precisas se obtienen de forma relativa, es decir, referidas al sistema astro-
nómico local y de alta precisión; ello implica transferir mediciones efectuadas en el sistema astronómico local
al global mediante observaciones adicionales y fórmulas complicadas; lo cual obliga a buscar sistemas menos
complejos.

309. 21
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
D) Sistema Elipsoidal Global.
Consiste en un caso mejorado del sistema astronómico global.
Así: pues la posición de un punto “P” quedará definida por sus tres coordenadas.
Ÿ Latitud geodésica (f)
Ÿ Longitud geodésica (l)
Ÿ Altura elipsoidal (h)
M
e
r
i
d
i
a
n
o
d
e
G
r
e
e
n
w
i
c
h
P
h
A
x
y
z
λ
φ
Elipsoide de
Revolución
Plano Meridiano
que contiene la Normal AP
Como verá usted, la superficie de referencia que reemplaza a la equipotencial es el elipsoide de revolución.
La ventaja de este sistema radica en que el elipsoide se basa en un modelo matemático definido y por ende las
coordenadas de un punto “p” serán fácilmente expresables matemáticamente.
Por otro lado es preciso destacar que latitud y longitud no son exactamente igual a sus homólogos astronómi-
cos, existe casi siempre una diferencia.
Un punto “p” puede quedar definido de dos formas:
. En términos de sus coordenadas geodésicas ( f ; l ; h )
. En términos de sus coordenadas cartesianas ( x ; y ; z )
2. Sistemas de referencia espaciales.
Respecto a los sistemas de referencia terrestre, las coordenadas de un punto fijo en el espacio variarían
constantemente en virtud a la rotación terrestre.
Es por ello que para determinar la posición de los astros lejanos que como tal, pueden ser considerados
fijos, se hace uso de las coordenadas astronómicas, gracias a la llamada esfera celeste, cuyo estudio no está
incluido en el presente texto.

310. 22
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Movimiento del eje de rotación terrestre
La dirección del eje de rotación terrestre, cambia con el tiempo respecto a la propia superficie terrestre.
El polo describe a lo largo del tiempo una trayectoria libre que es una curva más o menos circular de radio 6 metros
y período aproximado de 430 días, provocado por el carácter deformable de la tierra.
Superpuesta a ésta trayectoria libre, se encuentra una serie de oscilaciones provocadas por la influencia gravitatoria
del sol y la luna con una magnitud de 60 centímetros.
Este movimiento del polo afecta directamente a las coordenadas de los puntos sobre la superficie terrestre, dado que
el sistema de referencia irá cambiando. Lo más indicado es tomar como eje z de referencia al origen o centro de los
círculos de movimiento libre, quedando así determinado el eje de un modo convencional.
Si las coordenadas de los puntos se refieren al polo convencional, trendremos coordenadas absolutas, si se refieren
al polo instantáneo, tendremos coordenadas instantáneas.
No hay teoría científica que pueda predecir el movimiento del polo, así que se monitorea contínuamente mediante
observaciones. Esta materialización se realiza con observaciones astronómicas lo que da lugar al establecimiento de
tres polos diferentes.
1. Polo C.I.O. (Convencional International Origen). Definido como la posición media del polo entre 1900 y
1905
2. Polo B.I.H. (BUREAU International de L’Heure) creada en 1912; encargada del mantenimiento de la hora y de
la posición del origen de longitudes (posición media del observatorio astronómico de Greenwich).
La determinación de la latitud de sus observatorios, generó el polo BIH que proporciona estimaciones más fre-
cuentes (medias de 5 días) y precisiones de 1 metro en la determinación del movimiento del polo.
3. Polo I.P.M.S. (International Polar Motion Service). Generado a partir de determinaciones de latitud astro-
nómica en 80 estaciones y con precisión de un metro en la determinación del movimiento del polo.
NOTA
En 1984, la B.I.H. estableció un nuevo sistema de referencia terrestre, basada en las coordenadas cartesinas geocéntri-
cas de las estaciones fundamentales, donde técnicas espaciales habían sido aplicadas, este nuevo sistema coincide con
el polo C.I.O. astronómico si se tiene en cuenta las precisiones en la determinación del CIO, lo cual permite dar continui-
dad a las coordenadas determinadas antiguamente.

311. 23
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
4. Polo I.E.R.S. (International Earth Rotation And Reference Systems Service).
Creado en 1987, reemplazando a la BIH y a la IPMS para, entre otras cosas, monitorear el movimiento del polo,
basándose en técnicas espaciales de forma continua
MARCO DE REFERENCIA :
Es la materialización de un sistema de referencia convencional a través de observaciones, es decir, se trata de un
conjunto de puntos (lugares localizados en la superficie terrestre) con coordenadas y velocidades conocidas en ese
sistema de referencia convencional y que sirven para materializar en el espacio el sistema de referencia.
MARCO DE REFERENCIA TERRESTRE INTERNACIONAL (ITRF)
El sistema de referencia terrestre internacional convencional se materializa a través de las coordenadas de una serie
de estaciones distribuidas por todo el mundo en ese sistema de referencia, constituyendo el ITRF (Internacional Te-
rrestrial Reference Frame), establecido y mantenido por la IERS.
La historia de los diferentes ITRF comenzó en 1984, y, a partir de ahí se han obtenido las soluciones 88, 89, 90, 91,
92, 93, 94, 96, 97, 2000, 2005 y, recientemente la 2008, estas soluciones difieren unas de otras debido a la incorpo-
ración constante de nuevas estaciones, nuevas observaciones en las estaciones ya existentes, mejora en la precisión
de las mismas o nuevos métodos de procesamiento.
Estaciones que forman el ITRF2000 simbolizadas según el número de técnicas
espaciales diferentes que utilizan.

312. 24
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
SISTEMA DE REFERENCIA GEODÉSICO GLOBAL WGS84 ( WORLD GEODETIC SYSTEM 1984) :
Es un sistema geocéntrico elipsoidal, fundado y monitoreado por el Departamento de Defensa de los Estados Unidos
de Norte América, obtenido exclusivamente a partir de los datos de la constelación de satélites GPS. Es compatible
con el Sistema de Referencia Terrestre Internacional (ITRF).
WGS84, identifica cuatro parámetros :
Semieje mayor = a = 6,378,137.00 m
Aplanamiento = 1/f = 298.257223563
Constante de gravitación geocéntrica = GM = 3,986,004.418 x 108 m3/s2
Velocidad angular media de la tierra = ω = 7,292,115 x 10-11 rad/s
La orientación del eje Z, está definida por el Polo I.E.R.S. ; el eje x, por el meridiano origen definido por el I.E.R.S.
ACTUALIZACIÓN WGS84
Parámetros de transformación :
Parámetros de transformación entre WGS84 (G1674) y actualizaciones pasadas WGS84, así como algunas
realizaciones ITRF.
Desde A Época T1
m
T2
m
T3
m
D
ppb
R1
mas
R2
mas
R3
mas
Precisión
m
WGS84(G1150) WGS84(G1674) 2001.0 -0.0047 0.0119 0.0156 4.72 0.52 0.01 0.19 0.0059
ITRF2008 WGS84(G1674) 2005.0 0 0 0 0 0 0 0 0.10
ITRF2000 WGS84(G1150) 2001.0 0 0 0 0 0 0 0 0.10
ITRF94 WGS84(G873) 1997.0 0 0 0 0 0 0 0 0.10
ITRF91 WGS84(G730) 1994.0 0 0 0 0 0 0 0 0.10
ITRF90 WGS84(original) 1984.0 0.060 -0.517 -0.223 -11.0 18.3 -0.3 7.0 0.01
Nombre Datum-Época Observaciones Cambio
WGS84 1984 Primera realización, establecido por el Departamento de Defensa
en 1987, usando observaciones Doppler. También conocido como
WGS84 (1987), WGS84 (original), WGS84 (tránsito). Para fines de
topografía, WGS84 original, es idéntico al NAD83 (1986).
WGS84, está conectado al ITRF90 por una transformación Helmert
de siete parámetros.
N/A
WGS84
(G730)
1994 Actualización realizada por el Departamento de Defensa el
06/29/1994, basada en observaciones GPS.
G significa GPS y 730, es el número de semana GPS; basado en
ITRF91.
0.70 m.
WGS84
(G873)
1997 Actualización realizada por el Departamento de Defensa, el
01/29/1997, basada en observaciones GPS.
G significa GPS y 873, es el número de semana GPS; basado en
ITRF94.
0.20 m.
WGS84
(G1150)
2001 Actualización realizada por el Departamento de Defensa, el
01/20/2002, basada en observaciones GPS.
G significa GPS y 1150, es el número de semana GPS; basado en
ITRF2000.
0.06 m.
WGS84
(G1674)
2005 Actualización realizada por el Departamento de Defensa, el
02/08/2012, basada en observaciones GPS. G significa GPS y 1674,
es el número de semana GPS; basado en ITRF2008.
0.01 m.
m = metro; 1 mas = 0,001”; ppb = partes por billón.

313. 25
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
è WGS84 y ITRF
» Actualización Antigua: conocida comúnmente como DOPPLER Tránsito, y proporciona coordenadas de la
estación con una precisión de alrededor de un metro.
» Nuevas Actualizaciones: de WGS84, basados en los datos de GPS, como G730, G873 y G1150. Etas nue-
vas actualizaciones WGS84 son coincidentes con ITRF la altura de 10 centímetros.
Para estas actualizaciones no hay parámetros oficiales de transformación. Esto significa que se puede consi-
derar que ITRF coordenadas se expresan también en WGS84 al nivel 10 cm.
è WGS84, NAD83 y ITRF
WGS84 original, está de acuerdo escencialmente con NAD83 (1986).
El Datum de Norteamérica de 1983 (NAD83) se utiliza en todas partes de América del Norte, excepto México.
Este dato se realiza en el Estados Unidos contiguos y Alaska (Placa de Norteamérica) a través de las CORS Na-
cionales (estaciones de referencias de funcionamiento continuo) que proporciona la base para la obtención de
transformaciones rigurosos entre la serie ITRF y NAD83, asi como una gran variedad de aplicaciones científicas.
A partir de noviembre de 2011, la red CORS contiene más de 1800 estaciones, aportados por más, de 200 or-
ganizaciones diferentes, y la red continúa en expansión. La última realización de NAD83 se llama tecnicamente
NAD83 (2011/PA11/MA11) época 2010.00 que constituye el marco para la definición del sistema de referencia
espacial nacional (IEN). En Canadá NAD83 se vigila también a través del Sistema de Control Activo de Canadá.
Así, las dos organizaciones encargadas de la vigilancia y realizar cambios en el NAD83 son el Servicio Geodésico
Nacional (NGS), http://www.ngs.noaa.gov y los Recursos Naturales de Canadá (NRCan), http://www.nrcan.gc.ca.
y los recursos naturales de Canadá (NRCan), http://www.nrcan.gc.ca.
è Datum mexicana de 1993
De México Instituto Nacional de Estadística, Geográfica, e Informatica (INEGI), http://www.inegi.org.mx, la
agencia federal responsable de la geodesia y la cartografía del país, adoptó el marco geocéntrico ITRF92, época
1988.0, como base por su definición de referencia. La realización del datum se logra a través de la red Geodé-
sica Nacional Activa (RGNA) una red de 14 estaciones de receptores GPS permanentes. Recientemente, adop-
taron ITRF2008, .epoch 2010.0, como la nueva base para la definición mexicana Datum.
è WGS84, ITRF y SIRGAS
El sistema de referencia Geocéntrico para América del Sur 1995 (SIRGAS 1995) se estableció para apoyar un
marco geodésicoy cartografía unificada para el continente sudamericano. La mayoría de los países de América
del Sur y el caribe participaron en esta empresa con 58 estaciones de referencia que se extendió posteriormente
a América Central y del Norte. El marco de referencia adoptado era ITRF94, epoch 1,995,42. El Sistema de Re-
ferencia Geocéntrico para las Américas 2 000 (SIRGAS 2 000) fue realizado por un marco de 184 estaciones ob-
servadas en el 2 000 y ajustados en el ITRF2000, época 2 000.40 SIRGAS 2000 incluye vínculos con mareógrafos
y reemplaza SIRGAS 1995 para América del Sur, mientras que la expanción de SIRGAS hacia Centroamérica.
El nombre fue cambiado en 2001 para su uso en toda América Latina. hay varias páginas web con información
sobre SIRGAS, tales como: http://www.ibge.gov.br/home/geociencias/geodesia/sirgas.
è WGS84, ITRF y ETRS89
El ETRS89 (sistema Europeo de Referencia Terrestre de 1989) se basa en (TRF89, época 1989.0 y monitoreado
por una red de cerca de 250 estaciones de seguimiento GNSS permanentes conocidos como la Red Permanente
EUREF (EPN). El IAG Subcomisión EUREF es responsable del mantenimiento del Sistema Europeo de Refereren-
cia Terrestre (ETRS89). Visite el sitio web EUREF: http://www.euref.eu. La Oficina Central EPN se ecuentra en el
Observatorio Real de Belgica. http://www.epncb.oma.be.
è WGS84, ITRF y GDA94
El Datum Geocéntrico de Australia de 1994 (GDA94) se refería originalmente al marco ITRF92, en época 1994.0
GDA94 es controlada por la Red Australiana regional GNSS (ARGN) que actualmente está compuesta por una
red de 15 estaciones GPS de seguimiento permanente en Australia y sus territorios, con las 8 estaciones en Aus-
tralia conocidos como la Red Fiducial australiano (AFN). La organización responsable de la supervisión GDA94
es Geoscience Australia. http://www.auslig.gov.au.

314. 26
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
TIPOS DE COORDENADAS USADAS EN GEODESIA
Coordenadas cartesianas
Y
X
y
x
z
A
Z
Coordenadas geodésicas:
A= (x, y, z)
La posición de un punto queda definida gracias a los valores de
x, y, z.
Meridiano de
Greenwich
Ecuador
A
λ
φ
Coordenadas UTM:
Ver proyecciones cartográficas.
La posición de un punto queda definido gracias a los valores de la latitud geodésica (f)
y la longitud geodésica (l)

315. 27
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
PROYECCIONES CARTOGRÁFICAS
Proyección cartográfica es la representación de la superficie elipsoidal en un plano.
Es imposible llevar a cabo la proyección cartográfica sin evitar la presencia de algunos tipos de distorsiones.
Sin embargo se han elaborado proyecciones que mantienen alguna propiedad de la superficie elipsoidal “sin distor-
sión” a costa de distorsionar las otras propiedades; ello obedece al objetivo que se persigue.
Tiene la cualidad de mantener la distancia real entre dos puntos situados sobre la superficie del Elipsoide.
No obstante, es necesario aclarar que no es posible generar una proyección que conserve la distancia en todas las
direcciones para todos los puntos del mapa. En realidad la mayoría de las proyecciones cumple el principio de equi-
distancia para algunas líneas o puntos. Por ejemplo en la proyección de Mercator, la equidistancia se presenta en el
Ecuador, (ver figura A).
PROYECCIÓN EQUIDISTANTE
PROPIEDADES DE LAS PROYECCIONES CARTOGRÁFICAS
Proyección Conforme
Tiene la cualidad de conservar los ángulos formados por dos líneas, tanto en el elipsoide como en el plano carto-
gráfico; sin embargo es importante puntualizar que no existe ninguna proyección conforme que mantenga dicha
propiedad en todo el elipsoide. Este tipo de proyecciones conserva la forma de las figuras pero no el tamaño de éstas.
Por último es preciso acotar que una proyección conforme, se refiere a la conservación de ángulo, no de acimutes
o rumbos.
La proyección de Mercator es un ejemplo de estas propiedad; en el elipsoide, los paralelos y meridianos se cortan
perpendicularmente; en el plano cartógrafico proyectado conservan dicho ángulo perpendicular, (ver figura A)
En el presente caso, la línea ecuatorial es común al elipsoide y al cilindro, en virtud a ello, la distancia AB, no
sufre distorsión alguna.
Paralelos
Paralelos
Meridianos
Meridianos
ECUADOR
A B
A
B
Figura A

316. 28
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Proyección de MERCATOR
Consiste en circunscribir un cilindro hueco al elipsoide de referencia, tangente al plano Ecuatorial. El eje de cilindro
es coincidente con el eje de rotación de la tierra.
PROYECCIÓN CILÍNDRICA
Eje del
cilindro
Eje de rotación
de la tierra
Cilindro tangente al elipsoide en el
plano ecuatorial
Proyección Equivalente.
Tiene la propiedad de conservar la superficie (área) del elipsoide en el plano proyectado, a costa de distorsionar la
forma de las figuras.
Un ejemplo típico de ello está representado por la proyección cilíndra equivalente, en el cual los puntos del elipsoide
se proyectan paraleo al ecuador.

317. PA R A L E L O
PA R A L E L O
E C U A D O R
M
E
R
I
D
I
A
N
O
a
b
c
d
29
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Los meridianos se proyectan en líneas rectas paralelas al eje del cilindro.
Los paralelos se proyectan en líneas rectas paralelos al ecuador y desigualmente espaciado.
Desarrollando el Cilindro
Groenlandia

318. 30
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Análisis
Groenlandia es una isla muy cercana al polo norte con
un área de 2.1 millones de km2.
Sudamérica es un continente ubicado en el hemisferio
sur pero no muy cercano al polo sur, con un área 17,8
millones de km2 (mucho más extensa que Groenlan-
dia).
La proyección de MERCATOR muestra a Groenlandia
con una superficie mucho mayor que Sudamérica (14
veces su área original).
Groenlandia
Sudamérica
- Es una proyección conforme.
- El ecuador se representa mediante una línea recta sin deformaciónn (escala verdadera)
- Los meridianos se proyectan en líneas rectas paralelas al eje del cilindro.
- Los paralelos se proyectan en líneas rectas paralelas al ecuador y desigualmente espaciados.
- Los paralelos y meridianos se cortan en ángulos rectos.
- La proyección de Mercator, va exagerando el tamaño de las figuras a medida que nos alejamos
del plano ecuatorial (ver análisis).
CARACTERÍSTICAS
Observación
Este tipo de proyección es ventajoso en la navegación, pues el piloto de un barco puede mantener fijo el
timón siempre y cuando el rumbo sea constante.
Círculo
máximo
Loxodrómica
Meridiano 1
Meridiano 2
W70°
W50°
W30°
S10°
N10°
S30°
S50°
N30°
N50°
θ
θ
Meridiano 2
Meridiano 1
Loxodrómica

319. 31
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Consiste en circunscribir un cilindro hueco a un elipsoide, tangente a un Meridiano (meridiano origen), el eje del
cilindro es transversal (perpendicular) al eje de la tierra.
PROYECCIÓN TRANSVERSAL DE MERCATOR
Eje de
rotación
terrestre
Eje del
cilindro
Ecuador
Cilindro
4 3
θ
2 1 2’ 3’ 4’
A medida que el ángulo q crece, la distorsión de la proyección en área y distancia aumenta exa-
geradamente; en virtud a ello, convencionalmente se ha establecido como ángulo “q” máximo:
3 grados sexagesimales para un meridiano central.
PN
PS
Meridiano origen o central
Ecuador
Eje del cilindro
Eje de
rotación
terrestre

320. 32
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
¿La proyección trans-
versal de MERCATOR,
es aplicable para án-
gulos menores o igual
a 3° solamente?
Convencionalmente
si; no obstante, ello no
impide incrementar
el valor del ángulo θ,
si las circunstancias lo
ameritan.
¿Cuántas zonas de influencia existen?
Dado que el ángulo central de influencia corresponde a un ángulo de seis grados sexagesimales (3° a cada lado
del meridiano central), existen 60 cilindros tangentes, cada uno a un meridiano central diferente (sesenta zonas de
influencia).
Meridiano
central
Zona de
influencia Meridiano
central
Ecuador
No
aplica
No
aplica
3° 3°
¿Cuáles son los sesenta meridianos centrales?
Convencionalmente se ha establecido que el meridiano
central principal sea el meridiano de Greenwich; a partir
de él, se trazan los 60 meridianos centrales convencionales:
en realidad el meridiano de partida (zona) corresponde al
antimeridiano de Greenwich (el otro lado del observatorio
de Greenwich.)
Observatorio de
Greenwich
Antimeridiano de
Greenwich
λ=180°
λ=0
Plano
Ecuatorial
Esquemáticamente, presentamos a continuación, la ubicación de las 60 zonas.
Meridiano (lado opuesto de Greenwich)
Lado este respecto a Greenwich
Lado oeste respecto a Greenwich
Meridiano de
Greenwich
Ecuador
Zona
1
Zona
2
-180° -174° -168° 168° 174° 180°
-18° -12° -6° 6°
0
12° 18°
Zona
28
Zona
29
Zona
30
Zona
31
Zona
32
Zona
33
Zona
59
Zona
60
... ... ... ...

321. 33
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
l Es una proyección conforme.
l Tanto el meridiano central como el ecuador, se representan como lados rectos.
l No hay distorsión en el meridiano central (es una línea recta).
l Las distancias a lo largo del meridiano central son verdaderas.
l Los meridianos son ligeramente cóncavos con respecto al meridiano central.
l Los paralelos son líneas curvas cóncavos con respecto al polo más cercano.
l La distorsión aumenta a medida que nos alejamos del meridano central.
l La distorsión también aumenta cuando nos alejamos del ecuador hacia los polos, pero en
menor medida.
l Esta proyección es recomendable en regiones cuya extensión es mucho mayor en la direc-
ción norte-sur respecto a la dirección este-oeste.
CARACTERÍSTICAS

322. 34
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
PROYECCIÓN UNIVERSAL TRANSVERSAL DE MERCATOR (UTM)
Es un sistema similar a la proyección transversal de MERCATOR, la diferencia radica en que el cilindro transversal al eje de
rotación de la tierra, corta al elipsoide secantemente a lo largo de dos elipses (líneas estándar) paralelas al meridiano central.
Zona externa del
elipsoide respecto
al cilindro
Zona de influencia
correspondiente al
meridiano central.
Cilindro
Sección Meridiano central
Elipsoide
LE
LC
Línea
estándar
Meridiano
central
Línea
estándar
¿Cuál es el radio del cilindro?
El radio del cilindro, obedece a la
siguiente propiedad.
La intersección geométrica del cilindro
con el elipsoide, se realiza tal que
la distorsión del meridiano central
del elipsoide respecto al cilindro es
cuantitativamente 0.9996.
Lc = 0.9996 . (LE)

323. Sección 1-1 Sección 2-2 Sección 3-3
35
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
FACTOR DE ESCALA
Es aquel valor que permite proyectar la longi-
tud medida entre dos puntos en el elipsoide
de referencia sobre el plano cartográfico.
LP = (KESCALA) Lo
A
B
Lp
Elipsoide de
referencia
Lo
B’
A’
Plano
cartográfico
Analizando el factor de escala en la presente proyección cartográfica (UTM)
Cilindro
Elipsoide
Lo Lp
Cilindro
Elipsoide
Lo
Lp
Meridiano
Central
3
1
2
3
1
2
El elipsoide se
ubica dentro del cilindro.
La proyección de Lo
aumenta (Lp)
El elipsoide se
ubica fuera del cilindro.
La proyección de Lo
disminuye (Lp)
Analizando la zona
de influencia
correspondiente a un
meridiano central.
Lo Lp
El elipsoide se
ubica dentro del cilindro.
La proyección de Lo
aumenta (Lp)
Cilindro
Elipsoide
Línea
Estándar
Línea
Estándar
K 1
K 1
K 1
En Resumen :
Donde:
LP : longitud proyectada al plano
catográfico.
Lo : longitud medida en el elipsoi-
de de referencia.
KESCALA : factor de escala
Nota
Lp = K . Lo
K 1
Lp = K . Lo
K 1
Lp = K . Lo
K 1
La linea estándar no es
exactamente una recta

324. 36
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Esta proyección tiene
su rango de validez en-
tre la latitud 84° Norte
y 80° Sur. En las áreas
polares es convenien-
te el uso de la proyec-
ción estereográfica.
Dado que la proyección cartográfica UTM, es una modificación de la Proyección Transversal de Mercator (intersección se-
cante en reemplazo del encuentro tangente), se conservan los 60 meridianos convencionales y por tanto las sesenta zonas.
Observación 1
Observación 2
84°
80°
84° N
Ecuador
Meridiano
Central
80° S
Meridiano de Greenwich
Antimeridiano de
Greenwich
Zona
del
territorio
del
Perú
1 60 59 58
57
56
55
54
5
3
5
2
5
1
5
0
4
9
4
8
4
7
46
45
4
4
4
3
4
2
4
1
4
0
3
9
3
8
3
7
3
6
3
5
3
4
3
3
3
2
31
30
2
9
2
8
2
7
2
6
2
5
2
4
2
3
2
2
2
1
2
0
1
9
1
8
1
7
16
15
1
4
1
3
1
2
1
1
1
0
9
8
7
6
5
4
3 2
-174 -180 174 168
162
156
150
144
138
1
3
2
1
2
6
1
2
0
1
1
4
1
0
8
1
0
2
96
90
84
7
8
7
2
6
6
6
0
5
4
4
8
4
2
3
6
3
0
2
4
1
8
1
2
6
0
-6
-1
2
-
1
8
-
2
4
-
3
0
-
3
6
-
4
2
-
4
8
-
5
4
-
6
0
-
6
6
-
7
2
-7
8
-8
4
-90
-9
6
-1
0
2
-
1
0
8
-
1
1
4
-
1
2
0
-
1
2
6
-
1
3
2
-138
-144
-150
-156
-162 -168
-177 177 171
165
159
153
147
141
1
3
5
1
2
9
1
2
3
1
1
7
1
1
1
1
0
5
99
93
87
8
1
7
5
6
9
6
3
5
7
5
1
4
5
3
9
3
3
2
7
2
1
1
5
9
3
-3
--
6
-
1
5
-
2
1
-
2
7
-
3
3
-
3
9
-
4
5
-
5
1
-
5
7
-
6
3
-
6
9
-7
5
-8
1
-87
-93
-9
9
-
1
0
5
-
1
1
1
-
1
1
7
-
1
2
3
-
1
2
9
-135
-141
-147
-153
-159 -165 -171
N+

325. 37
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
El Perú abarca tres zonas : 17, 18 y 19.
l La zona 17, tiene como meridiano central: -81°
l La zona 18, tiene como meridiano central: -75°
l La zona 19, tiene como meridiano central: -69°
â Es una proyección conforme
â No hay distorsión en las líneas de intersección o estándar
â Las distancias a lo largo de las líneas estándar, son verdaderas
â Los meridianos cercanos al meridiano central son casi rectos (ligeramente cóncavas con respec-
to el meridiano central).
â Los paralelos son líneas curvas cóncavos con respecto al polo más cercano.
â La distorsión aumenta a medida que nos alejamos del meridiano central.
â La distorsión o escala también aumenta cuando nos alejamos del ecuador hacia los polos, pero
en menor medida.
â Esta proyección es recomendable en regiones cuya extensión es mucho mayor en la dirección
norte – sur que en el este – oeste.
CARACTERÍSTICAS
Zona
17
Zona
18
Zona
19
-84° -78° -72° -66°
-81° -75° -69°

326. 38
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Ejemplo 2:
El punto “A” tiene las siguientes coordenadas UTM.
N= 2 000 000 m
E= 340 000 m
Zona 35 N (norte)
Ubicar gráficamente su posición.
ORIGEN CONVENCIONAL DE COORDENADAS UTM
A manera de ilustración se tomará como ejemplo una sola zona, sin embargo es preciso acotar que la presente con-
vención es válida para todas las zonas.
Ejemplo 1:
El punto “A” tiene las siguientes coordenadas UTM
N= 450 000 m
E= 600 000 m
Zona 16 N (norte)
Ubicar gráficamente su posición.
» La coordenada norte tiene su origen en el
ecuador y su valor de inicio es cero metros.
» La coordenada este tiene su referencia en
el meridiano central y su valor de partida es
500 000 m.
a) Para el hemisferio Norte
0 m Ecuador
E=500
000
m
Meridiano
central
Norte
Este
0 m Ecuador 450 000 m
Zona 16
A
100 000 m
500
000
m
E=500 000+100000
N=0+450 000
A =
0 m
Ecuador
2 000 000 m
Zona 35
A
160 000 m
500
000
m
E=500 000 − 160 000
N=0+2 000 000
A =

327. 39
Profesor: JORGE MENDOZA DUEÑAS
TRANSFORMACIÓN DE COORDENADAS UTM A TOPOGRÁFICA
Ejemplo 3:
El punto “A” tiene las siguientes coordenadas UTM.
N= 8 000 000 m
E= 560 000 m
Zona 18 S (Sur)
Ubicar gráficamente su posición.
» La coordenada norte tiene su refe-
rencia en el ecuador y su valor es
10 000 000 m.
» La coordenada este tiene su referen-
cia en el meridiano central y su valor
de partida es 500 000 m.
b) Para el hemisferio Sur
N=10 000 000 m
Ecuador
Norte
Este
E=500
000
m
Meridiano
central
Zona 18 S
10 000 000 m
60 000 m
2 000 000 m
500
000
m
Ecuador
E=500 000+60 000
N=10 000 000 - 2 000 000
A =

328. CLASE 7

329. Equipos básicos de altimetría
49
49
49
49
49
A continuación se describen los instrumentos más usados en altimetría; no obstante, ello no
significa que dichos equipos se usen exclusivamente en altimetría; es más, existen equipos como
el teodolito y la estación total que se utilizan en la nivelación trigonométrica, sin embargo su
presentación se realizará en las páginas posteriores.
Instrumentos básicos de altimetría
• El nivel tubular • La mira
• El nivel de burbuja partida • El nivel de ingeniero
• El nivel esférico • El eclímetro.
• El telescopio
EL NIVEL TUBULAR (nivel tórico)
Consiste en un tubo cilíndrico hueco de vidrio
cerrado en ambos extremos, en cuyo interior con-
tiene en casi su totalidad de volumen un líquido
de baja viscosidad como bencina, éter, alcohol;
como quiera que el fluido no llena el 100% del
volumen interno, se forma una burbuja de aire.
La distancia entre divisiones es por conven-
ción 2 mm.
Este aparato tiene la propiedad generar un eje
o directriz horizontal (tangente al arco exter-
no) cuando la burbuja se encuentra centrada.
En topografía se utiliza este dispositivo para
generar una base horizontal, ya sea un plato,
un limbo o un anteojo; para dicho efecto exis-
ten ciertas metodologías.

330. Equipos básicos de altimetría
52
En realidad todo nivel tubular viene provisto de una caja metálica, la que a su vez contiene dos
tuercas que permite sujetar el nivel al aparato topográfico.
Precisión del nivel tubular
La precisión de estos aparatos dependen de la sensibilidad del mismo (S); éste a su vez depende
del ángulo central α que subtiende una de las divisiones (S = α)
Transformando la expresión a segundos.
206 265d
S =
R
 
 
 
Dado que convencionalmente d = 2 mm;las sensibilidad estará en función del radio de curvatura en mm.
Analizando: R = 82,5 metros ⇒ S = 5
R = 20,6 metros ⇒ S = 20
R = 6,9 metros ⇒ S = 60 = 1'
En realidad los niveles tubulares de sensibilidad 5 o cercanos a él son muy precisos, pero tienen el
inconveniente de desnivelarse con la más mínima vibración.
Los niveles de sensibilidad 20 o similar son menos precisos, por lo cual es más fácil su nivelación.
Los niveles tubulares de sensibilidad al minuto tienen una precisión gruesa, sin embargo
ofrecen poca dificultad en su nivelación.
d
S =
R
R = radio interno del tubo

331. Equipos básicos de altimetría
53
NIVEL DE BURBUJA PARTIDA (parábola)
Este tipo de nivel no es más que el mismo nivel tubular estudiado en las paginas anteriores, con
la diferencia que se le ha acoplado un sistema de prismas, como se muestra.
Como consecuencia óptica de este acoplamiento se apreciarán las mitades extremas de la bur-
buja en posición invertida.
Analizando
• Se demuestra que si la burbuja tiene un desplazamiento “x” en el nivel tubular,
los extremos de cada mitad de burbuja sufrirán un desplazamiento 2x.
• En promedio la apreciación óptica mínima de una persona normal es 0,2 mm.
• De la premisa anterior se deduce que el error mínimo que podemos come-
ter en apreciar la coincidencia de las burbujas invertidas es: 2x = 0,2; Lo cual
significa que el error en el desplazamiento de la burbuja será x = 0,1 mm y
no d = 2 mm como habíamos viso en el nivel tubular.
• Esto significa que trabajando con un nivel tubular y apoyándose en el pre-
sente sistema, se puede obtener una precisión 20 veces mayor
 
=
 
 
d 2 mm
x 0,1 mm
de lo normal.
Ventajas
• Con el nivel de burbuja partida es posible usar nive-
les tubulares de sensibilidad gruesa y obtener gran
precisión, dado que con el sistema de burbuja parti-
da multiplica la precisión normal en 20 veces aproxi-
madamente; así por ejemplo:
• Se verifica en el campo que haciendo coincidir los dos extremos de la burbuja se centra ésta
más rápidamente que observando su posición sobre las divisiones del tubo.
- Se recomienda realizar una pre-nivelación del aparato que contiene el nivel de
burbuja partida, generalmente se usa el nivel esférico para estos casos.
- El movimiento de las dos mitades extremas de la burbuja del nivel tubular se reali-
za con un tornillo de basculamiento.
Observaciónes
Nivel Tubular Precisión con nivel
de burbuja partida
S = 20 S = 1
S = 40 S = 2
S = 60 S = 3
Planta Vista Frontal

332. Equipos básicos de altimetría
54
NIVEL ESFÉRICO
Llamado también ojo de pollo; viene a estar constituido por un
casquete de vidrio en cuyo interior contiene generalmente alco-
hol; el conjunto engloba una burbuja de aire la cual por diferen-
cia de densidades se ubicará siempre en la parte superior.
El nivel esférico se usa generalmente para realizar una pre-
nivelación (nivelación aproximada) de algún aparato topo-
gráfico; por tal motivo su precisión es mucho menor que
los tubulares; su sensibilidad puede variar entre 3' y 6'.
El cuerpo del nivel esférico está debidamente protegido
de las influencias térmicas ya que su caja amortigua efi-
cazmente los efectos de las rápidas variaciones de la
intensidad de radiación y temperatura del ambiente.
De esta forma quedan compensadas ampliamente las
breves variaciones del punto de centrado o calado.
La plataforma que contiene al nivel esférico, puede estar confor-
mado por tres o cuatro tornillos nivelantes, no obstante también
existen equipos que prescinden de estos tornillos y en su lugar se
usa un dispositivo de rótula llamado tornillo de sujeción.
EL TELESCOPIO
Está constituído básicamente por una lente convergente, un microscopio y un sistema reticular montados
de forma que sus ejes principales coincidan para generar el eje óptico del instrumento.
La finalidad de un telescopio es observar objetos que están alejados respeto al operador.
La lente convergente se ubica en el objetivo, la cual puede deslizarse dentro de la armadura cilíndrica;
dicha lente se desplaza mediante el tornillo
de enfoque, gracias a esta lente se obtienen
imágenes reales e invertidas respecto a los
objetos observados.
El sistema reticular está compuesto por un
disco de vidrio sobre la cual están grabados
dos líneas rectas muy finas que definen la refe-
rencia horizontal y vertical del telescopio, di-
cho disco está ubicado físicamente en el plano
de la imagen A' B'. Así mismo el retículo va
adosado a un juego de tornillos que permite
centrar la cruz con el eje del anteojo.
Algunos retículos poseen hilos adiciona-
les los cuales sirven para medir distancia
por el método estadimétrico.

333. Equipos básicos de altimetría
55
El microscopio se ubica en el ocular y está compuesto comúnmente por dos lentes plano-
convexa montadas coaxialmente en un tubo metálico; sirve para amplificar los hilos del retículo
y la pequeña imagen del objeto observado dada por el objetivo; en algunos telescopios se ha
suprimido el cristal del retículo y la segunda lente del microscopio se coloca directamente en el
lugar del antiguo retículo y la cara plana de la misma lleva grabados los trozos con diamante, en
estos modelos, la primera lente es movible respecto a la segunda en el microscopio.
Defectos que limitan la calidad de la imagen
• La limpieza interna
No es recomendable la limpieza contínua del interior del telescopio, dado que habría que des-
montar el equipo y extraer las lentes.
Actualmente hay muchos telescopios que llevan internamente una lente móvil “Enfoque
interior” quedando la lente convergente del objetivo fijo de tal modo que el aclarador de
imagen se realiza con el movimiento del “Enfoque Interno”.
Su ventaja radica en la obtención de un aparato hermético dado que el lado exterior del ocular y
el objetivo son fijos; Sin embargo tiene el inconveniente de que dicha lente adicional de enfoque
absorbe luz, reduciendo así la claridad de la imagen.
• Paralaje
Si la imagen no se forma en el plano de la retícula se tendrá el fenómeno de paralaje, esto
significa que al moverse el operador levemente, observará diferentes lecturas a través del telesco-
pio, que dependen de la posición del ojo.
El paralaje desaparece variando la posición del retículo respecto al objetivo.
• Aberración esférica
Se produce cuando la imagen no se forma en un plano, sino más bien en una superficie
esférica; en esta situación la imagen se verá borrosa.
• Aberracion cromática
Se produce cuando el campo visual aparece coloreado con varios matices.
Estos dos últimos defectos se corrigen empleando un objetivo compuesto de una lente
exterior biconvexa de crown-glass y de otra interior cóncavo-convexa de flints-glass.
En todo telescopio de enfoque interno se puede distinguir dos ejes:
– El eje óptico; que une el centro óptico del objetivo y el ocular.
– El eje de colimación; que une el centro óptico del objetivo con el centro de la cruz filar.
Hoy en día se usan también lentes adicionales en el microscopio con la finalidad de obtener
imágenes derechas; no obstante esto diminuye la nitidez de la misma.

334. Equipos básicos de altimetría
56
Características técnicas de un telescopio
• Tipo de imagen
La imagen de los objetos o números pue-
den ser derecha o invertida; para trabajos
de alta precisión se recomienda usar equi-
pos que generen imágenes invertidas.
• Aumento
Determina el poder de amplificación de un ob-
jeto y se calcula mediante la siguiente relación:
A Aumento
I : Tamaño imagen
O : Tamaño objeto
Está claro entonces que el aumento puede es-
tar dado por:
1 1 1 1 1
; ; ; ; ; etc.
3 2 10 20 40
En adelante su denotación será como sigue:
1
3
; se representará por 3x; que significa 3 ve-
ces el diámetro del objeto.
1
20
; se representa por 20x; que significa 20 ve-
ces el diámetro del objeto, etc.
• Diámetro libre del objetivo (D)
Está determinado por el diámetro de la len-
te del objetivo; puede ser 20 mm; 24 mm;
30 mm; 41 mm, 45 mm; 50 mm; etc.
• Distancia mínima de enfoque (d)
Es la mínima distancia desde el objetivo
hasta la mira que permite tomar lecturas
con comodidad.
Puede ser 0,30 m; 0,40 m; 0,50 m; 1,60 m;
1,80 m; 2,0 m; etc.
I
A =
O
• Campo visual a 100 metros
Es el área circular a 100 metros del equi-
po que abarca la visual.
Puede ser 2,0 m, 3,0 m; 4,0 m; etc.
• Distancia de visada más larga
para lecturas en centímetros
Es la capacidad que tiene el anteojo para
poder disntiguir nítidamente dos puntos
de la mira separadas 1 cm y no como un
solo punto borroso.
Puede haber equipos con d = 200 m; 300 m;
400 m; etc.
• Distancia de visada más larga
para lecturas en milímetros
Es la capacidad que tiene el anteojo para
poder distinguir nítidamente dos pun-
tos de la mira separados 1 mm y no como
un solo punto borroso.

335. Equipos básicos de altimetría
57
LA MIRA
LA mira es una regla graduada en toda su longitud en centímetros, agrupados de 5 cm en 5 cm y
marcados de 10 cm en 10 cm, igualmente los metros de metro en metro (generalmente por el
cambio de color: rojo y negro).
Esta regla puede ser de una sola pieza (enteriza) o de dos o más piezas articuladas; generalmente
las miras son de tres o cuatro metros de longitud.
La mira puede estar conformada de madera, acero, plástico e invar..
Algunas miras llevan adosadas en su zona posterior un nivel esférico el cual permite indicar la
verticalidad de la regla cuando la burbuja queda calada.

336. Equipos básicos de altimetría
58
EL NIVEL DE INGENIERO (equialtímetro)
El nivel de ingeniero, es aquel instrumento topográfico, constituido básicamente de un telescopio
unido a un nivel circular más otro tubular o similar; el conjunto va montado generalmente a un trípode.
El objetivo de este aparato es obtener planos horizontales; consiguiendo de este modo conocer
el desnivel entre dos puntos.
En la actualidad existen muchos tipos de nivel, los más importantes son:
• Nivel óptico mecánico simple • Nivel óptico mecánico de alta precisión.
• Nivel óptico mecánico automático • Nivel electrónico
A) Nivel óptico mecánico simple
Es aquel en el cual tiene como componentes principales al telescopio, el nivel circular y el tubular
o parábola.
Equialtímetro con tornillos nivelantes y nivel tubular
Equialtímetro con tornillos nivelantes y nivel de burbuja partida

337. Equipos básicos de altimetría
59
B) Nivel óptico mecánico automático
Los equialtímetros automáticos se caracterizan por la particularidad principal de obtener
una línea de colimación horizontal con solo calar la burbuja del nivel esférico, obviando de
este modo el proceso de nivelación con el nivel tubular o de burbuja partida.
En realidad el nivel esférico permite llevar la línea de colimación dentro de 10' con respecto
a la horizontal.
Para incrementar la precisión de la línea de colimación se hace uso de un “compensador automático
que puede ser de péndulo, de prismas, de espejos o electromagnéticos”.
Si bien es cierto que estos equipos tienen la gran ventaja de ahorrar tiempo en el trabajo de campo,
dado que para cualquier movimiento acimutal del anteojo no se requiere ningún ajuste especial; sin
embargo tienen la desventaja de ser sensibles a las vibraciones inducidas por el viento, el tráfico, etc.
Equialtímetro con tornillo de sujeción y nivel tubular
Equialtímetro con tornillo de sujeción y nivel de burbuja partida

338. Equipos básicos de altimetría
60
C) Nivel óptico mecánico de alta precisión
A diferencia de los niveles anteriormente estudiados, éstos poseen en cada equipo un micrómetro de
placa plano – paralela con el cual se puede dar lectura de hasta el décimo de milímetro convirtiéndose
así en aparatos precisos, dado que los convencionales obtienen lecturas hasta el centésimo de metro.
A continuación se explicará las particularidades más importantes de
estos equipos.
Con estos equialtímetros se usa la mira invar. La cinta graduada lleva
dos divisiones de centímetros de precisión marcadas en la madera.
Una de las escalas de cifras tiene su origen en la base de la mira e
indica las alturas reales encima de la base (posición I). La otra escala
indica valores que son superiores en por lo menos 3 metros a los ante-
riores (posición II).
Este arreglo permite que se haga lecturas indepedientes, con el aumen-
to consiguiente de precisión de las observaciones, sirviendo al mismo tiempo de control.
Generalmente estas miras llevan una base metálica.
El telescopio de alta resolución permite visualizar una imagen clara del estadal, asimismo
está provisto de un retículo cuneiforme para que la lectura del estadal en sus graduaciones
sea más precisa.

339. Equipos básicos de altimetría
61
Con el acondicionamiento del micrómetro constituido por una placa plano – paralela fija en el
objetivo, se gradúa en el par de cuñas una de las rayas divisorias de la mira que se encuentra en el
centro del campo visual de manera que la raya divisora sea simétrica en la cuña al bascular la placa
plano – paralela ( con el micrómetro), la línea de puntería se desplaza paralelamente, leyéndose el
valor del desplazamiento directamente en el tambor graduado.
Lectura en mira 1,1400 +
Lectura en
micrométro 0,0036
Lectura final 1,1436 metros
Lectura en mira 4,2100 +
Lectura en
micrométro 0,0057
Lectura final 4,2157 metros
POSICIÓN I
POSICIÓN II
Existen equialtímetros simples y automáticos de alta precisión.
Nota

340. Equipos básicos de altimetría
62
A continuación ilustraremos nuestra teoría con ayuda del nivel automático de alta preci-
sión marca ZEISS NI002.

341. Equipos básicos de altimetría
63
La compesación pendular para la nivelacion automática de este equipo en particular se
realiza mediante el botón de conmutación. Las posiciones del compensador se han marca-
do en ambas superficies laterales del NI002 mediante puntos rojos. Un punto marca la
posición I del compensador, dos puntos la posición II.
Conmutador para lectura en posición II
Conmutador para lectura en posición I
Con este equipo se deberá llevar dos tablas de libreta de campo en un solo itinerario.

342. Altimetría
64
EL ECLÍMETRO
Se le llama también clisímetro y está compuesto por tres elementos primarios: un nivel tubular,
un tubo metálico y un transportador con doble graduación (sexagesimal y porcentaje).
Se usa en nivelaciones trigonométricas de poca precisión; no obstante, la rapidez que se consigue con el
uso del eclímetro, hace de éste el preferido de los camineros.
Es importante centrar la burbuja para poder tomar la lectura correspondiente, para ello se
requiere el apoyo del tornillo nivelante.
EL TRANSPORTADOR

343. 63
63
63
63
63

344. 66

345. 67

346. 68

347. Altimetría
69
Día Fecha Hora cm Fase lunar
vie 19-abr-02 21:11 55
sab 20-abr-02 03:49 34
sab 20-abr-02 12:02 88
sab 20-abr-02 19:47 46
sab 20-abr-02 23:37 52
dom 21-abr-02 05:24 34
dom 21-abr-02 13:11 91
dom 21-abr-02 20:27 40
lun 22-abr-02 01:27 58
lun 22-abr-02 06:59 34
lun 22-abr-02 14:08 98 Cuarto
lun 22-abr-02 21:02 34 Creciente
mar 23-abr-02 02:36 67
mar 23-abr-02 08:14 30
mar 23-abr-02 14:57 101
mar 23-abr-02 21:37 24
mie 24-abr-02 03:31 79
mie 24-abr-02 09:17 24
mie 24-abr-02 15:42 101
mie 24-abr-02 22:12 15
jue 25-abr-02 04:20 88
jue 25-abr-02 10:14 24
jue 25-abr-02 16:25 101
Día Fecha Hora cm Fase lunar
jue 25-abr-02 22:50 9
vie 26-abr-02 05:08 98
vie 26-abr-02 11:08 21
vie 26-abr-02 17:07 98
vie 26-abr-02 23:28 6
sab 27-abr-02 05:56 104
sab 27-abr-02 12:02 24
sab 27-abr-02 17:50 91
dom 28-abr-02 00:06 3 Luna
dom 28-abr-02 06:45 110 Llena
dom 28-abr-02 12:57 27
dom 28-abr-02 18:32 85
lun 29-abr-02 00:46 6
lun 29-abr-02 07:35 110
lun 29-abr-02 13:56 34
lun 29-abr-02 19:16 76
mar 30-abr-02 01:26 12
mar 30-abr-02 08:28 107
mar 30-abr-02 15:02 37
mar 30-abr-02 20:03 67
Preguntas y respuestas sobre el Bench Mark
¿Donde están geográficamente ubicados los
B.M.?
Los Bench Mark, están ubicados a lo largo y an-
cho de todo el globo terrestre y son establecidos
por instituciones especializadas en cada país; en
el Perú es el Instituto Geográfico Nacional (IGN)
la entidad que se ocupa de la colocación y man-
tenimiento de estas marcas permanentes.
¿Los B.M. se deben ubicar en algún pun-
to en particular?
Lo óptimo es que un B.M. se ubique en una
zona de suelo firme, sobre una extructura, pi-
lar o muro, en todos los casos de regular im-
portancia de modo que garantice su no demo-
lición en cinco años por lo menos.
En realidad, en nuestro país debería existir cier-
tas normas que reglamenten las dimensiones y
características de los cimientos para cada tipo
de suelo así como para ciertos casos generales.
¿Como es un B.M. en el terreno?
Físicamente un B.M. se representa mediante una
placa de bronce de 10 cm de diámetro soldado a una
barra de acero; este último colabora con la adheren-
cia entre el concreto y la placa. El disco de bronce
debe llevar grabado su código, la flecha de instala-
ción y el nombre de la institución que lo realizó.
¿Que es el N.M.M.?
El N.M.M. es el nivel medio del mar, cuya cota
absoluta toma el valor de ±0,000 metros, ese dato
es proporcionado por el mareógrafo el cual
promedia la marea alta, media y baja de un lugar.
En el Perú existen cinco mareógrafos a lo lar-
go de nuestro litoral, estos se ubican en:
• Talara (Piura) • San Juan (Marcona)
• Chimbote (Ancash) • Matarani (Arequipa)
• La Punta (Callao)
La Marina de Guerra del Perú, es la Institución
que se encarga de proporcionar el N.M.M.

348. Altimetría
70
¿Cómo se nivela un B.M.?
Generalmente para monumentar un B.M. primero se instala la placa de bronce en el lugar
elegido; luego se realiza una nivelación geométrica de alta precisión de circuito cerrado partien-
do de un B.M. anteriormente establecido. De este modo se determina la cota de la placa de
bronce a cuyo valor se le llama en adelante B.M.
¿Como saber el valor del B.M. de una placa de bronce de interes particular para un topógrafo?
La información de dicho dato corresponde al Instituto Geográfico Nacional, el cual lo efectúa
a pedido del interesado mediante un documento similar al que se muestra a continuación previo
pago por los derechos respectivos.

349. 71
Disco de metal
Vista de planta
En la figura superior, es fácil entender que con ayuda del equialtímetro es posible obtener directamente
la cota en “B”(101,00 m).
El plano o superficie horizontal que pasa por el instrumento es perpendicular a la vertical o plomada que pasa por
el centro del aparato, de lo cual se deduce que hay un solo plano horizontal para cada estación.
AGO-2016

350. 72
Dicha operación se realiza con ayuda de
los tornillos de las patas del trípode,
hasta centrar aproximadamente el nivel
circular.
Se realiza el centrado de la burbuja con ayuda de los
tornillos nivelantes.

351. Altimetría
73
– Cuando el equialtímetro no tiene tornillos nivelantes:
Se afloja el tornillo de sujeción del instrumento y moviendo éste coordinadamente con el
equipo, se realiza el calado del ojo de pollo.
Con ayuda del tercer tornillo se realiza el calado de la burbuja.
4º Se dirige la visual hacia el alineamiento elegido.
5º Se realiza el centrado definitivo, para lo cual se presentan dos posibilidades:
– Cuando el equipo tiene un nivel tubular:
Para calar la burbuja, se hace uso del tornillo nivelante que más se acerque al eje directriz
del nivel tubular.

352. Altimetría
74
– Cuando el equipo tiene un nivel de burbuja partida (parábola):
En este caso se realiza el centrado de la burbuja con ayuda del tornillo basculante.
• El quinto paso se repite para cada visual .
• En niveles automáticos, la puesta en estación termina en el 4º paso.
Observación

353. Altimetría
96
– Se traslada el equipo a uno de los extre-
mos, (en nuestro caso “A”) lo más cerca
que se puede a dicha estaca para evitar
la propagación de algún error. Se toma
la lectura (con el ojo del observador en
el objetivo).
– Con dicha lectura y el desnivel (A y B)
ya conocido se calcula la lectura que
deberá leerse en el punto “B”.
– Se gira el anteojo hasta ubicar la mira
en la estaca “B”; se toma la lectura
correspondiente, si dicho valor coincide con el calculado, el aparato está en perfecto
estado, de no ser así se suelta los tornillos verticales del retículo para subir o bajar los
retículos hasta que marque la lectura calculada.
Se recomienda volver a chequear de las tres condiciones para verificar el correcto ajuste realizado.
NIVELACIÓN INDIRECTA
Este método se basa en el uso de un instrumento u operación matemática mediante el cual se
calcula indirectamente el desnivel entre dos puntos.
Se emplea cuando no se requiere tanta precisión como para optar por una nivelación directa.
Nivelación trigonométrica
La trigonometría es el principio fundamental en este tipo de nivelación; en este método es preciso
contar como datos: el ángulo vertical “α” y la distancia inclinada entre A y B o la correspondiente
proyectada al horizonte, el objetivo es calcular el desnivel ∆h entre dos puntos.
Se emplea mucho en terrenos ondulados y donde hay quebradas; en las exploraciones y recono-
cimiento mediante la utilización del eclímetro y distancia a pasos. En trabajos de mayor preci-
sión , los ángulos se miden con teodolitos y las distancias con estadía.
Hoy en día este método se usa masivamente con ayuda de la estación total; no obstante ello, la
precisión por el método trigonométrico no es comparable con el geométrico.

354. 97
 
 
 
V = Lectura
140
282

355. Altimetría
98
B) Levantamiento con eclímetro
Este método sirve para determinar la
pendiente de una línea recta que une dos
puntos en el terreno; para ello es impor-
tante el uso de una mira.
Para determinar la pendiente entre los pun-
tos A y B; el operador se estaciona en el
punto A y coloca el eclímetro a la altura de
su ojo; se mide con cinta métrica la altura
que hay desde el punto “A” hasta el
eclímetro (h); se coloca la mira en el punto
“B”; se busca con el eclímetro la lectura “h” en la mira; con ello estamos consiguiendo trazar
imaginariamente una línea recta paralela a la línea AB del terreno.
El ángulo “α” en grado o en porcentaje será la pendiente de AB buscada.
Este método también se puede usar para replantear en el terreno pendientes preliminares.
Nivelación barométrica
Este método se fundamenta en el siguiente fenómeno físico: la presión atmosférica disminuye
al aumentar la altura respecto al nivel medio del mar.
Torricelli fue el primero en determinar la presión atmosférica con la demostración del princi-
pio que lleva su nombre.
Está claro entonces, que es posible determinar la presión producida por la atmósfera terrestre
para diferentes alturas respecto al nivel medio de mar.
En topografía se usa la nivelación barométrica para calcular el desnivel entre dos puntos mi-
diendo la presión atmosférica en cada uno de ellos.
Este tipo de nivelación se usa en los levantamientos de exploración o de reconocimiento, cuan-
do las diferencias de elevaciones son grandes como en zonas montañosas y/o colinas.
Si la densidad del aire que rodea a la Tierra fuese constante, el decrecimiento de la presión
atmosférica respecto a la altitud obedecería a una ecuación lineal, experimentalmente se de-
muestra que cuando la temperatura es cero grados centígrados:
∆h = 10,5 ∆P ....... Ecuación lineal patrón
∆h : Diferencia de altitudes (metros)
∆P : Diferencia de presión atmosférica (mmHg)
Como quiera que en la actualidad existen barómetros que miden la presión con aproxi-
mación al 0,1 mm de Hg: podemos obtener desniveles con precisión al metro.
Parámetros que afectan la ecuación lineal patrón
En realidad la densidad de nuestra atmósfera no es uniforme, pues cambia fundamentalmente
con la variación de la humedad y la temperatura.

356. Altimetría
99
La humedad; las diferentes cantidades de vapor de agua que se presentan en diversos lugares
hacen que a mayor vapor, mayor densidad.
La temperatura; a mayor temperatura, el aire se dilata, por tanto disminuye su densidad.
Fórmulas más comunes usadas en los barómetros de mercurio
A) Fórmula simplificada de Laplace B) Fórmula de Babinet
 
+
 
=  
 
 
 
A A B
BA
B
P T T
Z 18 400 log 1+ 0, 004
P 2
( )
A B
A B
BA
A B
2 T T
P P
Z 16 000 1 +
P P 1 000
 
+
−
 
=  
 
+  
 
ZBA : Desnivel entre los puntos A y B (metros)
PA : Presión atmosférica en el punto A cuando T = 0 °C (mm hg)
PB : Presión atmosférica en el punto B cuando T = 0 °C (mm hg)
TA : Temperatura del aire en el punto A
TB : Temperatura del aire en el punto B
Ejemplo de aplicación
Se ha medido la presión atmosférica en los
puntos A y B. Los datos obtenidos son los
siguientes:
PA = 760 mmHg cuando TA = 22 °C
PB = 720 mmHg cuando TB = 18 °C
Calcular el desnivel aplicando la fórmula
simplificada de Laplace y de Babinet
Solución:
• Aplicando la fórmula simplificada de Laplace
BA
760 22 18
Z 18 400 log 1 + 0, 004
72 2
 
+
 
=  
 
 
 
ZBA = 466,62 m
• Aplicando la fórmula de babinet
BA
760 720 22 18
Z 16 000 1+ 2
760 720 1 000
 
− +
   
=  
   
+
   
 
ZBA = 467,03 m
Recomendaciones
Sean A y B puntos sobre la superficie terrestre
donde se requiere una nivelación barométrica
– Evitar tomar lecturas barométricas en mo-
mentos de lluvias, altas temperaturas, fuer-
tes vientos, etc.
– Antes de tomar las lecturas hay que espe-
rar que el barómetro adquiera la tempera-
tura ambiente.
– Las lecturas barométricas se deben tomar
simultáneamente en ambos puntos.
– La nivelación barométrica se debe realizar
en una misma zona para no variar las ca-
racterísticas atmosféricas, como promedio
se puede recomendar no sobrepasar 15 km
para “D” y 1 000 metros para “∆h”.

357. Altimetría
100
Instrumentos básicos en la nivelación barométrica
En la actualidad los barómetros más usados en topografía son: El barómetro de Fortín y el
aneroide (altímetro), sin embargo por motivos didácticos se citará y describirá el barómetro de
Torricelli y el de cubeta además de las mencionadas.
A) El barómetro de Torricelli
Consiste en un tubo de vidrio calibrado, de aproxi-
madamente 80 – 90 centímetros de longitud, cerra-
do por un extremo y abierto por el otro; puede ser
de cualquier diámetro, sin embargo por su fácil
manejo se prefiere usar los de 5 a 8 milimetros, se
llena completamente dicho tubo con mercurio.
Así mismo es preciso contar con un recipiente (cu-
beta) conteniendo también mercurio.
Tapando el extremo libre del tubo se sumerge di-
cho tubo en la cubeta hasta hacer coincidir el cero de la graduación del tubo con el nivel libre del
mercurio en la cubeta; en esta posición se destapa el tubo, si nos encontramos al nivel del mar, a una
temperatura de 0
o
C y a 45
o
de latitud, el nivel del mercurio bajará hasta alcanzar una altura sobre
el nivel libre del mercurio de 760 mm; esto se debe a que el peso del mercurio del tubo se equilibra
con la presión del aire (presión atmosférica) el cual sería 760 mm de mercurio.
Se comprueba que para altitudes superiores al n.m.m la altura de mercurio disminuye.
Este aparato tiene la desventaja de tener que ser desmontado cada vez que sea trasladado, dado que
hay que hacer coincidir el cero de la graduación del tubo con el nivel libre del mercurio en la cubeta.
Si se fabricase un barómetro no desmontable, la coincidencia del cual se hace mención, casi nunca
se cumpliría porque si la presión aumenta, entra mercurio en el tubo y baja el nivel de la cubeta,
sucediendo lo contrario al disminuir la presión.
B) El barómetro de cubeta
Es un aparato muy similar al de Torricelli, sus
diferencias básicas son dos:
– La base de la cubeta es móvil (puede subir o
bajar) gracias a la acción de un tornillo va-
riando su capacidad a voluntad, se lleva has-
ta que enrase la superficie del mercurio con
el punto cero de la escala.
– No obstante tener marcado el cero de la gradua-
ción en el tubo, se ha adosado una punta de metal
o marfil (inmóvil) que acompañado con la cubeta
de vidrio nos puede avisar el enrase buscado.
Es imprescindible cuidar la verticalidad del tubo,
pues alguna inclinación del mismo daría lecturas erróneas de presión.
Estas modificaciones sirven para obtener un barómetro de Torricelli no desmontable y poder trasla-
darlo a diferentes lugares; sin embargo éste sigue siendo un aparato delicado y tedioso en su uso.

358. Altimetría
101
C) El barómetro de Fortín
Podría definirse como un barómetro de
cubeta portátil.
Consta de una cubeta de forma cilíndrica,
cuya parte superior “A” es de vidrio y la
inferior “B” de metal, y de un tubo que se
introduce en la cubeta, protegido por una
armadura metálica que está graduada en
medios milímetros, a lo largo de una ra-
nura que permite la observación de la co-
lumna de mercurio; un cursor “C”, lleva
un índice que puede colocarse al menisco
de la parte superior de la mencionada co-
lumna para leer con exactitud la altura.
En la parte superior de la cubeta está coloca-
da una gamuza que impide la salida del mer-
curio, pero permite la acción de la presión
atmosférica al dejar entrar el aire.
Para usar este
aparato, algunos
hacen uso de un
trípode y un ni-
vel circular para
garantizar la ver-
ticalidad del
tubo.
Para enrasar la
superficie libre
del mercurio
con la punta me-
tálica o de mar-
fil se hace girar
el tornillo “D”.
No obstante,
siendo un equi-
po portátil sigue
siendo molesto-
so y tedioso en su
transporte, por lo
que solo puede
emplearse fácil-
mente en estacio-
nes fijas.
D) El barómetro aneroide
Se le llama también altímetro y son los que
más se usan por su fácil traslado y opera-
ción, no obstante ser menos preciso que el
barómetro de Fortín.
Este instrumento consta de una caja cilíndrica
metálica que contiene en su interior una cáp-
sula cilíndrica con tapas de metal delgado con
acanaluras concéntricas que le dan mayor sen-
sibilidad a las diferencias de presiones; dentro
de la cápsula se ha hecho un vacío parcial.
Al variar la presión atmosférica, las tapas de la
cápsula vibran lo cual se transmite a una aguja
que va marcando en una escala circular de
graduaciones en milímetros equivalentes a los
de la columna de mercurio; en muchos
aneroides existe una escala adicional que indi-
ca la diferencia de altura.
- Las superficies del mercurio sufren los
efectos de capilaridad, lo que ocasiona
cierto error.
- La fórmula simplificada de Laplace
que es la que más se usa es válida para
una latitud de 45º , esto significa que
para latitudes diferentes (el caso co-
mún) habrá que hacer las correcciones
respectivas.
- Comúnmente en levantamientos
barométricos no se realizan la correc-
ción por capilaridad ni por latitud,
dado que sus valores son mínimos y no
tienen mayor incidencia en los traba-
jos preliminares.
Nota

359. Altimetría
102
Métodos para hacer levantamientos barométricos
En topografía es común hacer uso de los aneroides, puesto que los barómetros de Fortín pese a
su precisión requieren de mucho cuidado en su transporte.
Para tomar la lectura con el altímetro, se recomienda que éste se encuentre en posición horizontal, a la
altura del pecho de la persona y siempre evitar el contacto directo de los rayos solares.
A continuación citaremos los métodos más importantes.
A) Levantamiento con un aneroide
Es importante contar con la cota o B.M. del punto de partida.
Los instrumentos adicionales que nos deben acompañar son: un termómetro y un reloj o cronómetro.
En adelante asumiremos la lectura de presión o altitud, temperatura y tiempo de observación de
un punto, el promedio de los cinco valores que deberán tomarse con un lapso aproximado de dos
minutos entre cada observación en el mismo punto; se muestra a continuación la tabla modelo.
Pasos a seguir:
Campo
• Se coloca el altímetro en el punto de parti-
da, se toma como datos la presión, altitud,
temperatura y tiempo.
• Se traslada el aparato a cada uno de los
puntos cuya cota se desea conocer; en cada
uno de ellos se toma como datos: la pre-
sión, altitud, temperatura y tiempo.
• Se regresa al punto inicial y se vuelve a
tomar las lecturas mencionadas.
Gabinete
• Se calcula el error de cierre que viene a ser la
diferencia de la altitud de llegada con la alti-
tud de partida (ambas lecturas del altímetro).
• El error de cierre se reparte proporcionalmente
al tiempo en cada uno de los puntos levantados.
• Se calcula la cota de la superficie del terre-
no restando la altura (se recomienda cons-
tante) que hay entre el altímetro y el pun-
to propiamente dicho.
PUNTO A
Observación Presión(mmHg) Altitud(m) Temperatura(°C) Tiempo
1
2
3
4
5
Promedio
• Entre la cota o B.M. del punto de partida y su
correspondiente altitud compensada existirá
cierta diferencia; Se tomará como cota base o
patrón de dicho punto, el B.M. La diferencia
se suma algebraícamente a cada punto levan-
tado el cual será la cota buscada.
Altitud = Lectura – h

360. Altimetría
103
B) Levantamiento con dos aneroides
Es importante contar también con la cota o B.M. del punto de partida, asi como dos termó-
metros, dos radios de comunicación y dos relojes o cronómetros.
Asumiremos la ilustración en planta.
Pasos a seguir:
Campo
• Se colocan los dos altímetros en el punto
de partida , se toman las lecturas.
• Se traslada uno de los altímetros al siguien-
te punto y se toman las lecturas respecti-
vas tanto en el punto de partida como en
el siguiente punto en forma simultánea con
ayuda de la radio.
• Se vuelve a trasladar el altímetro “móvil”
al otro punto, mientras que el primero per-
manece en el punto de partida, en forma
simultánea se vuelve a tomar las lecturas.
• Se prosigue el mismo proceso moviendo
tan solo uno de los altímetros hasta regre-
sar al punto de partida.
Datos de campo:
Datos del barómetro fijo
Datos del barómetro móvil
Gabinete
• Se realiza el cálculo del error de índice, que
viene a ser la diferencias de altitudes
barométricas en el punto de partida (A) cuan-
do tiempo = 0
e = Altitud con barómetro móvil – Altitud con barómetro fijo
• Se aplica el error de índice a todas las
lecturas tomadas por el altímetro móvil;
de este modo se reduce todas las lecturas
respecto al altímetro fijo.
• Se calcula el desnivel da cada punto respecto al
punto de partida para un mismo instante para
luego hacer la corrección por temperatura.
• Entre la cota o B.M. del punto de partida y su
correspondiente altitud compensada existirá
cierta diferencia. Se tomará como cota base o
patrón de dicho punto, el B.M. La diferencia
se suma algebraicamente a cada punto levan-
tado el cual será la cota buscada.
Punto Altitud Temperatura Tiempo
A Dato Dato 0
A Dato Dato t1
A Dato Dato t2
A Dato Dato t3
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
A Dato Dato tn
Punto Altitud Temperatura Tiempo
A Dato Dato 0
1 Dato Dato t1
2 Dato Dato t2
3 Dato Dato t3
. . . .
. . . .
. . . .
. . . .
A Dato Dato tn

361. CLASE 9

362. Altimetría
75
Casos generales en una nivelación geométrica
A) Nivelación relativa
Cuando solo sea necesario conocer el desnivel entre los puntos de la zona de trabajo.
Para ello se asume una cota arbitraria a uno de los puntos lo suficientemente grande para no
tener en el curso de la nivelación cotas negativas, o bien al punto más bajo se le dá cota cero.
B) Nivelación absoluta
Cuando sea preciso trabajar con cotas absolutas.
En este caso se ubica el B.M. de un punto
cercano a la zona de trabajo; en el Perú, el
Instituto Geográfico Nacional nos puede
proporcionar dicho dato. A continuación
se lleva a cabo una nivelación de circuito
cerrado entre dicho B.M. y el punto más
cercano a la zona por nivelar.
Por último se realiza la nivelación en la zona establecida.
Elementos importantes de una nivelación geométrica
Puntos de nivel primario (Bancos de nivel)
Son los correspondientes a los puntos de control; éstas deben estar monumentadas.
Puntos de nivel secundario (Puntos de cambio)
Son aquellos puntos que sirven de apoyo para poder enlazar dos puntos de control; sobre dicho
punto de cambio se coloca la mira para efectuar las lecturas correspondientes.
Se recomienda que los puntos secundarios sean pintados si se tratase de pavimento ó estacados
provisionalmente en los jardines o tierra si fuese el caso; generalmente estos puntos deben
desaparecer al concluir el trabajo de gabinete.
Vista atrás L(+)
Es la lectura de la mira correspondiente al punto de cota conocida.
Vista adelante L(–)
Es la lectura de la mira correspondiente al punto de cota no conocida.

363. Altimetría
76
Nivel instrumental ( )
Es el nivel correspondiente al eje de colimación del instrumento.
- Existen miras que tienen
adosado un nivel esférico, el
cual ayuda a conseguir la ver-
ticalidad de la misma. (Fig. A)
- Enlaactualidadseutilizanmu-
chas miras que carecen del ni-
vel esférico; cuando por alguna
razón el portamira no consigue
colocar la regla verticalmente,
seaconsejabalancearlo;conello
el operador notará varias lectu-
ras en la mira, de los cuales deberá anotar el menor valor, ya que cuanto mayor se la
lectura en la mira, tanto mayor será el error debido a la inclinación dada. (fig.B)
Observación
Tipos de nivelación geométrica
A) Nivelación geométrica simple
Sirve para encontrar la cota de uno o más puntos del terreno por medio de una sola estación
instrumental.
Pasos a seguir
• Se coloca la mira en el punto de cota conocida (A)
• Se ubica el punto de cota por conocer (B).
• Se instala el nivel en un punto equidistante a los antes mencionados.
• La distancia nivel–mira no debe sobrepasar 120 metros; sin embargo es recomendable traba-
jar con una distancia máxima de 50 metros.
(Fig. B)
(Fig. A)
Fig. a

364. Altimetría
77
• Con ayuda del nivel se visa la mira en el punto de cota conocida: L(+) y se anota en la libreta de campo (fig. a).
• Se coloca la mira en el punto de cota por conocer.
• Con ayuda del nivel, se visa la mira en el punto de cota por conocer : L(-) y se anota en la
libreta de campo (fig. b).
Ejemplo Ilustrativo 1
Dado el punto “A” de cota 100,00 m; se desea
conocer la cota del punto “B”.
• Calculando la cota de “B”
Cota “B” = 101,85 – 0,72 = 101,13 m
• Comúnmente se hace uso de la siguiente tabla:
En el campo
Punto L(+) L(–) Cota
A 1,85 100,00
B 0,72
Calculando la cota de “B”
Punto L(+) L(–) Cota
A 1,85 101,85 100,00
B 0,72 101,13
• En general: = L(+) + Cota conocida
Cota por conocer = – L(–)
Solución:
• Ilustrando el proceso de campo en planta.
+
-
Fig. b

365. Altimetría
78
En la práctica, no siempre es posible ins-
talar el equipo equidistante a los puntos
involucrados; sin embargo se recomien-
da buscar en lo posible la equidistancia;
los motivos se explicarán más adelante.
Nota
Ejemplo ilustrativo 2
Dado el punto “A” de cota +100,00 m; se desea
conocer las cotas de los puntos B, C y D.
Solución
• Se instala el nivel en un punto, aproxima-
damente equidistante.
• En el campo
Punto L(+) L(–) Cota
A 1,85 100,00
B 0,72
C 2,40
D 1,23
• En el gabinete:
Punto L(+) L(–) Cota
A 1,85 101,85 100,00
B 0,72 101,13
C 2,40 99,45
D 1,23 100,62
B) Nivelación recíproca
Este método se utiliza cuando:
– Se desea comprobar si el eje óptico del anteojo del nivel es paralelo a la directriz del nivel tubular.
– No es posible colocar el instrumento en un lugar intermedio entre dos puntos de mira, ya
sea porque se interponga un río, un pantano o cualquier otro obstáculo.
Pasos a seguir
Se explicará los pasos con el apoyo de un ejemplo numérico.
– Se coloca el nivel en el extremo de la zona de cota conocida, mientras se instalan las
miras en los puntos A y B; para luego calcular la cota del punto B.
La distancia PA debe ser lo suficiente, tal que permita al operador visualizar sin dificul-
tad la lectura de la mira en “A”.

366. Altimetría
79
Calculando: cota “B” = 99,39 m
– Se traslada el nivel a un punto Q, tal que aproximadamente PA = QB ; para luego
calcular nuevamente la cota en “B”.
Calculando: cota “B” = 99,41 m
– La cota buscada será el promedio:
99,39 + 99,41
Cota “B” =
2
⇒ Cota “B” = 99,40 m
C) Nivelación compuesta
Es una sucesión de niveles simples relacionados entre sí; se utiliza cuando se requiere la diferencia de
nivel entre dos puntos muy distanciados o cuando la visibilidad desde una estación no lo permite.
Ejemplo ilustrativo
A continuación se explicará el presente método mediante un ejemplo numérico.
En el croquis se muestran dos puntos, en las cuales, el punto “A” tiene como cota: +100,00 m;
el problema consiste en determinar la cota del punto B.
No es difícil deducir la imposibilidad en realizar una nivelación simple, por lo cual se elige la
nivelación compuesta.

367. Altimetría
80
Pasos a seguir
– Se elige un punto: 1 (punto de cambio), con la condición de acercarnos al punto “B”.
– Se realiza una nivelación simple entre A y 1 como si B no existiese.
– Se calcula cota del punto 1.
– Se elige el punto “2” (punto de cambio) con la condición de acercarnos más aún hacia “B”.
– Se realiza una nivelación simple entre “1” y “2” como si los demás puntos no existiesen.
– Se calcula la cota del punto “2”
Punto L(+) L(–) Cota
1 0,56 101,68 101,12
2 2,53 99,15
Punto L(+) L(–) Cota
A 2,54 102,54 100,00
1 1,42 101,12

368. Altimetría
81
– Se elige el punto “3” (punto de cambio) con la condición de llegar al punto “B”.
– Se realiza una nivelación simple entre los puntos “2” y “3” como si los demás puntos no existiesen.
– Se calcula la cota del punto “3”
– Finalmente se realiza una nivelación simple entre los puntos “3” y “B”.
– Se calcula la cota del punto “B”, que es el resultado final.
Punto L(+) L(–) Cota
2 1,44 100,59 99,15
3 0,54 100,05

369. Altimetría
82
– Sintetizando: El recorrido en planta de la nivelación compuesta sería la siguiente:
Cota “B” = 100,79 m
Punto L(+) L(–) Cota
3 2,56 102,61 100,05
B 1,82 100,79
• En el campo
Es posible unir las tablas de las nivelacio-
nes simples independientes:
• En el gabinete
Punto L(+) L(–) Cota
A 2,54 102,54 100,00
1 0,56 101,68 1,42 101,12
2 1,44 100,59 2,53 99,15
3 2,56 102,61 0,54 100,05
B 1,82 100,79
Punto L(+) L(–) Cota
A 2,54 100,00
1 0,56 1,42
2 1,44 2,53
3 2,56 0,54
B 1,82
Enelpresenteejemploilustrativo, setomótrespuntosdecambio;enlaprácticaelnúmerode
dichos puntos lo elegirá el ingeniero.
Nota
Comprobación de una nivelación geométrica
Una vez realizado el cálculo de la libreta de campo, se debe efectuar la comprobación
de dicha nivelación, para ello se utiliza la actividad A y B.

370. Altimetría
83
A) Comprobación del cálculo matemático de la libreta
Muchas veces el cálculo de la libreta se realiza en campo, por ende está sujeto a posibles
errores, el cual se puede detectar con la siguiente expresión:
Σ Σ
L(+) – L(–) = Cota final – Cota inicial
En el ejemplo anterior:
ΣL(+) = 7,10 7,10 – 6,31 = 100,79 – 100,00
ΣL(–) = 6,31 0,79 = 0,79 ....... (conforme)
Cota final = 100,79
Cota inicial = 100,00 Lo cual significa que el cálculo es correcto.
Demostración:







Analizando cada nivelación simple:
L
1
(+) – L
2
(–) = Cota 2 – Cota 1
L
2
(+) – L
3
(–) = Cota 3 – Cota 2
L
3
(+) – L
4
(–) = Cota 4 – Cota 3
.
.
.
.
.
.
Ln – 1(+) – Ln(–) = Cota n – Cotan – 1
ΣL(+) – ΣL(–) = Cota n – Cota 1
ΣL(+) – ΣL(–) = Cota final – Cota inicial ....... (demostrado)
B) Comprobación de la nivelación propiamente dicha
La comprobación de la libreta de campo, no indica si la nivelación es correcta, para ello es
necesario verificar que el error accidental total sea menor que el máximo tolerable, el cual
dependerá de la precisión buscada.

371. Altimetría
84
Existen dos casos:
B-1) Cuando sólo sea conocido un banco de nivel
Generalmente se utiliza cuando el objetivo es determinar la cota de uno o varios puntos
específicos, partiendo de una cota conocida.
Para ello es necesario realizar la nivelación tanto de ida como de regreso.
Teóricamente la cota inicial debe ser exactamente igual a la cota final, dado que es el mismo
punto, en la práctica, siempre existe una diferencia entre dichas lecturas; a esta diferencia se
le llama error de cierre altimétrico, su aceptación dependerá de la precisión que se busca.
Solución:
• Sea E = Error de cierre altimétrico
E = Cota final – Cota inicial
E = 100,01 – 100,00
E = 0,01 m
• Dato:
Emax = 0,02 k
k =
8(50)
0, 4 km
1 000
=
Emax = 0,02 0, 4
Emax = 0,013 m
• Se observa: E Emax
Ejemplo ilustrativo
El croquis muestra dos puntos:
AyB;cota“A”=100,00mycota“B”=desconocida;
mediante una nivelación compuesta se deter-
mina la cota en “B” la cual es 120,00 m; para
comprobar dicha nivelación es preciso regre-
sar por cualquier otro recorrido.
La figura muestra que la cota de llegada es
100,01 m con lo cual el error de cierre
altimétrico es 0,01 m. Asumiendo que el máxi-
mo error tolerable en metros es:
Emax = 0,02 k (k = número de kilometros)
¿Es aceptable la nivelación?.
Con lo cual se da por aceptada la nivelación

372. Altimetría
85
B-2) Cuando se conozcan dos bancos de nivel
Generalmente se utiliza cuando el obje-
tivo es determinar la configuración
altimétrica del terreno a lo largo de una
línea definida planimétricamente y que
enlaza los puntos dados.
Para ello es necesario realizar la nivela-
ción de ida solamente.
Teóricamente la cota final calculada, debe ser exactamente igual a la cota final conocida, dado que es
el mismo punto; en la práctica, siempre existe una diferencia entre dichas lecturas; a esta diferencia se
le llama error de cierre altimétrico, su aceptación dependerá de la precisión que se busca.
Ejemplo ilustrativo
El croquis muestra dos puntos: A y B; cota “A” = 100,00 m; cota “B” = 101,60 m. Mediante una
nivelación compuesta, partiendo de la cota del punto “A”, se determina la cota de los puntos
que muestra la tabla. Sabiendo que la longitud total del itinerario es 800 metros y asumiendo
que el máximo error tolerable en metros es: Emax = 0,02 k (k = número de kilometros)
¿Es aceptable la nivelación?
Libreta de campo:
En el gabinete:
Solución
Punto L(+) L(–) Cota
A 1,63 101,63 100,00
1 1,82 102,25 1,20 100,43
2 1,76 102,65 1,36 100,89
3 1,93 103,17 1,41 101,24
4 2,16 103,71 1,62 101,55
5 1,87 103,65 1,93 101,78
B 2,06 101,59
Σ 11,17 9,58
Punto L(+) L(–) Cota
A 1,63 100,00
1 1,82 1,20
2 1,76 1,36
3 1,93 1,41
4 2,16 1,62
5 1,87 1,93
B 2,06
• Chequeando el cálculo matemático
ΣL(+) – ΣL(–) = Cota final – Cota inicial
11,17 – 9,58 = 101,59 – 100,00
1,59 = 1,59 ....... (conforme)
• Comprobando la nivelación propiamen-
te dicha:
E = error de cierre altimétrico
E = Cota “B” (real) – Cota “B” (calculado)
E = 101,60 – 101,59
E = 0,01 m
• Dato: Emax = 0,02 k = 0,02
800
1 000
Emax = 0,017 m
• Se observa: E Emax
Con lo cual se da por aceptada la nivelación

373. CLASE 10

374. Altimetría
78
En la práctica, no siempre es posible ins-
talar el equipo equidistante a los puntos
involucrados; sin embargo se recomien-
da buscar en lo posible la equidistancia;
los motivos se explicarán más adelante.
Nota
Ejemplo ilustrativo 2
Dado el punto “A” de cota +100,00 m; se desea
conocer las cotas de los puntos B, C y D.
Solución
• Se instala el nivel en un punto, aproxima-
damente equidistante.
• En el campo
Punto L(+) L(–) Cota
A 1,85 100,00
B 0,72
C 2,40
D 1,23
• En el gabinete:
Punto L(+) L(–) Cota
A 1,85 101,85 100,00
B 0,72 101,13
C 2,40 99,45
D 1,23 100,62
B) Nivelación recíproca
Este método se utiliza cuando:
– Se desea comprobar si el eje óptico del anteojo del nivel es paralelo a la directriz del nivel tubular.
– No es posible colocar el instrumento en un lugar intermedio entre dos puntos de mira, ya
sea porque se interponga un río, un pantano o cualquier otro obstáculo.
Pasos a seguir
Se explicará los pasos con el apoyo de un ejemplo numérico.
– Se coloca el nivel en el extremo de la zona de cota conocida, mientras se instalan las
miras en los puntos A y B; para luego calcular la cota del punto B.
La distancia PA debe ser lo suficiente, tal que permita al operador visualizar sin dificul-
tad la lectura de la mira en “A”.

375. Altimetría
79
Calculando: cota “B” = 99,39 m
– Se traslada el nivel a un punto Q, tal que aproximadamente PA = QB ; para luego
calcular nuevamente la cota en “B”.
Calculando: cota “B” = 99,41 m
– La cota buscada será el promedio:
99,39 + 99,41
Cota “B” =
2
⇒ Cota “B” = 99,40 m
C) Nivelación compuesta
Es una sucesión de niveles simples relacionados entre sí; se utiliza cuando se requiere la diferencia de
nivel entre dos puntos muy distanciados o cuando la visibilidad desde una estación no lo permite.
Ejemplo ilustrativo
A continuación se explicará el presente método mediante un ejemplo numérico.
En el croquis se muestran dos puntos, en las cuales, el punto “A” tiene como cota: +100,00 m;
el problema consiste en determinar la cota del punto B.
No es difícil deducir la imposibilidad en realizar una nivelación simple, por lo cual se elige la
nivelación compuesta.

376. Altimetría
91
Sea:
E1
: Error de cierre altimétrico en el sub-circuito 1 L1
: Longitud total del sub-circuito 1
E2
: Error de cierre altimétrico en el sub-circuito 2 L2
: Longitud total del sub-circuito 2
E3
: Error de cierre altimétrico en el sub-circuito 3 L3
: Longitud total del sub-circuito 3
.
. .
. .
. .
En : error de cierre altimétrico en el sub-circuito n L
n
: Longitud total del sub-circuito n
El error de cierre altimétrico del circuito total será:
2 2 2 2
total 1 2 3
E = E E E ... E
± + + + + n
Este error encontrado deberá ser menor que el máximo tolerable, el cual se calculará teniendo presente:
d = L1 + L2 + L3 + ... + Ln
Por último, se tendrá que realizar la compensación de cotas en cada sub-circuito independien-
temente unos de los otros.
Fenómenos físicos que afectan una nivelación
Cuando se requiera determinar el desnivel entre dos puntos separados a una distancia considerable,
hay que tomar en cuenta el error proveniente de la curvatura de la Tierra y la refracción atmosférica.
Influencia de la curvatura terrestre
Es conocido que todo plano o superficie horizontal es tangente a la superficie de nivel en un punto;
si la distancia entre dos puntos es pequeña la línea que las une se puede considerar tangente, pero
si es grande es imprescindible tomar en cuenta la curvatura de la superficie de nivel.
Ahora, para efectuar nivelaciones en ingeniería, se utilizan instrumentos ópticos que permiten
visualizar toda una horizontal sin importar la distancia
Si la distancia entre A y B no es mayor que 50
metros se puede considerar la superficie del ni-
vel instrumental y su respectiva horizontal con-
fundidos en un mismo plano.
Cota B = Nivel instrumental – Lectura visualizada

377. Altimetría
92
Si A y B están separadas por una distancia considerable, el plano horizontal y su respectivo nivel
instrumental provocan un error en la lectura:
Error por curvatura terrestre (Ec)
Cota B = Nivel instrumental + Ec – Lectura visualizada
Cota B = (Nivel instrumental – Lectura visualizada) + Ec
De donde se deduce que la corrección por curvatura terrestre siempre es positiva, es decir, hay
que sumarla algebraicamente a la cota del punto visado.
Ec : Error por curvatura terrestre
D : Distancia horizontal entre los puntos
R : Radio terrestre.
Influencia de la refracción atmosférica
Sabemos que todo rayo de luz que pasa de un medio a otro de diferente densidad cambia de
dirección, a este fenómeno se le llama refracción.
En el proceso de nivelación, el rayo que sale del anteojo del nivel y que se dirige a la mira, sufre dicha
refracción debido a que en su viaje tiene que atravesar diferentes capas de aire de diversas densidades,
ello hace que dicho rayo se vaya refractando en cada una de ellas, resultando curvilíneo.
2
D
Ec =
2R
+

378. Altimetría
93
De la figura: Cota “B” = (Nivel instrumental – ER) – Lectura visualizada
Cota “B” = (Nivel instrumental – Lectura visualizada) – ER
De donde se deduce que la corrección por refracción siempre es negativa, es decir hay que restar
algebraicamente a la cota del punto visado.
ER : Error por refracción
D : Distancia horizontal entre los puntos
R : Radio terrestre
Corrección de nivel aparente (C)
Cuando se realiza una nivelación entre dos puntos separados por una distancia considerable
hay que tener en cuenta el error de nivel aparente, que viene a ser la suma algebraica del error
por curvatura y el error por refracción; nótese que dicho error es positivo.
2
6 D
C =
14 R
 
⇒  
 
A continuación se muestran algunos valores de C para diferentes distancias.
D (m) C (m) D (m) C (m)
0 0,0000 210 0,0030
30 0,0000 240 0,0039
60 0,0002 270 0,0049
90 0,0005 300 0,0061
120 0,0010 330 0,0073
150 0,0015 360 0,0087
180 0,0022 390 0,0102
C R
C = E E
+
2 2
D –D
C =
2R 14R
 
+  
 
2
R
–D
E =
14R

379. 94

380. Altimetría
95
2
do
Perpendicularidad entre el hilo horizontal del retículo y el eje vertical
– Se enfoca el hilo horizontal sobre un punto fijo “P”, luego se gira el anteojo respecto al eje
vertical.
Si “P” continúa sobre el hilo horizontal no hay que hacer ninguna corrección.
– Si se aleja del hilo, se corrige mediante los tornillitos adjunto al anteojo.
3
ro
Paralelismo entre el eje de colimación del anteojo y el eje directriz del nivel tubular
Se comprueba y/o corrige mediante la llamada “prueba de las estacas”.
– Se colocan dos estacas en el suelo, a una distancia aproximada de 80 metros uno del otro.
– Procurar que el terreno sea horizontal.
– Se instala el equipo en un punto aproximadamente equidistante a las estacas y de prefe-
rencia en el alineamiento que los une.
– Se coloca una mira en cada estaca (garantizar la verticalidad de éstos, en su defecto habrá
que balancearlas) para luego tomar las lecturas correspondientes.
– Se calcula el desnivel entre los puntos A y B mediante la diferencia de las lecturas.
– El desnivel calculado será el verdadero, dado que por la equisdistancia, los errores ( si los
hubiesen) se anulan.
Desnivel (A y B) = 1,572 – 1,456
Desnivel (A y B) = 0,116 m

381. Altimetría
96
– Se traslada el equipo a uno de los extre-
mos, (en nuestro caso “A”) lo más cerca
que se puede a dicha estaca para evitar
la propagación de algún error. Se toma
la lectura (con el ojo del observador en
el objetivo).
– Con dicha lectura y el desnivel (A y B)
ya conocido se calcula la lectura que
deberá leerse en el punto “B”.
– Se gira el anteojo hasta ubicar la mira
en la estaca “B”; se toma la lectura
correspondiente, si dicho valor coincide con el calculado, el aparato está en perfecto
estado, de no ser así se suelta los tornillos verticales del retículo para subir o bajar los
retículos hasta que marque la lectura calculada.
Se recomienda volver a chequear de las tres condiciones para verificar el correcto ajuste realizado.
NIVELACIÓN INDIRECTA
Este método se basa en el uso de un instrumento u operación matemática mediante el cual se
calcula indirectamente el desnivel entre dos puntos.
Se emplea cuando no se requiere tanta precisión como para optar por una nivelación directa.
Nivelación trigonométrica
La trigonometría es el principio fundamental en este tipo de nivelación; en este método es preciso
contar como datos: el ángulo vertical “α” y la distancia inclinada entre A y B o la correspondiente
proyectada al horizonte, el objetivo es calcular el desnivel ∆h entre dos puntos.
Se emplea mucho en terrenos ondulados y donde hay quebradas; en las exploraciones y recono-
cimiento mediante la utilización del eclímetro y distancia a pasos. En trabajos de mayor preci-
sión , los ángulos se miden con teodolitos y las distancias con estadía.
Hoy en día este método se usa masivamente con ayuda de la estación total; no obstante ello, la
precisión por el método trigonométrico no es comparable con el geométrico.

382. 132
α

383. Altimetría
133
4. Calcular la altura H de piso a puente.
Solución
• De la figura:
Cota B = Cota A + (1,63) + (1,94)
Cota B = 100 + 1,63 + 1,94
Cota B = 103,57 m
• De la figura:
H = Cota B – 99,00 = 103,57 – 99
H = 4,57 m
5. Se muestra un corte longitudinal de un tunel; elaborar la libreta de campo y determinar las
cotas de los puntos: A, B, 1, 2, PC1 y PC2
Solución
• Cálculo de las cotas: A; 1; y 2
Pto V. Atrás V. Adelante Cota
BM 1,848 138,266 136,418
2 0,846 137,420
1 1,120 137,146
A 2,120 136,146
• Cálculo de las cotas: PC1; PC2 y B
Pto V. Atrás V. Adelante Cota
BM 1,345(+) 137,763 136,418
PC1 1,924(–) 138,325 2,486(+) 140,249
PC2 0,876(–) 139,773 2,324(+) 140,649
B 0,428(–) 139,345
• Analizando la nivelación en la estación B.
Nivel instrumental = Cota X + 2,080 = Cota Y + 2,895
Nivel instrument= 90,37 + 2,080 = Cota Y + 2,895
Cota Y = 89,555 m
• Finalmente: Nivelación recíproca
Cota Y =
89,573 + 89,555
2
Cota Y = 89,564 m

384. Altimetría
134
6. En la nivelación geométrica cuyo croquis y tabla se muestra, se usa un nivel descalibrado, siendo el error de
colimación 0,50 cm hacia arriba por cada 10,00 m de distancia horizontal. Determinar las cotas de los puntos.
Pto V. Atrás V. Adelante V.I. Cota
1,67 50,30
1 2,16
2 1,10
B 2,32 1,42
C 1,94 1,21
D 1,42 2,16
3 1,80
E 1,64
Solución
• Dado que el error de colimación es 0,005 m hacia arriba, para determinar el valor correcto,
habrá que efectuar:
Lectura correcta = Lectura – (0,005×n)
Siendo n = Número de decenas de metros
• Corrigiendo las lectura leídas:
Pto V. Atrás V. Adelante V.I. Cota
1,66 50,30
1 2,13
2 1,04
B 2,315 1,38
C 1,850 1,15
D 1,415 2,14
3 1,77
E 1,59
• Calculando la libreta.
Pto V. Atrás V. Adelante V.I. Cota
1,66 51,960 50,300
1 2,13 49,830
2 1,04 50,920
B 2,315 52,895 1,38 50,580
C 1,85 53,595 1,15 51,745
D 1,415 52,870 2,14 51,455
3 1,77 51,100
E 1,59 51,280
9. Se realiza una nivelación geométrica cerrada con un nivel láser; asumiendo que no existe
ningún tipo de error instrumental, se pide:
A) Determinar la cota de los puntos 1; 2; 3; 4.
B) Calcularelerrordecierrealtimétrico,asícomoelerrormáximotolerable(precisiónordinaria).
R(tierra) = 6370 km (C = +6D
2
/14R).
Nota: Se recomienda (para futuros trabajos) no realizar nivelaciones geométricas para
distancias tan grandes como la mostrada en el problema.

385. Altimetría
135
Solución:
• Elaborando la libreta de campo:
Pto V. Atrás V. Adelante Cota
A 1,40 107,623
1 1,22 1,62
2 1,20 1,87
3 1,71 0,42
4 0,80 1,87
A 0,508
• Calculando el error aparente para cada distancia
C = +6D2
/14R
150 0,002
360 0,009
120 0,001
390 0,01
330 0,007
30 0,000
60 0,000
210 0,003
• Realizando la corrección de nivel aparente
Pto V. Atrás V. Adelante Cota
A 1,402 107,623
1 1,221 1,629
2 1,201 1,880
3 1,710 0,427
4 0,80 1,879
A 0,511
• Calculando la libreta:
Pto V. Atrás V. Adelante Cota
A 1,402 109,025 107,623
1 1,221 108,617 1,629 107,396
2 1,201 107,938 1,880 106,737
3 1,710 109,221 0,427 107,511
4 0,80 108,142 1,879 107,342
A 0,511 107,631
Σ 6,334 6,5326
ΣV. Atrás – ΣV. Adelante = 0,008 m
Cota Final – Cota Inicial = 0,008 m
Luego: Ecierre = 0,008 m
• Cálculo del error tolerable máximo
=
max
E 0, 02 k (nivelaciónordinaria)
Del gráfico: k = 2,13
Emax = 0,029 m
Dado que: 0,008 m 0,029 m
La nivelación se dá por aceptada.
• Realizando la compensación de cotas.
× ×
= =
C i i
i
E d 0, 008 d
C
Perímetro 2 130
Pto Cota(m) di (m) Ci (m) Cota Comp. (m)
A 107,623 107,623
1 107,396 510,00 –0,002 107,394
2 106,737 1020,00 –0,004 106,733
3 107,511 1470,00 –0,006 107,505
4 107,342 1860,00 –0,007 107,335
A 107,631 2130 –0,008 107,623
10. Los puntos que se muestran en la tabla, for-
man el eje de un futuro camino rural, si la
subrasante de dicha vía estará conformada por
la línea recta imaginaria que une los puntos
superficiales A y 5, determinar el volumen de
tierra que se deberá cortar, así como el volu-
men de tierra que se deberá rellenar, si el an-
cho a explanar es de 1 metro a cada lado del eje.
Cota (B.M.) “A” = 107,623 m

386. Altimetría
136
Pto V. Atrás V. Adelante Cota Dist(m)
A 2,311 108,254
1 1,133 1,134 50
2 0,982 2,003 50
3 1,358 2,312 50
4 2,002 3,022 50
5 3,021 1,359 50
A 0,983 50
Solución
• Desarrollando el cálculo de la libreta.
Pto V. Atrás V. Ad. Cota Cota comp.
A 2,311 110,565 108,254 108,254
1 1,133 110,564 1,134 109,431 109,432
2 0,982 109,543 2,003 108,561 108,563
3 1,358 108,589 2,312 107,231 107,233
4 2,002 107,569 3,022 105,567 105,571
5 3,021 109,231 1,359 106,210 106,215
A 0,983 108,248 108,254
A(–) = 5402,5 m
2
∆A = A(+) – A(–) = 5 442,15 – 5 402,5
∆A = 39,65 m
2
................... (1)
• Área de corte: Entre 1 y 2
 
 
 
109, 432 + 108, 563
A(+) = 50
2
A(+) = 5 449,875 m
2
Calculando Y: En “2”
Y = –0,008156X + 108,254
X = 100 ⇒ Y = 107,438 m
 
 
 
107,846 + 107, 438
A(–) = 50
2
 
 
 
108, 254 + 109, 432
A(+) = 50
2
A(+) = 5442,15 m
2
Calculando Y: En “1”
Y = –0,008156X + 108,254
X = 50 ⇒ Y = 107,846 m
 
 
 
108, 254 + 107,846
A(–) = 50
2
• Área de corte: Entre A y 1 (fig. a).
A(–) = 5 382,10 m
2
∆A = A(+) – A(–) = 5 449,875 – 5 382,10
∆A = 67,775 m
2
.................(2)
• Área de corte: Entre 2 y 3 (fig. a)
 
 
 
108, 563 + 107, 233
A(+) = 50
2
A(+) = 5 394,900 m
2
Calculando Y: En “3”
Y = –0,008156X + 108,254
X = 150 ⇒ Y = 107,0306 m
 
 
 
107, 438 + 107, 0306
A(–) = 50
2
A (–) = 5 361,715 m2
∆A = A(+) – A(–) = 5 394,900 – 5 361,715
∆A = 33,185 m2
.................(3)
• Área de corte: Entre “3” y el punto de intersección.
Ecuacióndelarectadelterrenoentre“3”y“4”:
Fig. a: Y = –0,03324X + 112,219

387. El teodolito
137
 
 
 
106, 965 + 106, 623
A(+) = (50 – 8, 0689)
2
A(+) = 4 477,99 m
2
Terreno:
 
 
 
106, 965 + 105, 571
A(–) = (50 – 8, 0689)
2
A(–) = 4 455,934 m
2
∆A = 22,056 m
2
.................(5)
• Área de relleno: Entre 4 y 5 (fig. a)
Subrasante:
 
 
 
106, 623 + 106, 215
A(+) = 50
2
A(+) = 5 320,95 m
2
Terreno:
 
 
 
105, 571 + 106, 215
A(–) = 50
2
A (–) = 5 294,65 m2
∆A = 26,30 m2
.................(6)
• Área de relleno total: (5) + (6)
Área de relleno total = 48,356 m
2
Vrelleno = (48,356)(2)
Vrelleno = 96,712 m3
Ecuación de la subrasante:
Y = –0,008156X + 108,254
Intersectando: X = 158,0689
Y = 106,965
 
 
 
107, 233 + 106, 965
A(+) = 8, 0689
2
A(+) = 864,171 m
2
 
 
 
107, 0306 + 106, 965
A(–) = 8, 0689
2
A(–) = 863,355 m2
∆A = 0,816 m2
.................(4)
• Área de corte total: (1) + (2) + (3) + (4)
Área de corte total = 141,426 m
2
Dado que el ancho a explanar es 2 metros:
Vcorte = (141,426)(2)
Vcorte = 282,852 m
3
• Área de relleno: Entre punto de intersección
y “4”.
Subrasante (fig. a)
Y = –0,008156X + 108,254
X = 200 ⇒ Y = 106,623 m
• Figura a: Perfil longitudinal del terreno.
Fig. a

388. CLASE 11

389. Altimetría
86
Precisión de una nivelación compuesta
La precisión en una nivelación compuesta, está en relación directa al objetivo que se persigue;
así pues, si se requiere realizar un levantamiento preliminar, no justificaría usar un equipo de
alta precisión por cuanto ello llevaría consigo una mayor inversión económica.
No obstante cualquiera sea el caso, es necesario tomar ciertas precauciones cotidianas como:
– Revisar y ajustar el instrumento antes de ser usado.
– No apoyarse en el trípode y/o nivel.
– No instalar el equipo en zonas de posible vibración (como en las calzadas vehiculares).
– Tratar de nivelar en climas templados, dado que una alta o baja temperatura dilata o contrae
respectivamente la mira además de afectar al equipo.
– Evitar trabajar en épocas de viento y/o lluvias .
Sin embargo, por más precaución que se tenga, es imposible evitar la presencia de errores
accidentales. Es posible cuantificar la precisión mediante el error máximo tolerable, el valor de
dicho error está en función de dos parámetros:
• El error kilométrico (e).- Máximo error accidental del instrumento en un itinerario de 1 kilómetro.
• Número de kilometros (k).- La distancia en kilómetros del itinerario.
Emax : Error máximo tolerable (metros)
e : Error kilométrico (metros)
k : Número de kilometros
En el presente texto estableceremos la siguiente clasificación general para la nivelación geométrica.
Nivelación aproximada
Se usa en reconocimientos o levantamientos preliminares, las visuales pueden ser hasta 300
metros, la lectura en la mira puede tener una aproximación hasta de 5 cm, no es necesario que
el instrumento se encuentre equidistante respecto a los puntos por nivelar, el punto de apoyo
puede ser en terreno natural.
Emax = ±0,10 k
Nivelación ordinaria
Se emplea en trabajos de caminos, carreteras, ferrocarriles, trabajos comunes de topografía, etc. Las
visuales pueden ser hasta 150 metros, la lectura en la mira puede tener una aproximación hasta de 0,5
cm; el equipo debe ubicarse aproximadamente equidistante entre los puntos a nivelar, para ello basta
medir a pasos dichas distancias; el punto de apoyo de la mira debe ser un cuerpo sólido.
Emax = ±0,02 k
Emax : Error máximo tolerable (m)
k : Número de kilómetros del itinerario
Emax = e k

390. 87
EC
Ci
ai
dt

391. Altimetría
88
Ejemplo de aplicación
La siguiente tabla muestra los datos de una nivela-
ción cerrada; si se requiere una nivelación ordina-
ria; se pide realizar la compensación de cotas.
Pto L(+) L(–) Cota (m) d(m)
A 0,289 113,845
1,493 1,885 80,00
2 1,619 1,322 78,40
3 1,240 2,723 92,10
4 0,896 2,703 131,60
B 2,332 2,490 124,80
5 2,078 2,076 140,18
6 1,997 0,308 130,72
7 2,169 0,268 111,80
8 2,076 2,197 138,46
A 0,208 92,88
Pto L(+) L(–) Cota d(m)
A 0,289 114,134 113,845
1,493 113,742 1,885 112,249 80,00
2 1,619 114,039 1,322 112,420 78,40
3 1,240 112,556 2,723 111,316 92,10
4 0,896 110,749 2,703 109,853 131,60
B 2,332 110,591 2,490 108,259 124,80
5 2,078 110,593 2,076 108,515 140,18
6 1,997 112,282 0,308 110,285 130,72
7 2,169 114,183 0,268 112,014 111,80
8 2,076 114,062 2,197 111,986 138,46
A 0,208 113,854 92,88
Σ 16,189 16,18 1120,94
Desarrollando la tabla:
• Calculando el error de cierre.
Ecierre = Σ V. atras – Σ V. adelante
Ecierre = 0,009 m
• Calculando el error tolerable máximo.
Emax = ±0,02 d (en este caso)
Emax = ±0,02 1,12
Emax = ±0,021 m
• Comparando Ecierre con Emax
Ecierre Emax
La nivelación es conforme
• Compensando:
i cierre
i
( ) (E )
C =
dt
=
i
i
0, 009
C =
1 120,94
×
=
–6
i i
C = 8, 029 10
× =
• Compensación de cotas:
Pto Cota =i Ci Cota
compensada
A 113,845 113,845
112,249 80,00 – 0,001 112,248
2 112,420 158,40 – 0,001 112,419
3 111,316 250,50 – 0,002 111,314
4 109,853 382,10 – 0,003 109,850
B 108,259 506,90 – 0,004 108,255
5 108,515 647,08 – 0,005 108,510
6 110,285 777,80 – 0,006 110,279
7 112,014 889,60 – 0,007 112,007
8 111,986 1028.06 – 0,008 111,978
A 113,854 1120,94 – 0,009 113,845

392. Altimetría
89
B) En un itinerario abierto
El procedimiento es similar al de un itinerario cerrado.
i C
i
( ) (E )
C =
dt
a
Ci : Compensación en el punto “i”
ai : Distancia del punto inicial al punto “i”
EC : Error de cierre
dt : Distancia total
Ejemplo de aplicación
El siguiente croquis y tabla respectiva, muestra los datos de una nivelación abierta; si se
requiere una nivelación ordinaria; se pide realizar la compensación de cotas.
Desarrollando la tabla:
Pto L(+) L(–) Cota(m) d(m) Lado
A 2,105 163,221
1 1,860 1,270 79,30 A – 1
2 1,632 1,465 52,90 1 – 2
3 2,068 0,922 109,20 2 – 3
B 1,765 33,80 3 – B
Pto L(+) L(–) Cota d Lado
A 2,105 165,326 163,221
1 1,860 165,916 1,270 164,056 79,30 A – 1
2 1,632 166,083 1,465 164,451 52,90 1 – 2
3 2,068 167,229 0,922 165,161 109,20 2 – 3
B 1,765 165,464 33,80 3 – B
Σ 7,665 5,422 275,20
• Chequeando el cálculo matemático.
ΣL(+) – ΣL(–) = Cota “B” – Cota “A”
7,665 – 5,422 = 165,464 – 163,221
2,243 = 2,243 ....... (conforme)
• Calculando el error de cierre.
EC = Cota “B” (calculado) – Cota “B”(dato)
EC = 165,464 – 165,458
EC = +0,006 m

393. Altimetría
90
• Calculando el error tolerable.
Emax = ±0,02 k
Emax = ±0,02 0, 2752
Emax = ±0,01 m
• Comparando EC con Emax
EC Emax
La nivelación es conforme
Pto Cota =i Ci Cota
compensada
A 163,221 163,221
1 164,056 79,30 – 0,002 164,054
2 164,451 132,20 – 0,003 164,448
3 165,161 241,40 – 0,005 165,156
B 165,464 275,20 – 0,006 165,458
• Compensando:
i C
i
( ) (E )
C =
dt
=
i
i
0, 006
C =
275, 20
×
=
⇒ –5
i i
C = 2,18 10
× =
• Compensación de cotas:
Nivelación geométrica entre dos puntos extremadamente alejados
Cuando se trata de realizar una nivelación geométrica entre dos puntos muy distantes entre si;
se recomienda dividir el circuito total en sub-circuitos
Al nivelar en un circuito cerrado dos puntos muy alejados; es posible cometer una serie de errores, cuya presencia
ocasionaría un error de cierre altimétrico mayor que el máximo tolerable, lo cual obligaría al topógrafo a repetir posible-
mente todo el trabajo.
Los puntos que definen los sub-circuitos, deberán ser estacados con mucho cuidado de modo que posteriormente sean fácil-
mente ubicable y no altere el valor de su cota en ningún momento.
En cada sub-circuito se debe calcular su error de cierre altimétrico y cada uno de ellos debe ser menor que el máximo tolerable
respectivo.
Es posible que en uno de los sub-circuitos el error de cierre sea mayor que el tolerable; de ser así, el topógrafo deberá
repetir el trabajo tan solo en el sub-circuito comprometido.

394. Altimetría
91
Sea:
E1
: Error de cierre altimétrico en el sub-circuito 1 L1
: Longitud total del sub-circuito 1
E2
: Error de cierre altimétrico en el sub-circuito 2 L2
: Longitud total del sub-circuito 2
E3
: Error de cierre altimétrico en el sub-circuito 3 L3
: Longitud total del sub-circuito 3
.
. .
. .
. .
En : error de cierre altimétrico en el sub-circuito n L
n
: Longitud total del sub-circuito n
El error de cierre altimétrico del circuito total será:
2 2 2 2
total 1 2 3
E = E E E ... E
± + + + + n
Este error encontrado deberá ser menor que el máximo tolerable, el cual se calculará teniendo presente:
d = L1 + L2 + L3 + ... + Ln
Por último, se tendrá que realizar la compensación de cotas en cada sub-circuito independien-
temente unos de los otros.
Fenómenos físicos que afectan una nivelación
Cuando se requiera determinar el desnivel entre dos puntos separados a una distancia considerable,
hay que tomar en cuenta el error proveniente de la curvatura de la Tierra y la refracción atmosférica.
Influencia de la curvatura terrestre
Es conocido que todo plano o superficie horizontal es tangente a la superficie de nivel en un punto;
si la distancia entre dos puntos es pequeña la línea que las une se puede considerar tangente, pero
si es grande es imprescindible tomar en cuenta la curvatura de la superficie de nivel.
Ahora, para efectuar nivelaciones en ingeniería, se utilizan instrumentos ópticos que permiten
visualizar toda una horizontal sin importar la distancia
Si la distancia entre A y B no es mayor que 50
metros se puede considerar la superficie del ni-
vel instrumental y su respectiva horizontal con-
fundidos en un mismo plano.
Cota B = Nivel instrumental – Lectura visualizada

395. CLASE 13

396. Altimetría
115
CURVA DE NIVEL
Curva de nivel es una línea imaginaria que une los puntos que tienen igual cota respecto a un plano de
referencia (generalmente el nivel medio del mar).
El uso de las curvas de nivel, permite representar el relieve de un terreno con gran facilidad y precisión
respecto a otros métodos, dado que en conjunto representan cualitativa y cuantitativamente las elevacio-
nes, depresiones y accidentes del terreno.
Representación
Curvas de nivel más importantes
Por motivos didácticos mostraremos con ejemplos numéricos, las curvas más representativas.
1. El cerro
Representa las elevaciones, las curvas cambian de menor a mayor altitud, de modo que la de mayor
altitud es una curva cerrada dentro de las demás.
Cota A = Cota B = Cota C = Cota D

397. Altimetría
116
2. El hoyo
Representa una depresión, las curvas cambian de mayor a menor altitud, de modo que la de menor
altitud es una curva cerrada dentro de los demás.
3. Entrante (quebrada)
Se puede considerar como una porción de hoyo; está representada por curvas en forma de U, toda
el agua que caiga correrá formando corrientes por las quebradas en dirección hacia las cotas más baja.

398. Altimetría
117
4. Saliente
Puede considerarse como una porción de cerro y determina la línea divisoria de los valles.
Ejemplos de aplicación
Ejemplo 1

399. Altimetría
118
Ejemplo 2
Características de las curvas de nivel
1. Las curvas de nivel nunca se cortan
2. Lascurvasdenivelsonsiemprelíneascerradasaunquenosecierrenenelárearepresentadaenelplano.
3. Las curvas de nivel están separadas unas de otras por una distancia vertical constante llamada
equidistancia; ésta depende básicamente de la escala del plano; no obstante también de la topografía
del terreno.
4. Las equidistancias que se usan frecuentemente son:
– Para escalas superiores de 1/5000 ---------------------------------------- 1 metro
– Para escala de 1/5 000 ----------------------------------------------------- 2,5 metros
– Para escala de 1/10 000 ---------------------------------------------------- 5 metros
– Para escala de 1/25 000 ---------------------------------------------------- 10 metros
– Para escala de 1/50 000 ---------------------------------------------------- 20 metros
5. Las curvas de nivel están separadas una de otras por una distancia horizontal variable.
– En pendientes uniformes, el espaciamiento horizontal de las curvas de nivel es constante.
– En pendientes pronunciadas las curvas de nivel se encuentran casi juntas.
– En pendientes poco pronunciadas, las curvas de nivel se encuentran muy separadas.
6. En superficies planas, las curvas de nivel son rectas y paralelas entre sí.
7. Si las proyecciones de curvas de diferentes cotas coinciden, el terreno forma cantil y todos los puntos
se encontrarán prácticamente en un mismo plano vertical.
8. Las curvas de nivel no deben cruzar las estructuras artificiales.

400. Altimetría
119
Ejemplo Ilustrativo

401. 132
α

402. Altimetría
133
4. Calcular la altura H de piso a puente.
Solución
• De la figura:
Cota B = Cota A + (1,63) + (1,94)
Cota B = 100 + 1,63 + 1,94
Cota B = 103,57 m
• De la figura:
H = Cota B – 99,00 = 103,57 – 99
H = 4,57 m
5. Se muestra un corte longitudinal de un tunel; elaborar la libreta de campo y determinar las
cotas de los puntos: A, B, 1, 2, PC1 y PC2
Solución
• Cálculo de las cotas: A; 1; y 2
Pto V. Atrás V. Adelante Cota
BM 1,848 138,266 136,418
2 0,846 137,420
1 1,120 137,146
A 2,120 136,146
• Cálculo de las cotas: PC1; PC2 y B
Pto V. Atrás V. Adelante Cota
BM 1,345(+) 137,763 136,418
PC1 1,924(–) 138,325 2,486(+) 140,249
PC2 0,876(–) 139,773 2,324(+) 140,649
B 0,428(–) 139,345
• Analizando la nivelación en la estación B.
Nivel instrumental = Cota X + 2,080 = Cota Y + 2,895
Nivel instrument= 90,37 + 2,080 = Cota Y + 2,895
Cota Y = 89,555 m
• Finalmente: Nivelación recíproca
Cota Y =
89,573 + 89,555
2
Cota Y = 89,564 m

403. Altimetría
134
6. En la nivelación geométrica cuyo croquis y tabla se muestra, se usa un nivel descalibrado, siendo el error de
colimación 0,50 cm hacia arriba por cada 10,00 m de distancia horizontal. Determinar las cotas de los puntos.
Pto V. Atrás V. Adelante V.I. Cota
1,67 50,30
1 2,16
2 1,10
B 2,32 1,42
C 1,94 1,21
D 1,42 2,16
3 1,80
E 1,64
Solución
• Dado que el error de colimación es 0,005 m hacia arriba, para determinar el valor correcto,
habrá que efectuar:
Lectura correcta = Lectura – (0,005×n)
Siendo n = Número de decenas de metros
• Corrigiendo las lectura leídas:
Pto V. Atrás V. Adelante V.I. Cota
1,66 50,30
1 2,13
2 1,04
B 2,315 1,38
C 1,850 1,15
D 1,415 2,14
3 1,77
E 1,59
• Calculando la libreta.
Pto V. Atrás V. Adelante V.I. Cota
1,66 51,960 50,300
1 2,13 49,830
2 1,04 50,920
B 2,315 52,895 1,38 50,580
C 1,85 53,595 1,15 51,745
D 1,415 52,870 2,14 51,455
3 1,77 51,100
E 1,59 51,280
9. Se realiza una nivelación geométrica cerrada con un nivel láser; asumiendo que no existe
ningún tipo de error instrumental, se pide:
A) Determinar la cota de los puntos 1; 2; 3; 4.
B) Calcularelerrordecierrealtimétrico,asícomoelerrormáximotolerable(precisiónordinaria).
R(tierra) = 6370 km (C = +6D
2
/14R).
Nota: Se recomienda (para futuros trabajos) no realizar nivelaciones geométricas para
distancias tan grandes como la mostrada en el problema.

404. Altimetría
135
Solución:
• Elaborando la libreta de campo:
Pto V. Atrás V. Adelante Cota
A 1,40 107,623
1 1,22 1,62
2 1,20 1,87
3 1,71 0,42
4 0,80 1,87
A 0,508
• Calculando el error aparente para cada distancia
C = +6D2
/14R
150 0,002
360 0,009
120 0,001
390 0,01
330 0,007
30 0,000
60 0,000
210 0,003
• Realizando la corrección de nivel aparente
Pto V. Atrás V. Adelante Cota
A 1,402 107,623
1 1,221 1,629
2 1,201 1,880
3 1,710 0,427
4 0,80 1,879
A 0,511
• Calculando la libreta:
Pto V. Atrás V. Adelante Cota
A 1,402 109,025 107,623
1 1,221 108,617 1,629 107,396
2 1,201 107,938 1,880 106,737
3 1,710 109,221 0,427 107,511
4 0,80 108,142 1,879 107,342
A 0,511 107,631
Σ 6,334 6,5326
ΣV. Atrás – ΣV. Adelante = 0,008 m
Cota Final – Cota Inicial = 0,008 m
Luego: Ecierre = 0,008 m
• Cálculo del error tolerable máximo
=
max
E 0, 02 k (nivelaciónordinaria)
Del gráfico: k = 2,13
Emax = 0,029 m
Dado que: 0,008 m 0,029 m
La nivelación se dá por aceptada.
• Realizando la compensación de cotas.
× ×
= =
C i i
i
E d 0, 008 d
C
Perímetro 2 130
Pto Cota(m) di (m) Ci (m) Cota Comp. (m)
A 107,623 107,623
1 107,396 510,00 –0,002 107,394
2 106,737 1020,00 –0,004 106,733
3 107,511 1470,00 –0,006 107,505
4 107,342 1860,00 –0,007 107,335
A 107,631 2130 –0,008 107,623
10. Los puntos que se muestran en la tabla, for-
man el eje de un futuro camino rural, si la
subrasante de dicha vía estará conformada por
la línea recta imaginaria que une los puntos
superficiales A y 5, determinar el volumen de
tierra que se deberá cortar, así como el volu-
men de tierra que se deberá rellenar, si el an-
cho a explanar es de 1 metro a cada lado del eje.
Cota (B.M.) “A” = 107,623 m

405. Altimetría
136
Pto V. Atrás V. Adelante Cota Dist(m)
A 2,311 108,254
1 1,133 1,134 50
2 0,982 2,003 50
3 1,358 2,312 50
4 2,002 3,022 50
5 3,021 1,359 50
A 0,983 50
Solución
• Desarrollando el cálculo de la libreta.
Pto V. Atrás V. Ad. Cota Cota comp.
A 2,311 110,565 108,254 108,254
1 1,133 110,564 1,134 109,431 109,432
2 0,982 109,543 2,003 108,561 108,563
3 1,358 108,589 2,312 107,231 107,233
4 2,002 107,569 3,022 105,567 105,571
5 3,021 109,231 1,359 106,210 106,215
A 0,983 108,248 108,254
A(–) = 5402,5 m
2
∆A = A(+) – A(–) = 5 442,15 – 5 402,5
∆A = 39,65 m
2
................... (1)
• Área de corte: Entre 1 y 2
 
 
 
109, 432 + 108, 563
A(+) = 50
2
A(+) = 5 449,875 m
2
Calculando Y: En “2”
Y = –0,008156X + 108,254
X = 100 ⇒ Y = 107,438 m
 
 
 
107,846 + 107, 438
A(–) = 50
2
 
 
 
108, 254 + 109, 432
A(+) = 50
2
A(+) = 5442,15 m
2
Calculando Y: En “1”
Y = –0,008156X + 108,254
X = 50 ⇒ Y = 107,846 m
 
 
 
108, 254 + 107,846
A(–) = 50
2
• Área de corte: Entre A y 1 (fig. a).
A(–) = 5 382,10 m
2
∆A = A(+) – A(–) = 5 449,875 – 5 382,10
∆A = 67,775 m
2
.................(2)
• Área de corte: Entre 2 y 3 (fig. a)
 
 
 
108, 563 + 107, 233
A(+) = 50
2
A(+) = 5 394,900 m
2
Calculando Y: En “3”
Y = –0,008156X + 108,254
X = 150 ⇒ Y = 107,0306 m
 
 
 
107, 438 + 107, 0306
A(–) = 50
2
A (–) = 5 361,715 m2
∆A = A(+) – A(–) = 5 394,900 – 5 361,715
∆A = 33,185 m2
.................(3)
• Área de corte: Entre “3” y el punto de intersección.
Ecuacióndelarectadelterrenoentre“3”y“4”:
Fig. a: Y = –0,03324X + 112,219

406. El teodolito
137
 
 
 
106, 965 + 106, 623
A(+) = (50 – 8, 0689)
2
A(+) = 4 477,99 m
2
Terreno:
 
 
 
106, 965 + 105, 571
A(–) = (50 – 8, 0689)
2
A(–) = 4 455,934 m
2
∆A = 22,056 m
2
.................(5)
• Área de relleno: Entre 4 y 5 (fig. a)
Subrasante:
 
 
 
106, 623 + 106, 215
A(+) = 50
2
A(+) = 5 320,95 m
2
Terreno:
 
 
 
105, 571 + 106, 215
A(–) = 50
2
A (–) = 5 294,65 m2
∆A = 26,30 m2
.................(6)
• Área de relleno total: (5) + (6)
Área de relleno total = 48,356 m
2
Vrelleno = (48,356)(2)
Vrelleno = 96,712 m3
Ecuación de la subrasante:
Y = –0,008156X + 108,254
Intersectando: X = 158,0689
Y = 106,965
 
 
 
107, 233 + 106, 965
A(+) = 8, 0689
2
A(+) = 864,171 m
2
 
 
 
107, 0306 + 106, 965
A(–) = 8, 0689
2
A(–) = 863,355 m2
∆A = 0,816 m2
.................(4)
• Área de corte total: (1) + (2) + (3) + (4)
Área de corte total = 141,426 m
2
Dado que el ancho a explanar es 2 metros:
Vcorte = (141,426)(2)
Vcorte = 282,852 m
3
• Área de relleno: Entre punto de intersección
y “4”.
Subrasante (fig. a)
Y = –0,008156X + 108,254
X = 200 ⇒ Y = 106,623 m
• Figura a: Perfil longitudinal del terreno.
Fig. a

407. Taquimetría
379
3. Construcción de curvas de nivel
El levantamiento de curvas de nivel, es un caso particular del relleno topográfico.
La elección de los puntos a levantar taquimétricamente depende de dos factores: La topogra-
fía del terreno y el criterio del topógrafo, es por ello que él debe tener cierta experiencia y
buen sentido para que así, las curvas de nivel sean fiel reflejo de la configuración del terreno.
No obstante, a continuación se presentan ciertas recomendaciones importantes que a criterio
propio favorecen al orden y eficiencia de un levantamiento de curvas de nivel.
A) Proceso de campo
Ilustraremos con un ejemplo los pasos a seguir; para ello nos apoyaremos en el trabajo realizado por
los alumnos de la facultad de Ingeniería Civil de la Universidad Nacional de Ingeniería, Lima - Perú:
Gamarra Rivera, Carlos Alberto
Mallqui Rodriguez, José Eduardo
Callupe Morales, Armando Steve
A quienes felicitamos por la encomiable labor realizada.
Vista panorámica de la zona a levantar.

408. Taquimetría
380
1° En el proceso de reconocimiento de terreno, llevar a cabo un croquis de la zona, donde
planimétricamente se representen estructuras artificiales y naturales importantes, tales como:
Edificaciones, reservorios, carreteras, caminos, cercos, taludes, quebradas, divisorias de aguas, etc.

409. Taquimetría
381
2° Apoyándose en los puntos de control, proceder a levantar los puntos pertenecientes al
croquis realizado.
Para ello es recomendable asignar nombres estratégicos a los puntos por levantar y anotar-
los en el croquis.

410. Taquimetría
382
3° Realizar el levantamiento masivo de puntos; se recomienda llevar un orden establecido, en tal
sentido es preferible que los puntos por levantar formen un conjuntos de líneas o cuadrículas.
Es imprescindible levantar los puntos donde se presentan cambios de pendientes.
Al igual que en el segundo paso es muy importante la designación de nombres a los puntos por
levantar.

411. Taquimetría
383
B) Proceso de gabinete
En esta etapa es de vital importancia la presencia de la persona que estuvo a cargo del
croquis en el proceso de campo, dado su relación directa con el terreno.
Los pasos que se recomiendan seguir son las siguientes:
1° Se unen mediante líneas rectas los puntos considerados importantes en el dibujo del croquis
realizado en el proceso de campo.

412. Taquimetría
384
2° Se unen mediante líneas rectas los puntos masivamente levantados, formando triángulos y/
o rectángulos.
La configuración de las figuras geométricas obedecen al criterio y relación topógrafo-terreno.
No necesariamente habrá que unir todos los puntos.

413. Taquimetría
385
3° Como quiera que para dibujar una curva de nivel es necesario unir los puntos de igual cota,
y dado que generalmente dicha casualidad es siempre esquiva, se hace imprescindible
inducir una “multiplicación de puntos”.
Para dicho efecto se recurrirá al método de interpolación.
A continuación se explicará el procedimiento gráfico para realizar una interpolación líneal.
Asumiendo que se tienen como datos los puntos A y B cuyas cotas son 100,00 m y 110,00 m
respectivamente.
Datos: Punto A y B
Se une A y B mediante una línea recta.
Se traza una segunda línea recta convenientemente elegida.
Dado que de 100 a 110 m hay 10 unidades, se elige
10 espacios (con escalímetro) en la recta L.
Se une el extremo de L con el punto B, mediante una recta.

414. Taquimetría
386
Finalmente:
Esta metodología se puede realizar también analíticamente o mediante algún software
conocido basándonos siempre bajo el mismo principio: interpolación líneal.
Aplicando el método de interpolación líneal a nuestro ejemplo de aplicación y uniendo los
puntos de igual cota:
Aplicando el teorema de Thales se divide el segmento
AB en 10 partes iguales (en este caso).

415. Taquimetría
387
4° Se oculta o borra las figuras geométricas (triángulos o rectángulo) para luego presentar el plano final.

416. Taquimetría
388
Hoy en día con el uso de los software topográficos, pero obedeciendo los pasos explicados
se puede obtener un modelo digital del terreno e incluso representación tridimensional tal
como se muestra a continuación.
Modelo
digital
tridimensional
del
terreno.
Nótese
los
puntos
levantados
taquimétricamente.

417. Taquimetría
389
Observaciones:
A) Las curvas de nivel no deben cruzar las edificaciones.
Trabajo correcto : Los triángulos formados se encuentran al exterior de la edificación.
Trabajo incorrecto : Los triángulos formados se encuentran dentro y fuera de la edificación.

418. Taquimetría
390
Trabajo correcto : La interpolación se realiza al exterior de la edificación.
Trabajo incorrecto : La interpolación se realiza dentro y fuera de la edificación.

419. Taquimetría
391
Trabajo final correcto
Trabajo final incorrecto

420. Taquimetría
392
B) Cuando exista un talud, muro de contención o similar, es obligatorio levantar puntos en la
cima y al pie del mismo.
Trabajo correcto : Puntos levantados en la cima y al pie del talud.
Trabajo incorrecto : Puntos levantados solo en la cima del talud.
Punto Cota (m)
M1 117,638
M2 117,699
M3 117,703
M4 117,834
M5 117,860
M6 117,95
En la cima del talud
Punto Cota (m)
M7 113,393
M8 113,614
M9 113,709
M10 113,920
M11 114,240
M12 114,569
M13 115,088
Al pie del talud
Punto Cota (m)
M1 117,638
M2 117,699
M3 117,703
M4 117,834
M5 117,860
M6 117,95
En la cima del talud

421. Taquimetría
393
Trabajo final correcto
Trabajo final incorrecto

422. Taquimetría
394
C) En toda quebrada es imprescindible el levantamiento de puntos contenidos en su eje principal.
Trabajo correcto : Note Ud. la presencia de puntos levantados en el eje principal.
Trabajo incorrecto : No existen puntos levantados en el eje principal.

423. Taquimetría
395
Trabajo correcto : El eje principal divide la malla en: triángulos a la derecha y triángulos a la izquierda.
Trabajo incorrecto : Los triángulos sombreados no se encuentran ni a la derecha ni a la izquierda del eje principal.

424. Taquimetría
396
Trabajo final correcto
Trabajo final incorrecto

425. Taquimetría
397
Trabajo correcto : El punto de cota menor pertenece al eje principal. (quebrada real)
Trabajo incorrecto : Quebrada irreal

426. Taquimetría
398
Trabajo correcto : Se deben generar tres tipos de triángulos.
Triángulos a la derecha del borde derecho, a la izquierda del borde izquierdo y dentro de la calzada.
D) En toda carretera o camino, las curvas de nivel deben encontrarse aproximadamente paralelas entre sí.
Trabajo incorrecto : Se han generado triángulos que invaden simultáneamente la calzada y la zona izquierda del
borde izquierdo.

427. Taquimetría
399
Trabajo correcto : La interpolación se realiza independientemente en cada una de las tres zonas.
Trabajo incorrecto : Se han realizado interpolaciones que involucran simultáneamente a dos zonas.

428. Taquimetría
400
Trabajo final incorrecto
Trabajo fffal corrfcto

429. Taquimetría
401
1. Si la cota del punto M, es 47,767; calcular
la cota del punto N.
Datos del teodolito:
Constante aditiva = 0
Constante diastimométrica (K) = 100
PROBLEMAS DE APLICACIÓN
Solución:
• DV = (HS – HI)⋅
× α
100 sen 2
2
DV = (2,15 – 1,55)⋅
× × °
100 sen(2 56 32' 30)
2
DV = 27,598 m
• Cota M + 1,50 + DV = Cota N + 1,85
47,767 + 1,500 + 27,598 = Cota N + 1,85
Cota N = 75,015 m
2. Las siguientes lecturas se tomaron sobre
una mira colocada en forma vertical.
Calcúlese la distancia horizontal entre
el teodolito y la mira, y la elevación en
la mira, si el nivel del eje del instru-
mento es de 37,36 m.
Solución:
• Ilustrando el enunciado:
Ángulo vertical (α
α
α
α
α) Lectura hilo medio de la mira
+4° 13' 30 1,00
+5° 58' 20 3,00
37,36 = Cota A + h = Cota B + H – DH⋅tg α
(1) Cuando α = 4° 13' 30
Cota A + h = Cota B + 1,00 – DH⋅tg 4°13'30
(2) Cuando α = +5° 58' 20
Cota A + h = Cota B + 3,00 – DH⋅tg 5°58'20
• De (1) y (2)
DH = 65,06 m
• Además:
37,36 = Cota B + 1,00 – 65,06⋅tg 4° 13' 30
Cota B = 41,17 m

430. Taquimetría
402
3. Determinar la cota de B y la pendiente entre
A y B, con el siguiente registro de campo:
Teodolito nadiral.
Est. P.V. 5 H D.G.(m) H.M. 5 Vert. Cota(m)
E N 0° 00' 00 3 240,60
A 36° 36' 40 101,50 2,01 98° 37' 15
B 115° 25' 40 202,60 1,80 81° 22' 45
La altura del instrumento en la estación E
es 1,52 m.
Solución:
• Analizando la visual EA
3 240,60 + 1,52 + 15,21 = Cota A + 2,01
Cota A = 3 255,32 m
• Analizando la visual EB
3 240,60 + 1,52 = Cota “B” + 1,80 + 30,37
Cota B = 3 209,95 m
• Analizando las distancias horizontales.
115° 25' 40 – 36° 36' 40 = 78° 49' 00
Resolviendo el triángulo AEB:
dAB = 205,91 m
• Calculando la pendiente entre A y B.
P = –22%
4. Se realiza un levantamiento batimétrico
con ayuda de una estación total y una
ecosonda. Si los datos obtenidos en cam-
po son los que muestra la figura, calcular:
a) La Cota de B.
b) Las coordenadas absolutas de B.
Cota “A” = 100,00 m
A = (200,00 ; 250,00) m

431. Taquimetría
403
Solución:
• En el triángulo vertical sombreado:
α = 31° 22' 33
DH = 32,65⋅Cos α = 27,53
DV = 32,25⋅Sen α = 16,79
• Respecto al nivel de referencia horizontal:
Cota“A”+1,00=Cota“B”+10,27+0,80+DV
100,00 + 1,00 = Cota “B” + 10,27 + 0,80 + 16,79
Cota “B” = 73,14 m
• Analizando planimétricamente (N – E) la
posición de “B”.
∆x = DH⋅Sen Z
∆y = DH⋅Cos Z
– En nuestro caso:
∆x = 27,53⋅Sen (102° 20' 33) = 26,89 m
∆y = 27,53⋅Cos (102° 20' 33) = –5,89 m
– Coordenadas de “B”
Conociendo A = (200,00 ; 250,00) m
E = 200,00 + 26,89 = 226,89 m
N = 250,00 + (–5,89) = 244,11 m
Por tanto:
B = (226,89 ; 244,11) m
5. Desde el vértice A de una poligonal se ha
levantado taquimétricamente los puntos
1; 2; 3 y 4 obteniéndose:
Se dá como datos las coordenadas
planimétricas de los puntos A y B.
A = (100,00 ; 100,00) ; B = (144,826 ; 168,186)

432. Taquimetría
404
Se pide las coordenadas de los puntos 1; 2; 3 y 4 (x; y; z), sabiendo que el punto 4 se ha tomado con
una lectura de mira 1,61 m
Solución:
• Teniendo en cuenta que:
DH = (HS – HI)⋅ × α
2
100 Cos y DV = (HS – HI)⋅
× α
100 Sen 2
2
Teodolito : Cenital
Constante aditiva del teodolito : 0
Constante diastimométrica del teodolito : 100
Ángulo Vertical Hilo
Estación P.V. 5 H 5 V α Estadimétrico(m) DH(m) DV(m) Cota(m)
A 108,239
B 0° 00' 00
1 07° 57' 40 90° 14' 40 1,94
1,03
2 09° 45' 00 90° 13' 40 1,95
=1,49 m 1,01
3 46° 18' 20 89° 51' 20 1,55
1,42
4 81° 01' 20 89° 20' 10 1,80
1,40
• Calculando la cota del punto “4”
Ángulo Vertical Hilo
Estación P.V. 5 H 5 V α Estadimétrico(m) DH(m) DV(m) Cota(m)
A 108,239
B 0° 00' 00
1 07° 57' 40 90° 14' 40 –0° 14' 40 1,94 90,998 –0,388 107,851
1,03
2 09° 45' 00 90° 13' 40 –0° 13' 40 1,95 93,999 –0,374 107,865
=1,49 m 1,01
3 46° 18' 20 89° 51' 20 0° 08' 40 1,55 12,999 0,033 108,272
1,42
4 81° 01' 20 89° 20' 10 0° 39' 50 1,56 13,998 0,162 108,281
1,42
Cota “A” + 1,49 + 0,162 = Cota “4” + 1,61 ⇒ Cota “4” = 108,281 m

433. Ajustes en los circuitos topográficos aplicando el método de mínimos cuadrados
405
• Planimétricamente:
Considerando:
A = (100,000 ; 100,000) m
6. Tres puntos de control colineales X, Y, Z
tienen las siguientes coordenadas:
Lado d (m) ∆x = dsen Z ∆y = dcos Z
AB 33°19'16,42
A1 41°16'56,42 90,998 60,038 68,382
A2 43°04'16,42 93,999 64,193 68,667
A3 79°37'36,42 12,999 12,787 2,341
A4 114°20'36,4 13,998 12,753 –5,770
Punto E = 100 + ∆x N = 100 + ∆y Cota(m)
1 160,038 168,382 107,851
2 164,193 168,667 107,865
3 112,787 102,341 108,272
4 112,753 94,230 108,281
En la estación Q, al este de X, Y, Z, se
fijó un teodolito y se registró la siguien-
te información:
Calcular a, b y c
Datos estadimétricos del teodolito:
Constante aditiva = 0
Constante diastimométrica K = 100
HS, HI: Lectura estadimétrica
Punto Este(m) Norte(m)
X 285,00 320,00
Y 295,00 360,00
302,50 390,00
Estación de
Mira S H S V HS(m) HI(m)
X 0° 00' 02° 00' a 1,00
Y 19° 43' 0° 00' b 1,00
42° 52' 03° 00' c 1,00
• Estadimétricamente desde la estación Q.
Dreducida = (HS – HI)⋅100⋅Cos2
α
DX = (a – 1)⋅100⋅Cos2
(2° 00') = 99,878(a – 1)
DY = (b – 1)⋅100⋅Cos2
(0° 00') = 100,000(b – 1)
DZ = (c – 1)⋅100Cos2
(3° 00') = 99,726(c – 1)
• Analizando el gráfico:
(1)
( )
−
=
° α
99,878 a 1
41, 231
Sen 19 43' Sen
(a – 1) = 1,224⋅Sen α
(2)
( )
−
=
° ° − α
99, 726 c 1
30, 923
Sen 23 09' Sen (180 )
(c – 1) = 0,789⋅Sen α
(3) [72,154]2
= [99,878(a – 1)]2
+ [99,726(c – 1)]2
–
2[99,878(a–1)][99,726(c–1)]⋅Cos42°52'
– De (1), (2) y (3): a = 2,05 m
c = 1,68 m
– Del gráfico: b = 1,78 m
Tener presente: α = 120° 28' 30
Solución:
• Graficando el enunciado.

434. CLASE 14

435. Altimetría
120
PERFIL LONGITUDINAL
El perfil longitudinal topográfico a lo largo de un eje longitudinal en planta, es una línea quebrada que
proviene de la intersección de la superficie topográfica con el plano vertical que contiene al eje de dicha
planta.
Se utiliza para representar el relieve o accidente del terreno a lo largo de un eje longitudinal.
El perfil longitudinal se determina mediante la nivelación de un conjunto de puntos de la superficie de
la tierra situados a corta distancia entre sí y a lo largo de un alineamiento previamente establecido.
Los perfiles longitudinales se utilizan en el trazo de ejes de caminos, carreteras, de ferrocarriles, de
instalaciones de alcantarillado, etc.
Recomendaciones
– Con el fin de obtener un perfil donde se apre-
cie fácilmente el desnivel entre los diversos
puntos, se acostumbra tomar una escala ver-
tical mucho más grande que la horizontal. A
menudo se usa la relación 10 a 1
Como ejemplos se puede citar:
mente se toman puntos cada 20 metros (oca-
sionalmente se nivelarán cada 10 a 5 me-
tros, dependiendo de la topografía del te-
rreno y de los objetivos del levantamiento).
– No obstante seguir con la secuencia cons-
tante de 20 metros; será obligatorio nive-
lar ciertos puntos del itinerario como:
• Los puntos donde hay cambio de pen-
diente (A).
• Las cotas más altas y bajas del perfil.
• Los puntos altimétricamente extremos de
un escalón, talud o muro vertical, indican-
do que es cero la distancia horizontal entre
ellos (B y C).
Vertical Horizontal
1/10 1/100
1/20 1/200
1/25 1/250
1/50 1/500
1/100 1/1000
– Se deben nivelar puntos del terreno, obede-
ciendo una secuencia constante; general-

436. Altimetría
121
• El principio y fin de una estructura artificial (D y E).
• Las orillas y eje de un canal, quebrada, acequia, etc (F, G y H).
Métodos para la construcción de perfiles longitudinales
Según la precisión buscada, se pueden obtener perfiles directamente desde planos ó mediante
levantamientos topográficos realizados especialmente para tal fin.
I Método directo
Proviene especialmente de un levantamiento topográfico; es más preciso respecto al indirecto; se
puede obtener mediante una nivelación geométrica ó trigonométrica, ésta última se explicará más
adelante, dado que su principio está basado en la taquimetría.
Para obtener el perfil longitudinal de un alineamiento entre dos puntos, haciendo uso de la nivela-
ción geométrica, se presentan dos casos.
A) Cuando existen varios bancos de nivel
En el caso de tener uno o más bancos de nivel en el itinerario del eje longitudinal, se
recomienda trabajar por tramos, para de esta forma verificar que el error de cierre no sobrepa-
se al tolerable (Emax = e k )
Analizando el tramo 1:
– Se estaca los puntos a nivelar.
– Se nivela los puntos estacados.
– Se calcula el error de cierre con el punto “C” (en este caso).
– Se verifica: EC Emax = e k
– En caso que el error de cierre sea menor que el tolerable, se procede a repartir dicho error en
todos los puntos nivelados (compensación).
– A continuación se realiza la misma operación en el siguiente tramo.

437. Altimetría
122
B) Cuando sólo se cuenta con el B.M. o banco de nivel del primer punto
Enestecasosehacenecesariorealizarelrecorridodeidayvueltaparaverificarlaprecisiónbuscada.
Analizando el circuito.
– Se estaca los puntos a nivelar.
– Se nivela los puntos estacados.
– Se cierra el circuito,el recorrido de regreso puede realizarse por cualquier camino conveniente.
– Se verifica: EC Emax = e k
– En caso que el error de cierre sea menor que el tolerable se procede a repartir dicho error en los
puntos nivelados (compensación).
Ejemplo de aplicación
Se tiene una poligonal cerrada con cinco puntos de control estacados de la forma que se muestra, si el
único banco de nivel es el que corresponde al punto “A” (109,213 m); se pide dibujar el perfil longitudinal.
- Lasdistancias AP y CP puedenmedirseapasos,dadoquesuaplicaciónseráexclusiva-
mente para la determinación de la precisión del trabajo y la compensación respectiva.
- Cuando el eje longitudinal es muy extenso, se recomienda realizar varios sub-circuitos
cerrados.
Observaciones

438. Altimetría
123
Pto L(+) L(–) L.I. Cota d(m)
A 1,028 109,213
1 1,353 20
2 1,500 20
3 1,930 20
B 1,670 1,883 9
4 1,785 11
5 1,542 20
6 1,336 20
7 1,037 20
8 0,868 20
C 2,370 0,832 16,65
9 2,271 3,35
10 1,983 20
11 1,857 20
12 1,372 20
13 1,084 20
D 0,825 1,02 6,05
14 1,260 13,95
15 1,565 20
E 1,193 1,717 17,50
16 1,229 2,50
17 1,452 20
18 1,497 20
A 16,5
Libreta de campo Calculando y compensando cotas
Como muestra el siguiente gráfico, todo perfil longitudinal consta de dos partes:
Elgráficopropiamentedichoylaguitarra(datosnuméricos:cotasdistanciaspendientesetc).
Nota
Pto L(+) L(–) L.I. Cota d(m) Cota
Comp.
A 1,028 110,241 109,213 109,213
1 1,353 108,888 20 108,887
2 1,500 108,741 20 108,739
3 1,930 108,311 20 108,309
B 1,670 110,028 1,883 108,358 9 108,355
4 1,785 108,243 11 108,240
5 1,542 108,486 20 108,482
6 1,336 108,692 20 108,688
7 1,037 108,991 20 108,986
8 0,868 109,160 20 109,155
C 2,370 111,566 0,832 109,195 16,65 109,190
9 2,271 109,295 3,35 109,289
10 1,983 109,583 20 109,576
11 1,857 109,709 20 109,702
12 1,372 110,194 20 110,186
13 1,084 110,482 20 110,474
D 0,825 111,371 1,02 110,546 6,05 110,537
14 1,260 110,111 13,95 110,102
15 1,565 109,806 20 109,796
E 1,193 110,847 1,717 109,654 17,50 109,643
16 1,229 109,618 2,50 109,607
17 1,452 109,395 20 109,384
18 1,497 109,350 20 109,339
A 1,622 109,225 16,5 109,213

439. Altimetría
124

440. 125
890
895
890
885
870 875 880 895
890
885
880
875
870
885 880 875870 865
1
A
2
3
4
5
6
7
8
9 10
B

441. Altimetría
126
Denotaciones más comunes de las estacas en un perfil longitudinal
En la actualidad existen diferentes formas en denotar los puntos estacados en un perfil longitudinal; a
continuación se mostrará dos de ellos.
I Cuando las estacas base se de-
finen por el kilometraje
Veamos un ejemplo:
– El punto “A”; se inicia con el kilóme-
tro N° 160. (160 + 00)
– Los puntos que obedecen la secuen-
cia constante, están denotados por
un número que representa las dece-
nas de metros; así: 08, significa que
su ubicación en el eje de las abcisas es
el km 160 + 80 metros.
– Los puntos importantes del itinera-
rio; como quiera que no obedecen la
secuencia constante se denotarán
por dos sumandos, el primero in-
dica las decenas de metros y el se-
gundo las unidades; así: el punto B; 24 + 5,81; significa que su ubicación en el eje de las abcisas
es el km 160 + 240 metros + 5,81 metros.
Descripción Progresiva dacumulada (m) Cotaterreno(m)
A 160 + 00 0,00 660,00
160 + 02 20,00 660,00
160 + 04 40,00 559,50
160 + 06 60,00 660,00
160 + 08 80,00 654,00
6160 + 10 100,00 654,80
60 + 12 120,00 658,20
60 + 14 140,00 654,00
60 + 16 160,00 670,00
60 + 18 180,00 676,80
20 200,00 674,00
22 220,00 666,00
24 240,00 658,00
B 24 + 5,81 245,81 657,20
26 260,00 659,00
28 280,00 666,00
C 28 + 2,34 282,34 666,50
30 300,00 669,00
32 320,00 670,00

442. Altimetría
127
II
Cuando
las
estacas
base
se
definen
por
el
punto
hectométrico
Veamos
un
ejemplo:
–
El
punto
“A”;
se
inicia
con
el
hectómetro
cero
(0
+
00,00).
–
Lospuntos
intermedios
se
designan
por
la
numeración
del
hectómetro
inmediatamente
anterior
más
la
distancia
en
metros
que
la
separa
de
aquel.

443. Altimetría
128
Descripción Progresiva dacumulada (m) Cotaterreno(m)
A 0 + 00 0,00 220,00
160 + 20 20,00 222,50
160 + 40 40,00 223,00
160 + 60 60,00 220,50
160 + 80 80,00 225,00
6160 +1 + 00,00 100,00 226,00
60 + 20 120,00 228,00
60 + 40 140,00 230,00
B 60 +52,60 152,60 226,00
60 + 60 160,00 224,50
80 180,00 227,00
2 + 0,00 200,00 229,50
20 220,00 232,50
C 27,30 227,30 230,00
40 240,00 228,00
60 260,00 222,00
80 280,00 218,50
D 3 + 0,00 300,00 215,00

444. Altimetría
129
SECCIÓN TRANSVERSAL
Se le llama también perfil transversal y viene a ser el corte perpendicular al eje del perfil longitudinal en
cada estaca (por lo menos); generalmente se toman varios puntos a la derecha y a la izquierda, dependien-
do de la envergadura del proyecto.
El uso de las secciones transversales en un proyecto, está supeditado al ancho que compro-
mete al eje longitudinal; así tenemos que un sistema de alcantarillado y drenaje no
requiere de este tipo de secciones, dado que su ancho no lo amerita.
Sin embargo en proyectos de carreteras, vías de ferrocarril, diques, etc. Se hace impres-
cindible el levantamiento de secciones transversales, el ancho de éstas debe ser suficien-
te para cubrir el trabajo propuesto (5;10; 15; 20;50m;etc.acadaladodelejelongitudinal).
Observación

445. Altimetría
130
Recomendaciones
– Convencionalmente se establece que recorriendo el sentido creciente de la progresiva, las distan-
cias horizontales sobre los ejes transversales que se miden hacia la derecha serán positivas y las que
se midan hacia la izquierda serán negativas.
– Las escalas que se usan en ambos ejes, suelen ser los mismos y éstas obedecen a la precisión con que
hay que determinar el trazo horizontal transversal y cálculo del área de las secciones tranversales.
– No existe una secuencia constante entre los puntos a levantar en las secciones transversales;
más bien éstos obedecen a la topografía del terreno (accidentes, cambios de pendientes, etc.).
Método para la construcción de secciones transversales
I Método directo
Una vez estacados los puntos del itinerario del perfil longitudinal se procede ha realizar el levanta-
miento topográfico de las secciones transversales en campo.
Laaplicacióndeunanivelacióngeométrica,ensugranmayoríasehaceinnecesariaycostosa;seusaencasos
elproyectolocrea conveniente.
El uso de la taquimetría con estación total es el más recomendable dado su precisión y rapidez (ver
capítulo de taquimetría).
II Método indirecto
Una vez estacados los puntos del itinerario del perfil longitudinal se procede a graficar las secciones
transversales con ayuda de planos topográficos o fotogramétricos pre-establecidos; el procedimien-
to es similar al del perfil longitudinal.
Obviamente la precisión por este método no será la misma que por el método directo.
Ejemplo ilustrativo
Tomaremoscomoreferencialaprogresiva160+18;la tabla muestra la nivelación de la sección transver-
sal correspondiente a dicha progresiva.

446. Altimetría
131
TABLA
Sección transversal: Progresiva 160 + 18
Nombre Descripción Distancia Cota
1 Izquierdo 40,0000 652,959
2 Izquierdo 31,5975 658,560
3 Izquierdo 25,2316 663,389
4 Izquierdo 21,2602 666,453
5 Izquierdo 15,3041 670,019
6 Izquierdo 10,9228 672,253
7 Izquierdo 4,7526 674,891
8 Izquierdo 0,5854 676,640
18 0,0000 676,800
9 Derecho 6,5397 678,800
10 Derecho 9,7520 679,866
11 Derecho 11,6307 680,308
12 Derecho 18,8028 681,197
13 Derecho 19,8223 681,344
14 Derecho 20,0894 681,379
15 Derecho 21,5050 681,630
16 Derecho 30,4268 683,305
17 Derecho 32,1098 683,685
18 Derecho 38,5348 684,846
19 Derecho 40,0000 685,100