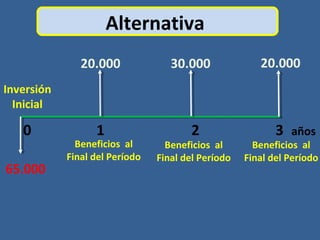
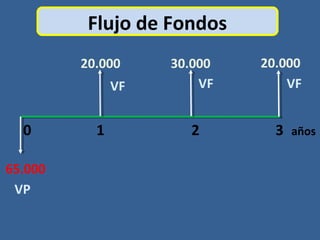
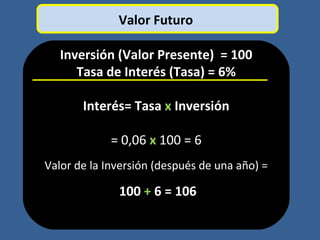
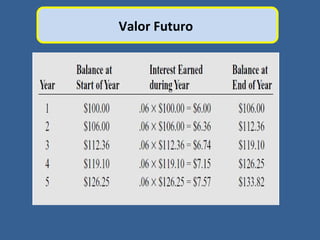
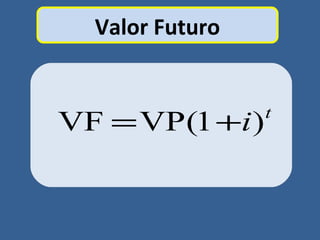
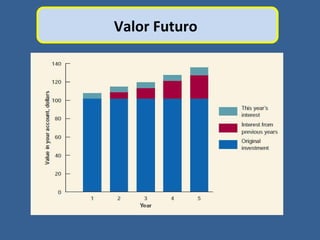
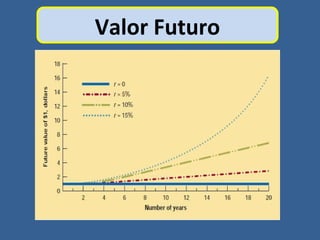
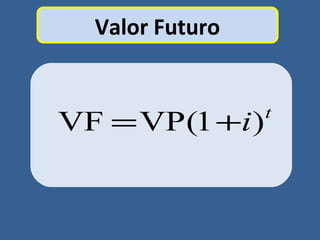
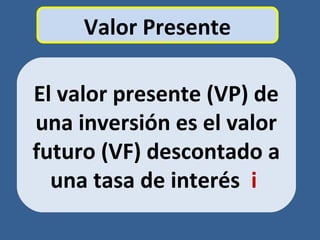
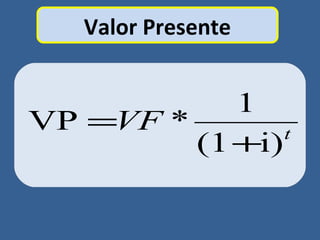
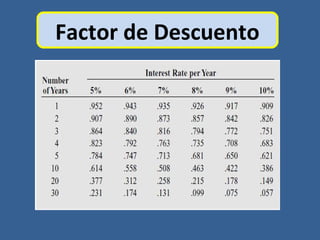
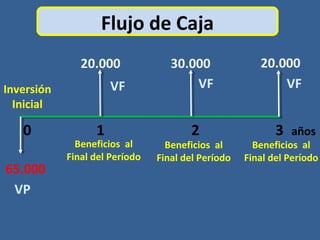
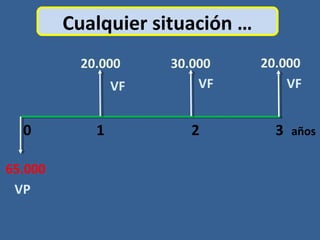
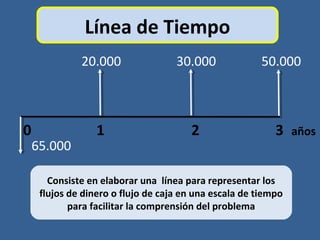
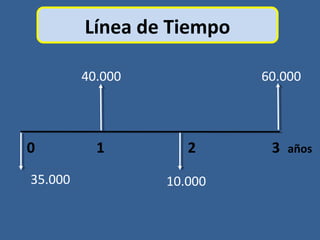
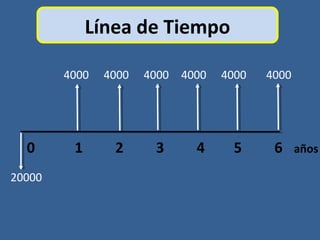
Este documento presenta conceptos básicos de matemáticas financieras como valor presente, valor futuro, tasa de interés compuesta e inversiones. Explica cómo calcular el valor futuro de una inversión inicial dada una tasa de interés compuesta aplicada durante cierto número de años, así como cómo determinar el valor presente requerido hoy para alcanzar un valor futuro específico. También muestra ejemplos numéricos y gráficos de líneas de tiempo para ilustrar flujos de efectivo en el tiempo.

1. Alternativa
0 1 2 3 años
Inversión
Inicial
20.000 30.000 20.000
65.000
Beneficios al
Final del Período
Beneficios al
Final del Período
Beneficios al
Final del Período

2. Evaluación Financiera …

3. Evaluación de Proyectos
Introducción a las Matemáticas
Financieras

4. Objetivos

5. Pregunta
¿Qué prefieres: recibir hoy
100.000 Bs. o recibir esa
misma cantidad dentro de
un año?
¡ La inflación es 0 !

6. Tasa de Interés
La tasa de interés es el valor
o precio del dinero

7. Valor Presente
Es el término que se utiliza
para designar el valor de
una cantidad de dinero HOY

8. Valor Futuro
Es el término que se utiliza
para designar el valor de una
cantidad de dinero que está
ubicada en un período
futuro “t”

9. Alternativa
0 1 2 3 años
Inversión
Inicial
20.000 30.000 20.000
65.000
Beneficios al
Final del Período
Beneficios al
Final del Período
Beneficios al
Final del Período

10. Flujo de Fondos
0 1 2 3 años
20.000 30.000 20.000
65.000
VP
VF VF VF

11. Inversión (Valor Presente) = 100
Tasa de Interés (Tasa) = 6%
Interés= Tasa x Inversión
= 0,06 x 100 = 6
Valor de la Inversión (después de una año) =
100 + 6 = 106
Valor Futuro

12. Es decir la inversión crece por el factor
(1+0,06) = 1,06
En general para cualquier Tasa de Interés
(la cual se denomina i, r, g )
El valor de la inversón final al primer año es
(1+i) veces la inversión inicial. Es decir:
VF= VP (1+i)
Valor Futuro

13. 0,06 x 106 = 6,36
Valor de la Inversión (después de dos años) =
106 + 6,36 = 112,36
Es decir la inversión ha crecido
100 (1+0,06)(1+0,06) =
100 (1,06)(1,06) =
100100 (1,06)2
= 112,36
Valor Futuro
Si mantenemos la Inversión durante otro año en el banco …

14. La inversión crecerá
100 (1+0,06)(1+0,06)(1+0,06) =
100100 (1,06)3
= 119,10
En este caso para determinar el valor final de
la inversión en cualquier año
VF= 100 (1+0,06)t
Valor Futuro
Si mantenemos durante otro año …

15. Valor Futuro

16. Valor Futuro
Si generalizamos:
El Valor Futuro (VF) de una inversión
efectuada hoy (VP), para una tasa de Interés
i en un horizonte de t años, puede
determinarse a través de la fórmula:
VF= VP (1+ i)t

17. Valor Futuro
VF VP(1 )t
i= +

18. Valor Futuro

19. Interés Compuesto
Se dice que el interés es compuesto
cuando se calculan los intereses de
una operación tomando en cuenta
el valor de los intereses
previamente generados, es decir se
calculan
intereses sobre los intereses

20. Valor Futuro

21. Valor Futuro
Veamos el comportamiento de
una inversión de US 1000 dólares
con distintas tasas de interés y
diferentes períodos de tiempo

22. Valor Presente
Hemos visto que 100 invertidos hoy al 6%
crecerán en una año a un valor futuro de 106.
Ahora si nos hacemos la pregunta de forma
inversa:
¿Cuánto debo invertir hoy para tener en un
horizonte de t años una determinada
cantidad, a una tasa de interés i ?

23. Valor Presente
¿Cuánto debo invertir hoy
para tener dentro de 1 año
Bs. 12.000 a una tasa de
interés del 15%?

24. Flujo de Fondos
0 1 año
VP=?
12.000

25. Valor Futuro
VF VP(1 )t
i= +

26. Valor Presente
VF
VP
(1 i)t
=
+

27. Valor Presente
El valor presente (VP) de
una inversión es el valor
futuro (VF) descontado a
una tasa de interés i

28. Valor Presente
1
VP *
(1 i)t
VF=
+

29. Factor de Descuento
1
(1 i)t
FD =
+

30. Factor de Descuento

31. Los cálculos con flujos de dinero en el
tiempo deben efectuarse en un instante
único para que sus valores sean
comparables.
El Dinero en el Tiempo

32. Flujo de Caja
0 1 2 3 años
Inversión
Inicial
20.000 30.000 20.000
65.000
Beneficios al
Final del Período
Beneficios al
Final del Período
Beneficios al
Final del Período
VP
VF VF VF

33. Cualquier situación …
0 1 2 3 años
20.000 30.000 20.000
65.000
VP
VF VF VF

34. Consiste en elaborar una línea para representar los
flujos de dinero o flujo de caja en una escala de tiempo
para facilitar la comprensión del problema
Línea de Tiempo
65.000
50.00030.00020.000
0 1 2 3 años

35. Línea de Tiempo
0 1 2 3 años
35.000
60.000
10.000
40.000

36. Línea de Tiempo
0 1 2 3 4 5 6 años
40004000 40004000 40004000
20000